Что является графиком y 2? – Обзоры Вики
Уравнение y=2 находится в форме точки пересечения наклона, где наклон равен 0, а точка пересечения y равна 2. Уравнение можно изобразить как уравнение y=0x+2 . График горизонтальная линия где все значения для y равны 2 .
Отсюда: является ли Y 2x 2 показательной функцией? Это график y = x2, и это действительно функция с показателем степени. Но это не экспоненциальная функция. В экспоненциальной функции независимая переменная или значение x является показателем степени, а основание является константой.
Как построить график EX?
Какова ось симметрии графика y 2 × 2? Ось симметрии линия х=1 , а вершина — точка (1, -1).
Какой тип функции y 2x 2? Это линейная функция, это линия. Это потому, что это просто y (без экспоненты) и просто x (опять же без экспоненты) и константа (+2). Для построения линии нужно будет нанести только две точки.
Как построить график квадрата Y параболы?
Также является ли Y 2 функцией? Объяснение: Функция — это отношение между двумя переменными в широком смысле. Ответ: соотношение x = y2 не является функцией.
Как изобразить параболу в вершинной форме?
com/embed/N44R1qoHPu4″ frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″> Является ли Y 2x функцией?
у = 2x2 — это парабола который открывается вверх. Не существует значения x, которое дает два возможных значения y, поэтому оно проходит тест вертикальной линии и является функцией.
Почему x2 не является функцией?
X=2 не является функцией, потому что это представляет собой линию, параллельную оси y и проходящую через точку (2,0). на этой линии бесконечное количество точек, поэтому при X = 2 y имеет бесконечное количество значений. Чтобы быть функцией, для любого X должно быть только одно значение y.
Какой наклон для 2? y=2 — горизонтальная линия, имеющая наклон нуля. x — единственная переменная, которая изменяется, так как y всегда равно 2. Поскольку у нас нет изменения y , у нас нет «подъема», поэтому наклон равен нулю.
Что такое y-пересечение Y 2? Перехват y для графика y = 2 просто точка (0,2) .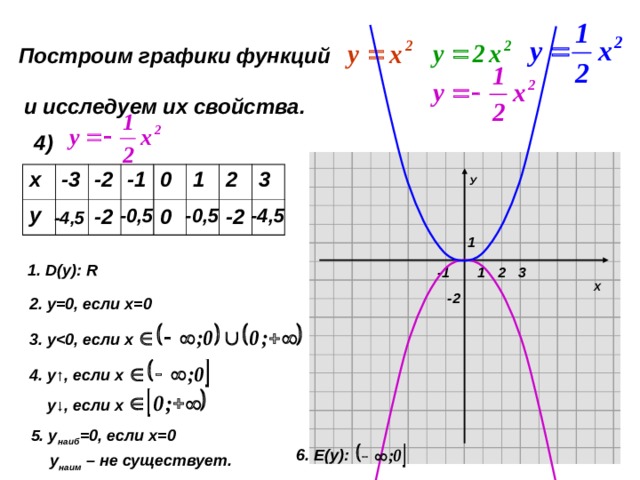
Как построить график бывшего без калькулятора?
Как вы рисуете уравнения?
Чтобы построить уравнение, используя наклон и точку пересечения по оси Y, 1) Запишите уравнение в форма y = mx + b чтобы найти наклон m и точку пересечения оси y (0, b). 2) Затем постройте точку пересечения по оси y. 3) От точки пересечения оси Y двигайтесь вверх или вниз, влево или вправо, в зависимости от того, положительный или отрицательный наклон.
Какова ось симметрии параболы y 2×2 1? Прямая X = – b/2a, проходит через вершину параболы и является осью симметрии. Х = (-2)/2(2), Х = – 1/2 является осью симметрии.
Как найти ось симметрии параболы?
Ось симметрии всегда проходит через вершину параболы .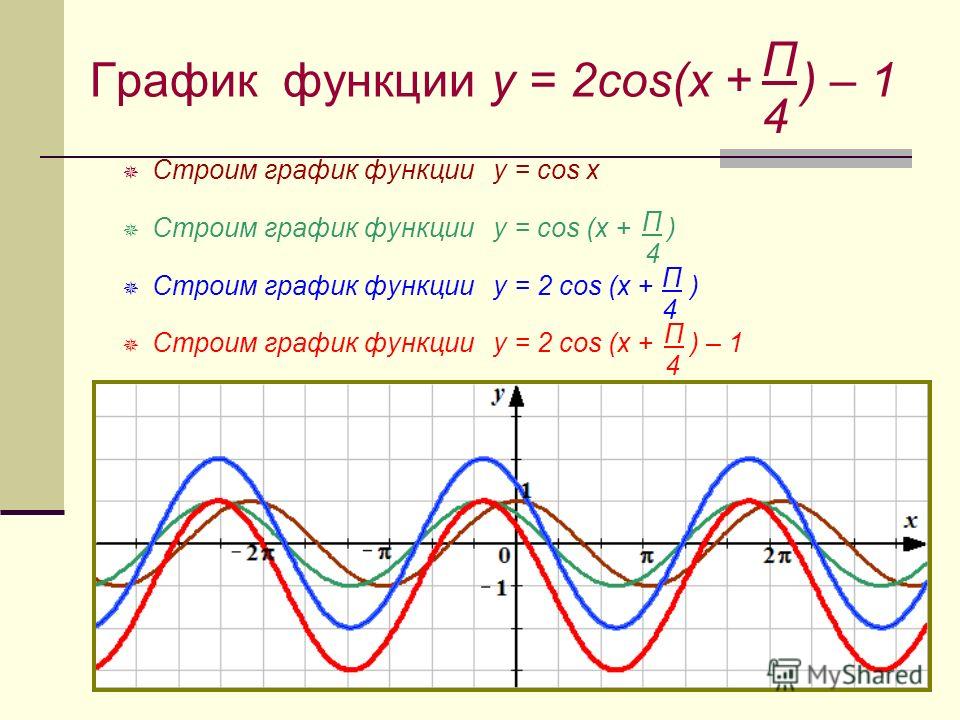
Координата x вершины есть уравнение оси симметрии параболы. Для квадратичной функции в стандартной форме y=ax2+bx+c осью симметрии является вертикальная линия x=−b2a .
Какова область определения y 2x 2? Домен выражения все действительные числа, за исключением случаев, когда выражение не определено. В этом случае нет действительного числа, которое делает выражение неопределенным. Диапазон — это набор всех допустимых значений y.
3-8Построение графика с наклоном и пересечением по оси y: примеры
Практические рекомендации
Purplemath
Теперь мы знаем, что, учитывая линейное уравнение в форме y = m x (2 b if m и b достаточно «красивы»), мы можем быстро и легко построить график, начав с точки пересечения y с b на оси y , а затем считая «вверх и вперед».
» к следующей точке, используя уклон. Итак, для этих следующих графиков давайте не будем делать никаких других «вычислений»; давайте просто работать прямо из уравнения.
Содержание продолжается ниже. Это означает, что линия пересечет ось y в точке y = −2. Я начну с построения этой первой точки:
Уравнение также говорит мне, что уклон равен
м = 3 / 5 . Это говорит мне о том, что, чтобы перейти от перехвата к следующей легкой точке, я должен подняться «на три и более пяти». Итак, я делаю подсчет и наношу следующую точку:
Продолжая двигаться в том же направлении (т. е. продолжая работать в обратном направлении), я поднимаюсь еще на три вверх и еще на пять назад, чтобы получить третью точку:
С тремя точками я могу провести свою линию:
И этот график «ответ», который они хотят.
Что делать, если уравнение не представлено в форме пересечения наклона? По моему опыту, обычно проще всего решить сначала « y =», потому что тогда все остальное будет намного проще.
Сначала я решу это уравнение для « y =»:
4 x + 3 y + 18 = 0
3 у = -4 х — 18
y = −(4/3) x − 6
Итак, я знаю, что линия пересечет ось
Уклон,
м = −4/3, значит, я буду двигаться «вниз на четыре и более трех». Но… хм…
Точка, которую я уже получил, находится очень далеко внизу моего графического окна. Было бы проще нанести точку до точки пересечения , а не точку после (которая находится ниже). Итак, вместо того, чтобы идти «вниз на четыре и более трех», я вернусь и пройду « назад, , три и , вверх, , четыре»:
Я сделаю еще одну точку таким же образом, а затем нарисую свою линию:
Иногда они дадут вам уравнение, где точка пересечения не так уж полезна.
Но вы все еще можете сделать график.
Сначала я решу « y =»:
3 x − 4 y + 5 = 0
3 х + 5 = 4 у
(3/4) x + 5/4 = y
Таким образом, линия пересекает ось y в точке
y = 5/4. В форме смешанных чисел (сюрприз! Это все еще полезно!), это «один плюс одна четвертая», поэтому я нарисую свою точку на четверть пути вверх от 9.0911 y = 1 до y = 2:
Но делать другие точки для этого графика может быть немного запутанно, особенно если я начну отсчет с этого отрезка. Я имею в виду, да, я могу подняться «на три и более четырех», но эта «одна четвертая» может быть надоедливой. Вместо этого я найду одну хорошую, аккуратную точку и буду работать с ней. Во-первых, я перестрою уравнение следующим образом:
y = (1/4)(3 x + 5)
кратно 4.