Правило пропорций: Пропорции. Основное свойство пропорции — урок. Математика, 6 класс.

Содержание

Пропорции математика. Пропорция – это равенство двух отношений. Соотношение.

Пропорция – это равенство, утверждающее, что два отношения равны. Пропорциональный — значит находящийся в определенном отношении к какой-либо величине. Четыре величины $4, 2, 8 $ и $4$ находятся в отношении, если $\frac{4}{2}=\frac{8}{4}$. Произведение крайних членов пропорции равно произведению средних.

Пропорция всегда включает равные коэффициенты. Когда соотношение остается постоянным, это соотношение называется пропорциональным.

Если $\frac{A}{B} = \frac{C}{D}$, то

Пропорция состоит из двух равных отношений. Однако если $\frac{A}{B}$ не равно $\frac{C}{D}$, то $A, B, C, D $ не называются пропорцией.

Три величины считаются пропорциональными, если отношение первого ко второму равно соотношению второго и третьего.

$A, B , C$ находятся в постоянной пропорции, если $\frac{A}{B} =\frac{C}{D}$

Если $A, B ,C $ находятся в постоянном отношении, то $B$ называется средней в пропорции.

В косвенной пропорции как одно значение увеличивается, так и другое значение уменьшается.

Задача 1. За $5$ дней и $12$ человек построили забор. Сколько дней это займет у $6$ людей?

Решение.

$12$ человек → $5$ дней
$6$ человек → $x$ дней
$\frac{12}{6} = \frac{x}{5}$
умножаем крест на крест члены пропорции и сокращаем на $6$:

$12*5=6x$

$60=6x$

$x=10$

Ответ: $6$ людей будут работать $10$ дней, чтобы закончить работу.

Задача 2. Найдите значение $x$, если $\frac{2}{5}=\frac{x}{15}$

Решение:

$2*15=5x$
$30 =5x$
Делим на 5 обе части равенства: $\frac{30}{5}=x$, откуда находим

Задача 3.

Что должно быть добавлено к каждому из четырех чисел 10, 18, 22, 38, чтобы сделать их пропорцией?

Решение:

$(10+x)(18+x)=(22+x)(38+x)$
$380+48x+2x=396+40x+2x$
$8x=16$
$x=2$

Задача 4. Найти четвертый член пропорции $6,10$ и $12$

Решение:

$\frac{6}{10}=\frac{12}{x}$

6×х = 120

x = 120/6

x = 20

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Пропорция

Если у двух отношений одинаковое частное, то их можно соединить знаком равенства, тогда это равенство будет уже

пропорцией.

Определение, Равенство двух отношений называется пропорцией.

Пропорции можно записывать в виде частного двух натуральных чисел, обыкновенными дробями, численно и буквенно. Например:
2 : 3 = 8 : 12;

Буквенная запись пропорции a : b = c : d — это общий
вид пропорции, где:

a и d — это крайние члены пропорции;

b и c — это средние члены пропорции.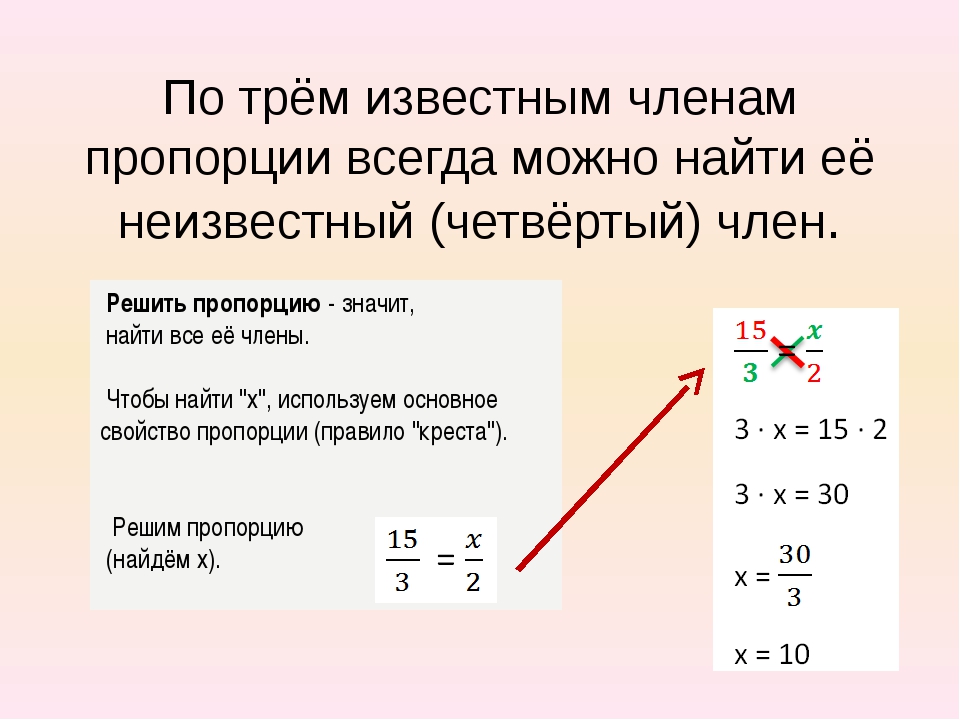

Основное свойство пропорции: a * d = b * c

Правило . Произведение средних членов истинной пропорции равно произведению ее крайних членов.

Правило. Средние и крайние члены пропорции можно менять местами, от этого пропорция не изменится.

Например, для истинной пропорции a : b = c : d верно: a * d = b * c

Истинными будут и пропорции

a : b = b : d, d : b = c : a, d : c = b : a.

В пропорции один из ее членов можно заменить буквой (обозначить буквой неизвестный член пропорции).

Например: 2 : 3 = x : 12 или x : 3 = 8 : 12.

В первом примере неизвестен средний член пропорции, а во втором — ее крайний член.

Пропорция с одним неизвестным часто встречается в решении задач (значение неизвестного — это ответ на вопрос задачи). Вычислить любой член пропорции можно по следующем правилу.

Правило . Неизвестный крайний член пропорции равен частному произведения средних членов пропорции и известного крайнего члена.

Неизвестный средний член пропорции равен частному произведения крайних членов пропорции и известного среднего члена.

Определение неизвестного члена пропорции :

x : b = c : d, x = (b * c) : d
a : b = c : x, x = (b * c) : a

a : x = c : d, x = (a * d) : c
a : b = x : d, x = (a * d) : b

Пропорции

Пропорция – это равенство, где с : d = n : m. При этом с, d, n, m являются действительными числами, которые отличные от 0. Числа d и n называются средними членами пропорции, а числа с и m называются крайними членами пропорции.

Для пропорций справедливы несколько следующих утверждений:

Произведение средних членов пропорции будет равняться произведение крайних членов той же пропорции.
Крайние члены пропорции всегда можно поменять местами, например, если с : d = n : m, то и m : d = n : c.
Средние члены пропорции всегда можно поменять местами, например, если c : d = n : m, то и c : n = d : m.

Пропорции довольно часто встречаются в различных математических задачах. При этом, как правило, один или несколько членов пропорции неизвестны. Давайте посмотрим, как же можно найти тот или иной член пропорции, зная значения всех остальных. Для начала, следует усвоить два простых правила:

Для того, чтобы найти крайний член пропорции, необходимо произведение средних членов поделить на известный крайний член.
Для того, чтобы найти средний член пропорции, необходимо произведение крайних членов пропорции поделить на известный средний член.

Пропорции

Два равных отношения образуют пропорцию

Основное свойство пропорции

ad = bc

Нахождение членов пропорции

bc
d

;

ad
c

;

ad
b

;

bc
a

Пропорции, равносильные между собой

a
b

c
d

;

a
c

b
d

;

d
b

c
a

;

d
c

b
a

Производная пропорция — следствие данной пропорции

a
b

c
d

в виде

ma + nb
pa + qb

mc + nd
pc + qd

где m, n, p, q — произвольные числа, причем p и q не равны нулю одновременно.

Отношения и пропорции в математике

В математике отношением называется то частное, которое получается при делении одного числа на другое. Ранее сам этот термин использовался только в тех случаях, когда было необходимо выражение какой-либо одной величины в долях другой, причем такой, которая однородна первой. К примеру, отношения использовались при выражении площади в долях другой площади, длины в долях другой длины и т.п. Решение этой задачи производилось с помощью деления.

Таким образом, сам смысл термина «отношение» был несколько иной, чем термина «деление»: дело в том, что второй означал разделение определенной именованной величины на любое совершенно отвлеченное абстрактное число. В современной математике понятия «деление» и «отношение» по своему смыслу абсолютно идентичны и являются синонимами. Например, и тот, и другой термин с одинаковым успехом применяют для отношения величин, являющихся неоднородными: массы и объема, расстояния и времени и т.

п. При этом многие отношения величин однородных принято выражать в процентах.

Пример

В супермаркете насчитывается четыреста наименований различных товаров. Из них двести произведено на территории Российской Федерации. Определить, каково отношение отечественных товаров к общему числу товаров, продаваемых в супермаркете?

400 – общее число товара

200 – РФ

Ответ: двести разделить на четыреста равняется ноль целых пять десятых, то есть пятьдесят процентов.

200 : 400 = 0,5 или 50%

В математике делимым принято называть предыдущий член отношения, а делителем – последующий член отношения. В приведенном выше примере предыдущим членом являлось число двести, а последующим – число четыреста.

Два равных отношения образуют пропорцию

В современной математике принято считать, что

пропорцией является два равным между собой отношения.

К примеру, если общее количество наименований товаров, продаваемых в одном супермаркете, – четыреста, а в России из них произведено двести, а те же значения для другого супермаркета составляют шестьсот и триста, то соотношение количества российских товаров к общему их числу, реализовываемых в обеих торговых предприятиях, одинаково:

1.Двести разделить на четыреста равняется ноль целых пять десятых, то есть пятьдесят процентов

200 : 400 = 0,5 или 50%

2.Триста разделить на шестьсот равняется ноль целых пять десятых, то есть пятьдесят процентов

300 : 600 = 0,5 или 50%

В данном случае имеется пропорция, которую можно записать следующим образом:

Если формулировать это выражение так, как это принято делать в математике, то говорится, что двести относится к четыремстам так же, как триста относится к шестистам. При этом двести и шестьсот называются крайними членами пропорции, а четыреста и триста – средними членами пропорции.

Произведение средних членов пропорции

Согласно одному из законов математики, произведение средних членов любой пропорции равняется произведению ее крайних членов. Если возвратиться к приведенным выше примерам, то проиллюстрировать это можно следующим образом:

Двести умноженное на шестьсот равняется сто двадцать тысяч;

200 × 600 = 120 000

Триста умноженное на четыреста равняется сто двадцать тысяч.

300 × 400 = 120 000

Из этого следует, что любой из крайних членов пропорции равен произведению ее средних членов, деленному на другой крайний член. По тому же самому принципу каждый из средних членов пропорции равен крайних ее членов, деленному на другой средний член.

Если вернуться к приведенному выше примеру пропорции, то:

Двести равняется четыреста умноженное на триста и деленное на шестьсот.

Эти свойства широко используются в практических математических вычислениях тогда, когда требуется найти значение неизвестного члена пропорции при известных значениях трех членов остальных.

Пропорции: крайние и средние члены, главное свойство

Равенство двух отношений называется пропорцией.

Пример.

10 : 5 = 6 : 3

или

Пропорцию

a : b = c : d

или

можно прочитать так: отношение a к b равно отношению c к d, или a относится к b, как c относится к d.

Члены пропорции: крайние и средние

Члены отношений, составляющих пропорцию, называются членами пропорции. Числа a и d называют крайними членами пропорции, а числа b и c — средними членами пропорции:

Эти названия условны, так как достаточно написать пропорцию в обратном порядке (переставить отношения местами):

c : d = a : b

или

и крайние члены станут средними, а средние — крайними.

Главное свойство пропорции

Произведение крайних членов пропорции равно произведению средних.

Пример. Рассмотрим пропорцию

Если воспользоваться вторым свойством равенства и умножить обе её части на произведение bd (для приведения обеих частей равенства от дробного вида к целому), то получим:

Сокращаем дроби и получаем:

ad = cb.

Из главного свойства пропорции следует:

Крайний член равен произведению средних, разделённому на другой крайний. То есть для пропорции :
Средний член равен произведению крайних, разделённому на другой средний. То есть для пропорции :

Нахождение неизвестного члена пропорции

Свойства пропорции позволяют найти любой из членов пропорции, если он неизвестен. Рассмотрим пропорцию:

x : 8 = 6 : 3.

Тут неизвестен крайний член. Так как крайний член равен произведению средних, разделённому на другой крайний, то

x = (8 · 6) : 3 = 16.

Золотое сечение как объяснение пропорций красоты

Над чем работают лучшие умы современной стоматологической науки? Над идеальной улыбкой, воплотившей в себе красоту и здоровье.

Что такое «красота»? Почему лицо и облик одного человека нам нравится, а другого — нет?

На эти вопросы пытались ответить учёные ещё тогда, когда не было ни только стоматологии как направления медицины, но и сама медицина находилась в стадии зарождения.

Оказывается, наше лицо и тело имеет определённые пропорции, кажущиеся на первый взгляд почти мистическими.

Хотя в наш просвещённый век многому можно найти научное и даже математическое объяснение.

Принято считать, что впервые закономерности соотношение размеров тела человека и отдельных его частей обобщил и сформулировал в 1855 г. немецкий исследователь Цейзинг в своём научном труде «Эстетические исследования». За основу своей теории он взял учение о «золотом сечении».

Ещё в VI веке до н.э. древнегреческий философ и математик Пифагор ввёл в научный обиход понятие «золотое деление». «Золотое деление» — это пропорциональное деление отрезка на неравные части. При этом меньший отрезок так относится к большему, как больший отрезок относится ко всему отрезку. a : b = b : c или с : b = b : а.

Так что же особенного в этом соотношении?

Оказывается, что всегда меньший отрезок относится к большему, как 0,382: к 0,618:

То есть, если АВ принять за единицу, АЕ/ЕВ=0,62/0,32 (в практических целях используют приближённые значения).

Один из примеров «золотого деления», с которым наверняка все знакомы, это — пентаграмма и, как представители её, так любимые людьми старшего поколения, «знак качества» и «звезда».

Все диагонали пятиугольника (пятиугольная звезда) делят друг друга на отрезки, связанные между собой «золотой пропорцией».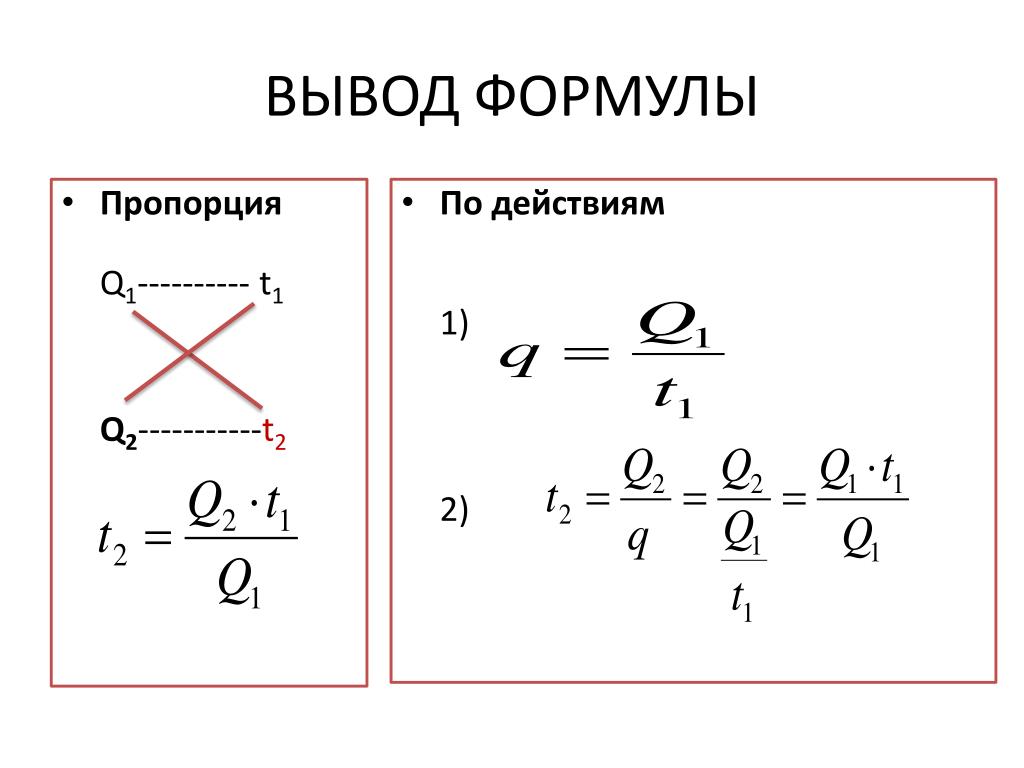

В настоящее время эта математическая закономерность носит название «золотое сечение», которое ввел в обиход ещё Леонардо да Винчи, который проводил сечения стереометрического тела, образованного правильными пятиугольниками. И каждый раз он получал соотношение сторон в «золотом делении». Он дал этому делению название «золотое сечение», принятое до сих пор.

Но не Пифагор впервые обнаружил закономерность «золотого сечения». Ещё древние египтяне и вавилоняне использовали эти знания в строительстве пирамид и изготовлении предметов обихода. Древние греки при проектировании своих зданий использовали пропорции «золотого сечения». В эпоху возрождения интерес к «золотому сечению» усилился. Художники нашли применение ему в искусстве. Учение о «золотом сечении» связано с именем гениального итальянского математика и монаха Луки Пачоли. В 1509 г. Была издана его книга «Божественная пропорция» с иллюстрациями Леонардо да Винчи (предположительно). Он причислял золотую пропорцию к «божественной сути» через триединство: бог сын, бог отец и святой дух, находящихся между собой в «золотой пропорции».

История «золотого сечения» связана ещё с одним известным итальянским математиком Фибоначчи. До наших времён дошёл ряд чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д., известный, как ряд Фибоначчи.

Особенность последовательности данных чисел заключается в том, что каждый её член, начиная с третьего, равен сумме двух предыдущих (2+3=5, 3+5=8), а отношение смежных чисел ряда приближается к отношению «золотого сечения» (21:34=0,617, а 34:55=0,618). В последствии все исследователи «золотого сечения» в растительном и животном мире, искусстве и анатомии приходили к этому ряду, как арифметическому выражению закона золотого деления. Интересно, что свой закон Фибонначи вывел, подсчитывая количество рождённых кроликов от пары кроликов за год.

Так в чём же ореол таинственности «золотого сечения»?

Всё, что растёт и приобретает какую-либо форму в живом мире нашей планеты — растёт вверх или закручивается по спирали. Спираль (например, морская раковина) — пример соотношения в пропорциях «золотого сечения». Спирали прослеживаются в расположении семян в шишках хвойных деревьев, в семенах подсолнечника и др.

Паук плетёт паутину по спирали, ДНК человека закручено по спирали.

А рост вверх? Растение живёт по тем же законам «золотого сечения». Самый большой участок стебля — до первого листочка. Затем следующие сегменты уменьшаются в пропорции «золотого сечения»: с : в = в : а

Удивительно то, что и человек в соотношении отдельных частей тела и расстояний между ними, подчиняется законам «золотого сечения».

Немецкий учёный Альберт Дюрер доказал, что рост человека делится в золотых пропорциях линией, проходящей через пупок и линией, проходящей через кончики средних пальцев опущенных рук.

Его труды продолжил Цейзинг. Он выяснил, что пропорции мужского тела колеблются в пределах 13 : 8 = 1, 625.

А пропорции женского тела в среднем находятся в соотношении 8 : 5 = 1,6.

Пропорции «золотого сечения» проявляются в отношении длины плеча, предплечья, кисти и пальцев и т. д.

Поразительно, но в лице человека можно проследить множество пропорций, подчиненных «золотому сечению». Причем, чем больше в лице человека соотношений в этой пропорции, тем красивее нам он кажется. Есть лица, при характеристике которых употребляют выражение «правильные черты лица». У этих людей основные пропорции наиболее близки к соотношению 1, 618: или 62 : 38.

Какие же пропорции в лице человека стремятся к «золотому сечению»?

Прежде всего, у людей с красивыми лицами наблюдается:

Идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это соотношение называется «динамической симметрией» или «динамическим равновесием».
Соотношение высоты верхней и нижней губы будет 1,618.
Высота надгубной складки (расстояние между верхней губой и нижней границей носа) и высота губ будут составлять соотношение 62 : 38.
Ширина одной ноздри суммарно с шириной переносицы относится к ширине другой ноздри в пропорции «золотого сечения».
Ширина ротовой щели также относится к ширине между наружными краями глаз, а расстояние между наружными уголками глаз — к ширине лба на уровне линии бровей, как все пропорции «золотого сечения».
Расстояние между линии смыкания губ до крыльев носа относится к расстоянию от линии смыкания губ до нижней точки подбородка, как 38 : 62: И к расстоянию от крыльев носа до зрачка — как 38 : 62 = 0.
Расстояние между линией верхней части лба до линии зрачков и расстояние между линией зрачков и линией смыкания губ имеет пропорцию «золотого сечения».

Можно продолжить этот список соотношения размеров гармоничного лица. Получается, правильную красоту можно математически просчитать и даже прибегнуть к хирургической корректировке с целью совершенствования внешности.

В настоящее время стоматология, наряду с пластической хирургией, занимается не только лечением заболеваний полости рта, но и эстетической медициной.

Удивительно, но и в стоматологии можно проследить пропорции «золотого сечения».

Красивая улыбка — это не только белоснежные здоровые ровные зубы, но и их правильное соотношение и расположение. И здесь мы опять сталкиваемся с закономерность «золотого сечения».

Вот некоторые примеры соотношений размеров и расстояний между зубами:

Ширина верхнего центрального резца относится к ширине нижнего центрального резца, как 62 : 38, т.е. 1, 618:, в соотношении «золотого сечения».
В этой же пропорции находится ширина двух верхних резцов к ширине двух нижних.
Расстояние между премолярами верхней челюсти относится к ширине четырёх верхних резцов, как 62 : 38.
Расстояние между дистальными поверхностями нижних клыков и щечными фиссурами моляров — пропорция 38 : 62.

И этот список можно продолжить.

Как же на практике можно использовать знание о «золотом сечении» и его влиянии на параметры в стоматологии?

Разумеется, искать применение золотых пропорций в эстетической стоматологии.

Расположение, размер и взаимное соотношение зубов в полости рта — всё это подчинено общему закону — «золотому сечению».

Вольно или невольно, осознанно или неосознанно врач использует эти пропорции при восстановлении коронковой части зуба, при протезировании или ортодонтических мероприятиях. Лучше, конечно, чтобы врач применял математическую составляющую в формировании вашей красоты и здоровья.

А мы теперь знаем, что человек — только часть живого мира на нашей планете, подчиняющийся общим законам мироздания. И доказательство тому — учение о «золотом сечении», дошедшее до нас уже даже не из предыдущего тысячелетия.

Время работы

Пн-Пт	10:00 — 22:00
Сб-Вс	10:00 — 20:00

Смирнова Ольга Игоревна Врач-стоматолог ортопед

Геометрическая Пропорция

370. Но если величины находятся в геометрической пропорции, произведение её крайних членов равно произведению их средних членов.
Если a:b = c:d, ad = bc
Согласно допущению, (Статьи. 341, 359.) $\frac{a}{b } =\frac{c}{d } $
Умножив на bd, (Аксиома 3.) $\frac{abd}{b } =\frac{cbd}{d } $
Упростив дроби, ad = bc.
Так 12:8 = 15:10, поэтому 12*10 = 8*15.

Соотв: Любой множитель может быть перенесён от одной средней величины к другой, без влияния на пропорцию. Если a:mb = x:y, то a:b = mx:y. При этом произведение средних величин в обоих случаях одинаково. И если na:b = x:y, то a:b = x:ny.

371. С другой стороны, если произведение двух величин равно произведению двух других, то четыре величины сформируют пропорцию, где они сгруппированы таким образом, что одна сторона уравнения будет содержать средние члены, а другая — крайние.
Если my = nh, то m:n = h:y, то есть$\frac{m}{n } =\frac{h}{y } $
Таким образом разделив my = nh на ny, мы получим$\frac{my}{ny} =\frac{nh}{ny } $
Упростив дроби, $\frac{m}{n } =\frac{h}{y } $.

Соотв. То же самое должно быть верно по отношению любых множителей, которые образуют две стороны равенства.
Если (a + b).c = (d — m).y, то a + b:d — m = y:c.

372. Если три величины пропорциональны, то произведение их крайних членов равно квадрату средних. Таким образом одновременно пропорциональны также второй член первой пары и предыдущий член последней. (Статья. 366.) Следовательно они должны быть умножены на себя, то есть возведены в квадрат.
Если a:b = b:c, тогда умножение крайних и средних членов, ac = b².
Следовательно, среднее пропорциональное двух величин может быть найдено путём извлечения квадратного корня из их произведения.
Если a:x = x:c, то x² = ac, и x√ac.

373. Из Статьи. 370 следует, что соотношение любого из крайних членов равно произведению средних, разделённых на другой крайний член. И любой из средних членов равен произведению крайних членов, разделённому на другой средний член.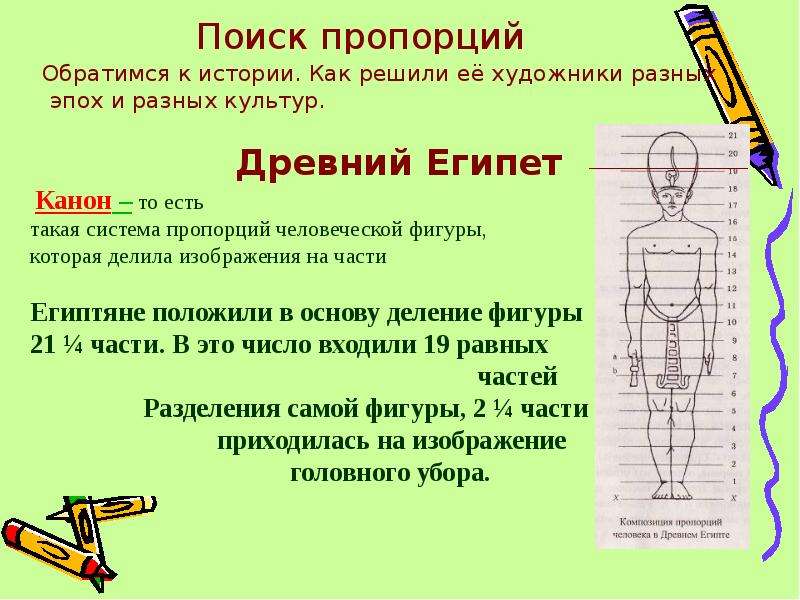
1. Если a:b = c:d, то ad = bc
2. Разделим на d, $a=\frac{bc}{d} $
3. Сначала разделим на c, $b=\frac{ad}{c} $
4. Разделим это на b, $c=\frac{ad}{b} $
5. Разделим на a, $d=\frac{bc}{a} $ ; Это значит, что
четвёртый член равен произведению второго и третьего, разделённому на первый.

На этом принципе основаны простые пропорции арифметики, которые часто называют Тройным Правилом. Три числа даны, чтобы найти четвёртое, которое получают путём умножения второго на третье и деления на первое.

374. Утверждение относительно произведений средних и крайних членов предоставляет очень простой и удобный критерий определения того, пропорциональны ли любые четыре величины. Нам только нужно перемножить средние и крайние члены. Если произведения равны, то величины пропорциональны. Если произведения не равны, то величины не пропорциональны.

375. В математических исследованиях, когда даны отношения нескольких величин, то они часто определены в виде пропорции. Но, как правило, необходимо, чтобы эта первая пропорция претерпела ряд трансформаций прежде, чем отчётливо выявится неизвестная величина или утверждение, которое мы хотели доказать. Она может пройти изменения, которые не окажут влияние на равенство отношений или которые обнаружат произведение средних членов равное произведению крайних.

В первую очередь очевидно, что любая перемена в расстановке, которая не окажет влияния на эти равенство этих двух произведений, не уничтожит пропорции. Поэтому, если a:b = c:d, то порядок этих величин может варьироваться, что в любом случае приведёт к ad = bc. Отсюда,

376. Если четыре величины пропорциональны, то порядок средних членов, или крайних членов, или членов обоих пар, может быть инвертирован без разрушения пропорции.
Если a:b = c:d,
И 12:8 = 6:4
тогда
1. Инвертируя средние члены,
a:c = b:d
12:6 = 8:4
то есть
Первый относится к третьему
Как второй к четвёртому.
Другими словами, отношение предыдущих членов равно отношению последующих.

Эта инверсия средних членов часто упоминается в геометрии под названием Альтернация.

2. Инвертируя крайние члены,
d:b = c:a
4:8 = 6:12
то есть,
Четвёртый относится ко второму,
Как третий к первому.

3. Инвертируя члены каждой пары,
b:a = d:c
8:12 = 4:6
то есть,
Второй относится к первому,
Как четвёртый к третьему.
Технически это называется Инверсией.
Каждое из этого также может варьироваться, меняя порядок двух пар. (Статья. 365.)

Соотв. Порядок всей пропорции может быть инвертирован.
Если a:b = c:d, то d:c = b:a.
В каждом из данных случаев будет немедленно видно, что вычисляя произведения средних и крайних членов, у нас получается ad = bc, и 12.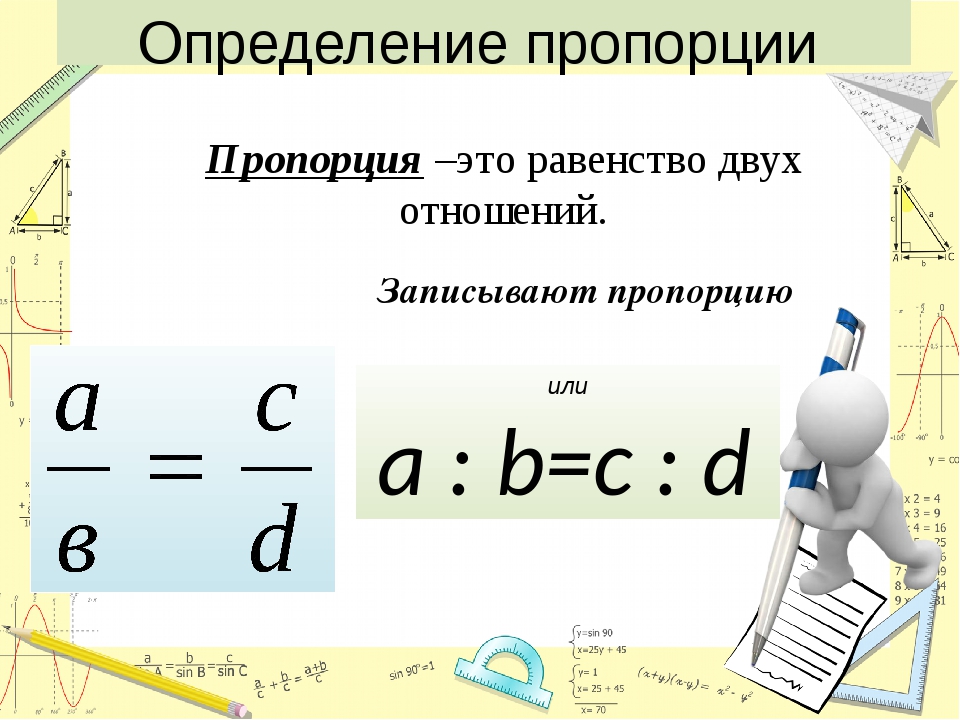 4 = 8.6.
Если члены только одной из пар инвертированы, то пропорция становится обратной. (Статья 367.)
Если a:b = c:d, то a относится к b, обратно тому, как d относится к c.

377. Разница в расположении не единственная алтернация, которую производят по отношению к членам пропорции. Часто бывает нужным умножить, разделить, возвести в степень и так далее. Во всех случаях искусство ведения исследования заключается в произведении некоторых изменений, при этом сохраняется постоянное равенство между отношением двух первых и двух последних членов. При решении уравнения, мы должны сохранять равенство сторон, так варьируя пропорцию, чтобы сохранить и равенство соотношений. И это достигается либо путём сохранения соотношений теми же, что и при альтернации членов, либо увеличивая или уменьшая одно из соотношений на столько же, как и другое. Большинство последующих доказательств направлены на чёткое выявление этого принципа и ознакомление с ним.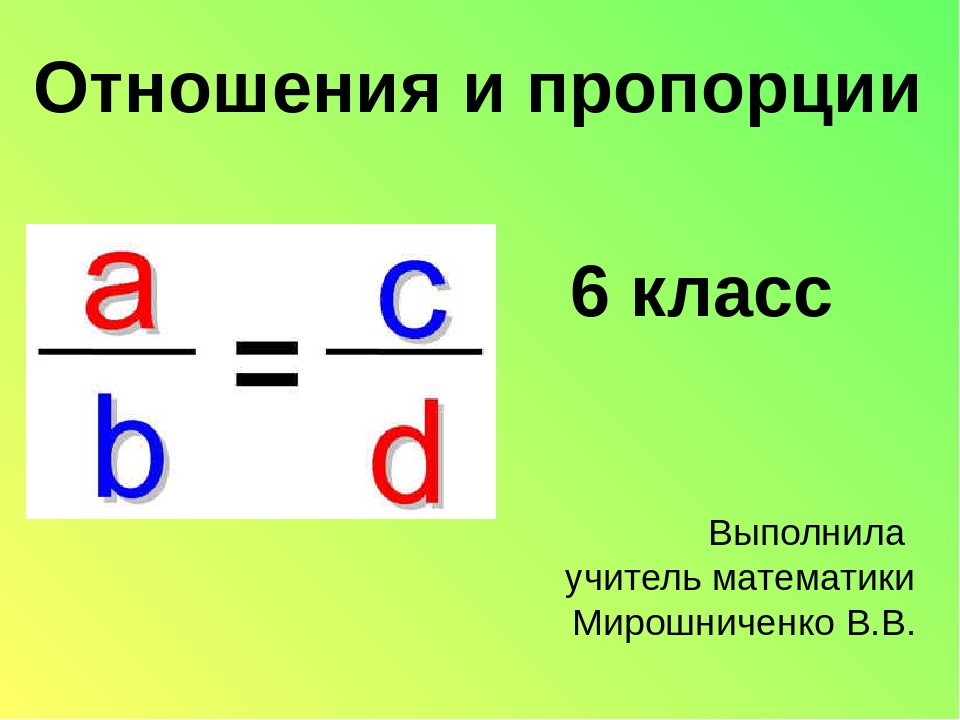 Некоторые из утверждений могут быть доказаны более простым способом, возможно, путём умножения крайних и средних членов. Но это не даст ясного понимания природы некоторых изменений в пропорциях.

Было показано, что если оба члена пары умножены или разделены на одинаковую величину, то их соотношение остаётся одинаковым (Статья. 355.) Так умножая предыдущий член (антецедента) проявится в умноженном соотношении, а деление последующего члена (консеквента) — в делении соотношения. (Статья. 352.) и следующие показывают, что умножение консеквента проявится в делении соотношения, а его деление — в произведении соотношения. (Статья. 353.) Так как соотношения в пропорции равны, то если их перемножить или разделить на одинаковую величину, то они всё ещё будут равны (Аксиома. 3.) Одно будет увеличено или уменьшено, так же как и второе. Отсюда,

378. Если четыре величины пропорциональны, два аналогичных или гомологичных члена могут быть умножены или разделены на одну и ту же величину, без нарушения пропорции.

Если аналогичные члены будут умножены или разделены, то их соотношения не поменяются. (Статья, 355.) Если гомологичные члены будут умножены или разделены, оба соотношения одинаково увеличатся или уменьшатся. (Статьи. 352, 353.)
Если a:b = c:d, то,
1. Умножая первые два члена, ma:mb = c:d
2. Умножая последние два члена, a:b = mc:md
3. Умножая два первых члена (антецедента), ma:b = mc:d
4. Умножая два последних члена (консеквента), a:mb = c:md
5. Разделив два первых члена, $\frac{a}{m}:\frac{b}{m}=c:d$
6. Разделив два последних члена, $a:b=\frac{c}{m}:\frac{d}{m }$
7. Разделив два антецедента, $\frac{a}{m}:b=\frac{c}{m}:d$ a/m:b = c/m:d
8. Разделив два консеквента, $a:\frac{b}{m}=c:\frac{d}{m}$ a:b/m = c:d/m.

Следствие. 1. Все члены могут быть умножены или разделены на одну и ту же величину.
ma:mb = mc:md, $\frac{a}{m}:\frac{b}{m}=\frac{c}{m}:\frac{d}{m} $.

Следствие. 2. В любом случае, в данной статье умножение консеквентов может быть заменено делением антецедентов той же самой пары, и деление консеквентов — умножением антецедентов. (Статья. 354, след.)

379. Часто бывает необходимо не только изменить члены пропорции и варьировать их расположение, но и сравнить одну пропорцию с другой. Из этого сравнения часто возникает новая пропорция, которая может быть необходима для решения задачи или перехода к доказательству. Один из самых важных случаев, когда сравниваемые два члена одной пропорции такие же как два в другой. Похожие члены могут исчезнуть, и новая пропорция может быть сформирована из оставшихся четырёх членов. Так,

380. Если два соотношения соответсвтенно равны третьему, то они также равны между собой.
Это не что иное, как 11ая аксиома, применяемая к соотношениям.
1. Если a:b = m:n
И c:d = m:n
тогда a:b = c:d,или a:c = b:d. (Статья.376.)
2. Если a:b = m:n
И m:n = c:d
то a:b = c:d,или a:c = b:d.

След. Если a:b = m:n
m:n > c:d
то a:b > c:d.
Так если соотношение m:n больше, чем c:d, то это показывает, что соотношение a:b, которое равно соотношению m:n, также больше чем соотношение c:d.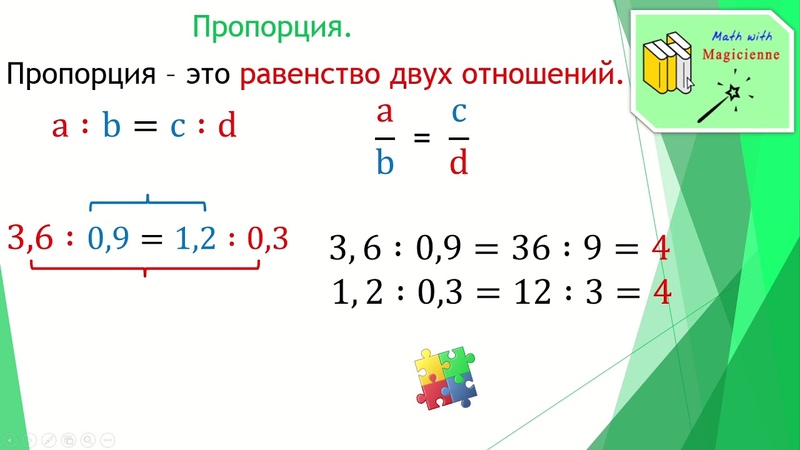

381. В этих примерах схожие члены двух пропорций это два первых и два последних. И порядок не важен. Порядок членов может быть изменён разными способами без влияния на равенство соотношений.

1. Похожими членами могут быть два антецедента, или два косеквента в каждой пропорции. Таким образом,
Если m:a = n:b
И m:c = n:d
тогда
Чередуем, m:n = a:b
И m:n = c:d
Отсюда a:b = c:d, или a:c = b:d, согласно последнему параграфу.

2. Антецеденты в одной пропорции, могут быть такими же как консеквенты в другой.
Если m:a = n:b
И c:m = d:n
Инветрируя и чередуя a:b = m:n
Чередуя c:d = m:n:
Поэтому a:b, и так далее как ранее.

3. Два гомологичных члена в одной из пропорций могут быть такими же, как два аналогичные члены в другой.
Если a:m = b:n
и c:d = m:n
Чередуя, a:b = m:n
И c:d = m:n
Поэтому, a:b, и так далее.

Всё это примеры равенства между соотношениями в одной пропорции с соотношениями в другой. В геометрии на предположение, к которому они принадлежат обычно ссылаются как на «ex aequo«или «ex aequali» (по справедливости). Второй случай в этой статье более всего отвечает объяснению Евклида. Но оба они все согласуются с одним и тем же принципом и часто к ним обращаются без разграничений.

382. Любое число пропорций может быть сравнено аналогичным способом, если два первых или два последних члена в каждой предыдущей пропорции такие же, как два первые и два последние члена в последующей.
Поэтому если a:b = c:d
И c:d = h:l
И h:l = m:n
И m:n = x:y
то a:b = x:y.
То есть два первых члена первой пропорции имеют такое же соотношение, как два последних члена последней пропорции. Это показывает, что соотношение всех пар одинаково.

И если члены не находятся в том же порядке как здесь, но могут быть упрощены к данному виду, применяется тот же самый принцип.
поэтому если a:c = b:d
И c:h = d:l
И h:m = l:n
И m:x = n:y
тогда чередуя
a:b = c:d
c:d = h:l
h:l = m:n
m:n = x:y.
Поэтому a:b = x:y, как и ранее.

Во всех примерах в этой и предшествующих статьях, два члена в одной пропорции, у которых есть равные члены в другой, не являются ни двумя средними членами, ни двумя крайними членами, а одним средним и одним крайним членом, из чего следует, что пропорция однородна и непрерывна.

383. Но если два средних или два крайних члена в одной пропорции такие же, как средние и крайние члены в другой, то оставшиеся четыре члена будут взаимно пропорциональны.
Если a:m = n:b
И c:m = n:d
тогда a:c = $\frac{1}{b}:\frac{1}{d} $, или a:c = d:b

Для ab = mn
И cd = mn
(Статья. 370) Поэтому ab = cd, и a:c = d:b.

В данном примере два средних члена в одной пропорции, такие же как те же в другой. Но принцип будет тем же, если крайние члены не равны или если крайние члены одной пропорции не равны средним членам другой.
Если m:a = b:n
И m:c = d:n
тогда a:c = d:b.

Или if a:m = n:b
И m:c = d:n
тогда a:c = d:b.
Теорема в геометрии, которая применима в данном случае обычно именуется словами «ex aequo perturbate» (по правде запутанная).

384. Другой способ варьировать члены в пропорции это сложение или вычитание.

Если к или от двух гомологичных членов пропорци вычитаются или прибавляются две другие величины, которые находятся в том же соотношении, то пропорция остаётся верной.

Соотношение не меняется, если добавить или отнять от него другое равное соотношение. (Статья. 357.)
Если a:b = c:d
И a:b = m:n
Тогда добавляя или отнимая от a и b, члены с равным соотношением m:n, мы получим
a+m:b+n = c:d, и a-m:b-n = c:d.
И добавляя или отнимая m и n к или от c и d, мы получим,
a:b = c+m:d+n, и a:b = c-m:d-n.

Здесь сложение и вычитание производится к и от аналогичных членов. Но путём чередования (Статья. 376,) эти члены будут гомологичными, и мы получим,
a+m:c = b+n:d, и a-m:c = b-n:d.

След. 1. Это добавление может распространяться на любое число равных соотношений.
Таким образом, если
a:b = c:d
a:b = h:l
a:b = m:n
a:b = x:y
Тогда a:b = c+h+m+x:d+l+n+y.

След. 2. Если a:b = c:d
И m:b = n:d
тогда a+m:b = c+n:d.

Чередуем a:c = b:d
И m:n = b:d
таким образом
a+m:c+n = b:d
или a+m:b = c+n:d.

385. Из последней статьи следует, что если в любой пропорции члены прибавляются или отнимаются друг от друга, то,

Если аналогичные и гомологичные члены добавляются или отнимаются от двух других, то пропорция сохраняется верной.
Таким образом, если a:b = c:d, и 12:4 = 6:2, тогда,

1. Добавляя два последних члена к двум первым.
a+c:b+d = a:b 12+6:4+2 = 12:4
и a+c:b+d = c:d 12+6:4+2 = 6:2
или a+c:a = b+d:b 12+6:12 = 4+2:4
и a+c:c = b+d:d 12+6:6 = 4+2:2.

2. Складывая два антецедента с двумя консеквентами.
a+b:b = c+d:d 12+4:4 = 6+2:2
a+b:a = c+d:c, т.д.. 12+4:12 = 6+2:6, т.д..
Это называется Композицией.

3. Отнимая два первых члена от двух последних.
c-a:a = d-b:b
c-a:c = d-b:d, т.д..

4. Отнимая два последних члена от двух первых.
a-c:b-d = a:b
a-c:b-d = c:d, т.д..

5. Отнимая консеквенты от антецедентов.
a-b:b = c-d:d
a:a-b = c:c-d, etc.
Преобразование, показанное в последней форме называется Конверсией.

6. Отнимая антецеденты от консеквентов.
b-a:a = d-c:c
b:b-a = d:d-c, etc.

7. Добывляя и вычитая,
a+b:a-b = c+d:c-d.
То есть сумма первых двух членов относится к их разности, как сумма двух последних к их разности.

След. Если любые сложные величины, расставленые как в предыдущих примерах, пропорциональны, то простые величины, из которых они состоят также пропорциональны.
Таким образом, если a+b:b = c+d:d, то a:b = c:d.
Это называется Делением.

386. Если соответствующие члены двух или более разрядов пропорциональных величин перемножить между собой, то произведение также будет пропорционально.

Это смешанные соотношения (Статья. 347,) или смешанные пропорции. Это нужно уметь отличать от того, что называется композицией, которая является сложением членов соотношения. (Статья 385. 2.)
Если a:b = c:d    12:4 = 6:2
И h:l = m:n    10:5 = 8:4
Тогда ah:bl = cm:dn    120:20 = 48:8.
Исходя из определения пропорции два соотношения первого разряда равны, как и соотношения второго разряда. И умножение соответствующих членов является умножением соотношений, (Статья. 352. соотв.), то есть умножением равных на равные (Аксиома. 3.), так что соотношения будут всё так же равными, и поэтому все четыре произведения должны быть пропорциональны.

Такое же доказательство применимо к любому числу пропорций.
Если
      a:b = c:d
      h:l = m:n
      p:q = x:y
Тогда ahp:blq = cmx:dny.
Из этого следует, что если члены пропорции перемножить на самих себя, то есть, если они возведены в какую-либо степень, то они всё равно будут пропорциональны.
Если a:b = c:d    2:4 = 6:12
   a:b = c:d    2:4 = 6:12
Тогда a²:b² = c²:d²    4:16 = 36:144
Пропорциональные величины также получаются реверсируя этот процесс, то есть вычисляя корни членов пропорции.
Если a : b:: c : d, тогда √a:√b = √c:√d.
Перемножив средние и крайние члены, ad = bc
И извлекя корень из обеих сторон, √ad = √bc
То есть, (Статья.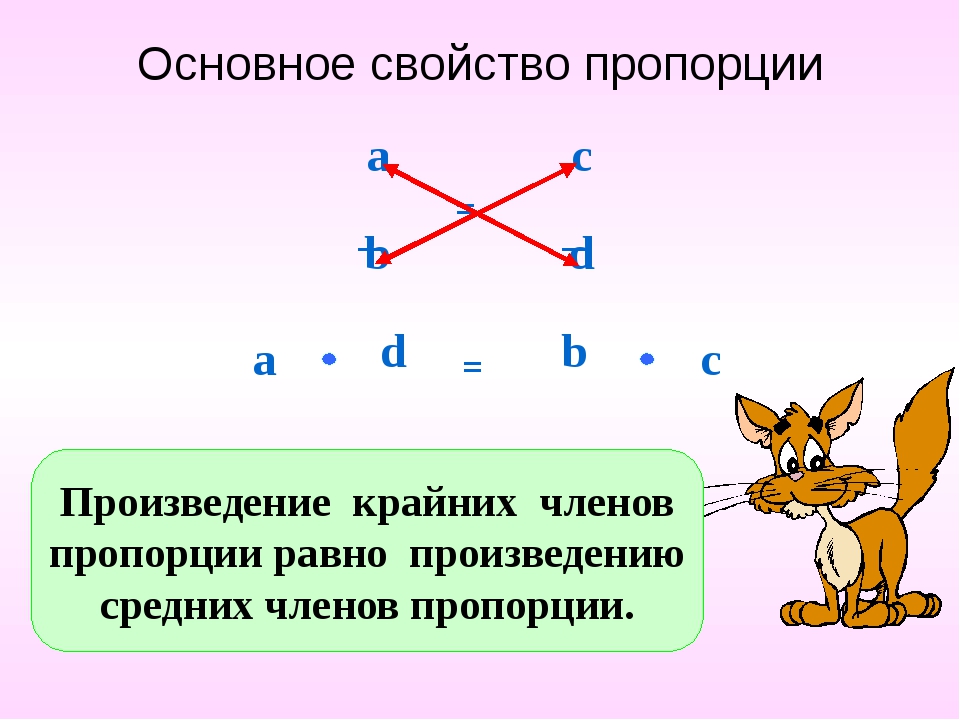 254, 371,) √a:√b = √c:√d.
Отсюда,

387. Если некоторые величины пропорциональны, то продукты их возведения в степень или извлечения корней пропорциональны.
Если a:b = c:d
Тогда aⁿ:bⁿ = cⁿ:dⁿ, и ^m√a:^m√b = ^m√c:^m√d.
И ^m√aⁿ:^m√bⁿ = ^m√cⁿ:√dⁿ, то есть, a^m/n:b^m/n = c^m/n:d^m/n.

388. Если члены одного разряда пропорций разделить на соответствующие члены другого разряда, то частные будут пропорциональны.
Это иногда называют решением соотношений.
Если a:b = c:d 12:6 = 18:9
И h:l = m:n 6:2 = 9:3
Тогда $\frac{a}{h}:\frac{b}{l }=\frac{c}{m}:\frac{d}{n} $ $\frac{a}{h}:\frac{b}{l }=\frac{c}{m}:\frac{d}{n} $.
Это просто реверсия процесса в Статье. 386, и может быть доказана похожим образом.
Это нужно уметь различать от того, что в геометрии называется разделением, которое является вычитанием членов соотношения. (Статья. 385. соотв.)

389. В сложных смешанных пропорциях, равные множители или делители двух аналогичных или гомологичных членов могут быть отвергнуты.
Если
a:b = c:d    12:4 = 9:3 b:h = d:l    4:8 = 3:6
h:m = l:n    8:4 = 6:15
Тогда a:m = c:n      12:20 = 9:15.
Это правило может быть применено к случаям, к которым относятся термины «ex aequo» и «ex aequo perturbate«. Смотрите Статьи. 381 и 383. Один из методов может служить для того, чтобы подтвердить другой.

394. Изменения, которые могут быть сделаны в пропорциях без нарушения равенства соотношений, так многочислены, что они стали бы обременительны к запоминанию, если бы их нельзя было бы упростить до нескольких общих принципов. Они обычно получаются,
1. Инвертируя порядок членов, Статья. 376.
2. Умножая или деля на одинаковую величину, Статья. 378.
3. Сравнивая пропорции, в которых есть схожие члены. Статьи. 380, 381, 382, 383.
4. Складывая или отнимая члены одинаковых соотношений, Статьи. 384, 385.
5. Умножая или деля одну пропорцию на другую, Статьи. 386, 387, 388.
6. Возводя в степень или извлекая корни членов, Статья. 387.

391. Когда четыре величины пропорциональны, если первая больше чем вторая, то третья будет больше чем четвёртая; если равны, то равны, а если меньше, то, соответственно, меньше.

Для одинаковых соотношений двух пар, если одно является соотношением равенства, то и второе тоже, и поэтому антецедент в каждой паре равен её консеквенту. (Статья. 345,) Если одно соотношение большего неравенства, то и второе тоже, и поэтому антецедент каждого из них больше чем соответствующий консеквент. А если одно соотношение меньшего неравенства, то и второе так же, и поэтому антецедент каждого из них меньше чем консеквент.
Пусть a:b = c:d; тогда если
a = b, c = d
a > b, c > d
a < b, c < d.

След. 1. Если первый член больше третьего, то тогда второй больше четвёртого, если равен — то равен, если меньше — то, соответсвенно, меньше.
В случае чередования, a:b = c:d становится a:c = b:d, без какого-либо чередования величин. Таким образом, если a = b, c = d, и т.д., как и ранее.

След. 2. Если a:m = c:n
и m:b = n:d
тогда if a = b, c = d, и т.д.
Для равенства соотношений, (Статья. 381. 2.) или смешанных соотношений, (Статьи. 386, 389.)
a:b = c:d. Таким образом, если a = b, c = d, и т.д. как ранее.

След. 3. Если a:m = n:d
и m:b = c:n
тогда if a = b, c = d.

391. b. Если четыре величины пропорциональны, то обратные им величины тоже пропорциональны и наоборот.
Если a:b = c:d, тогда $\frac{a}{h}:\frac{b}{l }=\frac{c}{m}:\frac{d}{n} $.
Для каждой из этих пропорций, при сокращении получаем ad = bc.

Пропорция

, золотое сечение и правило третей

Пропорция, золотое сечение и правило третей

Один из ключевых принципов дизайна для веб-дизайнеров пропорция , поскольку она применима на макроуровне (общий макет страницы) и микроуровне (например, отдельная диаграмма или виджет). Пропорция относится к соотношению размеров визуальных элементов друг к другу и ко всему целому. В искусстве этот принцип изучался на протяжении сотен лет, и одна вневременная пропорциональная зависимость, которая часто возникает для положительного эффекта в дизайне, — это золотое сечение или золотое сечение .

Золотое сечение

Отношение

относится к тому, как одно измерение соотносится с другим, а соотношение 1: 1,618 называется золотой серединой — отношение bc к ab совпадает с ab к ad . Если вы снова разделите каждое меньшее окно с тем же соотношением и соедините их углы, вы получите логарифмическую спираль . Эта спираль часто встречается в природе в ракушках, рогах, цветах и т. Д.

Может быть, люди генетически запрограммированы распознавать соотношение в золотой середине как приятное. Один необычный пример: исследования топ-моделей показали, что их лица имеют коэффициент 1,618.

Золотое сечение можно увидеть во многих древних архитектурных проектах, включая Парфенон. Сетка золотой середины, примененная к ландшафту

Правило третей

Многие дизайнеры и художники знают о правиле третей, согласно которому изображение делится на три части по вертикали и горизонтали, а линии и точки пересечения представляют собой места для размещения важных визуальных элементов.Правило третей может быть очень полезным руководством при создании дизайна.

Можно анализировать фотографии и рисунки, раскладывая сетки.

Сетка по правилу третей, примененная к ландшафту.

Сетка правила третей, примененная к портрету.

В качестве эксперимента я начал применять правило третей и золотое сечение к некоторым веб-сайтам:

Некоторые из этих веб-сайтов, например Amazon.com, имеют гибкий дизайн , что означает, что ширина увеличивается в соответствии с размером браузера пользователя. Как это может повлиять на пропорцию re?правило третей?

Пропорции — важный принцип дизайна и отличный инструмент, который помогает нам при принятии решений о макете. Но это не единственный инструмент; необходимо учитывать и другие элементы и принципы. При размещении визуальных элементов для создания эффективной композиции необходимо оценить другие элементы и принципы дизайна, включая форму, текстуру, цвет, преобладание, баланс и т. д.

Для получения дополнительной информации:

правил пропорции | ЭТО

От греков к золотому прямоугольнику

В соавторстве с Тоддом Мердоком

Что касается правил пропорции, я никогда не понимал всей картины. По крайней мере, до недавнего времени, не раньше, чем потратить последние на три года на изучение классических порядков с Тоддом Мердоком — одно исполнение SketchUp за раз. Теперь я знаю, почему мне было так сложно понять правила пропорции. Таких нет. Их не существует. Но есть рекомендации.

Я заметил растущий интерес к классическим порядкам — корням большинства архитектурного дизайна. Но так было не всегда. Когда я начал работать в строительстве, в начале 1970-х годов модернизм все еще привлекал внимание многих архитекторов, строителей и домовладельцев.К тому времени модернизм — от Фрэнка Ллойда Райта до Уолтера Гропиуса и движения Баухаус — повлиял на традиционные стили строительства, представив более мелкие и более обтекаемые формы, большие панорамные окна и раздвижные стеклянные двери, которые выводили наружу внутрь помещения вместе с консолями, странными. фигурные колонны и множество других аффектов.

Некоторые историки архитектуры высмеивают влияние модернизма, который часто отрицал стоечно-балочную структуру классических ордеров, что иногда приводило к глупым результатам.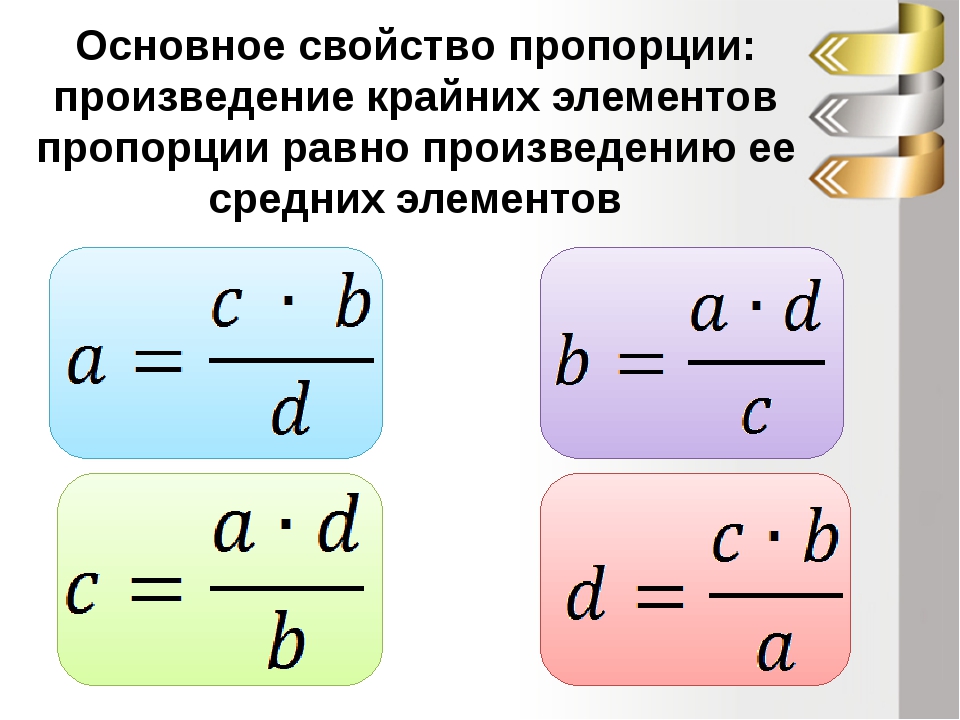 (Примечание: щелкните любое изображение, чтобы увеличить.)

Десять лет спустя, пытаясь понять, как спроектировать колониальную каминную полку для клиента из Лос-Анджелеса, я узнал, насколько сложно было изучать классические заказы. Сначала я обнаружил, что не существует единой простой для понимания системы дизайна или пропорции. Фактически, то, что я обнаружил в библиотеке моего местного университета, было запутанным набором систем и подходов к пропорциям. Но как плотнику мне нужен был только один! И все мне говорили, что классические ордена основывались на греческих храмах, на Парфеноне.Если бы это было правдой, как могло бы быть так много разных интерпретаций?

Как и большинству плотников, мне приходилось выполнять свою работу, поэтому я выбрал автора с наибольшим количеством титулов, Ашера Бенджамина, и, как оказалось, систему, которую легко понять. Подход Бенджамина казался… ну… доступным. К тому времени я построил несколько каминных панелей, но ни одна из них не казалась мне подходящей. На этот раз я хотел начать с действительно приятного дизайна, и мне нужно было знать, какой ширины и глубины должны быть пилястры, какой высоты антаблемент. должно быть, насколько далеко должен выступать карниз.Да, я хотел знать правила. У Бенджамина не было недостатка в правилах. И по какой-то глупой причине я все еще думал, что все они произошли от Парфенона!

Из-за того, что книга была такой маленькой, иллюстрации тесноваты, информация незначительна и почти непонятна, особенно пропорции классических орденов.

···

Бенджамин представил совершенно четкую систему пропорций для проектирования камина, когда он написал: «… разделите ширину или отверстие дымохода на восемь или девять частей; дайте одну восьмую или одну девятую ширине архитрава »(таблица XVII).

Мне понравилась простая система Бенджамина, разбивающая классические порядки на небольшое количество частей — от 11 частей для тосканских до 14 частей для коринфских. Я мог бы справиться с этим. Но затем я совершил ошибку, прочитав следующую книгу Ашера Бенджамина ( The American Builder’s Companion , 1827), где он полностью изменил правила и разбил тосканский порядок на ТРИДЦАТЬ ДЕВЯТЬ частей. И чтобы еще больше запутать, он описал размер каждой детали лепнины, используя систему, основанную на минутах ( Архитектор или Практический Дом Карпентер , 1830).Минуты! Какое отношение время имеет к пропорции?

Разбив заказ на 39 частей, Бенджамин смог определить размер каждой основной части, от цоколя и тора (плинтуса) до циматиума (короны). Для точных размеров Бенджамин создает новую единицу измерения, разделив диаметр основания колонны на 60 равных частей, называемых «минутами».

Все эти части (и минуты тоже!) Были слишком много для моего ума с арифметикой. Кроме того, за исключением некоторых причудливых декоративных элементов, таких как листья аканта, флейты и завитки, триглифы, метопы и модиллионные блоки, все заказы для меня выглядели почти одинаково! Но все же я был рад, что нашел правила, открыл последнее слово, узнал, как греки сориентировали Парфенон, римляне спроектировали Пантеон, и все это прямо от Ашера Бенджамина, истинного источника американской архитектуры.

Phooey.

Примерно пять лет спустя я вернулся в библиотеку и прочитал переизданный экземпляр книги Авраама Свона «Британский архитектор » (1758 г.). Какое потрясающее зрелище! Свон разбил тосканский порядок всего на ДЕВЯТЬ частей, что значительно упростило арифметику! И Свон разрушила все мои представления об универсальных правилах пропорции!

Система Авраама Свана для распределения тосканского ордена, состоящая только из ДЕВЯТИ частей, кажется намного проще, чем система Бенджамина — по крайней мере, на первый взгляд!

Но система Swan не так проста, когда вы детализируете размер каждой детали, которая по-прежнему требует многократных и трудоемких делений.Вместо того, чтобы разделить диаметр основания колонны на 60 минут, он делит его на 48 равных частей.

Итак, как могут быть две или даже три разные системы и измерения для пропорционального распределения классических порядков? Простой. Ни один из этих примеров не основан на конкретных греческих или римских руинах. Все они зависят от мнения и вкуса отдельного автора. На самом деле, единственное, что их объединяет, это то, что своим подходом они обязаны Витрувию (см. Историю ниже).

Понимание системы пропорций

Немногие плотники имеют возможность изучать классические порядки, и те, кто попробовал хотя бы беглый осмотр, сразу же сбиты с толку рисунками, датируемыми несколько веков назад, которые отображают каждый порядок в возрастающей высоте, от «коротких» тосканских до «высоких» композитных. .

Эта иллюстрация — с порядками, нарисованными с использованием одного и того же диаметра основания — вызвала больше путаницы, чем понимания! Первое впечатление — это то, что композитный и коринфский ордена выше тосканского ордена.Эти старые иллюстрации, основанные на диаметре, заставляют нас поверить в то, что тосканский орден не тяжелее, сильнее и существеннее, чем любой из последующих орденов, — что совсем не так!

Взгляните на Дрейтон-холл, один из самых знаковых образцов грузинской архитектуры в Америке, построенный примерно в 1738 году и с тех пор практически не тронутый.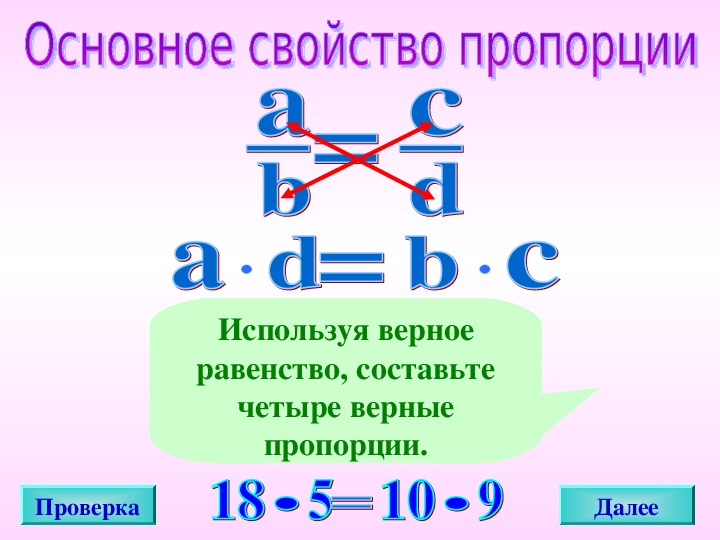

Портик поддерживается на первом этаже прочными тосканскими колоннами, способными выдержать вес пола и крыши над ним, в то время как более легкие ионные колонны поддерживают второй этаж и крышу.

Также обратите внимание, что ионные колонны опираются на пьедесталы, а перила красиво заканчиваются прямо под крышкой пьедестала. К сожалению, именно этот тип деталей или «порядок» сейчас отсутствует в большей части архитектурного дизайна.

Классические пропорции имеют больше смысла, если заказы нарисованы на одной высоте, а не на одном диаметре основания. В конце концов, плотники (как архитекторы и дизайнеры) должны работать с фиксированными отметками — высотой внешней стены, высотой внутреннего потолка.Вот почему такая иллюстрация, основанная на общей высоте, имеет гораздо больший смысл.

История

Теперь, когда Тодд предоставил понятное анимированное руководство по пониманию пропорций, давайте вернемся к Парфенону, древнему храму, который многие из нас ошибочно называют источником правил пропорциональности.

Жизнь веселая. То, чего вы избегаете в молодости, становится в старшем возрасте гораздо более привлекательным и привлекательным, например, находить красоту в пожилых людях — вы знаете, людям в возрасте от 50 до 60 лет — чего вы не можете себе представить в 20 лет Старый.Архитектура такая. Ценить классические порядки и ценить разнообразие систем, используемых для определения правильных пропорций, помогает ценить историю, и я имею в виду намного более давнюю, чем 50 или 60 лет.

Хотя Парфенон может и не входить в список семи чудес света, это самое важное архитектурное сооружение в западном мире, построенное греками примерно в 447 году до нашей эры. История здания — от проектирования и строительства до войн, пожаров и грабежей — необычна.Для зрителей рекомендую программу PBS Nova о Тайнах Парфенона. Читатели могут попробовать Mary Beard’s, Парфенон .

Витрувий, римский военный инженер и архитектор, опубликовал самую раннюю известную работу по архитектуре, De Architectura (Десять книг по архитектуре), где-то около I века до нашей эры, и он внимательно изучил Парфенон. Он особенно описал мельчайшие отклонения от идеально прямых линий, обнаруженные в стилобате или ступенях, ведущих к храму, в антазисе колонн и в том, что мы сегодня узнаем как слегка изогнутый архитрав, включая изгиб в самих панелях метопа.

447–438 до н. Э., Афины, Греция — Парфенон в сумерках — Изображение © Colin Dixon / Arcaid / Corbis

Витрувий разработал первую известную систему пропорций, используя «части» для определения каждого раздела заказа. Однако даже Витрувий описывает, как время повлияло на пропорции: «Это правда, что потомки, добившись прогресса в утонченности и деликатности чувств и найдя удовольствие в более тонких пропорциях, установили семь диаметров толщины как высоту дорической колонны, и девять — как у Iconic »(Morgan 104).[i]

В 1452 году Леон Батиста Альберти, автор и архитектор, опубликовал первую крупную работу по архитектуре итальянского Возрождения, De re aedificatoria («Об искусстве строительства»). Альберти основал многие из своих правил пропорции на работе Витрувия, написанной почти полторы тысячи лет назад.

В 1562 году, чуть более ста лет спустя, Джакомо Бароцци да Виньола, художник и архитектор, работавший в одно время с Микеланджело, измерил римские руины и памятники, а затем опубликовал Канон пяти архитектурных орденов .Как ранее объяснял Тодд, Виньола установил простейшую и наиболее влиятельную систему пропорционального распределения классических колонн и архитектурного орнамента.

Менее чем через десять лет Палладио измерил греческие руины и опубликовал свои выводы о пропорциях в Четыре книги архитектуры (1570), используя систему пропорций, почти такую же, как Виньола: например, ионная колонка Палладио — «девять». модули высотой… модуль (являющийся) нижним диаметром колонны »(Палладио, 19).[ii]

Из-за якобы тщательных измерений Палладио — но в значительной степени из-за умелого издательского мастерства — ему часто отдают должное за разработку настоящей системы пропорциональных правил, полностью основанной на классических порядках. Но именно система Виньолы оказала влияние на большинство авторов архитектуры.

И хотя Палладио считается одним из первых, кто измерил греческие руины, плотникам и подрядчикам следует задуматься, чтобы представить, насколько тщательно эти измерения могли быть выполнены.Как пишет Колдер Лот: «… пристальный взгляд на некоторые детали показывает, что Палладио не всегда был точен в своих изображениях многих черт. Мы можем предположить, что Палладио полагался на помощников для выполнения некоторых фактических измерений, когда он записывал записи и делал наброски на основе информации, передаваемой ему »(Loth 7355).

Генри Парк дает нам довольно хорошую подсказку о системе Палладио для измерения Парфенона. [Iv]

После Палладио множество архитектурных авторов написали и проиллюстрировали свои собственные версии приказов.В некоторых отношениях просто поразительно, сколько мужчин посвятили столько времени и энергии формированию своего видения классических порядков и своей системы пропорций. Среди этих архитекторов / авторов / иллюстраторов были Джеймс Гиббс (который работал в то же время, что и сэр Кристофер Рен и Иниго Джонс), Авраам Свон и Уильям Чемберс, которые оказали влияние — часто напрямую — на работу Ашера Бенджамина.

Правила или рекомендации?

Как сказал Бенджамин в предисловии к третьему изданию The American Builder’s Companion 1827 :

Далее я рассмотрел происхождение зданий, лепных украшений и заказов.Я попытался объяснить их настолько ясно и полно, что их нельзя неправильно понять. Сначала они были отобраны у нескольких авторов, нарисованы и обработаны. После тщательного изучения те части, которые я не одобрял, были изменены путем их повторной прорисовки и обработки и повторения этого процесса несколько раз, пока после самого тщательного и тщательного изучения каждой части четырех первых заказов я не получил подтверждения. по мнению, что никаких дальнейших изменений к лучшему сделать нельзя; В результате каких экспериментов видны эти порядки, они установлены по отдельности.[v]

Да, он действительно звучит немного самоуверенно. Немного позже в книге Бенджамин объясняет часть своих рассуждений по поводу интерпретации классических орденов: «Рисунок, прилагаемый здесь, а также дорический, ионический, коринфский и композитный ордера, я выбрал из нескольких авторов и сделал все изменения, которые, на мой взгляд, были необходимы, чтобы привести их в соответствие с практикой настоящего времени »(33).

Мы без сомнения знаем, что одним из авторов, на которого ссылается Бенджамин, является сэр Уильям Чемберс, потому что именно из более ранней работы Чемберса Бенджамин самым вопиющим образом плагиат, иногда несколько страниц за раз.На самом деле Бенджамин был серийным плагиатором, он не знал границ воровать работы других авторов и предполагать, что это были его собственные. Любой, кто интересуется полной историей Ашера Бенджамина и его источников, должен прочитать подробное исследование Эбботта Лоуэлла Каммингса. [Vi]

Хотя он не был плагиатором, Свон также признался в создании своих собственных дизайнов и включении уникальных пропорций для классических орденов:

Ибо я наблюдаю, что рисунки, опубликованные другими, по большей части были грандиозными и помпезными; которые, хотя они могут быть превосходными в своем роде, но редко используются, поскольку подходят только для очень больших зданий.
Но поскольку джентльменов с умеренным состоянием больше, чем с большим имуществом, которые могут быть склонны строить дома, я полагаю, что некоторые менее дорогие проекты могут быть приемлемы для публики, поскольку они имеют более общее применение, например, которые можно найти в нескольких следующие пластины »(Swan iii). [vii]

Дело в том, что то, что мы, возможно, считали прямыми измерениями, сделанными на древних руинах, не является чем-то подобным. Все эти влиятельные авторы создали свои собственные правила и выбрали свои собственные системы пропорций, основываясь на том, что, по их мнению, лучше всего подходит для каждого случая.

Очевидно, что каждый из исследованных нами авторов следовал некоторой форме стандартизированного дизайна, но художественная интерпретация имела больший авторитет, чем жесткие правила, что продемонстрировано различными примерами в этой иллюстрации тосканского ордена.

Внимательно читаете: мифы и заблуждения

Когда я учился в школе, один профессор однажды сказал мне: «Не верьте ни одному писателю, который ссылается на признанное или культовое литературное произведение. Большинство авторов никогда не читают фактический исходный материал; большинство авторов просто читают других авторов, которые цитировали исходный материал.Не будьте небрежным исследователем, — сказал он мне, — всегда читайте исходный материал самостоятельно. Возможно, ты единственный, кто это сделает ».

Давайте начнем с мифа о человеческом теле, являющемся источником всех архитектурных пропорций. Бесчисленные писатели, ораторы и интернет-пользователи повторяют эту историю. Вместо того, чтобы повторять это снова, давайте посмотрим на первоисточник — Витрувий, который писал: «Без симметрии и пропорции не может быть принципов в дизайне любого храма; то есть, если между его членами нет точной связи, как в случае с человеком хорошей формы »(Витрувий 72).

Так что же имел в виду наш учитель римского? Витрувий объясняет это хорошо, без двусмысленности. Он описывает, как человеческое тело «создано природой», и каждая его часть имеет идеальные пропорции, чтобы создать симметричное целое, «от подбородка до верхней части лба и самых нижних корней волос». Во втором абзаце «О симметрии» Витрувий даже отмечает пропорциональный размер человеческих стоп: «Длина стопы составляет одну шестую высоты тела; предплечья — одна четверть; и ширина груди тоже одна четвертая. ”

Но нигде автор не устанавливает и даже не намекает на связь или взаимосвязь между человеческими пропорциями и пропорциями классических орденов.

Витрувий просто использует симметрию и пропорции человеческого тела как пример естественной красоты, аналогию: «Точно так же в членах храма должна быть величайшая гармония в симметричных отношениях различных частей к окружающему миру. общая величина целого »(73).

Маркус Фрингс описывает оценку Витрувием естественных пропорций человеческого тела как «модель в первую очередь в силу совершенства симметричной формы, а не в присущих ей пропорциях, которые часто неправильно понимают; ср. [Frings 1998]. Человеческое тело, как пример модульного творения из природы, выбрано Витрувием в качестве парадигмы для требуемых правил пропорции »(Фрингс). [Viii]

Одна из возможных причин, по которой людей так сбивает с толку Витрувий, может заключаться в том, что римлянин обращает наше внимание на язык измерений, на то, как наша терминология получена из описаний анатомии человека: «Кроме того, именно от членов тела они получили основные идеи о мерах, которые, очевидно, необходимы во всех работах, таких как палец, ладонь, ступня и локоть. Они распределили их так, чтобы образовалось «совершенное число, называемое по-гречески τέλειον», и как совершенное число древние считали десятью. Ибо по количеству пальцев руки находится ладонь, а ступня — от ладони »(стр. 73).

К сожалению, писатели часто ошибочно полагают, что Витрувий описывает прямую корреляцию между размером ступни человека и размером диаметра колонны. Бред какой то. Это просто аналогия.

Золотой прямоугольник: еще один миф

Вернувшись к Витрувию, давайте более подробно рассмотрим происхождение картины Леонардо да Винчи Витрувианский человек и предполагаемую связь этой иллюстрации с золотым прямоугольником или золотой серединой.А затем мы рассмотрим Кинг-Конг из всех мифов — отношение золотого прямоугольника к Парфенону.

Та же часть из книги Витрувия «Десять архитектурных книг » вдохновила Леонардо да Винчи на рисунок Витрувианского человека. Обсуждая значение симметрии и пропорции, Витрувий писал:

Ибо, если человека положить плашмя на спину, с вытянутыми руками и ногами и с компасом по центру его пупка, пальцы рук и ног его двух рук и ног будут касаться окружности описываемого круга. И точно так же, как человеческое тело образует круговой контур, из него можно найти и квадратную фигуру. Ведь если мы измерим расстояние от подошв ступней до макушки головы, а затем применим эту меру к вытянутым рукам, то окажется, что ширина равна высоте, как в случае плоских поверхностей, которые идеально квадратные. (73)

Рисунок Леонардо да Винчи является точной копией описания Витрувием симметрии и пропорции человеческого тела.Хотя Витрувий нигде не ссылается на золотую середину и не полагается на иррациональные числа или отношения для какой-либо системы измерений. Далее, обсуждая древнее правило, согласно которому «в идеальных зданиях разные элементы должны находиться в точном симметричном отношении ко всей общей схеме», Витрувий обсуждает, почему греки остановились на десяти как на «совершенном числе», отчасти потому, что это число пальцы рук и ног на человеческом теле, и поскольку оно легко делится, но «как только достигается одиннадцать или двенадцать, числа, будучи чрезмерными, не могут быть идеальными, пока они не дойдут до десяти во второй раз» (стр. 73).

А в собственных записях да Винчи, которые на иллюстрации написаны зеркальным шрифтом, нет упоминания о золотом сечении. Художник просто цитирует оригинальную работу Витрувия, не оставляя сомнений в его цели — воспроизведении оригинальной работы Витрувия.

Из всех произведений человека, приписываемых золотому прямоугольнику — от Великих пирамид Гизы до Нотр-Дама, от Тайная вечеря до Моны Лизы — Парфенон, вероятно, является наиболее ярким примером, а также самым ярким примером. выдающееся заблуждение.Чтобы проследить связь между золотым прямоугольником и Парфеноном, я просмотрел все книги по архитектуре, которые попадались мне в руки.

Золотые прямоугольники, начерченные широкими линиями поверх архитектурных икон, являются домыслом; они игнорируют древнее происхождение классической пропорции, основанной на греческих и римских принципах.

В исследовании Мэри Берд 2010 г., Парфенон, никогда не упоминается золотой прямоугольник.

Фиск Кимбалл, американский архитектор, историк, 30 лет директор Художественного музея Филадельфии и уважаемый автор книги A History of Architecture (1918) — , одной из моих любимых и наиболее доступных книг по историческим архитектурным стилям — никогда. не упоминает золотой прямоугольник.

Спиро Костоф, автор книги История архитектуры — — справочника, общего для курсов по истории архитектуры в колледжах, и к которому я обратился, когда впервые начал изучать этот предмет — никогда не упоминается в Золотой прямоугольник.

И хотя в его обязательном Иллюстрированном словаре исторической архитектуры , похоже, есть иллюстрации для каждой архитектурной особенности, концепции и детали, Сирил Харрис не включает никакой информации о золотом прямоугольнике.

Марианна Кузато в своей замечательной работе Get Your House Right ( — обязательный путеводитель для строителей), действительно обсуждает Золотое сечение (в разное время описываемое как Золотое Сечение, Божественная пропорция и т. По словам Кузато, «Золотое сечение было впервые обнаружено и использовано в древности во время Золотого века Греции. Числовое приближение рациона было воплощено в архитектуре и теории итальянского Возрождения и вновь открыто в девятнадцатом веке »(стр.28).

Однако Роберт Адам в своей влиятельной работе « Классическая архитектура, » обсуждает золотой прямоугольник более глубоко и соглашается — по крайней мере в духе — с Кузато, когда он объясняет, что золотое сечение «обладает некоторыми уникальными и замечательными характеристиками. Многие из них были известны математикам в древности и в эпоху Возрождения, но нет никаких документальных свидетельств архитектурного интереса до XIX века. … Хотя нет никаких доказательств вечной красоты этой фигуры или ее сознательного использования в какой-либо период, кроме недавнего прошлого, ее характеристики представляют определенный интерес »(стр.116).

В то время как нынешние архитекторы, обученные золотому сечению, иногда используют формулу 1: 618 для проектирования внешних фасадов, грузинские колониальные дома, датируемые восемнадцатым веком, полагались на книги с образцами, изображающие пропорции классических орденов; Высота фриза, среди других деталей, была определена этими приказами, а не золотым сечением. (http://homewalldecor.us/modern-classic-house-architecture)

Маркус Фрингс, о котором я уже упоминал, вскакивает обеими ногами в спор в статье с обширными сносками — Золотое сечение в истории архитектуры. Фрингс, немецкий историк искусства и куратор музеев, не находит реального применения соотношения, возможно, вплоть до девятнадцатого века. Он прослеживает мифическую теорию до Луки Пачоли, математика эпохи Возрождения и близкого человека Леонардо да Винчи:

Золотое сечение давно не встречается в теории архитектуры. Впервые он появляется в девятнадцатом веке через Цейзинга и Фехнера, а затем становится известной модой в третьем и четвертом десятилетии двадцатого века, когда с ним знакомятся Нойферт и Ле Корбюзье.Нойферт возлагал большие надежды на обновление архитектуры через золотую середину, но вскоре он стал трезвым. Тем не менее он представляет его in extenso . После первых экспериментов Ле Корбюзье использует золотое сечение для разработки своего каталога мер, который имеет — из-за округлений и комбинаций — мало общего ни с золотым сечением, ни с рядами Фибоначчи. Фактически, Нойфер и Ле Корбюзье, кажется, используют золотое сечение как способ приукрасить свое собственное субъективное художественное творчество с помощью теории и соотношения.В любом случае золотое сечение, безусловно, играет роль в трудах этих теоретиков архитектуры. Однако до XIX века Золотое сечение просто отсутствовало в письменной архитектурной теории.

Frings напоминает читателям всех архитектурных авторов, которые упоминали золотой прямоугольник как основу своей работы, но ни разу не привели пример того, как они использовали принцип на практике.

Если вы не любите читать или не доверяете ученым, посмотрите сериал PBS Nova.Этой программе легко следовать, особенно когда рассказчик говорит с искренней простотой: «На протяжении веков многие ученые считали, что золотое сечение дало Парфенону огромную силу и идеальные пропорции — особенно соотношение высоты к ширине на его фасаде. Сегодня использование золотого сечения в Парфеноне в значительной степени дискредитировано ».

В программе с наглядной детализацией поясняется, что вместо соотношения золотого сечения (1: 1,618…) «соотношение, которое, по мнению большинства ученых, использовалось при строительстве Парфенона, составляет 4: 9, что соответствует высоте лица до его ширина, равная ширине столбцов и расстоянию между их центрами.”

Рассказчик в рубрике Нова продолжает:

Коррес и его команда исследовали все уголки Парфенона. И хотя здание выглядит прямым, они обнаружили, что на нем едва ли есть прямая линия.
Эти кривые не случайны. Начинают с фундамента, или стилобата. Каждая из 46 колонн имеет слегка изогнутый профиль и наклонена внутрь. Изогнуты даже наличники, мраморные балки, перекрывающие колонны, а также архитектурные элементы над ними.

Таким образом, каждая из панелей метопа (промежутки между триглифами вдоль фриза) также слегка изогнуты, имеют уникальную форму и размер, чтобы соответствовать каждой колонне. Этот факт также должен развеять миф о том, что в деталях фриза Парфенона наблюдается постоянное золотое сечение.

Но это еще не все! Тем, кто хочет получить подробную видеопрезентацию о золотом сечении, не пропустите академический и развлекательный видеоролик Кита Девлина, разоблачающий множество мифов, связанных с золотым прямоугольником, золотым сечением, золотым сечением и золотой серединой.

Наконец, вывод (своего рода)

Так что все это значит? Проще говоря, когда дело доходит до классического дозирования, нет никаких исчерпывающих источников или мистических наборов правил, которым можно было бы руководствоваться — только руководящие принципы. Плотники должны быть знакомы с «порядком» и иерархией основных элементов, но не должны зацикливаться на мелких деталях. Сделайте шаг назад и сначала посмотрите на всю картину. Например, когда вы строите навес для патио, не используйте стойки 4 × 4 — они выглядят слишком тонкими, слишком тонкими, они не дают человеческому глазу чувства комфорта или безопасности при выдерживании тяжелого груза.Как минимум, используйте стойки 6 × 6. И не используйте балку 6 × 6, используйте балку 6 × 8 или лучше, 6 × 10 или даже больше, в зависимости от пролета!

Но классические приказы — это больше, чем набор руководящих принципов. Как любит говорить Брент Халл, они предоставляют нам «грамматику»: классические порядки — это наш исходный материал для приятных и симметричных деталей, таких как сопоставление подоконников и направляющих стульев, определение размеров плинтуса и карниза, а также выбор пропорции выступов, таких как карнизы, полки каминных полок и дверные антаблементы в классическом стиле.

Но хватит уже о классических заказах! Следующая статья об архитектуре для плотников будет посвящена викторианскому периоду — апофеозу изделий из дерева.

Банкноты

[i] Vitruvious. Витрувиус, Десять книг по архитектуре, в переводе Морриса Хики Моргана. Дувр, 1960.

[ii] Палладио, Андреа. Четыре книги архитектуры . Дувр, 1965.

[iii] Лот, Колдер. « Можем ли мы доверять Палладио», http: // blog. classicist.org/?p=7355)

[iv] Фото: Генри Парк, рисунок лекции Королевской академии, изображающий студента на лестнице с прутом, измеряющего коринфский орден Храма Юпитера Стратора, Рим, SM 23/9/3, Воспроизведено Колдером Лотом с Разрешение Доверительных советов Музея Соуна в Лондоне.

[v] Бенджамин, Ашер. Компаньон Американских Строителей 1827 . Дувр, 1969, Предисловие к третьему изданию.

[vi] Каммингс, Эбботт Лоуэлл. Исследование источников, стилистической эволюции и влияния Руководств строителей Ашера Бенджамина .Оберлинский колледж, 1950.

[vii] Лебедь, Авраам. Грузинские архитектурные образцы и детали (1757 г.). Довер, 2005.

[viii] Фрингс, Маркус. «Золотое сечение в теории архитектуры», Nexus Network Journal, vol. 4, вып. 1 (зима 2002 г.), http://www.nexusjournal.com/Frings.html.

Правило 3: прямое и обратное

В сегодняшнем посте мы собираемся работать с пропорциями . На этот раз мы рассмотрим способ решения прямых и обратных пропорций: правило 3 .

Какое правило трех?

Правило из 3 — это операция, которая помогает нам быстро решать как прямые, так и обратные задачи пропорции слов.

Чтобы использовать правило 3, нам нужно трех значений: двух, которые пропорциональны друг другу, и третьего. Оттуда мы определим четвертое значение .

Прямое правило 3

Мы начнем с рассмотрения того, как применить в случае прямых пропорций .

Мы разместим 3 значения (которые мы назовем «a» , «b» и «c» ) и неизвестное значение, которое мы хотим вычислить ( «x» ) в таблице. Далее применим следующую формулу:

В качестве примера решим следующую задачу:

По прибытии в отель сотрудники дали нам карту с отображением достопримечательностей города и сказали, что 5 сантиметров на карте означают 600 метров в действительности. Сегодня мы хотим пойти в парк, который находится в 8 сантиметрах от отеля на карте. Как далеко от отеля находится парк?

Давайте составим таблицу с тремя значениями и неизвестным значением («x»), и мы найдем «x» с формулой , которую мы только что выучили.

Сантиметров на карте Реальных метров

Ответ: Парк расположен в 960 метрах от отеля.

Обратное правило 3

Теперь посмотрим, как применить правило 3 в случае обратных пропорций .

Мы поместим 3 значения и неизвестное значение в таблицу , так же, как мы сделали в предыдущем случае, , но , мы применим другую формулу:

Давайте посмотрим на пример:

Вчера 2 грузовика перевезли товар из порта на склад. Сегодня 3 грузовика, такого же размера, как вчера, должны будут совершить 6 рейсов, чтобы перевезти такое же количество товаров со склада в ТЦ. Сколько поездок вчера совершили грузовики?

Мы помещаем , значения в таблицу и применяем формулу для обратного правила 3 :

Грузовые автомобили Необходимые поездки

Ответ: Вчера 2 грузовика совершили 9 рейсов.

Что вы думаете об этом сообщении? Разве не легко применить правило трех для определения пропорций словесных задач!

Вы можете узнать больше о прямой и обратной пропорции из этой предыдущей публикации в нашем блоге: Правило трех проблем.

Помните, что с Smartick вы сможете выполнять упражнений, пропорции слов и и многое другое! Попробуй бесплатно!

Подробнее:

Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.

Пошаговые уроки рисования для мультфильмов и иллюстраций

Основы ландшафтной композиции

Композиция — один из самых сложных, но мощных и захватывающих аспектов живописи. Это техническая основа вашей картины. Без него картины визуально разваливаются.Тщательное рассмотрение состава перед нанесением краски на поверхность сделает ваш сеанс более приятным и внесет свой вклад в успех вашей картины.

Основы рисования: божественные пропорции и золотая спираль

Приятные формы, интересные совпадения, экзистенциальные разветвления и некоторая математическая реальность . .. использование этого уникального набора математических концепций может создать врожденный линейный баланс при формальном использовании для создания ваших произведений искусства.Это одно из тех странных мест, где наука взаимодействует с визуальной эстетикой, философией и смыслом жизни. Может быть.

Продвинутая композиция и золотое сечение

На самом деле это не предназначено для задания, но если вы усвоите все это и попытаетесь применить на практике, это значительно улучшит ваши композиционные навыки..

Состав: Правила третей

Правило третей — мощный композиционный прием, позволяющий сделать фотографии более интересными и динамичными. Это также, пожалуй, один из самых известных. В этой статье используются примеры, демонстрирующие, почему правило работает, когда его можно нарушить и как максимально использовать его для улучшения вашей фотографии.

Дизайн и божественная пропорция

Многие дизайнеры, независимо от того, имеют ли они традиционное образование или нет, испытывают проблемы с композицией. Я сидел с множеством дизайнеров, которые просто перемещали вещи, пока не почувствовали себя «правильными». Дизайн — это, по сути, коммуникация (я знаю, я знаю, я достаточно разглагольствую об этом, но это не одна из них), но средство коммуникации — это дизайн.Одним из ключевых компонентов средства коммуникации является композиция, а в школе дизайна это то, чему учат как нечто, что вы должны чувствовать, а не создавать логически. Меня это всегда беспокоило.

Божественные пропорции в ваших картинах

Я довольно хорошо научился планировать картины, используя этот классический метод в качестве основы для композиции. Я стал намного лучше понимать все искусство эпохи Возрождения, классицизма и барокко. Даже импрессионисты увлекались использованием композиций с геометрическим рисунком.

Элементы дизайна: пропорции и золотое сечение

«Золотое сечение» очаровывает художников и математиков более 2000 лет. Это математическая формула, наблюдаемая в природе и используемая художниками, архитекторами, дизайнерами и даже музыкантами бесчисленным количеством способов.

Золотая пропорция в художественной композиции

Древнегреческая цивилизация изучила формы, узоры и пропорции, существовавшие в окружающем их мире природы, и обнаружила, что среди них «Золотая пропорция» была самой простой, красивой и сложной из всех. Обнаруженный естественным образом в растительной и животной формах, он привел греков к теории о том, что та же естественная красота, которая существует в природе, должна использоваться в творениях, созданных руками человека (искусство, архитектура, музыка и т. Д.) если бы они тоже считались красивыми.

Золотое сечение — секрет эстетики?

Этот пост предназначен для графических дизайнеров, фотографов, архитекторов и других дизайнеров «форм», читающих мой блог. С момента открытия и исследования золотого сечения я могу искренне сказать, что моя эстетика резко улучшилась! Не говоря уже о (благодаря использованию некоторых инструментов, которыми я собираюсь с вами поделиться) о повышении производительности, которое я испытал!

Как добиться божественной пропорции / золотого сечения в ваших композициях

Теперь вы можете мгновенно нарисовать золотые сечения или другие божественные пропорции, чтобы облегчить композицию.Этот плагин может рисовать последовательности Фибоначчи, такие как золотые сечения, золотая спираль и золотые треугольники. Кроме того, он также может рисовать гармоничные треугольники и правило третей — на основе композиции через идентичность. Лучший способ использовать плагин — вывести рисунок на прозрачный верхний слой, который можно перемещать для обрезки.

Макет картины на холсте с соотношением золотого сечения

Поскольку золотое сечение проявляется в дизайне и красоте природы, его также можно использовать для достижения красоты и баланса в дизайне искусства.Но это всего лишь инструмент, а не правило для композиции. Золотое сечение широко использовалось Леонардо да Винчи. Обратите внимание, как все ключевые измерения комнаты и стола в «Тайной вечере» да Винчи были основаны на золотом сечении, которое в период Возрождения было известно как Божественная пропорция.

Класс живописи композиции: Правило третей

Правило третей — это простейшее композиционное правило для рисования.

Решение проблем с рисованием: применение правила третей

Если в картине есть что-то, что кажется вам неправильным, но вы не можете понять, что это такое, вернитесь к основам. Прищурьте глаза, чтобы проверить баланс светлых и темных тонов. Определите основные элементы в композиции, чтобы увидеть, как они связаны друг с другом, и проверьте, работают ли они с Правилом третей.

Композиция изображения — Правило третей (или золотое сечение)

Одно из основных правил композиции — правило третей. Это очень простое правило, которое любители часто игнорируют, и оно может значительно улучшить ваши фотографии. Вот как работает это правило: представьте, что вы рисуете линии поперек кадра, чтобы сформировать игровую доску типа «галстук-нолик».(у вас должно получиться девять одинаковых квадратов). Теперь изображение разделено на три части по горизонтали и вертикали. См. Схему расположения линий.

Фотография композиция с правилом третей (применимо также к искусству)

Чтобы повысить выразительность цифровых изображений, применяйте правила композиции изображения при съемке фотографий или моделировании их краев.

Правило третей — Композиция в искусстве

Правило третей, вероятно, одно из самых основных правил, которое веками использовалось в живописи. Это эмпирическое правило композиции, которое сегодня широко используется в изобразительном искусстве, включая живопись, фотографию и дизайн.

Правило третей

Пожалуй, наиболее известный принцип фотографической композиции — «Правило третей».

Божественная пропорция в дизайне

Божественная пропорция часто представлена золотой спиралью. Этот инструмент используют художники и скульпторы для достижения удивительно точных пропорций и эстетической композиции. В золотой спирали отношение длины стороны каждого квадрата к длине стороны следующего меньшего квадрата находится в золотом сечении; прямоугольники, образованные комбинацией квадратов, — золотые прямоугольники; и с каждой четвертью оборота спираль расширяется в Фи раз.

Ленивое правило третей

может сосчитать количество правил, которым я буду безоговорочно подчиняться, основываясь исключительно на страхе катастрофических последствий: я выключаю личную электронику во время посадки и взлета, я все время держу руки внутри аттракциона, я не делаю этого. В торговых автоматах я сопротивляюсь желанию перелезть через заборы зоопарка и больше не бросаюсь за пистолетом в кобуре полицейского в День дурака.Практически все остальное подлежит обсуждению.

Правило третей: почему оно работает и как использовать его в своем искусстве

В базовом прямоугольнике есть ряд мощных визуальных областей, которые художники могут использовать для улучшения своих композиций. О некоторых из этих областей мы уже говорили в нашем руководстве по золотому сечению и на уроке рабатмента на прошлой неделе.

Золотое сечение в искусстве и архитектуре

Появление этого соотношения в музыке, в моделях человеческого поведения, даже в пропорциях человеческого тела, — все указывает на его универсальность как принцип хорошей структуры и дизайна.

Учебное пособие: создание произведений искусства с использованием золотого сечения

На протяжении веков художники и дизайнеры использовали сумму — золотое сечение — для достижения пропорций.Вот как заставить его работать на вас. Люди, изучающие золотое сечение, находили его повсюду, от пирамид до Моны Лизы — и даже в природе, например, в прожилках листьев. В этом уроке Роберто Маррас показывает, как использовать золотое сечение в ваших работах, чтобы создавать пропорциональные части.

Иллюстратор: Золотое сечение / Божественные пропорции

Вы когда-нибудь задумывались, почему глубокое произведение искусства так приятно композиционно? Художник, вероятно, использовал Божественную пропорцию — феномен, который предполагает наличие математического уравнения, которое согласуется с эстетикой хорошей композиции.Давайте рассмотрим краткую историю Божественной пропорции и ее использования на протяжении веков.

Божественная пропорция

Интересно, что деление двух соседних чисел Фибоначчи (например, 8/5 или 21/13) друг на друга дает все более точное приближение к «Божественной пропорции», которую мы рассмотрим ниже, по мере того, как числа становятся больше.

Божественная пропорция

Любое объективное наблюдение, которое мы делаем, должно включать обсуждение пропорции, поскольку именно правило пропорции в исследовании природы заставляет нас наблюдать организованную вселенную и вселенную в хаосе, рациональных и иррациональных числах, гармонии и разногласиях, истине и ложности. .Эти описания — просто пропорциональные эффекты противостояния, присущего всем вещам.

Сила пропорции

Так как же найти эту особую пропорцию? Разделите прямую линию пополам так, чтобы отношение всей длины к большей части было таким же, как отношение большей части к меньшей части.Результат (примерно 1,62 к 1) — золотое сечение.

Используйте золотое сечение для создания приятного визуального баланса

В двух словах,
— это соотношение двух разных чисел. Отношение считается «золотым», если отношение большего числа к меньшему такое же, как отношение между двумя числами, сложенными вместе, и большим числом.Численно золотое сечение составляет примерно 1,618: 1. Но для вашего искусства вам не нужно беспокоиться о точном числе. С помощью линейки и карандаша вы можете быстро разделить весь холст, чтобы создать работоспособную основу для вашей композиции, разработанной с учетом золотого сечения.
Применение божественной пропорции к вашим веб-дизайнам (Также относится к настройке вашего искусства и рисунков)
В этой статье объясняется, что такое Божественная пропорция и что такое Правило третей, и описывается, как вы можете эффективно применить их оба в своих проектах.Конечно, есть много возможностей. Надеюсь, этот пост поможет вам найти свой путь к более эффективному и красивому веб-дизайну или, по крайней мере, предоставит некоторые хорошие отправные точки, на которых вы можете опираться или развиваться дальше.
Правило третей — идеальная пропорция?
Что такое правило третей?
Правило третей — не идеальная пропорция, как золотое сечение или квадрат. На самом деле это вовсе не пропорция.
Он не соответствует определенному соотношению ширины и ширины, например 8 x 10, 9 x 12, 4 x 3.
Вместо этого это метод компоновки изображения или макета путем разделения пространства — независимо от его соотношения сторон — на 9 равных частей: 3 ряда по 3.
Идея состоит в том, что после того, как вы разделите все пространство на трети по горизонтали и вертикали, вы намеренно составите свой дизайн, разместив наиболее важные элементы вдоль этих линий, особенно в одной из четырех центральных точек пересечения.
Правило третей слабо связано с правилом шансов , которое представляет собой универсальный принцип дизайна , который гласит, что использование нечетного количества элементов или повторений визуально более гармонично, чем использование четного числа.Три — первое нечетное или простое число, которое начинает передавать шаблон. Два ничего не делают. Чтобы табурет стал устойчивым, нужны три ножки.
Даже Adobe Photoshop® использует правило третей в своем инструменте обрезки, если вы не измените его настройки по умолчанию.
Составление по правилу третей.
Вы также можете разделить несколько разделов проекта на зоны и разместить контент внутри этих зон. Например, чтобы создать асимметричный баланс, вы можете разместить менее сложное или тяжелое содержимое в одной зоне и менее тяжелое содержимое в остальных зонах.
Например, вы можете разместить наиболее интересный контент в среднем вертикальном разделе, а разделы вверху и внизу оставить более открытыми. Это помогает привлечь внимание зрителя к наиболее важным областям дизайна.
Вы можете начать рисовать со стандартной рамки идеальных пропорций, например, 9 x 12 9 (это соотношение 4: 3), и разделить ее на три части.
Опять же, ключевой вопрос не в том, как вы разделите плоскость изображения (область внутри рамки или края вашего дизайна.Это то, как вы размещаете элементы в дизайне, чтобы направить взгляд туда, куда нужно.
Поскольку это сама по себе не идеальная или даже менее предпочтительная пропорция, а способ создания структуры, на которой вы вешаете свою композицию, существует большая гибкость в том, как вы ее используете, и независимо от того, используете ли вы ее вообще.
Использование правила третей не всегда необходимо. Есть и другие способы разделения пространства. Что делает использование правила третей полезным, так это то, что оно предотвращает создание мертвой точки в вашем дизайне.Размещение основного контента в центре дизайна сделает его статичным и, откровенно говоря, НАУЧНО!
Правило третей полезно тем, что оно не дает вам создать мертвую точку в вашем дизайне.
Будьте внимательны к людям, которые просматривают и используют ваши проекты. Делайте для них что-то интересное. Задействуйте их визуально, а затем концептуально. Композиция делает это возможным. Мертвую точку фокуса легко отбросить, например: «Двигайтесь прямо сейчас! Здесь не на что смотреть.”
Вот как использовать правило третей:
1] Нарисуйте общую систему координат. Это обычно прямоугольный контур или край, определяющий соотношение высоты и ширины вашего дизайна.
2] Нарисуйте две вертикальные линии равного расстояния, чтобы разделить плоскость изображения на равные трети по горизонтали.
3] Нарисуйте две горизонтальные линии через равные промежутки, чтобы разделить вертикальное пространство на равные трети.
Теперь у вас есть пространство дизайна или картинная плоскость, разделенная на 9 равных частей, три в поперечнике и три вниз, которые являются точной пропорцией всего пространства, но меньшего размера.
Есть четыре точки пересечения линий.
4] Составьте свой дизайн или изображение, разместив самые важные элементы на этих пересечениях.
Вы можете асимметрично сбалансировать дизайн, разместив контрастирующие или второстепенные элементы на противоположном по диагонали пересечении.
Использование правила третей создает больше интереса и динамики, чем центрирование объекта. Это предотвращает статический эффект «яблочка», потому что точка фокусировки не расположена в центре пространства.
Как решить пропорцию — Полный курс арифметики
(Евклид, VII.17.)
Мы уже видели, что соотношение будет сохранено, если мы разделим оба члена на одно и то же число.
Пример 5. Заполните эту пропорцию:
6: 7 =? : 28
Решение . 7 умножили на 4, чтобы получить 28. Следовательно, 6 также нужно умножить на 4:
6: 7 = 24: 28.
Чтобы решить эту пропорцию —
6: 7 =? : 28
— можно сказать:
«7 четыре раза превратится в 28. Четыре раза 6 равно 24.»
Все примеры и задачи в этом уроке должны быть простыми мысленными вычислениями.
Пример 6. Решите эту пропорцию:
2: 3 = 12:?
Решение . «2 переходит в 12 шесть раз. Шесть умноженное на 3 — 18.»
2: 3 = 12: 18.
Фактически, рассмотрите эти столбцы, кратные 2 и 3:
2 3
4 6
6 9
8 12
10 15
12 18
14 21
И так далее.
Итак, 2 равно двум третям от 3. (Урок 17.) И каждое кратное 2 равно двум третям от того же кратного 3:
4 составляет две трети от 6.
6 — это две трети от 9.
8 — это две трети от 12.
И так далее. Фактически, это единственные натуральные числа, в которых первое будет составлять две трети второго.
Обратите внимание, что каждая пара имеет общий делитель. И при делении на этот делитель частные в каждом случае равны 2 и 3. Это теорема об общем делителе. 2 и 3 — самые низкие члены. Это наименьшие числа, которые имеют отношение «две трети».«
Пример 7. Назовите три пары чисел, первая из которых составляет три пятых второй.
Решение . Элементарная пара — это 3 и 5. Чтобы создать другие, возьмите одно и то же число, кратное обоим: 6 и 10, 9 и 15, 12 и 20 и так далее.
Пример 8. 27 — это три четверти какого числа?
Решение . Пропорционально:
3: 4 = 27:?
«27 девять умножить на 3.Девять умножить на 4 — это 36 «.
3: 4 = 27: 36
27 — это три четверти от 36.
Только , кратное 3 может быть тремя четвертями другого числа, которое должно быть то же самое , кратное 4.
Так же, как 3 равно 4, любое количество тройок равно количеству четверок.
Пример 9. Решите эту пропорцию:
9: 45 = 2:?
Решение .Здесь надо смотреть прямо:
9 — пятая часть от 45. И 2 — пятая часть от 10.
9:45 = 2: 10.
Пример 10. Общий делитель. Заполните эту пропорцию:
12: 200 =? : 100.
Решение . С другой стороны, мы видим, что 200 было разделенным на на 2. Следовательно, 12 также нужно разделить на 2.
12: 200 = 6: 100
Вместо деления 12 и 200 на 2 можно взять половину.Половина 200 — 100. Половина 12 — 6.
Правило трех
Мы видим, что если мы знаем три члена пропорции, то всегда можем решить четвертое. Это называется Правило трех. Мы можем резюмировать это следующим образом.
1-й: 2-й = 3-й: 4-й.
• Если 4-й член неизвестен, а 3-й член является кратным
или частью 1-го (Пример 6),
, то 4-й член должен быть таким же кратным или частью 2-го.
(Аналогично, если 3-й член неизвестен, а 4-й член
кратен 2-му; Пример 5)
• Если 4-й член неизвестен, а 2-й член является кратным
или является частью 1-го (Пример 9),
, тогда 4-й член должен быть таким же кратным или частью 3-го.
Самое главное, мы применим это правило, чтобы найти, какой процент одно число от другого.
Что касается теоремы об общем делителе , это то, что мы называем симметричной версией теоремы об одном и том же кратном. Для этой пропорции
от 6 до 100, как от 12 до 200,
, в котором 3-й и 4-й члены появляются как двойники 1-го и 2-го, логически эквивалентно этой пропорции,
12 равно 200 как 6 равно 100,
, в котором 3-й и 4-й члены появляются как половинки 1-го и 2-го.
Пример 11. В классе соотношение девочек и мальчиков составляет 3: 4.
Есть 24 мальчика. Сколько там девушек?
Решение . Пропорционально
Девочки: Мальчики = 3: 4 =? : 24.
Обратите внимание, что 24 соответствует Мальчикам.
Итак, 4 переходит в 24 шесть раз. Таким образом, количество девушек в шесть раз больше 3: 18 .
Это еще один способ приблизиться к примеру 7 предыдущего урока. И следующий пример — это еще один способ приблизиться к Примеру 8 этого Урока.
Пример 12. Целое равно сумме частей. В классе количество девочек составляет 75% от количества мальчиков. Всего обучается 35 студентов. Сколько девочек и мальчиков?
Решение . Сказать, что девочки составляют 75% — три четверти — мальчиков,
означает, что соотношение девочек и мальчиков составляет 3: 4.Но это означает, что 3 из каждых 7 учеников — девочки (3 + 4 = 7), а 4 из каждых 7 — мальчики.
Следовательно, формируем пропорцию:
девочек: общее количество студентов =
3: 7 =? : 35.
Поскольку 35 равно 5 × 7, пропущенный член равен 5 × 3 = 15.
Всего 15 девушек. Итак, есть 20 мальчиков.
На этом этапе, пожалуйста, «переверните» страницу и выполните несколько задач .
или
Введение | Главная | Содержание
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]

золотое сечение | Примеры, определение и факты
Золотое сечение , также известное как золотое сечение , золотая середина или божественная пропорция , в математике иррациональное число (1 + квадратный корень из √5) / 2 , часто обозначается греческой буквой ϕ или τ, что приблизительно равно 1.618. Это отношение отрезка линии, разрезанного на две части разной длины, при котором отношение всего сегмента к таковому более длинного сегмента равно отношению более длинного сегмента к более короткому. Происхождение этого числа можно проследить до Евклида, который упоминает его как «крайнее и среднее соотношение» в Elements . С точки зрения современной алгебры, если длина более короткого сегмента равна одной единице, а длина более длинного сегмента — x единиц, возникает уравнение ( x + 1) / x = x / 1; это может быть преобразовано в квадратное уравнение x ² — x — 1 = 0, для которого положительным решением будет x = (1 + квадратный корень из √5) / 2, золотое сечение.
Древние греки признавали это свойство «разделения» или «разделения на части», фраза, которая в конечном итоге была сокращена до просто «раздел». Прошло более 2000 лет, когда и «сечение», и «сечение» были названы «золотыми» немецким математиком Мартином Омом в 1835 году. Греки также заметили, что золотое сечение обеспечивает наиболее эстетичную пропорцию сторон прямоугольника. , понятие, которое было усилено в эпоху Возрождения, например, благодаря работе итальянского эрудита Леонардо да Винчи и публикации De divina пропорционально (1509; Божественная пропорция ), написанной итальянским математиком Лукой Пачоли и проиллюстрированной Леонардо.
Витрувианский человек, рисунок Леонардо да Винчи ( ок. 1509), иллюстрирующий пропорциональный канон, установленный классическим римским архитектором Витрувием; в Академии изящных искусств Венеции.
Foto Marburg / Art Resource, New York
Золотое сечение встречается во многих математических контекстах. Его геометрически можно построить с помощью линейки и циркуля, и это происходит при исследовании архимедовых и платоновых тел. Это предел отношений последовательных членов последовательности чисел Фибоначчи 1, 1, 2, 3, 5, 8, 13,…, в котором каждый член после второго является суммой двух предыдущих, а также значение самой основной из непрерывных дробей, а именно 1 + 1 / (1 + 1 / (1 + 1 / (1 + ⋯.
В современной математике золотое сечение встречается при описании фракталов, фигур, которые проявляют самоподобие и играют важную роль в изучении хаоса и динамических систем.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
No related posts.

Пропорции математика. Пропорция – это равенство двух отношений. Соотношение.

Пропорция

Пропорции

Пропорции

Отношения и пропорции в математике

Два равных отношения образуют пропорцию

Произведение средних членов пропорции

Пропорции: крайние и средние члены, главное свойство

Члены пропорции: крайние и средние

Главное свойство пропорции

Нахождение неизвестного члена пропорции

Золотое сечение как объяснение пропорций красоты

Геометрическая Пропорция

, золотое сечение и правило третей

Пропорция, золотое сечение и правило третей

Золотое сечение

Правило третей

правил пропорции | ЭТО

От греков к золотому прямоугольнику

Понимание системы пропорций

История

Правила или рекомендации?

Внимательно читаете: мифы и заблуждения

Золотой прямоугольник: еще один миф

Наконец, вывод (своего рода)

Банкноты

Правило 3: прямое и обратное

Какое правило трех?

Прямое правило 3

Обратное правило 3

Пошаговые уроки рисования для мультфильмов и иллюстраций

Правило третей — идеальная пропорция?

Что такое правило третей?

Составление по правилу третей.

Правило третей полезно тем, что оно не дает вам создать мертвую точку в вашем дизайне.

Как решить пропорцию — Полный курс арифметики

золотое сечение | Примеры, определение и факты

Добавить комментарий Отменить ответ