Функция x от y – Что означает в математике запись y=f(x). Видеоурок. Алгебра 7 Класс

Что означает в математике запись y=f(x). Видеоурок. Алгебра 7 Класс

Итак, в данном уроке мы должны разобраться, что означает в математике запись . Во-первых, она говорит о том, что задана независимая переменная х, иначе говоря, аргумент. Например, утром ученик вышел из дома в школу, пока он идет, время идет независимо от него, время – пример независимой переменной.

Кроме того, данная запись задает зависимую переменную – функцию. Возьмем тот же пример, когда ученик идет из дома в школу, расстояние в этом случае будет зависимой переменной, так как через пять минут он пройдет, например, 200 метров, а через час километр, расстояние зависит от времени.

  – это закон соответствия, по которому каждому значению х – независимой переменной, ставится в соответствие единственное значение у – зависимой переменной. Условие единственности значения функции для каждого значения аргумента объясним все на том же примере. В некоторый момент времени ученик находится на расстоянии 500 метров от дома, и в этот же момент он не может быть еще и на расстоянии километра, то есть в один момент времени он может быть только в одном месте. Итак, реальные процессы таковы, что накладывают на функции упомянутое ограничение

Вспомним известные нам функции:

1) , функция равна константе. Для нашего примера это можно описать тем, что ученик находится в школе, то есть время идет, а расстояние от дома не меняется.

2) – прямая пропорциональность. Мы помним, что в зависимости от значения k функция может возрастать или убывать. Вспомним графики первых двух функций, для примера построим графики функций , , :

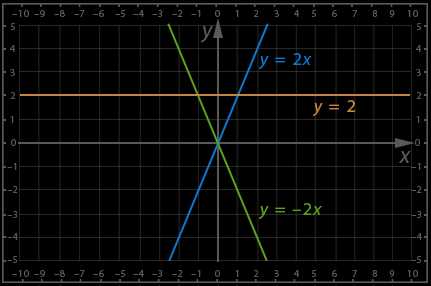
Рис. 1.

Напомним, что любой график прямой пропорциональности проходит через начало координат, при этом если k положительное, то функция возрастает, а если k отрицательное – функция будет убывать

3)   — линейная функция, она задается двумя параметрами – k и m. Возьмем пример: , построим график, напомним, что для этого достаточно взять две точки – составим таблицу:

х	0	-0,5
у	1	0

,

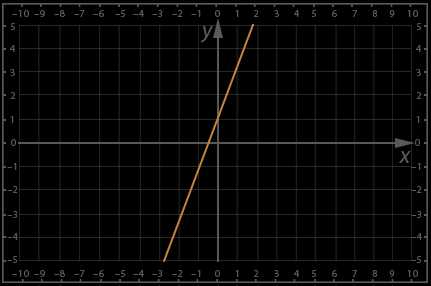
Рис. 2.

Напомним, что параметр m – это ордината точки пересечения графика с осью у, а параметр k как и в случае прямой пропорциональности отвечает за то, будет ли функция возрастать или убывать.

4)  – график данной функции парабола, напомним ее вид:

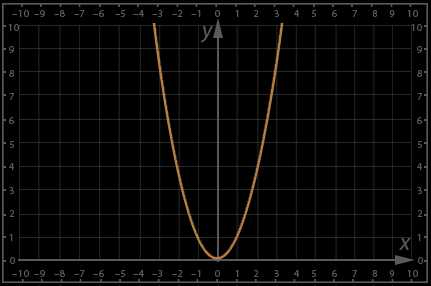
Рис. 3.

Отметим, что переменные можно называть как угодно, например вместо  можно написать , от этого вид функциональной зависимости не изменится.

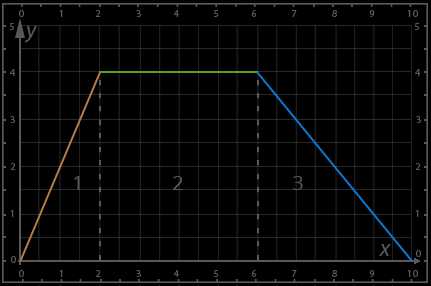
Рис. 4.

Вернемся к нашему примеру, где ученик идет в школу, находится в школе и возвращается домой. Расстояние будем откладывать по оси у, а время по оси х.

На участке 1 показано, как ученик идет в школу, расстояние его от дома увеличивается до конкретной точки – в этот момент он пришел в школу. Далее на участке 2 ученик находится в школе, расстояние его от дома остается неизменным. После этого на участке 3 он возвращается домой, причем скорость его меньше, чем когда он шел в школу, так как значение функции изменяется медленнее. В какой-то момент расстояние становится равным нулю – это означает, что ученик пришел домой.

Данный пример говорит нам о том, что функция может на разных участках быть описана по-разному.

Рассмотрим примеры:

Пример 1:

;

1) вычислить значение функции при , , , ,

2) построить график функции;

3) прочесть график и определить свойства данной функции.

Начнем с построения графика:

Для первого интервала, где  составим таблицу для нахождения двух точек:

Для второго интервала, где, также составим таблицу:

Итак, построим график:

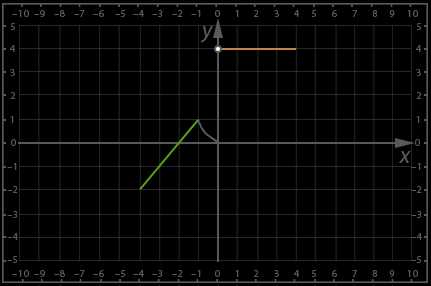
Рис. 5.

Теперь вычислим необходимые значения функции: , подставляем значение в функцию , так как  принадлежит интервалу . В эту же функцию подставляем и значение , . Значения  и   подставляем в функцию , так как эти значения х принадлежат интервалу , , ; значение  подставляем в функцию , так как оно входит в интервал , получаем

Нам осталось прочесть график. Итак, если аргумент возрастает , функция возрастает . Когда аргумент возрастает , функция убывает , наконец когда аргумент возрастает  функция остается неизменной и равна четырем. Область определения функции: , то есть данная функция существует только на этом интервале, и если нам нужно было бы вычислить значение в точке , мы не смогли бы этого сделать, так как в этой точке она не существует – не определена. Минимальное значение функции есть, и оно равно -2: ; y=0 при двух значениях аргумента:  и . Функция больше нуля при следующих значениях аргумента: 

 и .

Функция принимает отрицательные значения на следующем отрезке: .

Вывод: в данном уроке мы объяснили смысл записи  и провели обзор известных нам графиков функций. Мы узнали, что функция может быть задана на разных интервалах по-разному и рассмотрели пример подобного задания, в котором выполнили различные типовые задачи.

 

Список рекомендованной литературы

1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.

2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ 

3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.

 

Рекомендованные ссылки на ресурсы интернет

1. Портал Естественных Наук (Источник).

2. Интернет-портал Alexlarin.net  (Источник).

 

Рекомендованное домашнее задание

Задание 1: Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7, № 799, ст.167;

Задание 2: Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7, № 806, ст.168;

Задание 3: Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7, № 807, ст.168;

interneturok.ru

Число e. Функция y=e^x, ее свойства, график, дифференцирование

Напомним, что показательной называется функция вида . График выглядит так:

Рис. 1. График показательной функции

График функции возрастает, если ; если основание  лежит в пределах то функция убывает.

Вспомним основные свойства.

1.      . x может принимать любые действительные значения;

2.       может принимать любые положительные значения;

3.       Графики всех функций при любом значении  проходят через эту точку;

4.      Функция возрастает, если ;

5.      Функция убывает, если .

Итак, мы вспомнили, что такое показательная функция и каковы ее основные свойства.

Число

Рассмотрим две конкретные показательные функции с основанием

Вот график функции :

Рис. 2. График функции

Вот график функции :

Рис. 3. График функции

В точке , если проведем касательную к одному и второму графику, обнаружим, что касательная к первому графику наклонена к оси примерно на (меньше ).

Во втором случае касательная наклонена к оси примерно на (больше ).

Предполагаем, и вообще это доказано, что существует между основаниями  такое число , что график  имеет касательную в точке , которая наклонена к оси ровно на .

Рис. 4. Касательная к графику функции

Итак, в первом случае касательная наклонена под углом меньше , во втором случае касательная наклонена под углом больше . И, оказывается, есть такое число , что касательная в точке  наклонена к оси  под углом ровно  Это число , во-первых, расположено  и, во-вторых, иррационально. Вот выписано несколько десятичных знаков этого числа: . Таким образом, мы ввели очень важное число

Теперь рассмотрим свойства показательной функции с основанием

 

График функции выглядит так:

Рис. 5. График функции

Свойства аналогичны свойствам функции с основанием:

;

Функция возрастает;

Функция не ограничена сверху, но ограничена снизу;

Не существует ни наибольшего  ни наименьшего  значений;

Функция непрерывна;

Принимает все значения, когда ;

Функция выпукла вниз;

Функция дифференцируема. Что это значит практически? Что касательную к экспоненте можно провести в любой точке.

Таковы свойства данной функции.

Поговорим о производной этой функции. Что мы на данный момент о ней знаем и без доказательства понимаем?

Мы говорили, что функция  дифференцируема. Это значит, что касательная в любой точке существует, то есть производная существует в любой точке. Но как ее найти? Мы знаем, что производная в точке Доказан важный факт:

 При любом действительном значении  То есть отсюда видна особенность числа . Производная, то есть скорость роста функции в точке  равна значению функции в этой же точке. Это основная формула, которая позволит нам дифференцировать все показательные функции.

Теперь рассмотрим некоторые типовые задачи на производную функции

Пример 1.

Дано:

Найти: Производную

Решение.

Вот основная формула , мы умеем дифференцировать сложную функцию.

Ответ:=

Пример 2.

Дано:

Найти: Производную

Решение.

По тем же правилам, по которым мы дифференцируем все функции, продифференцируем и эту.

Ответ:=

Итак, зная основную формулу , мы можем решать примеры на нахождение производных.

Следующая стандартная задача на касательную.

Пример 3.

Дано:, абсцисса точки касания;

Найти: Уравнение касательной к данной кривой с абсциссой в .

Решение.

Вспоминаем уравнение касательной и стандартную методику ее построения:

Какие действия нужно сделать, чтобы составить уравнение касательной?

Найти координаты точки касания:

Итак, точка с координатами – это точка касания (рис. 6).

Рис. 6. Точка касания

Найти производную в любой точке

Найти конкретное значение производной в точке :

У нас все есть, чтобы заполнить уравнение касательной.

Заполняем, получаем:

Ответ:

Небольшой анализ:

Тангенс угла наклона

 

Ордината пересечения точки с осью :

Задача решена.

Пример 4.

Найти наименьшее значение функции.

Решение.

Имеем производную произведения:

Приравниваем производную к нулю и убеждаемся, что , так как по свойству показательной функции всегда больше нуля.

Итак, имеем единственную критическую точку (рис. 7).

Рис. 7. Критическая точка

Если , то и функция убывает. Если , то .

Мы уже говорили, что  – единственная критическая точка. Посчитаем значение функции в ней:

Рис. 8. Точка наименьшего значения функции

И получаем ответ: наименьшее значение функции достигается в точке . Рис. 8.

Ответ:

Итак, мы познакомились с числом , показательной функцией с основанием . На следующем уроке мы рассмотрим логарифмическую функцию с основанием .

 

Список литературы

1. Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Uztest.ru (Источник).
2. Schoolife.ru (Источник).
3. Terver.ru (Источник).

 

Домашнее задание

1. Найти производные функция в указанных точках:

а) ;

б) .

2. Найдите тангенс угла наклона касательной к графику функции  в точке с абсциссой :

а) ;

б) .

3. Алгебра и начала анализа, Мордкович А.Г.: № 1616, 1618, 1621, 1624.

 

interneturok.ru

Что означает запись y=y(x) и чем отличается от y=f(x)?

Запись y=y(x) попросту заменяет фразу «игрек зависит от икс», без конкретизации — как зависит. Запись y=f(x) помимо указанного смысла, довольно часто имеет цель уточнения: то есть зависит так, как определено конкретной ф-цией f(x).

это одно и тоже

это условная запись означающая что Y есть функция от переменной X. Т. е. под f(x) подразумевается какое то выражение с переменной x например y = 1/x + x Есть еще такая запись F=f(x), но это уже дифференциальных уравнениях используется.

y=y(x) и чем отличается от y=f(x)? Значится, это функции. Функции, которые определяют обрасть определения, значени, графики. Эти две функции имеют разный вид, но общее значение. В учебниках и условиях чаще всего применяется формула функции y=f(x), что означает перменную функции от перменной x. Тоесть, f(x), — это аргумент, а y — зависимая перменной. Всё это математическим языком, но а если по нашенски то игрик — это первая частьформулы, а ф от икс (именно так читается) вторая часть. Вобщем и первая и вторая это одно и тоже. Только F = Y Y= F В первой формуле y=y(x) — вместо F CNJBN Y, что является одним итем занчением!

touch.otvet.mail.ru

По графику функции найти x по y

Мы уже рассмотрели нахождение значения аргумента по заданному значению функции.

Теперь выясним, как по графику функции найти x по y.

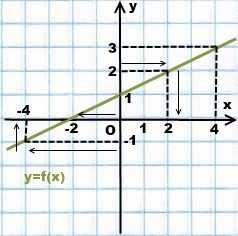
Рисунок 1

1) Пользуясь графиком линейной функции, изображенной на рисунке 1, найдите значение аргумента, если значение функции равно —1; 2; 0; 3.

Решение:

Аргумент — это x, функция — y.

Найти значение аргумента по значению функции — значит, по данному значению y найти x.

Начнём с y= -1. На оси Oy найдём точку с ординатой y= -1. Чтобы найти значение x, надо из точки на оси Oy попасть на график. Для этого нужно пойти либо влево, либо вправо. От точки y= -1 график находится слева, поэтому идём влево. Достигнув точки на графике, идём к оси Ox (в данном случае — вверх). Попадаем в точку с абсциссой x= -4. (Стрелочки помогают увидеть путь).

Следовательно, при y= -1 x= -4.

Если y=2, чтобы попасть из точки на оси Oy с ординатой y=2 на график, следует двигаться вправо. Идём вправо до графика. Достигнув точки графика, в которой y=2, идём вниз, до оси Ox. Попадаем в точку с абсциссой x=2.

Записываем: при y=2  x=2.

Если y=0, чтобы попасть на график функции, движемся влево. Дальше ни вверх, ни вниз двигаться не нужно, поскольку уже находимся на графике, в точке с абсциссой x= -2.

Записываем: при y=0  x= -2.

При y=3 идем вправо до графика, затем — вниз и получаем x=4.

Пишем: при y=3  x=4.

2) На рисунке 2 изображен график функции y=f(x).

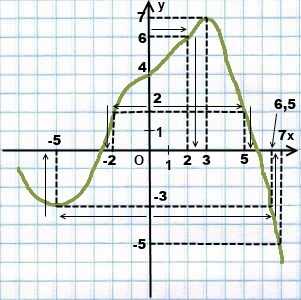
Рисунок 2

Пользуясь графиком, найдите значение аргумента, если значение функции равно 6; -3; 2; 4; -5; 7.

Решение:

Чтобы найти значение аргумента по заданному значению функции y= 6, от точки на оси Oy с ординатой y=6 идем вправо до пересечения с графиком функции. Достигнув точки на графике, идём вниз, к оси Ox. На оси абсцисс попали в точку с абсциссой x=2.

Записываем: при y=6  x=2.

При y= -3 график есть и слева, и справа от оси Oy. Идём влево и вверх, получаем x= -5. Идём вправо и вверх, получаем x=6,5.

Записываем: при y= -3 x= -5 и x=6,5.

Аналогично, при y=2 x= -2 и x=5.

Точка с ординатой  y=4 лежит на графике, идти никуда не надо, x=0.

При y= -5 идём вправо и вверх, приходим в точку с абсциссой x=7.

Пишем: при y= -5  x=7.

При y=7 идём вправо и вниз, получаем x=3.

www.algebraclass.ru

ее график и свойства при k0

 

Рассмотрим функцию y=k/y. Графиком этой функции является линия, называемая в математике гиперболой. Общий вид гиперболы, представлен на рисунке ниже. (На графике представлена функция y равно k разделить на x, у которой k равно единице.)

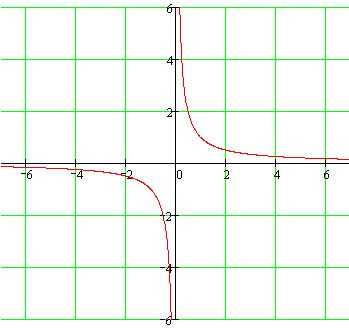
Видно, что график состоит из двух частей. Эти части называют ветвями гиперболы. Стоит отметить также, что каждая ветвь гиперболы подходит в одном из направлений все ближе и ближе к осям координат. Оси координат в таком случае называют асимптотами.

Вообще любые прямые линии, к которым бесконечно приближается график функции, но не достигает их, называются асимптотами. У гиперболы, как и у параболы, есть оси симметрии. Для гиперболы, представленной на рисунке выше, это прямая y=x.

Теперь разберемся с двумя общими случаями гипербол. Графиком функции y = k/x, при k ≠0, будет являться гипербола, ветви которой расположены либо в первом и третьем координатных углах, при k>0, либо во втором и четвертом координатных углах, при k<0.

Основные свойства функции y = k/x, при k>0

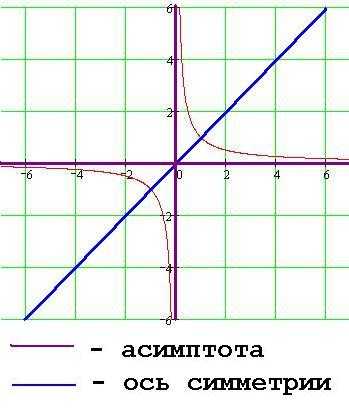
График функции y = k/x, при k>0

1. Точка (0;0) центр симметрии гиперболы.

2. Оси координат – асимптоты гиперболы.

3. Прямая y=x ось симметрии гиперболы.

4. Область определения функции все х, кроме х=0.

5. y>0 при x>0; y6. Функция убывает как на промежутке (-∞;0), так и на промежутке (0;+∞).

7. Функция не ограничена ни снизу, ни сверху.

8. У функции нет ни наибольшего, ни наименьшего значений.

9. Функция непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.

10. Область значений функции два открытых промежутка (-∞;0) и (0;+∞).

Основные свойства функции y = k/x, при k<0

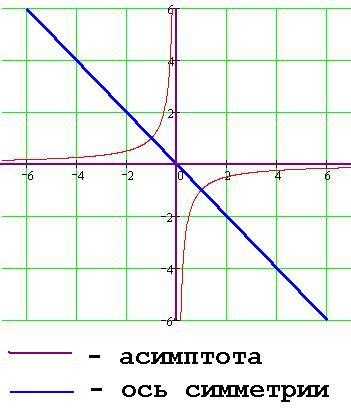
График функции y = k/x, при k<0

1. Точка (0;0) центр симметрии гиперболы.

2. Оси координат – асимптоты гиперболы.

3. Прямая y=-x ось симметрии гиперболы.

4. Область определения функции все х, кроме х=0.

5. y>0 при x0.

6. Функция возрастает как на промежутке (-∞;0), так и на промежутке (0;+∞).

7. Функция не ограничена ни снизу, ни сверху.

8. У функции нет ни наибольшего, ни наименьшего значений.

9. Функция непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.

10. Область значений функции два открытых промежутка (-∞;0) и (0;+∞).

Нужна помощь в учебе?

Предыдущая тема: Преобразование рациональных выражений: способы преобразований и примеры
Следующая тема:&nbsp&nbsp&nbspРациональные числа: определение, сумма, разность, умножение, деление

Все неприличные комментарии будут удаляться.

www.nado5.ru

Линейная функция

•Линейной функцией называется функция вида y=kx+b, где x-независимая переменная, k и b-любые числа.
•Графиком линейной функции является прямая.

1.Чтобы постороить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.

Например, чтобы построить график функции y= &frac13; x+2, удобно взять x=0 и x=3, тогда ординаты эти точек будут равны y=2 и y=3. Получим точки А(0;2) и В(3;3). Соединим их и получим график функции y= &frac13; x+2:

2. В формуле y=kx+b число k называется коэффицентом пропорциональности:
• если k>0, то функция y=kx+b возрастает
• если k

Коэффициент b показывает смещение графика функции вдоль оси OY:
• если b>0, то график функции y=kx+b получается из графика функцииy=kx сдвигом на b единиц вверх вдоль оси OY
• если b

На рисунке ниже изображены графики функций y=2x+3; y= ½ x+3; y=x+3

Заметим, что во всех этих функциях коэффициент k больше нуля, и функции являются возрастающими. Причем, чем больше значение k, тем больше угол наклона прямой к положительному направлению оси OX.

Во всех функциях b=3 – и мы видим, что все графики пересекают ось OY в точке (0;3)

Теперь рассмотрим графики функций y=-2x+3; y=- ½ x+3; y=-x+3

На этот раз во всех функциях коэффициент k меньше нуля, и функции убывают. Коэффициент b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)

Рассмотрим графики функций y=2x+3; y=2x; y=2x-3

Теперь во всех уравнениях функций коэффициенты k равны 2. И мы получили три параллельные прямые.

Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
• График функции y=2x+3 (b=3) пересекает ось OY в точке (0;3)
• График функции y=2x (b=0) пересекает ось OY в точке (0;0) — начале координат.
• График функции y=2x-3 (b=-3) пересекает ось OY в точке (0;-3)

Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции y=kx+b.
Если k0, то график функции y=kx+b имеет вид:

Если k>0 и b>0, то график функции y=kx+b имеет вид:

Если k>0 и b, то график функции y=kx+b имеет вид:

Если k, то график функции y=kx+b имеет вид:

Если k=0, то функция y=kx+b превращается в функцию y=b и ее график имеет вид:

Ординаты всех точек графика функции y=b равны b Если b=0, то график функции y=kx (прямая пропорциональность) проходит через начало координат:

3.Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a.

Например, график уравнения x=3 выглядит так:
Внимание! Уравнение x=a не является функцией, так одному значению аргумента соотвутствуют разные значения функции, что не соответствует определению функции.

4.Условие параллельности двух прямых:

График функции y=k₁x+b₁ параллелен графику функции y=k₂x+b₂, если k₁=k₂

5.Условие перепендикулярности двух прямых:

График функции y=k₁x+b₁ перепендикулярен графику функции y=k₂x+b₂, если k₁*k₂=-1 или k₁=-1/k₂

6.Точки пересечения графика функции y=kx+b с осями координат.

С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).

С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда x=-b/k. То есть точка пересечения с осью OX имеет координаты (-b/k;0):

www.tofmal.ru

3.Линейная функция вида y = kx + b

Линейной функцией называется функция вида y = kx + b, заданная на множестве всех действительных чисел. Здесь k – угловой коэффициент (действительное число), b – свободный член (действительное число), x – независимая переменная.

В частном случае, если k = 0, получим постоянную функцию y = b, график которой есть прямая, параллельная оси Ox, проходящая через точку с координатами (0; b).

Если b = 0, то получим функцию y = kx, которая является прямой пропорциональностью.

Геометрический смысл коэффициента b – длина отрезка, который отсекает прямая по оси Oy, считая от начала координат.

Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки.

Свойства линейной функции:

1) Область определения линейной функции есть вся вещественная ось;

2) Если k ≠ 0, то область значений линейной функции есть вся вещественная ось. Если k = 0, то область значений линейной функции состоит из числа b;

3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b.

a) b ≠ 0, k = 0, следовательно, y = b – четная;

b) b = 0, k ≠ 0, следовательно y = kx – нечетная;

c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида;

d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция.

4) Свойством периодичности линейная функция не обладает;

5) Точки пересечения с осями координат:

Ox:  y = kx + b = 0, x = -b/k, следовательно (-b/k; 0) – точка пересечения с осью абсцисс.

Oy:  y = 0k + b = b, следовательно (0; b) – точка пересечения с осью ординат.

Замечание.Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х. Если b ≠ 0 и k = 0, то функция y = b не обращается в ноль ни при каких значениях переменной х.

6) Промежутки знакопостоянства зависят от коэффициента k.

a) k > 0;  kx + b > 0, kx > -b, x > -b/k.

y = kx + b – положительна при x  из (-b/k; +∞),

y = kx + b – отрицательна при x  из (-∞; -b/k).

b) k < 0; kx + b < 0, kx < -b, x < -b/k.

y = kx + b – положительна при x  из (-∞; -b/k),

y = kx + b – отрицательна при x  из (-b/k; +∞).

c) k = 0, b > 0; y = kx + b положительна на всей области определения,

k = 0, b < 0; y = kx + b отрицательна на всей области определения.

7) Промежутки монотонности линейной функции зависят от коэффициента k.

k > 0, следовательно y = kx + b возрастает на всей области определения,

k < 0, следовательно y = kx + b убывает на всей области определения.

8) Графиком линейной функции является прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов

www.sites.google.com

No related posts.