Мнемонические приёмы запоминания при изучении тригонометрии
Мнемонические приёмы запоминания при изучении тригонометрии
Для многих ребят в школе тригонометрия – один из самых трудных, непонятных разделов математики. Уже с первых уроков идёт отторжение и нежелание изучать её, вникать в глубины, запоминать правила, значения функций. А как запомнить множество формул? На помощь пришла мнемотехника. Стала сама придумывать мнемотехнические правила, какие-то правила предложили ребята, что-то взяла из работ своих коллег.
8 класс
Определение тригонометрических функций острого угла прямоугольного треугольника
Для запоминания определений синуса и косинуса предлагаю закон «равновесия». Согласно этому закону к короткому слову (синус) надо соотнести длинное слово (противолежащий), к длинному слову (косинус) – короткое слово (прилежащий).
Синус противолежащий
К осинус прилежащий
Через некоторое время пришло озарение по запоминанию правила про тангенс.
Именно предлог «про» помог. И сейчас, когда я прошу напомнить определение про тангенс, специально делаю упор на предлог про и ребята хором отвечают – это отношение противолежащего катета к прилежащему. Назвали мы данный способ – правило «про».
9 класс
Определение синуса и косинуса угла
Для облегчения запоминания, что косинус угла – это абсцисса точки, а синус угла – это ордината точки единичной окружности используем закон соответствия. Предлагаю ребятам посмотреть на начальные буквы функций (косинус, синус), начальные буквы координат (абсцисса, ордината) и записать их в алфавитном порядке: в первом столбце – функции, во втором – координаты.
К осинус абсцисса (cos α x)
Синус ордината (sin α y)
Значения функций
Значения синуса и косинуса для углов 0, 30, 45, 60, 90 легко вычислить с помощью левой руки.
Для этого:
Пронумеруем пальцы от большого до мизинца, счет начинаем с нуля (рис. 1).
Затем из каждого числа извлечем корень и разделим на 2. Где возможно подсчитаем значения (рис. 2).
Д
Рис. 1
ля функции синус отсчет углов идет от большого пальца к мизинцу, для косинуса – от мизинца к большому, то есть:
Для sin Для cos
большой № 0 – соответствует 0, большой № 0 – соответствует 90,
указательный № 1 – соответствует 30, указательный № 1 – соответствует 60,
средний № 2 – соответствует 45, средний № 2 – соответствует 45,
безымянный № 3 – соответствует 60, безымянный № 3 – соответствует 30,
мизинец № 4 – соответствует 90. мизинец № 4 – соответствует 0.
Рис. 2
Рис. 1
Ребята, которые используют этот метод, отсчитывают угол в нужном направлении, смотрят на номер пальца и говорят значение функции.
Угол | № пальца | Значение |
0 | 0 | sin 0 = |
30 | 1 | sin 30 = |
45 | 2 | sin 45 = |
60 | 3 | sin 60 = |
90 | 4 | sin 90 = |
Угол | № пальца | Значение |
90 | 0 | cos 90 = |
60 | 1 | cos 60 = |
45 | 2 | cos 45 = |
30 | 3 | cos 30 = |
0 | 4 | cos 0 = |
10 класс
Знаки функций
Учащиеся прекрасно запоминают, что у тангенса и котангенса знаки располагаются крест-накрест, но забывают, у какой функции (синуса или косинуса), знаки расположены горизонтально, а у какой – вертикально.
В этом случае поможет следующее правило: произносить слова «синус» и «косинус» нужно нараспев, выделяя ударную гласную и фиксируя при этом, в каком направлении вытягивается рот. При произнесении слова «синус» ударная гласная «и» вытягивает рот в направлении «», значит, у синуса знаки расположены горизонтально. Аналогично, при произнесении слова «косинус», ударная гласная «о» вытягивает рот в направлении «↕», значит, у косинуса знаки расположены вертикально.
Четность и нечетность тригонометрических функций
Приём сладкоежек: последние три функции: синус, тангенс и котангенс – это друзья, они конфетки (знак «минус») не едят и как капризные детки их выплевывают, а вот Косинус, – сладкоежка и конфету съедает.
Формулы приведения (Лошадиное правило)
В старые добрые времена жил рассеянный математик, который при поиске ответа менять или не менять название функции (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс), смотрел на свою умную лошадь.
Она кивала головой вдоль той оси координат, которой принадлежала точка, соответствующая первому слагаемому аргумента π/2 ± α (3π/2 ± α) или π ± α (2π ± α). Если лошадь кивала головой вдоль оси ОУ (вертикального диаметра окружности), то математик считал, что получен ответ «да, менять», если вдоль оси ОХ (горизонтального диаметра окружности), то «нет, не менять».
Затем оставалось, только определить знак функции – это зависело от того в какой четверти располагалась это точка и знака тригонометрической функции в той или иной четверти.
Основное тригонометрическое тождество
Тождество можно ребятам преподнести в виде стишка.
Синус квадрат очень рад
К нему едет брат – косинус квадрат.
Когда встретятся они, окружность удивится:
Выйдет целая семья, то есть единица.
Тригонометрические формулы
Много трудностей обычно вызывает запоминание тригонометрических формул, и далеко не все ученики могут тут же вывести забытую формулу.
Поэтому можно рекомендовать запомнить, что sinx – функция «хорошая», а cosx – «плохая». Это означает, что для синуса в соответствующих формулах знак сохраняется, а для косинуса – меняется. Кроме того, функция синус – объединяющая функция, а косинус – разделяющая функция.
Формулы сложения
Для запоминания формул сложения для синуса и косинуса мы применяем правило сенокоса (sin – сено, cos – коси) :
Правило для синуса – сено коси, коси сено:
sin(x + y)=sinxcosy + cosxsiny
sin(x – y)=sinxcosy – cosxsiny
При записи формул надо вспомнить, что sinx – функция «хорошая» (знак сохраняется, то есть справа такой же знак, как и слева), также функция синус – объединяющая функция (справа стоят смешанные произведения синуса и косинуса).
Правило для косинуса – коси коси, сено сено:
cos(x + y)= cosxcosy – sinxsiny
cos(x – y)= cosxcosy + sinxsiny
При записи формул надо вспомнить, что cosx – функция «плохая» (знак справа меняется на противоположный), также функция косинус – разделяющая функция (справа произведения одноименных функций).
Формулы понижения степени
Важно понять структуру этих формул, в частности, такой момент – «степень понижается, а угол становится в два раза больше». Эти формулы очень похожи друг на друга, поэтому для лучшего их запоминания следует применять правило: «Единица минус – дает синус, а единица плюс – дает косинус».
Формулы корней простейших тригонометрических уравнений
Вспоминаем, что друзья – это Синус, Тангенс и Котангенс. У них во всех формулах стоит πn. А у единственной сладкоежки, у косинуса стоит 2πn. Ключевое слово – два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там – два. Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет 2πn.. А ещё наоборот бывает. Пропустит ученик знак ±, доберётся до конца, напишет правильно 2πn, да и спохватится.
Впереди-то два знака! Вернётся ученик к началу, да ошибку-то и исправит! Вот так.
Что такое закон синуса и косинуса? – Обзоры Вики
Чтобы решить треугольник, нужно найти длины каждой из его сторон и всех его углов. Правило синусов используется, когда нам дано либо а) два угла и одна сторона, или б) две стороны и угол, не заключенный между ними. Правило косинусов используется, когда нам даны либо а) три стороны, либо б) две стороны и угол между ними.
Отсюда, что такое правило синуса и косинуса? Правило синусов можно использовать, чтобы найти угол по 3 сторонам и углу, или по 3 углам и стороне найти угол. Чай правило косинуса можно найти сторону с 2-х сторон и прилежащий угол, или угол с 3-х сторон.
Является ли Аса законом синусов или косинусов? Поэтому три угла также называются А, В и С. Закон косинусы утверждает, что: … Примером ASA является ситуация, когда вам дана мера углов A и C и длина стороны b. Примером SSA является случай, когда вам даны стороны с, а и угол С.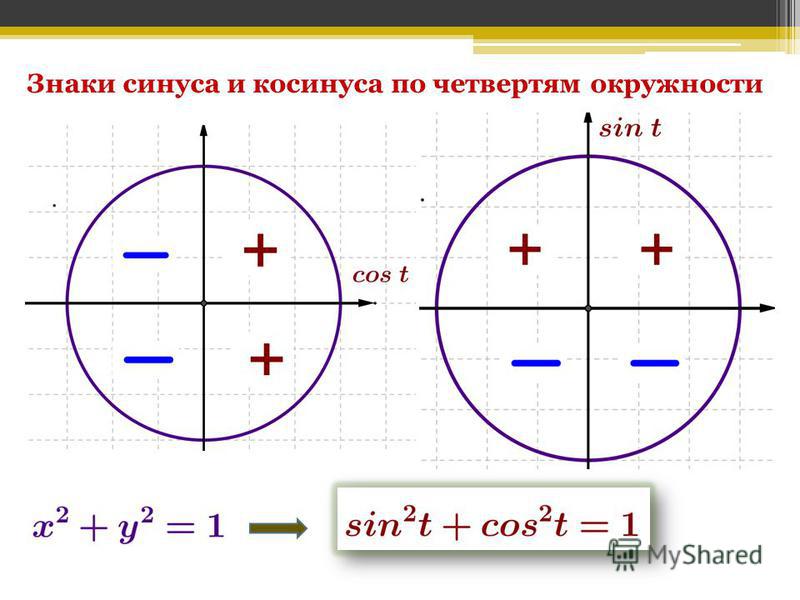
Дополнительно Является ли Аса законом синусов? Закон синусов – это соотношение между сторонами и углами непрямоугольных (косоугольных) треугольников. … Чтобы использовать закон синусов, вам нужно знать либо два угла, либо одну сторону треугольник (AAS или ASA) или две стороны и угол, противолежащий одной из них (SSA).
Какой закон вы используете для AAS? «ААС» — это когда мы знаем два угла и одну сторону (которая не лежит между углами). тогда Закон синуса найти каждую из двух других сторон.
Что такое правило синусов в математике?
Правило синусов гласит, что если a, b и c — длины сторон треугольника, а A, B и C — углы в треугольнике; с A напротив a и т. д., тогда asinA = bsinB = csinC.
Как вы помните правило синусов и косинусов? Отношения синуса, косинуса и тангенса в прямоугольном треугольнике можно запомнить, представив их в виде строк букв, например SOH-CAH-TOA на английском языке: Синус = Противоположный ÷ Гипотенуза. Косинус = Смежный ÷ Гипотенуза.
Что такое правило косинусов в математике? Утверждение: Правило косинусов гласит, что квадрат любой стороны треугольника равен разности между суммой квадратов двух других сторон и удвоенным произведением двух других сторон на косинус угла, противолежащего первой стороне.
Как решить закон косинусов?
Также Как найти закон косинусов? Закон косинусов гласит: c2 = a2 + b2−2ab cosC . Это похоже на теорему Пифагора, за исключением третьего члена, и если C — прямой угол, третий член равен 0, потому что косинус 90 ° равен 0, и мы получаем теорему Пифагора.
Что такое AAS в математике?
ААС (угол-угол-сторона) Два угла и не включенная сторона совпадают.
Закон косинусов SSA? Закон косинусов хорошо работает для решения треугольников, когда у вас есть две стороны и угол, но угол не находится между двумя сторонами.
… Кроме того, чтобы решить треугольник, который является SSA (илисторона-угол), используя закон косинусов, вы должны быть осторожны, чтобы найти правильный треугольник — есть две возможности.
Как вы используете закон косинусов ASA?
ASA: Если известны два угла и сторона треугольника, сначала вычтите эти угловые измерения из 180°, чтобы найти третий угол. Затем используйте закон синусов, чтобы установить пропорции, чтобы найти длины двух недостающих сторон.
Как решить закон косинусов СС?
Зачем нужен закон синусов? Закон синусов можно используется для вычисления оставшихся сторон треугольника, когда известны два угла и сторона— техника, известная как триангуляция.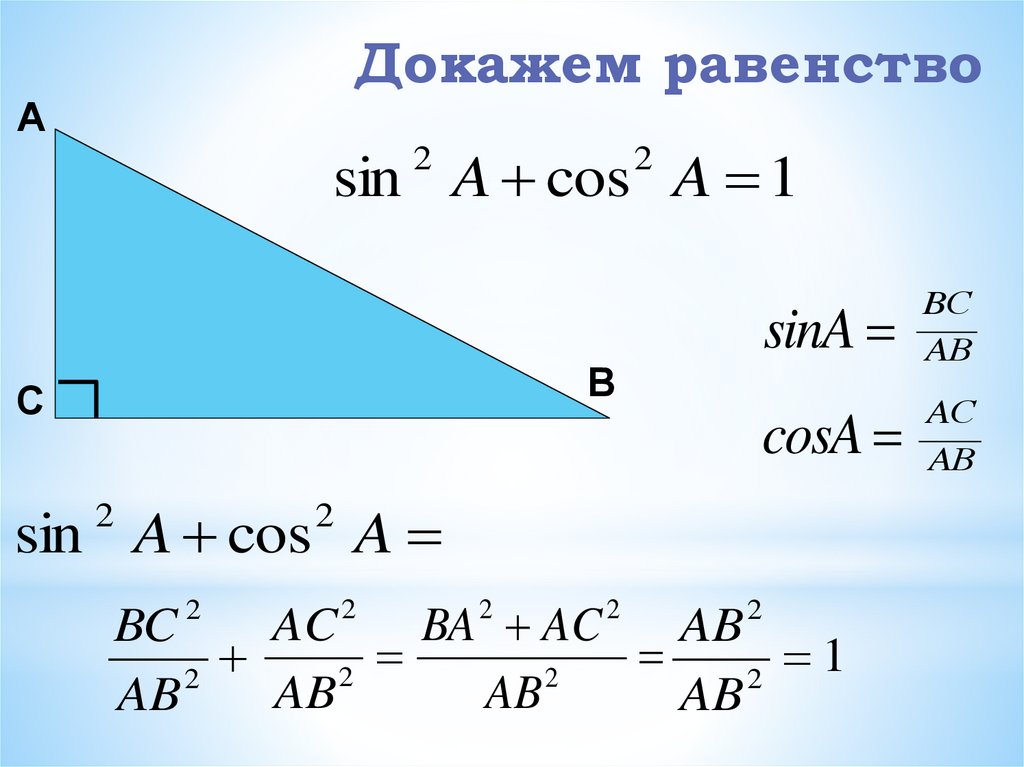
Его также можно использовать, когда известны две стороны и один из незамкнутых углов.
Как найти синус без калькулятора?
Когда можно использовать правило косинусов?
Правило косинусов можно использовать в любой треугольник, в котором вы пытаетесь связать все три стороны с одним углом. Если вам нужно найти длину стороны, вам нужно знать две другие стороны и противолежащий угол.
Что такое синусоидальный класс 11? Закон синуса или закон синуса гласит, что отношение длины стороны треугольника к синусу противолежащего угла, который одинаков для всех трех сторон. Это также известно как правило синусов.
Работает ли Sohcahtoa для всех треугольников?
В: Сохчатоа только для прямоугольных треугольников? А: Да, это относится только к прямоугольным треугольникам.
… A: У прямоугольного треугольника гипотенуза всегда противоположна углу 90 градусов и является самой длинной стороной.
Что такое правило проекции? Геометрическая интерпретация доказательства проекционных формул заключается в том, что длина любой стороны треугольника равна алгебраической сумме проекций на нее других сторон. В любом треугольнике ABC (i) a = b, потому что C + c, потому что B.
Понимание правила синусов и правила косинуса для выпускных экзаменов по математике
← Вернуться ко всем блогам
Федерико
18 февраля 2022 г.
любой треугольник. Каждому студенту выпускных экзаменов по математике необходимы практические знания тригонометрии, а правила синусов и косинусов будут незаменимы на вашем экзамене.
Каждый треугольник имеет шесть измерений: три стороны и три угла. Чтобы определить любые неизвестные углы или стороны, вам нужно знать по крайней мере три из этих измерений в любой комбинации, за исключением трех углов.
Вы можете использовать либо правило косинуса, либо правило синусов — выбор зависит от того, что вы ищете и что дано. В этом кратком уроке мы рассмотрим правила и способы их использования для решения вопросов по тригонометрии уровня GCSE.
1. Правило синусов
Треугольники не всегда удобно обозначать, поэтому очень важно выполнить следующий шаг, чтобы избежать путаницы. Возьмите любой треугольник ABC и обозначьте стороны a, b, c и соответствующие противоположные углы A, B, C , как на рисунке ниже.
Правило синусов гласит:
или
Давайте применим это к реальному примеру в стиле GCSE
Пример 1. Вычислим значение стороны
В этом случае мы используем правило синусов со сторонами сверху (первое).
Умножив обе стороны на , мы получим:
Пример 2. Вычислим значение угла
В этом примере мы используем правило синусов с синусами сверху (второе).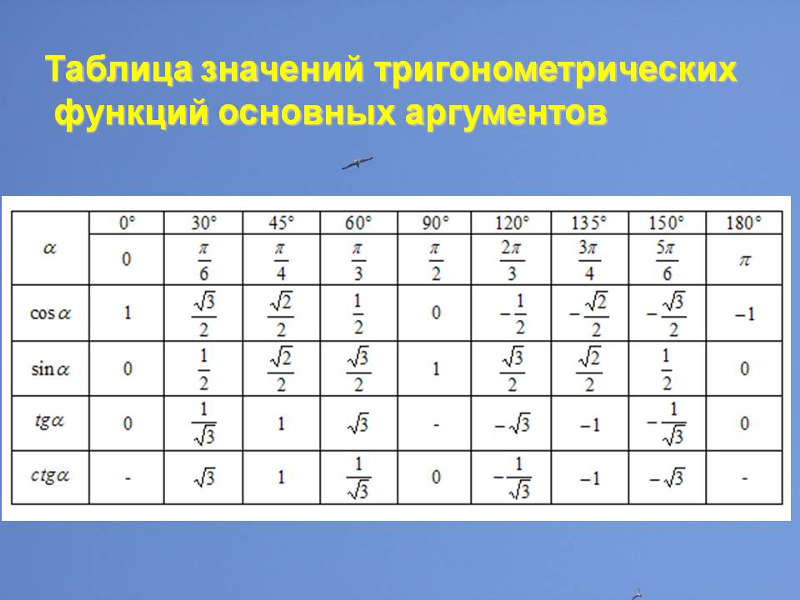
Нам также нужен калькулятор, чтобы вычислить арксинус.
Умножая обе части на 7, получаем:
Следовательно:
2. Правило косинуса
Правило косинуса можно использовать для нахождения неизвестных сторон треугольника, как показано на рисунке ниже. Его можно выразить с помощью следующих формул:
Приведенные выше формулы можно также изменить для вычисления неизвестных углов с помощью обратных операций: Вопросы уровня GCSE.
Пример 3. Определите значение стороны в следующем треугольнике
Используя правило косинусов 1, получаем:
Отсюда:
Пример 4: Вычисляем значение стороны в следующем треугольнике может получиться так:
В заключение, если вы не уверены в том, использовать ли правило синусов или правило косинусов, вы можете воспользоваться удобной тактикой.
Если вам даны две стороны и угол между ними, как в примере 3, вы можете использовать правило косинуса, чтобы вычислить недостающую сторону.
Если вам дана одна сторона и известен противоположный угол, а также другой угол или сторона (пример 2), вы можете использовать правило синусов, чтобы вычислить недостающую сторону. Если вам даны три стороны, вы можете использовать правило косинусов, чтобы определить любой угол.
Давайте начнем
Закажите бесплатную встречу. Составьте индивидуальный план урока. Мастер математики.
Запишитесь на уроки
Последние блоги
Читайте последние блоги
Подпишитесь
Получайте наши последние блоги и новости. Доставлено прямо в ваш почтовый ящик.
Спасибо, что подписались на получение обновлений. Проверьте свой почтовый ящик, чтобы подтвердить, что хотите получать последние доступные репетиторы.
Подписаться
Правила синусов и косинусов – Треугольники и тригонометрия – Mathigon
Для доступа к Mathigon включите JavaScript в браузере.
Изменить язык
Войти в Mathigon
или
Электронная почта или имя пользователя и парольНовая учетная запись Сбросить пароль
Mathigon использует файлы cookie для персонализации и улучшения этого веб-сайта.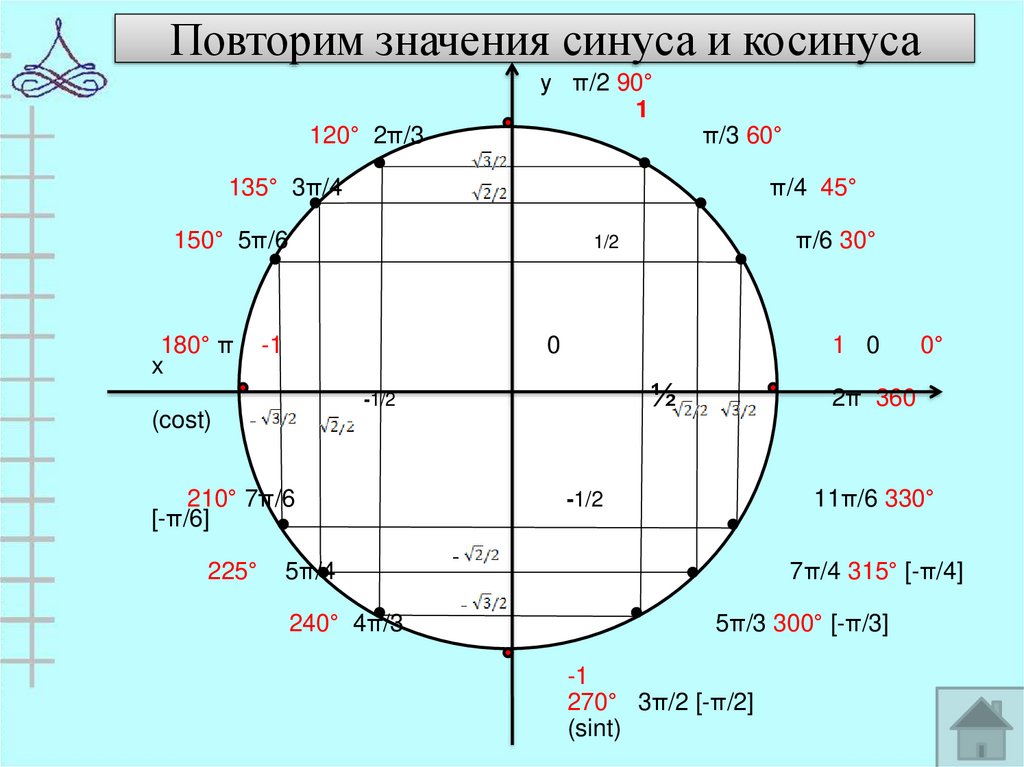
Политика конфиденциальности
Выберите одно из ключевых слов слева…
Пока все, что вы узнали о тригонометрии, применимо только к прямоугольным треугольникам. Но большинство треугольников не прямоугольные, и есть два важных результата, которые работают для всех треугольников
Правило синусов
B и C ,
sinAa=sinBb=sinCc
Правило косинуса
В треугольнике со сторонами a , b и c , и углами A , B и C ,
c2=a2bccab+b2−2abcos c2−2bccosA
СКОРО – Доказательство, примеры и приложения
Большое тригонометрическое исследование
Вы все еще помните поиск самой высокой горы на Земле из введения? С тригонометрией у нас наконец-то есть инструменты для этого!
Геодезисты в Индии измерили угол наклона вершины горы с двух разных точек, отстоящих друг от друга на 5 км. Результаты были 23° и 29°.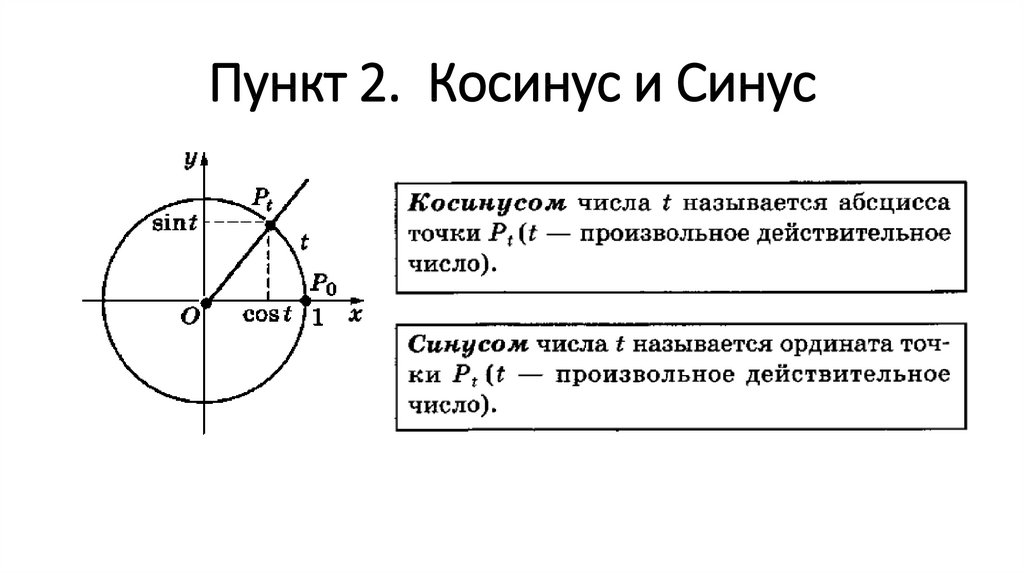
Поскольку угол α является дополнительным углом, мы знаем, что он должен быть равен °. Теперь мы можем использовать сумму внутренних углов треугольника, чтобы определить, что угол β равен °.
Теперь мы знаем все три угла треугольника, а также одну из сторон. This is enough to use the to find the distance d :
| sin151° | |
| d | =sin151°×5sin6° |
| =23.2 km |
Остался последний шаг: давайте посмотрим на большой прямоугольный треугольник. Мы уже знаем длину гипотенузы, но что нам действительно нужно, так это сторона. We can find it using the definition of sin :
| sin23° | = |
| height | =sin23°×23 |
=8. |