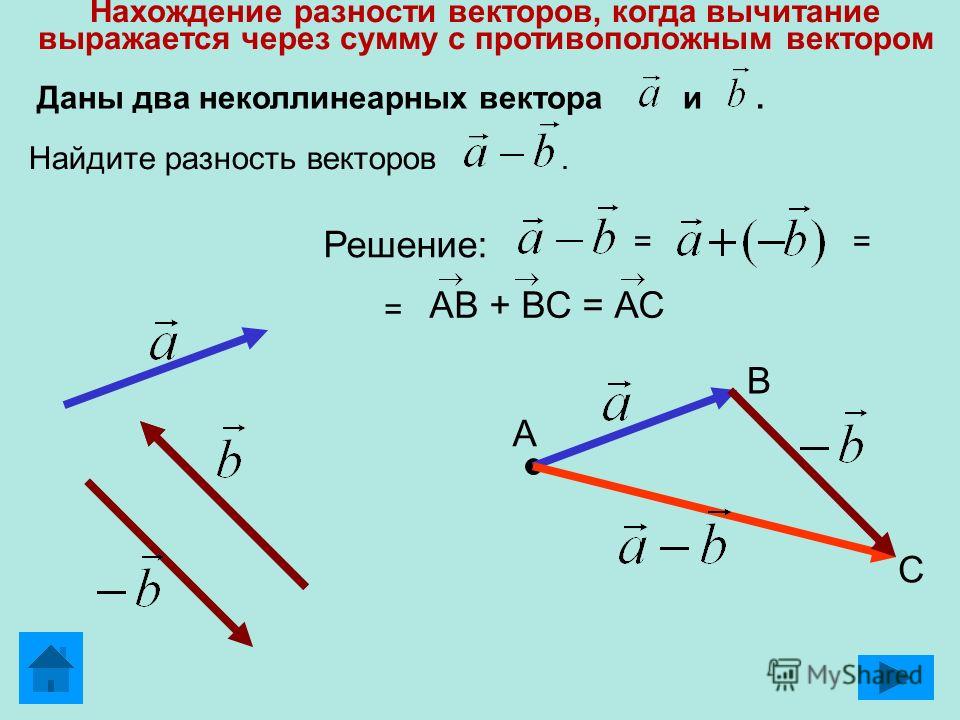
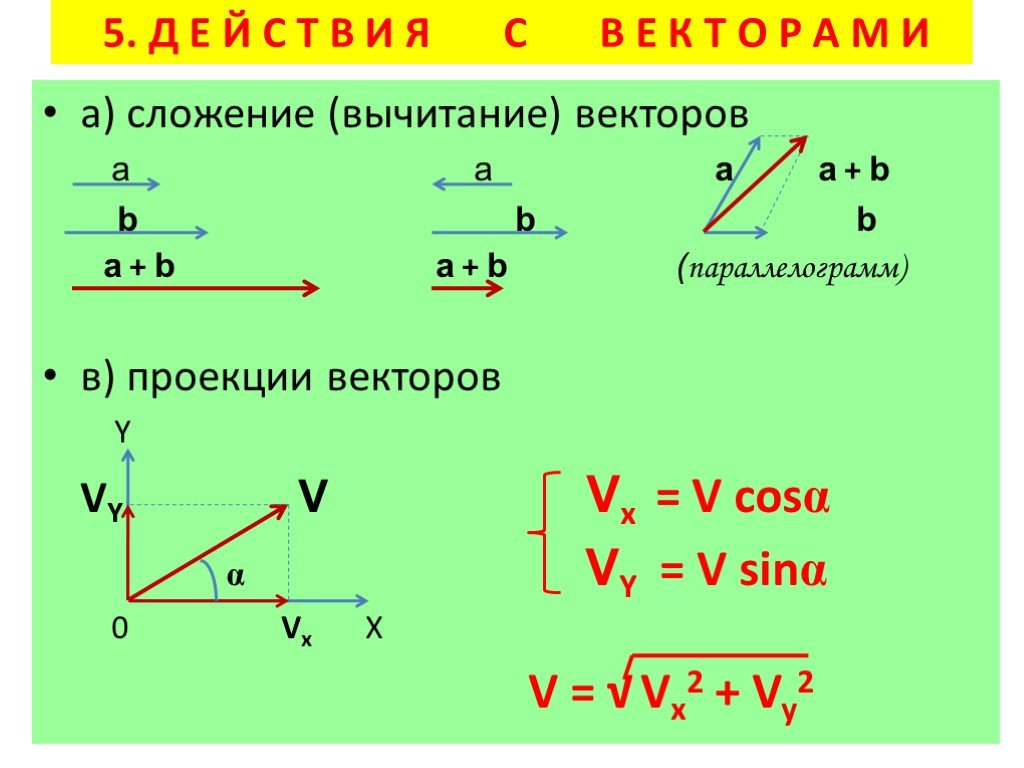
Правило сложения трех векторов: Правило параллелограмма. Законы сложения векторов — урок. Геометрия, 9 класс.

Содержание

Правило параллелепипеда. Разложение вектора

Содержание статьи

1. Правило параллелепипеда

2. Разложение вектора по двум неколлинеарным векторам

3. Пример задачи

Правило параллелепипеда

Для правила сложения трех векторов рассмотрим следующую задачу.

Пример 1

Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA_1}=\overrightarrow{AC_1}$

Рисунок 1.

Доказательство.

Воспользуемся свойством правила треугольника сложения двух векторов $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$, получим:

\[\overrightarrow{AC_1}=\overrightarrow{AC}+\overrightarrow{CC_1}=\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{CC_1}\]

Так как $\overrightarrow{DC}=\overrightarrow{AB},\ \ \overrightarrow{CC_1}=\overrightarrow{AA_1}$

То есть

\[\overrightarrow{AC_1}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA_1}\]

ч. т. д.

Из этой задачи получаем следующее правило для нахождения сложения трех векторов. Чтобы найти сумму трех векторов $\overrightarrow{a},\overrightarrow{b}\ и\ \overrightarrow{c}$ нужно от произвольной точки $O$ отложить векторы $\overrightarrow{AB}=\overrightarrow{a}$, $\overrightarrow{AC}=\overrightarrow{b}$ и $\overrightarrow{AA_1}=\overrightarrow{c}$ и построим параллелепипед на этих векторах. Тогда вектор диагонали $\overrightarrow{AC_1}$ и будет суммой этих трех векторов. Это правило называется правилом параллелепипеда для сложения трех векторов.

Разложение вектора по двум неколлинеарным векторам

Вспомним сначала, какие векторы называются компланарными.

Определение 1

Два вектора, которые параллельны одной плоскости называются компланарными.

Теорема 1

Произвольный вектор $\overrightarrow{p}$ можно разложить по трем некомпланарным векторам $\overrightarrow{a_1},\ \overrightarrow{a_2}$ и $\overrightarrow{a_3}$ с единственными коэффициентами разложения.

Математически это можно записать следующим образом

\[\overrightarrow{p}={\alpha }_1\overrightarrow{a_1}+{\alpha }_2\overrightarrow{a_2}+{\alpha }_3\overrightarrow{a_3}\]

Доказательство.

Существование: Пусть нам даны три некомпланарных вектора $\overrightarrow{a_1},\ \overrightarrow{a_2}$ и $\overrightarrow{a_3}$. Выберем произвольную точку $O$ и построим следующие векторы:

\[\overrightarrow{a_1}=\overrightarrow{OA},\ \overrightarrow{a_2}=\overrightarrow{OB},\ \overrightarrow{a_3}=\overrightarrow{OC}\ и\ \overrightarrow{p}=\overrightarrow{OP}\]

Рассмотрим следующий рисунок:

Рисунок 2.

Произведем следующие дополнительные построения. Проведем через точку $P$ прямую, которая будет параллельна вектору $\overrightarrow{OC}$. Пусть эта прямая пересекает плоскость $OAB$ в точке $P_1$. Далее, проведем через точку $P_1$ прямую, которая будет параллельна вектору $\overrightarrow{OB}$.

Пусть эта прямая пересекает прямую $OA$ в точке $P_2$ (смотри рисунок выше).

\[\overrightarrow{OP}=\overrightarrow{p}=\overrightarrow{OP_2}+\overrightarrow{P_2P_1}+\overrightarrow{P_1P}\]

Так как векторы $\overrightarrow{OP_2}$ и $\overrightarrow{OA}$ коллинеарны, то

\[\overrightarrow{OP_2}={\alpha }_1\overrightarrow{OA}={\alpha }_1\overrightarrow{a_1}\]

Так как векторы $\overrightarrow{P_2P_1}$ и $\overrightarrow{OB}$ коллинеарны, то

\[\overrightarrow{P_2P_1}={\alpha }_2\overrightarrow{OB}={\alpha }_2\overrightarrow{a_2}\]

Так как векторы $\overrightarrow{P_1P}$ и $\overrightarrow{OC}$ коллинеарны, то

\[\overrightarrow{P_1P}={\alpha }_3\overrightarrow{OC}={\alpha }_3\overrightarrow{a_3}\]

Тогда, получаем, что

\[\overrightarrow{p}=\overrightarrow{OP_2}+\overrightarrow{P_2P_1}+\overrightarrow{P_1P}={\alpha }_1\overrightarrow{a_1}+{\alpha }_2\overrightarrow{a_2}+{\alpha }_3\overrightarrow{a_3}\]

Существование разложения доказано.

Единственность: Предположим противное. Пусть существует еще одно разложение вектора $\overrightarrow{p}$ по векторам $\overrightarrow{a_1},\ \overrightarrow{a_2}$ и $\overrightarrow{a_3}$:

\[\overrightarrow{p}={\alpha ‘}_1\overrightarrow{a_1}+{\alpha ‘}_2\overrightarrow{a_2}+{\alpha ‘}_3\overrightarrow{a_3}\]

Вычтем эти разложения друг из друга

\[\overrightarrow{p}-\overrightarrow{p}={\alpha }_1\overrightarrow{a_1}+{\alpha }_2\overrightarrow{a_2}+{\alpha }_3\overrightarrow{a_3}-{\alpha ‘}_1\overrightarrow{a_1}-{\alpha ‘}_2\overrightarrow{a_2}-{\alpha ‘}_3\overrightarrow{a_3}\] \[\overrightarrow{0}=\left({\alpha }_1-{{\alpha }’}_1\right)\overrightarrow{a_1}+\left({\alpha }_2-{{\alpha }’}_2\right)\overrightarrow{a_2}+({\alpha }_3-{{\alpha }’}_3)\overrightarrow{a_3}\]

Из этого получаем

\[\left\{ \begin{array}{c} {{\alpha }_1-{{\alpha }’}_1=0,} \\ {{\alpha }_2-{{\alpha }’}_2=0} \\ {{\alpha }_3-{{\alpha }’}_3=0. } \end{array} \right.\]

Следовательно

\[\left\{ \begin{array}{c} {{\alpha }_1={{\alpha }’}_1,} \\ {{\alpha }_2={{\alpha }’}_2,} \\ {{\alpha }_3={{\alpha }’}_3.} \end{array} \right.\]

Теорема доказана.

Пример задачи

Пример 2

Пусть нам дана пирамида $OABCD$. Разложите вектор $\overrightarrow{OD}$ по векторам $\overrightarrow{OA},\ \overrightarrow{OB}\ и\ \overrightarrow{OC}$.

Решение.

Так как векторы $\overrightarrow{OA},\ \overrightarrow{OB}\ и\ \overrightarrow{OC}$ — стороны пирамиды, то они являются некомпланарными векторами. Тогда, по теореме 1, вектор $\overrightarrow{OD}$ можно разложить по этим векторам, причем разложение будет единственно. Для разложения будем пользоваться свойством сложения векторов и равенством векторов.

Видим, что

\[\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{AD}\] \[\overrightarrow{AD}=\overrightarrow{BC}=\overrightarrow{BO}+\overrightarrow{OC}=\overrightarrow{OC}-\overrightarrow{OB}\]

Следовательно

\[\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{OC}-\overrightarrow{OB}\]

Ответ: $\overrightarrow{OA}+\overrightarrow{OC}-\overrightarrow{OB}. $

Сообщество экспертов Автор24

Автор этой статьи Дата последнего обновления статьи: 27.04.2022

Какой вектор называется суммой двух векторов, правило треугольника сложения векторов

Для правильного отображения законов природы в физике требуется соответствующий математический инструментарий.

В геометрии и физике есть величины, характеризующиеся и числовым значением, и направлением.

Их целесообразно изображать направленными отрезками или векторами.

…

Оглавление:
Координаты на плоскости
Сумма векторов
Элементы алгебры

У таких величин есть начало (отображается точкой) и конец, обозначаемый стрелкой. Длина отрезка называется модулем (длиной).

Примеры:

скорость;
ускорение;
импульс;
сила;
момент;
силы;
перемещение;
напряженность поля и др.

Это интересно: как переводить градусы в радианы?

Координаты на плоскости

Зададим на плоскости отрезок, направленный из точки, А (x1,y1) в точку В (x2,y2).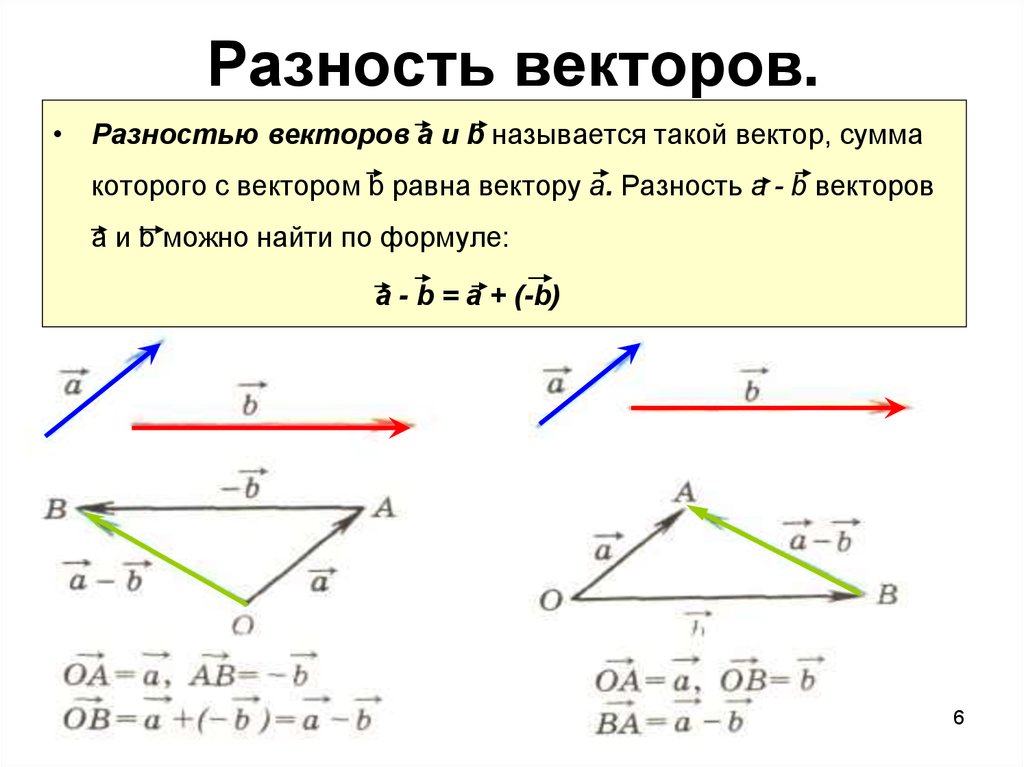 Его координатами a (a1, a2) являются числа а1=x2-x1, а2=y2-y1.

Модуль рассчитывается по теореме Пифагора:

У нулевого вектора начало совпадает с концом. Координаты и длина равны 0.

Сумма векторов

Существуют несколько правил для расчета суммы

правило треугольника;
правило многоугольника ;
правило параллелограмма.

Правило сложения векторов можно объяснить на задачах из динамики и механики. Рассмотрим сложение векторов по правилу треугольника на примере сил, воздействующих на точечное тело и последовательных перемещений тела в пространстве.

Допустим, тело переместилось сначала из точки A в точку B, а затем из точки B в точку C. Итоговое перемещение есть отрезок, направленный от начальной точки A к конечной точке C.

Результат двух перемещений или их сумма s = s1+ s2.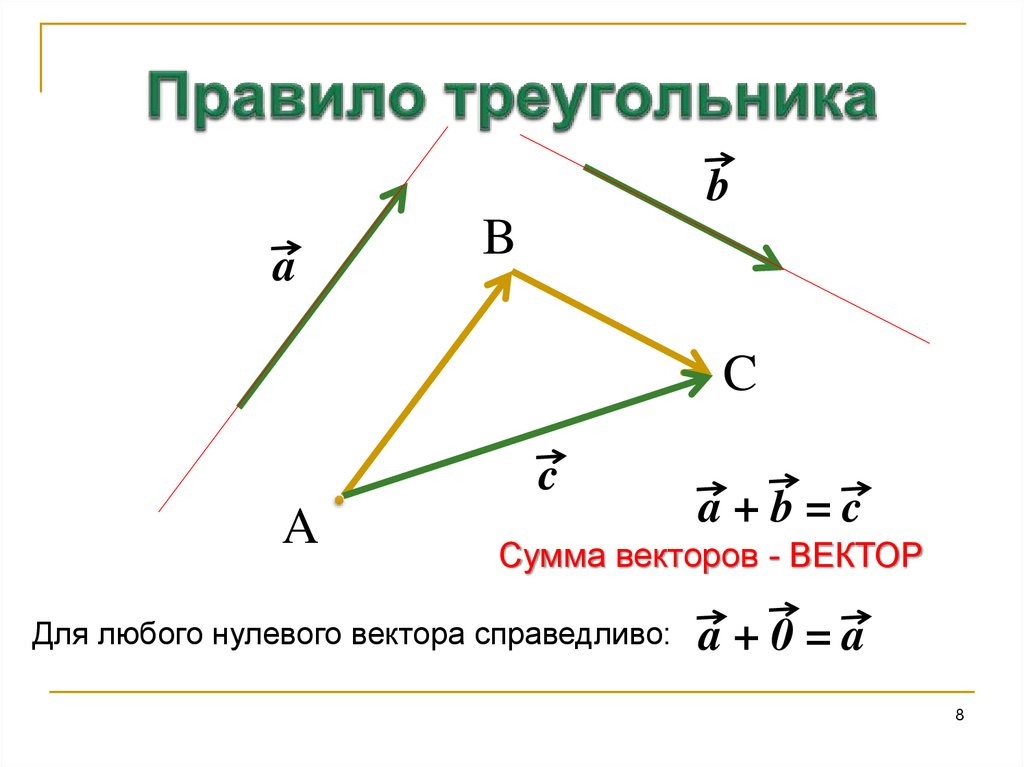 Такой способ называется правилом треугольника.

Стрелки выстраивают в цепочку одну за другой, при необходимости осуществляя параллельный перенос. Суммарный отрезок замыкает последовательность. Его начало совпадает с началом первого, конец — с концом последнего. В иностранных учебниках данный метод называется «хвост к голове».

Координаты результата c = a + b равны сумме соответствующих координат слагаемых c (a1+ b1, a2+ b2).

Сумма параллельных (коллинеарных) векторов также определяется по правилу треугольника.

Если два исходных отрезка перпендикулярны друг другу, то результат их сложения представляет собой гипотенузу построенного на них прямоугольного треугольника. Длина суммы вычисляется по теореме Пифагора.

Примеры:

Скорость тела, брошенного горизонтально, перпендикулярна ускорению свободного падения.
При равномерном вращательном движении линейная скорость тела перпендикулярна центростремительному ускорению.

Сложение трех и более векторов производят по правилу многоугольника, «хвост к голове»

Предположим, что к точечному телу приложены силы F1 и F2.

Опыт доказывает, что совокупное воздействие этих сил равнозначно действию одной силы, направленной по диагонали построенного на них параллелограмма. Эта равнодействующая сила равна их сумме F = F1 + F 2. Приведенный способ сложения называется правилом параллелограмма.

Длина в этом случае вычисляется по формуле

, где θ — угол между сторонами.

Правила треугольника и параллелограмма взаимозаменяемы. В физике чаще применяют правило параллелограмма, так как направленные величины сил, скоростей, ускорений обычно приложены к одному точечному телу. В трехмерной системе координат применяется правило параллелепипеда.

Обратите внимание: что такое луч в геометрии.

Элементы алгебры

Сложение является двоичной операцией: за один раз можно сложить только пару.
Коммутативность: сумма от перестановки слагаемых не изменяется a + b = b + a. Это ясно из правила параллелограмма: диагональ всегда одна и та же.
Ассоциативность: сумма произвольного числа векторов не зависит от порядка их сложения (a + b)+ c = a +(b + c).
Суммирование с нулевым вектором не меняет ни направление, ни длину: a +0= a .
Для каждого вектора есть противоположный. Их сумма равна нулю a +(-a)=0, а длины совпадают.

Вычитание направленного отрезка равносильно прибавлению противоположного. Координаты равны разности соответствующих координат. Длина равна:

Для вычитания можно использовать видоизмененное правило треугольника.

Умножение на скаляр

Результатом умножения на скаляр будет вектор.

Координаты произведения получаются перемножением на скаляр соответствующих координат исходного.

Скаляр — числовая величина со знаком плюс или минус, больше или меньше единицы.

Примеры скалярных величин в физике:

масса;
время;
заряд ;
длина;
площадь;
объем;
плотность;
температура;
энергия.

Примеры:

Перемещение равномерно движущегося тела равно произведению времени и скорости s = vt .
Импульс тела — масса, умноженная на скорость p = mv .
Второй закон Ньютона. Произведение массы тела на ускорение равно приложенной равнодействующей силе ma=F.
Сила, действующая на заряженную частицу в электрическом поле, пропорциональна заряду F = qE.

Скалярное произведение направленных отрезков a и b равно произведению модулей на косинус угла между ними. Скалярное произведение взаимно перпендикулярных отрезков равно нулю.

Пример:

Работа является скалярным произведением силы и перемещения A = Fs .

Найдите сумму трех векторов?

Ответ

Проверено

193,8 тыс.+ просмотров

Подсказка: Во-первых, давайте представим эти три вектора через i, j и k. Чтобы решить вопрос, нам нужно добавить все компоненты i векторов по отдельности, затем компоненты j и, наконец, компоненты k всех трех векторов.

Полный пошаговый ответ:
Здесь допустим три вектора.
Первый вектор: $a = {x_1}i + {y_1}j + {z_1}k$, второй вектор: $b = {x_2}i + {y_2}j + {z_2}k$, а третий вектор равен $c = {x_3}i + {y_3}j + {z_3}k$.
Применим сложение двух векторов a и b. Для этого нам нужно добавить все компоненты i векторов отдельно, затем компоненты j и, наконец, компоненты k всех трех векторов.
Следовательно,
$ \Rightarrow a + b = \left( {{x_1}i + {y_1}j + {z_1}k} \right) + \left( {{x_2}i + {y_2}j + {z_2 }k} \right)$
Это равно
$ \Rightarrow a + b = \left( {{x_1} + {x_2}} \right)i + \left( {{y_1} + {y_2}} \right)j + \left( {{z_1} + {z_2}} \right)k$
Теперь добавим вектор c с приведенным выше выражением.
$ \Rightarrow a + b + c = \left[ {\left( {{x_1} + {x_2}} \right)i + \left( {{y_1} + {y_2}} \right)j + \left ( {{z_1} + {z_2}} \right)k} \right] + \left( {{x_3}i + {y_3}j + {z_3}k} \right)$
Это равно
$ \Rightarrow a + b + c = \left( {{x_1} + {x_2} + {x_3}} \right)i + \left( {{y_1} + {y_2} + {y_3}} \right)j + \left( {{z_1} + {z_2} + {z_3}} \right)k$
Следовательно, сумма трех векторов $a = {x_1}i + {y_1}j + {z_1}k$, $b = {x_2}i + {y_2}j + {z_2}k$, а $c = {x_3}i + {y_3}j + {z_3}k$ равно $a + b + c = \left( {{x_1 } + {x_2} + {x_3}} \right)i + \left( {{y_1} + {y_2} + {y_3}} \right)j + \left( {{z_1} + {z_2} + {z_3 }} \right)k$ .

Примечание: Сложение векторов отличается от обычного сложения, поскольку векторы имеют направление. Здесь i, j и k представляют направления x, y и z соответственно. Таким образом, при сложении или вычитании векторов мы должны складывать или вычитать значение только того же направления. Мы также должны быть осторожны со знаком. Следовательно, мы должны позаботиться о квадранте, в котором лежит вектор.
Мы можем напрямую сложить три вектора заданного вопроса.
Первый вектор: $a = {x_1}i + {y_1}j + {z_1}k$, второй вектор: $b = {x_2}i + {y_2}j + {z_2}k$, а третий вектор равен $c = {x_3}i + {y_3}j + {z_3}k$.
Применим сложение двух векторов a и b. Для этого нам нужно добавить все компоненты i векторов отдельно, затем компоненты j и, наконец, компоненты k всех трех векторов.
Следовательно,
$ \Rightarrow a + b + c = \left( {{x_1}i + {y_1}j + {z_1}k} \right) + \left( {{x_2}i + {y_2}j + {z_2}k} \right) + \left( {{x_3}i + {y_3}j + {z_3}k} \right)$
Это равно
$ \Rightarrow a + b + c = \left ( {{x_1} + {x_2} + {x_3}} \right)i + \left( {{y_1} + {y_2} + {y_3}} \right)j + \left( {{z_1} + {z_2 } + {z_3}} \right)k$

Недавно обновленные страницы

Рассчитать изменение энтропии, связанное с конверсией класса 11 химии JEE_Main

Закон, сформулированный доктором Нернстом, является первым законом термодинамики класса 11 химии JEE_Main

Для реакции при rm0rm0rmC и нормальном давлении класса A 11 химия JEE_Main

Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC класс 11 химия JEE_Main

Для реакции rm2Clg в rmCrmlrm2rmg признаки 11 класса химии JEE_Main

Изменение энтальпии перехода жидкой воды в химический класс 11 JEE_Main

Рассчитайте изменение энтропии при переходе в химический класс 11 JEE_Main

Закон, сформулированный доктором Нернстом, представляет собой Первый закон термодинамики 11-го класса химии JEE_Main

Для реакция при rm0rm0rmC и нормальном давлении А химический класс 11 JEE_Main

Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC химический класс 11 JEE_Main

0003

Изменение энтальпии перехода жидкой воды класса 11 по химии JEE_Main

Тенденции сомнений

Дополнение к вектору

Введение

Все измеряемые величины могут быть классифицированы либо как векторные величины, либо как скалярные величины. Скалярные величины полностью описываются одним числом (с соответствующими единицами), представляющим величину величины; примерами являются масса, время, температура, энергия и объем. Для векторных величин, таких как скорость, сила и ускорение, величина сопровождается свойством направления. (Векторы будут обозначаться цифрой A и единичные векторы на î

.) Когда в расчетах используются скалярные величины, применяются обычные правила арифметики; но когда речь идет о векторных величинах, процесс усложняется, поскольку необходимо учитывать направление вектора. В этом эксперименте будут рассмотрены три метода добавления векторов: графический, аналитический и экспериментальный.

Теория

Векторная величина может быть представлена графически прямой линией со стрелкой на конце. Направление, в котором указывает стрелка, дает смысл вектора, а длина линии указывает величину вектора. Например, сила в 3 Н, действующая горизонтально, может быть описана линией длиной в три единицы (каждая единица соответствует 1 Н), как показано на рисунке 1.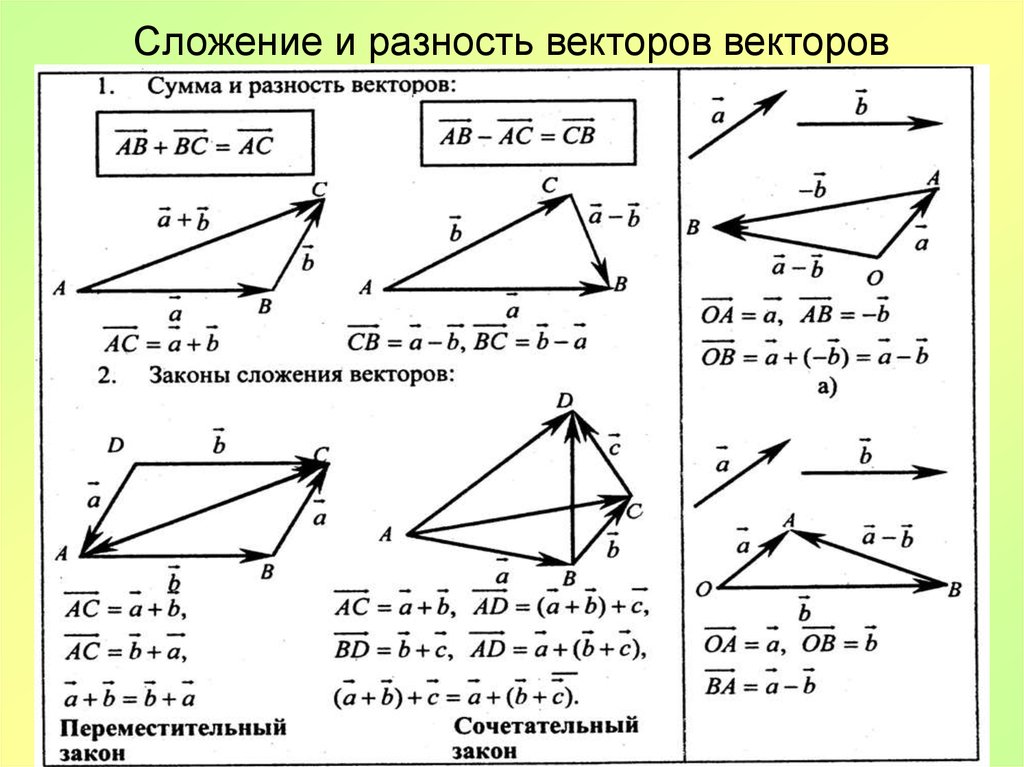

Рисунок 1 : Вектор R имеет как величину, так и направление.

Когда для описания процесса используются два или более векторов, их можно заменить одним результирующим вектором, который несет эквивалентную информацию. В качестве примера рассмотрим автомобиль, который едет из точки O в точку P , сначала проехав 50 км на северо-запад, затем 20 км на запад и, наконец, 40 км на север. Теперь вместо перехода к пункту P в серии из трех шагов, представленных векторами A , B и C , автомобиль может следовать более прямому пути, указанному вектором R . Этот вектор R , называемый равнодействующим, эквивалентен комбинации трех векторов A , B и C , поскольку автомобиль по-прежнему начинается в точке O и заканчивается в точке P .

Это можно записать символически как

(1)

Р = А + Б + С .

Рисунок 2 : Графическое сложение векторов A , B и C

Следует отметить, что в данном случае все пути, представляющие движение от O до P , эквивалентны R и друг другу. Итак, на рисунке 3

( 2 )

Рисунок 3 : Один и тот же результат R получается независимо от порядка добавления векторов.

Хотя этот графический метод, в котором последовательные векторы располагаются «голова к хвосту», полезен в качестве визуального описания, его точность ограничена тем, что может быть получено с помощью инструментов для рисования.

Когда требуются результаты более точные, чем те, которые дает графический анализ, применяются аналитические методы. Чтобы использовать аналитические методы для сложения векторов, все векторы описываются с помощью единичных векторов. Единичный вектор — это вектор, имеющий величину один (без каких-либо единиц) с заданной ориентацией. Его единственное использование — описание определенного направления в пространстве. В 9В системе координат 0095 x-y принято назначать единичный вектор х в направлении положительной оси х , а единичный вектор х — в направлении положительной оси y . Любой отдельный вектор может быть выражен как сумма двух (или более) векторов-компонентов. На рисунке 4 вектор A имеет величину A и ориентацию θ от оси x .

Рисунок 4 : Вектор A графически разделен на компоненты A _x и A _y .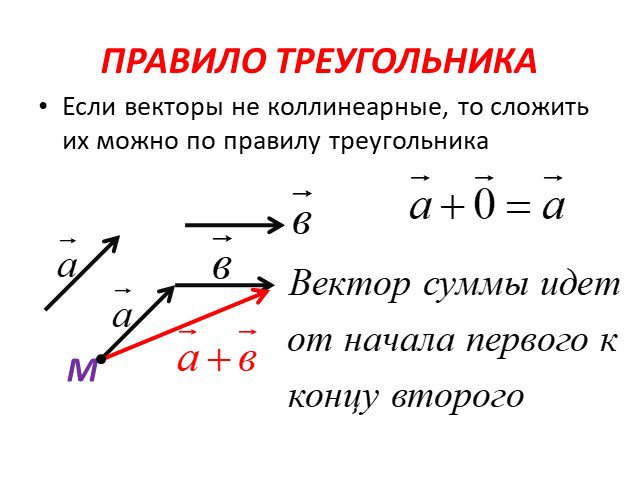

This vector can be considered to be the resultant of two component vectors: A _x = A _x î pointing along the î direction and A _y = А _у х указывая в направлении х ; или символически следующим образом.

( 3 )

A = A _x î + A _y ĵ

( 4 )

A = A _x + А _у

Компонент A _x is positive or negative as A _x is in the + î or – î direction, and A _y is positive or negative as A _y находится в направлении + х или – х . Величина компонентов A может быть рассчитана из определений тригонометрических функций.

( 5 )

грех θ =

или же

( 6 )

A _y = A sin θ

а также

( 7 )

cos θ =

или же

( 8 )

A _x = A cos θ .

Кроме того,

( 9 )

тангенс θ =

( 10 )

θ = арктангенс

и по теореме Пифагора величина A равна

( 11 )

|А| .

При аналитическом добавлении векторов каждый вектор сначала записывается в форме своих компонентов, затем x -компоненты всех векторов складываются алгебраически (уделяя строгое внимание знаку) для получения результирующего x -компонента, и y -компоненты всех векторов складываются, чтобы получить результирующую y -компоненту. Предположим, добавлены два параллельных вектора. Для графического метода «голова к хвосту» вектор B помещается на острие стрелки вектора A (или наоборот), а результирующий R проводится от O до вершины . B , как показано на рис. 5.

Рисунок 5 : Графическое векторное сложение двух векторов

На рисунке 6 векторы C и D добавлены аналитически. В математических терминах векторы можно записать

( 12 )

C = C _x î + C _y ĵ

( 13 )

D = D _х î + D _y ĵ

( 14 )

R = R _x î + R _y ĵ .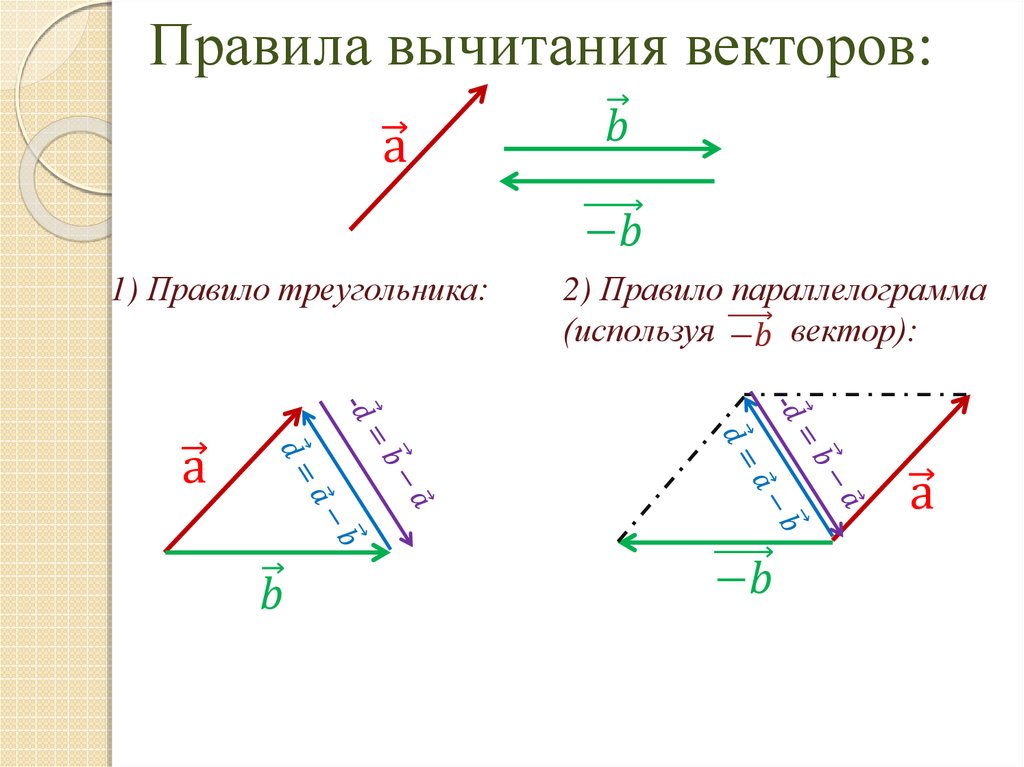

Рисунок 6 : Векторы C и D разделены на компоненты графически и аналитически вместе с их результирующим вектором R .

Так как результат R , is the sum of the vectors C and D

( 15 )

R = C + D

( 16 )

R = C _x î + C _y ĵ + D _x î + D _y ĵ

( 17 )

R = ( С _х + D _x ) î + ( C _Y + D _y ) 777777777777777777777777 гг.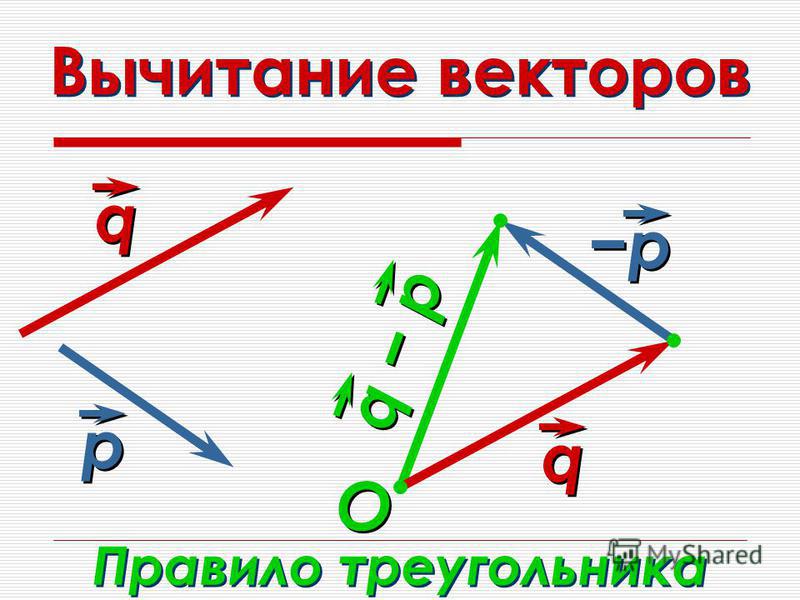

Сравнение с уравнением (14) R = R _x х + R _y 7 х 900. дает значения для x — и y -компонентов результата:

( 18 )

R _x = C _x + D _x

( 19 )

R _y = C _{1 D 1 + 9021}

Из компонентов R величина и направление равнодействующей равны

( 20 )

|Р| =

R _x ² + R _y ²

( 21 )

θ = арктангенс .

Если добавляется более двух векторов, уравнения

(18)
R _x = C _x + D _x
и
(19)
R _y = C _{y 14 D _y .}
можно обобщить до
(22)
R _x = A _x + B _x + C _x + D _x +
(23)
R _y +
(23)
R _y =
(23)
R _y =
(23)
R _y =
(23).0215 + B _y + C _y + D _y +
и связи уравнений
(20)
|R| =
R _x ² + R _Y ²
и
(21)
и
(21)
и
.
можно применять для получения величины и направления равнодействующей.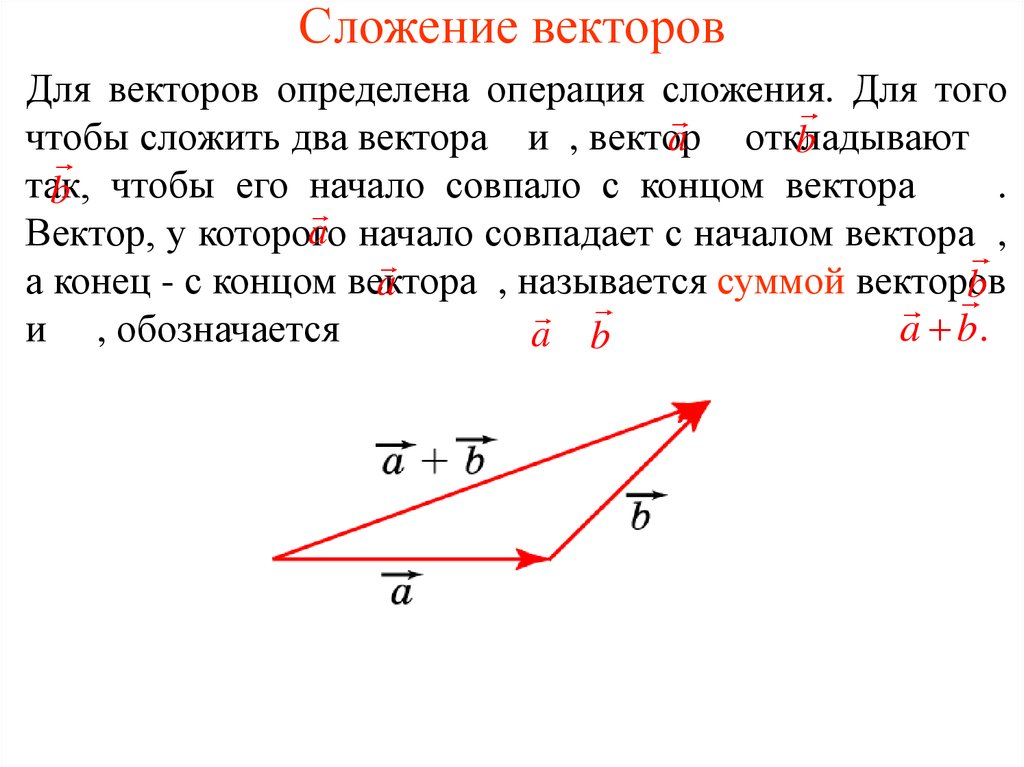 Когда добавляемые векторы представляют силы, отрицание равнодействующей называется уравновешивающей (или антирезультантной) сил. Равновесная сила – это единственная сила, которая в сочетании с другими силами приводит систему в равновесие. Обратите внимание, что равновесие равно по величине, но противоположно по направлению равнодействующей векторов.
Цель
Цель этой лаборатории состоит в том, чтобы найти уравновешивающую силу для одной или нескольких известных сил, используя таблицу сил, и сравнить этот результат с результатами, полученными с помощью графических и аналитических методов.
Аппаратура
линейка транспортир
Три шкива
Набор щелевых масс
Три массовые вешалки
Силовой стол с центральным штифтом и кольцом
Пузырьковый уровень
Рисунок 7 : Устройство
Процедура
Пожалуйста, распечатайте рабочий лист для этой лабораторной работы. Этот лист понадобится вам для записи ваших данных.
Таблица сил состоит из горизонтально установленной поверхности с градуировкой по периметру. Штифт, вставленный в центр стола, удерживает кольцо на месте, когда система не сбалансирована. Кольцо — это объект, который будет находиться в равновесии, а натяжение трех прикрепленных к нему струн обеспечит уравновешивание сил. При условии, что трением в шкивах можно пренебречь, натяжение каждой струны равно направленному вниз весу груза, размещенного на ее концах (это будет темой дальнейшего обсуждения в классе). Шкивы могут быть зажаты под любым желаемым углом, а направление каждой силы указывается положением метки шкива на круглой шкале таблицы.
A: Экспериментальный метод определения равнодействующей двух векторов
Перед использованием силового стола важно, чтобы он был ровным. С помощью пузырькового уровня проверьте горизонтальность платформы силового стола.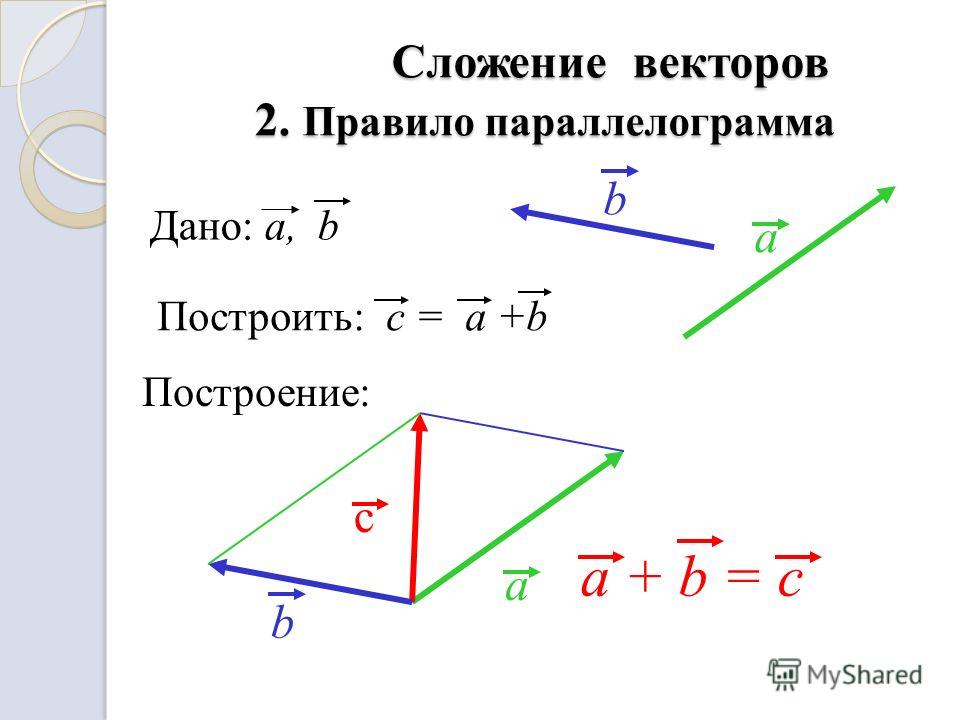 Если это не так, используйте регулировочные винты, чтобы сделать необходимые регулировки, пока поверхность не станет горизонтальной.
1
Используя значения, предоставленные WebAssign для случая 1, расположите шкивы в угловых положениях двух векторов, указанных на диаграмме.
Осторожно:
Обратите внимание, что очень легко перетянуть зажимы, удерживающие шкивы на поверхности стола, поэтому будьте осторожны, затягивая эти зажимы только на долю оборота после того, как зажим коснется поверхности стола (затяните от руки).
Подвесьте грузы, перечисленные для каждого вектора, над соответствующим шкивом. Обязательно учитывайте вес держателя при расчете массы струн. Как только эти грузы будут на месте, используйте третий шкив и систему грузов, чтобы найти уравновешивающий вектор, связанный с двумя векторами, которые вам даны. Отрегулируйте угол силы на столе, а также массу, пока не найдете равновесную конфигурацию.
2
Аккуратно постучите по кольцу, чтобы немного сместить его от центра; если кольцо возвращается в исходное положение, то оно находится в равновесии. Когда кольцо окажется в равновесии, осторожно снимите центральный штифт и еще раз постучите по кольцу, чтобы немного сместить его. Если кольцо не возвращается в центральное положение, замените центральный штифт и отрегулируйте массу и положение шкива для равновесия, пока не будет установлено равновесие. Для тела, находящегося в равновесии, результирующая сила, действующая на тело, равна нулю. Для трех векторов, представленных в таблице сил
A + B + C = 0
или
A + B = −C,
, где C — уравновешивающая. Результат R двух векторов на карточке с заданиями равен
R = A + B
, поэтому
R = −C
, а результат равен отрицательному значению равновесия.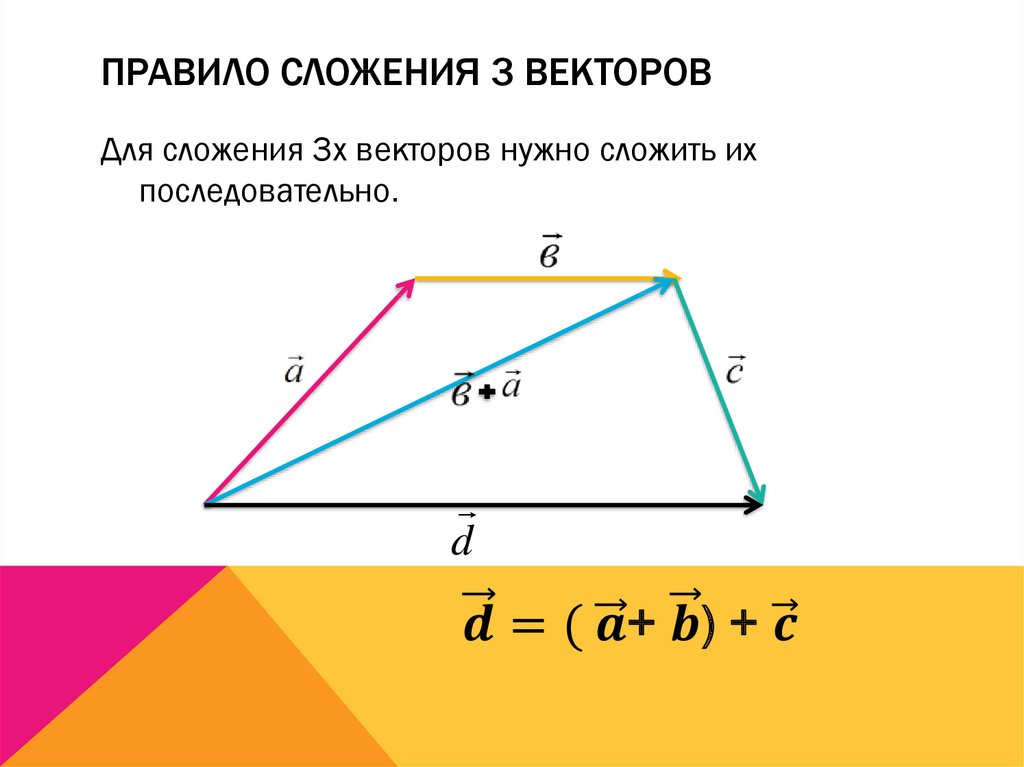
3
Запишите положение равновесия с точностью до доли градуса и запишите его величину с точностью до наименьшей доступной массы. Нарисуйте расположение векторов так, как оно нарисовано на карточке с заданиями, и включите на диаграмме эквилибрант, найденный из таблицы сил. Держите угол равновесия фиксированным.
4
Держите угол равновесия фиксированным. Чтобы найти экспериментальную неопределенность величины равновесия, добавьте к шкиву (или уберите с него) вес, достаточный для того, чтобы кольцо на силовом столе значительно отклонилось от своего положения равновесия. Величина, на которую изменилась масса, является мерой экспериментальной неопределенности величины вектора. Запишите эту неопределенность в наименьшей доступной массе (не забудьте указать правильные единицы измерения).
5
Поместите кольцо в равновесие еще раз. Сохраняя фиксированную величину равновесия, найдите экспериментальную неопределенность в направлении равновесия, слегка перемещая шкив до тех пор, пока кольцо не перестанет находиться в равновесии. Изменение угла, необходимого для того, чтобы вывести кольцо из положения равновесия, представляет собой экспериментальную неопределенность в направлении равновесия. Запишите эту неопределенность с точностью до доли градуса.
6
Повторите процедуры 1–5 для случая 2.
B: Графический метод определения равнодействующей двух векторов
1
На листе линейной миллиметровой бумаги сложите два вектора, показанные в случае, используя метод «голова к хвосту», описанный на рисунке 3.
2
Нарисуйте векторы в масштабе (используя максимально возможный масштаб) и точно измерьте угол с помощью предоставленного транспортира.
3
Нарисуйте результирующую и равновесную на диаграмме и измерьте и запишите величину и направление двух векторов. Сделайте это для обоих случаев.
C: Аналитический метод определения равнодействующей двух векторов
1
На наборе координатных осей x-y начертите примерно в масштабе и в любой удобной ориентации два вектора, указанные в деле.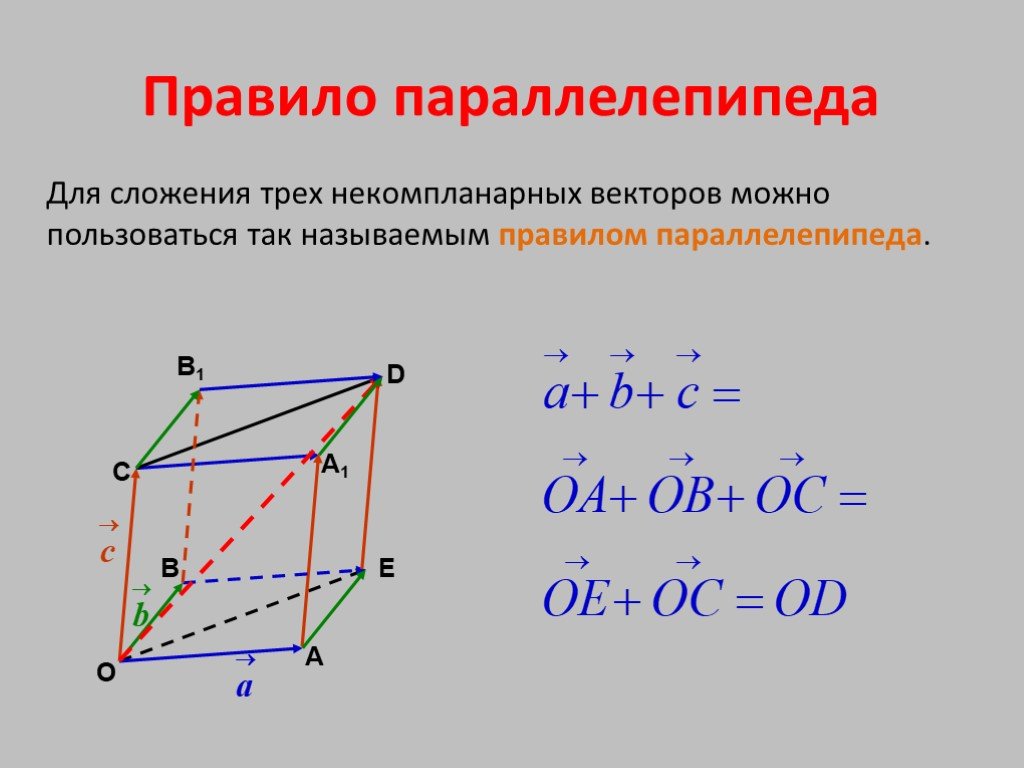 Разрешите каждый вектор в его x — и и -компоненты и перечислите их в таблице над схемой.
2
Из этих значений получить компоненты x — и y для равнодействующей и, используя уравнения
(20)
|R| =
R _x ² + R _Y ²
и
(21)
и
(21)
и
.
, определите величину и направление равнодействующей и нарисуйте ее на эскизе. Сделайте это для обоих случаев.
D: Расчеты
1
Определите % ошибки для величины равнодействующей, полученной экспериментальным и аналитическим методами.
2
Определить % разницы величины равнодействующей, полученной экспериментальным и графическим методами.
No related posts.