Философия деления на… или исповедь сумасшедшего / Хабр
Вступление
Сразу следует указать что в данной статье не будет глубокой математики. Будет лишь рассуждение на указанную в заголовке тему. Всё далее описанное лишь мнение автора. Не более того. Почти.
Небольшое дополнение: «мера» и «величина» являются слишком расплывчатыми понятиями, а некоторыми они считаются и синонимичными. Автор же решил строго использовать их в разных представлениях, для однозначности — мерами выступают названия единиц измерения, а величинами выступают численные значения, полученные в результате введённых условий или измерений. Причина, по которой мера указана в виде обычной единицы («/1» в квадратных скобках далее), а не какого-то символьного названия, состоит в том, что при работе с обычными числами в нашем воображении мы не опираемся на какую-либо известную человечеству меру в своих мысленных расчётах, а просто напрямую работаем с числами («чистые вычисления»).
Особенность математики
И хотя многим очевидно, что аксиоматизация основана всегда на наблюдениях физической действительности (то есть на опыте), почему-то эти многие концентрируются исключительно на самой математике, то есть структуре (форме) без содержания. Потому они иногда не представляют что делают, но знают как. Большинство пытавшихся подойти к описанной проблеме, подобно кошке, которая преследует свой хвост, упорно ходит по кругу. Здесь, по всей видимости, проявляется то самое профессиональное закостенение, о котором написал Лоренц в своей прекрасной работе.
Сравнение, как важнейший инструмент познания
Всё познаётся в сравнении.Рене Декарт
Для начала следует сразу обозначить что все математические операции происходят у людей благодаря возможности выявления общих признаков. То есть, благодаря постановке условия и соотношению условия с объектами происходит сам по себе счёт. Отсюда выводятся операции арифметики. Проще говоря, через сравнение происходил первоначальный счёт. Многие физические величины являются принятыми стандартами (эталонами), примеры которых бережно хранятся в Париже. Это подразумевает под собой то, что установлена первоначальная единица, на основе которой выводятся численные представления (
) физических явлений. Проще говоря проводится тот же подсчёт. “Вещами в себе” (термин, предложенный великим философом – Иммануилом Кантом) представляются нам такие предметы бытья, которые мы не можем постигнуть разумом, в силу несовершенства человеческих возможностей.
Элементарное сравнение вещей и составление на этой основе категорий даёт нам возможность проводить систематизацию объектов познания, что приводит к получению какого-то обработанного знания (“вещи в себе” становятся не полными “явлениями”, ведь мы можем не знать всех свойств чего-либо). Если бы мы не могли определять различий между телами (формы, цвета, вкуса, размера и так далее), то для нас все предметы так и остались бы “вещами в себе”. Кант устанавливал, что выделение категорий – это основа внеопытного (
) мышления, которое напрямую связано с математической разновидностью познания, то есть сразу можно обозначить что благодаря выделению равенства или неравенства (схожести) мы устанавливаем (производим) только после этого возможность самого счёта. Конечно же, отсутствие внеопытного мышления исключает возможность его проведения (исключение человеческой «функции» сравнения делает невозможным счёт). Множества, к слову, представляют из себя категории объектов, у которых присутствует какие-то условия наличия элементов.
Возьмём в качестве объекта рассмотрения слиток серебра (популярный объект мысленного эксперимента). Мы можем выделить его массу исходя из экспериментального сопоставления с принятой единицей в системе СИ (килограмм). Мы, также, можем выделить его длину и ширину исходя из экспериментального сопоставления с принятой единицей в системе СИ (метр). Если мысленно отбросить принятые меры и все известные объекты, кроме самого слитка, то перед нами будет лишь объект познания данный нам в наших субъективных, чувственных представлениях (что по-прежнему будет частью внеопытного знания объекта, ведь полностью отключить мышление нельзя (как и обойтись без прошлого опыта, определение которого весьма затруднительно)). Мы не сможем сопоставить с ним какое-либо число просто потому, что не сможем его ни с чем сравнивать. Исходя из всего этого, легко прийти к выводу, что численное представление физической величины имеет под собой связь с элементарным сравнением (сопоставлением) вообще (это очевидно, но обозначить необходимо для ясности суждения).
Если поменять нашу единицу измерения (эталон), то мы можем получить любое численное представление (в рамках действительных чисел) одного и того же слитка, исходя из правила (теоремы) замены масштаба. Представим, что слиток весил один килограмм, то есть был полностью сопоставлен с принятой единицей измерения по массе. Но если мы не будем пользоваться традиционным эталоном (килограммом), а заменим его половиной принятой ранее единицы измерения (килограмма), то получим, что наш слиток весит две “принятых единицы”. Конечно же, в таком случае, масштаб будет распространяться на все сопоставляемые предметы (в рамках рассмотрения) для возможности их сравнения, но это не отменяет возможности изменения численных представлений сопоставляемых величин в принятых рамках (действие правила (теоремы) масштабов). Таким образом, я выделяю отдельно численное представление (величину), получаемое за счёт сравнения с принятой единицей измерения (мерой). Мы можем сравнивать слиток серебра в двести килограмм и другой слиток серебра в четыреста половин килограмма, что подразумевает использование разных численных представлений и разных принятых единиц измерения (мер).
Конечно же они будут равны, при одинаковой мере. Учёт единиц измерения играет важную роль в физике, что помогает избежать ошибок (и парадоксов) при вычислениях. Но математика позволяет себе игнорировать такой подход, не смотря на то, что можно выводить любые численные представления исходя из выбора “принятой единицы”.
Важнейшая проблема математического подхода
Математика может быть определена как доктрина, в которой мы никогда не знаем ни о чём говорим, ни того, верно ли то, что мы говорим.Бертран Рассел
Когда нам приходиться работать с величинами, то мы по-умолчанию считаем их одномерными (выведенными через одну, общую меру). Это относится к многочисленным учебным вычислениям математиков, которые не учитывают меры в решениях. Такой подход сразу же создаёт определённую ориентацию. «Идеальные представления», выработанные математически, не позволяют полно соотносить явления действительности, в силу сложности самих явлений (слишком много факторов, которые нельзя сразу учесть).
Возникает проблема, при которой «идеальное представление» может быть само изначально не полным, а его проверка становится совершенно невозможной (опыт не может однозначно подтвердить это). Всё это достаточно подтверждается существованием такого замечательного параметра как точность («идеальное представление» (какой-нибудь всемирный закон) выведено на основании опыта и само же определяется опытом, что довольно забавно). Юмор ещё может состоять в том, что изначальные условия получения «идеальных представлений» могут уже не соотноситься с текущей действительностью (вселенная тогда и сейчас). Исходя из той же биологии (на примере которой легче это увидеть), наша действительность постоянно меняется, как и меняемся мы. Столетия назад выработанные законы могут перестать выполнять свою роль через какое-то время в силу изменения самой действительности (не сообщая уже о научных революциях). Видимо, в силу перечисленных проблем постепенно меняется подход к измерениям и стандартизации (становится более подозрительным
).
Но к чему всё это?
Автор данной статьи сошлётся на второй раздел книги Конрада Лоренца («Возникновение новых системных свойств»), в котором учёный указывает на не очевидные изменения параметров при формировании (комбинировании) систем из отдельных элементов, где каждый отдельный элемент демонстрирует свои особенности, но, при сочетании с другими, эти особенности искажаются — то есть устраняется линейная последовательность причин. Таким образом я хочу обратить внимание на то, что наблюдаемые явления не всегда могут следовать математическому подходу (да даже той же арифметике в простейших случаях) как некоторым известно. А если учесть что сама математика возникает при обработке опыта нашим разумом (с другими функциями человеческого организма), то решение математических проблем посредством опытной проверки не является чем-то уж преступным.
Ноль, как число
Не мало уже есть разборов относительно представления нуля, а потому раздел будет краток.
Проблема нуля и деления на него
Почему-то люди окончательно удостоверились, что в результате умножения числа на ноль результатом будет сам ноль. Конечно же у этого вывода есть основания. Автор с ними согласен, но всё же необходимо немного разобраться. Возьмём всё тот же злосчастный слиток серебра и умножим на пять. Получим пять слитков. Увеличилась величина, а мера осталась той же. Возьмём слиток и умножим на ноль. Получим количество слитков — 0. Мера всё та же. Берём надоевший слиток и делим на два. Результатом будет половина слитка. Мера та же. Изменилась величина. Или нет? Что мешает сообщить, что мера изменилась? Бессмысленность. Поделив слиток на единицу мы получаем всё тот же слиток. Поделив же слиток сам на себя мы получаем чистую величину без меры (количество). Можно легко вспомнить что знаменателем всех действительных чисел, по-умолчанию, является единица. Та самая единица, которая, по сути, является мерой (эталоном) подсчёта нашей величины.
Деление на ноль, как познавательный процесс
Уничтожается мера. Наше представление, благодаря которому выработана (подсчитана) величина, уничтожается. Каждый раз человек, проводивший математические операции на неопределённых величинах, всё время делал это неосознанно. Он брал признак (условие), по которому вырабатывал в воображении величину и выполнив необходимые для себя вычисления избавлялся от этого представления (из кратковременной памяти). Имея наблюдаемый пример, в котором мы позволяем себе поделить на ноль какое-то слагаемое, мы просто избавляем пример от этого слагаемого (получается что оно просто игнорируется, ведь мера, в данном случае, уже не совпадает при сопоставлении самих слагаемых — её просто нет для этого). Если провести аналогию с языками программирования, то поделив переменную какого-то типа на ноль, мы, фактически, должны удалить память (выделенную даже на «обёртку» (именованный указатель)), выделенную под эту переменную (это слишком радикально по описанным далее причинам).
У автора сложилось представление, при котором данная операция тесно связана с теорией информации, познавательной (когнитивной) психологией и всеми остальными «точными» (не может позволить себе автор назвать науки точными, в которых нет точных вычислений, для чего достаточно вспомнить представления пределов с бесконечно малыми (большими) величинами, не говоря уже о различителях (иррациональных) числах) науками.
Проблема систематизации
Сперва, по всей видимости, получили операцию умножения (через сумму), и уже потом для неё и была выведена, как обратная, — операция деления. Особенность в том, что умножение коммутативно, ассоциативно, дистрибутивно и так далее, в отличии от деления. То есть, по свойствам уже нет такого же сопоставления, как при суммировании и вычитании. Никакой логической симметрии уже здесь не наблюдается, если так можно выразиться. При умножении и делении на ноль возникает знаменитая дилемма, ведь любое число умноженное на ноль всегда будет равно нулю, не говоря уже о делении, пока что.
Что же делать в таком случае?
Предложение
Подобно тому, как в какое-то время люди решили ввести комплексные числа, для решения кубических уравнений, можно ввести особую разновидность чисел для решения проблемы возврата значения при делении и умножении на ноль. На первый взгляд всё это бессмысленно. На второй бессмысленность по прежнему очевидна, но автор не просто так затронул естественные науки и познавательную психологию. При условии, что меры расчёта могут быть друг с другом сопоставлены в самых различных математических вычислениях, должна появиться необходимость при учёте различных мер и особенностей подсчёта величин. Сам учёт будет являться необходимой информацией, формирующей возвратное значение при делении и умножении в различных, запутанных задачах физики и стандартизации (не говоря уже о расчёте систем с подключаемыми подсистемами и элементами).
При умножении на ноль любой величины сама величина становится нулевой, но мера остаётся неизменной.
Учёт возвращаемых параметров при умножении и делении на ноль должен зависеть от применения и оправданности, но уже на этом шаге можно вывести что для уничтожения величины является обратной операция уничтожения представления (меры). Сами эти операции, конечно же, в рамках обычных вычислений не имеют смысла (хотя это покажет будущее и опыт).
Исходя из этого, в квадратных скобках остаётся информация о предыдущей величине и мере умножаемого или делимого на ноль числа.
Конечно же нужно добавить пометки ([*;/] или [/;*]), уточняющие на каких местах предыдущая величина и мера, ведь при умножении на ноль необходимо ставить на первое место меру, которая осталась. При делении же необходимо ставить на первое место предыдущую величину, а уже потом меру, которая уничтожена. Получающиеся «памятные числа» не могут взаимодействовать с другими числами посредством арифметики, хотя должны взаимодействовать друг с другом, в силу наличия одинаковых мер, но это уже устанавливает сам вычисляющий. Складывая метры с литрами нельзя всё подвести под одну величину. Такова действительность. Другое дело, что числа одномерны, при использовании сами по себе.
Ввод правил арифметических действий довольно прост. Достаточно сопоставлять величины одинаковых мер. Для подгонки просто следовать правилу приведения масштабов, используя имеющиеся меры, то есть умножать имеющуюся величину на меру.
Автор не сильно задумывался над тем, какие символы для обозначения оставшихся мер и величин использовать, да и квадратные скобки взял просто так, но если каким-то чудом его идеи получат применения и смысл у других людей, то просьба всё же использовать русские символы для уникальности изображения и внедрения русской, культурной традиции.
Небольшие размышления на тему «неопределённостей»
Обозначенная проблема деления на ноль породила несколько общеизвестных неопределённостей. Но при выводе предыдущих идей они не кажутся такими уж нерешаемыми.
Автор статьи выступает резко против использования пределов (неопределённых функций, у которых метод достижения заданной величины не обозначен) при данном обозрении, ведь для достижения многих величин, пусть и самих по себе неопределённых, всегда можно попробовать подойти к их оценке, иначе сами величины были бы нами не воспринимаемы (к вопросу сравнения).
В данной формуле путем замен легко выводится прошлый результат:
Как видно, пределы совершенно не нужны для восприятия установленных, (например) действительных чисел. Когда идёт речь о пустоте, то подразумевается состояние всё же определённое (отсутствие чего-то по условию, как результат), хотя в действительности абсолютно пустых состояний ещё никто не видел (правда при таком подходе условие размыто).
Важная проблема появляется при сопоставлении бесконечностей с нулём, но всё дело в том, что сами бесконечности неопределённы. Стоит только им придать функциональный вид и многие выводы при оценке сами собой напрашиваются через индукцию. Вспоминаются прекрасные рассуждения Георга Кантора о «мощностях», благодаря которым и появились множества.
Допустим у нас имеются функции F(x) и G(x):
Разве при делении данных функций у нас не получится явный ответ?
Более того, что мешает дать оценку быстроты достижения различных бесконечностей, при учёте тех же канторовских «мощностей»? Да ни что.
Деление одной бесконечности на другую должно равняться единице хотя бы потому, что обозначение одинаковое. В противном случае, введение функционального представления бесконечностей является необходимой нуждой, которая поможет определять их различие даже в символьном отображении. Исходя из принятия бесконечности, как результата, легко прийти к выводам:
Имей мужество пользоваться собственным разумом.Иммануил Кант
Это очередная попытка прикоснуться к неизведанному (вроде так писал коллега по озабоченности проблемой деления на ноль), которая здесь (на ресурсе) уже не раз проводилась. Просто автор считает что нужно использовать другие методы, нежели математические, в вопросах определения различных оснований. Например достаточно самоощущения (
).
Я плохо представляю, что происходит с людьми: они учатся не путем понимания.Они учатся каким-то другим способом — путем механического запоминания или как-то иначе. Их знания так хрупки!
Ричард Фейнман
Они учатся каким-то другим способом — путем механического запоминания или как-то иначе. Их знания так хрупки!Литература:
Конрад Лоренц: «Оборотная сторона зеркала»;
Рене Декарт: «Рассуждение о методе, чтобы верно направлять свой разум и отыскивать истину в науках»;
Иммануил Кант: «Критика чистого разума»;
Александров Александр Данилович: «Геометрия».
Почему минус на минус дает плюс?… -reshimne.ru
Новые вопросы
Ответы
При умножении отрицательных чисел друг на друга получаем положительный результат. Противоположностьчего-то , например -5 это противоположность 5, то -5×(-5)= -(-25) то есть противопожность минус 25 , то есть двадцать пять 25
Это что-то типо определённого правила как жи ши.
Похожие вопросы
30 баллов срочно.
Вычислите точки пересечения парабол y=2x ²+3х-1 и у=-х ²-5х+2
и определите в каких координатных четверях находятся эти точки…
Найдите неизвестный член пропорции:
2 целых 1/2:0,4=(4-x):1 целая 3/5…
А18
(выбор ответа)
срочно пожалуста!…
ax+ay-bx-by
__________
ax-ay-bx+by
При x= -3 y= -5 a=61,4 b=118
Если что- ___ Это дробная черта))…
Вычисление логарифмов
9-25 включительно, пожалуйста…
Найдите периметр равнобенного треугольника ADC с основанием AD, если AD=7см, DC=8см.
…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
открытых учебников | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно.
Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.
Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без торговой марки)
Эти версии одного и того же контента без торговой марки доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, изменять или развивать их любым способом, при этом единственным требованием является предоставление соответствующей ссылки на Siyavula.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
целых задач на сложение умножение деление вычитание
Значение отрицательных чисел
Отрицательные числа — это числа меньше нуля. Какой смысл говорить о числах меньше нуля? Ну, вы слышали о температурах ниже нуля, но даже это несколько искусственно, потому что, если бы вы использовали шкалу Кельвина, вам все равно не пришлось бы с ними иметь дело. Есть и другие вещи, которые соответствуют отрицательным числам, например, ниже уровня моря, но это не значит, что вы постоянно будете иметь дело с температурой или высотой. Возможно, лучшая причина иметь отрицательные числа — чисто математическая, поскольку она делает нашу систему счисления более полной и с ней легче работать. В частности, когда вы занимаетесь алгеброй и работаете с неизвестными величинами, лучше, если большинство, если не все операции, которые вы можете записать, выполнимы, а отрицательные числа позволяют вычитать большие числа из меньших.
Это встречается и в реальном мире, но это не очень приятная тема. Если у вас есть 5 долларов, и вы тратите 7 долларов, то вы должны 2 доллара, что может быть представлено как наличие -2 долларов.
Мы можем представлять отрицательные числа на числовой прямой, записывая их слева от 0, так как на числовой строке меньшие числа записываются слева от больших чисел. Когда вы сравниваете отрицательные числа друг с другом, вы должны быть осторожны, потому что те, которые кажутся большими, на самом деле меньше. Если у вас долг в 7 долларов, у вас меньше денег, чем если бы у вас был долг в 5 долларов.
Противоположности
Другая веская причина использования отрицательных чисел заключается в том, что они позволяют складывать то, что называется обратным, что также полезно при изучении алгебры. У каждого числа есть число, которое можно прибавить к нему, чтобы получить ноль, и это число называется его противоположностью. Чтобы найти противоположное число, вы просто меняете его знак, так что противоположное положительному числу — это отрицательное число, а противоположное отрицательному числу — положительное число.
Символ для противоположного такой же, как и для отрицательного, поэтому это может немного сбить с толку. Но на самом деле не так уж важно определить, какое значение знака «минус» подходит, потому что в любом случае это одно и то же. Если бы вы хотели, вы могли бы просто думать обо всех минусах как о противоположных значениях, потому что, когда они используются для обозначения отрицательного числа, это число противоположно положительному числу, на котором в любом случае стоит знак минус, так что получается к тому же. Но все, что вам действительно нужно сделать, это интерпретировать знак минус как указание на отрицательность всякий раз, когда это имеет смысл, и в противном случае воспринимать его как противоположное значение. В основном это означает, что первый знак минус в числе означает отрицательное значение, а любые последующие означают противоположное.
Сложение
На самом деле сложение чисел со знаком представляет собой объединение сложения и вычитания в одну операцию, подобно тому как умножение дробей объединяет умножение и деление в одну операцию.
Сложение положительных чисел — это сложение, а сложение отрицательных чисел — это вычитание. Если вы хотите подумать об этом на числовой прямой, вы начинаете с 0, и когда вы добавляете положительное число, вы уходите на столько же вправо, а когда вы добавляете отрицательное число, вы уходите на столько же влево.
Правила сложения
Если вы проработаете это в каждом конкретном случае, вы сможете придумать правила сложения чисел плюс и минус. Глядя на возможности комбинаций знаков, можно увидеть, что есть 4 возможности.
+ +
Здесь ничего нового, просто добавьте как обычно.
+ —
Вы идете направо, а потом налево, поэтому они дерутся друг с другом, и вы не уходите далеко. Не обращайте внимания на знаки и вычтите большее из меньшего. Больший из них выигрывает в том, в каком направлении вы движетесь, поэтому он определяет знак вашего ответа.
— +
Вы идете налево, а потом направо, так что они снова дерутся, поэтому, как и в прошлом случае, вы игнорируете знаки и вычитаете больший минус меньший, и больший побеждает и определяет знак вашего ответа.
— —
Теперь вы идете налево, а затем снова идете налево, поэтому, чтобы определить, как далеко вы идете, вы игнорируете знаки и добавляете, и, поскольку вы окажетесь слева от 0, знак вашего ответа будет отрицательным.
На самом деле вы можете разбить эти правила на два случая, и это даст вам более простую формулировку правил.
- Like Signs — добавьте и знак станет общим знаком.
- Разные знаки — вычтите и используйте знак большего.
Абсолютное значение
Вы могли заметить, что я пару раз упоминал об игнорировании знаков в приведенном выше объяснении. Чтобы избежать необходимости говорить об игнорировании знаков в таких объяснениях и в других случаях, когда это требуется, удобно иметь имя для числа, лишенного своего знака, и имя, данное для этого, является абсолютным значением. Абсолютное значение числа — это просто число без знака. Это означает, что если число положительное, его абсолютное значение есть само, но если оно отрицательное, то это число, которое вы получите, если лишить его знака минус, то есть соответствующее положительное число.
На числовой прямой абсолютное значение можно представить также как расстояние от 0. Обозначение абсолютного значения числа x равно |x|. Так, например, |7|=7, но |-4|=4. Ответ на оценку абсолютного значения всегда положителен.
Вычитание
С числами со знаком нам действительно не нужно вычитание, но иногда реальный мир или интуитивные причины заставляют нас думать о проблеме с точки зрения вычитания, поэтому нам нужно определение, которое подходило бы для вычитания чисел со знаком. Наше исходное вычитание положительных чисел, таких как 7-5, можно исправить, добавив отрицательное, поскольку 7+-5 дает тот же ответ, что и 7-5, поэтому мы можем обобщить это до определения вычитания любых двух чисел со знаком. Таким образом, чтобы вычесть два числа со знаком, вы превращаете это в задачу на сложение, заменяя второе число на противоположное. Если вы знаете о делении дробей, то могли заметить, что это очень похоже на тот случай, когда вы делите мое умножение на обратное.
Чтобы вычесть, измените знак второго числа и прибавьте. И это действительно все, что нужно. Вы просто должны помнить, чтобы сделать это, и это требует практики.
Одна вещь, которую я заметил, может сбивать с толку при вычитании, это то, что отрицательный знак является тем же символом, что и знак вычитания, поэтому вы должны убедиться, что вы не перепутаете их и не заставите их выполнять двойную функцию. Один из способов сделать это правильно — нарисовать кружок с двумя числами и кружок другого цвета вокруг знака вычитания. Для этого сначала обведите первое число. Затем следующий знак минус, который вы видите, — это знак вычитания, так что обведите его другим цветом. Любой последующий знак «минус» должен быть знаком «минус», прикрепленным к числу, поэтому обведите все, что осталось, первым цветом. Затем, чтобы изменить вычитание на сложение, сделайте это. Сначала скопируйте первое число, то, что в первом круге. Затем напишите знак сложения вместо исходного знака вычитания, который находится в другом цветном круге.
Затем запишите противоположное следующему числу, которое обведено тем же цветом, что и первое число.
Пример 1:
Решение:
Объяснение:
Два числа представляют собой кружки красного цвета и знак операции синего цвета. Запишите первое число, 2. Затем измените операцию на сложение. Затем измените знак второго числа. Это была положительная 7, так что теперь она становится -7. Теперь для задачи на сложение у нас есть разные знаки, поэтому они борются друг с другом, одно число говорит нам идти вперед, а другое число говорит нам идти назад, поэтому мы вычитаем и получаем 4, но поскольку отрицательное значение было большим. , это -4.
Пример 2
Решение:
Объяснение:
На этот раз первое число равно -4, а второе число — 9, обведено золотым кружком, а знак минус обведен зеленым.
Сначала запишите -4. Затем измените операцию на сложение и запишите сложение плюс знак вниз. Затем измените знак второго числа на 9, что сделает его -9. Теперь для задачи на сложение нам нужно сложить два отрицательных числа. Так как они имеют один и тот же знак, они оба хотят, чтобы мы шли в одном направлении, поэтому мы складываем их, чтобы получить 13. Но поскольку они оба отрицательные числа, это отрицательное число 13.
Пример 3:
Решение:
Объяснение:
На этот раз первое число равно 6, а второе число равно -7. Скобки здесь совсем не нужны. Они здесь только для того, чтобы облегчить чтение, чтобы знаки минус не совпадали друг с другом. Затем меняем задачу на задачу на сложение. Сначала запишите 7. Затем измените вычитание на сложение, поэтому запишите для этого знак плюс. Это изменяет знак второго числа с отрицательного на положительный, чтобы сделать его положительным 7 вместо отрицательного 7.
Теперь для сложения, это просто добавление к положительным числам, что мы уже знали, как делать, прежде чем узнать об отрицательных числах.
Пример 4:
Решение:
Объяснение:
Опять же, скобки на самом деле не нужны. Два числа — это -5 и -6, поэтому, чтобы превратить их в задачу на сложение, мы добавляем -5 и 6. В этой задаче на сложение у нас разные знаки, но на этот раз положительный больше, поэтому мы вычитаем и получаем положительный ответ.
Умножение
Теперь давайте посмотрим на различные комбинации плюса и минуса для умножения чисел со знаком.
+ +
Здесь нет отрицательных чисел, так что ничего нового.
+ —
Умножение на положительные числа означает повторное сложение, поэтому то же самое должно быть верно и при умножении на отрицательное число.
Повторное добавление отрицательного числа дает отрицательное число, а абсолютное значение, то есть размер без знака минус, является просто произведением двух абсолютных значений. Это означает, что когда вы умножаете положительное число на отрицательное число, вы умножаете два числа, игнорируя знаки, и знак ответа отрицательный.
— +
Мы хотим, чтобы умножение было коммутативным, поэтому его нужно делать так же, как +-.
— —
Это немного сложнее понять, и я никогда не видел убедительной физической интерпретации этого. В основном вы должны принять это на том основании, что это единственный математически непротиворечивый способ определить его с учетом других определений. Есть несколько способов думать об этом. Если — это -, то — каким-то образом должно быть что-то другое, значит, это должен быть +. Или вы можете думать об этом так: поскольку -+ есть — то умножение на минус должно изменить знак, поэтому при умножении минуса на минус первый минус должен изменить знак второго на плюс.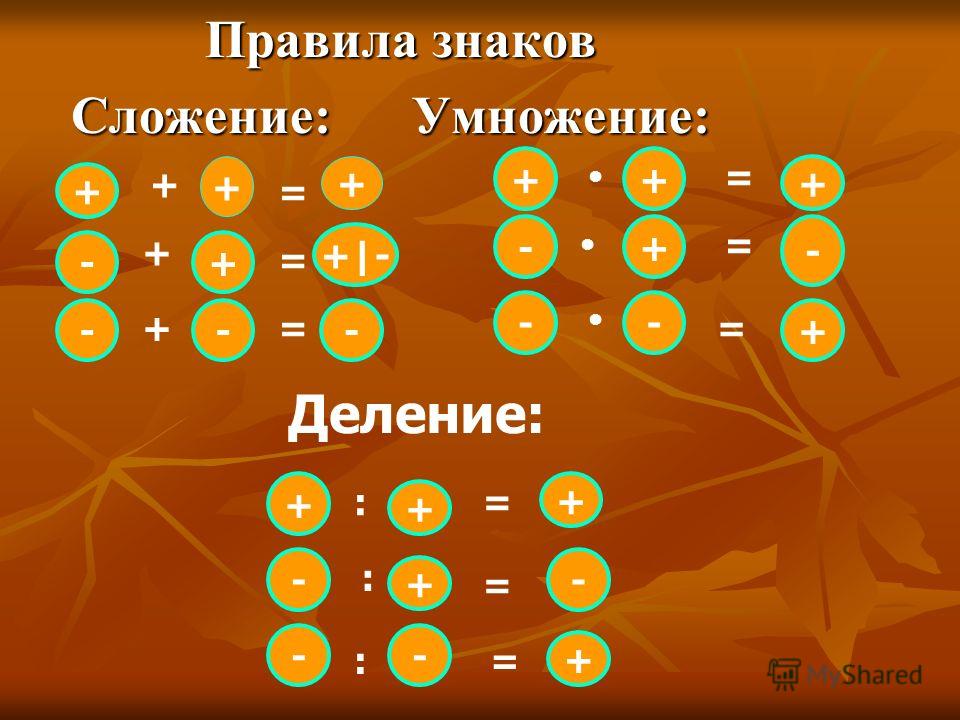
Интересный более формальный способ увидеть это — использовать свойство дистрибутивности. Возьмите пример с цифрами, чтобы сделать его более дружелюбным.
но и по распределительному свойству
-5(6+-6)=(-5)(6)+(-5 )(-6)=-30+(-5)(-6).
Таким образом, чем бы ни было (-5)(-6), прибавив его к -30, вы должны получить 0, и единственное, что вы можете прибавить к -30 и получить 0, это 30. В любом случае, как бы вы это ни видели , кажется, что произведение двух отрицаний может быть только положительным. Я знаю, что две ошибки не дают права, но, как это ни странно, в математике произведение двух отрицаний действительно является положительным.
Я думаю, что если вас беспокоит мысль о том, что отрицательные числа, умноженные на отрицательные, становятся положительными, я думаю, что умножение на самом деле является гораздо более сложной операцией, чем сложение, и это определенно не то же самое, что сложение.
Если вы думаете, что это не может быть правдой, потому что две ошибки не делают правильно, вы должны понять, что объединение двух ошибок добавляет их, а не умножает. Умножение двух отрицательных чисел — это нечто другое. Если умножение — это многократное сложение, что значит многократно складывать что-то отрицательное число раз? Это не имеет буквально большого смысла. Прежде чем вы сможете решить, каким должно быть отрицательное число, умноженное на отрицательное, вы должны сначала решить, что подразумевается под умножением на отрицательное число. В какой-то степени мы определяем отрицательное время как отрицательное, не думая об этом, а просто определяя его единственным способом, который имел бы смысл, учитывая приведенные выше соображения, но если бы мы задумались о том, что означает умножение на отрицательное, возможно, лучший способ думать об этом было бы как многократное вычитание. Поскольку умножение на положительное число является повторным сложением, имело бы смысл думать об умножении на отрицательное число как о многократном вычитании, и это действительно сделало бы произведение двух отрицательных чисел положительным, поскольку вычитание отрицательного числа равносильно добавлению положительного.
.
Дополнительно для экспертов: если вы более продвинутый ученик, преподаватель или родитель, изучивший квадратные уравнения, и вы хотели бы узнать о другой причине, по которой минус умножить на минус — это плюс, прочитайте мою статью Геометрический подход к завершению уравнения. Квадрат.
Опять же, как и со сложением, мы можем облегчить запоминание, сократив его до двух случаев, и здесь это действительно намного проще, чем со сложением, потому что при умножении вы всегда умножаете, так что вам нужно беспокоиться только о том, что будет знак ответа.
- Всегда умножать
- Как знаки, знак +
- Различные знаки, знак —
Большие произведения
Для умножения также интересно посмотреть, что происходит, когда вы умножаете несколько разных чисел. Что происходит тогда, так это то, что каждый раз, когда у вас есть два минуса, вы собираетесь вместе и делаете плюс. так что для каждого знака минус ответ переключается между — и +, поэтому, чтобы определить знак вашего ответа, вам просто нужно подсчитать минусы и посмотреть, четный он или нечетный.
Если оно четное, то ответ +, а если нечетное, то ответ — -.
Умножение и сложение
Интересно сравнить правила умножения с правилами сложения, чтобы не перепутать их.
- Для умножения вы всегда умножаете, а для сложения иногда добавляете, а иногда вычитаете.
- И для умножения, и для сложения вы делаете разные вещи в зависимости от того, одинаковые знаки или разные.
- Для умножения похожие знаки означают, что ответ равен +, а для сложения подобные знаки означают, что вы складываете, а знак является общим знаком.
- Для умножения разные знаки означают, что ответ равен -, а для сложения разные знаки означают, что вы вычитаете, и знак является знаком большего.
- Умножение ++=+, Сложение ++=+.
- Умножение +-=-, Сложение +-=знак большего.
- Умножение -+=-, Сложение -+=знак большего.
- Умножение —=+, Сложение —=-.
Степени
Степени означают многократное умножение, поэтому из правил умножения вы должны уметь возводить числа в степени.
Когда вы возводите отрицательные числа в степень, вы также можете использовать наше правило подсчета знаков минус. Когда вы возводите отрицательное число в четную степень, у вас есть четное количество знаков минус, поэтому ответ +. когда вы возводите отрицательное число в нечетную степень, получается нечетное количество знаков минус, поэтому ответ будет -.
Немного об обозначениях
Есть кое-что, с чем нужно быть осторожным при записи отрицательных чисел, возведенных в степени. Когда вы хотите обозначить отрицательное число, возведенное в степень, вы всегда заключаете его в круглые скобки. Поэтому, когда вы хотите написать -2 в пятой степени, вы пишете это
причина этого в том, что, поскольку умножение на -1 ставит перед числом знак минус, мы думаем о знаках минус у чисел как равных умножение в порядке действий. Это означает, что степени выполняются до того, как к числам присоединяются знаки минус, поэтому, если вы напишете
это не означает, что -2 возводится в 5-ю степень, вместо этого, поскольку степень выполняется первой, это означает, что 2 возводится в 5-ю степень, а затем к этому числу присоединяется знак минус.