Угловой диаметр это: УГЛОВОЙ ДИАМЕТР | это… Что такое УГЛОВОЙ ДИАМЕТР?

Видимый размер — frwiki.wiki

Для одноименных статей см. Диаметр и угловой .

«Угловой радиус» перенаправляется сюда. Чтобы узнать о других значениях, см. Радиус .

Видимый диаметр звезды, наблюдаемой невооруженным глазом

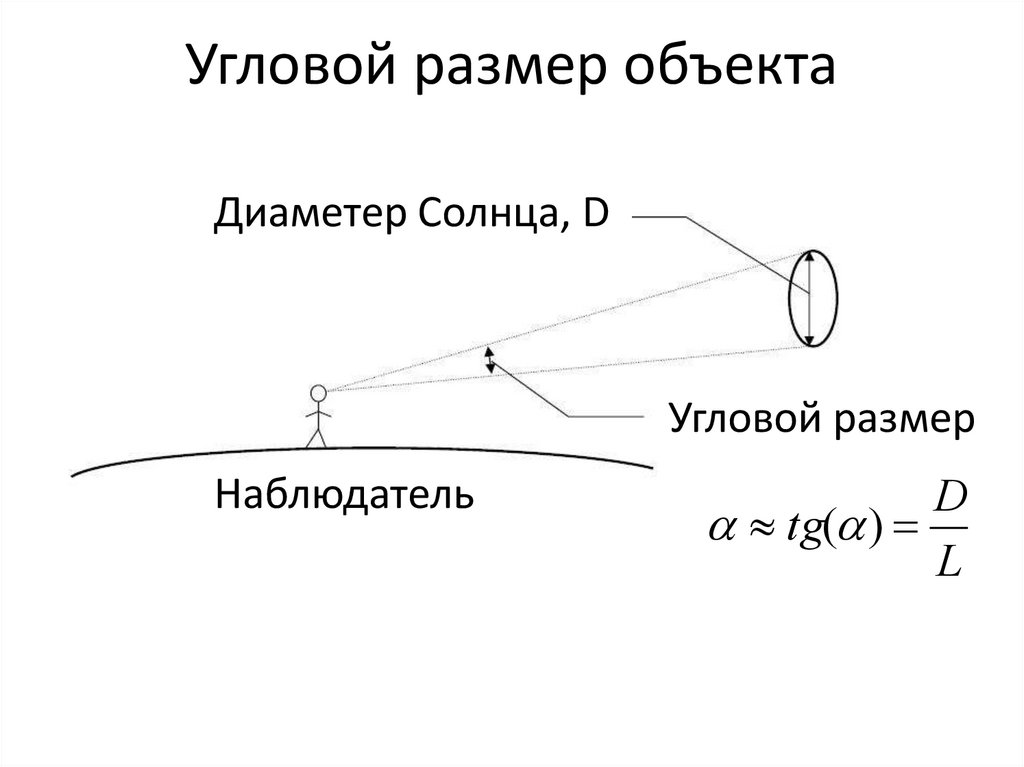
Видимый размер или углового размер или видимый диаметр или угловой диаметр объекта виден на расстоянии это угловое расстояние между ее крайними точками в точке наблюдения, то есть угол между линиями , которые соединяют концы объекта и наблюдатель. Мы можем связать это понятие с понятием телесного угла или трехмерного угла.

Угловой диаметр является единственной мерой непосредственно доступны в астрономии . В топографии или морского судоходства , то видимый размер объектов, размерность которых мы знаем , позволяет рассчитать их расстояние. Этот расчет предполагает, что свет распространяется по прямой линии. В астрономии это не всегда так, особенно рядом с массивным телом, таким как звезда или тем более черная дыра .

Кажущийся размер объектов при оценке без использования инструментов является объектом визуальных иллюзий, серьезно искажающих суждение. Влияет на восприятие цветов.

Резюме

• 1 Расчет
  • 1.1 Случай протяженного объекта
  • 1.2 Случай шара
• 2 Земельные заявки
• 3 Кажущийся диаметр в астрономии
  • 3.1 Космология
  • 3.2 Случай черной дыры
• 4 Человеческое восприятие
  • 4.1 Иллюзия видимого размера
  • 4.2 Цвет
• 5 Приложения
  • 5.1 Библиография
  • 5.2 Статьи по теме
  • 5.3 Внешние ссылки
• 6 Примечания и ссылки

Расчет

Видимый полудиаметр θ звезды

Расчет немного отличается для протяженного объекта и для сферы. В обоих случаях мы получаем приблизительную линейную зависимость между расстоянием, размером и кажущимся диаметром.

Это понятие полезно для понимания затмений с тонкостью различения между полным затмением и кольцевым затмением . Он также используется в геометрической оптике , особенно при исследовании телескопов .

Для определения или прогнозирования этого угла можно использовать несколько методов.

Случай протяженного объекта

Угловой размер объекта (δ) как функция его диаметра (d) и расстояния (D).

Объект, имеющий размер d в ориентации, перпендикулярной направлению наблюдения, если смотреть с центром на расстоянии D , пересекает угол δ . Половина размера объекта и линии, соединяющие положение наблюдателя в середине объекта и на одном из его концов, образуют прямоугольный треугольник, угол которого в точке наблюдения равен половине δ и для которого , по определению,

загар⁡δ2знак равноd2D{\ displaystyle \ tan {\ frac {\ delta} {2}} = {\ frac {\ frac {d} {2}} {D}}}.

Мы получаем это сразу

δзнак равно2арктан⁡(d2D){\ displaystyle \ delta = 2 \ arctan \ left ({\ frac {d} {2D}} \ right)}

Для достаточно удаленных объектов, т. е. таких, что расстояние D велико по сравнению с размером d , это выражение можно записать

δ≈dD{\ displaystyle \ delta \ приблизительно {\ frac {d} {D}}}( δ в радианах ).

При D > 3 × d упрощенная оценка (называемая гауссовым приближением ) верна с точностью до 1%.

Таким образом, мы можем рассчитать расстояние до объекта, зная одно из его измерений, измеряя угол в радианах или миллирадианах ( угловой мил ). Размер объекта, расстояние до которого оценивается, должен быть перпендикулярен и центрирован на оси наблюдения.

Случай шара

Угловой диаметр сферы

Когда объект представляет собой шар , это условие выполняется независимо от положения наблюдателя. Точная формула , отличается от протяженного объекта, расстояние находясь на гипотенузе в треугольнике  :

грех⁡δ2знак равноd2D{\ displaystyle \ sin {\ frac {\ delta} {2}} = {\ frac {\ frac {d} {2}} {D}}},

откуда :

δзнак равно2Arcsin⁡(d2D){\ displaystyle \ delta = 2 \ arcsin \ left ({\ frac {d} {2D}} \ right)}.

Приближение остается:

δ≈dD{\ displaystyle \ delta \ приблизительно {\ frac {d} {D}}}.

Земельные заявки

Взгляд в топографии

Угловой диаметр можно использовать для расчета расстояния до объекта, если известен его фактический размер.

В топографии можно измерить расстояние по горизонтали, поместив измерительный стержень со спиртовым уровнем, указывающим вертикальность, в одной точке и измерив в другой точке его видимый размер. Во избежание накопления ошибок приближения избегаются. Поскольку длина измерительной доски всегда одинакова, в таблице указано соответствие между углом и расстоянием.

Стадий дальномер используется с тестовым образцом для измерения расстояния пути измерения длиной qu’intercepte фиксированного угла.

Горький

В морской навигации , А телескоп или градуированные биноклей указывают на видимый размер объекта в мил (миллирадианах), выражение углового размера , таких как объект 1 единицу размера видно на 1000 единиц расстояния перехватывает 1  мил . В описании достопримечательностей указывается их размер. Ориентир длиной t метров, пересекающий угол m мил, находится на расстоянии t ÷ m в километрах . Высокая точность не требуется.

Соотношение, которое дает расстояние от углового размера от угла в точке наблюдения, также дает расстояние от точки до разницы в угле обзора от расширенной базы в дальномере .

То же соотношение используется в геометрической оптике , в частности при изучении телескопов . В оптике величина — это диоптрия , обычно используемая в расчетах. Вычисления в диоптриях упрощают формулу углового расстояния, заменяя знаменатель. Таким образом, мы переходим от фокусного расстояния к оптическому увеличению , которое напрямую является множителем углового расстояния в телескопе. 1D{\ displaystyle \ scriptstyle {\ frac {1} {D}}}

Видимый диаметр в астрономии

В астрономии видимый диаметр звезды — это изначально единственные данные, которые у нас есть. Расстояние и размер определяются расчетным путем.

Два объекта очень разных размеров могут иметь одинаковый угловой размер. Это часть Луны и Солнца составляет около половины степени (9 мил), но их диаметр и расстояние от Земли отличаются на коэффициент примерно 400, с Луны на 400000 и Солнца в 150.000.000  километров. .

Видимые диаметры (в минутах и секундах дуги ) от Солнца , Луны , планет и карликовых планет в Солнечной системе , наблюдаемые с Земли

Объект	Минимум	Максимум	Средний в нижнем соединении	Средний в оппозиции	Ref.
солнце	31 ′ 27 ″	32 ′ 32 ″
Меркурий	0 ′ 4,5 ″	0 ′ 13 ″	0 ′ 11 ″
Венера	0 ′ 9,7 дюйма	1 ′ 6 ″	1 ′ 0,2 ″
маршировать	0 ′ 3,5 ″	0 ′ 25,1 дюйма		0 ′ 17,9 дюйма
Луна				31 ′ 36 ″
Юпитер	0 ′ 29,8 дюйма	0 ′ 50,1 дюйма		0 ′ 46,9 дюйма
Сатурн	0 ’14 . 5 «	0 ′ 20,1 дюйма		0 ′ 19,5 дюйма
Уран	0 ′ 3,3 дюйма	0 ′ 4,1 дюйма		0 ′ 3,9 ″
Нептун	0 ′ 2,2 ″	0 ′ 2,4 ″		0 ′ 2.3 ″
Плутон	0 ′ 0,06 ″	0 ′ 0,11 ″		0 ′ 0,08 ″

Космология

В космологии , когда расстояние становится порядка размера наблюдаемой Вселенной, возникает необходимость учитывать влияние расширения Вселенной на угловой диаметр объектов. В частности, для данного физического размера угловой диаметр объекта не уменьшается с расстоянием для достаточно удаленных объектов.

Случай черной дыры

Для более общей статьи см черная дыра .

Видимый размер θ из черной дыры больше , чем у классического объекта одного и того же радиуса. Эффекты отклонения света, описываемые общей теорией относительности, заставляют его «казаться» больше, чем его фактический размер.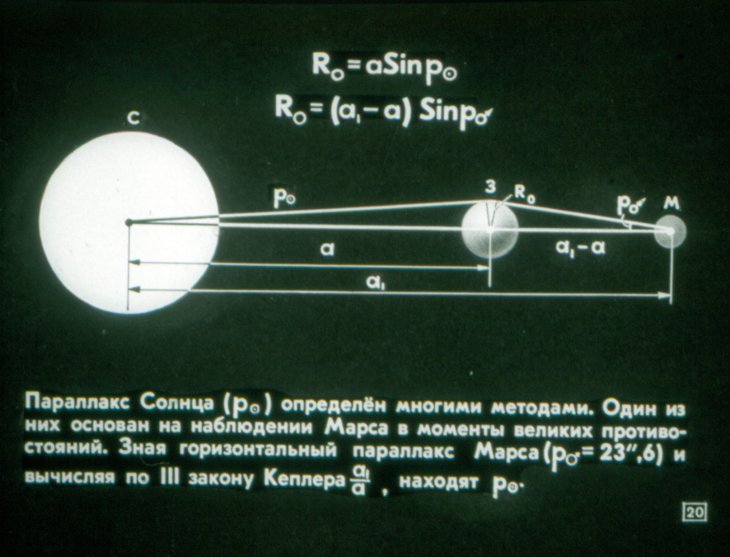 {2}}}}

R _s — это радиус Шварцшильда черной дыры, который можно рассматривать здесь как ограничивающий «поверхность» черной дыры (хотя в действительности черная дыра не имеет материальной поверхности). Формула дает угловой диаметр примерно в 2,5 раза больше, чем дает обычная оценка.

Пример:

Сверхмассивная черная дыра , связанная с Стрельца А * , в центре нашей галактики , находится на расстоянии около 8,5 

кпса . Его масса порядка 2,6 миллиона солнечных масс , поэтому радиус Шварцшильда составляет около 7,5 миллионов километров . На расстоянии 8,5  кпк , или 2,6 × 10 ²⁰  м , его видимый диаметр должен наивно составлять 5,9  × 10 ⁻¹¹  радиан , или 12 угловых микросекунд . Добавив недостающий фактор , угловой диаметр затем падает до примерно 30 дуговых микросекунд, который теперь доступен для очень длинной базы интерферометрии в радио области . 332{\ displaystyle \ textstyle {\ frac {3 {\ sqrt {3}}} {2}}}

Человеческое восприятие

Иллюзия видимого размера

Луна выглядит больше , когда он находится вблизи горизонта. Птолемей , измеряя видимый размер Луны приборами, уже отмечает, что это иллюзия. С тех пор мы обсудили причину этого восприятия.

Целью этой статьи является случай, когда использование инструмента дает меру . Во многих случаях, таких как видимый размер Луны, а также Солнца, расположенного близко к горизонту, восприятие размера сильно различается в зависимости от того, используется ли устройство или нет. Помимо иллюзий, встречающихся в природе, некоторые из них специально созданы для архитектурных целей , и такие впечатления, как камера Эймса, демонстрируют их драматически. В психологи из восприятия , отмеченная в конце XIX — ^го  века, визуальное восприятие размера и расстояний связаны между собой . Закон Эммерт  (в) указывает на то, что окружающие предметы определяют размер и воспринимаемое расстояние от образа сетчатки. Эта тема все еще исследуется.

Цвет

Видимый размер предметов незначительно влияет на восприятие их цвета. Международная комиссия по освещению составлена цветовые таблицы для угловых размеров 2 °, что соответствует размеру макулов , в 1931 г. Было установлено , что эти таблицы только предсказать , приемлемы восприятие цвета до к явному размеру около 4 °. Новые измерения побудили CIE опубликовать в 1964 году дополнительные таблицы, действительные для угла 10 °.

Приложения

Библиография

• Ричард Тайлле , Лоик Злодей и Паскаль Февр , Физический словарь , Брюссель, Де Бок ,2013, стр.  192–193
• (ru) Субраманян Чандрасекар , Математическая теория черных дыр , Oxford University Press (1983) ( ISBN  0198503709 ) .
• Ричард Грегори , Глаз и мозг: психология зрения [«  Глаз и мозг: психология зрения  »], Университет Де Бока ,2000 г.( 1- ^е  изд. 1966 г.)
  • (ru) Ричард Грегори , Видение сквозь иллюзии , Oxford University Press ,2009 г.

Статьи по Теме

• Диаметр
• Телесный угол
• Угловое расстояние
• Расстояние углового диаметра
• Диоптрия

Внешние ссылки

• Тезис DEA, чтобы понять связь между видимым диаметром и затмениями
• http://phys-chimie.voila.net/seconde/physique/chap1/longueur/diametre_apparent/diametre.htm
• http://www. astrosurf.com/denisjarry/diamappa.htm

Примечания и ссылки

• Эта статья частично или полностью взята из статьи «  Угловой размер черной дыры  » (см. Список авторов ) .

• Эта статья частично или полностью взята из статьи «  Угловой диаметр  » (см. Список авторов ) .

1. ↑ Для квадрата, видимого на расстоянии, в 40 раз превышающем его сторону, скажем, от 2,5  см до одного метра, 30  миллирадиан по диагонали.

1. ↑ (in) »  Sun Fact Sheet  » (по состоянию на 28 июля 2014 г. )
2. ↑ (in) »  Mercury Fact Sheet  » (по состоянию на 28 июля 2014 г. )
3. ↑ (in) »  Venus Fact Sheet  » (по состоянию на 28 июля 2014 г. )
4. ↑ (in) »  March Fact Sheet  » (по состоянию на 28 июля 2014 г. )
5. ↑ (in) »  Moon Fact Sheet  » (по состоянию на 28 июля 2014 г. )
6. ↑ (in) »  Jupiter Fact Sheet  » (по состоянию на 28 июля 2014 г. )
7. ↑ (in) »  Saturn Fact Sheet  » (по состоянию на 28 июля 2014 г. )
8. ↑ (in) »  Uranus Fact Sheet  » (по состоянию на 28 июля 2014 г. )
9. ↑ (in) »  Neptune Fact Sheet  » (по состоянию на 28 июля 2014 г. )
10. ↑ (in) «  Информационный бюллетень о Плутоне  » (по состоянию на 28 июля 2014 г. )
11. ↑ Грегори 2000 гл. 10 «Иллюзий»; Григорий 2009 , стр.  200-202.
12. ↑ Роберт Сев , Наука о цвете: физические и перцепционные аспекты , Марсель, Chalagam,2009 г. , стр.  72.
13. ↑ Sap 2009 , стр.  107.

<img src=»https://fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>

Каковы угловые диаметры солнца и луны. Основные данные о луне

Наверняка многие входят в ступор, когда слышат фразы вроде «диаметр Луны составляет половину градуса» или «угловое расстояние между компонентами двойной звезды равно 5 секунд дуги». Какие в небе могут быть секунды, минуты и градусы? Попробуем с этим разобраться, а также научиться измерять расстояния между небесными объектами при помощи собственных рук.

Когда он отошел от экватора, его угловой диаметр явно уменьшился бы. Диагональный диаметр Фобоса также изменяется во время его блуждания по небу — на востоке он имел бы 8, в зените и 12. Для сравнения — солнце, видимое с Марса, имеет угловой диаметр 21.

Фобос — это темный объект, который, как представляется, состоит из аналогичного материала, такого как астероиды типа С, обнаруженные во внешнем поясе астероидов. Однако низкая плотность Фобоса указывает на то, что он состоит не только из скал — это, вероятно, смесь горных пород и льда. Это также может указывать слабые, но непрерывные выбросы газа обнаруженного России зонда Фобос зонд имеет неисправность, прежде чем он мог бы определить состав газа, но это может быть паром.

Всем известно, что условно небо можно представить в виде сферы, на которую спроецированы изображения космических объектов. А наблюдатель всегда находится в ее центре. В связи с этим измерения на небе вполне разумно выражать в градусной мере. Таким образом, если у нас имеется две точки на небе, то расстояние между ними будет представлять из себя угол, образованный прямыми, проведенными из этих точек в глаз наблюдателя. Сложно? Тогда зацените картинку.

Поверхность Фобоса покрыта кратерами. Воздействие, вызвавшее подъем кратера, должно было почти разорвать маленькую луну и, вероятно, вызвать появление видимых канав и полос. Фобос широко считается планетоидом, захваченным Марсом. Некоторые полагают, что это может произойти даже не из основного пояса астероидов, а из внешних областей солнечной системы.

Когда мы смотрим на небо, создается впечатление, что все объекты, которые мы видим на нем, находятся на равном расстоянии от Земли. Уже в древности предполагалось, что все объекты, видимые в небе, лежат на поверхности небесной сферы. Исследователи того времени считали, что небесные тела, такие как планеты, Солнце и Луна, кружатся между сферой неподвижных звезд и Земли. Последний часто покрывал звезды, поэтому он должен был быть ближе. Кометы считались на протяжении многих веков объектами в атмосфере Земли.

Сразу все стало понятно, не так ли? между двумя объектами на изображении есть угол α.

Всего в окружности 360, а в ее половине — 180 градусов. Таким образом, между двумя противоположными точками на горизонте 180°. между горизонтом и точкой зенита — 90°.

Как мы определяем расстояния в космосе сегодня? Ответ на этот вопрос станет предметом этого урока. Во время некоторых солнечных затмений наблюдатель на Земле наблюдает за экраном Луны, идеально охватывающим щит Солнца. Благодаря этому можно наблюдать корону, то есть самую внешнюю часть солнечной атмосферы.

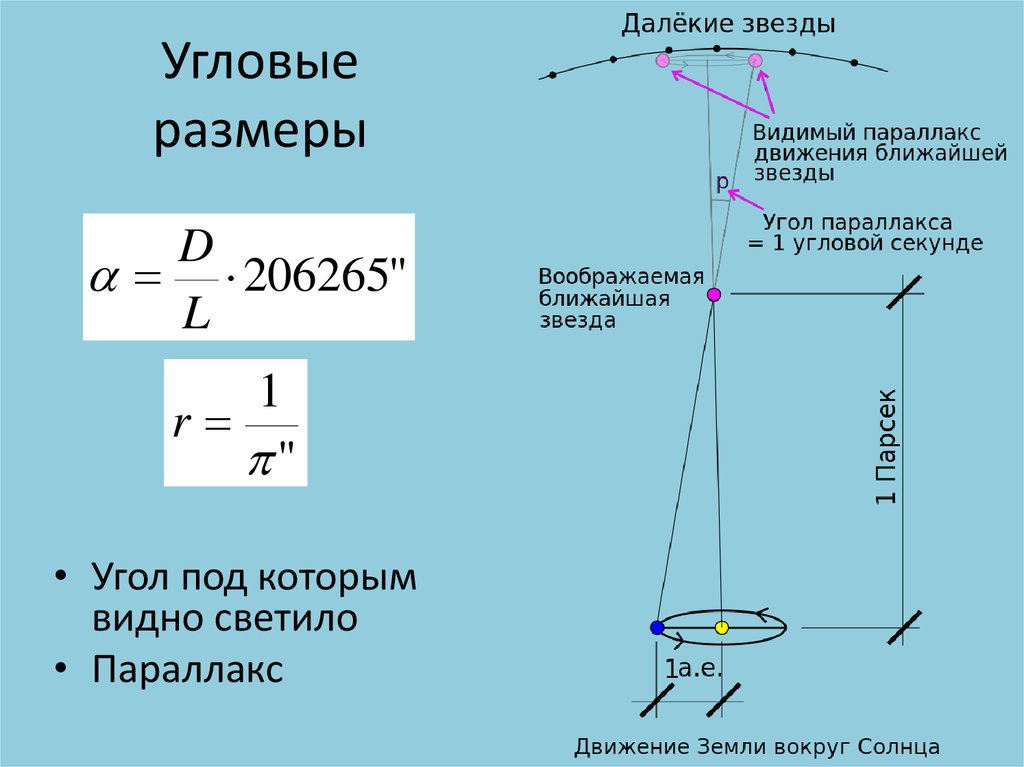
Каково явление параллакса

Распознавать углы вершины и смежные углы и использовать их свойства, распознавать острые треугольники, прямоугольные и тупоугольные треугольники, равносторонние и равнобедренные треугольники, использовать теорему о сумме углов треугольника. Определить расстояния до отдаленных точек, используя явление параллакса, интерпретировать светлый год как единицу расстояния, использовать астрономическую единицу для описания расстояния в солнечной системе. Как мы знаем, как далеко от нас идут дела? Мы используем здесь свойства атмосферы и глаза — чем дальше объект находится, тем больше он затуманен.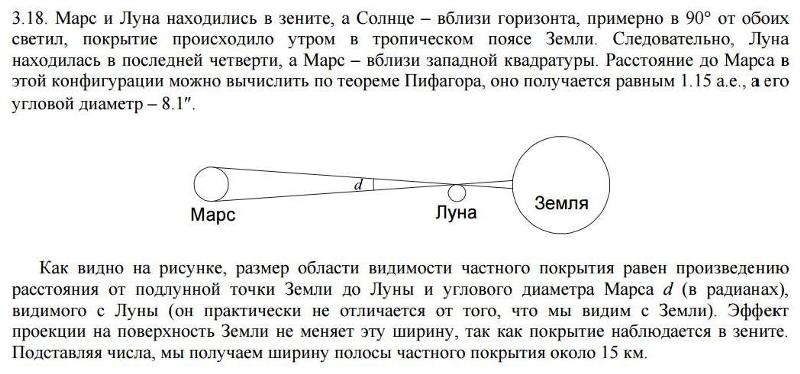

На рисунке в начале статьи указаны расстояния между некоторыми звездами в созвездиях Большой и Малой медведиц . По ним можно «откалибровать» пальцы для небесных измерений. Средние результаты приблизительно таковы:

Как это работает? Просто полностью вытяните руку и расположите пальцы так, как на изображении, чтобы измерить угловое расстояние между интересующими вас объектами.

Он также имеет меньшие угловые размеры. Если элемент близок к нам, мы видим много деталей, если далеко — просто общий план. В общем, мы видим объекты ближнего и дальнего, благодаря которым мы имеем шкалу сравнения. Однако мы скучаем по луне, солнцу и звездам, потому что они слишком далеко. Мы видим звезды как точки, независимо от расстояния, которое они от нас.

Следует отметить, что основными препятствиями для развития наблюдательной астрономии были: отсутствие возможности измерения расстояния и отсутствие учета влияния вращения Земли. Почему было так сложно определить угол параллакса? Расстояния до звезд оказались намного большими, чем ожидалось. Параллакс ближайшей звезды составляет приблизительно 0, 78. Это звезда по имени Проксима Центавра. Слово «Проксима» просто означает «ближайший». Эта звезда расположена в южном полушарии неба, в созвездии Кентавра.

Градусы — довольно большая величина для небесных тел. Говоря об их размерах и расстояниях между ними, часто используют минуты (′) и секунды (″) дуги. Здесь все предельно просто: в одном градусе 60 минут, а в одной минуте… сами догадаетесь, сколько секунд? Секунда дуги — величина очень маленькая. Примерно такой угловой диаметр имеет пятирублевая монета с расстояния в 4 километра. Невооруженный глаз, каким бы орлиным он ни был, никогда не увидит ее.

Какие единицы используются для описания расстояния звезд и планет?

Вместе с двойной звездой Центавра создает трехзвездную систему. Обозначение первого параллакса для звезд не было единственным свидетельством движения Земли вокруг Солнца. Чтобы описать расстояние, астрономы используют единицу, непосредственно связанную с углом параллакса. Это устройство, и его определение очень просто.

Например: проксимальный параллакс равен 0, 78, поэтому его расстояние от Земли. Это удобная единица — две самые близкие нам звезды далеки друг от друга около 1 парсека. Также используются кратные единицы: килопарсек и мегапарсек. Благодаря тригонометрии, которую вы скоро узнаете в школе, вы можете рассчитать, сколько километров оно подходит в одном парсеку.

И напоследок приведу примеры угловых расстояний и размеров на небесной сфере .

Солнце и Луна имеют диаметр 0,5° (30′).
Расстояние между составляет 12′.
Невооруженный глаз человека способен видеть объекты с угловым размером минимум 1′.
Венера достигает диаметра 1′.
Максимальный угловой размер Юпитера — 45″, а Сатурна — 22″.
В 100-мм телескоп нельзя увидеть объекты с угловым диаметром менее полутора секунд дуги.

Популярным подразделением, используемым в научно-популярных статьях, является одно. Рассчитайте, сколько километров и метров — 1 световой год, и сколько световых лет — один парсек. Мы уже знаем, как определить расстояние до звезд. Однако галактика намного больше; расстояние до других галактик также намного больше. Как определяются такие огромные расстояния? Мы упомянем об этом позже в учебнике.

Можно ли использовать другие методы для определения расстояний? Открытие трех законов Кеплера, описывающих планетарное движение, позволило нам рассчитать расстояния от планет до Солнца. Предположим, однако, что единица расстояния, равная 1, соответствует расстоянию между Землей и Солнцем.

• Средний суточный параллакс Луны 57″02″,61.
• Среднее расстояние Луны от Земли 384 400 км.
• Наибольшее удаление Луны от Земли в апогее 405 500 км.
• Наименьшее удаление Луны от Земли в перигее 363 300 км.
• Видимый угловой диаметр Луны на среднем расстоянии от Земли 31″05″,16 = 1865″, 16.
• Наибольший видимый угловой диаметр Луны 32″53″,5.
• Наименьший видимый угловой диаметр Луны 29″28″,1.
• Диаметр Луны 3476,0 км = 0,2725 экв. диаметра Земли (примерно 3/11 земного).
• Объем Луны 21,99·10 9 км 3 = 0,02 объема Земли (примерно 1/50 земного).
• Площадь поверхности Луны 37,96·10 6 км 2 = 0,074 площади поверхности Земли (примерно 1/14 земной).
• Масса Луны 7.35·10 25 г. = 0,0123 массы Земли (1/81,30 земной).
• Средняя плотность Луны 3,34 г/см 3 = 0,607 средней плотности Земли.
• Ускорение силы тяжести па поверхности Луны 1,623 м/с 2 = 0,166 земного (примерно 1/6 земного).
• Первая космическая скорость для Луны 1,68 км/с.
• Вторая космическая скорость для Луны (скорость освобождения) 2,38 км/с.
• Средний эксцентриситет лунной орбиты 0,055 (линейный эксцентриситет 21 000 км).
• Эксцентриситет лунной орбиты меняется от 0,044 до 0,072.
• Наклон лунной орбиты к эклиптике 5°08″43″,4.
• Наклон лунной орбиты к эклиптике меняется от 5°17″ до 4°59″.
• Средний наклон лунного экватора к орбите 6°41″.
• Наклон лунного экватора к орбите меняется от 6°51″ до 6°31″.
• Наклон лунного экватора к эклиптике 1°32″47″.
• Наклон лунной орбиты к земному экватору меняется от 18°18″ до 28°36″.
• Наибольшее значение либрании по долготе 7°54″.
• Наибольшее значение либрации по широте 6°50″.
• Параллактическая либрация около 1°.
• Невидимая с Земли часть поверхности Луны составляет 41% всей лунной поверхности.
• Либрационные зоны составляют 18% всей лунной поверхности.
• Видимая угловая скорость движения Луны по небу 13°,2 в сутки (примерно 30″ в час).
• Средняя скорость движения Луны по орбите 1,023 км/с (примерно 3681 км/час).
• Ускорение Луны в ее движении вокруг Земли 0,272 см/с 2 .
• Сидерический месяц, равный периоду вращения Луны, 27 сут. 07 час. 43 мин. 11,47 с = 27,321661 суток (примерно 655,7 час).
• Синодический месяц, равный периоду смены фаз Луны (фазовому циклу), 29 сут. 12 час. 44 мин. 02,78 с = 29,5305882 суток (примерно 708,7 час).
• Продолжительность синодического месяца меняется вследствие эллиптичности лунной орбиты от 29,25 сут. до 29,83 сут, (примерно на 13 час).
• Тропический месяц 27,321582 суток.
• Аномалистический месяц 27,554551 суток.
• Драконический месяц 27,212220 суток.
• Период вращения линии узлов 6798 сут. = 18,61 лет.
• Период вращения линии апсид 3232 сут. = 8,85 лет.
• Угловая скорость вращения линии апсид примерно 40° в год.
• Максимум отраженного излучения Луны приходится примерно на длину волны 0,6 мкм.
• Максимум собственного излучения Луны приходится примерно на длину волны 7 мкм.
• Визуальная звездная величина Луны в истинное полнолуние — 12 m ,91.
• Освещенность от Луны на расстоянии Земля — Луна в истинное полнолуние 0,449 лк.
• Геометрическое альбедо Луны в истинное полнолуние 0,147.
• Фазовый интеграл Луны в системе истинного полнолуния 0,509.
• Сферическое альбедо Луны в истинное полнолуние 0,075.
• Средняя визуальная звездная величина Луны в полнолуние, наблюдаемая с Земли, —12 m ,71 (полная Луна светит в 465 000 раз слабее Солнца).
• Средняя яркость полной Луны, наблюдаемой с Земли, 0,251 сб.
• Средняя освещенность, создаваемая полной Луной, находящейся в зените, на земной поверхности, перпендикулярной к направлению падающих лучей, 0,25 лк.
• Среднее альбедо всей лунной поверхности 12,44%.
• Среднее альбедо материковых областей Луны 13,45%.
• Среднее альбедо морских областей Луны 7,30%. Показатель цвета Луны В — V = +1 m ,2.
• Среднее значение максимальной степени поляризации света лунной поверхностью (при фазовых углах 100—110°) 6—8%.
• Максимальная степень поляризации материковых областей Луны 6,5-7,5%.
• Максимальная степень поляризации морских областей Луны 12—16%.
• Температура поверхности Луны в подсолнечной точке около + 130° С.
• Температура поверхности Луны на ночной стороне около — 160 — 170° С.
• Концентрация газов у поверхности Луны в дневное время на освещенной стороне 104 см -3 (10 -13 концентрации молекул газов в земной атмосфере).
• Концентрация газов у поверхности Луны в ночное время (на темной стороне) 2·10 5 см -3 .
• Общая площадь морских образований на поверхности Луны составляет 16,9%.
• Площадь морей на видимом полушарии Луны составляет 31,2% поверхности.
• Площадь морей на обратном полушарии Луны составляет 2,6% поверхности.
• Среднее отношение глубины к диаметру лунных кратеров 0,2.
• Средняя толщина слоя реголита 2—3 м.
• Возраст древних материковых пород Луны 4,3—4,6 млрд. лет.
• Средний возраст лунных базальтов Имбирийской системы 3,7 млрд.лет.
• Средний возраст лунных базальтов Эратосфеновской системы 3,2 млрд. лет.
• Возраст кратера Коперник 0,85 млрд. лет.
• Средняя мощность лунной коры на видимом полушарии 60 км.
• Средняя мощность лунной коры на обратном полушарии 100 км.
• Плотность анортозитовых пород Луны 2,9 г/см 3 .
• Плотность базальтовых пород Луны 3,3 г/см 3 .

Как рассчитать угловой диаметр Солнца

Обновлено 7 декабря 2019 г.

Кевин Бек

Солнце является основным источником энергии для всех процессов на Земле. Он долгое время был законным источником удивления для людей разных культур, которые осознали его фундаментальную сущность еще до того, как смогли понять, что это такое или из чего оно сделано.

Задумывались ли вы когда-нибудь над тем, какой большой «кусок» неба занимает солнце по отношению ко всему? Например, если вы думаете о небе как о гигантской полусфере, покрывающей все, что над вами и вокруг вас, от каждой точки на горизонте до зенита прямо над головой, какую часть этого поглощает важнейшее солнце?

Ответ может вас удивить, и путь к нему поучителен как в геометрии, так и в астрономии.

Факты о Солнце

Земля вращается вокруг Солнца на среднем расстоянии около 93 миллионов миль, или миль (150 миллионов километров, или км; 1,5 × 10 ¹¹ м). Его диаметр или расстояние в самом широком месте составляет около 870 000 миль (1 400 000 км или 1,4 × 10 ⁹ м), что делает его почти в 100 раз шире Земли. Солнечному свету требуется около восьми минут, чтобы достичь Земли, а это значит, что если он вдруг исчезнет, ​​у вас будет достаточно времени, чтобы прослушать одну или две песни, прежде чем вы поймете, что что-то не так.

Достаточно ли одной этой информации, чтобы понять, насколько большим «выглядит» солнце? Для этого вы обращаетесь к величине в тригонометрии, называемой угловым диаметром.

Что такое угловой диаметр?

Угловой диаметр — это, по сути, угол, а не диаметр. Это угол, под которым объект «поднимается», как его видит наблюдатель на определенном расстоянии. Это можно измерить в градусов (°) или радиан (рад). Один круг занимает 360° и 2π рад, поэтому 1 рад = 360/2π = 57,3°.

Если бы вы смотрели на север и стояли перед массивным полукуполом, достигающим точно в зенит над вами и точками на горизонте на востоке и западе, то купол имел бы угловой диаметр 90° (π /2 рад).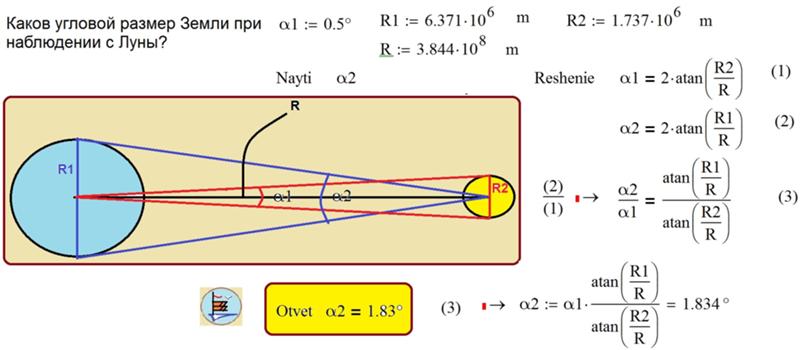 Это означает, что он занимает половину вашего доступного поля зрения. Если вы полностью повернете голову на восток или на запад, ничего не изменится, но если вы повернетесь лицом к югу, вы увидите все оставшиеся 90° неба, если вы повернете голову на восток, а затем на на запад от этой южной позиции.

Расчет углового диаметра

Важно помнить, что угловой диаметр не является неотъемлемым свойством объекта. Солнце имело бы больший угловой диаметр на Меркурии, ближайшей к Солнцу планете, чем на Земле, а на далеком Сатурне он был бы намного меньше.

Формула для углового диаметра α объекта диаметром D на расстоянии r :

α = 2 \arctan \bigg(\frac{D}{2r}\bigg) 9{11}\text{ m}}\bigg) \\ &= 2 \arctan (0,0047) \\ &= 2 × 0,270° \\ &= 0,54° \end{aligned}

Таким образом, солнце занимает примерно половину градус неба – примерно 1/360 часть доступных 180° неба.

Солнце и Луна: угловой диаметр

Если вы заметили, что луна и солнце кажутся примерно одинакового размера (решение затруднено тем фактом, что вы не можете или не должны смотреть прямо на солнце невооруженным глазом) вы правы.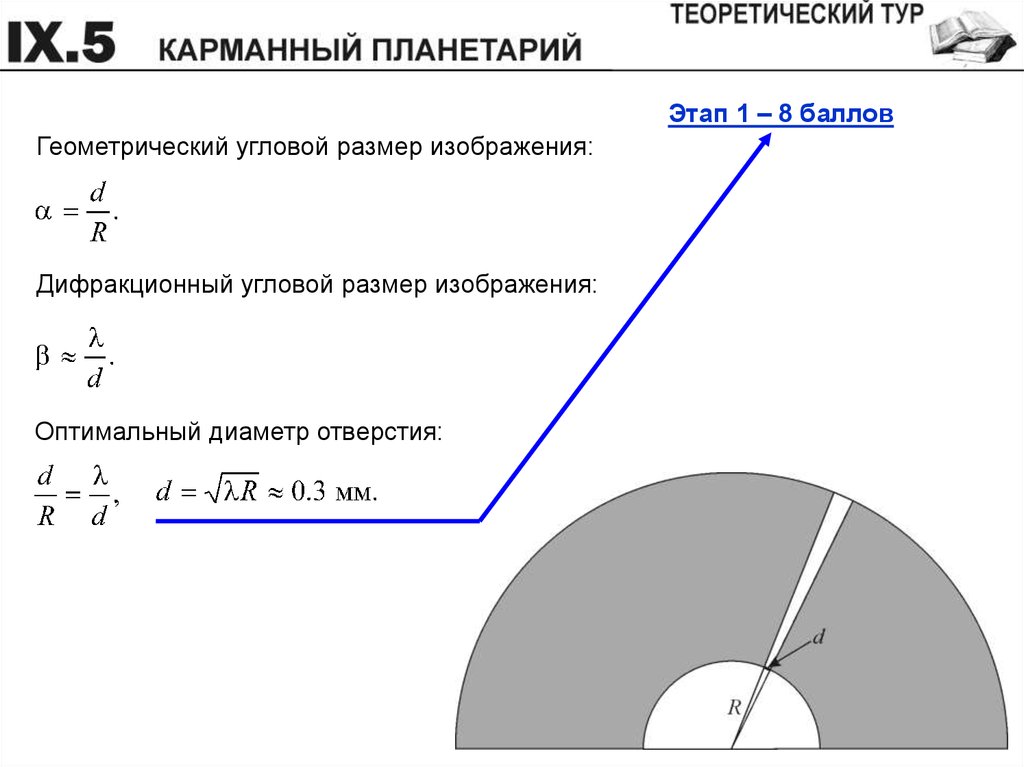 Диаметр Луны примерно в 400 раз меньше диаметра Солнца, но она также примерно в 400 раз ближе к Земле, чем Солнце.

Угловой размер | Imaging the Universe

Ресурсы: Рабочий лист (PDF),   Онлайновый рабочий лист (PDF), Онлайновый рабочий лист (текстовый документ), Stellarium Web, Карты Google, Рулетки, Метры, Линейки, Бумага, Лента, Скрепки, Зажимы для переплета 

Терминология: Формула малого угла, формула процентной погрешности

Всякий раз, когда вы смотрите на объект, вы измеряете его угловой размер — количество места, которое он занимает в поле вашего зрения, в градусах, минутах ( 1/60 1 градуса) и секунды (1/60 1 минуты или 1/3600 1 градуса). Или вы можете количественно определить угловой размер в радианах, если вы склонны к математике. Вы не можете напрямую измерить размер объекта в сантиметрах или дюймах, если не подойдете к нему и не воспользуетесь линейкой. Вы знаете, что удаленные объекты кажутся маленькими, а близлежащие объекты кажутся большими, поэтому, когда вы смотрите на объект, ваш мозг объединяет угловой размер объекта с вашим предположением о расстоянии до него, чтобы дать вам представление о его реальном размере.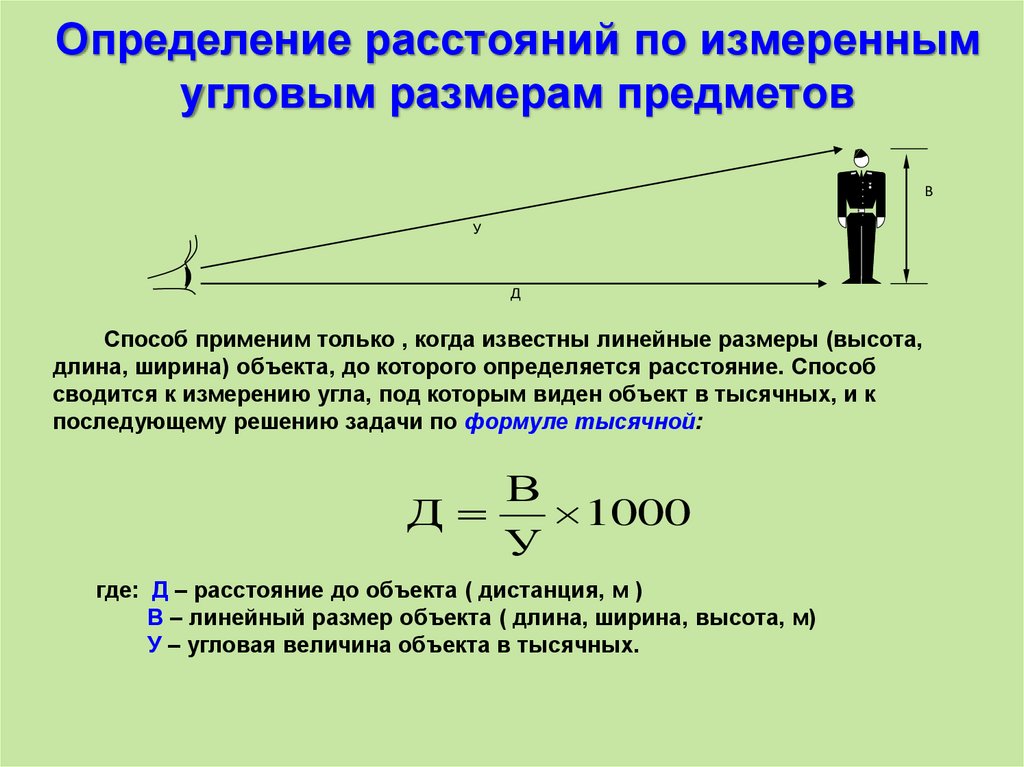

Люди развили бинокулярное зрение, чтобы помочь нам угадывать расстояние до объектов, которые могут повлиять на наше выживание (например, львов, тигров и медведей — о боже!). Чтобы определить расстояние до чего-либо, наш мозг также использует кажущиеся размеры хорошо известных объектов рядом с интересующим объектом, таких как здания и деревья в непосредственной близости от объекта. В астрономии размеры более неопределенны; объекты, которые кажутся близкими друг к другу в небе, на самом деле могут находиться на расстоянии многих световых лет друг от друга. Нашим основным измерением размера в астрономии является угловой размер.

Чтобы узнать истинный физический размер объекта, мы должны сначала записать угловой размер и найти расстояние до объекта каким-либо независимым методом. И наоборот, если известен физический размер объекта, его можно объединить с его видимым угловым размером, чтобы определить расстояние до него. В этих отношениях всегда можно рассчитать третью желаемую величину, если известны две величины; это делается с помощью формулы малого угла.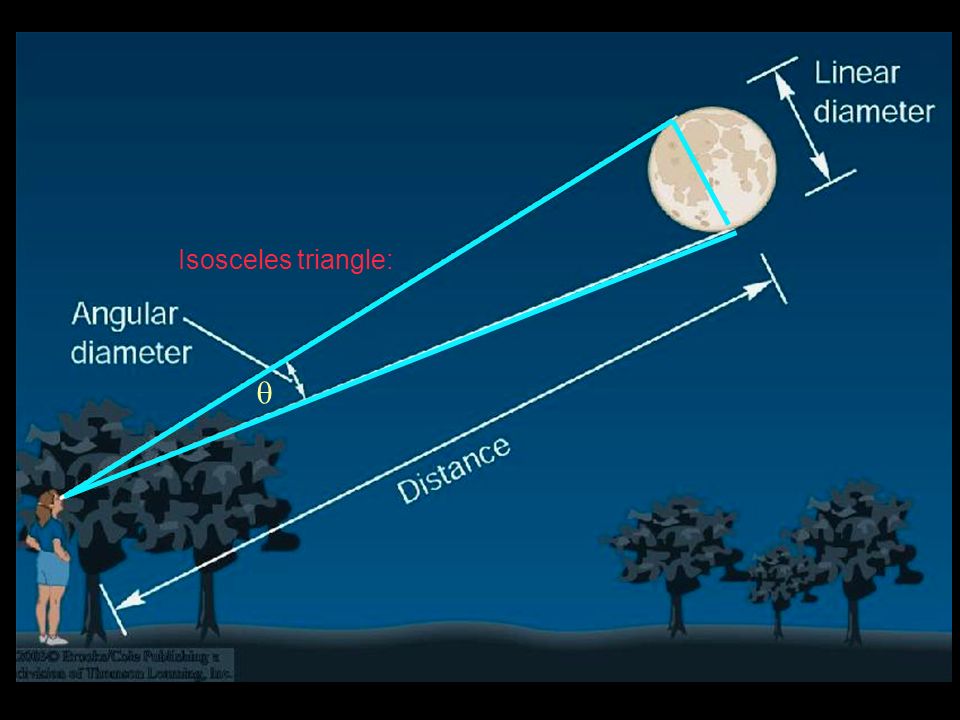

Сложные и точные инструменты существуют и могут быть созданы для измерения угловых размеров объектов, но набор инструментов для грубого измерения можно найти на конце руки большинства людей. Поскольку люди построены в основном с одинаковыми пропорциями, если вы держите руки вытянутыми ладонями вперед, ваши руки будут иметь примерно одинаковый угловой размер в поле вашего зрения, независимо от того, высокий вы, низкий, большой или маленький. Ваши пальцы и суставы можно использовать для грубых измерений угловых размеров и расстояний на небе, как показано на диаграмме справа.

Существуют и другие полезные линейки угловых размеров. Например, полная Луна имеет размер почти ровно полградуса, если смотреть с поверхности Земли. Некоторые созвездия и астеризмы простираются на определенное количество градусов неба.

Цели обучения: Учащиеся узнают, как расстояние до объекта, его физический размер и угловой размер соотносятся друг с другом, и узнают, как астрономы используют это соотношение для определения размеров удаленных объектов.