Примеры на сложение дробей: Сложение и вычитание дробей с разными знаменателями — урок. Математика, 5 класс.

Сложение дробей, формулы и примеры решений

Содержание:

• Сложение дробей с одинаковыми знаменателями
• Сложение дробей с разными знаменателями
• Сложение смешанных дробей

Сложение дробей с одинаковыми знаменателями

Определение

Суммой двух дробей с одинаковыми знаменателями называется дробь, числитель которой равен сумме числителей исходных дробей, а знаменатель — знаменателю дробей, то есть

$\frac{a}{b}+\frac{c}{b}=\frac{a+c}{b}$

Чтобы сложить две дроби с одинаковым знаменателем, надо сложить их числители и результат записать в числитель, а знаменатель оставить без изменения.

Пример

Задание. Найти сумму дробей  $\frac{3}{11}$  и  $\frac{7}{11}$ 

Решение.   $\frac{3}{11}+\frac{7}{11}=\frac{3+7}{11}=\frac{10}{11}$

Ответ.   $\frac{3}{11}+\frac{7}{11}=\frac{10}{11}$

Если в результате сложения получается дробь, числитель и знаменатель которой можно сократить, то для конечного результата выполняем и сокращение дроби.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти сумму дробей  $\frac{3}{14}$  и  $\frac{11}{14}$ 

Решение. Складываются дроби с одинаковым знаменателем, поэтому просто складываем числитель, а знаменатель оставляем исходный:

$\frac{3}{14}+\frac{11}{14}=\frac{14}{14}$

Полученная дробь $\frac{14}{14}$ является неправильной, у которой числитель равен знаменателю, и такая дробь равна единице, то есть

$\frac{3}{14}+\frac{11}{14}=\frac{14}{14}=1$

Ответ.   $\frac{3}{14}+\frac{11}{14}=1$

Сложение дробей с разными знаменателями

Определение

Чтобы сложить дроби с разными знаменателями, вначале надо привести их к общему знаменателю, а далее складывать как дроби с общим знаменателем.

{3}}{8}=\frac{2 \cdot 8+1 \cdot 3}{24}=\frac{16+3}{24}=\frac{19}{24}$

Ответ.   $\frac{2}{3}+\frac{1}{8}=\frac{19}{24}$

Замечание. После первого знака равенства справа вверху у каждой дроби указан дополнительный множитель к ней.

Сложение смешанных дробей

Определение

Чтобы сложить смешанные дроби, надо отдельно найти сумму целых частей и отдельно сумму дробных частей.

Пример

Задание. Вычислить сумму дробей  3$\frac{2}{5}$  и  4$\frac{7}{10}$ 

Решение. В данном случае складываем отдельно целые и дробные части:

$3 \frac{2}{5}+4 \frac{7}{10}=(3+4)+\left(\frac{2}{5}+\frac{7}{10}\right)$

Так как знаменатели дробных частей разные, то приводим дроби к общему знаменателю, который равен 10, так как НОК знаменателей 5 и 10. Соответственно дополнительные множители, как частные общего знаменателя и знаменателей дробей, равны 2 и 1:

$3 \frac{2}{5}+4 \frac{7}{10}=7+\frac{2^{2}}{5}+\frac{7^{1}}{10}=7+\frac{2 \cdot 2+7 \cdot 1}{10}=7+\frac{11}{10}=7 \frac{11}{10}$

Так как дробная часть представляет собой неправильную дробь, то выделяем целую часть:

$3 \frac{2}{5}+4 \frac{7}{10}=7 \frac{11}{10}=7\left(1+\frac{1}{10}\right)=8 \frac{1}{10}$

Ответ.   $3 \frac{2}{5}+4 \frac{7}{10}=8 \frac{1}{10}$

Читать следующую тему: вычитание дробей.

Задачи на сложение и вычитание дробей

Лёгкий

Задача 1

Вычислите сумму дробей: [tex]\frac{1}{5}+\frac{2}{5}[/tex]

[tex]\frac{2}{5}[/tex]

[tex]\frac{1}{5}[/tex]

[tex]\frac{3}{10}[/tex]

[tex]\frac{3}{5}[/tex]

Задача 2

Найдите значение [tex]\frac{3}{7}+\frac{2}{7}[/tex]

[tex]\frac{5}{14}[/tex]

[tex]\frac{5}{7}[/tex]

[tex]\frac{1}{7}[/tex]

[tex]\frac{6}{7}[/tex]

Задача 3

Вычислите [tex]\frac{1}{3}+\frac{2}{3}[/tex]

$\frac{4}{3}$

$\frac{2}{3}$

$1$

$3$

Задача 4

Посчитайте значение: [tex]\frac{2}{15}+\frac{5}{15}[/tex]

$\frac{7}{30}$

$\frac{7}{15}$

$\frac{10}{15}$

$\frac{1}{3}$

Задача 5

Найдите сумму дробей: [tex]\frac{8}{11}+\frac{4}{11}[/tex]

[tex]\frac{12}{22}[/tex]

[tex]\frac{13}{11}[/tex]

[tex]\frac{10}{11}[/tex]

[tex]\frac{12}{11}[/tex]

Задача 6

Вычислите [tex]\frac{2}{187}-\frac{2}{187}[/tex]

$0$

$1$

$2$

$\frac{1}{187}$

Задача 7

Вычислите [tex]\frac{13}{39}-\frac{8}{39}[/tex]

$\frac{5}{39}$

$5$

$\frac{4}{39}$

$\frac{21}{39}$

Задача 8

Найдите значение [tex]\frac{18}{19}-\frac{11}{19}[/tex]

$\frac{7}{9}$

$\frac{29}{19}$

$\frac{6}{19}$

$\frac{7}{19}$

Задача 9

Найдите значение [tex]\frac{15}{8}-\frac{14}{8}[/tex]

[tex]\frac{1}{8}[/tex]

[tex]8[/tex]

[tex]\frac{2}{8}[/tex]

[tex]\frac{13}{8}[/tex]

Задача 10

Найдите значение [tex]\frac{19}{27}-\frac{6}{27}[/tex]

[tex]\frac{1}{3}[/tex]

[tex]\frac{12}{27}[/tex]

[tex]\frac{14}{27}[/tex]

[tex]\frac{13}{27}[/tex]

Задача 11

Найдите сумму дробей [tex]\frac{2}{5}[/tex] и [tex]\frac{1}{5}[/tex]

[tex]\frac{1}{5}[/tex]

[tex]\frac{2}{5}[/tex]

[tex]\frac{3}{5}[/tex]

[tex]\frac{4}{5}[/tex]

Задача 12

Вычислите [tex]\frac{5}{6}+\frac{10}{6}[/tex]

$\frac{15}{3}$

$\frac{50}{36}$

$\frac{5}{3}$

$\frac{5}{2}$

Задача 13

Определите значение [tex]\frac{6}{7}-\frac{4}{7}[/tex]

[tex]\frac{1}{7}[/tex]

[tex]\frac{2}{7}[/tex]

[tex]\frac{3}{7}[/tex]

[tex]2[/tex]

Задача 14

Вычтите [tex]\frac{5}{13}[/tex] из [tex]\frac{14}{13}[/tex]

[tex]\frac{19}{13}[/tex]

[tex]\frac{9}{13}[/tex]

[tex]1\frac{9}{13}[/tex]

[tex]\frac{8}{13}[/tex]

Задача 15

Вычислите [tex]\frac{3}{18}+\frac{15}{18}[/tex]

[tex]1[/tex]

[tex]\frac{1}{18}[/tex]

[tex]\frac{17}{18}[/tex]

[tex]\frac{19}{18}[/tex]

Задача 16

Найдите значение [tex]\frac{2}{7}+\frac{3}{7}-\frac{5}{7}[/tex]

[tex]\frac{1}{7}[/tex]

[tex]1[/tex]

[tex]\frac{6}{7}[/tex]

[tex]0[/tex]

Задача 17

Выполните сложение дробей: [tex]\frac{8}{91}+\frac{13}{91}[/tex]

[tex]\frac{20}{91}[/tex]

[tex]\frac{21}{91}[/tex]

[tex]\frac{22}{91}[/tex]

[tex]\frac{23}{91}[/tex]

Задача 18

Вычтите дроби: [tex]\frac{15}{45}-\frac{5}{45}[/tex]

[tex]\frac{3}{5}[/tex]

[tex]\frac{3}{9}[/tex]

[tex]\frac{20}{45}[/tex]

[tex]\frac{2}{9}[/tex]

Задача 19

Сложите дроби: [tex]\frac{5}{6}+\frac{4}{6}[/tex]

[tex]\frac{4}{3}[/tex]

[tex]1\frac{1}{2}[/tex]

[tex]\frac{9}{12}[/tex]

[tex]\frac{5}{3}[/tex]

Задача 20

Сложите дроби: [tex]\frac{43}{56}+\frac{13}{56}[/tex]

[tex]\frac{54}{56}[/tex]

[tex]\frac{55}{56}[/tex]

$1$

$2$

Задача 21

Найдите сумму дробей: [tex]\frac{1}{10}+\frac{7}{10}[/tex]

[tex]\frac{4}{5}[/tex]

[tex]\frac{3}{5}[/tex]

[tex]\frac{7}{10}[/tex]

[tex]\frac{9}{10}[/tex]

Задача 22

Выполните вычитание дробей: [tex]\frac{5}{18}-\frac{1}{18}[/tex]

[tex]\frac{1}{9}[/tex]

[tex]\frac{1}{4}[/tex]

[tex]\frac{3}{9}[/tex]

[tex]\frac{2}{9}[/tex]

Задача 23

Сложите дроби: [tex]\frac{5}{18}[/tex] и [tex]\frac{16}{18}[/tex]

[tex]1\frac{5}{6}[/tex]

[tex]\frac{8}{6}[/tex]

[tex]1\frac{1}{6}[/tex]

[tex]\frac{5}{6}[/tex]

Задача 24

Вычтите дроби: [tex]\frac{6}{10}-\frac{1}{10}[/tex]

[tex]\frac{1}{5}[/tex]

[tex]\frac{1}{2}[/tex]

[tex]\frac{2}{5}[/tex]

[tex]\frac{7}{10}[/tex]

Лёгкий

Прислать задачу

Правильный:

Неверный:

Неразрешенные задачи:

Добавление дробей | Как складывать дроби + примеры

Сегодня мы рассмотрим несколько примеров сложения дробей .

Прежде чем читать этот пост, вы можете просмотреть предыдущий пост, в котором мы шаг за шагом объясняем, как складывать дроби.

Начнем с простейших примеров:

Сложение дробей с одинаковым знаменателем

Например:

Единственное, что нам нужно сделать, это добавьте числители и оставьте знаменатель в покое . Ответ: :

Сложение чисел и дроби

Например:

Первое, что нам нужно сделать в этом случае, это преобразовать 2 в дробь. Как вы уже знаете, мы можем просто поставить 1 в знаменателе любого числа, не меняя его значения:

Когда у нас есть две дроби, мы можем начать искать общий знаменатель . В этом примере это довольно просто, потому что это число является наименьшим общим кратным 1 и любого числа. Итак:

Теперь нам нужно только умножить 2 x 4, и мы получим:

… и теперь мы подставляем это в нашу задачу на сложение:

Сложение дробей с взаимно простыми знаменателями

Помните, что два числа взаимно просты, если их наибольший общий делитель равен 1 . Например, в задаче:

Знаменатели взаимно просты, потому что:

Задачи такого рода решить просто, потому что единственное, что нам нужно сделать, чтобы найти новые числители, — это умножить каждый числитель на знаменатель другой дроби, как показано ниже:

И мы просто умножаем знаменатели вместе. Итак, получаем:

и

И осталось только сложить две дроби вместе:

Сложение дробей в целом

Например:

Нам нужно вычислить наименьшее общее кратное знаменателя :

Что нам делать дальше? Давайте сломаем это. Сначала рассмотрим дробь:

Чтобы найти числитель , нам нужно разделить НОК на знаменатель дроби:

Нам нужно умножить числитель дроби на 2. Итак:

И мы видим, что новый числитель равен 6.

Для знаменателя нам просто нужно использовать GCM (18):

Теперь мы просто делаем то же самое с другой дробью. Чтобы найти числитель, нам нужно разделить:

И умножить на числитель:

Затем мы подставляем в GCM в качестве знаменателя, что дает нам:

Теперь все это осталось нужно сложить дроби вместе

…

И все!

На самом деле мы складываем все дроби таким образом, первые примеры были проще благодаря GCM, с которым было легче работать. Однако способ решения проблем всегда оставался одним и тем же.

Подводя итог, шагов для сложения дробей :

• Найдите GCM двух знаменателей.
• Разделите GCM на знаменатель и умножьте его на числитель, чтобы преобразовать каждую дробь в дробь, в которой GCM является новым знаменателем.
• Когда мы сделали два предыдущих шага со всеми дробями, расставим их по порядку и добавим их числители.

Если вы хотите продолжить изучение математики, зарегистрируйтесь на Smartick сегодня!

Удачи в сложении дробей — немного потренировавшись, вы увидите, что это совсем несложно, и у вас все получится!

Подробнее:

• Автор
• Последние сообщения

Smartick

Команда создания контента.

Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.

Последние сообщения Smartick (посмотреть все)

Дроби: сложение и вычитание дробей

Урок 3: сложение и вычитание дробей

/en/фракции/сравнение-и-сокращение-фракций/содержание/

Сложение и вычитание дробей

На предыдущих уроках вы узнали, что дробь является частью целого. Дроби показывают, сколько у вас есть чего-то, например, 1/2 бака бензина или 1/3 стакана воды.

В реальной жизни вам может понадобиться складывать или вычитать дроби. Например, вы когда-нибудь проходили 1/2 мили на работу, а затем шли еще 1/2 мили обратно? Или слить 1/4 литра бензина из бензобака, в котором было 3/4 литра? Вы, вероятно, не думали об этом в то время, но это примеры , складывающего и , вычитающего дроби.

Просмотрите слайд-шоу, чтобы узнать, как решать задачи на сложение и вычитание с дробями.

• Представим, что в рецепте торта сказано добавить в тесто 3/5 стакана масла.

• Вам также понадобится 1/5 стакана масла, чтобы смазать сковороду. Чтобы узнать, сколько всего масла вам понадобится, вы можете сложить вместе этих дробей.

• Когда вы складываете дроби, вы просто добавляете первых чисел или числителей .

• Это потому, что нижние числа или знаменателя показывают, сколько частей составит целое.

• Мы не хотим менять количество частей, составляющих целую чашку (5). Мы просто хотим выяснить, сколько частей нам нужно всего.

• Итак, нам нужно только сложить числители наших дробей.

• Мы можем сложить дроби так, чтобы числители выстроились. Это облегчит их добавление.

• И это все, что нам нужно сделать, чтобы настроить пример сложения с дробями. Теперь наши фракции готовы к добавлению.

• Мы сделаем то же самое, чтобы настроить пример вычитания. Допустим, у вас было 3/4 бака бензина, когда вы приступили к работе.

• Если вы используете 1/4 бака, чтобы добраться до дома, сколько у вас останется? Мы можем вычесть этих дробей, чтобы узнать.

• Точно так же, как при сложении, мы будем складывать наши дроби, чтобы числители выровнялись.

• Это потому, что мы хотим вычесть 1 часть из 3 частей.

• Теперь, когда наш пример настроен, мы готовы к вычитанию!

Попробуйте!

Попробуйте решить эти задачи на сложение и вычитание с дробями. Не пытайтесь их решить!

Утром вы пробегаете 4/10 мили. Позже вы бежите 3/10 мили.

У вас было 7/8 пачки масла, и вы использовали 2/8 пачки во время приготовления обеда.

Ваш бензобак заполнен на 2/5, и вы заправляете еще 2/5 бака.

Решение задач на сложение с дробями

Теперь, когда мы знаем, как писать задачи на сложение с дробями, давайте попрактикуемся в решении некоторых из них. Если вы можете складывать целые числа, вы готовы складывать дроби.

Щелкните слайд-шоу, чтобы узнать, как складывать дроби.

• Давайте продолжим наш предыдущий пример и добавим следующие части: 3/5 стакана масла и 1/5 стакана масла.

• Помните, что когда мы складываем дроби, мы не складываем знаменатели.

• Это потому, что мы находим, сколько всего частей нам нужно. Числители показывают, какие части нам нужны, поэтому мы добавим 3 и 1.

• 3 плюс 1 равно 4. Убедитесь, что 4 выровнены с числами, которые вы только что добавили.

• Знаменатели останутся прежними, поэтому мы напишем 5 внизу нашей новой дроби.

• 3/5 плюс 1/5 равно 4/5. Итак, вам понадобится 4/5 стакана масла всего , чтобы приготовить торт.

• Возьмем другой пример: 7/10 плюс 2/10.

• Как и прежде, мы будем добавлять только числители. В этом примере числители 7 и 2.

• 7 плюс 2 равно 9, поэтому мы напишем это справа от числителей.

• Как и в нашем предыдущем примере, знаменатель остается прежним.

• Итак, 7/10 плюс 2/10 равно 9/10.

Попробуйте!

Попробуйте решить некоторые из приведенных ниже задач на сложение.

Решение задач на вычитание с дробями

Вычитание дробей очень похоже на обычное вычитание. Если вы можете вычитать целые числа, вы можете вычитать и дроби!

Просмотрите слайд-шоу, чтобы узнать, как вычитать дроби.

• Давайте воспользуемся нашим предыдущим примером и вычтем 1/4 бака бензина из 3/4 бака.

• Как и в дополнение, мы не собираемся менять знаменатели.

• Мы не хотим менять количество деталей, из которых состоит целый бак бензина. Мы просто хотим знать, сколько деталей у нас останется.

• Начнем с вычитания числителей. 3 минус 1 равно 2, поэтому мы напишем 2 справа от числителя.

• Как и при сложении, знаменатель нашего ответа будет таким же, как и другие знаменатели.

• Итак, 3/4 минус 1/4 равно 2/4. Когда вы вернетесь домой, у вас останется 2/4 бака бензина.

• Попробуем решить другую задачу: 5/6 минус 3/6.

• Начнем с вычитания числителей.

• 5 минус 3 равно 2. Итак, мы поставим 2 справа от числителя.

• Как обычно, знаменатель остается прежним.

• Итак, 5/6 минус 3/6 равно 2/6.

Попробуйте!

Попробуйте решить некоторые из приведенных ниже задач на вычитание.

После сложения или вычитания дробей иногда может получиться дробь, равная сократил до более простой дроби.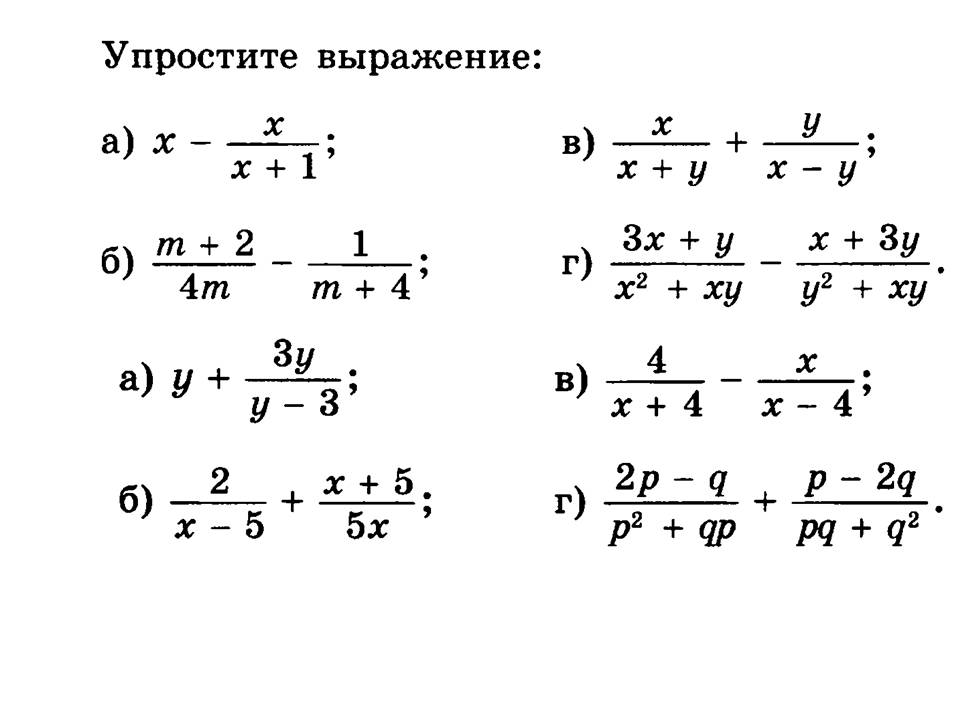 Как вы узнали из раздела «Сравнение и сокращение дробей», всегда лучше сократить дробь до ее простейшей формы , когда это возможно. Например, 1/4 плюс 1/4 равно 2/4. Поскольку 2 и 4 можно разделить на 2, мы можем уменьшить 2/4 до 1/2.

Сложение дробей с разными знаменателями

На прошлой странице мы узнали, как складывать дроби с одинаковыми знаменателями, например 1/4 и 3/4. Но что, если вам нужно сложить дроби с разных знаменателя ? Например, в нашем рецепте торта можно сказать, что нужно медленно смешать 1/4 стакана молока, а затем добавить еще 1/3 стакана.

В разделе «Сравнение и сокращение дробей» мы сравнили дроби с другим нижним числом или знаменателем. Нам пришлось изменить дроби, чтобы их знаменатели были одинаковыми. Для этого мы нашли наименьший общий знаменатель или LCD .

Мы можем складывать или вычитать дроби, только если у них одинаковые знаменатели.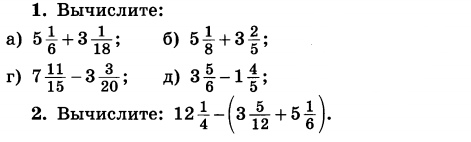 Поэтому нам нужно найти наименьший общий знаменатель, прежде чем складывать или вычитать эти дроби. Когда дроби имеют одинаковый знаменатель, мы можем складывать или вычитать, как обычно.

Просмотрите слайд-шоу, чтобы узнать, как складывать дроби с разными знаменателями.

• Добавим 1/4 и 1/3.

• Прежде чем мы сможем сложить эти дроби, нам нужно изменить их так, чтобы они имели одинаковый знаменатель .

• Для этого нам нужно найти LCD , или наименьший общий знаменатель чисел 4 и 3. и 4, значит 12 это наша ЖК-дисплей .

• Поскольку 12 — это LCD, это будет новый знаменатель наших дробей.

• Теперь изменим числители дробей так же, как мы изменили знаменатели.

• Во-первых, давайте посмотрим на дробь слева: 1/4.

• Чтобы преобразовать 4 в 12, мы умножаем его на 3.

• Поскольку знаменатель умножался на 3, мы также умножаем числитель на 3.

• 1 умножить на 3 равно 3.

• 1/4 равно 3/12.

• Теперь посмотрим на дробь справа: 1/3. Мы также изменили его знаменатель на 12.

• Наш старый знаменатель был 3. Мы умножили его на 4, чтобы получить 12.

• Мы также умножим числитель на 4. 1 умножить на 4 равно 4.

• Итак, 1 /3 равно 4/12.

• Теперь, когда наши дроби имеют одинаковый знаменатель, мы можем сложить их, как обычно.

• 3 плюс 4 равно 7. Как обычно, знаменатель остается прежним. Таким образом, 3/12 плюс 4/12 равно 7/12.

Попробуйте!

Попробуйте решить приведенные ниже задачи на сложение.

Вычитание дробей с разными знаменателями

Мы только что видели, что дроби можно складывать только тогда, когда у них один и тот же знаменатель. То же самое верно, когда мы вычитаем дроби. Прежде чем мы сможем вычитать, нам нужно изменить наши дроби, чтобы у них был один и тот же знаменатель.

Просмотрите слайд-шоу, чтобы узнать, как вычитать дроби с разными знаменателями.

• Попробуем вычесть 1/3 из 3/5.

• Во-первых, мы изменим знаменатели обеих дробей, чтобы они были одинаковыми, найдя наименьший общий знаменатель .

• Похоже, 15 — это наименьшее число, которое можно разделить без остатка на 3 и 5, поэтому 15 — это наш ЖК-дисплей.

• Теперь изменим нашу первую дробь. Чтобы изменить знаменатель на 15, мы умножим знаменатель и числитель на 3.

• 5 умножить на 3 равно 15. Итак, наша дробь теперь равна 9/15.

• Теперь изменим вторую дробь. Чтобы изменить знаменатель на 15, мы умножим оба числа на 5, чтобы получить 5/15.

• Теперь, когда наши дроби имеют одинаковый знаменатель, мы можем вычитать, как обычно.

• 9 минус 5 равно 4. Как всегда, знаменатель остается прежним. Итак, 9/15 минус 5/15 равно 4/15.

Попробуйте!

Попробуйте решить приведенные ниже задачи на вычитание.

Сложение и вычитание смешанных чисел

На последних нескольких страницах вы практиковались в сложении и вычитании различных дробей. Но для некоторых проблем потребуется один дополнительный шаг. Например, можете ли вы сложить приведенные ниже дроби?

В разделе «Введение в дроби» вы узнали о смешанных числах . Смешанное число имеет как дробь , так и целое число . Например, 2 1/2 или 9.0003 два с половиной . Другой способ записать это будет 5/2, или пять половин . Эти два числа выглядят по-разному, но на самом деле они одинаковы.

5/2 — это неправильная дробь

. Это просто означает, что верхнее число на больше, чем нижнее число на . Несмотря на то, что неправильные дроби выглядят странно, их можно складывать и вычитать так же, как обычные дроби. Смешанные числа складывать непросто, поэтому сначала вам придется преобразовать их в неправильные дроби.

• Сложим эти два смешанных числа: 2 3/5 и 1 3/5.

• Нам нужно преобразовать эти смешанные числа в неправильные дроби. Начнем с 2 3/5.

• Как вы узнали из Урока 2, мы умножаем целое число 2 на нижнее число 5.

• 2 умножить на 5 равно 10. числитель , 3.

• 10 + 3 равно 13.

• Так же, как когда вы добавить дроби, знаменатель останется прежним. Наша неправильная дробь 13/5.

• Теперь нам нужно преобразовать наше второе смешанное число: 1 3/5.

• Сначала умножим целое число на знаменатель. 1 x 5 = 5.

• Далее мы добавим 5 к числителям. 5 + 3 = 8.

• Как и в прошлый раз, знаменатель остался прежним. Итак, мы изменили 1 3/5 на 8/5.

• Теперь, когда у нас изменил наши смешанные числа на неправильные дроби, мы можем складывать, как обычно.

• 13 плюс 8 равно 21.

  No related posts.