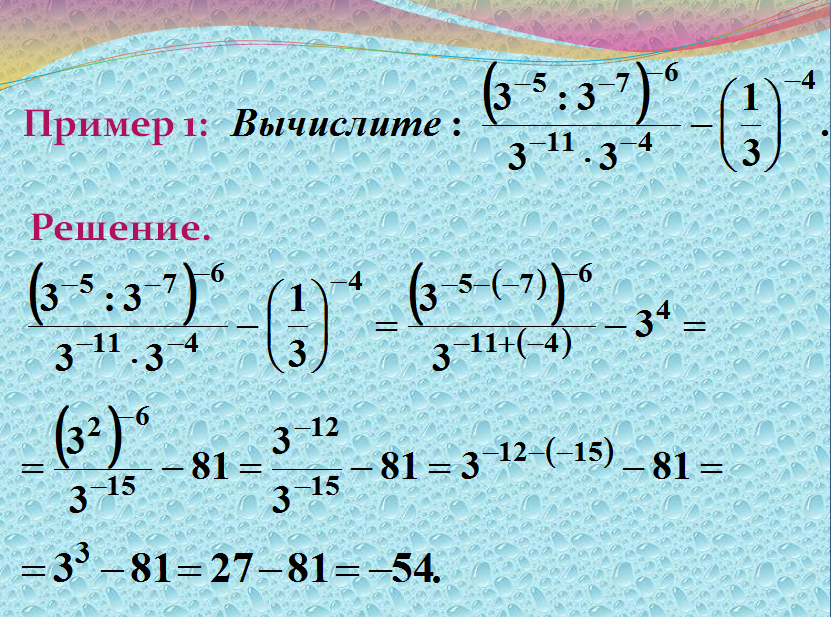Примеры решения свойства степеней: Свойства степеней, действия со степенями

alexxlab / / Разное

Свойства степени с натуральным показателем

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Свойства степени с натуральным показателем

Учитель математики Муниципального бюджетного
общеобразовательного учреждения Багаевской
средней общеобразовательной школы № 1
Алимова Надежда Ивановна
К этому уроку ученики знают понятие степени
с натуральным показателем, основные
свойства степени с натуральным
показателем, умеют применять свойства при
решении примеров, владеют навыками
упрощения выражений
Оборудование: мультимедийная презентация,
сигнальные карточки, перфокарты, учебник, тесты с
выбором ответа, карта для самооценки, смайлики для
рефлексии.
Необходимое аппаратное и программное
обеспечение
(мультимедийный проектор, программные средства)
Программы MS PoverPoint, MS Word.
Компьютер и мультимедийный проектор
лабиринт
1). х
16
2). х
16
х
х 32
н
:х
х 16
и
х0
и
х
б
3).(х 31 )1
4).( х х)
16
0
2
8
5).х х
6).х
15
7).(х
х
16 2
)
8). (х10 )10
31
х
15
х 10
х
100
х 17
а
р
т
л

4. Историческая справка

• С чем связана «путеводная нить»?
• Войдём в лабиринт
1. Что называется степенью
числа а с натуральным
показателем n?
2. Как перемножить две
степени с одинаковыми
основаниями?
3. Как разделить две степени с одинаковыми основаниями?
4. Как возвести степень в степень?
5. Как возвести произведение в степень?
6. Как возвести дробь в степень?
Степенью числа а с натуральным
показателем n называется
произведение n множителей,
каждый из которых равен a.
a a
a
…
a
n
n
множителей
Чтобы перемножить две степени
с одинаковыми основаниями
нужно основание оставить
прежним, а показатели сложить.
a а а
n
т
n m
a :а а
n
т
n m
Чтобы найти частное
двух степеней с
одинаковыми
основаниями нужно
основание оставить
прежним, а из
показателя делимого
вычесть показатель
делителя.
(a b) а b .
т
m
Чтобы возвести степень в степень нужно
основание оставить прежним, а показатели
перемножить.
m
Чтобы возвести дробь в
степень нужно в эту
степень возвести
числитель и знаменатель
дроби
n
a n a
( ) n
b
b .
• б) Соедините «Нитью Ариадны» верные равенства
а b
(5а 3b 5 ) 2
2)
а 2b 6
1 4 3 3
( а b )
2
3)
25а b
(а b )
1)
4)
5)
12 15
6 10
1 12 9
а b
8
1 6 9
а y
64
4
5 3
1 2 3 3
( а b )
4
(а b )
3 2
1)
2)
(-5) 2 ( 5) 3 0
( 7) ( 5) 3 0
2
3
4
3)
( 1) 2 ( 1)14 14 0 ( 1) 6
4)
3 n 3 n 3 n 33 n
5)
5n 5n 5n
3
n
5
+
+
+
+
Проверь себя!
Минотавр повержен!
Пройдём ещё один круг «лабиринта», а
впереди финишная прямая
Работа по группам
1 группа
1) Вычислить
2)
(33 3) 5 3 4
(37 ) 3
При каком значении k выполняется
равенство
5k 2
( 2 ) 5 8.
5
2 группа
1) Вычислить
(7 5 7) 5 7 7
(7 7 ) 5
2) При каком значении k выполняется равенство
4k 2
( 3 ) 4 6.
4
1 группа.
1) Решение:
(33 3) 5 34 3
3 27.
7 3
(3 )
Ответ: 27.
2)
5k 2 52k
( 2 ) 4 5 2 k 4 ;
5
5
5 2 k 4 58 ;
2k 4 8;
2k 8 4;
2k 12;
2 группа.
1) Решение:
(7 5 7) 5 7 7 (7 6 ) 5 7 7 7 37
2
7
49
7 5
35
35
(7 )
7
7
Ответ: 49.
2)
4 k 2 4 2k
( 3 ) 6 4 2 k 6 ;
4
4
4 2 k 6 4 6 ;
2k 6 6;
2k 6 6;
k 6.
2k 12;
Ответ: при k= 6 выполняется
равенство
k
5 2
( 2 ) 5 8.
5
k 6.
Ответ: при k= 6
выполняется
равенство
4k 2
( 3 ) 4 6.
4
ГИА — 2014
Задание 21.
Задание 21.
3
Сократить дробь:
33
.
2
2
3 11
Решение:
333
333
333
3 2
1
33
33
33.
2
2
2
2
3 11
(3 11)
33
Ответ: 33.

Мы выполнили большую и важную
задачу. А вот какую, вы мне скажите
сами.
Ответы учеников:
*Вспомнили и закрепили все
свойства,
*Применяли данные свойства для
решения заданий,
*Отрабатывали решения,
*Работали в группах, консультируя
друг друга,
*Рассмотрели решение задания из II
части ГИА -2014 по математике.

English     Русский Правила

Урок алгебры в 7-м классе «Свойства степени с натуральным показателем»

Ключевые слова: алгебра, степень с натуральным показателем

Цели:

  • формировать представление о свойствах степеней с одинаковым основанием;
  • формировать умение применять свойства степеней для упрощения выражений и нахождения их значения;
  • формировать умение выполнять действия оценки.

Планируемые результаты: обучающиеся научатся формулировать и доказывать свойства степени с натуральным показателем; применять свойства степени с натуральным показателем для вычисления значения выражения и преобразования выражений, содержащих степень; продолжат учиться анализировать и оценивать свою работу.

Оборудование: ноутбук, мультимедийный проектор, презентация, карточки с раздаточным материалом.

Ход урока

1. Самоопределение к деятельности

Добрый день! С каким новым понятием мы познакомились на прошлом уроке? (степень с натуральным показателем)

Начать урок хочу с высказывания М.В.Ломоносова «Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь»

2. Актуализация знаний и фиксирование индивидуального затруднения в пробном действии

Для начала вспомним, что называют степенью числа а? (обучающиеся дают определение степени с натуральным показателем)

1. Представьте в виде степени:

  • 5·5·5
  • а·а·а·а·а·а
  • (-2)·(-2)·(-2)·(-2)

2. Вычислите устно:

  • 115;
  • (-1)5;
  • 0,32;
  • (-2)4;
  • -24;
  • 132012 · 02013 · (-31)2014 .

3. Дома вам было предложено найти значение двух выражений, содержащих степени. Обсудим их решение:

3. Выявление причины затруднения и постановка цели

В чем, по вашему мнению, причина затруднения? (громоздкие вычисления)

Какую цель мы можем поставить перед собой на этот урок? (найти способ упрощать выражения, содержащие степень)

Вернемся к заданию, вызвавшему затруднение, в конце урока. А я вам предлагаю подумать над более простой задачей.

4. Проблемное изложение нового знания

1. Вычислите:

  • 23·25     (23·25 =(2·2·2) ·(2·2·2·2·2)=2·2·2·2·2·2·2·2=28=256)
  • 31·34     (31·34 =3·(3·3·3·3)= 3·3·3·3·3=35=243)

Обратите внимание на подчеркнутые части равенства. Найдите связь между левой и правой частями. Попробуйте сформулировать ее в общем виде.

(аn· аk=an+k)

То, что мы записали, всего лишь предположение. Его предстоит еще доказать (обучающие под руководством учителя доказывают)

а n· аk=an+k.

Сформулируйте доказанное свойство степеней с натуральным показателем в виде правила. (При умножении степеней с одинаковым основанием показатели складываются).

2. Вычислите (подсказка – замените знак деления чертой дроби):

26 : 24                (22=4)
38 : 35                (33=27) 

Какую вы наблюдаете закономерность? (При делении степеней с одинаковым основанием из показателя делимого вычитают показатель делителя).
Запишите  данное свойство в виде формулы (аn : аk=an–k).

Действительно, аn : аk=an–k, n>k.

3. Докажите самостоятельно  свойство (an)k = an·k

. Сформулируйте соответствующее правило.

5. Первичное закрепление с проговариванием во внешней речи

Скажите, пожалуйста, для чего в математике необходимы свойства, в том числе и степеней? (для упрощения числовых выражений, буквенных выражений).

1. Устно, с подробными комментариями.

Упростите выражения № 17.1(а,б), 17.3(а,б),17.15(а,б),17.19(а,б)

2. Работа в парах: письменно в тетрадях, с подробными комментариями вслух: найдите значение числовых выражений № 17.32 (а,б)

6. Самостоятельная работа с самопроверкой по эталону

Упростите выражения:

  • x5 · x8
  • m14 : m
  • (a5)13
  • (b7)3 · (b5)4

Сравните свои решения с эталоном, представленном на слайде, подчеркните ошибки, определите тип ошибки, исправьте ее (обучающиеся сравнивают решения, отмечают правильно решенные примеры, исправляют ошибки).

На доске указаны:

типы ошибок:

  • ошибка вычислительная
  • ошибка в применении свойств степени

критерии оценки:

  • 7 – отлично
  • 6 – хорошо
  • 5-4 – будь внимательнее
  • 3-0 – необходимо еще раз проработать теоретический материал
7. Включение нового знания в систему знаний и повторение

Вернемся к числовому выражению, решение которого вызвало у вас затруднение. Найдите значение этого выражения.

Чем вы воспользовались для нахождения значения данного выражения? (свойствами степеней)

Сформулируйте эти свойства.

Примените свойства степеней для решения уравнения: № 17.42.(а)

8. Рефлексия учебной деятельности на уроке

Подведем итог нашего урока:

— Какую задачу ставили?

— Удалось ли решить поставленную задачу?

— Каким способом?

— Что на уроке у вас получилось хорошо?

— Какие трудности остались?

— Над чем еще надо поработать?

— Где можно применить новое знание?

Домашнее задание: п. 37, № 37.2, 37.9, 37.16

Использование свойств углов для решения задач

Результаты обучения

  • Найти дополнение угла
  • Найдите дополнение угла

Знакома ли вам фраза «сделать [латекс]180[/латекс]?» Она означает сделать полный поворот лицом в противоположном направлении. Это происходит из-за того, что мера угла, образующего прямую, составляет [латекс]180[/латекс] градусов. См. изображение ниже.


Угол образован двумя лучами, имеющими общий конец. Каждый луч называется стороной угла, а его общая точка вершиной. Угол называется по его вершине. На изображении ниже [латекс]\угол А[/латекс] — это угол с вершиной в точке [латекс]А[/латекс]. Мера [латекс]\угол А[/латекс] записывается как [латекс]м\угол А[/латекс]. 9\циркуляр[/латекс].

В этом и следующем разделах вы познакомитесь с некоторыми распространенными геометрическими формулами. Мы адаптируем нашу стратегию решения задач для приложений геометрии. Геометрическая формула назовет переменные и даст нам уравнение для решения.

Кроме того, поскольку все эти приложения будут включать геометрические фигуры, будет полезно нарисовать фигуру, а затем подписать ее информацией из задачи. Мы включим этот шаг в стратегию решения задач для приложений геометрии.

Используйте стратегию решения задач для геометрических приложений.

  1. Прочтите задачу и убедитесь, что вы понимаете все слова и идеи. Нарисуйте рисунок и обозначьте его данными.
  2. Определите , что вы ищете.
  3. Назовите то, что вы ищете, и выберите переменную для ее представления.
  4. Переведите в уравнение, написав соответствующую формулу или модель для данной ситуации. Замените предоставленную информацию. 9\циркуляр[/латекс].

    1. Найдите его дополнение

    2. Найдите его дополнение

    Решение

    1.
    Шаг 1. Прочтите проблему. Нарисуйте рисунок и подпишите его с помощью данной информации.
    Шаг 2. Определите , что вы ищете. Дополнение [латексного]40°[/латексного]угла.
    Шаг 3. Имя. Выберите переменную для ее представления. Пусть [latex]s=[/latex]мера добавки.
    Шаг 4. Перевести.

    Напишите подходящую формулу для ситуации и замените данную информацию.

    		 [латекс]м\угол А+м\угол В=180[/латекс]

    [латекс]s+40=180[/латекс]

    Шаг 5. Решите уравнение. [латекс]s=140[/латекс]
    Шаг 6. Проверка:

    [латекс]140+40\stackrel{?}{=}180[/латекс]

    [латекс]180=180\галочка[/латекс]

    Шаг 7. Ответьте на вопрос. Дополнение к углу [латекс]40°[/латекс] составляет [латекс]140°[/латекс].
    2.
    Шаг 1. Прочтите проблему. Нарисуйте рисунок и подпишите его с помощью данной информации.
    Шаг 2. Определите , что вы ищете.
    Дополнение угла [латекс]40°[/латекс].
    Шаг 3. Имя. Выберите переменную для ее представления. Пусть [latex]c=[/latex]мера дополнения.
    Шаг 4. Перевести.

    Напишите подходящую формулу для ситуации и замените данную информацию.

    		 [латекс]м\угол А+м\угол В=90[/латекс]
    Шаг 5. Решите уравнение. [латекс]с+40=90[/латекс]

    [латекс]с=50[/латекс]

    Шаг 6. Проверка:

    [латекс]50+40\stackrel{?}{=}90[/латекс]

    [латекс]90=90\четверка\галочка[/латекс]

    Шаг 7. Ответьте на вопрос. Дополнение угла [латекс]40°[/латекс] равно [латекс]50°[/латекс].

     

    попробуй 9\circ[/latex] больше, чем меньший угол. Найдите величину обоих углов.

    Показать решение

     

    попробуйте

    Использование свойств углов для решения задач | Преалгебра |

    Результаты обучения

    • Найти дополнение угла
    • Найдите дополнение угла

    Вам знакома фраза «сделать

    180»?180\text{‘?}180?

    Это означает сделать полный поворот лицом в противоположном направлении. Это происходит из-за того, что градусная мера угла, образующего прямую, равна 9.0011

    180180180

    градуса. См. изображение ниже. Угол образован двумя лучами, имеющими общий конец. Каждый луч называется стороной угла, а его общая точка вершиной. Угол называется по его вершине. На изображении ниже

    ∠A\angle A∠A

    — это угол с вершиной в точке

    AAA

    . Мера

    ∠A\угол A∠A

    записывается как

    м∠Am\угол Am∠A

    .

    ∠А\угол А∠А 9\circ \text{}.{}m∠A+m∠B=90∘.

    В этом и следующем разделах вы познакомитесь с некоторыми распространенными геометрическими формулами. Мы адаптируем нашу стратегию решения задач для приложений геометрии. Геометрическая формула назовет переменные и даст нам уравнение для решения.

    Кроме того, поскольку все эти приложения будут включать геометрические фигуры, будет полезно нарисовать фигуру, а затем подписать ее информацией из задачи. Мы включим этот шаг в стратегию решения задач для приложений геометрии.

    Используйте стратегию решения задач для геометрических приложений.

    1. Прочтите задачу и убедитесь, что вы понимаете все слова и идеи. Нарисуйте рисунок и обозначьте его данными.
    2. Определите , что вы ищете.
    3. Назовите то, что вы ищете, и выберите переменную для ее представления.
    4. Переведите в уравнение, написав соответствующую формулу или модель для данной ситуации. Замените предоставленную информацию.
    5. Решите уравнение, используя хорошие методы алгебры.
    6. Проверьте ответ в задаче и убедитесь, что он имеет смысл.
    7. Ответьте на вопрос полным предложением.

    Следующий пример покажет, как вы можете использовать стратегию решения задач для приложений геометрии, чтобы ответить на вопросы о дополнительных и дополнительных углах.

    пример

    Угол равен 9\circ40∘

    . Найдите 1. его дополнение и 2. его дополнение.

    Раствор

    1.
    Шаг 1. Прочтите проблему. Нарисуйте рисунок и подпишите его с помощью данной информации.
    Шаг 2. Определите , что вы ищете. Дополнение к углу

    40°40°40°

    .
    Шаг 3. Имя. Выберите переменную для ее представления. Пусть

    s=s=s=

    мера добавки.
    Шаг 4. Перевести.

    Напишите формулу, подходящую для ситуации, и замените полученную информацию.

    м∠A+m∠B=180м\угол A+m\угол B=180м∠A+m∠B=180

    с+40=180с+40=180с+40=180

    Шаг 5. Решите уравнение.

    с=140с=140с=140

    Шаг 6. Проверка:

    140+40=?180140+40\stackrel{?}{=}180140+40=?180

    180=180✓180=180\checkmark180=180✓

    Шаг 7. Ответьте на вопрос. Дополнение к углу

    40°40°40°

    равно

    140°140°140°

    .
    2.
    Шаг 1. Прочтите проблему. Нарисуйте рисунок и подпишите его с помощью данной информации.
    Шаг 2. Определите , что вы ищете.
    Дополнение угла

    40°40°40°

    .
    Шаг 3. Имя. Выберите переменную для ее представления. Пусть

    c=c=c=

    — мера дополнения.
    Шаг 4. Перевести.

    Напишите формулу, подходящую для ситуации, и замените полученную информацию.

    м∠A+m∠B=90м\угол A+m\угол B=90м∠A+m∠B=90

    Шаг 5. Решите уравнение.

    с+40=90с+40=90с+40=90

    с=50с=50с=50

    Шаг 6. Проверка:

    50+40=?9050+40\stackrel{?}{=}9050+40=?90

    90=90✓90=90\quad\checkmark90=90✓

    Шаг 7. Ответьте на вопрос. Дополнение к

    40°40°40° 9\circ30∘

    больше, чем меньший угол. Найдите величину обоих углов.

    Показать решение

    Решение:

    Шаг 1. Прочтите задачу. Нарисуйте рисунок и подпишите его с помощью данной информации.
    Шаг 2. Определите , что вы ищете. Меры обоих углов.
    Шаг 3. Имя. Выберите переменную для ее представления.

    Больший угол на 30° больше меньшего угла.

    		 Пусть

    a=a=a=

    мера меньшего угла

    a+30=a+30=a+30=

    мера большего угла
    Шаг 4. Перевести.

    Напишите соответствующую формулу и замените ее.

    м∠А+м∠В=180м\угол А+м\угол В=180м∠А+м∠В=180

    Шаг 5. Решите уравнение.

    (а+30)+а=180(а+30)+а=180(а+30)+а=180

    2a+30=1802a+30=1802a+30=180

    2a=1502a=1502a=150

    a=75a=75a=75

    мера меньшего угла.

    а+30а+30а+30

    мера большего угла.

    75+3075+3075+30

    105105105

    Шаг 6. Проверка:

    м∠A+m∠B=180м\угол A+m\угол B=180м∠A+m∠B=180

    75+105=?18075+105\stackrel {?}{=}18075+105=?180

    180=180✓180=180\quad\checkmark180=180✓

    Шаг 7. Ответьте на вопрос. Меры угла:

    75°75°75°

    и

    105°105°105°

    .

    попробуй

    Лицензии и атрибуции

    Лицензионный контент CC, конкретное атрибуция