Площади многоугольников и тающий лёд
Григорий Мерзон
«Квантик» №9, 2018
Формула Пика
Как найти площадь многоугольника на клетчатой бумаге? Можно подсчитать число клеток, которые полностью накрыты фигурой, и ещё как-то учесть клетки, накрытые фигурой частично, — скажем, прибавить половину от числа этих клеток. И сказать, что площадь фигуры (в клеточках) приблизительно равна полученной сумме.
А можно вместо клеток, полностью или частично накрытых многоугольником, считать узлы сетки (вершины клеток) строго внутри многоугольника или на его границе.
Действительно, вокруг каждого узла сетки можно нарисовать по единичному квадратику. И если узел лежит на границе многоугольника, то этот квадратик накрыт многоугольником только частично. А если узел лежит внутри, то обычно и квадратик накрыт многоугольником полностью… впрочем, иногда всё же не полностью — но мы и считаем площадь только приближённо.
Но чудесным образом последний рецепт всегда даёт почти правильный ответ! А именно, верна Формула Пика. Площадь S многоугольника с вершинами в узлах сетки можно найти по формуле
Площадь S многоугольника с вершинами в узлах сетки можно найти по формуле
S=i+b2−1,
где i — число узлов сетки строго внутри многоугольника, b — число узлов сетки на его границе.
Подчеркнём, что это уже не приближённая, а точная формула!
Интересно, что хотя длины сторон у многоугольников обычно совершенно не целые, формула Пика гарантирует, что площадь всегда получится целой или полуцелой.
Тающий лёд
Формула Пика известна с XIX века, и с тех пор у неё появилось много доказательств, но большинство из них не такие уж простые. Мы обсудим предложенный в 1997 году швейцарским математиком Кристианом Блаттером мысленный эксперимент с тающим льдом, который сразу объясняет формулу Пика.
Поставим на каждый узел сетки по одинаковому цилиндрическому столбику изо льда. Каждый столбик очень тонкий (пересекается только с теми сторонами многоугольника, которые проходят через центр столбика) и весит 1 грамм.
Построим вокруг каждого столбика забор в виде единичного квадратика, после чего растопим весь лёд (во всех квадратиках вода растекается одинаково и симметрично относительно центра своего квадратика). Вся клетчатая плоскость будет равномерно залита водой, и в каждой ячейке площади 1 будет по 1 грамму воды. То есть количество воды в нашем многоугольнике (в граммах) будет равно его площади (в клетках).
С другой стороны, задумаемся, откуда эта вода попала в наш многоугольник. Посмотрим на какую-нибудь конкретную сторону многоугольника. Если через неё внутрь многоугольника втекла вода из какого-то столбика, то точно столько же воды из симметричного столбика (симметричного относительно середины этой стороны) через неё из многоугольника вытекло.
То есть внутри многоугольника ровно столько воды, сколько в нём было льда! А сколько в нём было льда? Каждый из узлов сетки внутри многоугольника даёт вклад 1 грамм, общий вес получается i граммов. Узлы на сторонах обычно дают по 12 грамма, но только если это не вершина, для вершины этот вес меньше — так что и общий вес узлов на границе получается не b2 граммов, а меньше.
Насколько меньше? Продлим немного каждую сторону, обходя многоугольник вдоль сторон по часовой стрелке. На рисунке ниже красная часть дополняет каждую из синих частей до половины круга. Но красные части в сумме дают ровно один круг! Ведь, обходя многоугольник по контуру, мы в каждой вершине поворачиваемся на угол, соответствующий красной части, пока не вернёмся в исходную точку, сделав как раз полный оборот.
То есть суммарный вес льда внутри многоугольника равен i+b2−1, и мы получили формулу Пика!
Художник Мария Усеинова
Понятие площади многоугольника. Формула Пика.
Площадь многоугольника. Формула Пика.
Приступаем к изучению понятия площади фигур. Как понять, что такое площадь? Ниже приведены два рисунка. Как вы думаете, чем они отличаются? В чём существенная разница между ними?
На первом рисунке фигура имеет только границу, а на втором рисунке, кроме границы, закрашена вся внутренняя её область.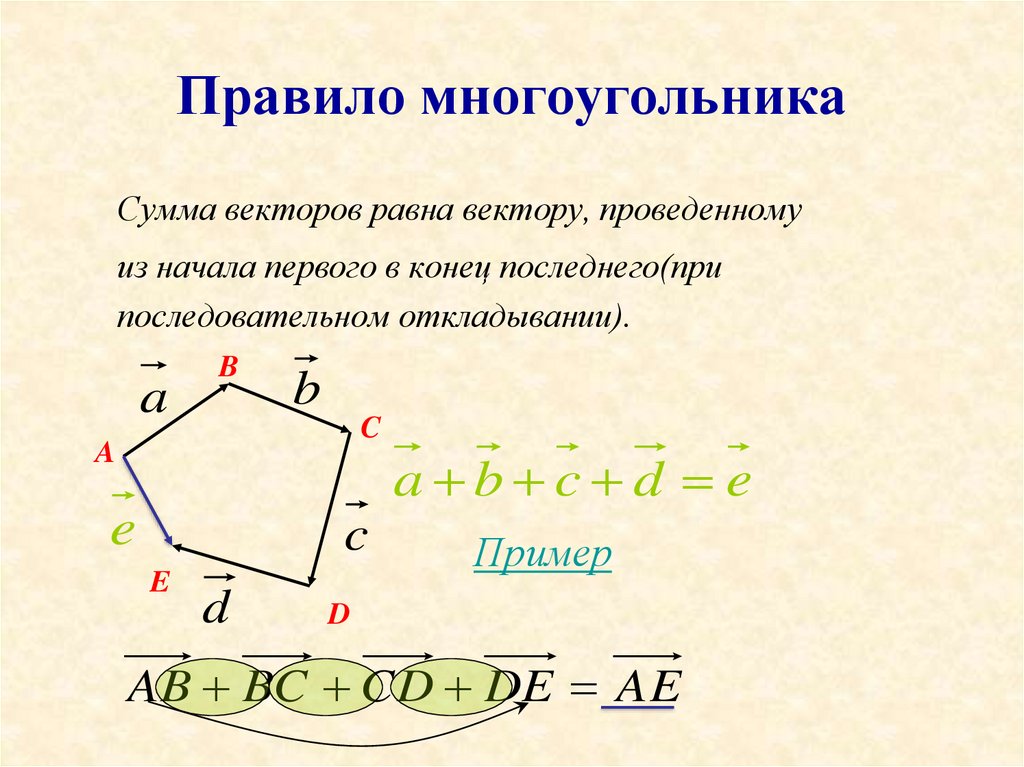
Определение: Площадь – это положительная величина, численное значение которой обладает следующими свойствами:
Равные фигуры имеют равную площадь.
На рисунке изображены равные многоугольники и , значит, их площади равны.
Обратное утверждение неверно. Фигуры могут иметь одинаковую площадь, при этом сами они не равны. Это равновеликие фигуры.
Определение: Равновеликими называются фигуры, имеющие одинаковую площадь.
Например, площадь квадрата равна 4 ед2 (он состоит из 4 единичных квадратов), и площадь прямоугольника равна 4 ед2 (он тоже состоит из 4 единичных квадратов). Фигуры разные, а площади у них равны, значит, они равновеликие.
П
лощадь фигуры равна сумме площадей частей, на которые эта фигура разделена отрезками.
Многоугольник разделён диагоналями, исходящими из одной вершины (например, ) на пять частей (треугольников). Значит, площадь всего многоугольника равна сумме площадей частей, на которые этот многоугольник разделён. Причём, делить многоугольник можно как угодно, главное, чтобы можно было найти площадь получившихся частей.
П
лощадь квадрата со стороной, равной единице измерения (1 мм, 1 см, 1 м и т.д.), равна единице.
Е
сли какой-либо многоугольник нарисован на клетчатой бумаге (квадратной решётке), то существует универсальный способ определения его площади. Этот способ придумал австрийский математик Пик ещё в 1899 году. Разберём его на примере.
На рисунке изображён многоугольник, площадь которого нужно найти. Отметим синим цветом целочисленные точки (т.е. точки, которые лежат в уголках клеток), расположенные на границе этого многоугольника, а жёлтым цветом целочисленные точки, лежащие внутри многоугольника.
Георг Пик вывел формулу для нахождения площади фигуры, используя только количество целочисленных точек:здесь В – количество точек внутри фигуры; Г – количество точек на границе этой фигуры.
Используя эту формулу, найдём площадь нашего многоугольника.
Этот способ нахождения площади имеет и практическое применение. Например, если необходимо найти площадь фигуры неправильной формы, то на эту фигуру накладываем сетку (как на рисунке вверху) и используем формулу Пика.
Например, если необходимо найти площадь фигуры неправильной формы, то на эту фигуру накладываем сетку (как на рисунке вверху) и используем формулу Пика.
Найдём таким же образом площадь кольца.
Найдём площадь этого же кольца по известной формуле площади круга:
Сравнивая полученные результаты при разных способах вычисления, мы видим, что в случае нахождения площади круга или кольца погрешность достаточно серьёзная.
Поэтому, нужно запомнить, что формула Пика точно работает только для многоугольников!
Найдите площади фигур, изображённых на квадратной решётке, используя формулу Пика:
Разделите шестиугольник на части разными способами. Для каждого случая сделайте рисунок. Запишите, как будет вычисляться площадь пятиугольника, учитывая разделение.
Определите, какие фигуры на рисунке имеют одинаковую площадь. Найдите их площади.
П
рямоугольники разделены на равные квадраты со стороной 1 ед. Посчитайте, сколько квадратов содержится в каждом прямоугольнике. Какова площадь каждого прямоугольника? Подумайте, как найти площадь прямоугольника, не пересчитывая все квадраты?
Н
айдите равновеликие многоугольники.
2
{2}$ и т. д. Существуют заранее определенные формулы для вычисления площади прямоугольника, квадрата, треугольника, круга, ромба, трапеции и воздушного змея. Однако для вычисления площади многоугольника она рассчитывается как комбинация двух или более правильных многоугольников.Давайте научимся находить площади многоугольников.
Многоугольник — 2D-плоскость Рисунок
Многоугольник – это двумерная замкнутая форма, ограниченная прямыми сторонами, называемыми сторонами или ребрами. У него нет изогнутых сторон. Точки, в которых встречаются две стороны, являются вершинами (сингулярными вершинами) многоугольника. Каждая вершина содержит две стороны, образующие угол.
У него нет изогнутых сторон. Точки, в которых встречаются две стороны, являются вершинами (сингулярными вершинами) многоугольника. Каждая вершина содержит две стороны, образующие угол.
Полигоны названы по количеству присутствующих в них сторон. Некоторые из общих полигонов
| Number of Sides | Name of the Polygon | |
| $3$ | Triangle (Prefix is Tri meaning $3$) | |
| $4$ | Quadrilateral (Prefix is Quadri означает $4$) | |
| $5$ | Pentagon (префикс Penta meaning $5$) | |
| $6$ | Hexagon (Prefix is Hexa meaning $6$) | |
| $7$ | Heptagon (Prefix is Hepta meaning $7$) | |
| $8$ | Octagon (префикс — OCTA , означающий $ 8 $) | |
| $ | NONAGN (префикс — NONA Значение $ | |
| $ | DECAGON (PREFIX | |
| $ | DECAGON (PREFIX | |
| $ | $(PREFIX | |
| $ | (PREFIX | |
| (PREFIX | ||
Примечание:
- Суффикс «гон» в многоугольнике — это греческое слово, означающее сторону
- «Поли» — это также греческое слово, означающее «много»
Правильные и неправильные многоугольники
Многоугольник делится на правильный и неправильный многоугольник в зависимости от длины его сторон. Как следует из названия, длина всех сторон одинакова, а также мера каждого угла равна. Следовательно, можно использовать фиксированную или общую формулу, чтобы найти периметр многоугольника, используя любой из следующих
- количество сторон
- мера внутреннего угла
- мера внешнего угла
В случае неправильного многоугольника длина сторон разная, а также разная мера углов. Следовательно, чтобы найти периметр неправильного многоугольника, необходимо знать длину всех сторон.
Площадь многоугольника — обычный
Прежде чем перейти к формуле нахождения площади многоугольника, давайте разберемся с некоторыми терминами, с ней связанными.
Центр правильного многоугольника: Центр правильного многоугольника — это точка, от которой все вершины равноудалены.
Радиус правильного многоугольника: Радиус правильного многоугольника — это отрезок с одной конечной точкой в центре и другой конечной точкой в одной из вершин. Таким образом, в $n$-стороннем правильном многоугольнике имеется $n$ радиусов.
Примечание: Центр и радиус правильного многоугольника такие же, как центр и радиус окружности, описанной вокруг этого правильного многоугольника.
Апофема правильного многоугольника: Апофема правильного многоугольника — это отрезок, один конец которого находится в центре, а другой — в середине одной из сторон. Апофема правильного многоугольника — это серединный перпендикуляр к той стороне, на которой он имеет свою конечную точку.
Центральный угол правильного многоугольника: Центральный угол правильного многоугольника — это угол, вершина которого является центром, а лучи или стороны которого содержат концы сторон правильного многоугольника.
Примечание: $n$-сторонний правильный многоугольник имеет $n$ апофем и $n$ центральных углов, мера каждого из которых равна $\frac {360}{n}$ градусов. Каждая апофема представляет собой биссектрису центрального угла, содержащего сторону, на которую простирается апофема.
СКАЧАТЬ БЕСПЛАТНО КАРТОЧКИ ПО МАТЕМАТИКЕ:
Красиво оформленные карточки для печати, которые помогут вам запомнить все важные математические понятия и формулы.
Нахождение длины Апофемы
Рассмотрим пятиугольник с центром $O$ и длиной каждой стороны $s$. Далее рассмотрим $\треугольник OAB$ на одной из сторон $AB$. (Таких треугольников в пятиугольнике будет $5$).
Мера центрального угла $\theta = \frac {360}{n}$ градусов (в случае пятиугольника $n = 5$).
Примечание:
- $OC$ — апофема пятиугольника
- $\треугольник OAB$ равнобедренный треугольник, где $OA = OB$ (радиусы многоугольника)
- Апофема $OC$ делит пополам $\angle AOB$, т.
 {2}} {4 \ tan \ frac {\ theta} {2}} $. 9{2}}{4 \tan \frac {180}{n}}$
{2}} {4 \ tan \ frac {\ theta} {2}} $. 9{2}}{4 \tan \frac {180}{n}}$ Теперь посмотрим, как $\frac {1}{2} \times a \times p$ равно сумме площадей треугольников, составляющих правильный многоугольник.
Рассмотрим пятиугольник (пятиугольник). Его можно разделить на треугольники по $5$. Один из таких треугольников показан на рисунке ниже.
Площадь треугольника $\frac {1}{2} \times s \times a$.
Площадь пятиугольника, показанного на рисунке, равна сумме площадей $5$ треугольников, т. е. $\text {Площадь пятиугольника} = 5 \times \frac {1}{2} \times s \times a = \frac {1 }{2} \times \left(5 \times s \right) \times a = \frac {1}{2} \times p \times a$ (где $p$ — периметр пятиугольника). 9{2}$
Правильные и неправильные дробиПлощадь многоугольника – неправильная
Неправильный многоугольник – это плоскозамкнутая фигура, не имеющая равных сторон и равных углов.
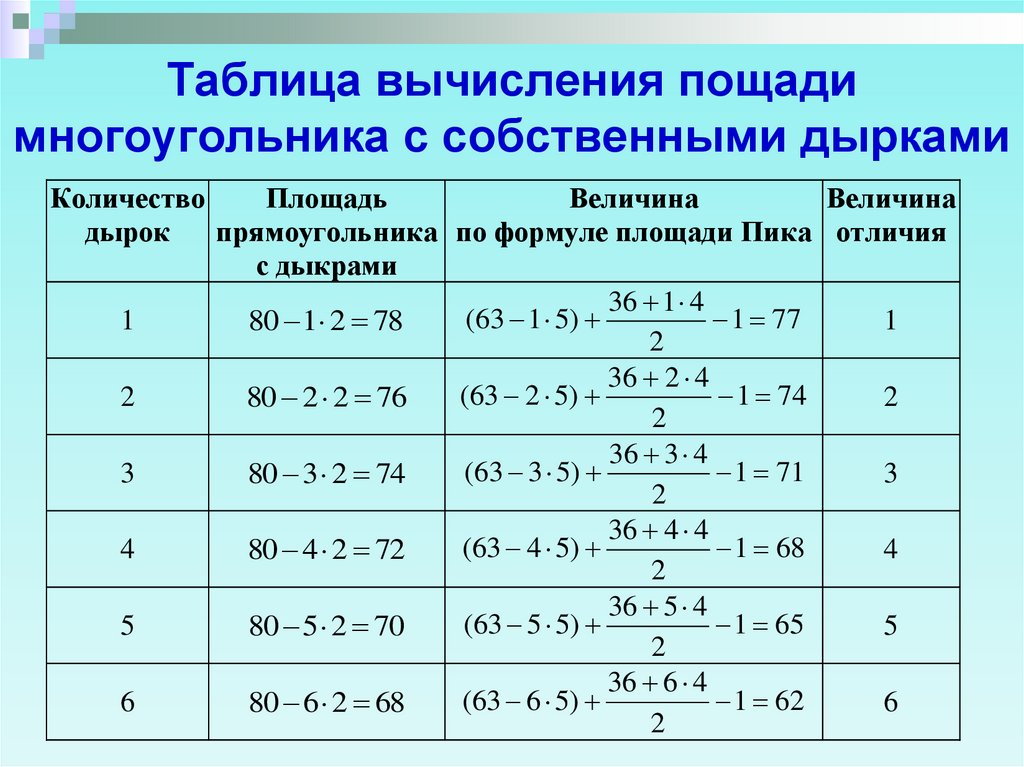
 Таким образом, чтобы вычислить площадь неправильного многоугольника, мы разобьем неправильный многоугольник на множество правильных многоугольников так, что известны формулы их площадей.
Таким образом, чтобы вычислить площадь неправильного многоугольника, мы разобьем неправильный многоугольник на множество правильных многоугольников так, что известны формулы их площадей.Рассмотрим многоугольник (неправильный четырехугольник), показанный ниже.
Разделите четырехугольник на два треугольника, соединив вершины $B$ и $D$. (Проведение диагонали $BD$).
Теперь с помощью формулы площади треугольника можно вычислить площади $\треугольника ABD$ и $\треугольника BCD$, а также вычислить площадь неправильного четырехугольника $ABCD$, сложив площади двух треугольников.
Площадь четырехугольника $ABCD = $ (Площадь $\треугольника ABD$) + (Площадь $\треугольника BCD$).
Площадь полигонов с координатами
Чтобы найти площадь многоугольника с известными координатами, первым делом нужно найти длину каждой стороны многоугольника, используя формулу расстояния. 9{2}}$.
Теперь выполните одно из следующих действий
- Если многоугольник правильный, найдите площадь по формуле.

- Если многоугольник неправильный, найдите площадь, разбив его на несколько меньших многоугольников, таких как треугольники, квадраты, прямоугольники и т. д.
Примеры
Пример 1: Найти площадь четырехугольника с вершинами $\left(4, 10 \right)$, $\left(9, 7 \right)$, $\left(11, 2 \right)$, и $\left(2, 2\right)$. 9{2}} = \sqrt{49 + 64} = \sqrt{113} = 10,63$ единиц
Чтобы найти площадь треугольника, воспользуемся формулой Герона.
Площадь $\треугольника ABC$
$a = AB = 5,83$ единиц, $b = BC = 5,39$ единиц и $c = AC = 10,63$ единиц
Полупериметр $s = \frac {a + b + c}{2} = \frac {5,83 + 5,39 + 10,63}{2} = 10,92$ единиц
Площадь = $\sqrt{s \left(s – a \right)\left(s – b \right)\left(s – c \right)} = \sqrt{10,92 \left(10,92 – 5,83 \right) \слева(10,92 – 5,39{2}$.
Заключение
Многоугольник – это двумерная замкнутая форма, ограниченная прямыми сторонами, называемыми сторонами или ребрами.
 Многоугольник может быть правильным или неправильным многоугольником. Вы можете найти площадь правильного многоугольника, используя предопределенную формулу, тогда как, чтобы найти площадь неправильного многоугольника, прежде всего, разделите многоугольник на количество многоугольников, формула площади которых известна, а затем найдите площадь неправильный многоугольник путем сложения площадей всех образованных таким образом многоугольников.
Многоугольник может быть правильным или неправильным многоугольником. Вы можете найти площадь правильного многоугольника, используя предопределенную формулу, тогда как, чтобы найти площадь неправильного многоугольника, прежде всего, разделите многоугольник на количество многоугольников, формула площади которых известна, а затем найдите площадь неправильный многоугольник путем сложения площадей всех образованных таким образом многоугольников.Практические задачи
- Найдите площадь равностороннего треугольника со стороной $7 см$.
- Найдите площадь квадрата со стороной $9 мм$.
- Найдите площадь правильного пятиугольника со стороной $11 см$.
- Найдите площадь правильного шестиугольника со стороной $5 m$.
- Найдите площадь правильного семиугольника со стороной $7 см$.
- Найдите площадь правильного восьмиугольника со стороной $4 в $.
- Найдите площадь правильного девятиугольника со стороной $12 см$.
- Найдите площадь правильного десятиугольника со стороной $6 см$.

Рекомендуемое чтение
- Площадь прямоугольника – определение, формула и примеры
- Площадь квадрата – определение, формула и примеры
- Площадь треугольника – формулы, методы и примеры
- Площадь круга – формула, вывод и примеры
- Площадь ромба – формулы, методы и примеры
- Площадь воздушного змея – формулы, методы и примеры
- Периметр многоугольника (с формулой и примерами)
- Периметр трапеции – определение, формула и примеры
- Периметр воздушного змея – определение, формула и примеры
- Периметр ромба – определение, формула и примеры
- Окружность (периметр) круга – определение, формула и примеры
- Периметр квадрата – определение, формула и примеры
- Периметр прямоугольника – определение, формула и примеры
- Периметр треугольника – определение, формула и примеры
- Что такое 2D-фигуры — имена, определения и свойства
Часто задаваемые вопросы
Как определяется площадь многоугольника?
Площадь многоугольника — это область, занимаемая многоугольником.
 Многоугольники могут быть правильными и неправильными. Основными многоугольниками, которые используются в геометрии, являются треугольник, квадрат, прямоугольник, пятиугольник, шестиугольник и т. д.
Многоугольники могут быть правильными и неправильными. Основными многоугольниками, которые используются в геометрии, являются треугольник, квадрат, прямоугольник, пятиугольник, шестиугольник и т. д. Какова формула площади правильного многоугольника? 9{2}}{4 \tan \frac {180}{n}}$, где $s$ — длина стороны.
Как найти площадь неправильного многоугольника?
Чтобы вычислить площадь неправильного многоугольника, мы разобьем неправильный многоугольник на множество правильных многоугольников, для которых известны формулы их площадей.
Вам также может понравиться
Геометрическая прогрессия – значение, формулы и примеры
Содержание Что такое геометрическая прогрессия? Примеры геометрической прогрессии 9-й член0003
Читать далее
Арифметическая прогрессия – значение, формулы и примеры
Содержание Что такое арифметическая прогрессия? Примеры арифметической прогрессии Член
Читать далее
Последовательность и серия – типы, различия и формулы
Содержание Что такое последовательность и серия? Сигма-обозначение серии Общее
Читать далее
Площадь правильных многоугольников: формулы, примеры и уравнения
Все вокруг нас имеет определенную форму, будь то стол, часы или продукты питания, такие как бутерброды или пицца.
 Особенно в геометрии мы видели и изучали различные формы, такие как треугольники или квадраты и многие другие. Эти формы являются некоторыми примерами многоугольников. Напомним, что многоугольник — это двумерная замкнутая фигура, образованная прямыми линиями.
Особенно в геометрии мы видели и изучали различные формы, такие как треугольники или квадраты и многие другие. Эти формы являются некоторыми примерами многоугольников. Напомним, что многоугольник — это двумерная замкнутая фигура, образованная прямыми линиями.В этой статье мы поймем концепцию области r правильных многоугольников , найдя апофему .
Что такое правильные многоугольники?
Правильный многоугольник — это тип многоугольника, в котором все стороны равны друг другу, а также равны все углы. Кроме того, мера всех внутренних и внешних углов соответственно равна.
Правильные многоугольники — это геометрические фигуры, у которых все стороны имеют одинаковую длину (равносторонние) и все углы имеют одинаковую величину (равноугольные).
Правильные многоугольники включают равносторонние треугольники (3 стороны), квадраты (4 стороны), правильные пятиугольники (5 сторон), правильные шестиугольники (6 сторон) и т.
 д.
д.Правильные многоугольники, StudySmarter Originals правильный многоугольник (то есть не имеет равных длин сторон и равных углов), то его можно назвать неправильным многоугольником. Например, прямоугольник или четырехугольник можно назвать неправильным многоугольником.
Свойства и элементы правильного многоугольника
Давайте сначала рассмотрим свойства и элементы правильного многоугольника, прежде чем приступить к обсуждению его площади.
Любой правильный многоугольник имеет различные части, такие как радиус, апофема, сторона, вписанная окружность, описанная окружность и центр. Давайте обсудим понятие апофемы.
Апофема многоугольника – это отрезок, идущий от центра многоугольника к середине одной из сторон. Это означает, что он перпендикулярен одной из сторон многоугольника.
Апофема правильного многоугольника, StudySmarter Originals
Апофема — это линия, идущая от центра к одной стороне, перпендикулярная этой стороне и обозначаемая буквой а.

Чтобы найти апофему многоугольника, нам сначала нужно найти его центр. Для многоугольника с четным числом сторон это можно сделать, проведя как минимум две линии между противоположными углами и посмотрев, где они пересекаются. Перекресток будет центром. Если у многоугольника нечетное количество сторон, вам нужно вместо этого провести линии между одним углом и серединой противоположной стороны.
Диагонали и центр правильного многоугольника, Studysmarter Originals
Свойства правильного многоугольника включают:
- Все стороны правильного многоугольника равны.
- Все внутренние и внешние углы соответственно равны.
- Каждый угол правильного многоугольника равен n-2×180°n.
- Правильный многоугольник существует с 3 или более сторонами.
Формула площади правильного многоугольника
Теперь вы знаете все, что нужно для того, чтобы воспользоваться формулой для нахождения площади правильного многоугольника. Формула площади правильного многоугольника:
Площадь=a×p2
, где a — апофема, а p — периметр.
 Периметр правильного многоугольника можно найти, умножив длину одной стороны на общее количество сторон.
Периметр правильного многоугольника можно найти, умножив длину одной стороны на общее количество сторон.Вывод формулы площади с использованием прямоугольного треугольника
Давайте посмотрим на вывод этой формулы, чтобы понять, откуда она взялась. Мы можем вывести формулу площади правильных многоугольников, используя прямоугольный треугольник для построения n треугольников одинакового размера внутри многоугольника с n сторонами. Затем мы можем сложить все площади отдельных треугольников вместе, чтобы найти площадь всего многоугольника. Например, у квадрата четыре стороны, поэтому его можно разделить на четыре треугольника, как показано ниже.
Деление квадрата на четыре равные части, StudySmarter Originals
Здесь x — длина одной стороны, a — апофема. Возможно, вы помните, что площадь треугольника равна b×h3, где b — основание треугольника, а h — высота.
В этом случае
b=x и h=a,
, поэтому площадь одного треугольника внутри квадрата может быть выражена как:
a×x2
Поскольку треугольников четыре, нам нужно умножить это на четыре, чтобы получить общую площадь квадрата.
 Это дает:
Это дает:⇒ 4×a×x2=a×4×2
Рассмотрим термин 4x. Возможно, вы уже заметили, что периметр квадрата — это сумма его четырех сторон, равная 4x. Итак, мы можем подставить p=4x обратно в наше уравнение, чтобы получить общую формулу площади правильного многоугольника:
Площадь=a×p2
Нахождение площади правильных многоугольников с помощью тригонометрии
Длина апофемы или периметра не всегда может быть дано в вопросе о правильных многоугольниках. Однако в таких случаях мы можем использовать наши знания тригонометрии для определения недостающей информации, если мы знаем длину стороны и величину угла. Давайте рассмотрим, как тригонометрия связана с правильными многоугольниками, на следующем примере сценария.
Дан правильный многоугольник с n сторонами, радиусом r и длиной стороны x.
Правильный многоугольник с n(=5) сторонами, StudySmarter Originals
Мы знаем, что угол θ будет равен 360°n. Рассмотрим один участок многоугольника, как показано на рисунке ниже.
 В этом разделе мы рисуем апофему из центра, разделяя ее на два прямоугольных треугольника.
В этом разделе мы рисуем апофему из центра, разделяя ее на два прямоугольных треугольника.Одна часть правильного многоугольника, StudySmarter Originals
Мы знаем, что ∠BAC равно θ, тогда ∠BAD&∠DAC будет θ2 соответственно, так как апофема является серединным перпендикуляром из центра. Теперь, вычислив площадь любого из прямоугольных треугольников, мы можем найти площадь правильного многоугольника. Следовательно, площадь прямоугольного треугольника равна:
Площадь=12×a×x2
где, a=rcosθ2,x2=rsinθ2.
Площадь сечения многоугольника в два раза больше площади прямоугольного треугольника.
⇒ Площадь одной части многоугольника=2×площадь прямоугольного треугольника=a×x2
Теперь, учитывая все части многоугольника, вся площадь многоугольника в n раз больше площади одной части.
⇒Площадь правильного многоугольника=n×площадь одной части многоугольника=n×(a×x2)
Площадь правильных многоугольников примеры и задачи
Рассмотрим несколько решенных примеров и задач на площадь правильных многоугольников.

Найдите площадь заданного правильного многоугольника.
Правильный многоугольник, Studysmarter Originals
Решение: Здесь дано, что a=14, сторона=283. Итак, периметр p равен:
p=3×side=3×283=145,5
Следовательно, площадь правильного многоугольника равна:
id=»2951752″ role=»math» Area=a×p2=14 ×145,52=1018,5
Найдите площадь шестиугольника со стороной 4 см и апофемой 3,46 см.
Решение: Поскольку апофема уже дана в вопросе, нам нужно только найти периметр шестиугольника, чтобы использовать формулу площади.
Площадь=a×p2
Периметр — это длина одной стороны, умноженная на количество сторон.
⇒p=4×6=24 см
Теперь, подставляя все значения в формулу площади, получаем:
Площадь=24×3,462=41,52 см2
Предположим, квадратный ярд имеет длину 3 фута. Какова площадь этого двора?
Решение: Нам дан квадратный многоугольник с длиной x=3ft.
 Нам нужно вычислить значение апофемы, чтобы найти площадь.
Нам нужно вычислить значение апофемы, чтобы найти площадь.Квадратный многоугольник со стороной 3 фута, StudySmarter Originals
Сначала разделим квадрат на четыре равные части. Угол одного сечения многоугольника (относительно центра) равен θ=360°n=360°4=90°. Поскольку каждое сечение можно разделить на два прямоугольных треугольника, угол, связанный с одним прямоугольным треугольником, равен θ2=90°2=45°.
Теперь мы можем использовать тригонометрическое соотношение для вычисления прямоугольного треугольника. Значение апофемы a можно найти как:
tanθ2=oppsideadjsidetan45°=32a⇒a=32tan45°=321=1,5
Теперь, подставив все значения в формулу, вычислим площадь правильного многоугольника:
Площадь=n×a×x2=4×1,5×1,5=9 футов2
Итак, площадь двора составляет 9 квадратных футов.
Площадь правильных многоугольников. Ключевые выводы
- Правильный многоугольник бывает равносторонним и равноугольным.
- Апофема многоугольника – это отрезок, идущий от центра многоугольника к середине одной из сторон.

- Если многоугольник правильный, найдите площадь по формуле.


 {2}} {4 \ tan \ frac {\ theta} {2}} $. 9{2}}{4 \tan \frac {180}{n}}$
{2}} {4 \ tan \ frac {\ theta} {2}} $. 9{2}}{4 \tan \frac {180}{n}}$  Таким образом, чтобы вычислить площадь неправильного многоугольника, мы разобьем неправильный многоугольник на множество правильных многоугольников так, что известны формулы их площадей.
Таким образом, чтобы вычислить площадь неправильного многоугольника, мы разобьем неправильный многоугольник на множество правильных многоугольников так, что известны формулы их площадей.
 Многоугольник может быть правильным или неправильным многоугольником. Вы можете найти площадь правильного многоугольника, используя предопределенную формулу, тогда как, чтобы найти площадь неправильного многоугольника, прежде всего, разделите многоугольник на количество многоугольников, формула площади которых известна, а затем найдите площадь неправильный многоугольник путем сложения площадей всех образованных таким образом многоугольников.
Многоугольник может быть правильным или неправильным многоугольником. Вы можете найти площадь правильного многоугольника, используя предопределенную формулу, тогда как, чтобы найти площадь неправильного многоугольника, прежде всего, разделите многоугольник на количество многоугольников, формула площади которых известна, а затем найдите площадь неправильный многоугольник путем сложения площадей всех образованных таким образом многоугольников.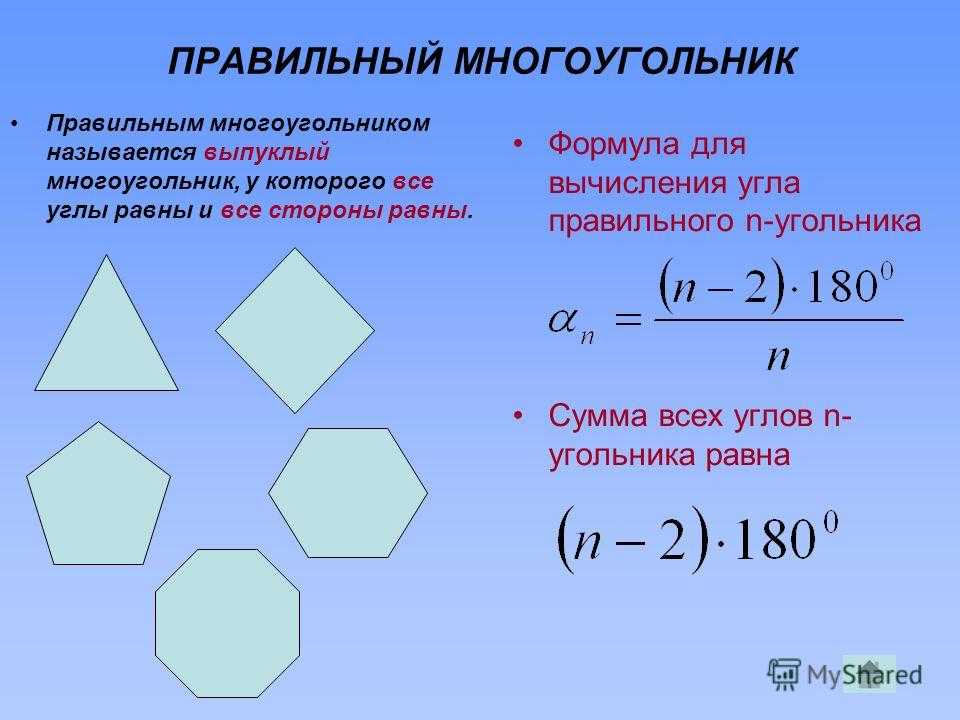
 Многоугольники могут быть правильными и неправильными. Основными многоугольниками, которые используются в геометрии, являются треугольник, квадрат, прямоугольник, пятиугольник, шестиугольник и т. д.
Многоугольники могут быть правильными и неправильными. Основными многоугольниками, которые используются в геометрии, являются треугольник, квадрат, прямоугольник, пятиугольник, шестиугольник и т. д.  Особенно в геометрии мы видели и изучали различные формы, такие как треугольники или квадраты и многие другие. Эти формы являются некоторыми примерами многоугольников. Напомним, что многоугольник — это двумерная замкнутая фигура, образованная прямыми линиями.
Особенно в геометрии мы видели и изучали различные формы, такие как треугольники или квадраты и многие другие. Эти формы являются некоторыми примерами многоугольников. Напомним, что многоугольник — это двумерная замкнутая фигура, образованная прямыми линиями. д.
д.
 Периметр правильного многоугольника можно найти, умножив длину одной стороны на общее количество сторон.
Периметр правильного многоугольника можно найти, умножив длину одной стороны на общее количество сторон. Это дает:
Это дает: В этом разделе мы рисуем апофему из центра, разделяя ее на два прямоугольных треугольника.
В этом разделе мы рисуем апофему из центра, разделяя ее на два прямоугольных треугольника.
 Нам нужно вычислить значение апофемы, чтобы найти площадь.
Нам нужно вычислить значение апофемы, чтобы найти площадь.