Примеры системы массового обслуживания: Системы массового обслуживания. Подробное решение задачи

Система массового обслуживания с неограниченной очередью. Экономико-математические модели

Краткая теория

---

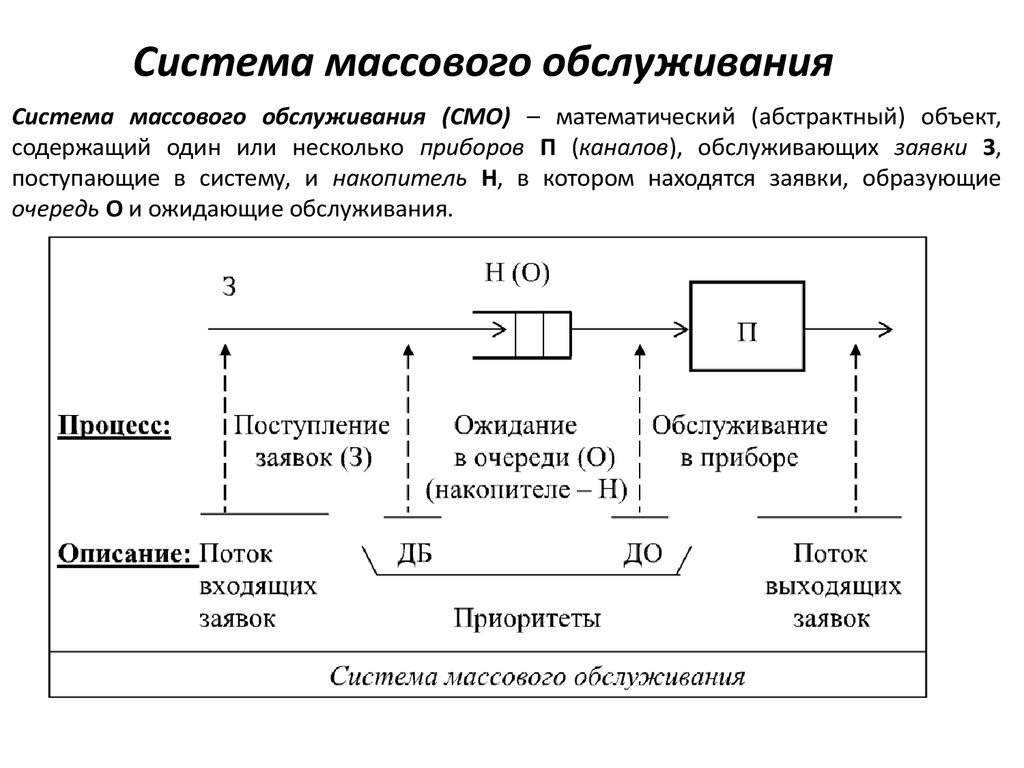
Пусть в n-канальную систему массового обслуживания (СМО) поступает с интенсивностью  простейший поток требований. Длительность обслуживания распределена по показательному закону со средним временем обслуживания .  Если же все каналы обслуживания заняты, то вновь поступившее требование становится в очередь за ранее поступившими не обслуженными требованиями. Освободившийся канал приступает к обслуживанию очередного требования из очереди. Определим основные характеристики работы такой системы. Так как число требований, стоящих в очереди, может быть бесконечно большим, то и число состояний системы также может быть бесконечно большим.

Вероятность свободного состояния системы:

Последнее выражение получено при условии , которое является условием стационарности СМО.

В случае  система не справляется с обслуживанием, очередь неограниченно возрастает. Отношение  обозначается через  и называется уровнем загрузки системы:

Определим основные характеристики многоканальной СМО с ожиданием. Вероятность получения отказа равна нулю. Относительная пропускная способность —это величина, которая дополняет вероятность отказа до единицы: .  Абсолютная пропускная способность . Определим среднее число занятых каналов: каждый занятый канал обслуживает в единицу времени в среднем  заявок, а вся система —  заявок. Тогда:

Коэффициент занятости каналов обслуживания:

Образование очереди возможно, когда вновь пост пившее требование застанет в системе не менее n требований, т. е. когда в системе будет находиться , , требований.

Эти события независимы, поэтому вероятность того, что все каналы заняты, равна сумме вероятностей ,   Отсюда вероятность образования очереди:

Среднее число заявок в очереди  можно вычислить как математическое ожидание, складывая произведения  возможного числа заявок на вероятность того, что число заявок будет в очереди:

Среднее число заявок, связанных с системой:

Определим среднее время ожидания заявки в очереди . Очередь образуется, если все  каналов заняты. Так как интенсивность обслуживания , то поток освобожденных каналов имеет интенсивность . Если заявка поступила в момент, когда заняты все  каналов и очереди нет, то время ожидания составит в среднем , а если застанет одно требование в очереди, то , и так далее. Среднее время ожидания заявок в очереди найдем, суммируя произведения среднего времени ожидания на соответствующую вероятность:

Среднее время пребывания заявок в системе:   

Формулы Литтла:  

Среднее число простаивающих каналов обслуживания:

Коэффициент простоя каналов:

Пример решения задачи

---

На строительном складе работают четыре кладовщика. Поток посетителей имеет пуассоновское распределение с интенсивностью 2 заявки в минуту. Время обслуживания имеет показательное распределение со средним значением 1,5 минуты на заявку. Определить показатели работы склада.

Решение

Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:

ВКонтакте
WhatsApp
Telegram

Я буду работать с вами, над вашей проблемой, пока она не решится.

Имеем:

Отсюда следует, что вероятность того, что все четыре кладовщика простаивают, равна 0,05. Определим другие показатели работы системы.

Абсолютная пропускная способность склада, т. е. количество обслуживаемых в единицу времени требовании,  (заявки в минуту). Среднее число занятых кладовщиков . Вероятность образования очереди, т. е. вероятность того, что в момент обращения заказчика все четыре кладовщика заняты:

Среднее число заявок в очереди:

Среднее время простаивания в очереди:

Среднее число заявок в системе:

Среднее время пребывания заявки в системе:

Среднее число простаивающих кладовщиков: 

Основы теории массового обслуживания

 

 

При исследовании операций часто приходится сталкиваться с анализом эффективности работы систем массового обслуживания. Примеры СМО: телефонная станция, ремонтные мастерские, билетные кассы, АЗС, железнодорожная сортировочная станция.

В теории массового обслуживания понятие очереди является одним из основных.

Определение: Очередью называется линейная цепочка выстроившихся один за другим объектов, нуждающихся в обслуживании.

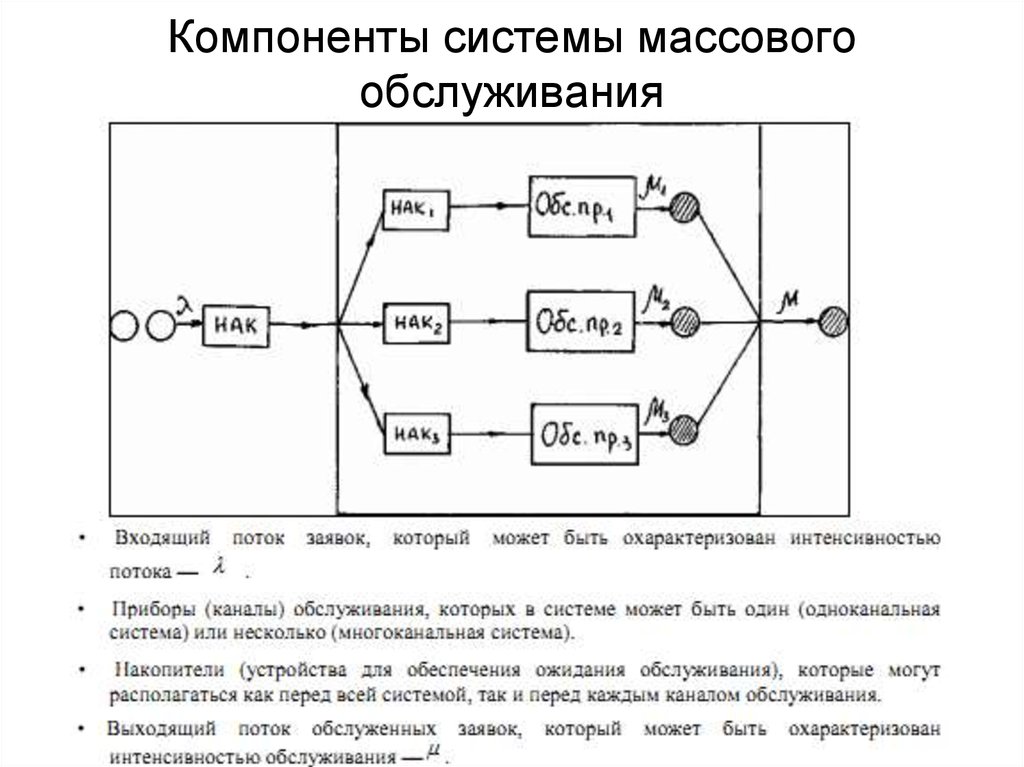
Все системы массового обслуживания имеют следующие основные элементы:

а) Входной поток – это поток поступающих требований или заявок на обслуживание. Если поступление требований или заявок на обслуживание и процедура обслуживания выполняется строго по графику, то очереди можно избежать. На практике эти процессы носят случайный характер, и для их описания следует привлекать методы теории вероятностей.

Обычно требования в СМО поступают по одному. Такие системы называются системами с единичным поступлением. Однако бывают ситуации, когда требования поступают группами. Причем число требований в группе может быть заданным или случайным (число вагонов в железнодорожном составе, поступающих на сортировочную станцию). В этом случае речь идет о системе с групповым поступлением требований.

Возможны ситуации, когда поступившие требования могут отказываться от обслуживания и покидать систему (система с потерями). Система, в которой обслуживаются все поступающие требования, называется системой массового обслуживания с ожиданиями.

б) Механизм обслуживания. СМО различаются числом обслуживающих приборов, количеством обслуживаемых одновременно требований, продолжительностью обслуживания. Здесь также есть характеристики, которые носят случайный характер.

Процесс обслуживания требований может состоять из нескольких этапов, выполняемых последовательно на различных обслуживающих устройствах. Такую систему называют многофазной.

в) Дисциплина очереди или правила поведения очереди. Это правила, в соответствии с которыми обслуживающий механизм принимает поступившую заявку на обслуживание. Например, “первым пришел – первым обслуживается”, “последним пришел – первым обслуживается”, “случайный отбор заявок” и т.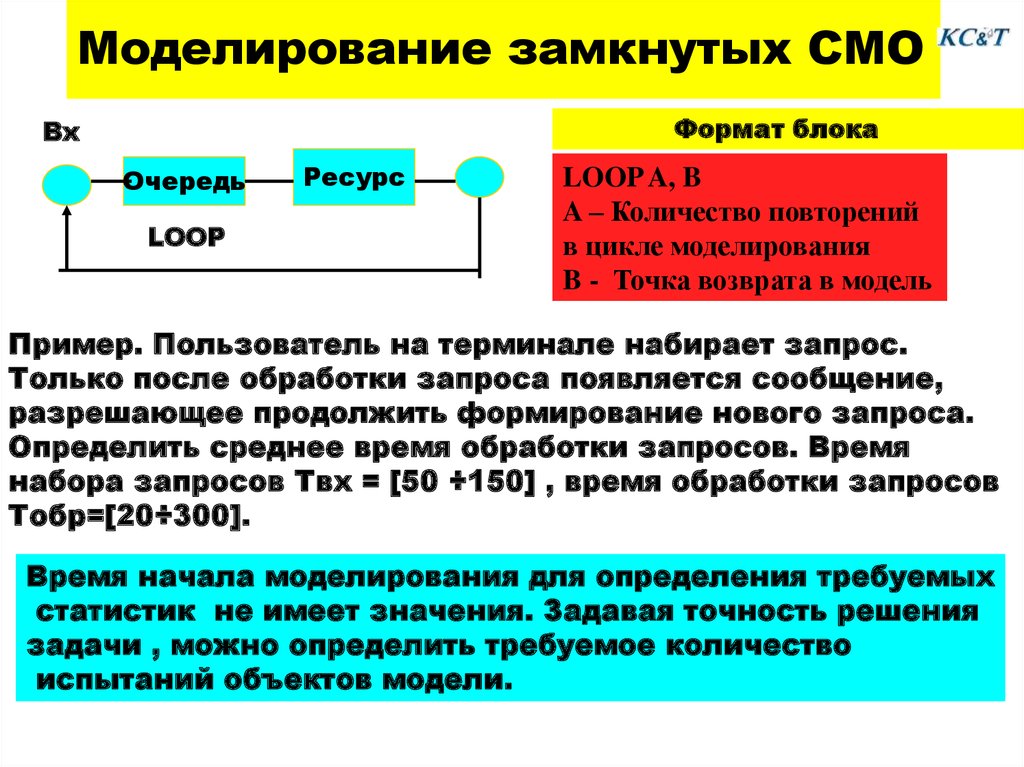 п.

Существуют так называемые приоритетные СМО и соответствующие им приоритетные дисциплины очереди. Причем, требование с более высоким приоритетом в момент своего поступления могут прервать процесс обслуживания требований с более низким приоритетом. Это

СМО с абсолютным приоритетом. Если прерывание не допустимо, то говорят о СМО с относительным приоритетом.

г) Выходящий поток – поток требований покидающих СМО после обслуживания. Этот поток играет важную роль, так как может быть сам входящим потоком для других СМО. Часто, обслуженные требования возвращаются в эту же систему. В этом случае имеют место замкнутые СМО. Примером может быть организация ремонта станочного парка предприятия, когда отремонтированные станки возвращаются в систему, образуя входящий поток.

Предмет теории массового обслуживания связан с установлением зависимости между характеристиками потока заявок, числом каналов, их производительностью, правилами работы СМО и эффективность обслуживания.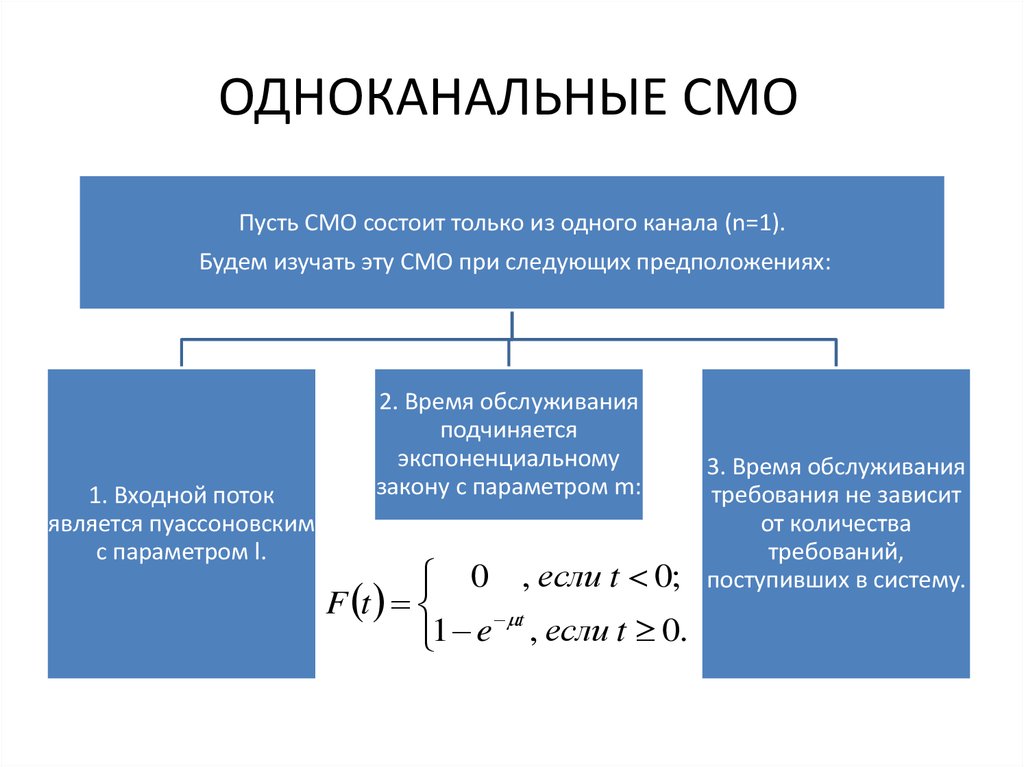

Характеристики эффективности СМО:

1)      Среднее число обслуживаемых заявок СМО в единицу времени;

2)      Среднее число заявок, покидающих СМО не обслуженными;

3)      Среднее время ожидания в очереди и т.п.

Случайный характер потока заявок и длительности их обслуживания приводит к тому, что в СМО протекает случайный процесс. Если случайный процесс марковский, то удается описать работу СМО с помощью аппарата обыкновенных дифференциальных уравнений и выразить характеристики обслуживания через параметры СМО и потоки заявок.

Для того, чтобы протекающий в системе процесс был марковский, нужно чтобы все потоки событий, переводящие систему из одного состояния в другое, были пуассоновскими. Если потоки не пуассоновские, тогда для исследования основных характеристик такой системы используется метод численного моделирования.

При изучении СМО можно выделить три класса задач: задача анализа поведения систем, статические задачи, операционные задачи.

Задачи анализа поведения системы заключаются в том, чтобы с помощью математических моделей, отражающих свойства СМО, выявить определяющие поведение этих систем в процессе их функционирования. К основным операционным характеристикам относятся:

Q(t) – длина очереди в момент времени t, т.е. число требований находящихся в системе;

W(t) – продолжительность ожидания обслуживания относительно требования, которое поступило в момент времени t;

I_n – продолжительность n-го периода простоя системы.

На практике часто используется показатель, который называется степенью загруженности обслуживающего прибора или коэффициентом нагрузки:

.

Статистические задачи, возникающие при исследовании систем массового обслуживания, связаны с оценкой основных процессов, которые протекают в системе. При этом общая модель приводится в количественное соответствие с конкретной СМО на основе статистического анализа эмпирических данных. Это позволяет оценить фигурирующие в модели параметры.

Операционные задачи возникают при проектировании систем массового обслуживания, управлении СМО и оценке их эффективности. Некоторые из этих задач по своей природе относятся к разряду статистических.

При рассмотрении систем массового обслуживания часто используются обозначения предложенные Кендаллом. Они позволяют описать СМО с помощью следующих трех элементов: вид входного потока, распределение продолжительности обслуживания, число обслуживающих приборов.

Используются следующие обозначения:

M – пуассоновское или экспоненциальное распределение;

D – постоянная величина;

E_k – распределение Эрланга;

G – произвольное распределение;

GI – распределение в случае независимых событий.

Например, система M /D /s – система с s приборами, обслуживающая поступающие требования за строго определенный интервал времени, поступающие требования образуют пуассоновский поток.

Введенная классификация должна дополняться правилами формирования очереди, от которых будет зависеть полученный результаты.

 

 

Рассмотрим СМО, которая состоит из одного канала (одного обслуживающего прибора). На нее поступает стационарный пуассоновский поток заявок с интенсивностью

l = l(t). Заявка, заставшая канал занятым, получает отказ и покидает систему. Обслуживание заявки продолжается в течение случайного времени T_обсл., имеющему экспоненциальную плотность вероятности:

f(t) = me^—mt.

Из сказанного следует, что мы имеем дело с системой типа М/М/1.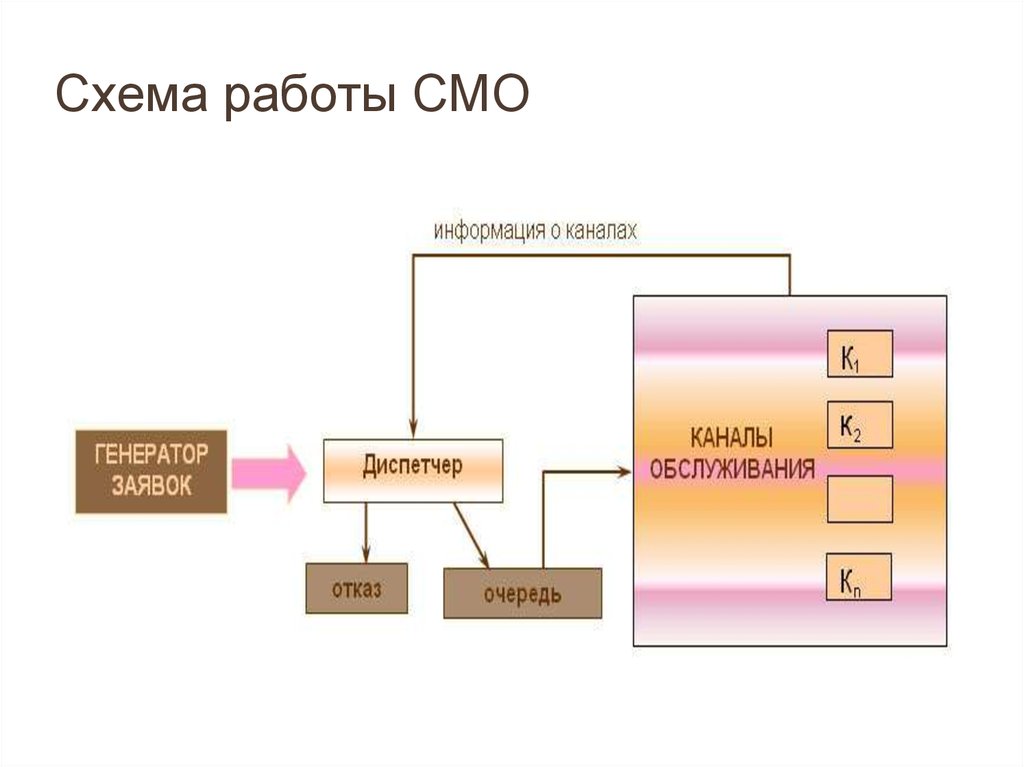 Ее размеченный граф имеет вид:

              

 

 

Возможно два состояния:

Q₀ – канал свободен;

Q₁ – канал занят.

Из Q₁ в Q₀ систему переводит поток заявок, а из Q₁ в Q₀ поток обслуживаний. Обозначим вероятности состояний p₀(t) и p₁(t) и составим для них дифференциальные уравнения Колмогорова. Получим:

Если учесть, что p₁+p₀ = 1, то получим одно уравнение:

.

Можно показать, что при начальных условиях p₀(0) = 1, p₁(0) = 0, решение имеет вид:

.

Начальное условие p₀(0) = 1 означает, что в начальный момент канал заведомо свободен. Зависимости p₀(t) и p₁(t) показаны на рисунке.

 

Важной характеристикой СМО с отказами является относительная пропускная способность q, которая равна доли обслуженных требований от общего числа поступивших в систему

q = 1 – P_отк.,

P_отк. – вероятность отказа в обслуживании поступившему требованию. В нашем случае:

P_отк. = p₁ и y = m/(l + m).

Абсолютная пропускная способность А – это среднее число требований, обслуживаемых системой в единицу времени:

.

Пример: АЗС имеет одну заправочную колонку. Заявка (требование) – автомобиль, пришедший на заправку. АЗС не имеет места для ожидания, поэтому автомобиль, пришедший на заправку в момент, когда колонка занята, покидает АЗС. Средняя продолжительность заправки  мин, средняя интенсивность потока автомобилей l = 0,3 (авт. в минуту). Все потоки событий простейшие. Определить предельные величины:

1)      относительной пропускной способности q;

2)      абсолютной пропускной способности А;

3)      вероятность отказа.

Решение: Имеем одноканальную СМО с отказами. Т.к. время обслуживания имеет экспоненциальное распределение, то

Относительная пропускная способность:

,

т.е. в установившемся режиме будет обслуживаться около 42,5% машины.

Абсолютная пропускная способность:

A = l * q = 0,425 * 0,3 = 0,127,

т.е. в среднем заправляется 0,127 машин/мин.

Вероятность отказа: P_отк. = 1 – q = 0,575.

Определим номинальную пропускную способность АЗС как

,

что почти  вдвое больше, чем фактическая пропускная способность. Это объясняется стохастической природой входного потока и время обслуживания.

(тип СМО – М/М/n)

 

Схема СМО показана на рисунке

 

 

Поток поступающих требований – пуассоновский со средней интенсивностью l. Число мест для ожидания равно m. Время обслуживания имеет экспоненциальное распределение с параметром m.

Если поступающее требование застает узел обслуживания занятым и свободных мест в очереди нет, то это требование покидает СМО. Если при поступлении требования свободно несколько обслуживающих устройств, то оно поступает на любое из них с равной вероятностью.

Максимально в СМО одновременно может находиться n + m требований. Состояние системы будем нумеровать по числу находящихся в ней требований: Q₀ – все каналы свободны; Q₁ – занят один канал; Q_n – заняты все каналы; Q_n+1 – одно требование стоит в очереди;

Q_n+m – все каналы заняты, все места в очереди заняты.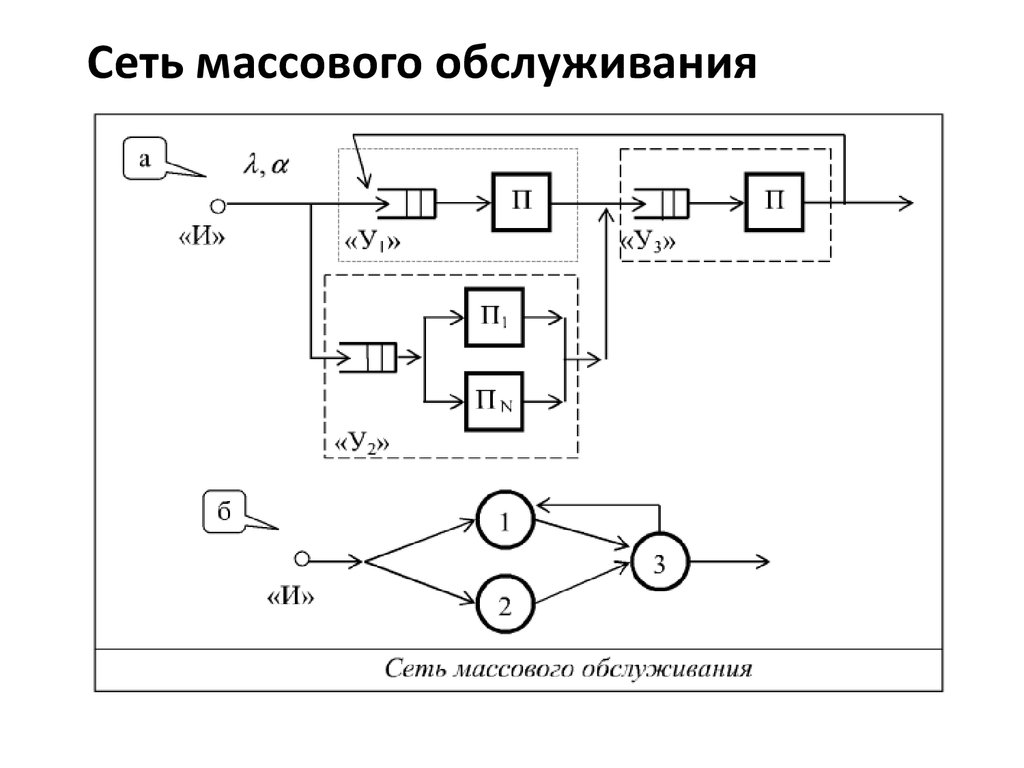 Граф состояний имеет вид:

 

 

Если очереди нет, то систему из состояния Q_k в Q_k-1 переводит поток, интенсивность которого равна km.

Граф представляет рассмотренную схему “гибели и размножения”. Используя полученные результаты можно записать выражение для финальных вероятностей. Обозначим r = l/m.

 

;

 

1)      Вероятность того, что все обслуживающие устройства свободны p₀. (1)

2)      Вероятность того, что занято k обслуживающих устройств p_k. (2)

3)      Вероятность того, что все обслуживающие устройства заняты и l требований в очереди (l£m) (из 3)

Вероятность отказа в обслуживании:

4)      Среднее число устройств, занятых обслуживанием требований:

Если выполнить суммирование:

5)      Среднее число простаивающих устройств:

6)      Коэффициенты прочности и занятости:

7)      Относительная пропускная способность:

8)      Абсолютная пропускная способность:

A = l q;

9)      Среднее число требований, находящихся в очереди. Очередь существует тогда, когда все обслуживающие устройства заняты:

10)  Среднее число требований в системе:

11)  Среднее время ожидания в очереди. Если заявка застанет занятыми не все каналы, ей вообще не придется ждать облуживания. Если заявка придет в момент, когда заняты все n каналов, а очереди нет, ей придется ждать среднее время 1/nm (nm — интенсивность потока освобождения n каналов). Если заявка придет в СМО и застанет в очереди одну заявку, то она будет ждать 2/nm и т.д. Если заявка застанет в очереди m заявок, то она ждать не будет.

Формула Литтла.

12)  Среднее время пребывания заявки в СМО. Время пребывания заявки в СМО:

t_сис = t_ож + t, t_ож – время ожидания в очереди;

<t_сис> = <t_ож> + <t>;

<t> = (1-q)0 + q<t_обсл> = q /m;     <t_обсл> = 1/m;

<t_сис> = W + q/m;

Прежде чем рассмотреть пример, рассмотрим n-канальную СМО с неограниченной очередью (m®¥). Можно показать, что условием существования финальных вероятностей является r/n < 1. Если r/n ³ 1, то очередь растет до бесконечности. Для системы с неограниченной очередью:

Напоминаем выражение для СМО с ограниченной очередью:

 — формула Литтла.

Пример. Касса по продаже железнодорожных билетов с двумя окошками представляет собой двухканальную СМО с неограниченной очередью, которая устанавливается сразу к двум окошкам. Касса продает билеты сразу в два пункта А и В. Интенсивность потока заявок для обоих пунктов одинакова и равна l_А = l_B = 0,45. Интенсивность результирующего потока

l = l_A + l_B = 0,9. Касса в среднем тратит на обслуживание одного пассажира две минуты (время обслуживания имеет экспоненциальное распределение). Пассажиры не довольны большой очередью у кассы. Поступило предложение создать две специализированные кассы, продающие билеты одна только в пункт А, другая в пункт В. Оценить эффективность такого предложения при условии, что поток пассажиров – простейший.

Найдем среднюю длину очереди L_очи среднее время ожидания в очереди.

Вариант1.

Двухканальная СМО. l = 0,9. m = 0,5. r = l/m = 1,8. r/2 = 0,9 < 1 – условие существования финальных вероятностей выполняется.

P₀ » 0,0525 (вероятность присутствия заявок в системе)

L_оч = 7,68чел W_оч = 8,54 мин.

Вариант2.

Две одноканальные СМО. l = 0,9. i =1,2. m = 0,5. r = 0,9.

L_оч = 8,1чел;  W_оч = 18 мин.

Второй вариант значительно хуже первого. Это можно объяснить тем, в первом варианте меньше средняя доля времени, которую  простаивает каждый из двух пассажиров. Если он не занят обслуживанием пассажира, покупающего билет в А он может заняться обслуживанием пассажира, покупающего билет в В и наоборот. Во втором варианте незанятый кассир сидит. Следует также отметить, что обе СМО работают на пределе своих возможностей. Если немного увеличить время обслуживания, то r станет больше 1 и очередь начнет неограниченно возрастать.

 

   

Ошибка

Перейти к основному содержанию

Вся размещенная на ресурсе информационная продукция предназначена для детей, достигших возраста шестнадцати лет (16+)

Извините, не удалось найти запрашиваемый Вами файл

Подробнее об этой ошибке

Перейти на… Перейти на…Новостной форумКомплексные числа (с приложениями к задачам электротехники)Лекционный материал по теме «Комплексные числа»Разбор типовых задач задач по теме «Комплексные числа»Примеры решения задач по теме «Комплексные числа»КОМПЛЕКСНЫЕ ЧИСЛАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийТеория функций комплексного переменного. Операционное исчислениеПрезентация по теме «Комплексные числа»Дополнительный материал к темеОсновы линейной алгебры с приложениями в других разделах математикиЛекционный материал по теме «Матрицы. Определители»Лекционный материал по теме «Системы линейных алгебраических уравнений (СЛАУ). Применение СЛАУ в экономике»Лекционный материал по теме «Линейные операторы»Примеры решения по теме «Системы линейных алгебраических уравнений»ЛИНЕЙНАЯ АЛГЕБРАКомплексные числа. Основы линейной алгебры. Системы линейных уравненийЛинейная алгебра для экономистовМатрицы. ОпределителиВекторная алгебра.Аналитическая геометрияЛекционный материал по теме «Векторная алгебра. Линейные операции над векторами»Лекционный материал по теме «Скалярное, векторное и смешанное произведения векторов»Примеры решения задач по теме «Векторная алгебра. Линейные операции над векторами»Примеры решения задач по теме «Скалярное, векторное и смешанное произведения векторов»ВЕКТОРНАЯ АЛГЕБРАВекторная алгебра и аналитическая геометрияПрезентация по теме «Векторная алгебра»Векторная алгебра. Аналитическая геометрияТеоретический материал по теме «Метод координат на плоскости и в пространстве»Лекционный материал по теме «Прямая на плоскости»Лекционный материал по теме «Кривые второго порядка»Лекционный материал по теме «Прямая в пространстве»Лекционный материал по теме «Плоскость в пространстве»Лекционный материал по теме «Поверхности второго порядка»Примеры решения задач по теме «Прямая на плоскости»Примеры решения задач по теме «Кривые второго порядка»Примеры решения задач по темам «Прямая и плоскость в пространстве»АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯВекторная алгебра и аналитическая геометрияСправочный материал «Прямая на плоскости»Справочный материал «Кривые второго порядка»Справочный материал «Прямая и плоскость в пространстве»Линейная алгебра для экономистовПрезентация по теме «Прямая на плоскости»Презентация по теме «Уравнения плоскости и прямой в пространстве»▶ Виртуальный тренажер «Прямая на плоскости» 👨‍🎓Введение в анализНачала анализаЛекционный материал по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Лекционный материал по теме «Предел функции, основные теоремы о пределах.Замечательные пределы. Бесконечно малые функции»Лекционный материал по теме «Непрерывность функции»Примеры решения задач по теме «Множества, функции, основные характеристики функций. Основные элементарные функции»Примеры решения задач по теме «Предел функции. Раскрытие математических неопределенностей»Примеры решения задач по теме «Непрерывность функции»ВВЕДЕНИЕ В АНАЛИЗУпражнения для самостоятельного решения Тест «Введение в анализ»Презентация по теме «Введение в анализ»1. Понятие функцииПрименение функций в экономической теории и практикеПрименение пределов в экономических расчетахПриложение понятия непрерывности функций в экономике▶ Виртуальная справочная «Тригонометрические функции» 👨‍🎓Дифференциальное исчисление функций одной переменнойПриложения дифференциального исчисления функции одной переменнойЛекционный материал по теме «Дифференциальное исчисление функции одной переменной»Лекционный материал по теме «Основные теоремы дифференциального исчисления. Правила Лопиталя»Лекционный материал по теме «Формулы Тейлора и Маклорена»Лекционный материал по теме «Приложения дифференциального исчисления»Примеры решения задач по теме «Дифференциальное исчисление функций одной переменной»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙТест «Основные правила и формулы дифференцирования»Тест «Дифференциальное исчисление функций одной переменной»Основы дифференцирования. Часть 1Основы дифференцирования. Часть 2Основы дифференцирования. Часть 3Приложения производной Исследование функций, Примеры решения задачПрименение производных при решении экономических задачИнтегральное исчисление функции одной переменнойЛекционный материал по теме «Неопределенный интеграл»Лекционный материал по теме «Определенный интеграл»Практическое занятие 1. Непосредственное интегрирование (неопределённый интеграл)Практическое занятие 2. Интегрирование заменой переменной (неопределённый интеграл)Практическое занятие 3. Интегрирование по частям. Интегрирование выражений, содержащих квадратный многочлен (неопределённый интеграл)Практическое занятие 4. Интегрирование рациональных дробей (неопределенный интеграл)Практическое занятие 5. Определенный интегралПримеры решения задач по теме «Неопределенный интеграл»Примеры решения задач по теме «Определенный интеграл»ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙТест «Таблица основных неопределенных интегралов»Тест «Интегрирование функций одной переменной»1. Неопределенный интеграл. Основы интегрирования2. Интегрирование иррациональных выражений 3. Интегрирование тригонометрических выражений 4. Определенный интегралДифференциальное исчисление функций нескольких переменныхЛекционный материал по теме «Функции нескольких переменных»Примеры решения задач по теме «Функции нескольких переменных»ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХТест «Дифференциальное исчисление функций нескольких переменных»1. Функции нескольких переменныхПрименение функций нескольких переменных в экономикеОбыкновенные дифференциальные уравненияОбыкновенные дифференциальные уравнения и их приложенияДифференциальные уравнения первого порядкаДифференциальные уравнения высших порядковСистемы дифференциальных уравнений и устойчивость их решенийЛекционный материал по теме «Дифференциальные уравнения 1-го порядка»Лекционный материал по теме «Дифференциальные уравнения высших порядков»Примеры решения задач по теме «Дифференциальные уравнения»ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯТест «Обыкновенные дифференциальные уравнения»1. Дифференциальные уравнения 1-го порядка2. Дифференциальные уравнения высших порядковСпециальные разделы высшей математикиСпециальные разделы высшей математики: практикум Кратные, криволинейные и поверхностные интегралы. Элементы теории поляПоверхностные интегралы. Векторный анализЛекционный материал по теме «Двойные интегралы»Примеры решения задач по теме «Двойные интегралы»КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ2. Двойные интегралыРядыЛекционный материал по теме «Числовые ряды»Лекционный материал по теме «Функциональные ряды»Примеры решения задач по теме «Ряды»1. Числовые ряды2. Функциональные ряды3. Разложение функций в степенные рядыТеория функций комплексного переменного. Операционное исчисление.Основы теории функций комплексного переменногоОперационное исчисление.Теория функций комплексного переменного. Операционное исчислениеТеория вероятностей Теория вероятностей (случайные события)Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы: практикумЛекционный материал по теме «Основные подходы к определению вероятности»Лекционный материал по теме «Алгебра событий. Основные теоремы о вероятности»Лекционный материал по теме «Дискретные случайные величины»Лекционный материал по теме «Непрерывные случайные величины»Лекционный материал по теме «Числовые характеристики случайных величин»Лекционный материал по теме «Моменты и другие характеристики распределений»Лекционный материал по теме «Нормальное распределение»Практическое занятие 1. КомбинаторикаПрактическое занятие 2. Действия над событиями. Вероятность событияПрактическое занятие 3. Теоремы умножения и сложения вероятностей событийПрактическое занятие 4. Формула полной вероятности Практическое занятие 5. Схема Бернулли. Локальная и интегральная теоремы ЛапласаПрактическое занятие 6. Дискретные случайные величины. Числовые характеристикиПрактическое занятие 7. Непрерывные случайные величины. Классические законы распределения НСВПримеры решения задач по теме «Комбинаторика»Примеры решения задач по теме «Классическое определение вероятности»Примеры решения задач по теме «Теоремы сложения и умножения»Примеры решения задач по теме «Формула полной вероятности. Формулы Байеса»Примеры решения задач по теме «Схема независимых испытаний Бернулли»Примеры решения задач по теме «Дискретные случайные величины»Примеры решения задач по теме «Основные числовые характеристики дискретных случайных величин»Примеры решения задач по теме «Непрерывные случайные величины»Примеры решения задач по теме «Основные числовые характеристики непрерывных случайных величин»Примеры решения задач по теме «Классические законы распределения дискретных случайных величин»Примеры решения задач по теме «Классические законы распределения непрерывных случайных величин»Таблица значений функции ЛапласаТЕОРИЯ ВЕРОЯТНОСТЕЙТест по разделу «Случайные события»Тест по теме «Числовые характеристики случайных величин»Тест по теме «Дискретные случайные величины»Тест по теме «Непрерывные случайные величины»Основные подходы к определению вероятностиАлгебра событий. Основные теоремы о вероятностиТеория вероятностей (Лыткина Е.М.,Чихачев А.С., 2013)Математическая статистикаОсновы математической статистикиМатематическая статистика: практикумПримеры решения задач по математической статистикиМАТЕМАТИЧЕСКАЯ СТАТИСТИКАТест по разделу «Математическая статистика». Тема «Статистическое распределение. Точечные и интервальные оценки параметров распределения»Тест по разделу «Математическая статистика». Тема «Статистические гипотезы. Корреляционный и регрессионный анализ»Вероятность, случайные процессы, математическая статистикаСтатистический метод и основы его примененияВероятностно-статистические методы на примере задач исследования работы железнодорожного транспорта Марковские процессы и СМО. Учебное пособиеЛекционный материал по теме «Марковский процесс с дискретным временем»Лекционный материал по теме «Марковский процесс с непрерывным временем»Примеры решения задач по теме «Марковские процессы»СЛУЧАЙНЫЕ ПРОЦЕССЫЛабораторные работы Вероятность, случайные процессы, математическая статистикаТеория вероятностей. Случайные процессы. ПрактикумЛекция «Марковские процессы»Цепи МарковаСистемы массового обслуживания (СМО)СМОВыбор группы*Тест «Таблица основных неопределенных интегралов»*Тест «Интегрирование функций одной переменной»*Тест «Дифференциальное исчисление функций нескольких переменных»*Тест «Обыкновенные дифференциальные уравнения»*Тест по разделу «Случайные события»*Тест по теме «Дискретные случайные величины»*Тест по теме «Непрерывные случайные величины»*Тест по теме «Числовые характеристики случайных величин»*Тест «Введение в анализ»*Тест «Основные правила и формулы дифференцирования»*Тест «Дифференциальное исчисление функций одной переменной»*Экзаменационный тест «Таблица основных неопределенных интегралов»*Экзаменационный тест «Интегрирование функций одной переменной»*Экзаменационный тест «Дифференциальное исчисление функций нескольких переменных»*Экзаменационный тест «Обыкновенные дифференциальные уравнения»Контрольная работа. Дифференциальное исчисление функций нескольких переменныхКонтрольная работа. Неопределенный интеграл (методы интегрирования)Контрольная работа. Неопределенный интеграл (интегрирование рациональных дробей)Контрольная работа. Определенный интегралКонтрольная работа. Обыкновенные дифференциальные уравненияКонтрольная работа 1. Теория вероятностей (случайные события)Контрольная работа 2. Теория вероятностей (характеристики дискретной случайной величины)Контрольная работа 3. Теория вероятностей (характеристики непрерывной случайной величины)Контрольная работа 4. Теория вероятностей (классические законы распределения дискретной случайной величины)Контрольная работа 5. Теория вероятностей (классические законы распределения непрерывной случайной величины)Экзамен Математика (2 семестр). СОД.1,2,3-19-1 (И,З)ЭКЗАМЕН. Математика (3 семестр)_СОД.1,2,3-19 (з)

Что такое система массового обслуживания? Определение, примеры и преимущества

Что такое система массового обслуживания?

На первый взгляд, ответ очевиден: это система, предназначенная для помощи в очередях.

Хотя этот ответ не совсем неверен, имена могут быть обманчивы. Легко принять решение об организации очередей как должное, если вы не полностью понимаете все, что оно влечет за собой.

Так что берите тетради и точите карандаши! Мы идем по авантюрной дороге к управление очередью .

Вы узнаете, почему важно управление очередями, как работают системы очередей и какие преимущества дает использование решения для организации очередей в вашем бизнесе.

Приступим к делу.

Системы массового обслуживания: оглавление

Чтобы сделать это руководство более понятным, оно разделено на главы. Не стесняйтесь читать все сверху вниз или переходите к разделу, который вас больше всего интересует.

• Управление очередью: что это такое и почему это важно
• Введение в системы массового обслуживания
• Принципы работы систем массового обслуживания
• Применение систем массового обслуживания в различных отраслях промышленности
• Преимущества системы массового обслуживания
• Краткий обзор систем массового обслуживания

83 Что такое очередь и почему это важно

Ранее мы определили управление очередью как набор принципов, направленных на управление потоком клиентов и оптимизацию работы в очереди.

Чтобы добавить к этому, управление очередями — это не то, что требуется один или два раза. Чтобы управление очередями приносило результаты, оно должно быть непрерывным процессом .

На бумаге огромное количество посетителей – это хорошо для вашего бизнеса. Это много потенциальных продаж, которые только и ждут, чтобы это произошло!

Проблема возникает, когда наплыв клиентов превышает возможности сотрудников. Чем меньше служащих, тем меньшей толпой клиентов они могут управлять.

Результаты? 51% потребителей в США сменили поставщика услуг в 2012 году из-за плохого обслуживания клиентов.

Предоставленные сами по себе, обслуживающие клерки не могут не чувствовать себя ошеломленными, когда сталкиваются с толпами посетителей, похожими на гуннов. Они могут победить только при наличии инструментов управления очередью.

Управление очередью в первую очередь касается областей очереди — т. е. мест, где возникают очереди. Но что такое очередь?

Можно сказать, что это очередь людей, ожидающих предоставления услуг или товаров. Но вы также можете сформулировать это как приложение к проблеме «спрос превышает предложение».

Как уже говорилось выше, «приток клиентов (спрос) превышает возможности сотрудников (предложение)».

Управление очередью помогает поддерживать это хрупкое равновесие.

Введение в системы очередей

Системы очередей прошли долгий путь развития. Они перешли от простых физических барьеров к современному программному обеспечению виртуальных очередей

Существует много типов решений для организации очередей, но их самые простые случаи также являются одними из наименее эффективных.

Возьмем, к примеру, барьеров толпы .

Барьеры или стойки обычно используются в гостиницах, банках, кинотеатрах, на массовых мероприятиях и в других местах. Их основная цель — контроль толпы за счет ограничения доступа к определенным областям.

С одной стороны, кажется логичным использовать физические инструменты для управления потоком клиентов, которые физически присутствуют в вашем офисе.

С другой стороны, наш цифровой век требует чего-то более сложного. Помещение ваших посетителей в лабиринт веревочных барьеров также имеет неблагоприятное влияние на их психологическое состояние .

Помните: 12 положительных впечатлений от обслуживания клиентов компенсируют один отрицательный опыт.

Очевидно, ситуация требует более изящных решений.

Современное цифровое решение для управления очередью работает на другом уровне, чем простые инструменты управления толпой.

Цифровая система очереди дает клиентам ощущение свободы действий, поскольку они регистрируются для получения услуг с помощью киосков самообслуживания — интерактивных терминалов, размещенных в местах с высокой проходимостью.

После регистрации покупателю необходимо посмотреть на экран с соответствующей статистикой: ваше место в очереди, количество людей перед вами, пункт обслуживания, в который вам нужно обратиться и т. д.

С четкими инструкциями и текстом уведомления о сообщениях, процесс постановки в очередь быстрее, чем когда-либо . Кассы работают эффективно, время ожидания сокращается, а опыт покупок значительно улучшается.

Тем временем персонал получает ценные показатели, такие как длина очереди, время ожидания и другую информацию, предоставляемую системами управления очередью, которые работают над дальнейшим улучшением обслуживания.

Что именно делает процесс постановки в очередь гладким? Давайте рассмотрим принципы работы систем массового обслуживания .

Элементы системы очередей

Управление очередями — и, соответственно, системы очередей — основано на трех основных принципах организации очередей. Это справедливость , участие в очереди и объясненное ожидание .

Давайте рассмотрим каждый из этих принципов один за другим.

Справедливая очередь

Никому не нравятся перепрыгивающие через очередь и перерезающие линии. Но обычно, сталкиваясь с явными случаями перехода без очереди, люди не высказывают своего недовольства и предпочитают вести себя вежливо.

Только 10% людей в очереди предотвращают перерезание очереди.

Однако это означает, что они будут набрасываться на вашу систему очередей, которая позволяет людям не стоять в очереди без последствий.

В результате ваш бизнес теряет уважение из-за неспособности эффективно справиться с этой ситуацией.

Справедливое обращение означает, что все принимают правила очереди и свое место в ней. Если есть список приоритетов, его необходимо сообщить заранее.

Если есть прыгуны в очереди, они должны столкнуться с последствиями или, что еще лучше, вообще предотвратить их.

Отсутствие порядка в ваших очередях вызывает тревогу и беспокойство. Люди боятся покинуть свое место и обычно не доверяют своим товарищам по очереди.

Это создает неблагодарную атмосферу обслуживания клиентов.

Справедливость в очередях нельзя недооценивать. Обеспечение справедливости ваших очередей является одним из наиболее важных аспектов хорошего управления очередями.

Читать далее: Взвешивание вариантов: может ли обход очереди быть справедливым?

Занятие в очереди

Хотите верьте, хотите нет, но течение времени не является объективной вещью. Во многом это зависит от уникального восприятия времени человеком.

То, что вы стоите в очереди, не сокращает время ожидания. На самом деле, это может сделать ваше время ожидания еще более длительным.

Когда клиенты не заинтересованы, их внимание сосредоточено на том, сколько времени они ждали.

Воспринимаемое время ожидания часто кажется больше, чем фактическое время, проведенное в очереди .

Именно по этой причине вы видите журналы и брошюры, разбросанные в залах ожидания. Даже простое занятие может отвлечь вас от того факта, что вы ждете, и эффективно убить время.

Но можно поступить иначе.

Когда нет страха потерять место в очереди, покупатели могут делать все, что хотят — пользоваться телефоном, ходить по магазину, общаться с обслуживающим персоналом и т. д.

Решение для организации очередей, избавляющее от проблемы «восприятия времени», убивает двух зайцев одним выстрелом.

Во-первых, это делает покупки более удобными . Как воспринимаемое, так и фактическое время ожидания сокращается, что значительно улучшает имидж вашего бизнеса в глазах посетителей.

Во-вторых, это также может привести к дополнительному доходу . Просматривая ваш магазин, ваши посетители могут найти что-то, что они хотели бы купить прямо сейчас или в какой-то момент в будущем.

По сути, это реклама и мерчандайзинг в одном лице.

Объяснение времени ожидания клиента

Во-первых, объяснение ожидания означает, что клиенты должны знать, как долго им придется ждать. В парках развлечений это происходит в виде знаков вне очереди, указывающих, сколько времени ожидания ожидается.

Во-вторых, объясненное ожидание означает, что любой сбой в процессе постановки в очередь должен иметь четко указанную причину. Когда клерки не обслуживают клиентов, у них должна быть четкая, поддающаяся проверке причина .

Конечно, занятого клерка легко спутать с праздным. И даже когда клиент подозревает, что служащий бездельничает, в большинстве случаев вспышки не происходит.

Тем не менее, вы все равно должны учитывать психологию ваших клиентов.

Человеческий мозг работает загадочным образом. Наши эмоции часто омрачают наше восприятие реальности, поэтому неопределенных ожиданий могут казаться длиннее известных, ограниченных ожиданий .

Но вы также должны учитывать это: люди, стоящие в очереди без понятия, почему они так долго ждут, чувствуют себя бессильными.

Ваша компания, с другой стороны, должна улучшить их жизнь и заставить их чувствовать себя лучше.

Когда есть явная причина задержки, по крайней мере, клиенты имеют конкретную информацию и не впадают в полную паранойю.

Естественно, продолжительность периода, в течение которого ваши клиенты готовы ждать, также зависит от ценности вашего продукта или услуги . Или, скорее, это зависит от воспринимаемой ценности.

Это не значит, что вы можете пренебрегать управлением очередями, когда считаете, что предлагаете что-то исключительное, но есть много нюансов, которые вы должны учитывать.

Типы систем массового обслуживания в различных отраслях

Сначала вы можете подумать, что системы массового обслуживания подходят только для розничной торговли, где количество клиентов, которых вы можете обслужить за ограниченное время, имеет наибольшее значение.

Тем не менее, управление толпой — это проблема, которую стоит решать во многих других отраслях — от здравоохранения до правительства, образования и банковского дела.

Давайте посмотрим, как решения с очередями могут помочь в каждом случае.

Управление очередями в розничной торговле

Наиболее очевидным применением управления очередями являются обычные магазины. Если они не могут эффективно управлять своими линиями, они рискуют потерять клиентов в пользу своих конкурентов.

Длительное время ожидания и неуправляемые очереди — бич бизнеса во всем мире. Внедрение системы очередей для розничной торговли — это то, что позволяет превратить это время ожидания в беспроблемное обслуживание клиентов.

Посетители, которых встречает правильное управление очередью, также могут превратиться в лояльных клиентов — но об этом позже.

Управление очередями в здравоохранении

Насколько тяжело время ожидания в здравоохранении? 21% пациентов идут в другое место, чтобы получить рецепт из-за длительного времени ожидания.

Дело в том, что пациенты, в отличие от клиентов, не могут позволить себе роскошь ждать. Даже когда это не вопрос жизни или смерти, пациентов не хотят проводить в больнице больше времени, чем необходимо .

Система управления очередью в здравоохранении поможет контролировать поток пациентов, создавая лучшую атмосферу как для персонала больницы, так и для пациентов.

Для первых важно снять с себя бремя и помочь им лучше управлять своим временем. Для последних все дело в уменьшении их беспокойства и разочарования.

Управление очередью в образовании

Несмотря на то, что в розничной торговле и здравоохранении бывают часы пик, нигде они не проявляются так ярко, как в образовании.

Школы должны учитывать приток студентов и потенциальных студентов во время зачисления, а также в начале и конце семестров.

Затем также есть перерывы, когда студенты посещают приемную комиссию, чтобы получить ответы на свои вопросы.

Что произойдет, если вы внедрите в школе систему очередей? Это помогает с организацией упорядоченных очередей , предотвращая скопление студентов в часы пик.

Обслуживание посетителей в государственных учреждениях

Правительственные учреждения — паршивая овца в этом списке. Они не слишком беспокоятся об уровне обслуживания своих клиентов, так как люди приходят к ним за услугами, которые больше никто не может предоставить.

В розничной торговле, как и почти во всех других отраслях, дополнительный покупатель является потенциальной продажей или доходом . Для государственных учреждений это дополнительных расходов .

Им нужна система управления очередями именно потому, что они не хотят тратить время на управление и обслуживание своих посетителей. Чем быстрее вывод, тем лучше.

Как видите, решения для организации очередей приносят множество преимуществ всем отраслям, которым приходится иметь дело с более чем одним клиентом одновременно.

Некоторые отрасли, например государственные учреждения, заинтересованы в том, чтобы решить проблему очередей. Другие, такие как розничная торговля и здравоохранение, хотят улучшить ситуацию с обслуживанием клиентов.

Решение для организации очередей — незаменимый инструмент, помогающий в обоих аспектах управления посетителями.

Преимущества системы массового обслуживания

«Аспект очередей» и «улучшение ситуации с обслуживанием клиентов» звучат хорошо, но достаточно расплывчато. Что-то сказал бы продавец змеиного масла.

Итак, давайте перейдем к конкретике. А именно, какие преимущества решение для организации очередей может принести вашему бизнесу.

Повышение лояльности клиентов

В наш современный век, когда удержание клиента более рентабельно, чем привлечение нового, лояльность клиентов является важной темой для обсуждения .

Учитывая, что в настоящее время клиенты более избирательны и не боятся переходить на новый бренд, вы должны сделать так, чтобы вашим клиентам нравился опыт, который они получают.

Даже мельчайшие детали имеют значение. Длительное время ожидания, возможно, не было решающим фактором несколько десятилетий назад, но сейчас сокращение времени ожидания играет важную роль в создании положительного клиентского опыта.

Такие факторы, как ожидаемое ожидание, длина очереди и соотношение времени ожидания к времени обслуживания, создают или разрушают бизнес.

Базовая математика предполагает, что меньшее время ожидания равно большему времени, потраченному на покупки . Даже если это не влияет на покупательские привычки ваших клиентов, это заставляет их уйти в хорошем настроении.

Последние минуты, которые мы проводим у прилавка, самые важные.

Покупатель сам решает, понравился ли ему в целом процесс покупки или нет. Никакое дополнительное обслуживание клиентов после этого не затмит первое впечатление.

Повышая удобство покупок, решения для управления очередями помогут вашему бизнесу превратить посетителей в постоянных клиентов. Постоянный клиент не только чаще посещает ваш бизнес, но и склонен покупать больше.

Короче говоря, лояльные клиенты являются основой успеха, и решения для организации очередей помогают вам получить их легче.

Сбор данных о клиентах

Решения для организации очередей не только помогают улучшить ваш бизнес сейчас, но и помогут улучшить его в будущем. И они делают это с помощью данных клиентов .

Вам не нужно нанимать и обучать дополнительный персонал или устанавливать специальные датчики для получения точных показателей посещаемости. Решение для организации очередей удваивается как решение для подсчета посетителей.

Поскольку система очереди автоматически отслеживает всех зарегистрированных клиентов, вы получаете легкий доступ к количеству посетителей, спросу в очереди и времени ожидания.

Другими словами, система очередей помогает вам получать подробную розничную аналитику в режиме реального времени :

1. Количество посетителей.
2. Количество неявок.
3. Определение областей с низкой/высокой посещаемостью.
4. Узнайте время ожидания, простоя и обслуживания.

Точные числа, собранные и обработанные решениями для организации очередей, помогут вашему бизнесу Воспользуйтесь возможностями продаж и и улучшите свой сервис .

Возможность сравнения текущих данных с прошлыми аналогами помогает понять, в правильном ли направлении вы движетесь.

Эффективное использование персонала

Мы уже упоминали «разгрузку сотрудников», но что именно это означает?

Вы должны понимать, что управление посетителями требует много работы . Поприветствовать их, записать их, показать им дорогу — это много времени, которое тратит каждый посетитель.

Когда вы умножаете эту сумму на количество ежедневных посетителей, становится очевидным, сколько времени тратится на то, что можно автоматизировать.

Решение для организации очередей призвано сделать жизнь лучше не только ваших клиентов, но и сотрудников . Как только их время освобождается для выполнения более важных задач, обслуживание клиентов улучшается как на дрожжах.

Возвращаясь к аспекту данных СМК, аналитика помогает определить, является ли использование персонала эффективным или нет.

Он может показать недостатки в управлении персоналом, выявляя клерков, которым трудно управлять своими посетителями.

Может пора провести дополнительное обучение? Как насчет перераспределения сотрудников в эту проблемную зону? Или, может быть, вам нужно добавить еще одну точку обслуживания?

Выбор за вами. Но это решение для организации очередей, которое поможет вам сделать этот выбор информированным .

Краткий обзор систем массового обслуживания

Чтобы повторить то, что мы уже узнали, система очереди является неотъемлемой частью обслуживания современного бизнеса .

Решение для организации очередей необходимо в каждой отрасли, от розничной торговли до образования, и потребность в этом возрастает по мере того, как посетители стремятся к большему комфорту.

Основное внимание в управлении очередями уделяется удовлетворению клиентов, но ценность системы очередей не ограничивается решением очередей.

Управление очередью помогает сократить время ожидания и обслуживания клиентов, повысить эффективность обслуживания и сотрудников, тем самым увеличивая доход.

Предоставляя своим клиентам справедливое, разумное и объясненное время ожидания, вы создаете базу лояльных клиентов для своего бизнеса.

Взгляните на предприятия, которые уже используют решения для организации очередей для улучшения своих услуг. Разве это не та компания, частью которой вы хотели бы стать?

Благодаря бесплатной 14-дневной пробной версии Qminder вы на один шаг приблизились к построению бизнеса, о котором всегда мечтали вы и ваши клиенты.

Повысьте эффективность своего бизнеса с помощью Qminder

Определение, история и реальные приложения

1. Что такое теория массового обслуживания?
2. Как возникла теория массового обслуживания?
3. Какие существуют типы систем массового обслуживания?
4. Почему важна теория массового обслуживания?
5. Каковы приложения теории массового обслуживания?
6. Как психология очереди влияет на организацию очередей?

1. Что такое теория массового обслуживания?

Теория массового обслуживания (или теория массового обслуживания) относится к математическому изучению формирования, функции и загруженности очередей или очередей.

В своей основе ситуация с очередями состоит из двух частей.

1. Кто-то или что-то, кто запрашивает услугу, обычно называемую клиентом, заданием или запросом.
2. Кто-то или что-то, что завершает или предоставляет услуги, обычно называемое сервером.

Для иллюстрации возьмем два примера. Если посмотреть на ситуацию с очередями в банке, клиенты — это люди, которые хотят внести или снять деньги, а официанты — банковские кассиры. При рассмотрении ситуации очереди принтера клиенты — это запросы, которые были отправлены на принтер, а сервер — это принтер.

Теория массового обслуживания тщательно изучает всю систему ожидания в очереди, включая такие элементы, как частота прибытия клиентов, количество серверов, количество клиентов, вместимость зоны ожидания, среднее время завершения обслуживания и дисциплина обслуживания в очереди. Дисциплина обслуживания очереди относится к правилам очереди, например, ведет ли она себя на основе принципа «первым пришел — первым вышел», «последний пришел — первым ушел», приоритетом или обслуживанием в случайном порядке.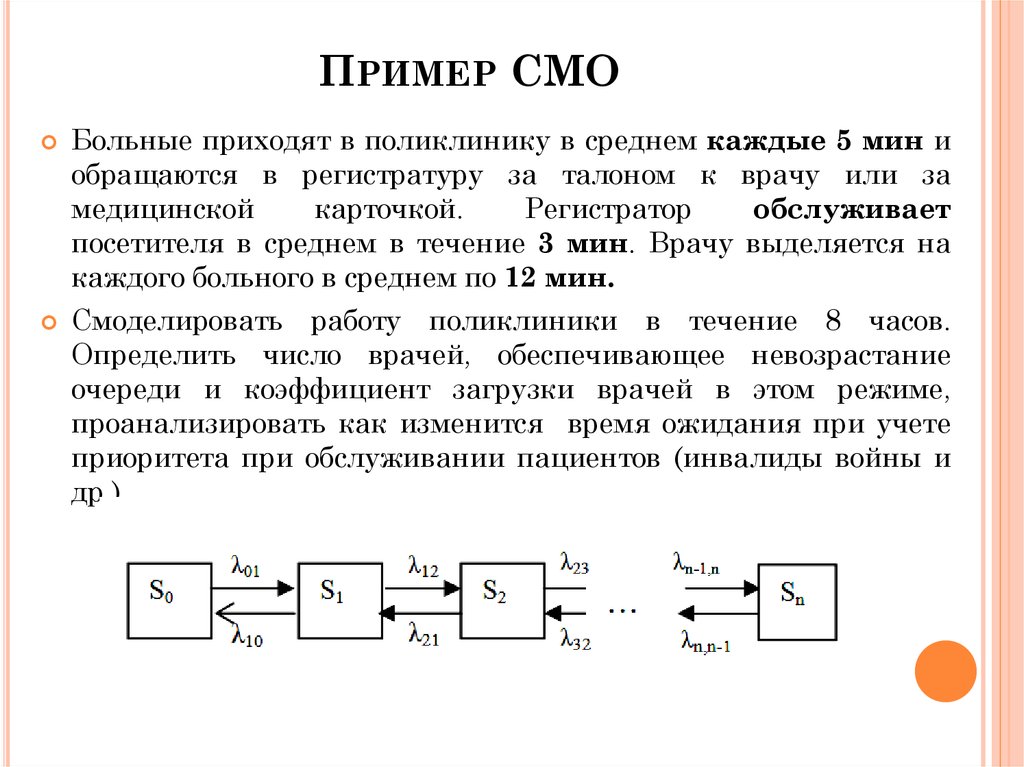

2. Как возникла теория массового обслуживания?

Теория массового обслуживания была впервые представлена ​​в начале 20 ^-х века датским математиком и инженером Агнером Крарупом Эрлангом.

Эрланг работал на Копенгагенской телефонной станции и хотел проанализировать и оптимизировать ее работу. Он стремился определить, сколько цепей необходимо для обеспечения приемлемого уровня телефонного обслуживания, чтобы люди не находились «в ожидании» (или в телефонной очереди) слишком долго. Ему также было любопытно узнать, сколько телефонных операторов необходимо для обработки заданного объема звонков.

Кульминацией его математического анализа стала статья 1920 года «Время ожидания телефона», которая послужила основой прикладной теории массового обслуживания. Международная единица телефонного трафика названа в его честь эрлангом.

Изображение с Reddit

3. Какие существуют типы систем массового обслуживания?

Теория массового обслуживания использует нотацию Кендалла для классификации различных типов систем массового обслуживания или узлов.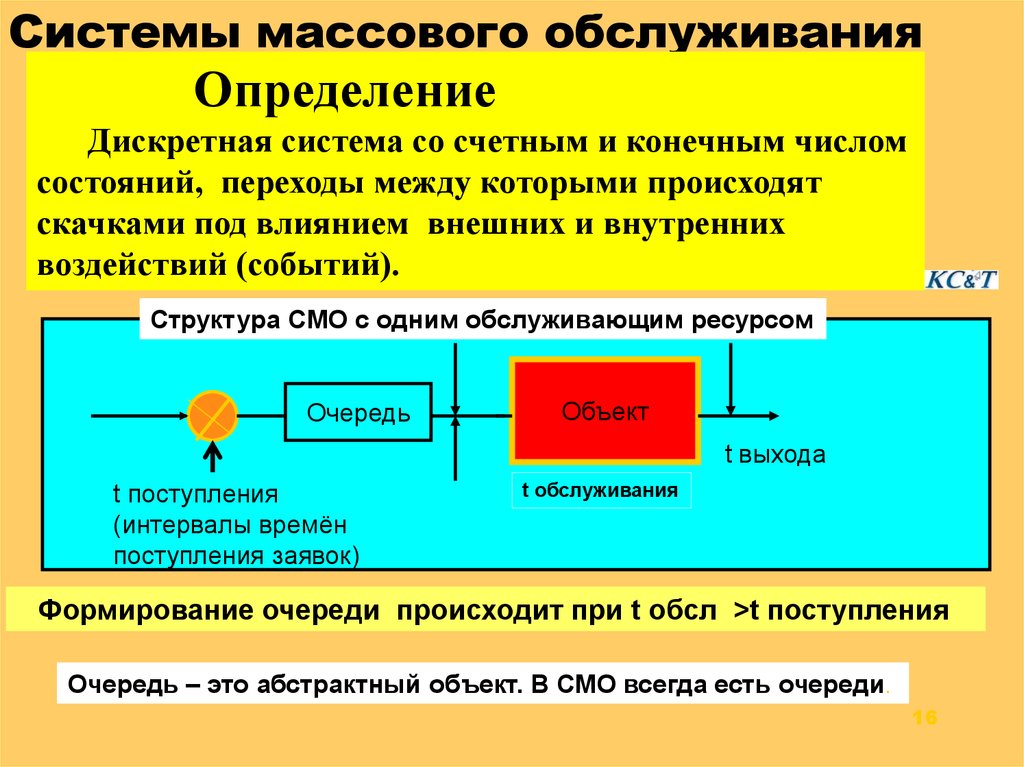 Узлы массового обслуживания классифицируются с использованием обозначения A/S/c/K/N/D где:

• A процесс прибытия
• S математическое распределение времени обслуживания
• c количество серверов
• K емкость очереди, опускается, если не ограничена
• N — количество возможных клиентов, опускается, если не ограничено
• Д — это дисциплина организации очереди, предполагается, что первый пришел — первый обслужен, если опущен

Например, представьте себе банкомат.

Может обслуживать: одного клиента за раз; в порядке «первым пришел – первым вышел»; со случайно распределенным процессом поступления и временем распределения обслуживания; неограниченная емкость очереди; и неограниченное количество возможных клиентов.

Теория очередей описывает эту систему как очередь M/M/1 («M» здесь означает марковский, статистический процесс для описания случайности).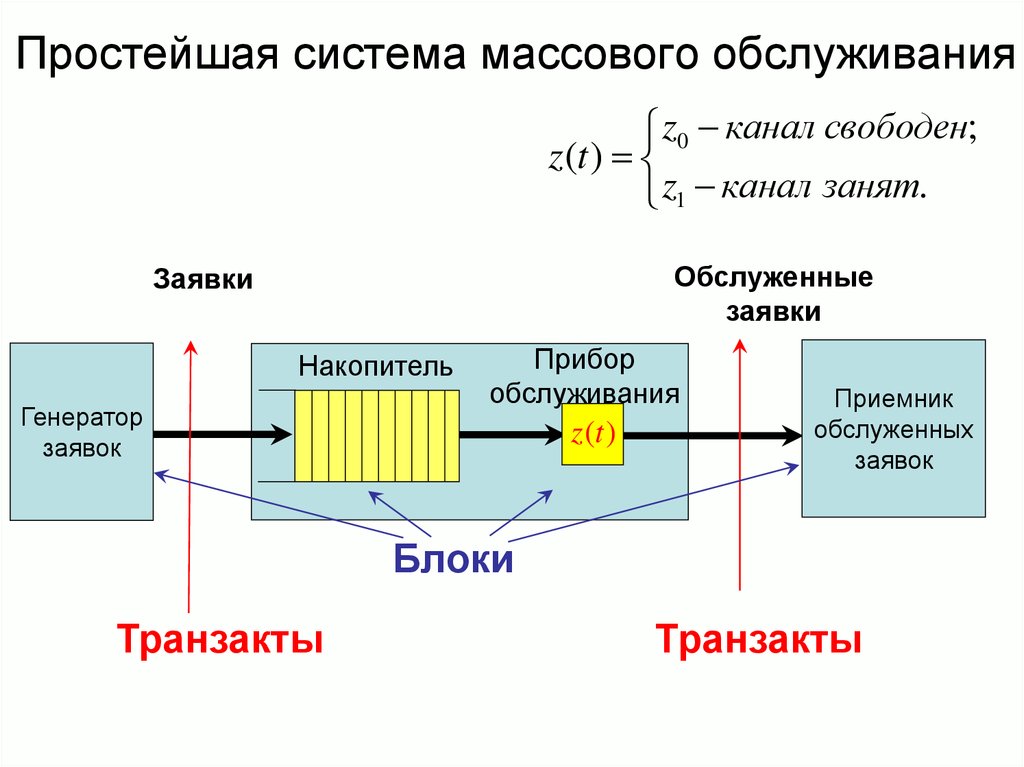

Калькуляторы теории массового обслуживания часто требуют выбора системы массового обслуживания из нотации Кендалла перед вычислением входных данных.

4. Почему важна теория массового обслуживания?

Ожидание в очереди является частью повседневной жизни, потому что как процесс оно имеет несколько важных функций. Очереди — это справедливый и важный способ справиться с потоком клиентов при ограниченных ресурсах. Отрицательные результаты возникают, если процесс очереди не установлен для борьбы с избыточной емкостью.

Например, когда на веб-сайт переходит слишком много посетителей, веб-сайт будет работать медленнее и давать сбой, если у него нет способа изменить скорость обработки запросов или способа поставить посетителей в очередь.

Связанный: Что такое система онлайн-очередей?

Или представьте себе самолеты, ожидающие посадки на взлетно-посадочную полосу. При избытке самолетов отсутствие очереди будет иметь серьезные последствия для безопасности, поскольку все самолеты пытаются приземлиться одновременно.

Теория очередей важна, потому что она помогает описать особенности очереди, такие как среднее время ожидания, и предоставляет инструменты для оптимизации очередей. С точки зрения бизнеса теория очередей позволяет создавать эффективные и экономичные системы рабочих процессов.

5. Каковы приложения теории массового обслуживания?

Теория массового обслуживания является мощной, потому что повсеместное распространение ситуаций с очередями означает, что существует бесчисленное множество разнообразных приложений теории массового обслуживания.

Теория массового обслуживания применялась, среди прочего, к:

• телекоммуникациям
• транспорт
• логистика
• финансы
• аварийно-спасательные службы
• вычисления
• промышленное строительство
• управление проектами

Прежде чем мы рассмотрим некоторые конкретные приложения, полезно понять закон Литтла, формулу, которая помогает применять теорию массового обслуживания во многих из этих приложений.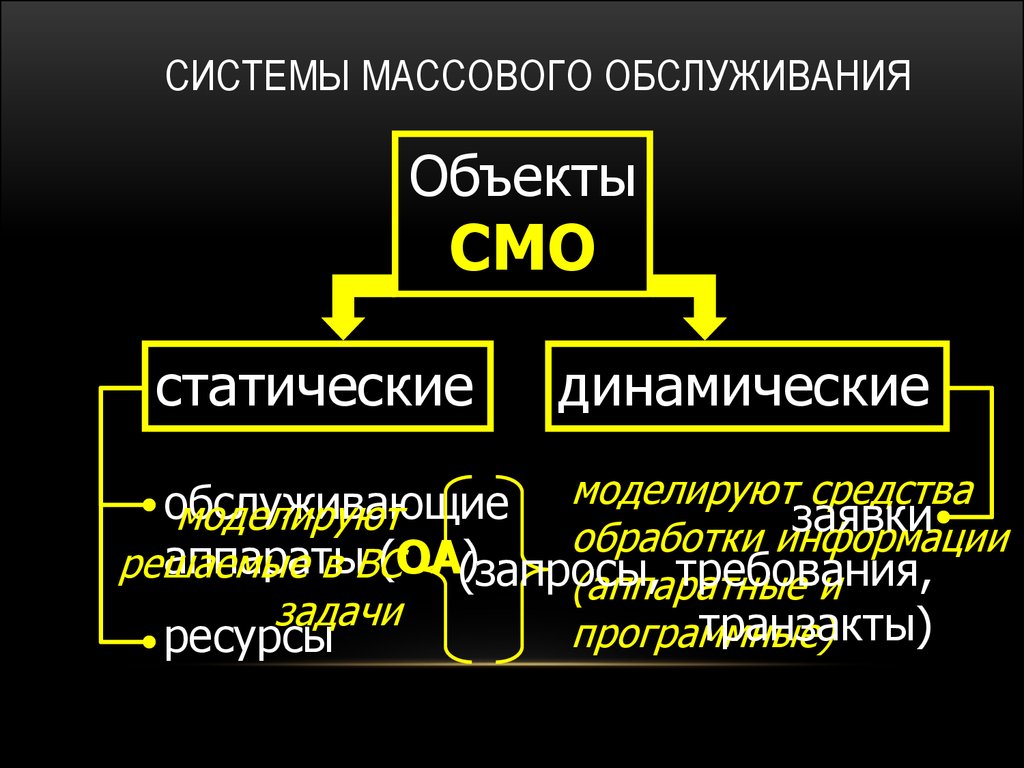

Знаете ли вы 6 простых правил психологии очереди?

Выяснить

Закон Литтла

Закон Литтла связывает пропускную способность системы массового обслуживания, среднее время, проведенное в системе, и среднюю скорость прибытия в систему, не зная никаких других характеристик очереди. Формула достаточно проста и записывается следующим образом:

или преобразованный для решения для двух других переменных, так что:

, где:

• L является средним числом клиентов в системе
L .
• λ (лямбда) — средняя скорость поступления в систему
• З среднее время пребывания в системе

Процессы управления проектами, такие как Lean и Kanban, не существовали бы без закона Литтла. Они имеют решающее значение для бизнес-приложений, в которых закон Литтла может быть записан простым английским языком как:

 

 

Применение закона Литтла к реальным ситуациям просто на основе двух других входных данных.

Очередь в кафе

Например, если вы стоите в очереди в Starbucks, Закон Литтла может оценить, сколько времени потребуется, чтобы вам принесли кофе.

Предположим, что в очереди 15 человек, один сервер и 2 человека обслуживаются в минуту. Чтобы оценить это, вы должны использовать закон Литтла в форме:

 

 

Показывающий, что вы можете ожидать свой кофе 7,5 минут. Очередь в виртуальной комнате ожидания добавление факторов для учета неявок и повторных входов:

 

 

Где:

• L количество пользователей впереди в очереди
• λ (лямбда) — скорость перенаправлений на веб-сайт или в приложение, пользователей в минуту
• N коэффициент неявки
• R скорость повторного входа в очередь
• W расчетное время ожидания в минутах

Оптимизация процесса

Мы можем посмотреть на пример оптимизации процесса для военных, любезно предоставленный Process.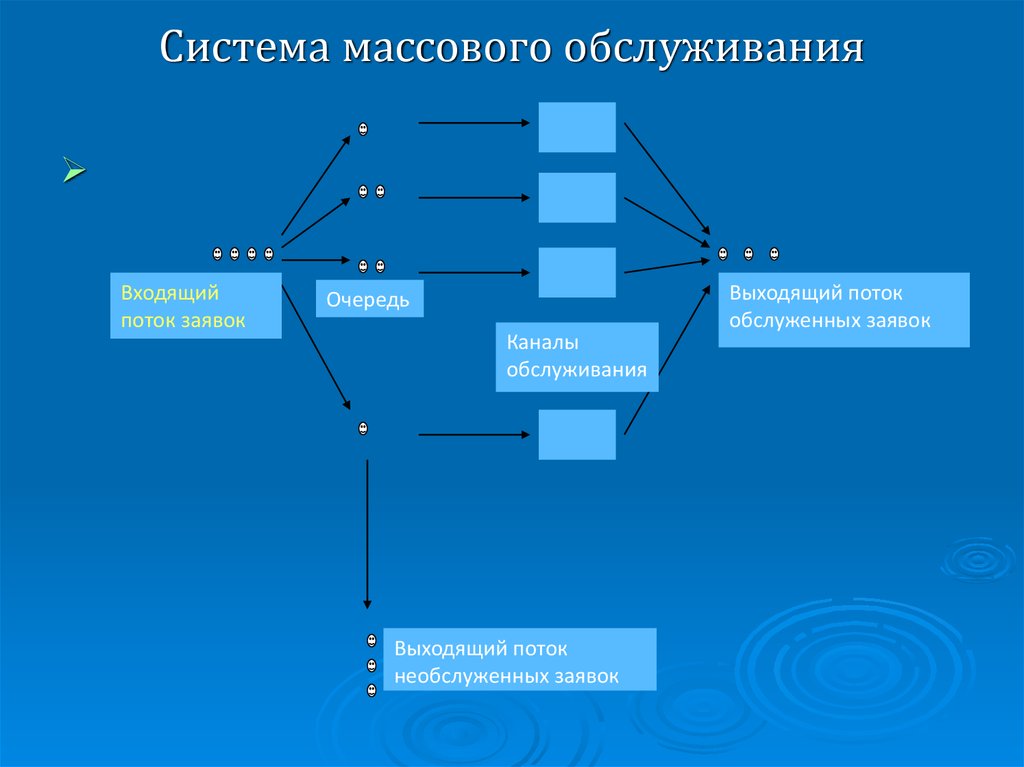 st.

В этом примере из реальной жизни военным нужно было определить идеальное время обслуживания бомбардировщиков-невидимок B-2. Самолетов В-2 всего 20, и они должны быть готовы в любой момент. Но они требуют частого обслуживания, которое может составлять от 18 до 45 дней. Использование закона Литтла поможет найти баланс между используемыми и обслуживаемыми самолетами.

Изображение skeeze с сайта Pixabay

 

На основе анализа графика полетов было подсчитано, что три бомбардировщика B-2 будут находиться на техническом обслуживании в любой момент времени. Скорость, с которой бомбардировщики попадали на техническое обслуживание, также была рассчитана примерно каждые 7 дней. Итак:

• L = количество элементов в незавершенном производстве (обслуживание) = 3
• A = скорость прибытия/отбытия = 1 каждые 7 дней = 1/7 дня
• Вт = среднее количество времени, затрачиваемое на техническое обслуживание = ???

В соответствии с законом Литтла у нас остается:

Таким образом, целевое время выполнения работ по техническому обслуживанию бомбардировщика B-2 должно было составлять 21 день для удовлетворения потребностей как имеющихся самолетов, так и регулярных расписаний полетов.

6. Как психология очереди влияет на организацию очередей?

Теория очередей помогает объяснить математические принципы работы очередей. Но когда в очередях участвуют люди, психология очереди также важна для понимания опыта очереди.

Исследования в области психологии очереди показывают, что не продолжительность ожидания определяет, насколько положительным или отрицательным будет впечатление от очереди, а то, как люди чувствуют себя во время ожидания.

Связанный: Психология очереди раскрыта в 6 простых правилах

Например, свободное время кажется длиннее, чем занятое. Отвлечения или возможность сделать что-то еще, пока вы стоите в очереди, заставляет время чувствовать, что оно идет быстрее. И неопределенное ожидание кажется более продолжительным, чем известное, ограниченное ожидание.

Вот почему опция обратного звонка на линиях обслуживания клиентов так популярна. Вы можете почувствовать, как тревога утихает, когда вы получаете возможность перезвонить через 10 минут, освобождая вас, чтобы заняться чем-то другим, вместо того, чтобы слушать эту ужасную музыку в течение неизвестного количества времени.

В ситуациях очередей с участием людей — например, на веб-сайтах, использующих онлайн-систему очередей — психологические правила, управляющие очередями, так же важны, как и математические.

1. Что такое теория массового обслуживания?
2. Как возникла теория массового обслуживания?

Знаете ли вы 6 простых правил психологии очереди?

Выяснить

Определение теории массового обслуживания

Что такое теория массового обслуживания?

Теория массового обслуживания — это раздел математики, изучающий, как формируются линии, как они функционируют и почему они выходят из строя. Теория очередей исследует каждый компонент ожидания в очереди, включая процесс прибытия, процесс обслуживания, количество серверов, количество системных мест и количество клиентов, которые могут быть людьми, пакетами данных, автомобилями или чем-то еще.

Реальные приложения теории массового обслуживания охватывают широкий спектр предприятий. Его результаты могут быть использованы для обеспечения более быстрого обслуживания клиентов, увеличения потока трафика, улучшения доставки заказов со склада или разработки сетей передачи данных и колл-центров.

Как направление исследования операций, теория очередей может помочь принять бизнес-решения о том, как построить более эффективные и экономичные системы рабочих процессов.

• Теория массового обслуживания — это изучение движения людей, объектов или информации по линии.
• Изучение перегрузки и ее причин в процессе используется для создания более эффективных и экономичных услуг и систем.
• Теория очередей, часто используемая в качестве инструмента управления операциями, может решать проблемы с персоналом, планированием и обслуживанием клиентов.
• Некоторая очередь допустима в бизнесе. Если никогда нет очереди, это признак избыточной пропускной способности.
• Теория массового обслуживания направлена ​​на достижение баланса между эффективностью и доступностью.

Как работает теория массового обслуживания

Очереди могут возникать всякий раз, когда ресурсы ограничены. Некоторое ожидание в очереди допустимо в любом бизнесе, поскольку полное отсутствие очереди предполагает дорогостоящий избыток производственных мощностей.

Теория массового обслуживания направлена ​​на разработку сбалансированных систем, которые обслуживают клиентов быстро и эффективно, но не требуют слишком больших затрат, чтобы быть устойчивыми.

На самом базовом уровне теория очередей включает в себя анализ прибытия в учреждение, такое как банк или ресторан быстрого питания, и анализ процессов, действующих в настоящее время для их обслуживания. Конечным результатом является набор выводов, направленных на выявление любых недостатков в системе и предложение способов их устранения.

Происхождение теории массового обслуживания можно проследить до начала 1900-х годов в исследовании телефонной станции Копенгагена Агнером Крарупом Эрлангом, датским инженером, статистиком и математиком. Его работа привела к созданию теории эффективных сетей Эрланга и области анализа телефонных сетей.

По сей день основная единица телекоммуникационного трафика в голосовых системах называется «эрланг».

Параметры очереди

В теории массового обслуживания изучаемый процесс разбивается на шесть различных параметров. К ним относятся процесс прибытия, процесс обслуживания и ухода, количество серверов, порядок организации очереди (например, первый пришел, первый ушел), вместимость очереди и количество клиентов.

Очереди не обязательно являются негативным аспектом бизнеса, поскольку их отсутствие свидетельствует о избыточных мощностях.

Преимущества теории массового обслуживания

Теория очередей как метод управления операциями обычно используется для определения и оптимизации потребностей в персонале, планирования и инвентаризации с целью улучшения общего обслуживания клиентов. Он часто используется практиками Six Sigma для улучшения процессов.

Психология очереди

Психология массового обслуживания связана с теорией массового обслуживания. Это компонент очередей, который имеет дело с естественным раздражением, которое испытывают многие люди, которые вынуждены стоять в очереди на обслуживание, ждут ли они кассы в супермаркете или ожидания загрузки веб-сайта.

Вариант обратного звонка во время ожидания разговора с представителем клиента по телефону — один из примеров решения проблемы нетерпения клиента. Более старомодным примером является система, используемая многими гастрономами, которые выдают номера обслуживания клиентов, чтобы люди могли отслеживать свое продвижение к началу очереди.

Supositorio предлагает бесплатные онлайн-калькуляторы теории массового обслуживания с выбором моделей массового обслуживания.

Пример теории массового обслуживания

Статья профессора Стэнфордской высшей школы бизнеса Лоуренса Вейна и др. использовал теорию очередей для анализа множества возможных аварийных ответных мер в случае воздушной биотеррористической атаки в общественном месте. Модель указывала на конкретные действия, которые можно было бы предпринять, чтобы сократить время ожидания неотложной помощи, тем самым уменьшив потенциальное число смертей.

Теория массового обслуживания полезна, хотя и не столь безотлагательна, при управлении логистикой многих предприятий. Например, операционный отдел компании по доставке, скорее всего, будет использовать теорию очередей, чтобы сгладить перегибы в своих системах перемещения посылок со склада к покупателю. В этом случае изучаемая «линия» состоит из коробок с товарами, ожидающих доставки покупателям.

Применяя теорию очередей, бизнес может разрабатывать более эффективные системы, процессы, механизмы ценообразования, кадровые решения и стратегии управления прибытием, чтобы сократить время ожидания клиентов и увеличить количество клиентов, которые могут быть обслужены.

Часто задаваемые вопросы по теории массового обслуживания

Вот ответы на некоторые часто задаваемые вопросы о теории массового обслуживания.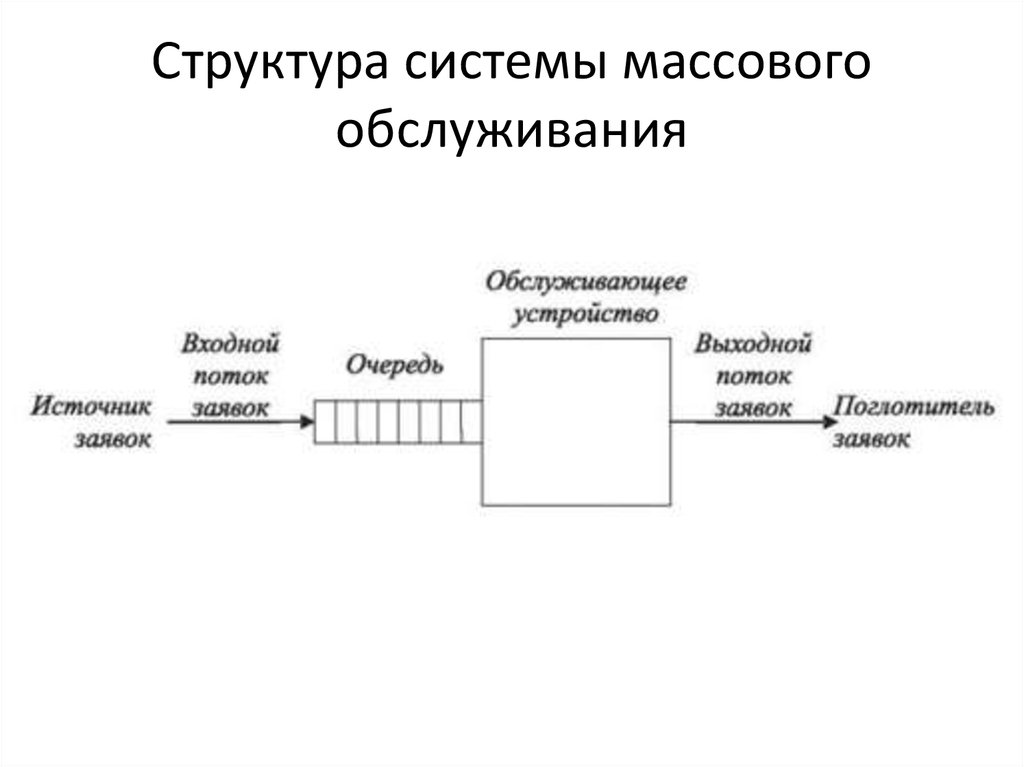

Как вы используете теорию очередей?

Теория массового обслуживания используется для выявления и исправления точек перегрузки в процессе. Очередь может состоять из людей, вещей или информации. В любом случае, они вынуждены ждать обслуживания. Это неэффективно, плохо для бизнеса и раздражает (когда очередь состоит из людей).

Теория массового обслуживания используется для анализа существующего процесса и определения альтернатив с лучшим результатом.

Кто изобрел теорию массового обслуживания?

Агнеру Крарупу Эрлангу, датскому математику, статистику и инженеру, приписывают создание не только теории очередей, но и всей области организации телефонного трафика.

В начале 20 века Эрланг возглавлял техническую лабораторию в Copenhagen Telephone Co. Его обширные исследования времени ожидания в автоматизированных телефонных службах и его предложения по более эффективным сетям были широко приняты телефонными компаниями.

Каковы основные элементы теории массового обслуживания?

Изучение очереди с использованием теории очередей разбивает ее на шесть элементов: процесс прибытия, процесс обслуживания и отправления, количество доступных серверов, дисциплина обслуживания очереди (например, «первым пришел — первым вышел»), вместимость очереди.