Математика Тригонометрия Единичный круг Прекалькуляция Тригонометрические функции, Математика, метка, кунг-фу png
Математика Тригонометрия Единичный круг Прекалькуляция Тригонометрические функции, Математика, метка, кунг-фу pngтеги
- метка,
- кунг-фу,
- мультфильм,
- число,
- упражнение,
- тригонометрические функции,
- физика,
- предкалькул,
- радиан,
- шаолин,
- тригонометрия,
- шаолин Кунг-фу,
- синус,
- алгебра,
- математика,
- боевые искусства,
- боевые действия,
- закон косинусов,
- идентичность,
- поведение человека,
- геометрия,
- уравнение,
- единица измерения Круг,
- png,
- прозрачный png,
- без фона,
- бесплатная загрузка
- Размер изображения
- 2984x2957px
- Размер файла
- 3.
 18MB
18MB - MIME тип
- Image/png
изменить размер PNG
высота(px)
Некоммерческое использование, DMCA Contact Us
- тригонометрическое уравнение, единичный круг Тригонометрия Синус Тригонометрические функции, математика, угол, текст png 1600x1600px 364.45KB
- Единица круга Математика Тригонометрия Площадь, круг, угол, симметрия png 2403x2400px 191.29KB
- Сферическая тригонометрия Тригонометрические функции Единичный круг Математика, Математика, угол, текст png 1600x1024px 110.66KB org/ImageObject»> Единица окружности Радиан Линия Угол, прицел, угол, симметрия png 2375x2267px 24.69KB
- Математика Треугольник Синус Тригонометрия, Математика, угол, текст png 881x840px 15.44KB
- Прямоугольный треугольник Тригонометрия Теорема Пифагора Геометрия, треугольная геометрия, угол, белый png 569x600px 8.67KB
- Угол Радиана Степень Математика Поворот, Угол, угол, текст png 1052x1095px 446.34KB
- График функции Закон косинусов Синусоида Козено, деление, угол, текст png 5003x2243px 170.83KB
- Единица окружности Тригонометрия Тригонометрические функции Плоскость, круг, круг, тригонометрия png
768x768px
37.

- Ряд Фурье Фундаментальная частота Преобразование Фурье Синусоида, Прямоугольная волна, угол, белый png 790x592px 103.35KB
- Закон косинусов Тригонометрия Треугольник Математика, плавающий треугольник, синий, угол png 1000x582px 28.88KB
- Wikimedia Commons Тригонометрия Круг Тригонометрические функции Синус, круг, угол, треугольник png 2000x1938px 139.74KB
- Обратные тригонометрические функции Тригонометрия Единица окружности, линия радиана, угол, текст png 1280x834px 153.84KB
- Брюс Ли, Дракон: история Брюса Ли Дао Джит Кун До Рисование, ручная роспись Брюс Ли, Акварельная живопись, знаменитости png
640x600px
245.
 94KB
94KB - математическая иллюстрация, элементарный математический номер, математические границы, текст, график функции png 2254x2174px 227.7KB
- Треугольник Теорема Пифагора Синус Тригонометрические функции Тригонометрическая единица Пифагора, треугольник, угол, текст png 2000x1747px 73.28KB
- Прямоугольный треугольник Тригонометрия Тригонометрические функции Синус, cos, угол, текст png 2000x1500px 70.69KB
- Desmos График функции Математика Единица окружности, граф, угол, текст png
2400x2400px
49.
 17KB
17KB - Система уравнений Математика Квадратичное уравнение Решение уравнений, рукописная математическая формула, угол, текст png 1920x2010px 152.49KB
- Прямоугольный треугольник Тригонометрия Прямоугольный треугольник, угол, белый png 1103x1063px 45.89KB
- Закон синусов Сферическая тригонометрия Закон косинусов Сфера, треугольник, угол, треугольник png 1029x1024px 85.38KB
- График функции Синусоида Математика Закон косинусов, Математика, угол, текст png 2000x897px 158.63KB
- Использование тригонометрии Геометрия Математика Угол, Тадж Махал, угол, здание png
1600x997px
165.
 31KB
31KB - Прямоугольный треугольник Математика Тригонометрия, треугольник, угол, текст png 1024x601px 22.94KB
- Прямоугольный треугольник Тригонометрия Тригонометрические функции, треугольник, угол, текст png 765x792px 25.42KB
- Закон синусов Тригонометрия Треугольник, треугольник, угол, текст png 1200x867px 29KB
- Закон косинусов Закон синусов Треугольник Теорема Пифагора Тригонометрия, треугольник, угол, текст png 1280x768px 43.5KB
- Тригонометрия Тригонометрические функции Прямоугольный треугольник, треугольник, угол, текст png
745x768px
11.
 8KB
8KB - Брюс Ли Вин Чун Боевые искусства Android, смешанный мастер боевых искусств, знаменитости, кунг-фу png 1024x1024px 530.48KB
- Математика Математическая тревога Умножение Учитель Геометрия, Математика, фиолетовый, синий png 1024x928px 585.6KB
- Единица окружности Угол Тригонометрия Рабочий лист, Угол окружности, угол, текст png 2550x3300px 398.91KB
- Тай-чи Китайские боевые искусства Ушу Мультфильм, мультипликационный персонаж фитнес, белый, ребенок png 600x871px 214.65KB
- Прямоугольный треугольник Тригонометрия Теорема Пифагора Математика, треугольник, угол, белый png
728x768px
9.

- Радиан Единица окружности Угол, окружность, радиан, круг png 800x336px 20.85KB
- Угол Степень Градиан Sexagesimal, Угол, угол, белый png 1257x1024px 19.54KB
- Треугольник Доказательство тригонометрических тождеств Синус Тригонометрические функции Тригонометрия, треугольник, угол, симметрия png 768x768px 24.84KB
- Обратная гиперболическая функция Обратная тригонометрическая функция Обратная функция Арккозин, креативный текст, угол, текст png 886x1024px 35.58KB
- Единичный круг Синус Тригонометрия Математика, круг, угол, белый png
600x600px
21.
 71KB
71KB - Козено График функции Параметрическое уравнение Синус, Угол, угол, треугольник png 808x657px 29.44KB
- Закон косинусов Закон синусов Тригонометрические функции Тригонометрия, Математика, угол, текст png 744x576px 43.69KB
- Единица окружности Тригонометрия Козено Прекалькулус, круг, угол, текст png 512x512px 140.94KB
- Музыка капоэйры Grupo Capoeira Бразилия Джит Кун До Данс, арбуз, текст, спорт png 512x515px 63.21KB
- Аналитическая геометрия Алгебра Математика, электричество человек, лицо, рука png 480x522px 32.77KB
- Специальный прямоугольный прямоугольный прямоугольный угол, угол, белый png 598x767px 15.88KB
- Монастырь Шаолинь Китайские боевые искусства Шаолинь Кунг-фу Каратэ, каратэ, спорт, кунг-фу png 1020x1019px 96.2KB
- Угол Линия График функции Тригонометрия Тригонометрические функции, Угол, угол, текст png 1280x721px 10.35KB org/ImageObject»> Линейное движение Математика Геометрия Расчет Бал, Математика, угол, текст png 870x1024px 34.75KB
градусная и радианная мера угла, интервалы и отрезки, свойства точки
- Понятие тригонометрии
- Числовая окружность
- Градусная и радианная мера угла
- Свойства точки на числовой окружности
- Интервалы и отрезки на числовой окружности
- Примеры
п.1. Понятие тригонометрии
Тригонометрия – это раздел математики, в котором изучаются тригонометрические функции и их использование.
Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.
Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.
п.2. Числовая окружность
Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.
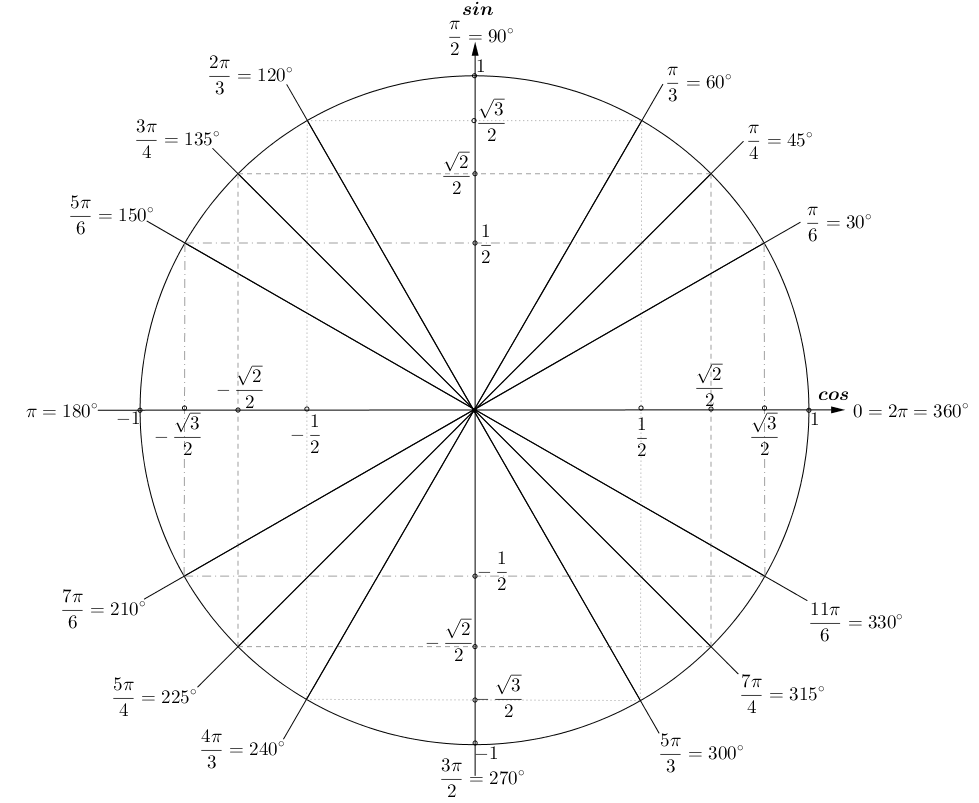
| Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета, ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным; по часовой стрелке – отрицательным.  |
Например:
| Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°. |
п.3. Градусная и радианная мера угла
Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).
В целом, более обоснованной и естественной для измерения углов является радианная мера.
Радианной мерой угла называется отношение длины дуги окружности, заключенной между сторонами угла и центром в вершине угла, к радиусу этой окружности. {\circ} $$
{\circ} $$
| 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° | 360° |
| \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) | \(\frac{2\pi}{3}\) | \(\frac{3\pi}{4}\) | \(\frac{5\pi}{6}\) | \(\pi\) | \(\frac{3\pi}{2}\) | \(2\pi\) |
п.4. Свойства точки на числовой окружности
Построим числовую окружность. Обозначим O(0;0), A(1;0)
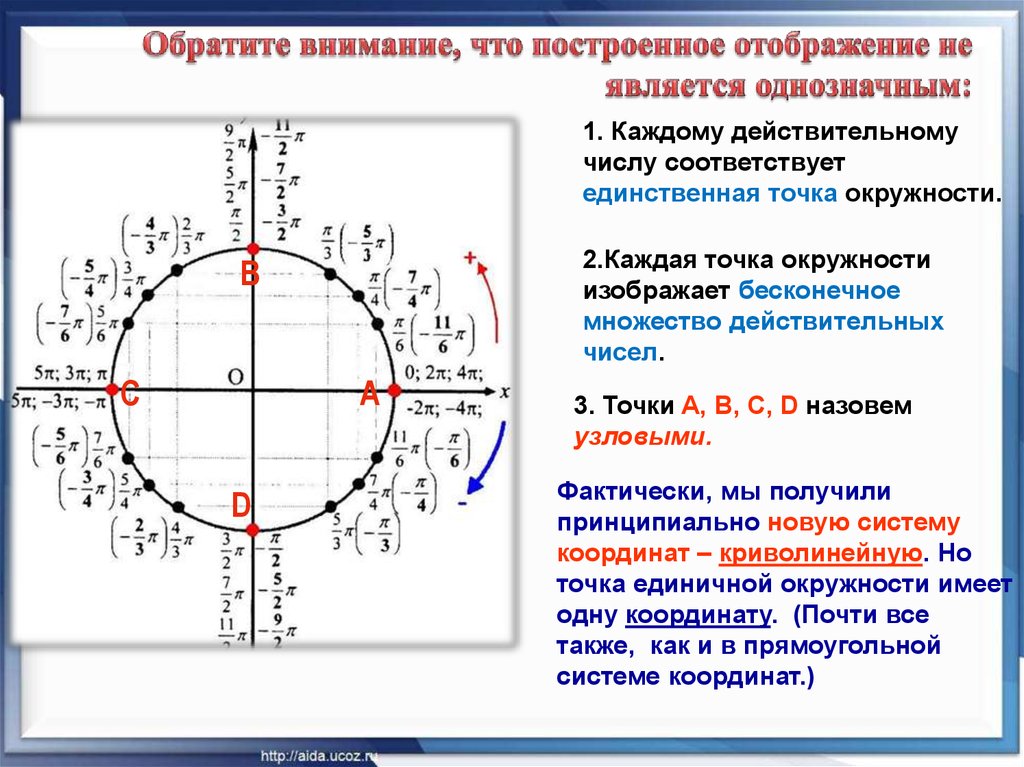
| Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M — искомая. При t<0 двигаемся по окружности по часовой стрелке, описывая дугу ⌒ AM=t. 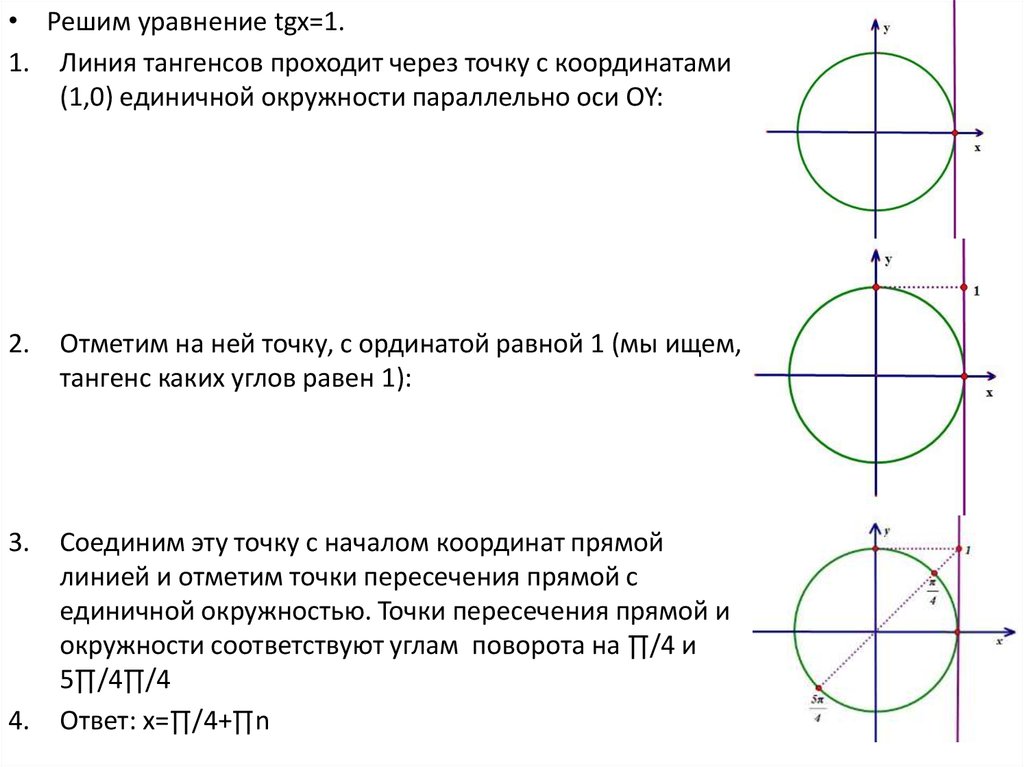 Точка M — искомая. Точка M — искомая. |
Например:
| Отметим на числовой окружности точки, соответствующие \(\frac{\pi}{6},\ \frac{\pi}{4},\ \frac{\pi}{2},\ \frac{2\pi}{3},\ \pi\), а также \(-\frac{\pi}{6},\ -\frac{\pi}{4},\ -\frac{\pi}{2},\ -\frac{2\pi}{3},\ -\pi\) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности. |
Каждой точке M(t) на числовой окружности соответствует бесконечное множество действительных чисел t с точностью до полного периода 2π:
$$ M(t) = M(t+2\pi k),\ \ k\in\mathbb{Z} $$
Например:
| Отметим на числовой окружности точки, соответствующие \(\frac{\pi}{6},\ \frac{13\pi}{6},\ \frac{25\pi}{6}\), и \(-\frac{11\pi}{6}\). Все четыре точки совпадают, т.к. \begin{gather*} M\left(\frac{\pi}{6}\right)=M\left(\frac{\pi}{6}+2\pi k\right)\\ \frac{\pi}{6}-2\pi=-\frac{11\pi}{6}\\ \frac{\pi}{6}+2\pi=\frac{13\pi}{6}\\ \frac{\pi}{6}+4\pi=\frac{25\pi}{6} \end{gather*} |
п.
 5. Интервалы и отрезки на числовой окружности
5. Интервалы и отрезки на числовой окружностиКаждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.
Например:
| Числовой промежуток | Соответствующая дуга числовой окружности |
| Отрезок | |
| $$ -\frac{\pi}{6} \lt t \lt \frac{\pi}{3} $$ а также, с учетом периода $$ -\frac{\pi}{6}+2\pi k\lt t\lt\frac{\pi}{3}+2\pi k $$ | |
| Интервал | |
| $$ -\frac{\pi}{6} \leq t \leq \frac{\pi}{3} $$ а также, с учетом периода $$ -\frac{\pi}{6}+2\pi k\leq t\leq\frac{\pi}{3}+2\pi k $$ | |
| Полуинтервал | |
| $$ -\frac{\pi}{6} \leq t \lt\frac{\pi}{3} $$ а также, с учетом периода $$ -\frac{\pi}{6}+2\pi k\leq t\lt\frac{\pi}{3}+2\pi k $$ | |
п.
 {\circ}\\ \frac{17\pi}{6}=\frac{18-1}{6}\pi=3\pi-\frac{\pi}{6}\rightarrow \pi-\frac{\pi}{6}=\frac{5\pi}{6}\\ \frac{27\pi}{4}=\frac{28-1}{4}\pi=7\pi-\frac{\pi}{4}\rightarrow \pi-\frac{\pi}{4}=\frac{3\pi}{4} \end{gather*}
{\circ}\\ \frac{17\pi}{6}=\frac{18-1}{6}\pi=3\pi-\frac{\pi}{6}\rightarrow \pi-\frac{\pi}{6}=\frac{5\pi}{6}\\ \frac{27\pi}{4}=\frac{28-1}{4}\pi=7\pi-\frac{\pi}{4}\rightarrow \pi-\frac{\pi}{4}=\frac{3\pi}{4} \end{gather*}Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.
| Сравниваем каждое число с границами четвертей: \begin{gather*} 0,\ \ \frac\pi2\approx\frac{3,14}{2}=1,57,\ \ \pi\approx 3,14\\ 3\pi\ \ 3\cdot 3,14\\ \frac{3\pi}{2}\approx \frac{3\cdot 3,14}{2}=4,71,\ \ 2\pi\approx 6,28 \end{gather*} |
\(\frac\pi2\lt 2\lt \pi \Rightarrow \) угол 2 радиана находится во 2-й четверти
\(\pi\lt 4\lt \frac{3\pi}{2} \Rightarrow \) угол 4 радиана находится в 3-й четверти
\(\frac{3\pi}{2}\lt 5\lt 2\pi \Rightarrow \) угол 5 радиана находится в 4-й четверти
\(7\gt 2\pi\), отнимаем полный оборот: \(0\lt 7-2\pi\lt \frac\pi2\Rightarrow\) угол 7 радиан находится в 1-й четверти.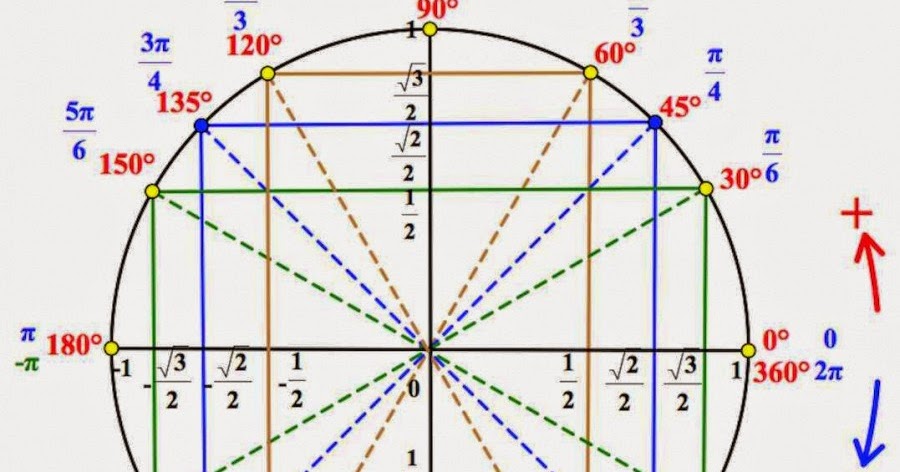
Пример 5. Изобразите на числовой окружности множество точек \((k\in\mathbb{Z})\), запишите количество полученных базовых точек.
| $$ \frac{\pi k}{2} $$ | $$ -\frac{\pi}{4}+2\pi k $$ |
Четыре базовых точки, через каждые 90° | Две базовых точки, через каждые 180° |
| $$ \frac{\pi}{3}+\frac{2\pi k}{3} $$ | $$ -\frac{\pi k}{5} $$ |
Три базовых точки, через каждые 120° | Пять базовых точек, через каждые 72° |
Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.
| $$ \left[0;\ \frac{\pi}{3}\right] $$ | $$ \left(-\frac{\pi}{4};\ \pi\right] $$ |
| $$ \left[\frac\pi2;\ \frac{5\pi}{4}\right) $$ | $$ (1;\ 3) $$ |
| \begin{gather*} 1\ \text{рад}=\frac{180^{\circ}}{\pi}\approx 57,3^{\circ}\\ 3\ \text{рад}=\frac{180^{\circ}}{\pi}\cdot 3\approx 171,9^{\circ} \end{gather*} |
Тригонометрия и окружность .
 Магия математики [Как найти x и зачем это нужно]
Магия математики [Как найти x и зачем это нужно]Пока что наши знания о тригонометрических функциях ограничиваются прямоугольными треугольниками. Для решения повседневных задач этого, в принципе, более чем достаточно. Но разве вам не интересно узнать, как они ведут себя в других углах, а не только в тех, значения которых колеблются исключительно в диапазоне от 0° до 90° (ведь в прямоугольном треугольнике один из углов всегда прямой, а два оставшихся – острые)? Конечно, интересно, и именно этим мы и займемся в этом разделе – посмотрим на тригонометрические функции через призму единичного круга и разберемся в особенностях поведения синусов, косинусов и тангенсов углов других типов.
Надеюсь, вы не забыли, что единичным называется такой круг, радиус которого равен 1, а центр расположен в точке начала координат (0, 0). Для него отлично работает уравнение x? + y? = 1, которое получилось у нас в прошлой главе из теоремы Пифагора.
Давайте попробуем найти некую точку (x, y), расположенную на окружности выше и левее точки (1, 0) и образующую с центром круга и осью x острый угол A:
Для того чтобы найти x и y, нам нужно начертить прямоугольный треугольник и применить к нему наши формулы косинусов и синусов:
Другими словами, значения координат (x, y) составят (cos A, sin A).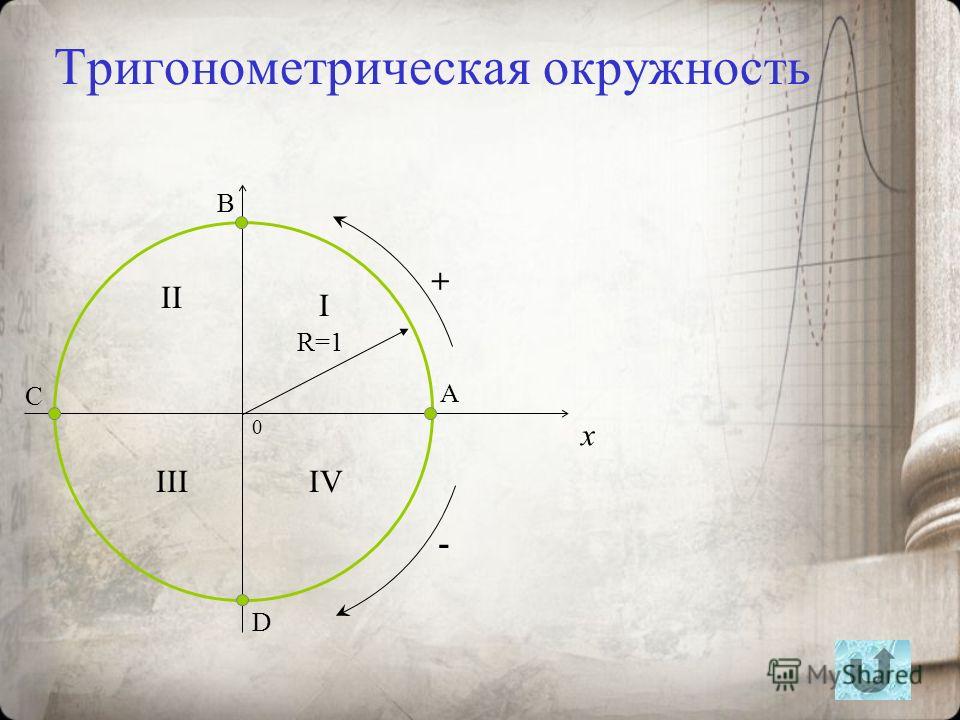 Если обобщать, то при радиусе, равном r, (x, y) = (r cos A, r sin A).
Если обобщать, то при радиусе, равном r, (x, y) = (r cos A, r sin A).
Для любого угла A нам нужно определить (cos A, sin A), то есть место расположения на окружности его вершины. При этом cos A будет соответствовать значению координаты по оси x, а sin A – по оси у, вот так:
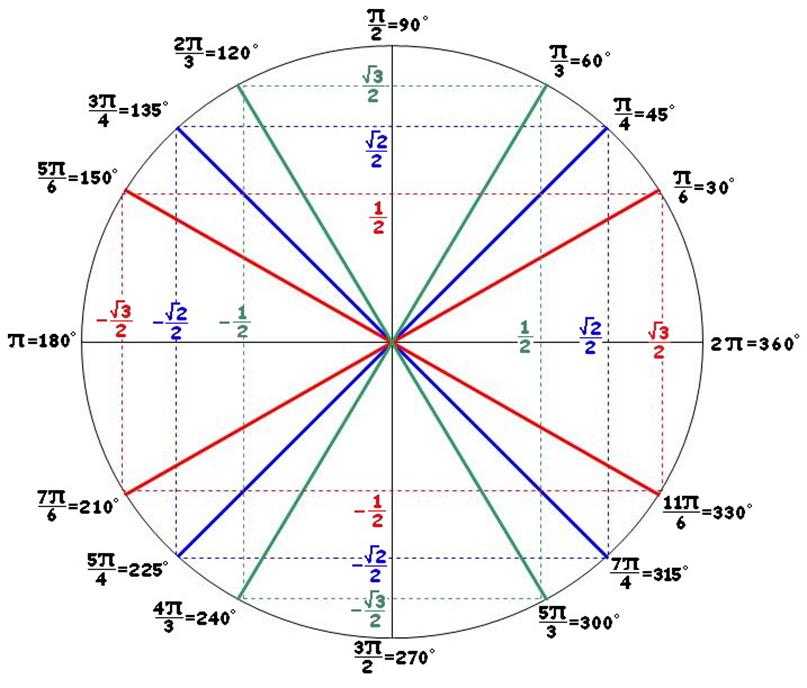
А вот еще одно общее представление. Только теперь мы разделим единичный круг на много углов с шагом 30° (и сделаем один шаг в 45° для большей наглядности) – так мы получим углы из уже очень хорошо знакомых нам треугольников. Помните, я советовал вам выучить значения косинусов и синусов для углов 0°, 30°, 45°, 60° и 90°?
К углам этим можно прийти с помощью простого отражения значений, содержащихся в первой четверти окружности.
Прибавление или вычитание 360° на величину угла никак не повлияет (мы просто обойдем вокруг него с одной или другой стороны), а значит, для любого ?A
sin (A ± 360°) = sin A cos (A ± 360°) = cos A
Имея дело с отрицательными значениями углов, мы двигаемся по окружности слева направо: так, угол, равный –30°, ничем, по сути, не отличается от угла, равного 330°. Обратите внимание, что сдвиг на A градусов по часовой стрелке приводит нас к той же x-координате, что и сдвиг на те же A градусов против часовой стрелки. Y-координата же при этом сменит знак на противоположный. Другими словами, для любого значения угла A
Обратите внимание, что сдвиг на A градусов по часовой стрелке приводит нас к той же x-координате, что и сдвиг на те же A градусов против часовой стрелки. Y-координата же при этом сменит знак на противоположный. Другими словами, для любого значения угла A
cos (–A) = cos A sin (–A) = –sin A
Например,
cos (–30°) = cos 30° = ?3/2 sin (–30°) = –sin 30° = –1/2
Обратное происходит, когда мы «отзеркаливаем» ?A через ось y. Значение y-координаты получившегося таким образом дополнительного угла 180 – A остается неизменным, а значение x-координаты меняет знак на противоположный. То есть
cos (180 – A) = –cos A sin (180 – A) = sin A
Скажем, при A = 30°
cos 150° = –cos 30° = –?3/2 sin 150° = sin 30° = 1/2
Остальные тригонометрические функции определяются по старой схеме (например, tan A = sin A/cos A).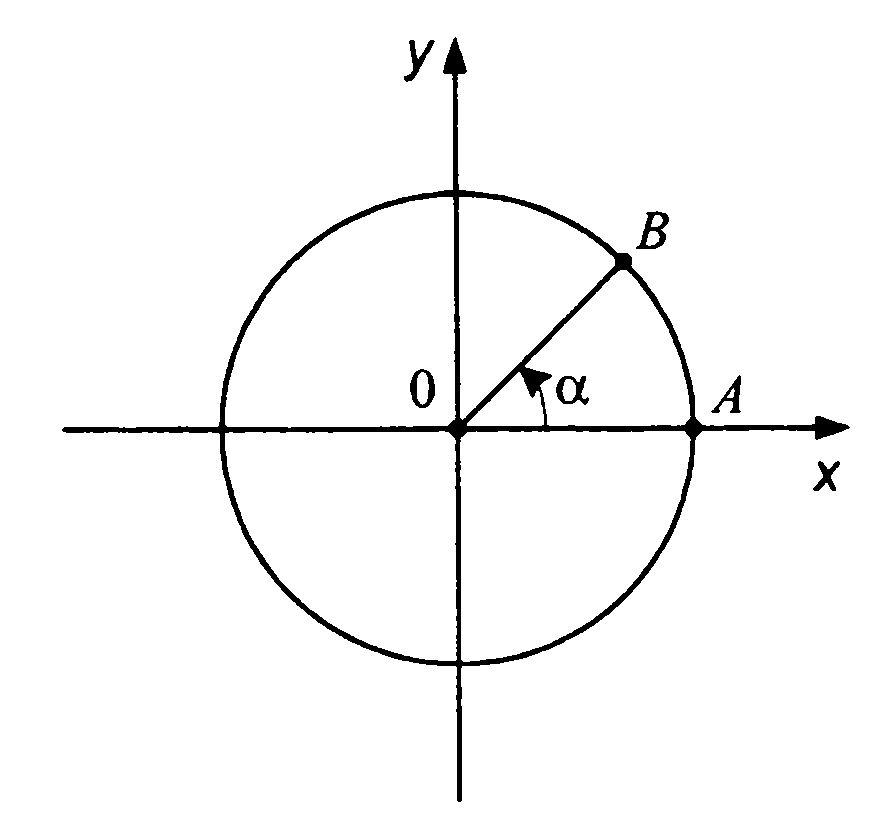
Оси x и y «разрезают» поверхность окружности на четыре сектора-квадранта. Пронумеруем их римскими цифрами по часовой стрелке – I, II, III и IV, – начиная с правой верхней, то есть с диапазона углов от 0° до 90°. Квадрант II, таким образом, охватит диапазон от 90° до 180°, квадрант III – от 180° до 270°, а квадрант IV – от 270° до 360°. Обратите внимание, что в разных квадрантах разные тригонометрические функции будут вести себя по-разному: положительные значения синуса мы получим в квадрантах I и II, косинуса – в квадрантах I и IV, тангенса – в квадрантах I и III. Чтобы это запомнить, некоторые из моих учеников любят повторять «Все студенты таскают калькуляторы» (посмотрите на первые буквы в каждом слове этой «запоминалки»: «в» – «все функции» в квадранте I, «с» – «синусы» в квадранте II, «т» – «тангенсы» в квадранте III, «к» – «косинусы» в квадранте IV).
Ну и еще немного терминологии. Для определения неизвестных значений углов нужны обратные тригонометрические (циклометрические, круговые) функции. Например, обратным синусом 1/2 будет sin–1(1/2)[32]. Такого рода функция говорит нам, что мы имеем дело с неким ?A, синус которого равен 1/2. А так как мы знаем, что sin 30° = 1/2, получаем
Например, обратным синусом 1/2 будет sin–1(1/2)[32]. Такого рода функция говорит нам, что мы имеем дело с неким ?A, синус которого равен 1/2. А так как мы знаем, что sin 30° = 1/2, получаем
sin–1(1/2) = 30°
Функция sin–1 (которая также называется арксинусом) всегда даст нам угол в диапазоне от –90° до 90°, но мы-то с вами знаем, что есть и другие углы с тем же значением синуса – синус 150°, например, будет также равен 1/2. То же происходит и с любым кратным 360° значением, прибавляемым к 30° или 150° – синусы будут равны.
Для треугольника с длинами сторон 3, 4 и 5 (см. рисунок) калькулятор может рассчитать ?A тремя различными способами, каждый из которых будет основан на своей обратной функции:
?A = sin–1(3/5) = cos–1(4/5) = tan–1(3/4) ? 36,87° ? 37°
Самое время применять все эти знания на деле. В «геометрической» главе мы доказали теорему Пифагора, с помощью которой можно вычислить длину гипотенузы прямоугольного треугольника, зная длины его катетов. Здесь же, в главе «тригонометрической», мы можем сделать практически то же самое для любого треугольника. В этом нам поможет закон косинусов.
В «геометрической» главе мы доказали теорему Пифагора, с помощью которой можно вычислить длину гипотенузы прямоугольного треугольника, зная длины его катетов. Здесь же, в главе «тригонометрической», мы можем сделать практически то же самое для любого треугольника. В этом нам поможет закон косинусов.
Теорема (закон косинусов): Длина стороны c любого треугольника ABC, в котором стороны a и b образуют ?C, соответствует
c? = a? + b? – 2ab cos C.
Для примера взгляните на изображенный ниже треугольник ABC. Между двумя его сторонами с длинами 21 и 26 лежит угол 15°. Согласно закону косинусов, длина третьей стороны с составит
c? = 21? + 26? – 2(21)(26) cos 15°
А так как cos 15° ? 0,9659, уравнение упрощается сначала до c? = 62,21, а потом и до c ? 7,89.
Отступление
Доказательство: Чтобы доказать эту теорему, рассмотрим три частных случая – в зависимости от того, будет ли ?C прямым, острым или тупым. Если ?C – прямой, его косинус будет равен cos 90° = 0, что упрощает закон косинусов до c? = a? + b?, то есть до уже доказанной нами теоремы Пифагора.
Если ?C – острый (как на рисунке), опустим перпендикуляр из ?B к стороне AC до лежащей на ней точки D. Получим два треугольника. Применим теорему Пифагора к CBD – a? = h? + x? и придем к
h? = a? – x?
Треугольник же ABD можно просчитать как c? = h? + (b – x)? = h? + b? – 2bx + x?, то есть
h? = c? – b? + 2bx – x?
Составим из двух равных h? частей уравнение:
c? – b? + 2bx – x? = a? – x?
Следовательно,
c? = a? + b? – 2bx
В треугольнике CBD cos C = x/a, поэтому x = a cos C. Следовательно, если ?C является острым, то
Следовательно, если ?C является острым, то
c? = a? + b? – 2ab cos C
Если же ?C – тупой, дополним треугольник ABC прямоугольным треугольником CBD, как на рисунке:
Для него, как и для получившегося большого, верна теорема Пифагора: a? = h? + x? и c? = h? + (b + x)?. Как и в случае с острым ?C, соединим уравнения:
c? = a? + b? + 2bx
В треугольнике CBD cos (180° – C) = x/a, то есть x = a cos (180° – C) = –a cos C. И мы вновь приходим к искомому:
c? = a? + b? – 2ab cos C?
Кроме того с помощью функций можно рассчитать площадь треугольника.
Сопутствующая теорема: В любом треугольнике ABC со сторонами a и b и лежащим между ними ?C
Отступление
Доказательство: Площадь треугольника с длиной основания b и высотой h равна Все три треугольника, рассмотренные при доказательстве закона косинусов, имеют основание b. Определим высоту h. В остроугольном треугольнике обратим внимание на то, что sin C = h/a, то есть h = a sin C. В тупоугольном треугольнике sin (180° – C) = h/a, поэтому опять имеем h = a sin (180° – C) = a sin C. В прямоугольном же треугольнике h = a, что равно a sin C, потому что C = 90°, а sin 90° = 1. Следовательно, так как во всех трех случаях h = a sin C, площадь треугольников составит что и требовалось доказать.
Следствия этой теоремы очевидны:
Другими словами, в треугольнике ABC (sin C)/c равен его удвоенной площади, разделенной на произведение длин трех его сторон. Какой угол выбрать, по большому счету не так уж и важно – (sin B)/b или (sin A)/a дадут нам тот же результат. И это доказывает одну очень полезную теорему.
Теорема (закон синусов): В любом треугольнике ABC, длины сторон которого соответственно равны a, b и c,
Закон синусов – это еще один способ вычислить высоту нашей горы. На этот раз мы сосредоточимся на a – диагонали, пролегающей между нами и вершиной:
Способ № 5 (закон синусов): В треугольнике ABD ?BAD = 32°, а ?BDA = 180° – 40° = 140°. Следовательно, ?ABD = 8°. Согласно закону синусов получаем
Умножим обе части на sin 32°, что даст нам a = 300 sin 32°/ sin 8° ? 1143 метров. А так как sin 40 ? 0,6428 = h/a, то
А так как sin 40 ? 0,6428 = h/a, то
h = a sin 40 ? (1143)(0,6428) = 735
что полностью совпадает с ответом, к которому мы пришли в прошлом разделе.
Отступление
Не менее замечательна в этом отношении формула Герона, с помощью которой можно найти площадь треугольника по длинам его сторон a, b и c. Сначала мы находим полупериметр p:
А потом и площадь S:
S = ?p(p – a)(p – b)(p – c)
Например, если взять треугольник со сторонами 3, 14 и 15 (узнаете первые пять цифр числа ??), полупериметр будет равен (3 + 14 + 15)/2 = 16, а площадь, таким образом, – ?(16(16 – 3)(16 – 14)(16 – 15)) = ?416 ? 20,4.
Несложно, правда? Уверен, внимательный читатель не сможет не заметить здесь закон косинусов, слегка приправленный алгеброй.
Единичный круг · Алгебра и тригонометрия
Единичный круг · Алгебра и тригонометрияВ этом разделе вы:
- Найдите значения функции для синуса и косинуса
30° или (π6), 45° или (π4),
и
60∘ или (π3). - Определение области определения и диапазона функций синуса и косинуса.
- Найти опорные углы.
- Используйте опорные углы для оценки тригонометрических функций.
Хотите острых ощущений? Тогда подумайте о поездке на Singapore Flyer, самом высоком в мире колесе обозрения. Расположенное в Сингапуре колесо обозрения поднимается на высоту 541 фут — чуть больше десятой мили! Описанное как колесо обозрения, всадники наслаждаются захватывающими видами, путешествуя от земли к вершине и снова вниз по повторяющейся схеме. В этом разделе мы рассмотрим этот тип вращательного движения по окружности. Для этого нам нужно сначала определить тип круга, а затем поместить этот круг в систему координат. Тогда мы можем обсудить круговое движение в терминах пар координат.
Для этого нам нужно сначала определить тип круга, а затем поместить этот круг в систему координат. Тогда мы можем обсудить круговое движение в терминах пар координат.
Нахождение тригонометрических функций с помощью единичной окружности
Мы уже определили тригонометрические функции в терминах прямоугольных треугольников. В этом разделе мы переопределим их в терминах единичного круга. Напомним, что единичный круг — это круг с центром в начале координат и радиусом 1, как показано на [ссылка]. Угол (в радианах), который t
точки пересечения образуют дугу длины s.
Используя формулу s=rt,
и зная, что r=1,
мы видим, что для единичного круга s=t.
Оси x- и y- делят координатную плоскость на четыре четверти, называемые квадрантами. Мы помечаем эти квадранты, чтобы имитировать направление положительного угла. Четыре квадранта обозначены I, II, III и IV.
Для любого угла t,
мы можем обозначить пересечение конечной стороны и единичного круга его координатами (x,y).
Координаты x
и y
будут выходами тригонометрических функций f(t)=cos t
и f(t)=sin t,
соответственно. Это означает, что x=cos t 90 003
andy=sin t.
Единичная окружность
Единичная окружность имеет центр в точке (0,0)
и радиус 1.
В единичной окружности длина дуги, на которую она опирается, равна радианной мере центрального угла t.
Позвольте (x,y)
быть концом на единичной окружности дуги длины дуги с.
(x,y)
координаты этой точки могут быть описаны как функции угла.
Определение функций синуса и косинуса по единичному кругу
Функция синуса связывает действительное число t
к y -координата точки пересечения соответствующего угла с единичной окружностью. Точнее, синус угла t
равно y -значению конечной точки на единичной окружности дуги длины t.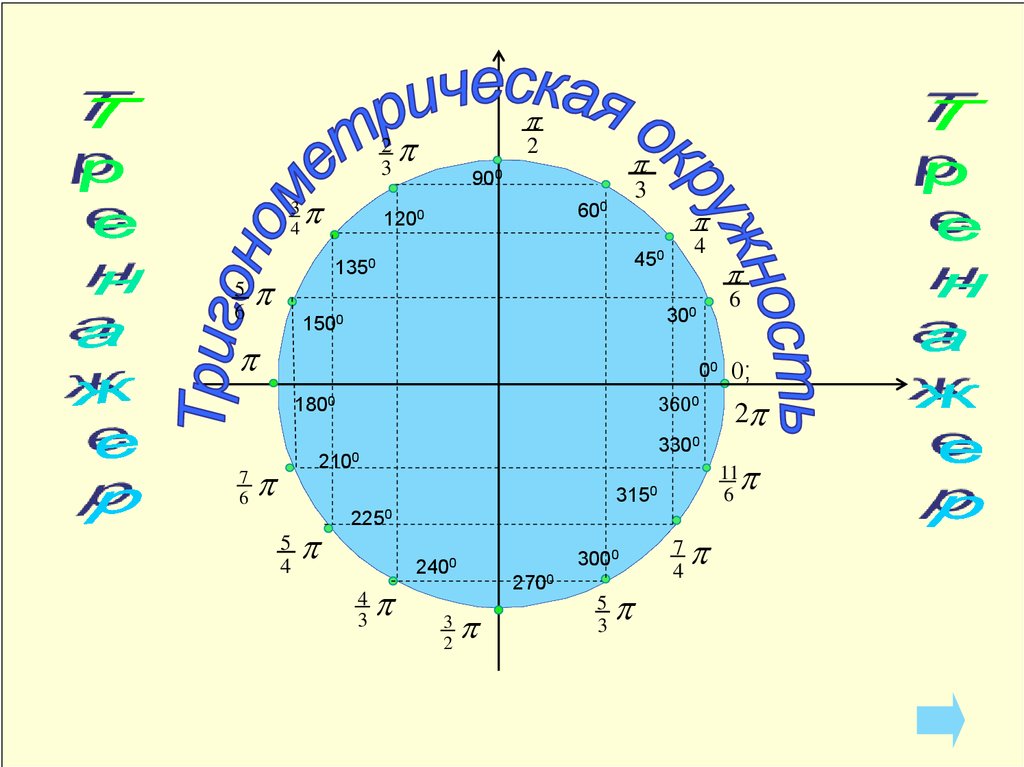
В [ссылка] синус равен y.
Как и все функции, синусоидальная функция имеет вход и выход. Его вход является мерой угла; его вывод — y -координата соответствующей точки на единичной окружности.
Функция косинуса угла t
равно x -значению конечной точки на единичной окружности дуги длины t.
В [ссылка] косинус равен x.
Поскольку известно, что синус и косинус являются функциями, нам не всегда нужно записывать их в скобках: sin t
совпадает с sin(t)
и стоимость
совпадает с cos(t).
Аналогично, cos2t
— обычно используемое сокращение для (cos(t))2.
Имейте в виду, что многие калькуляторы и компьютеры не распознают стенографию. Если вы сомневаетесь, используйте дополнительные скобки при вводе вычислений в калькулятор или компьютер.
Функции синуса и косинуса
If t
— действительное число и точка (x,y)
на единичной окружности соответствует центральному углу t,
затем
cos t=x
sin t=y
*Дана точка *P (x,y)
на единичной окружности, соответствующей углу t,
найти синус и косинус.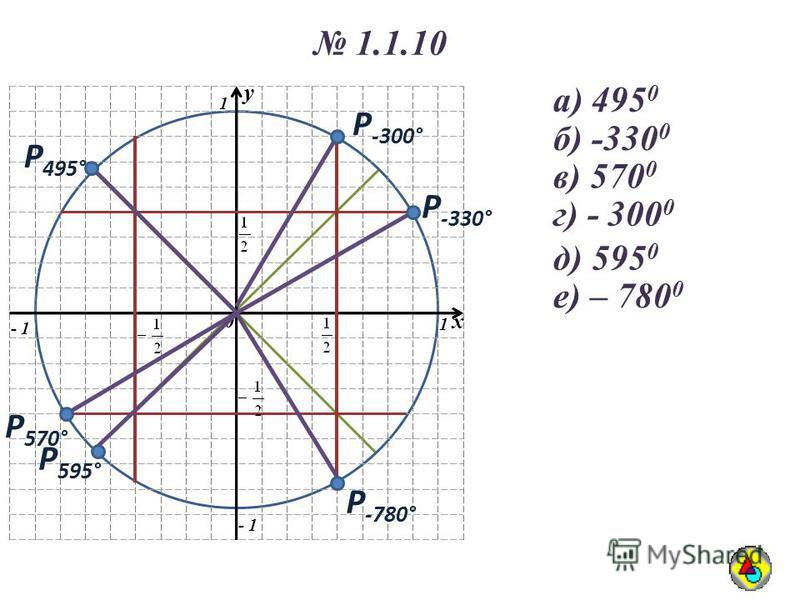 **
**
- Синус
t
равно y — координате точки
P:sin t = y. - Косинус
t
равно x -координата точки
P:cos t=x.
Нахождение значений функции для синуса и косинуса
Точка P
— точка на единичной окружности, соответствующая углу t,
, как показано на [ссылка]. Найдите cos(t)
и sin(t).
Мы знаем, что cos t
– это координата x соответствующей точки на единичной окружности, а sin t
– это y -координата соответствующей точки на единичной окружности. Итак:
х=cos t=12y=sin t=32
Некоторый угол t
соответствует точке на единичной окружности в точке (−22,22)
, как показано на [ссылка]. Найдите cos t
и sin t.
cos(t)=−22,sin(t)=22
Нахождение синусов и косинусов углов на оси
Для квадрантральных углов соответствующая точка на единичной окружности лежит на оси x- или y .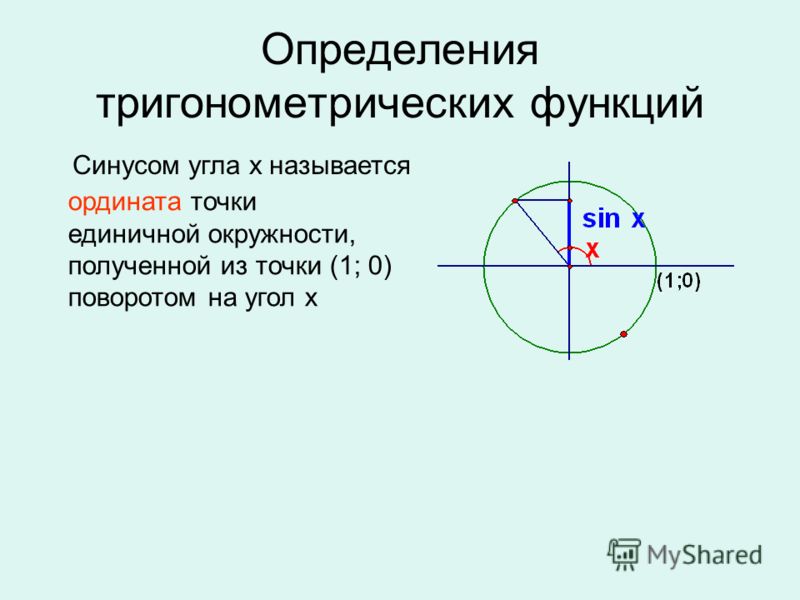 В этом случае мы можем легко вычислить косинус и синус по значениям x
В этом случае мы можем легко вычислить косинус и синус по значениям x
и г.
Вычисление синусов и косинусов вдоль оси
Найти cos(90°)
и sin(90°).
Перемещение 90°
против часовой стрелки вокруг единичной окружности от положительной оси x приводит нас к вершине окружности, где (x,y)
координаты (0,1),
, как показано в [ссылка].
Затем мы можем использовать наши определения косинуса и синуса.
x=cos t=cos(90°)=0y=sin t=sin(90°)=1
Косинус 90°
равен 0; синус 90°
равен 1,
Найдите косинус и синус угла π.
cos(π)=−1,sin(π)=0
Пифагорейская идентичность
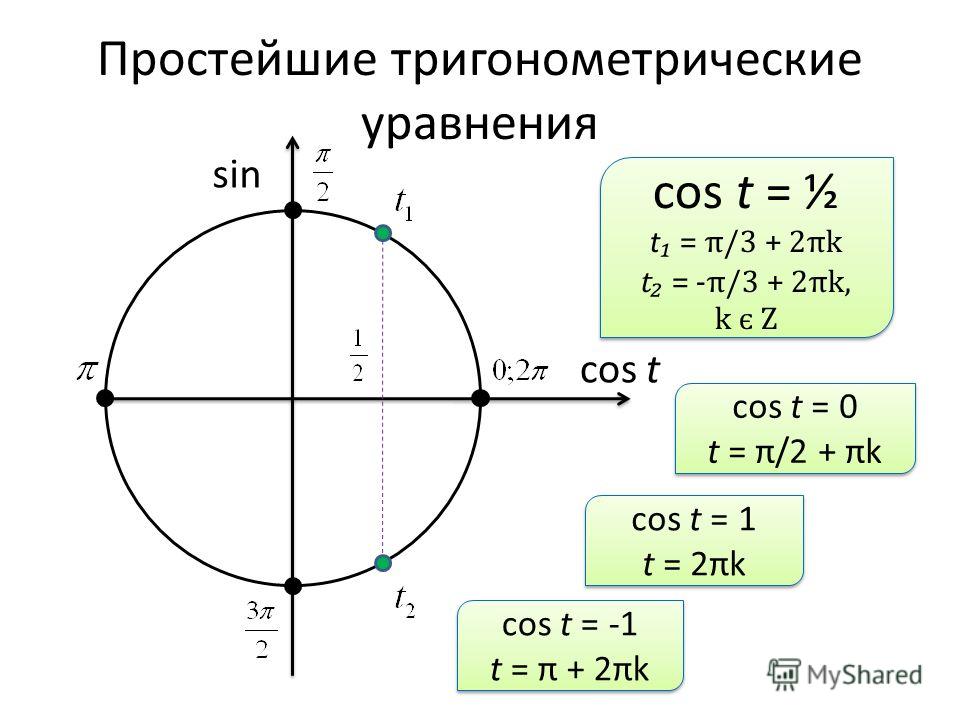
Теперь, когда мы можем определить синус и косинус, мы узнаем, как они соотносятся друг с другом и с единичным кругом. Напомним, что уравнение для единичного круга имеет вид x2+y2=1.
Потому что x=cos t
и y=sin t,
мы можем заменить x
и y
, чтобы получить cos2t+sin2t=1.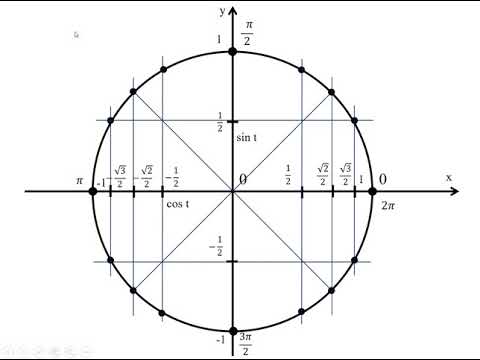
Это уравнение, cos2t+sin2t=1,
известен как Пифагорейская Идентификация . См. [ссылка].
Мы можем использовать тождество Пифагора, чтобы найти косинус угла, если мы знаем синус, или наоборот. Однако, поскольку уравнение дает два решения, нам нужно дополнительное знание угла, чтобы выбрать решение с правильным знаком. Если мы знаем квадрант, в котором находится угол, мы можем легко выбрать правильное решение.
Пифагорейское тождество
Пифагорейское тождество утверждает, что для любого действительного числа t
cos2t+sin2t=1
Зная синус некоторого угла
tи его положение в квадранте, найдите косинус
t.
- Подставить известное значение
sin t
в пифагорейскую идентичность.
- Решить для Стоимость.
- Выберите решение с соответствующим знаком для x — значения в квадранте, где
т
находится.

Нахождение косинуса по синусу или синуса по косинусу
Если sin(t)=37
и t
находится во втором квадранте, найти cos(t).
Если мы опустим вертикальную линию из точки на единичной окружности, соответствующей t,
, мы создадим прямоугольный треугольник, из которого мы можем увидеть, что тождество Пифагора — это просто один из случаев теоремы Пифагора. См. [ссылка].
Подстановка известного значения синуса в тождество Пифагора,
cos2(t)+sin2(t)=1cos2(t)+949=1cos2(t)=4049cos(t)=±4049=±407= ±2107
Поскольку угол находится во втором квадранте, мы знаем, что значение x- является отрицательным действительным числом, поэтому косинус также отрицателен.
cos(t)=−2107
Если cos(t)=2425
и t
находится в четвертом квадранте, найдите sin(t).
sin(t)=−725
Нахождение синусов и косинусов специальных углов
Мы уже изучили некоторые свойства специальных углов, такие как преобразование радианов в градусы, и мы нашли их синусы и косинусы, используя прямоугольные треугольники.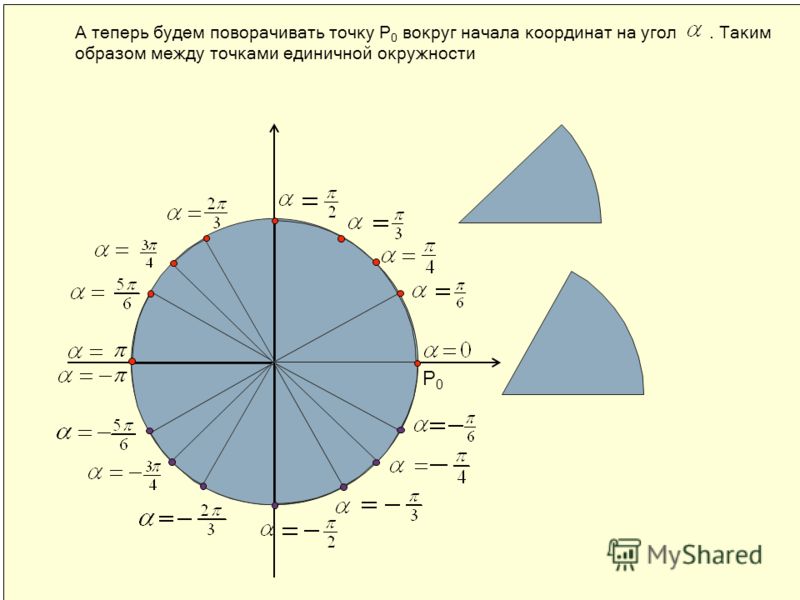 Мы также можем вычислить синусы и косинусы специальных углов, используя тождество Пифагора.
Мы также можем вычислить синусы и косинусы специальных углов, используя тождество Пифагора.
Нахождение синусов и косинусов 45°
Уголки
Сначала рассмотрим углы 45°
или π4,
, как показано в [ссылка]. А 45°–45°–90°
Треугольникравнобедренный, поэтому x- и y -координаты соответствующей точки на окружности совпадают. Поскольку значения x- и y одинаковы, значения синуса и косинуса также будут равны.
At t=π4,
, что составляет 45 градусов, радиус единичной окружности делит пополам первый квадрантный угол. Это означает, что радиус лежит вдоль линии y=x.
Единичный круг имеет радиус, равный 1, поэтому прямоугольный треугольник образуется ниже линии y=x
имеет стороны x
и y (y=x),
и радиус = 1. См. [ссылка].
Из теоремы Пифагора получаем
х2+у2=1
Затем мы можем заменить y=x.
х2+х2=1
Далее объединяем одинаковые термины.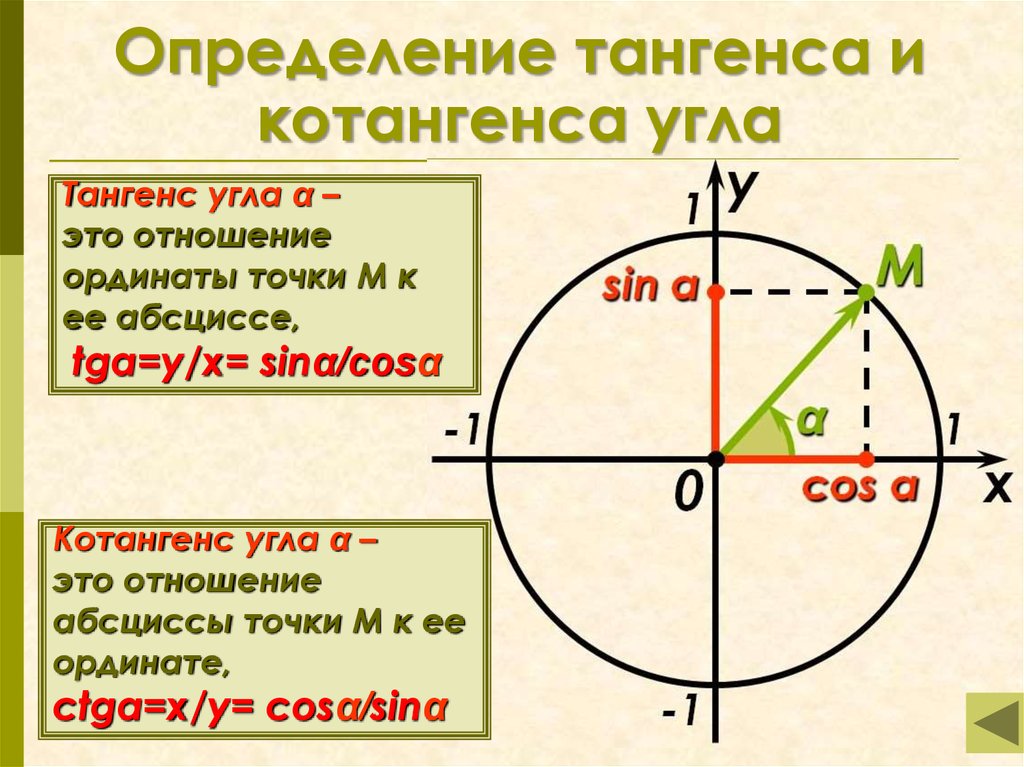
2×2=1
И найти x,
получаем
х2=12х=±12
В квадранте I x=12.
Ат t=π4
или 45 градусов,
(x,y)=(x,x)=(12,12)x=12,y=12cos t=12,sin t=12
Если мы затем рационализируем знаменатели, мы получим
cos t=1222=22sin t=1222=22
Следовательно, (x,y)
координаты точки на окружности радиусом 1
под углом 45°
ар (22,22).
Нахождение синусов и косинусов 30°
и 60°
Уголки
Далее найдем косинус и синус под углом 30°,
или π6.
Сначала нарисуем треугольник внутри круга с одной стороной под углом 30°,
и еще один под углом −30°,
, как показано в [ссылка]. Если полученные два прямоугольных треугольника объединить в один большой треугольник, обратите внимание, что все три угла этого большего треугольника будут равны 60°,
., как показано в [ссылка].
Поскольку все углы равны, стороны также равны. Вертикальная линия имеет длину 2y,
Вертикальная линия имеет длину 2y,
, и поскольку все стороны равны, мы также можем заключить, что r=2y
или y=12р.
Так как sin t=y,
sin(π6)=12r
А так как r=1
в нашем единичном круге,
грех(π6)=12(1)=12
Используя тождество Пифагора, мы можем найти значение косинуса.
cos2(π6)+sin2(π6)=1cos2(π6)+(12)2=1cos2(π6)=34Используйте свойство квадратного корня.cos(π6)=±3±4=32Поскольку y положительный, выберите положительный корень.
(x,y)
координаты точки на окружности радиусом 1
под углом 30°
ар (32,12).
At t=π3 (60°),
радиус единичной окружности, 1, служит гипотенузой прямоугольного треугольника с углами 30-60-90 градусов, BAD,
, как показано в [ссылка]. Угол А
имеет меру 60°.
В точке B,
рисуем угол ABC
с мерой 60°.
Мы знаем, что сумма углов треугольника равна 180°,
, поэтому мера угла C
также 60°.
Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника ABC
— это одинаковая длина, и мы знаем, что одна сторона — это радиус единичного круга, все стороны должны иметь длину 1.
Мера угла ABD
— 30°. Угол ABC
— двойной угол ABD,
, поэтому его мера равна 60°. БД
— биссектриса AC,
., поэтому он режет AC
.пополам. Это означает, что AD
равно 12
радиус, или 12.
Обратите внимание, что AD
это x -координата точки B,
, который находится на пересечении угла 60° и единичной окружности. Это дает нам треугольник BAD
.с гипотенузой 1 и стороной x
длины 12.
Из теоремы Пифагора получаем
х2+у2=1
Замена x=12,
получаем
(12)2+y2=1
Решение для y,
получаем
14+y2=1y2=1−14y2=34y=±32
Так как t=π3
имеет оконечную сторону в квадранте I, где y- координата положительная, выбираем y=32,
положительное значение.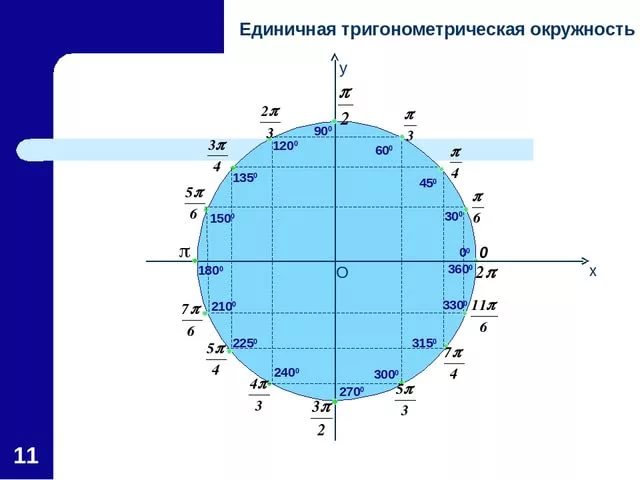
Ат t=π3
(60°), (x,y)
координаты точки на окружности радиусом 1
под углом 60°
а (12,32),
так что мы можем найти синус и косинус.
(x,y)=(12,32)x=12,y=32cos t=12,sin t=32
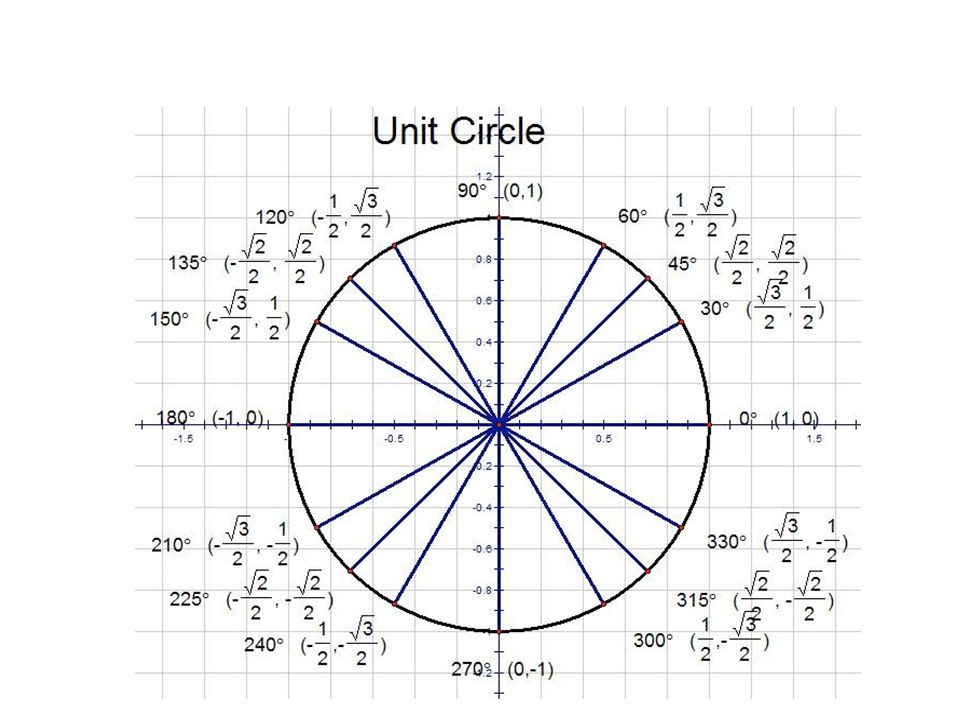
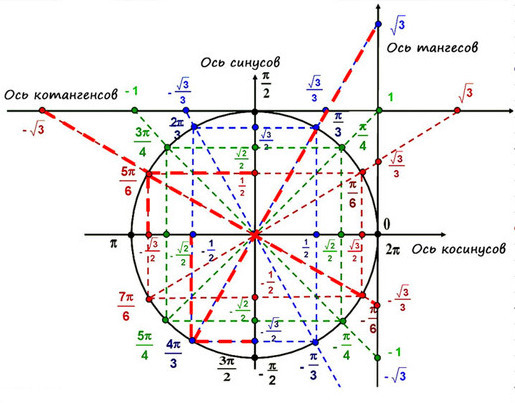
Теперь мы нашли значения косинуса и синуса для всех наиболее часто встречающихся углов в первом квадранте единичной окружности. [ссылка] суммирует эти значения.
| Уголок | 0 |
или 30°
или 45°
или 60°
или 90°
| Косинус | 1 | 32 |
| 0 | ||
| Синус | 0 | 12 |
[ссылка] показывает общие углы в первом квадранте единичной окружности.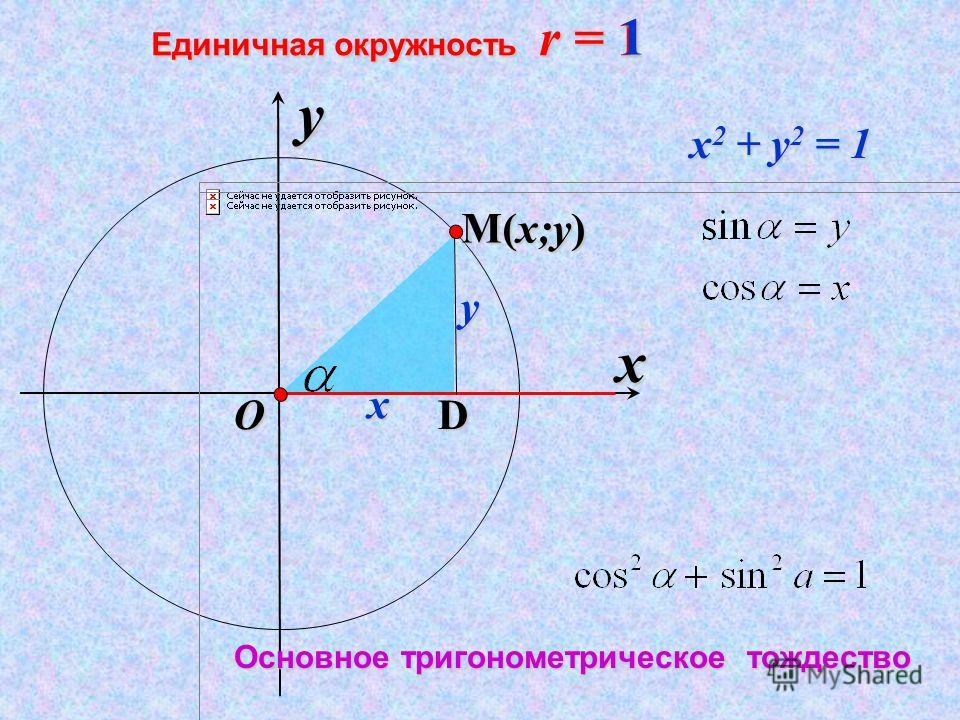
Использование калькулятора для нахождения синуса и косинуса
Чтобы найти косинус и синус углов, отличных от специальных углов, обратимся к компьютеру или калькулятору. Имейте в виду : Большинство калькуляторов можно установить в режим «градусы» или «радианы», которые сообщают калькулятору единицы измерения для входного значения. Когда мы оцениваем cos(30)
на нашем калькуляторе, он оценит его как косинус 30 градусов, если калькулятор находится в режиме градусов, или как косинус 30 радиан, если калькулятор находится в режиме радиан.
Зная угол в радианах, используйте графический калькулятор, чтобы найти косинус.
- Если в калькуляторе есть режимы в градусах и в радианах, установите его в режим в радианах.
- Нажмите клавишу COS.
- Введите значение угла в радианах и нажмите клавишу закрытия скобок «)».
- Нажмите ВВОД.
Использование графического калькулятора для нахождения синуса и косинуса
Вычисление cos(5π3)
с помощью графического калькулятора или компьютера.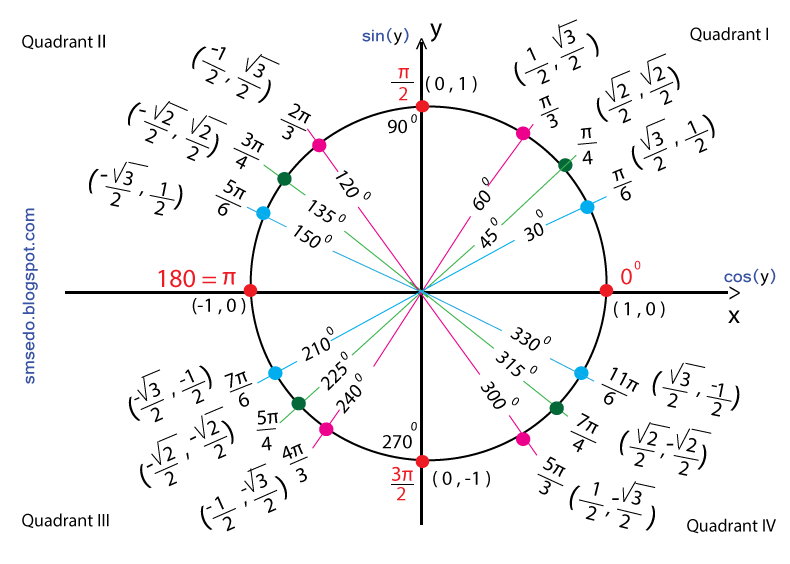
Введите следующие нажатия клавиш:
COS( 5 × π ÷ 3 ) ENTER
cos(5π3)=0,5
Анализ
Мы можем найти косинус или синус угла в градусах прямо на калькуляторе с режимом градусов . Для калькуляторов или программного обеспечения, использующего только радианный режим, мы можем найти знак 20°, 9Например, 0003
, включив коэффициент преобразования в радианы как часть ввода:
SIN( 20 × π ÷ 180 ) ENTER
Вычислить sin(π3).
приблизительно 0,866025403
Определение области значений и диапазона функций синуса и косинуса
Теперь, когда мы можем найти синус и косинус угла, нам нужно обсудить их области определения и диапазоны. Каковы области определения функций синуса и косинуса? То есть, каковы наименьшее и наибольшее числа, которые могут быть входными данными функций? Поскольку углы меньше 0
и углы больше 2π
все еще может быть нанесено на единичную окружность и иметь реальные значения x, y и r,
нет нижнего или верхнего предела углов, которые могут быть входными данными для функций синуса и косинуса. Входными данными для функций синуса и косинуса является поворот от положительной оси x , и это может быть любое действительное число.
Входными данными для функций синуса и косинуса является поворот от положительной оси x , и это может быть любое действительное число.
Каковы диапазоны функций синуса и косинуса? Каковы наименьшее и максимальное возможные значения их выхода? Мы можем увидеть ответы, изучив единичный круг, как показано на [ссылка]. Границы x -координата [−1,1].
Границы координаты y также равны [−1,1].
Таким образом, диапазон функций синуса и косинуса составляет [−1,1].
Нахождение опорных углов
Мы обсудили нахождение синуса и косинуса для углов в первом квадранте, но что, если наш угол находится в другом квадранте? Для любого заданного угла в первом квадранте существует угол во втором квадранте с таким же значением синуса. Поскольку значение синуса равно y -координата на единичной окружности, другой угол с таким же синусом будет иметь такое же значение y , но противоположное x -значение. Следовательно, его значение косинуса будет противоположно значению косинуса первого угла.
Следовательно, его значение косинуса будет противоположно значению косинуса первого угла.
Аналогично, в четвертом квадранте будет угол с тем же косинусом, что и исходный угол. Угол с тем же косинусом будет иметь то же значение x , но будет иметь противоположное значение y . Следовательно, его значение синуса будет противоположно значению синуса исходного угла.
Как показано в [ссылка], угол α
имеет то же значение синуса, что и угол t;
значения косинуса противоположны. Угол β
имеет то же значение косинуса, что и угол t;
значения синуса противоположны.
sin(t)=sin(α)andcos(t)=−cos(α)sin(t)=−sin(β)andcos(t)=cos(β)
Напомним, что опорным углом угла является острый угол, t,
, образованный конечной стороной угла t
и горизонтальной оси. Базовый угол всегда представляет собой угол между 0
и 90°,
или 0
и π2
радиана. Как мы видим из [ссылка], для любого угла в квадрантах II, III или IV существует опорный угол в квадранте I.
**По углу между 0
и 2π,
найдите его исходный угол.**
- Угол в первом квадранте является собственным исходным углом.
- Для угла во втором или третьем квадранте опорным углом является
\|π−t\|
или
\|180°−t\|. - Для угла в четвертом квадранте опорный угол равен
2π−t
или
360°−t. - Если угол меньше
0
или больше
2π,добавить или вычесть
2πстолько раз, сколько нужно, чтобы найти эквивалентный угол между
0и
2π.
Нахождение исходного угла
Нахождение исходного угла 225°
, как показано в [ссылка].
Поскольку 225°
находится в третьем квадранте, базовый угол равен
\|(180°−225°)\|=\|−45°\|=45°
Найдите опорный угол 5π3.
№3
Использование опорных углов
Теперь давайте еще раз вспомним колесо обозрения, представленное в начале этого раздела.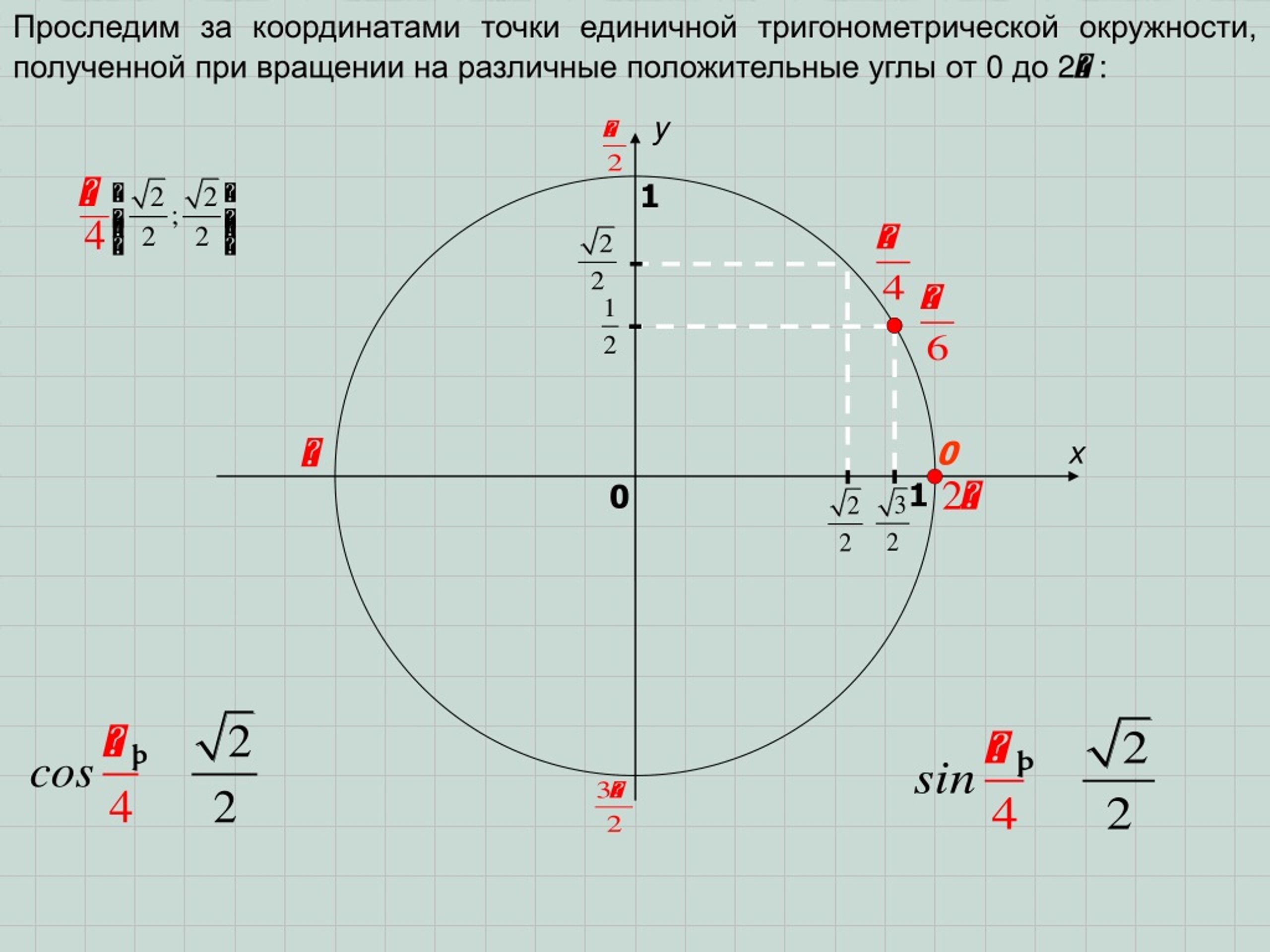 Предположим, всадник делает снимок, остановившись в двадцати футах над уровнем земли. Затем всадник вращается на три четверти круга. Какова новая высота всадника? Чтобы ответить на такие вопросы, как этот, нам нужно оценить функции синуса или косинуса при углах, превышающих 90 градусов или под отрицательным углом. Опорные углы позволяют вычислять тригонометрические функции для углов вне первого квадранта. Их также можно использовать для нахождения (x,y)
Предположим, всадник делает снимок, остановившись в двадцати футах над уровнем земли. Затем всадник вращается на три четверти круга. Какова новая высота всадника? Чтобы ответить на такие вопросы, как этот, нам нужно оценить функции синуса или косинуса при углах, превышающих 90 градусов или под отрицательным углом. Опорные углы позволяют вычислять тригонометрические функции для углов вне первого квадранта. Их также можно использовать для нахождения (x,y)
координаты для этих углов. Мы будем использовать опорный угол угла поворота в сочетании с квадрантом, в котором лежит конечная сторона угла.
Использование опорных углов для оценки тригонометрических функций
Мы можем найти косинус и синус любого угла в любом квадранте, если знаем косинус или синус его исходного угла. Абсолютные значения косинуса и синуса угла такие же, как у опорного угла. Знак зависит от квадранта исходного угла. Косинус будет положительным или отрицательным в зависимости от знака числа 9.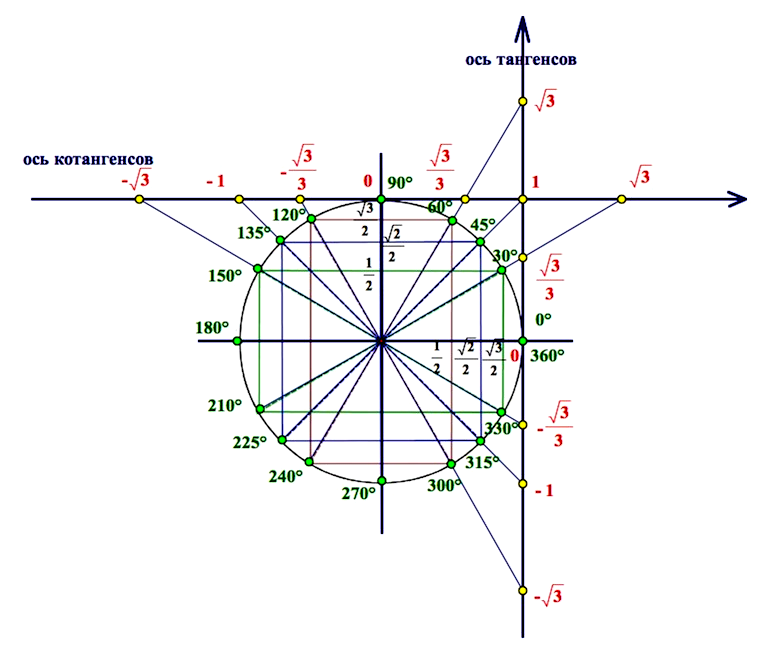 0033 x -значения в этом квадранте. Синус будет положительным или отрицательным в зависимости от знака значений и в этом квадранте.
0033 x -значения в этом квадранте. Синус будет положительным или отрицательным в зависимости от знака значений и в этом квадранте.
Использование опорных углов для нахождения косинуса и синуса
Углы имеют косинусы и синусы с тем же абсолютным значением, что и их опорные углы. Знак (положительный или отрицательный) можно определить по квадранту угла.
Для заданного угла в стандартном положении найдите опорный угол, а также косинус и синус исходного угла.
- Измерьте угол между конечной стороной заданного угла и горизонтальной осью. Это опорный угол.
- Определить значения косинуса и синуса опорного угла.
- Присвойте косинусу тот же знак, что и значениям x в квадранте исходного угла.
- Присвойте синусу тот же знак, что и y -значения в квадранте исходного угла.
Использование опорных углов для нахождения синуса и косинуса
- Используя эталонный угол, найдите точное значение
cos(150°)
и
грех(150°).
- Используя базовый угол, найдите
cos 5π4
и
грех 5π4.
- 150°
находится во втором квадранте. Угол, который он образует с осью x , равен
. 180°−150°=30°,, поэтому опорный угол равен
. 30°.Это говорит нам о том, что 150°
имеет те же значения синуса и косинуса, что и 30°,
кроме знака.
cos(30°)=32andsin(30°)=12
С 150°
находится во втором квадранте, координата x точки на окружности отрицательна, поэтому значение косинуса отрицательно. Координата y положительна, поэтому значение синуса положительно.
cos(150°)=-32andsin(150°)=12
- 5π4
находится в третьем квадранте. Его исходный угол равен
. 5π4−π=π4.Косинус и синус числа
π4равно
22.
В третьем квадранте оба
хи
yотрицательны, поэтому:
cos5π4=−22andsin5π4=−22
- Используйте исходный угол
315°
найти
cos(315°)и
грех(315°). - Используйте опорный угол
−π6
, чтобы найти
cos(-π6)и
грех(-π6).
- cos(315°)=22, sin(315°)=–22
- cos(−π6)=32,sin(−π6)=−12
Использование опорных углов для поиска координат
Теперь, когда мы узнали, как находить значения косинуса и синуса для специальных углов в первом квадранте, мы можем использовать симметрию и опорные углы, чтобы заполнить значения косинуса и синуса для остальных специальных углов на единичный круг . Они показаны в [ссылка]. Уделите время изучению (x,y)
координаты всех главных углов в первом квадранте.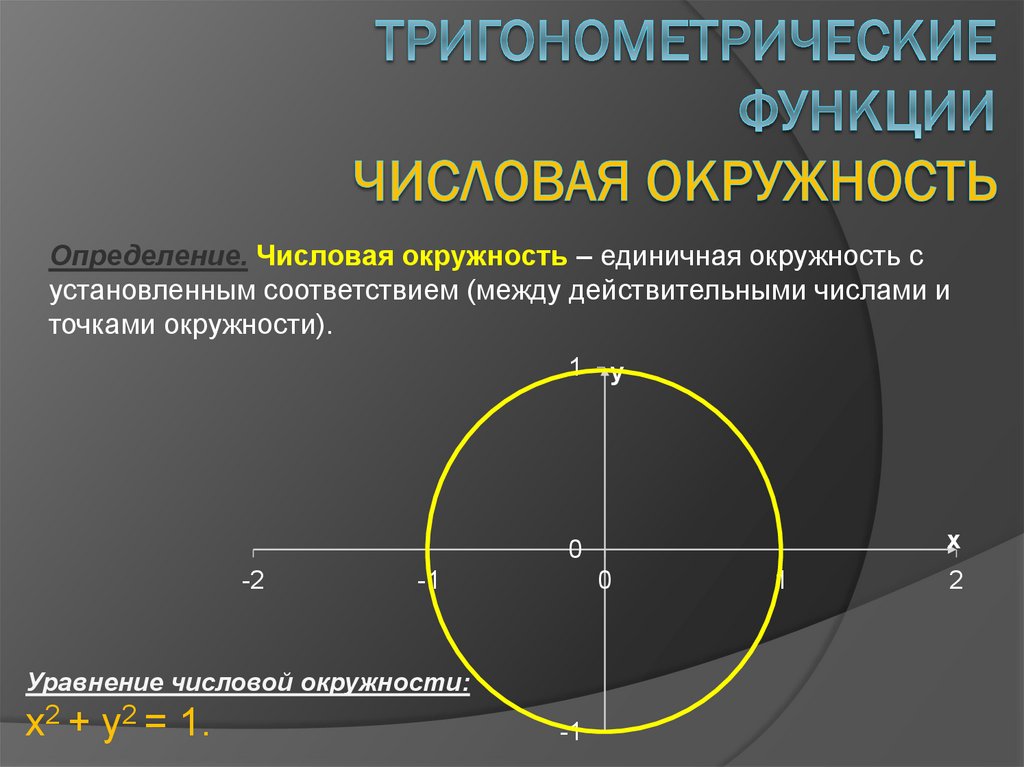
Помимо изучения значений специальных углов, мы можем использовать эталонные углы, чтобы найти (x,y)
координаты любой точки на единичной окружности, используя то, что мы знаем об опорных углах вместе с тождествами
х=costy=sin t
Сначала мы находим опорный угол, соответствующий данному углу. Затем мы берем значения синуса и косинуса опорного угла и присваиваем им знаки, соответствующие y — и x — значения квадранта.
**Зная угол точки на окружности и радиус окружности, найдите (x,y)
координаты точки.**
- Найдите исходный угол, измерив наименьший угол к х -ось.
- Найдите косинус и синус опорного угла.
- Определите соответствующие знаки для
х
и
yв данном квадранте.
Использование единичной окружности для нахождения координат
Найдите координаты точки на единичной окружности под углом 7π6.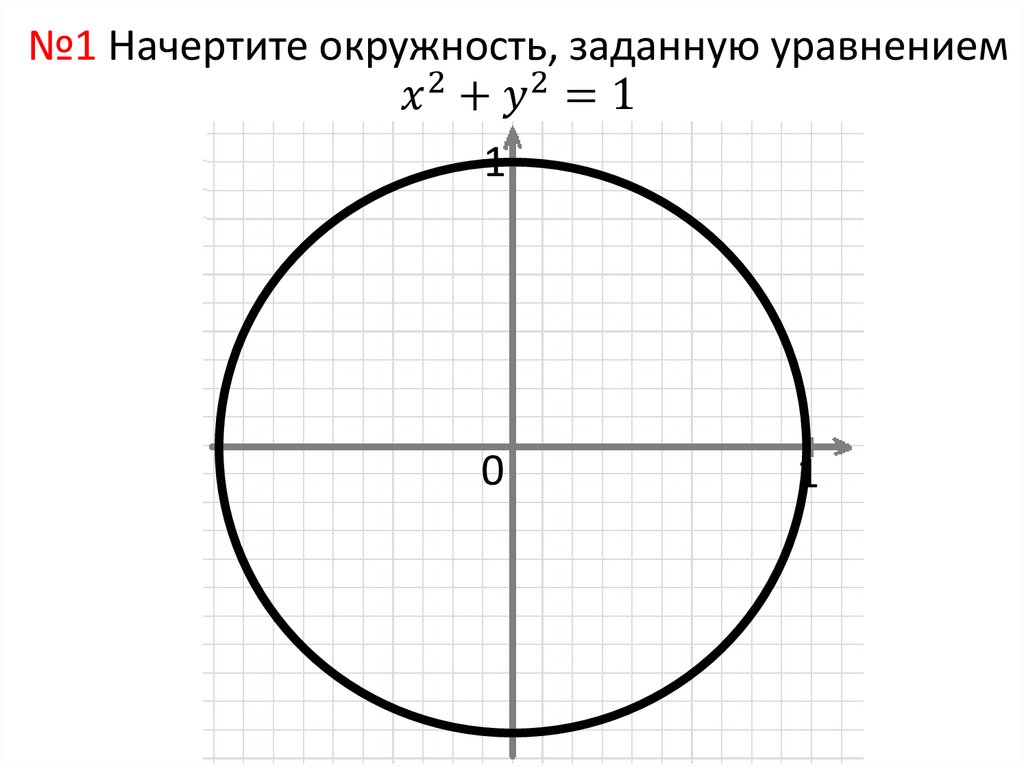
Мы знаем, что угол 7π6
находится в третьем квадранте.
Сначала найдем опорный угол, измерив угол относительно оси x . Чтобы найти исходный угол угла, крайняя сторона которого находится в квадранте III, мы находим разность угла и π.
7π6−π=π6
Далее найдем косинус и синус опорного угла.
cos(π6)=32sin(π6)=12
Мы должны определить соответствующие знаки для x и y в данном квадранте. Поскольку наш первоначальный угол находится в третьем квадранте, где и x
, и y
отрицательны, то и косинус, и синус отрицательны.
cos(7π6)=−32sin(7π6)=−12
Теперь мы можем вычислить (x,y)
координат, используя тождества x=cos θ
и y=sin θ.
Координаты точки (−32,−12)
на единичном круге.
Найдите координаты точки на единичной окружности под углом 5π3.
(12,−32)
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с функциями синуса и косинуса.
- Тригонометрические функции с использованием единичной окружности
- Синус и косинус от блока
- Синус и косинус единичной окружности и числа Пи, деленные на шесть
- Синус и косинус единичной окружности и числа Пи, деленные на четыре
- Тригонометрические функции с использованием опорных углов
Ключевые уравнения
| Косинус | cos t=x |
| Синус | sin t=y |
| Пифагорейская идентичность | cos2t+sin2t=1 |
Ключевые понятия
- Нахождение значений функций для синуса и косинуса начинается с рисования единичной окружности с центром в начале координат и радиусом в 1 единицу.

- Используя единичную окружность, синус угла
t
равно y -значение конечной точки на единичной окружности дуги длиной
t, тогда как косинус угла
tравно x -значению конечной точки. См. [ссылка].
- Значения синуса и косинуса наиболее непосредственно определяются, когда соответствующая точка на единичной окружности попадает на ось. См. [ссылка].
- Когда известен синус или косинус, мы можем использовать тождество Пифагора, чтобы найти другой. Тождество Пифагора также полезно для определения синусов и косинусов специальных углов. См. [ссылка].
- Калькуляторы и программы для построения графиков полезны для нахождения синусов и косинусов, если известна правильная процедура ввода информации. См. [ссылка].
- Областью определения функций синуса и косинуса являются все действительные числа.
- Диапазон функций синуса и косинуса [−1,1].
- Синус и косинус угла имеют то же абсолютное значение, что и синус и косинус исходного угла.

- Знаки синуса и косинуса определяются из значений x и y в квадранте исходного угла.
- Опорный угол угла – это размерный угол,
т,
образован конечной стороной угла
tи ось абсцисс. См. [ссылка].
- Опорные углы можно использовать для нахождения синуса и косинуса исходного угла. См. [ссылка].
- Справочные углы также можно использовать для определения координат точки на окружности. См. [ссылка].
Раздельные упражнения
Устный
Опишите единичный круг.
Единичная окружность — это окружность радиусом 1 с центром в начале координат.
Что представляют собой координаты x- и y- точек на единичной окружности?
Обсудите разницу между котерминальным углом и опорным углом.
Котерминальные углы — это углы, имеющие общую конечную сторону. Базовый угол – это величина наименьшего острого угла, t,
, образованного конечной стороной угла t
и горизонтальной осью.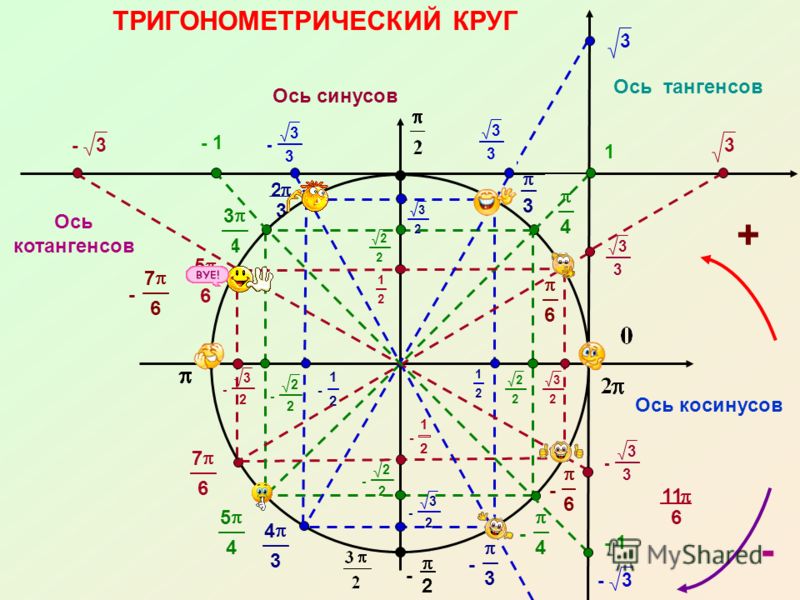
Объясните, чем косинус угла во втором квадранте отличается от косинуса его исходного угла в единичной окружности.
Объясните, чем отличается синус угла во втором квадранте от синуса его исходного угла в единичной окружности.
Значения синусов равны.
Алгебраический
В следующих упражнениях используйте заданный знак функций синуса и косинуса, чтобы найти квадрант, в котором конечная точка определяется t
ложь.
sin(t)<0
и cos(t)<0
sin(t)>0
и cos(t)>0
I
sin(t)>0
и cos(t)<0
sin(t)>0
и cos(t)>0
IV
В следующих упражнениях найдите точное значение каждой тригонометрической функции.
sin π2
sin π3
32
cos π2
cos π3
12
sin π4
cos π4
22
грех π6
sin π
0
sin 3π2
cos π
-1
cos π6
32
Цифровой
Для следующих упражнений укажите опорный угол для заданного угла.
240°
60°
100°
80°
135°
45°
−11π3
π3
В следующих упражнениях найдите опорный угол, квадрант конечной стороны, а также синус и косинус каждого угла. Если угол не является одним из углов единичной окружности, воспользуйтесь калькулятором и округлите его до трех знаков после запятой.
300°
60°,
Квадрант IV, sin(300°)=−32,cos(300°)=12
135°
45°,
Квадрант II,sin(135°)=22,cos(135°)=−22
120°
60°,
Квадрант II, sin(120°)=32,cos(120°)=−12
150°
30°,
Квадрант II, sin(150°)=12,cos(150°)=−32
7π6
π6,
Квадрант III, sin(7π6)=−12,cos(7π6)=−32
3π4
π4,
Квадрант II, sin(3π4)=22,cos(4π3)=−22
2π3
π3,
Квадрант II, sin(2π3)=32,cos(2π3)=−12
7π4
π4,
Квадрант IV, sin(7π4)=−22,cos(7π4)=22
Для следующих упражнений найдите требуемое значение.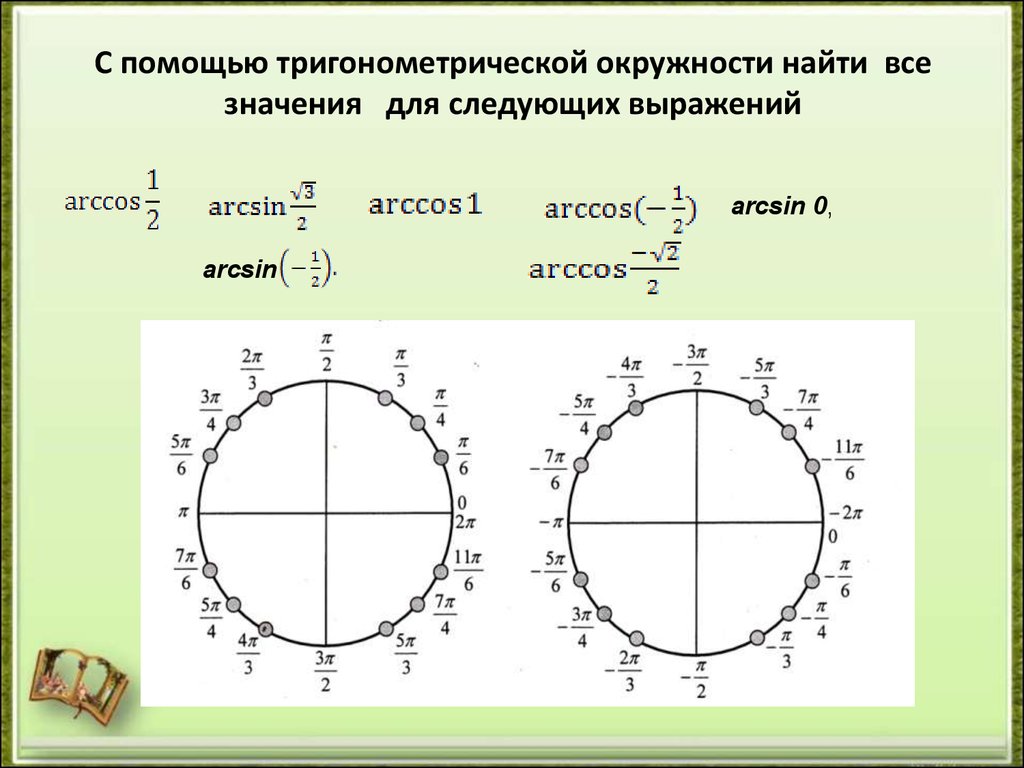
Если cos(t)=17
и t
находится в четвертом квадранте, найдите sin(t).
Если cos(t)=29
и t
находится в первом квадранте, найдите sin(t).
779
Если sin(t)=38
и t
находится во втором квадранте, найдите cos(t).
Если sin(t)=−14
и t
находится в третьем квадранте, найти cos(t).
−154
Найдите координаты точки на окружности радиусом 15, соответствующей углу 220°.
Найдите координаты точки на окружности радиусом 20, соответствующей углу 120°.
(−10, 103)
Найдите координаты точки на окружности радиусом 8, соответствующей углу 7π4.
Найдите координаты точки на окружности радиусом 16, соответствующей углу 5π9.
(–2,778, 15,757)
Укажите область определения функций синуса и косинуса.
Укажите диапазон функций синуса и косинуса.
[–1, 1]
Графический
В следующих упражнениях используйте заданную точку на единичной окружности, чтобы найти значение синуса и косинуса t.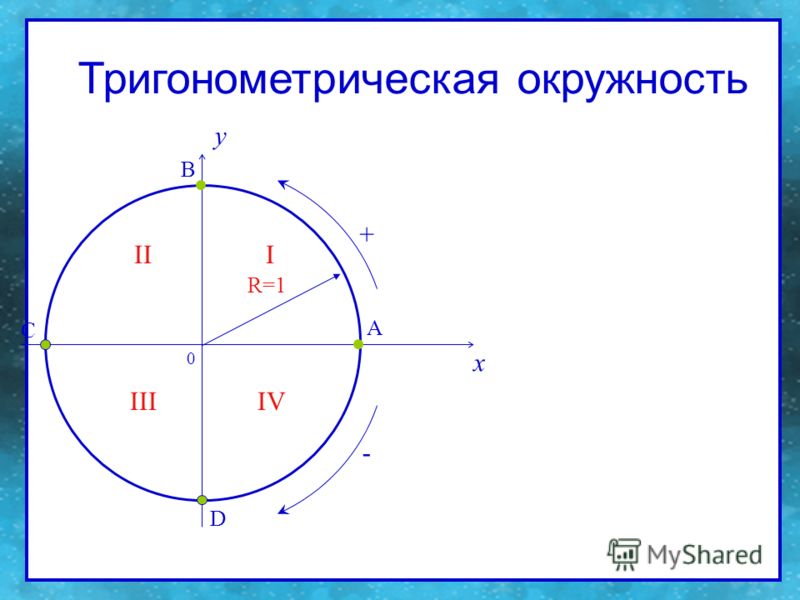


sint=12,cost =−32
![График окружности с вписанным углом t. Точка (1/2, отрицательный квадратный корень из 3 из 2) находится на пересечении конечной стороны угла и края окружности.0003
![График окружности с вписанным углом t. Точка (отрицательный квадратный корень из 2 из 2, отрицательный квадратный корень из 2 из 2) находится на пересечении конечной стороны угла и края круга.] (/ алгебра-тригонометрия-книга/ресурсы/CNX_Precalc_Figure_05_02_204.jpg)
sint =−22, стоимость=−22
 Точка (1/2, квадратный корень из 3 из 2) находится на пересечении конечной стороны угла и края окружности.0003
Точка (1/2, квадратный корень из 3 из 2) находится на пересечении конечной стороны угла и края окружности.0003

sint=32,cost =−12
 jpg)
jpg)
sint=0, cost=−1


sint=−0,596, cost=0,803


sint=0,761,cost=-0,649

 jpg)
jpg)
sint=1,cost=0
Технология
Для оценки следующих упражнений используйте графический калькулятор.
грех 5π9
cos 5π9
−0,1736
sin π10
cos π10
0,9511
грех 3π4
cos 3π4
−0,7071
sin 98°
cos 98°
−0,1392
cos 310°
sin 310°
−0,7660
Расширения
Для следующих упражнений оцените.
sin(11π3) cos(−5π6)
sin(3π4) cos(5π3)
24
sin(−4π3) cos(π2)
sin(−9π4) cos(−π6)
−64
sin(π6) cos(−π3)
sin(7π4)cos(−2π3)
24
, потому что (5π6) потому что (2π3)
cos(−π3)cos(π4)
24
грех(−5π4) sin(11π6)
sin(π)sin(π6)
0
Реальные приложения
Для следующих упражнений используйте этот сценарий: Ребенок входит в карусель, которой требуется одна минута, чтобы сделать один оборот.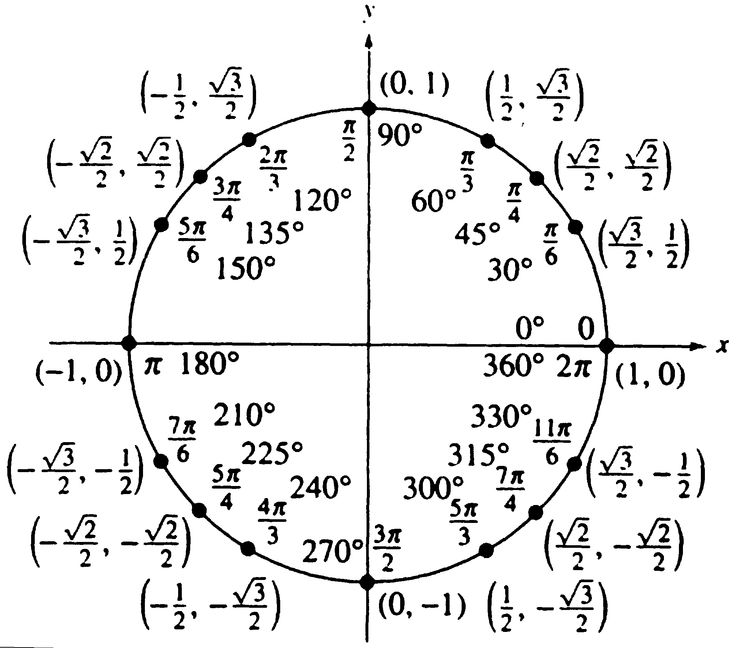 Ребенок входит в точку (0,1),
Ребенок входит в точку (0,1),
, то есть строго на север. Предположим, что карусель вращается против часовой стрелки.
Каковы координаты ребенка через 45 секунд?
Каковы координаты ребенка через 90 секунд?
(0,–1)
Каковы координаты ребенка через 125 секунд?
Когда у ребенка появятся координаты (0,707,–0,707)
, если поездка длится 6 минут? (Ответов несколько.)
37,5 секунд, 97,5 секунд, 157,5 секунд, 217,5 секунд, 277,5 секунд, 337,5 секунд
Когда у ребенка появятся координаты (–0,866,–0,5)
, если поездка длится 6 минут?
Глоссарий
- Функция косинуса
- x -значение точки на единичной окружности, соответствующей заданному углу
- Пифагорейская идентичность
- следствие теоремы Пифагора, утверждающее, что квадрат косинуса данного угла плюс квадрат синуса этого угла равен 1
- функция синуса
- y -значение точки на единичной окружности, соответствующей заданному углу
Эта работа находится под лицензией Creative Commons Attribution 4.
 0 International License.
0 International License.Вы также можете бесплатно скачать на http://cnx.org/contents/[email protected]
Атрибуция:
- По вопросам, касающимся этой лицензии, обращайтесь по адресу [email protected].
- Если вы используете данный учебник в качестве библиографической ссылки, то цитировать его следует следующим образом: Колледж OpenStax, алгебра и тригонометрия. OpenStax CNX. http://cnx.org/contents/[email protected].
- Если вы распространяете этот учебник в печатном формате, вы должны указать на каждой физической странице следующее указание авторства: «Загрузите бесплатно по адресу http://cnx.org/contents/[email protected]».
- Если вы распространяете часть этого учебника, вы должны сохранять при каждом просмотре страницы в цифровом формате (включая, помимо прочего, EPUB, PDF и HTML) и на каждой физической печатной странице следующее указание авторства:
«Скачать бесплатно на http://cnx.
 org/contents/[email protected].»
org/contents/[email protected].»
Круги единиц и стандартное положение (видео и практика)
TranscriptPractice
Привет, и добро пожаловать в этот обзор круга единиц! В этом видео мы рассмотрим, что такое единичный круг и для чего он используется.
Прежде чем мы перейдем к самой единичной окружности, давайте поговорим о градусах и радианах. В большинстве случаев, когда вы измеряете угол , вы измеряете его в градусах . Например, прямой угол имеет 90 градусов, прямой угол имеет 180 градусов, и для каждого числа между ними есть угол.
Но на самом деле есть еще один способ измерить угол, и это измерение в радианах . Измерение в радианах связывает угол с \(\pi \), поэтому \(\pi \) будет почти во всех измерениях угла при измерении в радианах.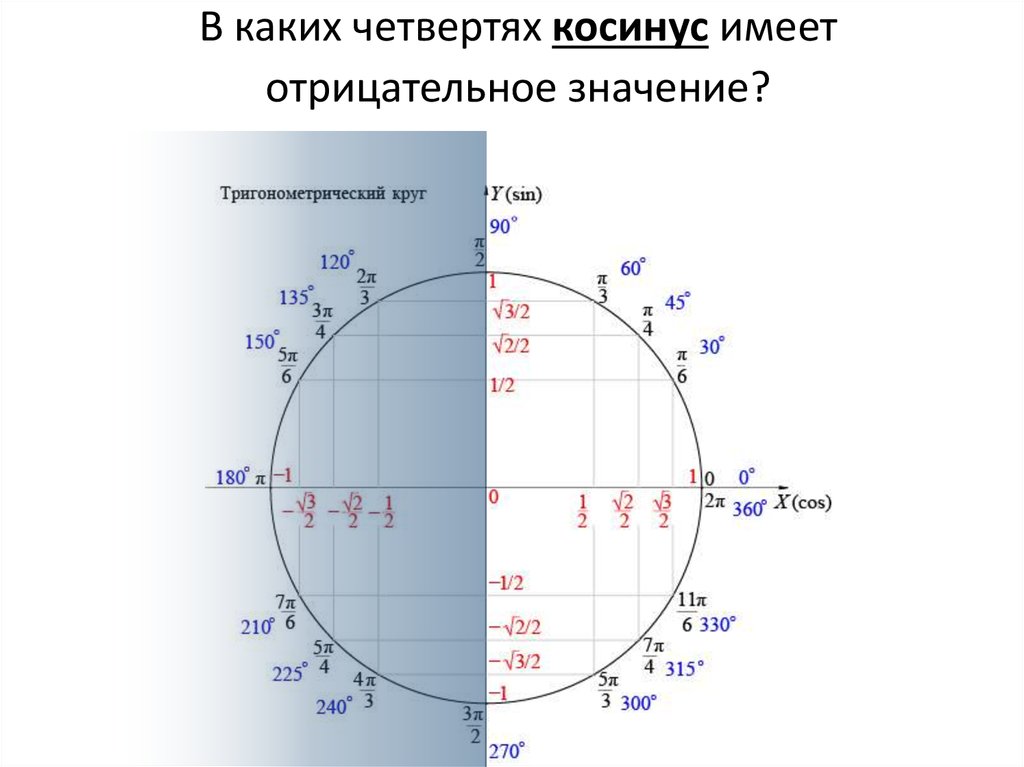
Поскольку \(\pi \) — это отношение длины окружности к ее диаметру, имеет смысл использовать радианы чаще всего при работе с окружностями. 9{\circ}}{\pi \text{ рад}}\), что затем упрощается до \(30°\).
Теперь давайте посмотрим, как это относится к единичному кругу.
Единичная окружность — это окружность радиусом в одну единицу, центр которой находится в начале координат. Это может показаться довольно распространенным, и вы можете быть взволнованы, если думаете, что я попрошу вас найти длину окружности или площадь. С радиусом один, это было бы не очень сложно. Но сегодня мы посмотрим на этот круг через призму тригонометрии.
Тригонометрия — это наука о том, как стороны и углы треугольника соотносятся друг с другом. Теперь вам, наверное, интересно, какое отношение круги и треугольники имеют друг к другу, и это отличный вопрос! Одним из наиболее распространенных применений тригонометрии является нахождение мер угла по двум сторонам прямоугольного треугольника. Если мы внимательно посмотрим на наш круг, мы действительно сможем найти в нем прямоугольные треугольники. Вот пример:
Если мы внимательно посмотрим на наш круг, мы действительно сможем найти в нем прямоугольные треугольники. Вот пример:
Мы знаем, что радиус равен 1, и мы можем использовать SOHCAHTOA, чтобы найти, что противоположная сторона равна \(\frac{1}{2}\), а смежная сторона равна \(\sqrt{3}\) .
Единичный круг представляет собой набор наиболее распространенных прямоугольных треугольников, поэтому мы используем его для запоминания триггерных значений наиболее распространенных углов. Координатные точки, в которых мера определенного угла попадает на окружность, дают нам значения синуса и косинуса. Например, для луча, исходящего из угла \(60°\), точка, в которой луч попадает на единичную окружность, находится в точке \((\frac{1}{2},\frac{\sqrt{3}}{2 })\). Координата \(x\) дает нам значение косинуса для этого угла, а координата \(y\) дает нам значение синуса. Если вам нужно найти значение тангенса, просто положите синус на косинус или координату \(y\) на координату \(x\). Возвращаясь к нашему примеру с \(60°\), \(\sin{60^{\circ}}=\frac{\sqrt{3}}{2}\), наша \(y\)-координата, \(\cos{60^{\circ}}=\frac{1}{2}\), наша \(x\)-координата и \(\tan{60^{\circ}}=\frac{ \frac{\sqrt{3}}{2}}{\frac{1}{2}}\), что упрощается до \(\sqrt{3}\).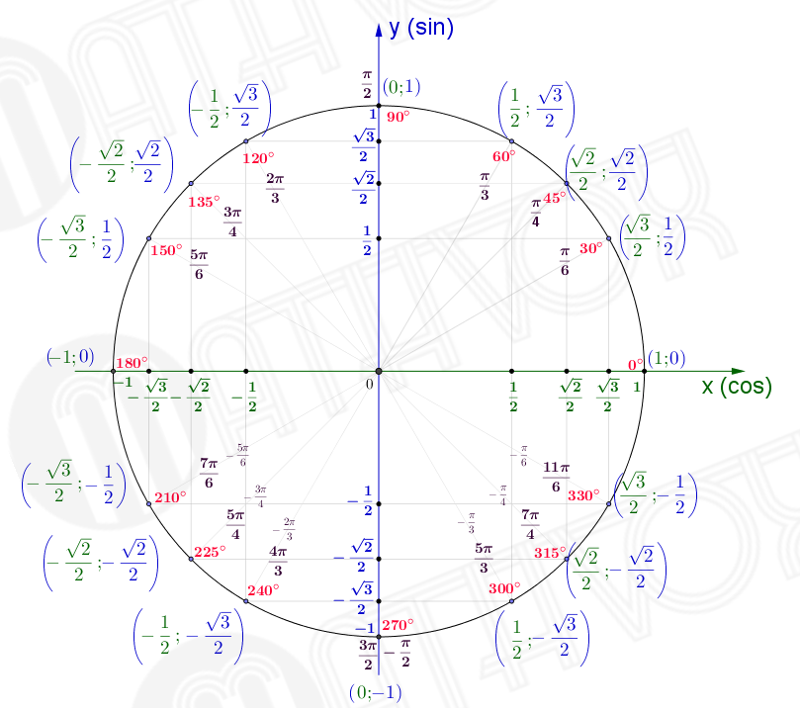
Важно отметить, что при обсуждении этих угловых измерений углы должны находиться в стандартном положении. Стандартное положение просто означает, что вершина угла находится в начале окружности и что один луч угла находится на положительной оси \(x\). Другой луч угла помещается на меру угла, образованную движением против часовой стрелки по окружности. Если угол не находится в стандартном положении, важно поместить его в стандартное положение, прежде чем использовать точки для поиска значений триггера. 9{\circ}\). Затем мы используем нашу единичную окружность с углами в стандартном положении, чтобы найти триггерные значения обычных угловых измерений.
Надеюсь, этот отзыв был вам полезен. Спасибо за просмотр и удачной учебы!
Вопрос №1:
Каково значение cos 90°? Используйте единичный круг.
\(0\)
\(1\)
\(\frac{1}{2}\)
\(\frac{\pi}{2}\)
Показать ответ
Ответ:
В паре координат \((x,y)\) на единичной окружности координата x — это косинус угла, образованного точкой, началом координат и осью x .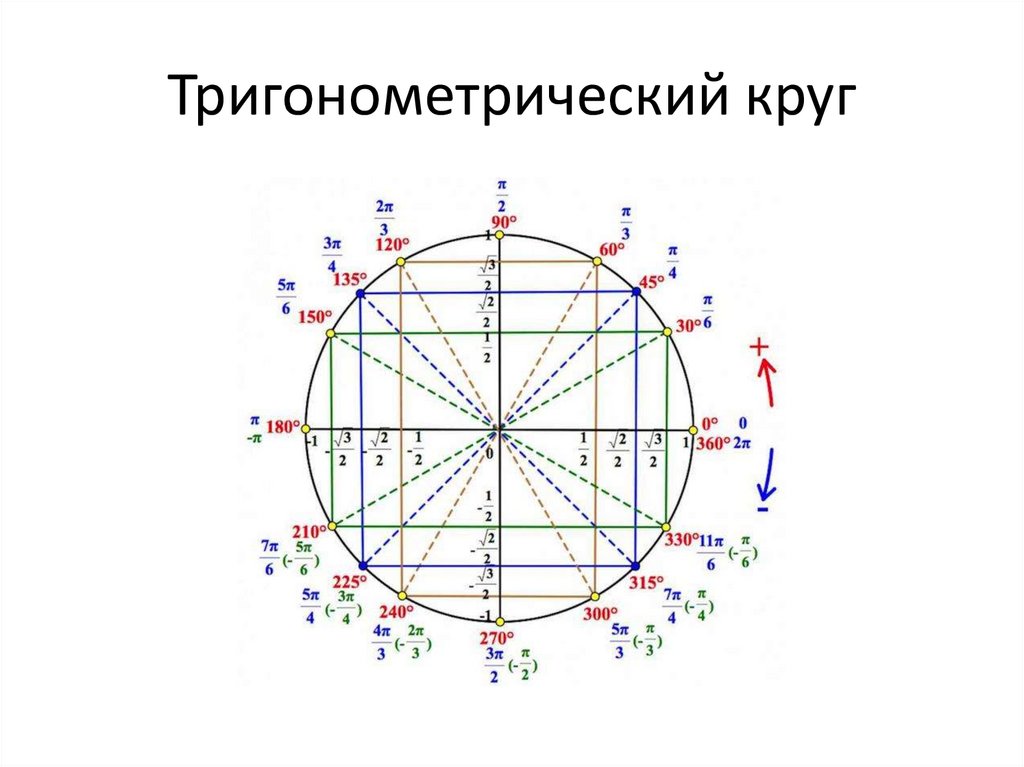
Скрыть ответ
Вопрос № 2:
Каково значение sin \(\frac{3π}{4}\)? Используйте единичный круг.
\(\frac{1}{2}\)
\(-\frac{\sqrt{2}}{2}\)
\(\frac{\sqrt{2}}{2} \)
\(\frac{\sqrt{3}}{2}\)
Показать ответ
Ответ:
В паре координат \((x,y)\) на единичной окружности , координата y — это синус угла, образованного точкой, началом координат и осью x .
Скрыть ответ
Вопрос № 3:
Каково значение тангенса \(\frac{5π}{4}\)? Используйте единичный круг.
\(0\)
\(-1\)
\(-\frac{1}{2}\)
\(1\)
Показать ответ
Ответ:
2 Функция тангенса находится путем деления значения
y на x -значение.
\(-\frac{\sqrt{2}}{2}\div-\frac{\sqrt{2}}{2}=1\), поэтому загар \(\frac{5π}{4}=1 \)
Скрыть ответ
Вопрос № 4:
180 градусов = ______________ радиан.
\(\frac{π}{2}\)
\(2π\)
\(π\)
\(\frac{3π}{2}\)
Показать ответ
Ответ:
Мы можем решить это, умножив 180 градусов на коэффициент преобразования \(\frac{π\text{ рад}}{180\text{ градусов}}\). Это упрощается до π рад.
Скрыть ответ
Вопрос № 5:
\(\frac{5π}{3}\) рад = __________ градусов.
30
330
270
300
Показать ответ
Ответ:
)\frac{180\text{ градусов}}{π}.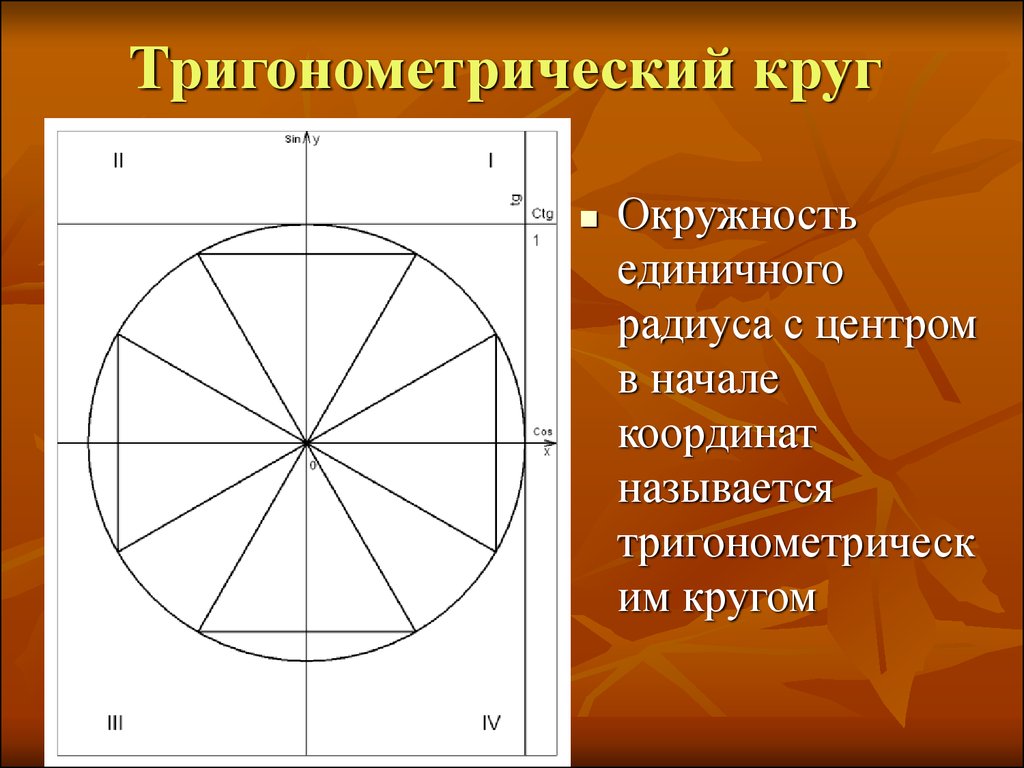 Это упрощает до 300 градусов.
Это упрощает до 300 градусов.
Скрыть ответ
Вопрос №6:
Тангенс каких двух углов равен \(\frac{\sqrt{3}}{3}\)?
30 ° и 150 °
30 ° и 210 °
150 ° и 210 °
150 ° и 330 °
Покажите ответ
Ответ:
. Тангентный угол — угла. (\ frac{\ text {sin}} {\ text {cos}} \). Мы знаем, что x — и y -координаты точек на единичной окружности представляют косинус и синус угла соответственно. Будем искать координаты, где отношение \(\frac{y}{x}=\frac{\sqrt{3}}{3}\). х – и y -координаты для углов 30° и 210° упрощаются до \(\frac{\sqrt{3}}{3}\).
Скрыть ответ
Вопрос № 7:
Чему равен косинус \(\frac{4π}{3}\)?
\(-\frac{1}{2}\)
\(-\frac{\sqrt{3}}{2}\)
\(\frac{1}{2}\)
\(\frac{\sqrt{3}}{2}\)
Показать ответ
Ответ:
Мы знаем, что x -координаты точки на единичной окружности представляют косинус. Найдите \(\frac{4π}{3}\), что эквивалентно 240° в координате \((-\frac{1}{2},-\frac{\sqrt{3}}{2}) \). Координата x точки равна \(-\frac{1}{2}\) и косинусу \(\frac{4π}{3}\).
Найдите \(\frac{4π}{3}\), что эквивалентно 240° в координате \((-\frac{1}{2},-\frac{\sqrt{3}}{2}) \). Координата x точки равна \(-\frac{1}{2}\) и косинусу \(\frac{4π}{3}\).
Скрыть ответ
Вопрос № 8:
\(\text{sin }Ɵ=\frac{1}{2}\), где 0°
\(\frac{π}{6 }\)
\(\frac{π}{3}\)
\(\frac{5π}{6}\)
\(\frac{5π}{3}\)
Показать ответ
Ответ:
Так как нам сказали, что значение Ɵ находится в первом квадранте, и мы знаем, что y -координата точки на единичной окружности представляет синус, мы можем искать точку на единице круг где y -координата \(\frac{1}{2}\). Единственная точка в первом квадранте с координатой y \(\frac{1}{2}\) представляет собой угол 30°, который равен \(\frac{π}{6}\) в радианах.
HID мог бы спросить: что хорошего в единичном круге? Далее следует небольшой пересмотр некоторых комментариев, которые я размещал два или три раза за последние несколько лет в рассылке для (в основном американских средних школ) учителей AP-исчисления.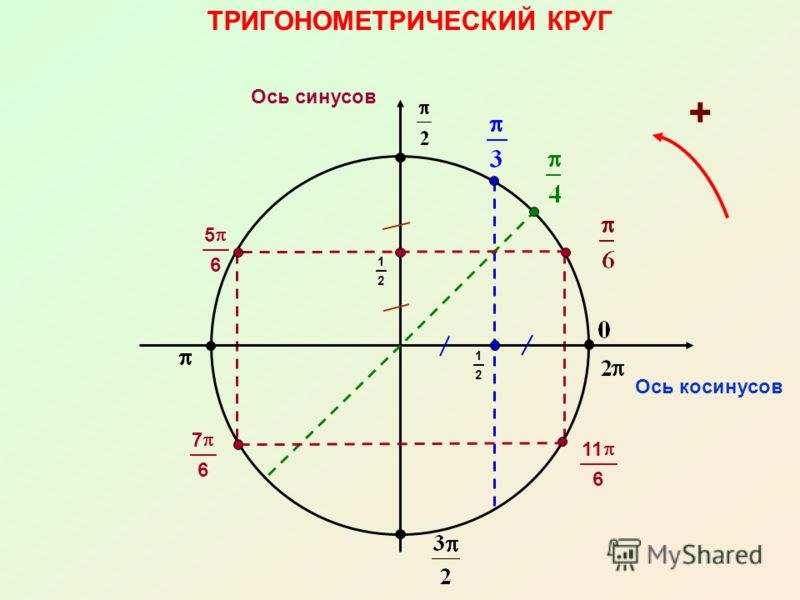
Под «единичным кругом» я подразумеваю определенную концептуальную основу для многих важных фактов и свойств триггера, а НЕ большой круг, нарисованный на листе бумаги, углы которого обозначены градусными мерами 30, 45, 60, 90, 120, 150 и т. д. (и/или с соответствующими мерами в радианах), а также точным значением синуса и косинуса этих углов.
Я обнаружил, что правильное понимание единичного круга дает огромную экономию на запоминании, поскольку позволяет эффективно каталогизировать и перепроверить большое количество соответствующих фактов о триггерных функциях. Все, что вам нужно знать, это то, что косинус идет с координатой $x$, а синус идет с координатой $y$, и для этого вы просто помните, что это алфавит: * c *osine идет с $x$ и * s *ine идет с $y$.
Используя это понимание единичной окружности, мы можем получить значения синуса и косинуса при целых кратных 90 градусах, поскольку они будут соответствовать точкам единичной окружности, которые находятся на положительной оси $x$, отрицательной $ ось x$, положительная ось $y$ или отрицательная ось $y$, и для каждой из этих возможностей мы знаем, каковы будут обе координаты точки.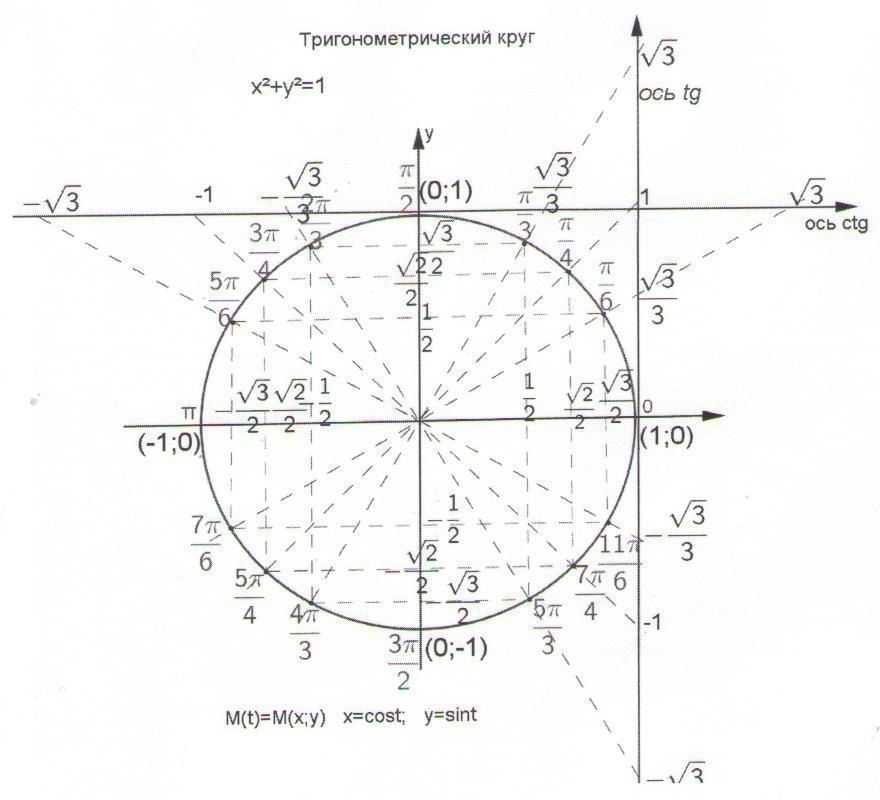 {2} x = 1$, из чего возникает очень многое другое. (По сути
все, если вы будете достаточно усердно работать. См. [1] [2].)
{2} x = 1$, из чего возникает очень многое другое. (По сути
все, если вы будете достаточно усердно работать. См. [1] [2].)
[1] Энди Рой Магид, «Тригонометрические тождества», Mathematics Magazine 47 № 4 (сентябрь 1974 г.), 226–227.
[2] Дэвид Эрл Доббс, «Доказательство триггерных тождеств для первокурсников», Mathematics and Computer Education 14 # 1 (зима 1980 г.), 39–42.
Используя это понимание единичного круга, мы можем получить знаки синуса и косинуса в каждом из 4 квадрантов.
Используя это понимание единичного круга, мы можем сделать вывод, что $\sin(-\theta) = -\sin(\theta)$ и $\cos(-\theta) = \cos(\theta)$. [На практике, когда вы знаете, что каждый из синусов и косинусов является либо четной, либо нечетной функцией, и вы знаете о свойствах отражения графика для четных и нечетных функций, легко понять, что есть что, посмотрев на то, как $x$ — и $y$-координаты для $-45$ градусов сравниваются с $x$- и $y$-координатами для 45 градусов.]
Используя это понимание единичной окружности, мы знаем, когда задан интервал, увеличивается ли синус на этом интервале, уменьшается на этом интервале или ни то, ни другое. Мы также знаем это для косинуса. [На самом деле, поскольку справа от $0$ синус возрастает, а косинус убывает, и оба они положительны, отсюда следует, что косинус — это тот, для которого вы должны использовать отрицательный знак при записи его производной. Это предполагает, что вы помните, что производная синуса — это косинус, а производная косинуса — синус, по модулю одного из них, требующего отрицательного знака. Однако я не ожидал (и никогда не видел) такого от студентов.] 92 = 1$, что дает нам $x = \frac{\sqrt{3}}{2}$. Поскольку $\frac{\sqrt{3}}{2} > \frac{1}{2}$ (возведите в квадрат обе стороны или просто обратите внимание, что $\sqrt{3} > 1$), должно быть, что это значения для точки $(x,y)$ на единичной окружности такие, что $x > y$, так что это должно быть для 30 градусов (учитывая, что мы знаем, что $\frac{1}{2}$ может быть значение синуса и/или косинуса только для углов первой четверти среди углов с градусной мерой 30, 45, 60). Так как $x = \frac{1}{2}$ и $y = \frac{\sqrt{3}}{2}$ также удовлетворяют $x^2 + y^2 = 1$ (дополнительных действий не требуется; просто переключите порядок сложения в предыдущем случае), а здесь $x < y$, это должны быть значения для 60 градусов.
Мы также знаем это для косинуса. [На самом деле, поскольку справа от $0$ синус возрастает, а косинус убывает, и оба они положительны, отсюда следует, что косинус — это тот, для которого вы должны использовать отрицательный знак при записи его производной. Это предполагает, что вы помните, что производная синуса — это косинус, а производная косинуса — синус, по модулю одного из них, требующего отрицательного знака. Однако я не ожидал (и никогда не видел) такого от студентов.] 92 = 1$, что дает нам $x = \frac{\sqrt{3}}{2}$. Поскольку $\frac{\sqrt{3}}{2} > \frac{1}{2}$ (возведите в квадрат обе стороны или просто обратите внимание, что $\sqrt{3} > 1$), должно быть, что это значения для точки $(x,y)$ на единичной окружности такие, что $x > y$, так что это должно быть для 30 градусов (учитывая, что мы знаем, что $\frac{1}{2}$ может быть значение синуса и/или косинуса только для углов первой четверти среди углов с градусной мерой 30, 45, 60). Так как $x = \frac{1}{2}$ и $y = \frac{\sqrt{3}}{2}$ также удовлетворяют $x^2 + y^2 = 1$ (дополнительных действий не требуется; просто переключите порядок сложения в предыдущем случае), а здесь $x < y$, это должны быть значения для 60 градусов.

 94KB
94KB 17KB
17KB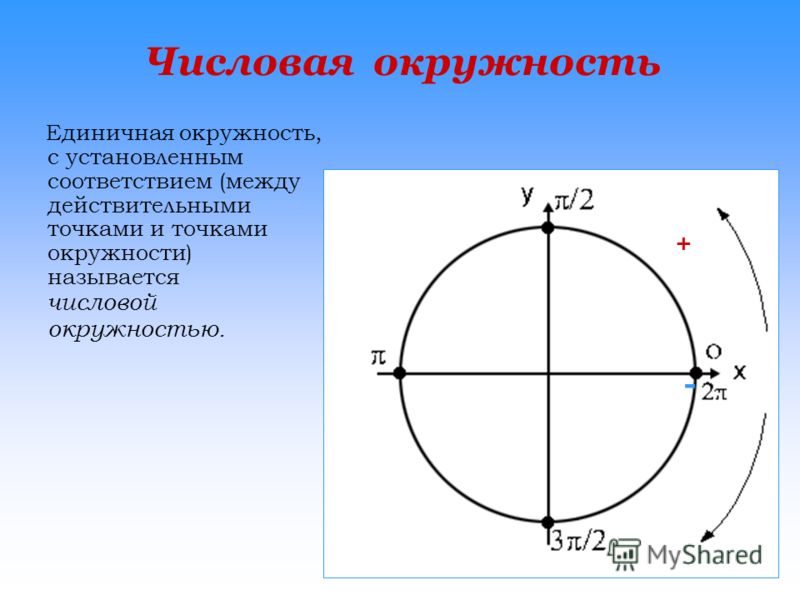 31KB
31KB 8KB
8KB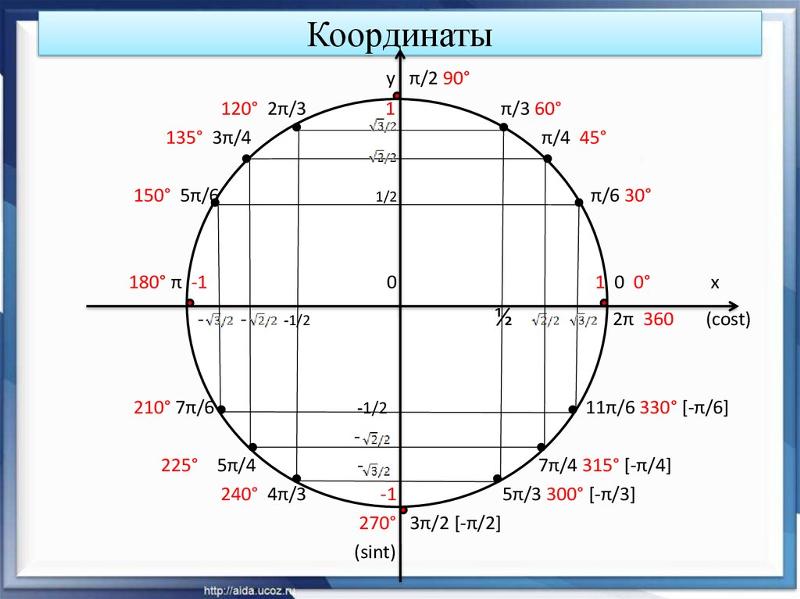
 71KB
71KB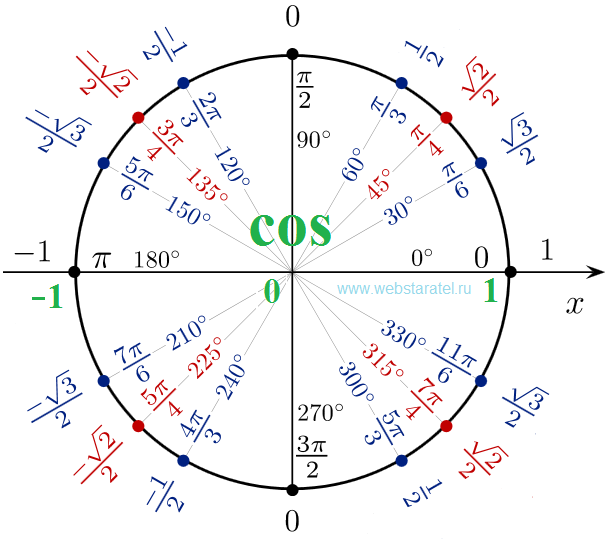
 org/contents/
org/contents/