Таблица истинности онлайн
Данный онлайн калькулятор строит таблицу истинности для любого логического выражения. Чтобы начать, введите логическое выражение в поле ввода.
Калькулятор таблицы истинности
Составить таблицу истинностилогического выражения:abcdУстановить калькулятор на свой сайт
Калькулятор поддерживает следующие логические операции:
Логическая операция «не» (отрицание, инверсия)
Данная операция обозначается символом
. Для её ввода в наш онлайн калькулятор можно использовать либо символ ¬, либо значок восклицательного знака !. Операция отрицания является унарной (содержит один операнд) и обладает наивысшим приоритетом (выполняется первой) среди логических операций.
Таблица истинности логической операции «не» имеет вид:
Логическое «и» (конъюнкция, логическое умножение)
Данная операция обозначается символом
.
Таблица истинности логической операции «и» имеет вид:
Логическое «или» (дизъюнкция, логическое сложение)
Данная операция обозначается символом
. Для её ввода в наш онлайн калькулятор можно использовать либо символ ∨, либо два значка ||. Операция дизъюнкция является бинарной.
Таблица истинности логической операции «или» имеет вид:
Логическая операция «исключающее или» (сложение по модулю 2)
Данная операция обозначается символом
. Для её ввода в наш онлайн калькулятор можно использовать либо символ ⊕, либо функцию
.
Таблица истинности логической операции «исключающее или» имеет вид:
Логическая операция «не и» (штрих Шеффера)
Данная операция обозначается символом
. Для её ввода в наш онлайн калькулятор можно использовать либо символ ↑, либо значок |.
Для её ввода в наш онлайн калькулятор можно использовать либо символ ↑, либо значок |.
Таблица истинности логической операции «не и» имеет вид:
Логическая операция «не или» (стрелка Пирса)
Данная операция обозначается символом
. Для её ввода в наш онлайн калькулятор можно использовать либо символ ↓, либо функцию
.
Таблица истинности логической операции «не или» имеет вид:
Логическая операция «эквивалентность»
Данная операция обозначается символом
. Для её ввода в наш онлайн калькулятор можно использовать либо символ ⇔, либо конструкцию (знак меньше, знак равно, знак больше).
Таблица истинности логической операции «эквивалентность» имеет вид:
Логическая операция «исключающее не или»
Данная операция обозначается символом
. Для её ввода в наш онлайн калькулятор можно использовать либо символ ⊙, либо функцию
.
Для её ввода в наш онлайн калькулятор можно использовать либо символ ⊙, либо функцию
.
Таблица истинности логической операции «исключающее не или» имеет вид:
Стоит отметить, что таблицы истинности для бинарных логических операций «эквивалентность» и «исключающее не или» совпадают. В случае, если указанные операции являются -арными, их таблицы истинности различаются. Отметим, что -арную операцию в наш калькулятор можно ввести только в виде соответствующей функции, например , и результат такого выражения будет отличаться от результата выражения . Потому что последнее интерпретируется как , в то время как в случае с — операция «эквивалентность» выполняется сразу с учетом всех аргументов.
Логическая операция «импликация»
Данная операция обозначается символом
. Для её ввода в наш онлайн калькулятор можно использовать либо символ ⇒, либо конструкцию => (знак равно, знак больше).
Для её ввода в наш онлайн калькулятор можно использовать либо символ ⇒, либо конструкцию => (знак равно, знак больше).
Таблица истинности логической операции «импликация» имеет вид:
При формировании таблицы истинности сложного (составного) логического выражения необходимо использовать представленные выше таблицы истинности соответствующих логических операций.
Другие полезные разделы:
Оставить свой комментарий:
2 — Таблицы истинности логической функции
1. Логическая функция Fзадаётся выражением F = (¬z) ∧ x ∨ x ∧ y. Определите, какому столбцу таблицы истинности функции Fсоответствует каждая из переменных x, y, z? В ответе напишите буквы x, y, z без пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
2. Логическая функция Fзадаётся выражением F = a ∧ b ∨ a ∧ (¬c). Определите, какому столбцу таблицы истинности функции Fсоответствует каждая из переменных a, b, c? В ответе напишите буквы a, b, cбез пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
3. Логическая функция Fзадаётся выражением F = ¬x ∧ y ∧ z ∨ ¬x ∧ ¬z. На рисунке приведены все строки таблицы истинности, в которых функция равна 1. , y, z? В ответе напишите буквы x, y, zбез пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
4. Логическая функция Fзадаётся выражением F = x ∧ (y ∧ z ∨ y ∧ ¬w ∨ ¬w ∧ ¬z). На рисунке приведены все строки таблицы истинности, в которых функция равна 1. Определите, какому столбцу соответствует каждая из переменных x, y, z, w? В ответе напишите буквы x, y, z, w без пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
5. Логическая функция Fзадаётся выражением F = (¬x ∨ y ∨ z) ∧ (¬x ∨ ¬z). На рисунке приведены все строки таблицы истинности, в которых функция равна 0. Определите, какому столбцу соответствует каждая из переменных x, y, z? В ответе напишите буквы x, y, zбез пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
6. Логическая функция Fзадаётся выражением F = (¬x ∨ z) ∧ (¬x ∨ ¬y ∨ ¬z). На рисунке приведены все строки таблицы истинности, в которых функция равна 0. , y, z? В ответе напишите буквы x, y, zбез пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
7. Логическая функция Fзадаётся выражением F = x ∨ ¬w ∨ y ∧ ¬z. На рисунке приведены все строки таблицы истинности, в которых функция равна 0. Определите, какому столбцу соответствует каждая из переменных x, y, z, w? В ответе напишите буквы x, y, z, w без пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
8. Логическая функция Fзадаётся выражением F = x ∨ (¬y ∨ z ∨ ¬w) ∧ (y ∨ ¬z). На рисунке приведены все строки таблицы истинности, в которых функция равна 0. Определите, какому столбцу соответствует каждая из переменных x, y, z, w? В ответе напишите буквы x, y, z, wбез пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
9. Логическая функция Fзадаётся выражением F = ¬x ∨ ¬y ∧ ¬z ∨ ¬z ∧ ¬w ∨ ¬y ∧ w. На рисунке приведены все строки таблицы истинности, в которых функция равна 0. Определите, какому столбцу соответствует каждая из переменных x, y, z, w? В ответе напишите буквы x, y, z, wбез пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
10. Логическая функция Fзадаётся выражением F = ¬x ∨ y ∧ z ∨ y ∧ ¬w ∨ ¬z ∧ ¬w. На рисунке приведены все строки таблицы истинности, в которых функция равна 0. Определите, какому столбцу соответствует каждая из переменных x, y, z, w? В ответе напишите буквы x, y, z, w без пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
Построение таблиц истинности — презентация онлайн
Похожие презентации:
Элементы алгебры логики. Математические основы информатики. (8 класс)
Элементы алгебры логики. Математические основы информатики
Элементы алгебры логики. Математические основы информатики
Элементы алгебры логики математические основы информатики
Элементы алгебры логики. Математические основы информатики. 9 класс
Алгоритм решения задач средствами алгебры логики
Элементы алгебры логики. Математические основы информатики
Элементы алгебры логики. Математические основы информатики
Элементы алгебры логики. Математические основы информатики. Логические задачи
Элементы алгебры логики. Математические основы информатики
ЭЛЕМЕНТЫ
АЛГЕБРЫ ЛОГИКИ
Построение таблиц
истинности
Построение таблиц истинности для
логических выражений
подсчитать n — число переменных в выражении
подсчитать общее число логических операций в выражении
установить последовательность выполнения логических операций
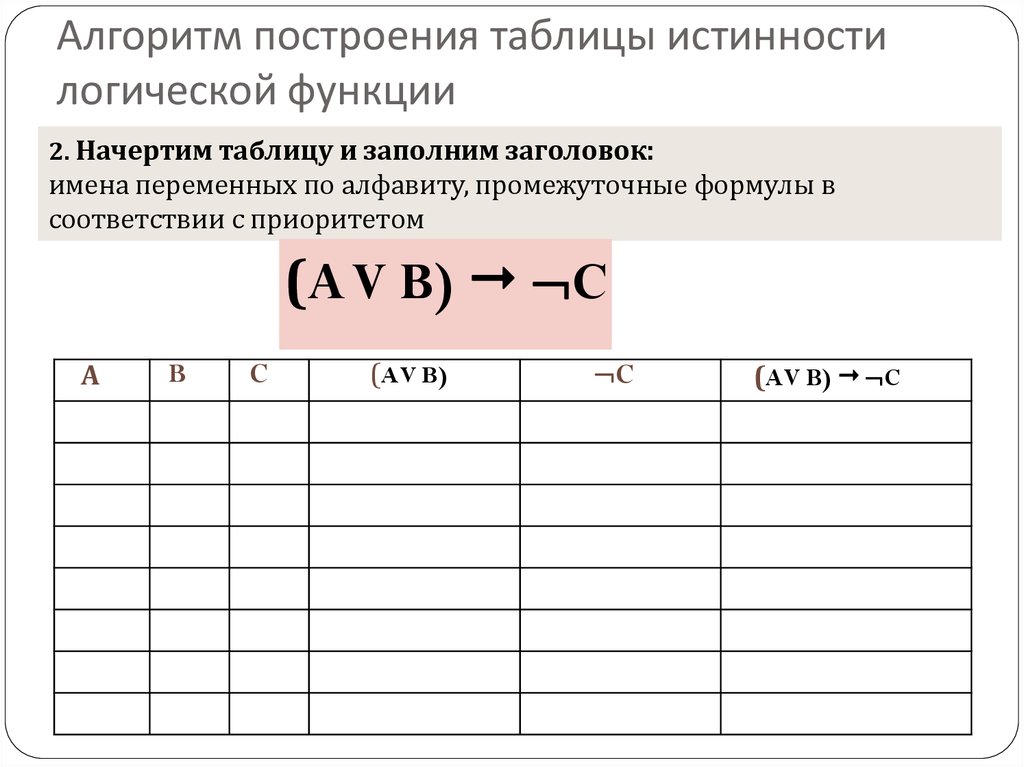
заполнить шапку таблицы, включив в неё переменные и операции
определить число строк в таблице без шапки: m =2n
выписать наборы входных переменных
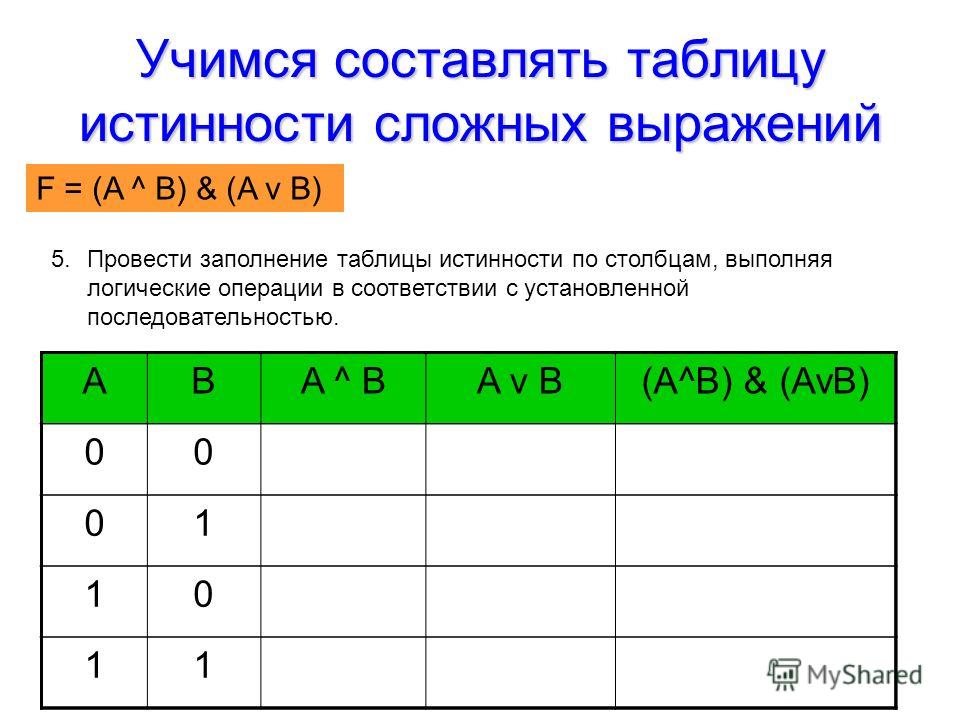
провести заполнение таблицы по столбцам, выполняя логические
операции в соответствии с установленной последовательностью
Решение задач
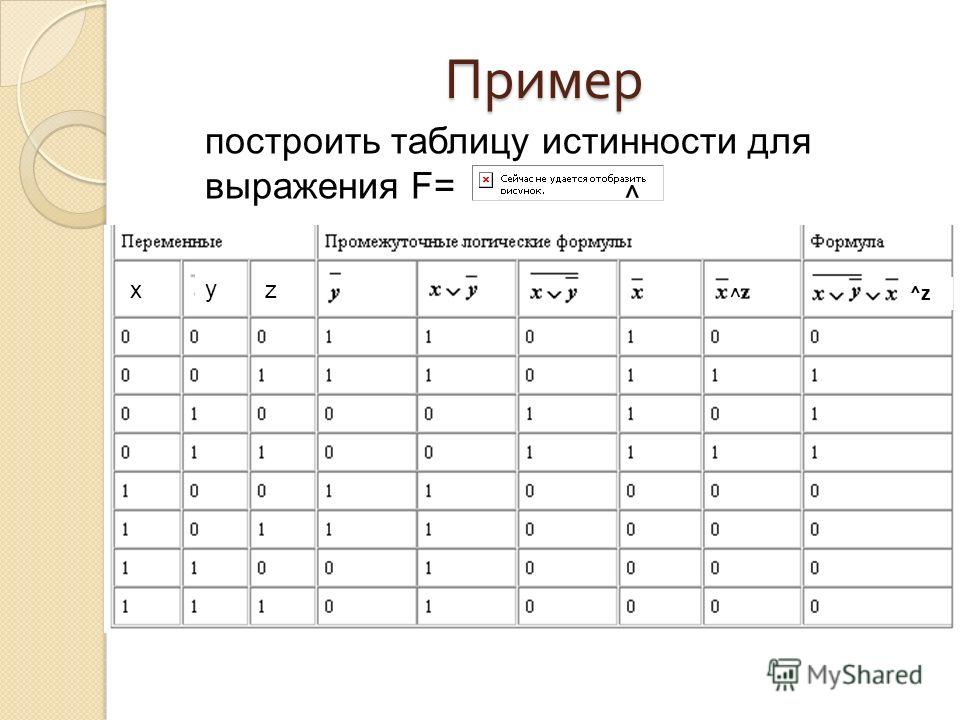
Составить таблицу истинности для формулы
F ( A, B) ( A B) ( A В)
А
В
A B
0
0
0
0
1
1
1
0
1
1
1
1
A
A В
F
Решение задач
Составить таблицу истинности для формулы
F ( A, B) ( A B) ( A В)
А
В
A B
A
0
0
0
1
0
1
1
1
1
0
1
0
1
1
1
0
A В
F
Решение задач
Составить таблицу истинности для формулы
F ( A, B) ( A B) ( A В)
А
В
A B
A
A В
0
0
0
1
1
0
1
1
1
1
1
0
1
0
0
1
1
0
1
F
Решение задач
Составить таблицу истинности для формулы
F ( A, B) ( A B) ( A В)
А
В
A B
A
A В
F
0
0
0
1
1
0
0
1
1
1
1
1
1
0
1
0
0
0
1
1
1
0
1
1
Свойства логических
операций
Логические законы и тождества
Тождества
Логического сложения
Логического умножения
1) А v 0 = А
1) А 0 = 0
2) А v 1 = 1
2) А 1 = А
3) А v А = А
3) А А = А
4) А v А = 1
4) А А = 0
Логические законы и тождества
Законы
1) А=А (Закон тождества)
2) А ( A B)=А (Закон поглощения)
Задание: доказать справедливость данного
закона (раскрыть скобки с помощью законов
распределения и повторения)
3) А (A B)=А (Закон поглощения)
Задание: доказать справедливость данного
закона (раскрыть скобки с помощью законов
распределения и повторения)
Доказательство закона с помощью таблицы
истинности
Распределительный закон для логического сложения:
A v (B & C) = (A v B) & (A v C).

A
B
C
0
B&C
0
A v (B & C)
0
0
0
0
0
1
0
0
0
1
0
0
1
1
0
1
0
1
1
0
0
0
1
0
1
1
1
0
1
1
1
0
0
1
AvB
0
1
0
1
0
1
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
1
A v C (A v B) & (A v C)
0
0
Умножаем
Складываем
Умножаем
Равенство
(АvB)
ВА
наиСC
В
(В&С)
навыделенных
ии(AvC
выводим
выводим
и выводим
)и выводим
результат.
результат.
результат.
столбцов
результат.
распределительный закон.
1
1
доказывает
Решение логических
Решение логических задач
Задача. Коля, Вася и Серёжа гостили летом у бабушки.
Однажды один из мальчиков нечаянно разбил любимую
бабушкину вазу.
На вопрос, кто разбил вазу, они дали такие ответы:
Серёжа: 1) Я не разбивал.
 2) Вася не разбивал.
2) Вася не разбивал.Вася: 3) Серёжа не разбивал. 4) Вазу разбил Коля.
Коля: 5) Я не разбивал. 6) Вазу разбил Серёжа.
Бабушка знала, что один из её
внуков (правдивый), оба раза сказал
правду; второй (шутник) оба раза
сказал неправду; третий (хитрец) один
раз сказал правду, а другой раз неправду. Назовите имена правдивого,
шутника и хитреца.
Кто из внуков разбил вазу?
Решение. Пусть К =«Коля разбил вазу»,
В =«Вася разбил вазу»,
С =«Серёжа разбил вазу».
Представим в таблице истинности высказывания каждого
мальчика. Так как ваза разбита одним внуком, составим не
всю таблицу, а только её фрагмент, содержащий наборы
входных переменных: 001, 010, 100.
K
B
C
Утверждение
Серёжи
С
0
0
1
0
1
0
1
0
0
В
Утверждение
Васи
С
K
Утверждение
Коли
К
C
Решение. Пусть К =«Коля разбил вазу»,
В =«Вася разбил вазу»,
С =«Серёжа разбил вазу».
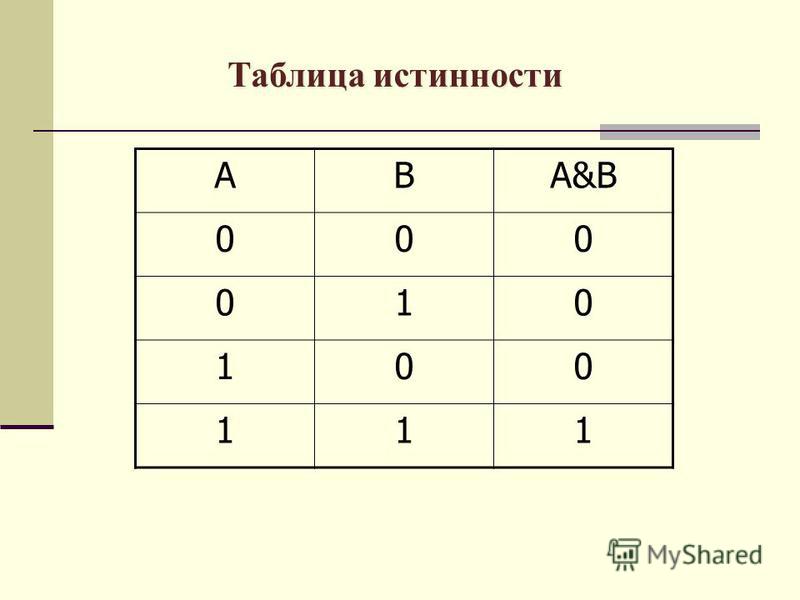
Представим в таблице истинности высказывания каждого
мальчика. Так как ваза разбита одним внуком, составим не
всю таблицу, а только её фрагмент, содержащий наборы
входных переменных: 001, 010, 100.
K
B
C
Утверждение
Серёжи
С
В
0
0
1
0
1
0
1
0
1
0
1
0
0
1
1
Утверждение
Васи
С
K
Утверждение
Коли
К
C
Решение. Пусть К =«Коля разбил вазу»,
В =«Вася разбил вазу»,
С =«Серёжа разбил вазу».
Представим в таблице истинности высказывания каждого
всю таблицу, а только её фрагмент, содержащий наборы
входных переменных: 001, 010, 100.
K
B
C
Утверждение
Серёжи
Утверждение
Васи
С
В
С
K
0
0
1
0
1
0
0
0
1
0
1
0
1
0
1
0
0
1
1
1
1
Утверждение
Коли
К
C
Решение.
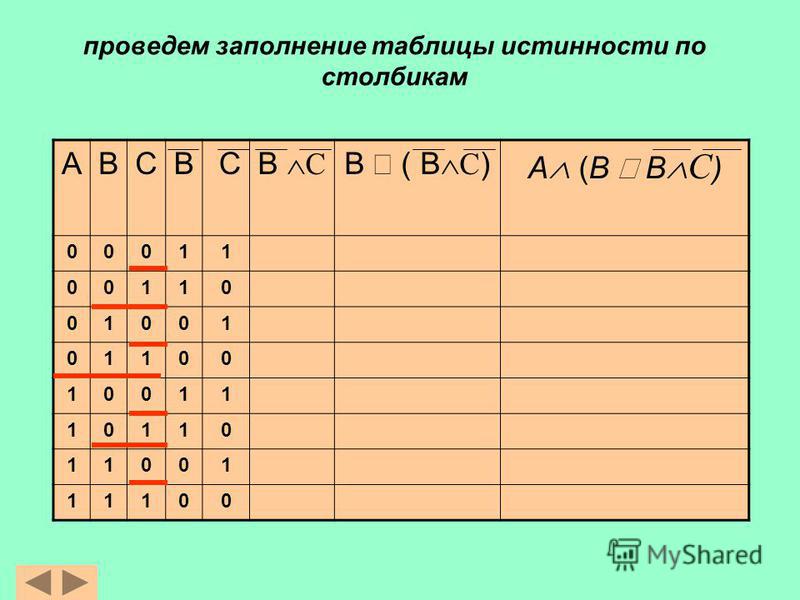 Пусть К =«Коля разбил вазу»,
Пусть К =«Коля разбил вазу»,В =«Вася разбил вазу»,
С =«Серёжа разбил вазу».
Представим в таблице истинности высказывания каждого
мальчика. Так как ваза разбита одним внуком, составим не
всю таблицу, а только её фрагмент, содержащий наборы
входных переменных: 001, 010, 100.
K
B
C
Утверждение
Серёжи
Утверждение
Васи
Утверждение
Коли
С
В
С
K
К
C
0
0
1
0
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
0
1
1
1
1
0
0
Исходя из того, что знает о внуках бабушка, следует искать
в таблице строки, содержащие в каком-либо порядке три
комбинации значений: 00, 11, 01 (или 10). Это первая строка.
Вазу разбил Серёжа, он — хитрец. Шутником оказался Вася.
Имя правдивого внука — Коля.
Логические элементы
Логические элементы
Логический элемент – устройство, которое после
обработки двоичных сигналов выдаёт значение одной из
логических операций.

А
&
В
И (конъюнктор)
А
1
В
ИЛИ
(дизъюнктор)
А
НЕ (инвертор)
Опорный конспект
Высказывание – это предложение на любом языке, содержание которого
можно однозначно определить как истинное или ложное.
Основные логические
операции
Инверсия
Конъюнкция
Дизъюнкция
А
Ā
A
B
A&B
A
B
AVB
0
1
0
0
0
0
0
0
1
0
0
1
0
0
1
1
1
0
0
1
0
1
1
1
1
1
1
1
Приоритет выполнения логических операций: ¬, &, V.
English Русский Правила
Калькулятор таблицы истинности / Генератор
Запишите логическую формулу, и калькулятор мгновенно вычислит для нее значения таблицы истинности с помощью показанных шагов.
Введите уравнение
| Символы | |
| Отрицание | ~ |
| Соединение (И) | и |
| Разделение (OR) | против |
| Условный | -> |
| Биусловный | <-> |
| Шеффер Инсульт | | |
| Абсурд | # |
РЕКЛАМА
Содержание
| 1 | Что такое дощатый фут в пиломатериалах (BF)? |
| 2 | Бортовой фут Формула: |
| 3 | Подставка для досок Единицы: |
| 4 | Важно Толщина: |
| 5 | Как рассчитать доски? |
| 6 | Что вы подразумеваете под термином «Измерение поверхности»? |
| 7 | Что подразумевается под номинальным размером? |
| 8 | Как вы определяете линейное измерение? |
Получите виджет!
Добавьте этот калькулятор на свой сайт, чтобы пользователи могли выполнять простые расчеты.
Получить код
Обратная связь
Насколько легко было пользоваться нашим калькулятором? Сталкивались ли вы с какой-либо проблемой, сообщите нам!
ОБРАТНАЯ СВЯЗЬ
Онлайн-калькулятор таблицы истинности предоставит значения таблицы истинности для заданных формул логической логики. Утверждения пропозициональной логики могут быть только истинными или ложными.
Многие операторы могут быть объединены логическими связями для формирования новых операторов. Решатель таблицы истинности генерирует все комбинации истинных и ложных утверждений и вычисляет соответствующее истинностное содержание логического выражения.
Что такое таблица истинности? Таблица истинности представляет собой табличное представление всех комбинаций значений для входов и соответствующих им выходов. Это математическая таблица, в которой показаны все возможные результаты, которые могут возникнуть во всех возможных сценариях. Он используется для логических задач, таких как логическая алгебра и электронные схемы.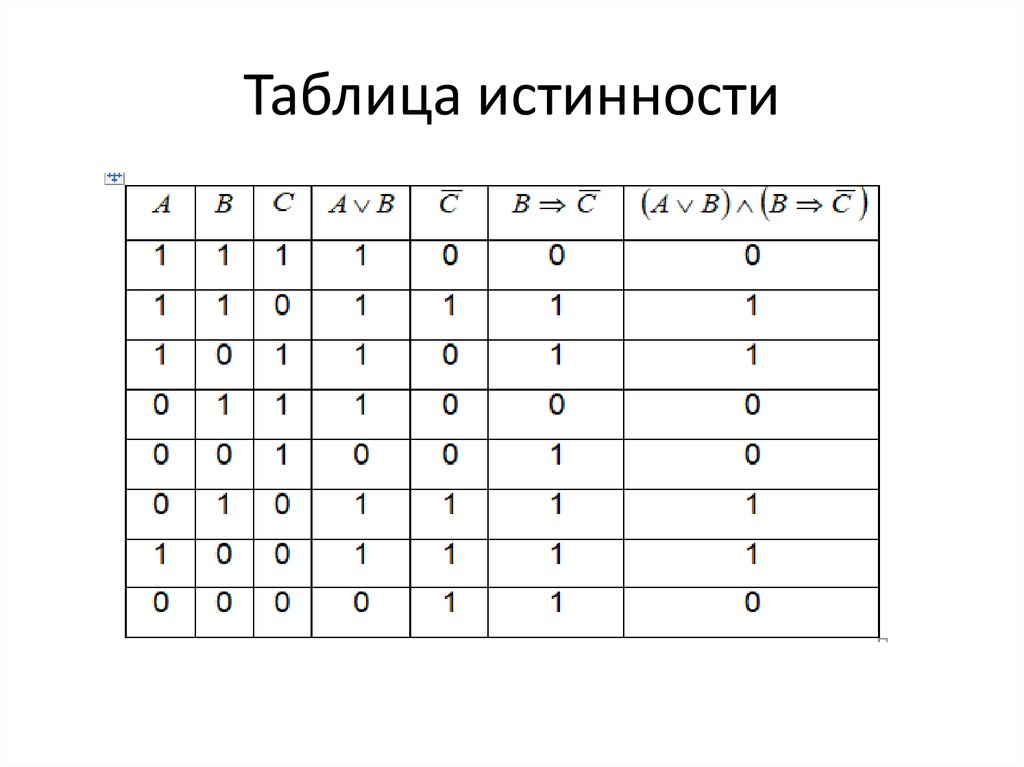
Предложение — это набор декларативных утверждений со значением истинности «истина» или значением истинности «ложь». Пропозициональные выражения состоят из связок и пропозициональных переменных. Мы используем заглавные буквы для обозначения пропозициональных переменных (A, B). Связки соединяют пропозициональные переменные.
Как составить таблицу истинности?Связки:
В калькуляторе таблицы истинности логики высказываний используются различные связки, а именно −
- ИЛИ (∨)
- И (∧)
- Отрицание/ НЕ (¬)
- Импликация / если-то (→)
- Если и только если (⇔)
- Абсурд (#)
- Инсульт Шеффера (|)
Два утверждения A и B логически эквивалентны, если выполняется любое из следующих двух условий –
- Биусловное утверждение A⇔B является тавтологией.

- Таблицы истинности каждого утверждения имеют одни и те же переменные истинности.
Пример:
Докажите, что ~(P ∨ Q) и [(~P) ∧ (~Q)] эквивалентны
Решение:
Калькулятор таблиц истинности выполняет тестирование методом сопоставления таблиц истинности
3
Здесь мы видим, что значения истинности ~(P ∨ Q) и [(~P) ∧ (~Q)] одинаковы, следовательно, все утверждения эквивалентны.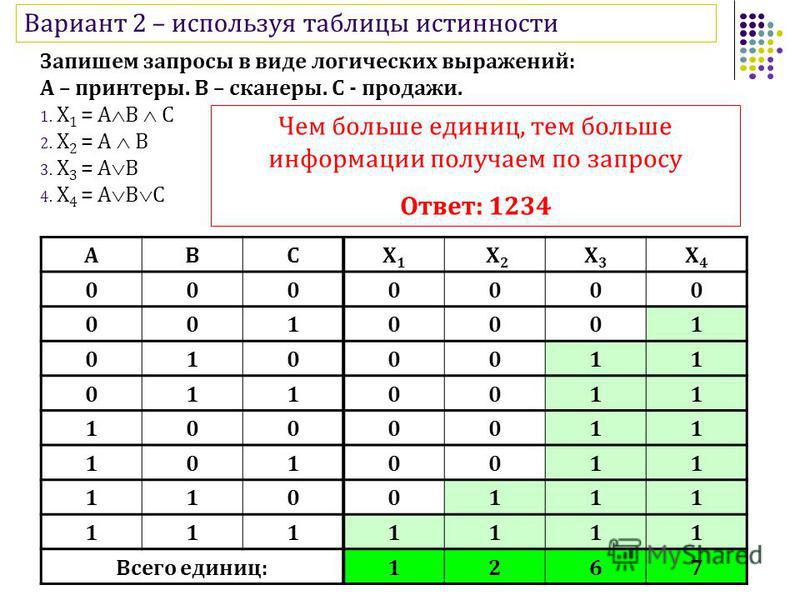
Онлайн-генератор таблицы истинности предоставляет подробную таблицу истинности, выполнив следующие шаги:
Ввод:- Сначала введите логическое уравнение с символами.
- Нажмите кнопку расчета для получения результатов.
- Наш калькулятор построит таблицу истинности для 4-х переменных данного выражения.
Используйте этот онлайн-генератор таблиц истинности для создания таблиц истинности многомерной логики высказываний. Логика высказываний имеет дело с утверждениями, которые могут быть значениями истинности, «истинными» и «ложными». Цель состоит в том, чтобы проанализировать эти утверждения по отдельности или вместе.
Артикул: Из источника Википедии: Унарные операции, Логическая истина, Логическая ложь, Логическое тождество, Логическое отрицание, Бинарные операции, Логическая конъюнкция (И), Логическая дизъюнкция (ИЛИ), Логическая импликация.
Генератор таблиц истинности онлайн для студентов колледжа — Полная помощь по заданию
У вас есть какие-либо опасения по поводу решения таблицы истинности для логических вентилей, исчисления высказываний или булевой алгебры? Если да, используйте наш генератор таблиц истинности . Студенты со всего мира и из каждого университета по всему миру используют наш генератор таблиц истинности для получения точных результатов и экономии времени. Если эта концепция таблицы истинности для вас является чем-то новым, прочитайте эту статью, чтобы понять, о чем эта таблица и как работает генератор таблиц истинности ABC.
Переменные (разделенные запятыми)
Выражения (разделенные запятыми)
Таблица истинности показывает, как истинность и ложность сложносочиненного предложения зависят от истинности и ложности ясного предложения, из которого оно получено. В таблице есть столбец для всех входных переменных, обычно представленных как P и Q, a и b или x и y.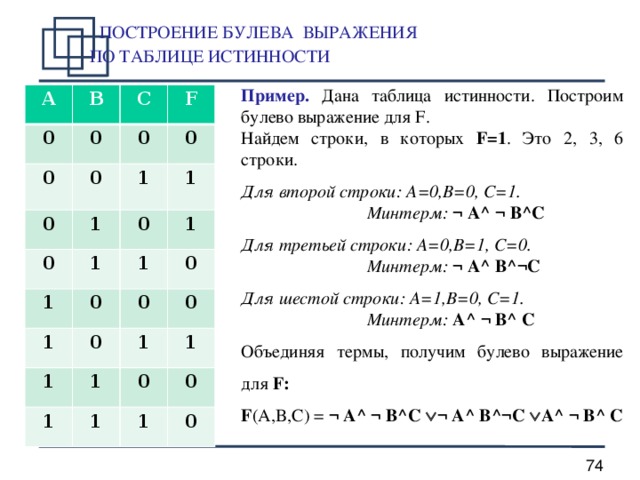 В другом столбце представлены все результаты логических операций, как А и Б. Все строки таблицы содержат возможную конфигурацию вставленных в них переменных и результат операции для вставленных значений.
В другом столбце представлены все результаты логических операций, как А и Б. Все строки таблицы содержат возможную конфигурацию вставленных в них переменных и результат операции для вставленных значений.
Если вы новичок и ничего не знаете о таблицах истинности, то генератор таблиц истинности с TotalAssignmentHelp.com может показаться просто еще одним приложением, в котором вы вставляете символы и показываете несколько случайных предложений. Но не беспокойся; статья расскажет вам о таблице и о том, как использовать генератор логических вентилей из таблицы истинности.
Прочитав приведенные выше указатели, вы поймете, что использовать наш генератор таблиц истинности ABC легко. Когда вы поймете каждый из операторов, вы сможете ввести любую переменную и работать с ней без помощи друзей или членов семьи.
Плата за использование генератора таблиц истинности для решения операций AND, XOR или NOR не взимается. Вы можете самостоятельно управлять инструментом, не нанимая услуги эксперта, связанного с TotalAssignmentHelp.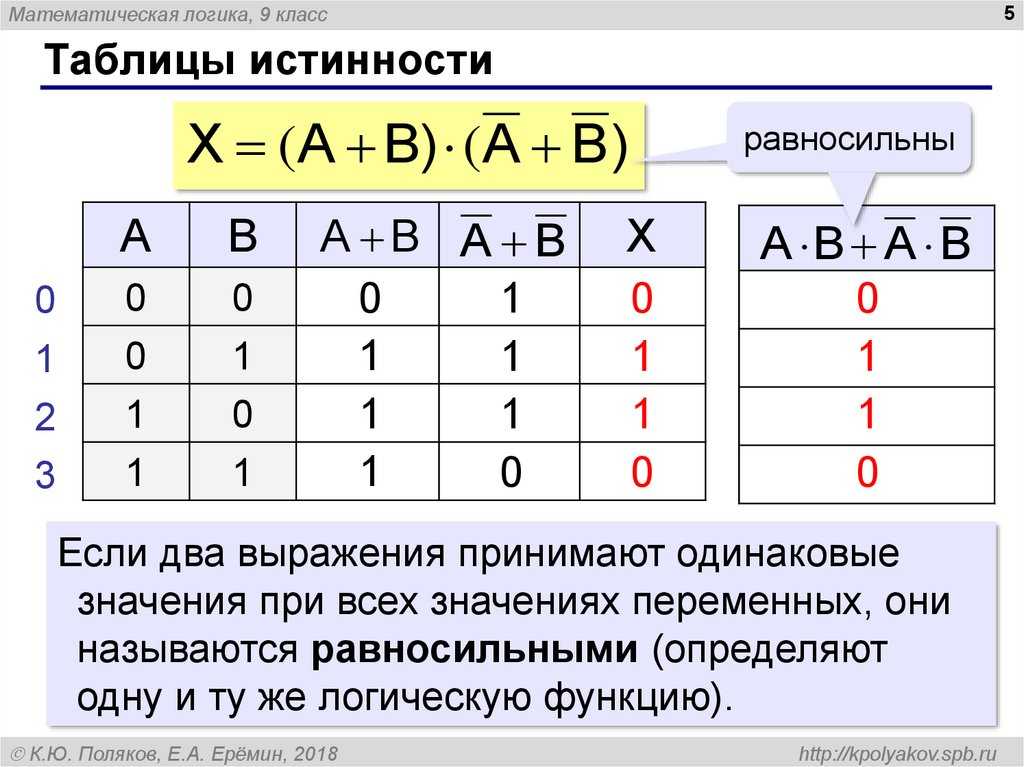 com, или вкладывать деньги в найм услуг любого другого онлайн-инструмента. Генератор таблицы истинности логических вентилей обладает следующими качествами:
com, или вкладывать деньги в найм услуг любого другого онлайн-инструмента. Генератор таблицы истинности логических вентилей обладает следующими качествами:
Использование без каких-либо ограничений : Нет условий, связанных с использованием генератора таблицы истинности для логических вентилей. Генератор можно использовать любое количество раз, не ограничивая частоту его использования. Задачи, связанные с булевой алгеброй или исчислением высказываний, можно быстро решить с помощью генератор таблицы истинности от TotalAssignmentHelp.com.
Современный алгоритм : мы использовали современный алгоритм глубокого обучения при разработке генератора логической схемы на основе таблицы истинности. Обновленные функции стола помогают работать лучше при каждом использовании. Это, в свою очередь, позволяет получать 100-процентно точные результаты при каждом использовании. Итак, зачем ждать, чтобы использовать наш генератор таблиц истинности для решения всех задач на основе таблиц.
Круглосуточная поддержка службы поддержки клиентов : Если вы столкнулись с какой-либо ошибкой при использовании нашего генератора таблиц истинности, вы можете связаться с нашим отделом обслуживания клиентов, который остается онлайн весь день. Если вы не можете связаться с нами по телефону или в сообщениях, вы можете зайти в онлайн-режим на нашем веб-сайте и пообщаться с нами, или вы даже можете отправить электронное письмо на наш идентификатор с указанием ошибок, с которыми вы столкнулись при работе с инструментом.
Генератор логических таблиц истинности может решить все проблемы, связанные с И-НЕ, бинарными логическими операторами, вентилями НЕ-ИЛИ и т.д. Кроме того, за использование таблицы с вашего кармана не возьмут денег.
Способен ли генератор таблицы истинности пропозициональной логики давать быстрые результаты? У вас есть задание, связанное с булевой алгеброй или цифровой электроникой, которое нужно срочно сдать? Если да, вы можете использовать наш генератор таблиц истинности логики высказываний для получения ответов на все задачи независимо от крайнего срока. Вы получите точный результат, не тратя время на каждое использование. Генератор таблиц истинности дискретных математических функций имеет следующие особенности:
Вы получите точный результат, не тратя время на каждое использование. Генератор таблиц истинности дискретных математических функций имеет следующие особенности:
Может работать с любого устройства : Страница, связанная с генератором таблиц истинности, может быть открыта на любой платформе, будь то телефон, планшет, настольный компьютер или ноутбук. Инструмент был создан для совместимости с платформами IOS, Windows и Android. Таким образом, вам не требуется приобретать какое-либо конкретное устройство для открытия или запуска результатов при использовании нашего генератора таблиц истинности.
Его можно использовать в любое время : Как уже говорилось ранее, использование услуг генератора таблиц истинности логики высказываний не требует никаких скрытых затрат. Плата за подписку не взимается, и инструмент можно использовать в любое время дня. Его можно использовать из любого места, и единственным требованием является устройство и стабильное подключение к Интернету.
Быстрый результат : Как только вы поместите формулу или задачу в таблицу, вы сможете быстро получить результат. Генератор таблицы истинности пропозициональной логики быстро генерирует результаты. Если у вас есть готовый оператор или выражение для ввода в инструмент, вы увидите, что генератор отразит результаты в течение нескольких секунд.
Итак, не тратя время на поиск других генераторов таблиц истинности онлайн , воспользуйтесь услугами TotalAssignmentHelp.com.
Ограничены ли услуги TotalAssignmentHelp.com генераторами таблиц истинности? Нет, наши услуги не ограничиваются набором инструментов. Эти услуги являются дополнительными услугами, которые мы предоставляем вместе с услугами по написанию. Наша основная цель — удовлетворить потребности студентов в академическом письме, включая написание заданий, отчеты, эссе, диссертации, домашние задания и т. д. У нас есть группа экспертов из разных академических областей, которые предоставляют безупречные услуги по написанию работ для студентов. Например, если у вас есть набор вопросов, связанных с логикой высказываний или булевой алгеброй, которые требуют некоторого объяснения, вы можете воспользоваться нашими услугами академического письма.
Например, если у вас есть набор вопросов, связанных с логикой высказываний или булевой алгеброй, которые требуют некоторого объяснения, вы можете воспользоваться нашими услугами академического письма.
Эксперты, которых мы наняли для решения ваших академических проблем, обладают высокой квалификацией и хорошо разбираются в своих дисциплинах, включая таблицу истинности, выражения, операторы и т. д. Таким образом, использование наших услуг принесет вам следующие преимущества:
Выполнение заданий в срок : Когда эксперта просят ответить на логический вопрос или вопрос, связанный с условными воротами, он использует правильную логику для ответа на все вопросы, независимо от их сложности. Они гарантируют подачу задания вовремя, чтобы представить его без каких-либо предпоследних при опоздании. Но если у вас мало времени и вы не можете разместить запрос на задание, используйте наш генератор таблиц истинности для проверки ответов.
Помощь в рамках вашего бюджета : Наши услуги недороги, и каждый студент может выбрать сумму из своего кармана.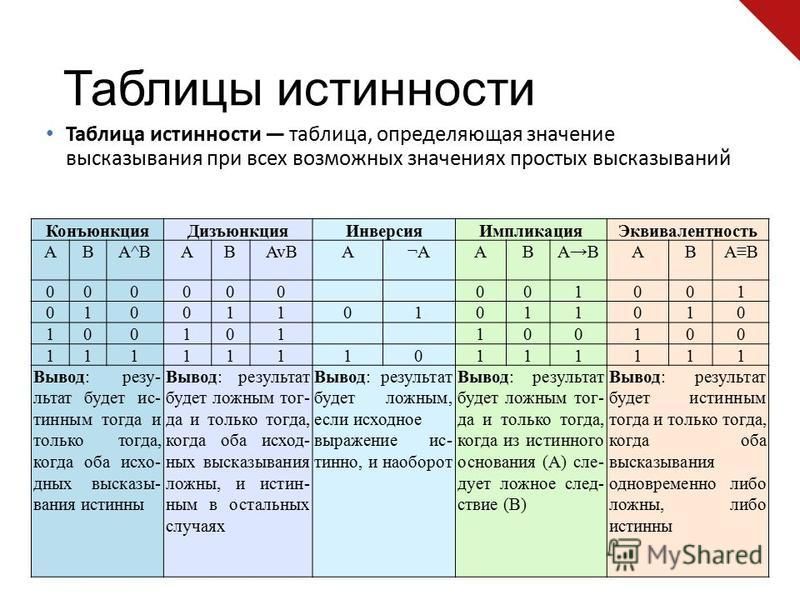 Бюджетные задания не ограничиваются набором конкретных студентов; вместо этого они доступны для всех студентов со всего мира. Наряду с низкими ценами на выполнение заданий, мы предоставляем значительные скидки студентам, оформившим у нас оптовые заказы, первокурсникам, реферальные бонусы и т. д. Мы также проверяем все задания на плагиат и их качество после сдачи экспертом. , и эти услуги бесплатны.
Бюджетные задания не ограничиваются набором конкретных студентов; вместо этого они доступны для всех студентов со всего мира. Наряду с низкими ценами на выполнение заданий, мы предоставляем значительные скидки студентам, оформившим у нас оптовые заказы, первокурсникам, реферальные бонусы и т. д. Мы также проверяем все задания на плагиат и их качество после сдачи экспертом. , и эти услуги бесплатны.
Неограниченное количество правок : После получения задания, если учащийся считает, что оно не на должном уровне, он всегда может попросить внести изменения на основе своих входных данных. Если вы считаете, что решить ваши задачи с помощью генератора таблиц истинности невозможно, вы всегда можете обратиться к нам за услугами по написанию заданий. После того, как задание выполнено, вносимые нами исправления не подлежат оплате. Мы рассматриваем запросы на доработку как возможность выполнить качественную работу, исправив ранее допущенные ошибки. Для авторов это полезный опыт, позволяющий избежать таких ошибок в будущих задачах.
Бесплатный доступ к образцам : Мы подготовили набор образцов, относящихся к разным темам и дисциплинам. Если студент застрял при решении каких-либо проблемных вопросов, он может проверить наши бесплатные образцы, доступные на нашем веб-сайте. Образцов много, и вы можете отсортировать их по своему усмотрению. Например, у нас есть образцы, связанные с темами управления, техническими описаниями, обзорами литературы, задачами по программированию, таблицами истинности, операциями P и Q и т. д.
Работа без плагиата : Задания, которые мы делаем, или проблемы, которые мы решаем, не содержат плагиата. Мы с гордостью можем сказать, что наши специалисты могут выполнять работу без плагиата, даже если они работают над несколькими задачами одновременно. Нелегко выполнить задачу без плагиата, но наши специалисты всегда старались предоставить оригинальный контент. Подлинность содержания в заданиях оценивается с помощью различных программ для проверки на плагиат, таких как Turn-it-in и Grammarly.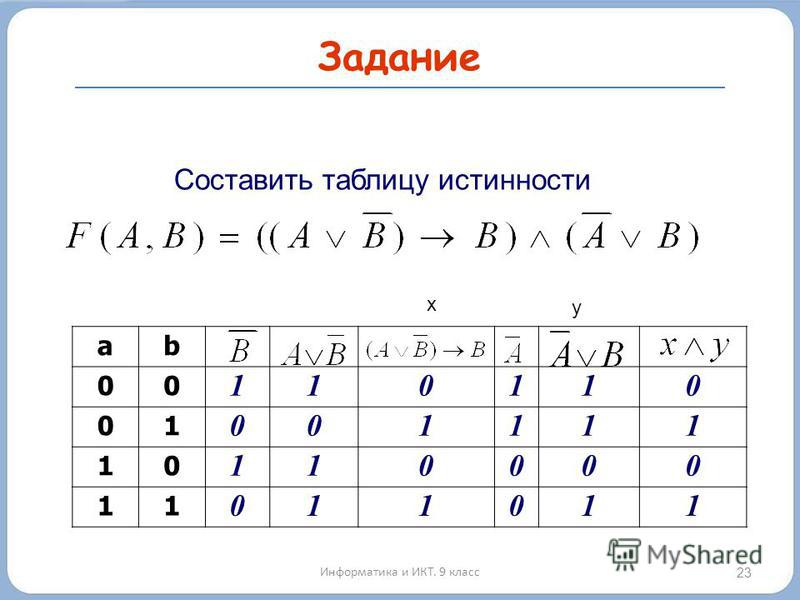 com.
com.
Поддержание качества : Если вы обращаетесь за помощью к письменному онлайн-сайту для написания своего задания и не получаете качественного обслуживания, то такая помощь бесполезна. Мы думаем, что было бы лучше написать свои задания, а не помощь от низкопробных поставщиков услуг. О нашем качестве можно судить по отзывам, опубликованным разными студентами, и по чтению содержания наших образцов работ на нашем веб-сайте. Поддержание качества является приоритетом, который наша внутренняя команда по контролю качества тщательно проверяет перед тем, как передать какое-либо задание учащемуся.
Поэтому, если вы хотите получить полные оценки за оставшиеся задания, воспользуйтесь нашей помощью прямо сейчас.
Заказать сейчас
Заказать сейчас
Популярные вопросы, которые ищут в Интернете Что такое генератор таблиц истинности? Генератор таблиц истинности используется для построения таблицы истинности для формулы пропозициональной логики. Логические операторы могут быть вставлены в таблицу в различных форматах. Единственное, что необходимо сделать, это выбрать оператора и ввести свое требование. Наконец, введите выражение и получите нужную таблицу из инструмента.
Логические операторы могут быть вставлены в таблицу в различных форматах. Единственное, что необходимо сделать, это выбрать оператора и ввести свое требование. Наконец, введите выражение и получите нужную таблицу из инструмента.
Чтобы решить логическое выражение, вам необходимо выполнить следующие шаги:
Какое значение имеют P и Q в таблице истинности? P и Q — это связки, используемые в таблице истинности для отображения составных предложений. Отрицание представлено как «¬p», что означает «не p», а союз представлен как «p ∧ q», что означает «p и q». Дизъюнкция представлена как «p ∨ q», что означает «p или q или оба». Исключающее ИЛИ представляется как «p ⊕ q», что означает «либо p, либо q, но не оба». Импликация представлена как «p → q», что означает «если p, то q». Бикондиционал представлен как «p ↔ q», что означает «p тогда и только тогда, когда q».
(∨) на самом деле таблица представляет собой клин, представляющий слово, которое соединяет два дизъюнкта с выражением «или» в качестве наиболее знакомого примера. Другими словами, включающее «или» означает истинную природу одного из дизъюнктов, тогда как исключающее «или» означает, что одно дизъюнктное является истинным, но не оба.
Применимы ли таблицы истинности в реальных сценариях?Таблица истинности в математике используется для определения истинности сложного утверждения. Возможно, вам не потребуется ежедневно составлять таблицу истинности, но важно применять логику таблицы, чтобы установить, является ли утверждение истинным или ложным. Возьмите, например. это можно обосновать с помощью таблицы истинности, что «если я выиграю, я перейду на следующий уровень».
Что в логике означают P и Q? Если значение истинности утверждения одинаково, то можно сказать, что предложение идентично или логически похоже.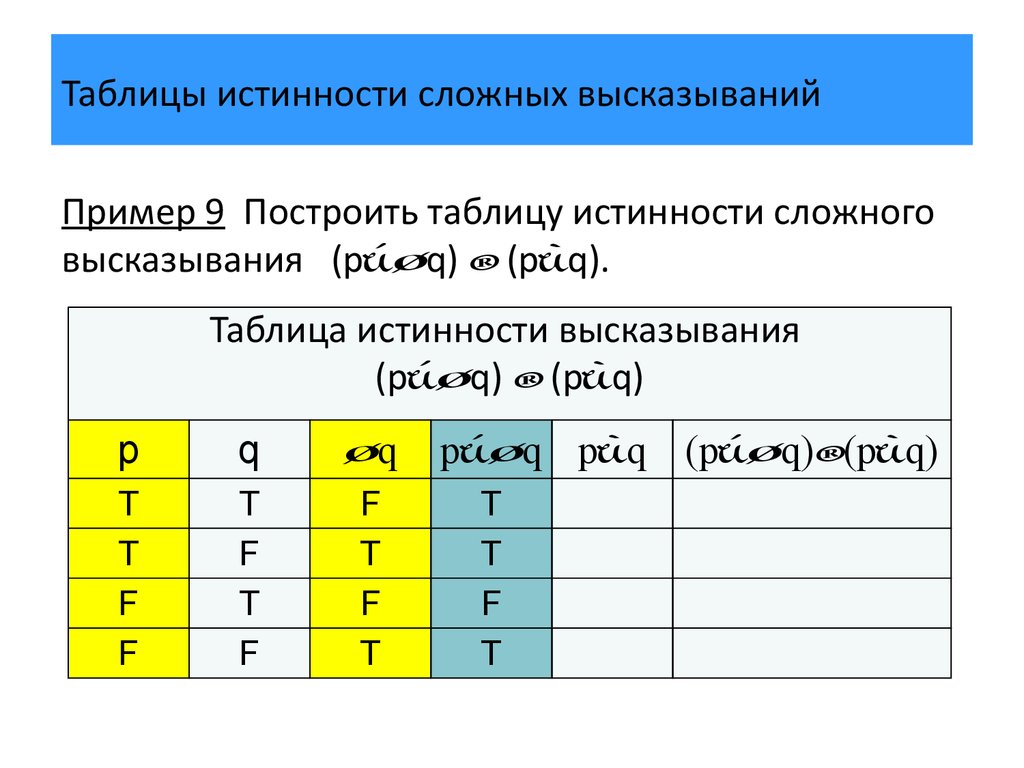 Следовательно, p считается истинным, если q истинно, и наоборот. P считается ложным, если q ложно, и наоборот. Следовательно, можно сказать, что p и q логически эквивалентны. Подводя итог, можно сказать, что p = q, если p и q логически равны.
Следовательно, p считается истинным, если q истинно, и наоборот. P считается ложным, если q ложно, и наоборот. Следовательно, можно сказать, что p и q логически эквивалентны. Подводя итог, можно сказать, что p = q, если p и q логически равны.
Пять символов логических операторов: точка, клин, тильда, тройная черта и подкова. Используйте наш генератор таблиц истинности для решения математических задач.
Генератор таблиц истинности — Мгновенное создание логических таблиц истинности
Генератор таблиц истинности — Мгновенное создание логических таблиц истинности
Логический инструмент для создания таблицы истинности онлайн
Введите логическое выражение
Поделиться
Твитнуть
Как использовать ?
- Введите свое логическое выражение в поле поиска
- Используйте буквы для переменных, символы для логических операторов
- Нажмите кнопку «Получить таблицу истинности»
- Таблица истинности будет отображаться
- Нажмите кнопку «Расширенная таблица истинности» для операций с пропозициональной логикой
| Оператор | Символ для ввода | Пример |
|---|---|---|
| ИЛИ | | | А | Б | С |
| И | и | А и Б и С |
| НЕ | ! | ! А |
| И-НЕ (И + НЕ) | ! (* и *) | ! (А и В и С) |
| ИЛИ (ИЛИ + НЕ) | ! (* | *) | ! (А | Б | С) | 9 Б
Таблица истинности
Таблица истинности представляет собой представление логического выражения в табличном формате.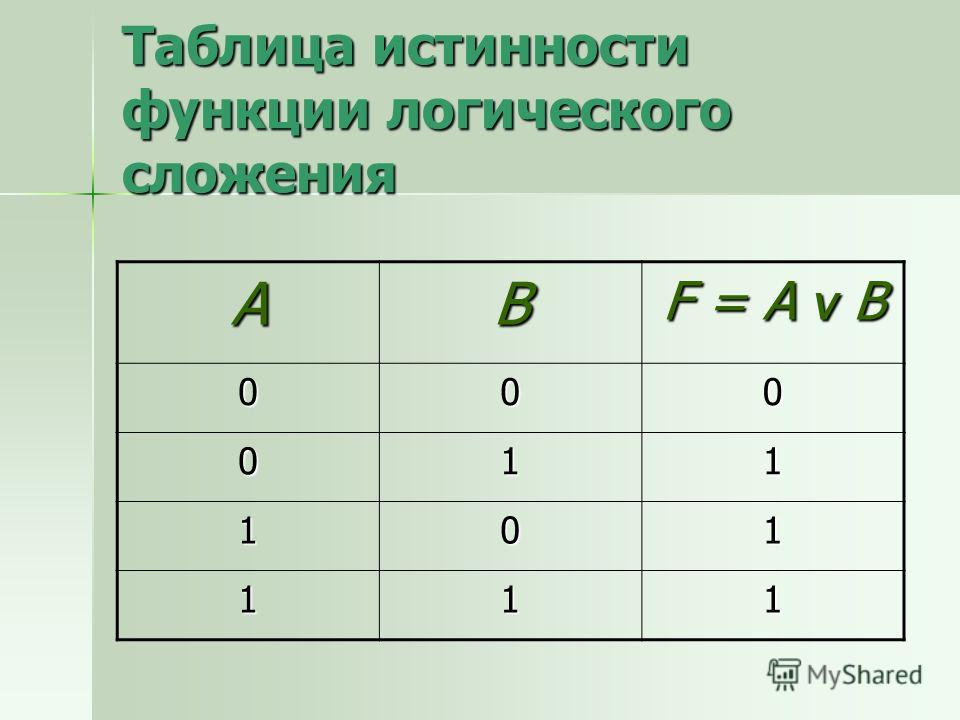 Он в основном используется в математике и информатике.
Он в основном используется в математике и информатике.
Представление выполняется с использованием двухзначной логики — 0 или 1. Вы также можете ссылаться на них как на True (1) или False (0). Он используется для просмотра выходного значения, сгенерированного из различных комбинаций входных значений.
Символы логических вентилей
Эти входные значения представляют собой различные переменные и символы (обычно называемые ЛОГИЧЕСКИМИ ВОРОТАМИ). Ниже представлены ВОРОТА и символы
- И (символически: &)
- ИЛИ (символически: +)
- НЕ (символически: !)
- НО (обозначает: НЕ ИЛИ)
- НЕ-И (Обозначает: Не-И)
Примеры таблиц истинности
В каждой таблице истинности каждое утверждение обычно представлено двоичной цифрой или переменной. Для лучшего понимания взгляните на приведенные ниже примеры.
Для лучшего понимания взгляните на приведенные ниже примеры.
Таблица истинности шлюза OR
| Символ | А | Б | А+В |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 0 | 1 | 1 | |
| 1 | 1 | 1 |
Таблица истинности вентилей И
| Символ | А | Б | АБ |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 1 |
Таблица истинности логических элементов И-НЕ
| Символ | А | Б | !(А.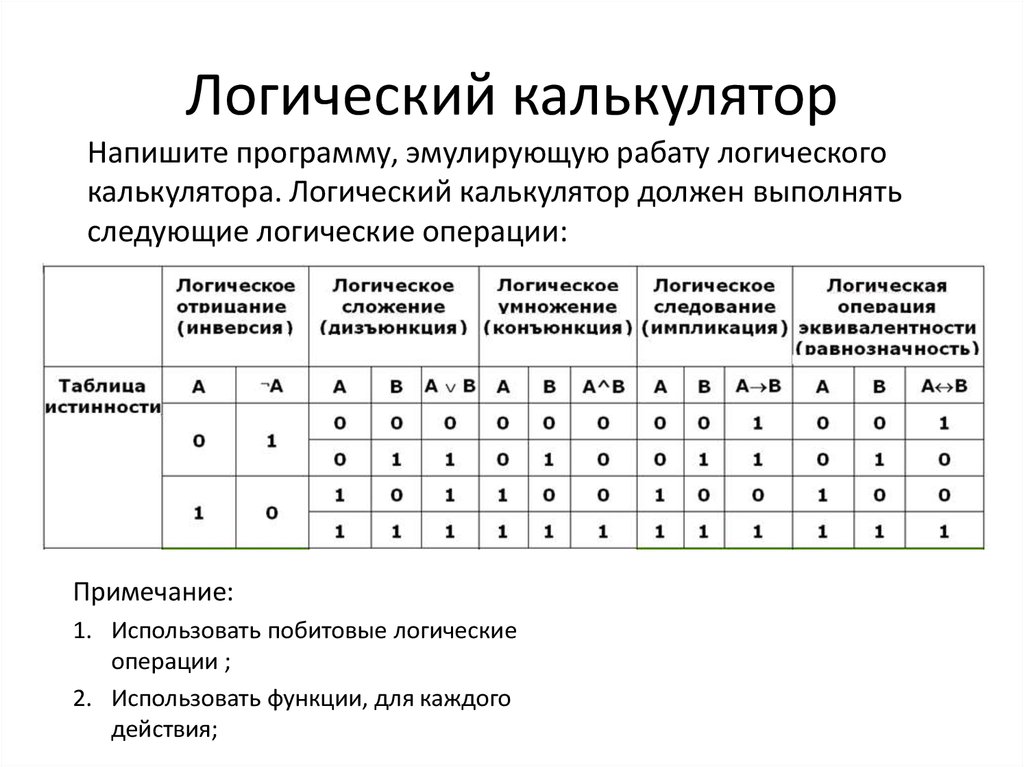 Б) Б) |
|---|---|---|---|
| 0 | 0 | 1 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
Таблица истинности шлюза NOR
| Символ | А | Б | !(А+В) |
|---|---|---|---|
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 0 |
Таблица истинности шлюза НЕ
| Символ | А | !А |
|---|---|---|
| 0 | 1 | |
| 1 | 0 |
Генератор таблиц истинности
Таблица истинности представляет собой математическую таблицу и основу для всех вычислительных нужд.

 Определите, какому столбцу соответствует каждая из переменных
Определите, какому столбцу соответствует каждая из переменных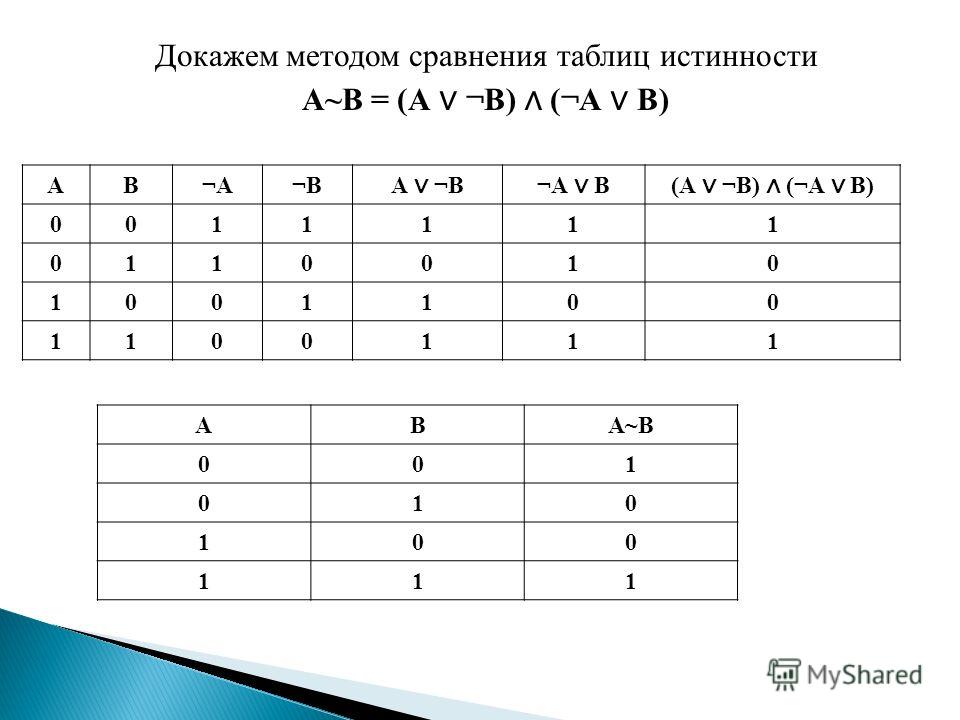
 Определите, какому столбцу соответствует каждая из переменных
Определите, какому столбцу соответствует каждая из переменных