6 класс решение дробных уравнений
Вы искали 6 класс решение дробных уравнений? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и дробные уравнения 6 класс как решать, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «6 класс решение дробных уравнений».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 6 класс решение дробных уравнений,дробные уравнения 6 класс как решать,дробные уравнения как решать 6 класс,дробные уравнения как решать 7 класс,как найти корень уравнения дробного,как решать дробные уравнения 6 класс,как решать квадратные уравнения с дробями,как решать уравнения по алгебре 7 класс с дробями,как решать уравнения с дробями 6 класс,как решать уравнения с дробями 6 класс примеры,как решить уравнение 6 класс с дробями,как решить уравнение с дробями 6 класс,как решить уравнение с дробями 9 класс,как решить уравнения 6 класс с дробями,примеры уравнения 6 класс с дробями,примеры уравнения с дробями 6 класс,решение уравнений дробных 6 класс,решение уравнений с дробями 6 класс,решение уравнений с дробями 6 класс объяснение,решить уравнение 6 класс с дробями,решить уравнение квадратное уравнение с дробями,решить уравнение с дробями 6 класс,уравнение 6 класс с дробями,уравнение с дробями 6 класс,уравнение с дробями 6 класс примеры и решение,уравнения 6 класс примеры с дробями,уравнения 6 класс с дробями,уравнения 6 класс с дробями примеры,уравнения 6 класс с обыкновенными дробями,уравнения с дробями 6 класс,уравнения с дробями 6 класс примеры,уравнения с дробями 6 класс примеры с ответами,уравнения с обыкновенными дробями 6 класс.
Решить задачу 6 класс решение дробных уравнений вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Мерзляк 6 класс — § 7. Основное свойство дроби
- Ответы к учебнику для 6 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1.
Сформулируйте основное свойство дроби.
Если числитель и знаменатель умножить или разделить на одно и то же число, то получиться равная ей дробь:
Решаем устно
1. Прочитайте дроби и назовите в каждой из них числитель и знаменатель.
— пять седьмых: числитель 5, знаменатель 7;
— одна девятая: числитель 1, знаменатель 9;
— семь двенадцатых: числитель 7, знаменатель 12;
— двенадцать двенадцатых: числитель 12, знаменатель 12;
— три восьмых: числитель 3, знаменатель 8;
— пять третьих: числитель 5, знаменатель 3.
2. В школьном саду растёт 14 яблонь и 13 вишен. Какую часть всех деревьев составляют: 1) яблони; 2) вишни?
14 + 13 = 27 (шт) — деревьев растёт в саду всего.
Значит:
- яблони составляют всех деревьев;
- вишни составляют всех деревьев.
Ответ: 1) яблони — ; 2) вишни — всех деревьев.
3. Когда сгорела половина свечки и ещё 5 см, то высота свечки стала 5 см. Какой была высота свечки первоначально?
- Когда сгорела половина свечки осталась другая половина свечки.
- Потом сгорело ещё 5 см и 5 см осталось. Значит оставшаяся половина свечки была 5 + 5 = 10 см.
- Две половины свечки равны между собой. Значит высота свечки 10 • 2 = 20 см.
Ответ: 20 см.
Упражнения
187. Начертите координатный луч, взяв за единичный отрезок, длина которого в 20 раз больше стороны клетки тетради. Отметьте на луче точки, соответствующие числам:
Какие из этих чисел изображаются на луче одной и той же точкой? Запишите соответствующие равенства.
188. Начертите координатный луч, взяв за единичный отрезок, длина которого в 18 раз больше стороны клетки тетради. Отметьте на луче точки, соответствующие числам:
Какие из этих чисел изображаются на луче одной и той же точкой? Запишите соответствующие равенства.
189. Умножьте на 4 числитель и знаменатель каждой из дробей . Запишите соответствующие равенства.
1)
2)
3)
4)
5)
190. Разделите на 3 числитель и знаменатель каждой из дробей . Запишите соответствующие равенства.
1)
2)
3)
4)
5)
191. Укажите пропущенное значение числителя или знаменателя, при котором данная запись будет верной:
1)
2)
3)
4)
5)
6)
192. Объясните, почему верно равенство:
1) — равенство верно, так как и числитель, и знаменатель умножили на число 7.
2) — равенство верно, так как и числитель, и знаменатель разделили на число 20.
3) — равенство верно, так как и числитель, и знаменатель умножили на число 11.
4) — равенство верно, так как и числитель, и знаменатель разделили на число 6.
193. Запишите три дроби, равные:
1)
2)
3)
4)
194. Какие изданных равенств неверны:
1) — верно, так как
2) — неверно, так как
3) — неверно, так как
4) — верно, так как
195. Каждую из данных дробей замените равной ей дробью, знаменатель которой равен 42:
1)
2)
3)
4)
5)
6)
196. Каждую из данных дробей замените равной ей дробью, знаменатель которой равен 72:
1)
2)
3)
4)
5)
6)
197. Запишите:
1) число 3 в виде дроби, знаменатель которой равен 6
2) число 13 в виде дроби, знаменатель которой равен 5
3) число 1 в виде дроби, знаменатель которой равен 29
198. Запишите:
1) число 5 в виде дроби, знаменатель которой равен 8
2) число 10 и виде дроби, знаменатель которой равен 14
3) число 16 в виде дроби, знаменатель которой равен 16
199.
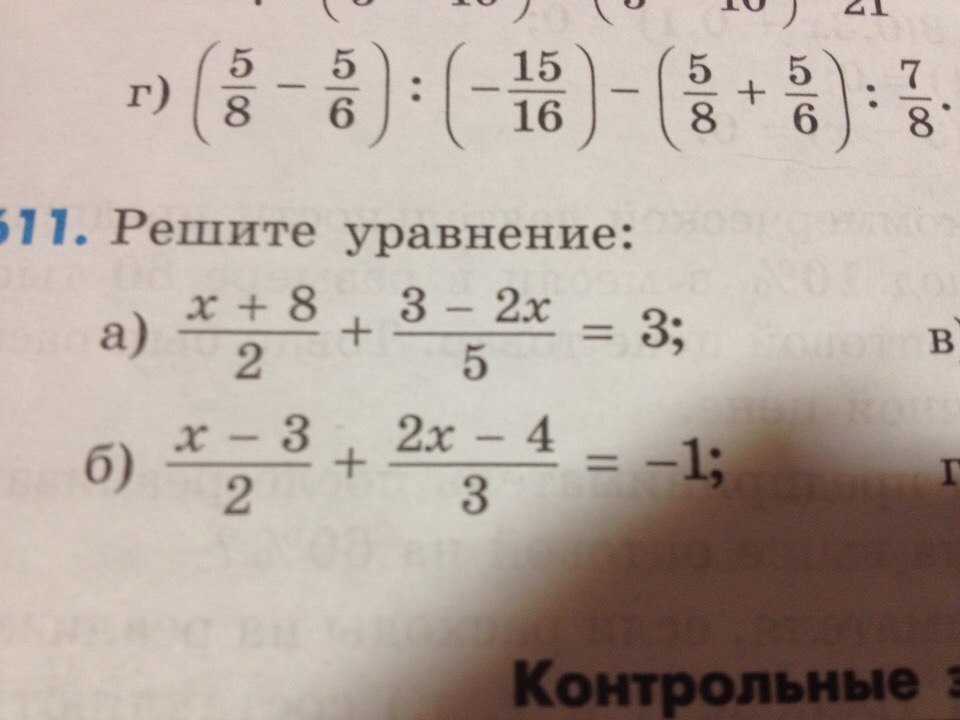Пользуясь основным свойством дроби, найдите значение а, при котором верно равенство:
1) — равенство будет верно при a = 1, так как
2) — равенство будет верно при a = 4, так как
3) — равенство будет верно при a = 5, так как
4) — равенство будет верно при a = 20, так как
200. Пользуясь основным свойством дроби, найдите значение a, при котором верно равенство:
1) — равенство будет верно при a = 2, так как
2) — равенство будет верно при a = 48, так как
3) — равенство будет верно при a = 10, так как
4) — равенство будет верно при a = 72, так как
201. Решите уравнение:
202. Решите уравнение:
Упражнения для повторения
203. Леденец стоит 16 сольдо. У Буратино есть 20 монет по 10 сольдо. Какое наибольшее количество леденцов может купить Буратино, чтобы продавцу не нужно было давать ему сдачу?
1) Найдём наименьшее общее кратное (НОК) чисел 16 и 10.
Для этого разложим данные числа на произведение степеней простых множителей:
- 10 = 2 • 5
- 16 =
Значит НОК (10, 16) = = 16 • 5 = 80.
2) 10 • 20 = 200 (сольдо) — всего у Буратино.
3) Найдём наибольшее число, которое кратно и 16, и 10, и, при этом, меньше 200. Для этого запишем все числа меньшие 200 и кратные 80 (НОК (10, 16)) и выберем наибольшее из них:
- 80, 160.
Значит наибольшее количество денег, на которое Буратино может купить леденцы без сдачи, это 160 сольдо.
4) 160 : 16 = 10 (шт) — леденцов может купить Буратино без сдачи.
Ответ: 10 шт.
204. Число делится нацело на 2, на 5 и на 9. Каким ещё числам кратно это число?
1) Разложим числа 2, 5 и 9 на простые множители:
- 2 = 2, так как это простое число;
- 5 = 5, так как это простое число;
- 9 = 3²
Значит делителями задуманного числа будут все возможные числа, которые получатся в результате перемножения между собой простых множителей, а также числа 1:
- 1
- 2 • 1 = 2
- 3 • 1 = 3
- 5 • 1 = 5
- 2 • 3 = 6
- 3 • 3 = 9
- 2 • 5 = 10
- 5 • 3 = 15
- 2 • 3 • 3 = 18
- 2 • 3 • 5 = 30
- 5 • 3 • 3 = 45
- 2 • 3 • 3 • 5 = 90
Ответ: задуманное число кратно числам: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90.
205. В среднем сердце человека делает 75 ударов в минуту. Сколько ударов делает сердце в течение суток? Сколько литров крови оно перекачивает за 1 мин, если сердце перекачивает за сутки 8 640 л крови?
1) 60 • 24 = 1 440 (минут) — в одних сутках.
2) 1 440 • 75 = 108 000 (шт) — ударов делает сердце за 1 сутки.
3) 8 640 : 1 440 = 6 (л) крови перекачивает сердце за 1 минуту.
Ответ: 108 000 ударов за сутки, 6 литров крови за минуту.
206. Начертите острый угол ABC. Проведите луч BD так, чтобы угол ABD был прямым, а угол BCD:
1) тупым
- ∠ABC — острый;
- ∠ABD — прямой;
- ∠BCD — тупой.
2) острым
- ∠ABC — острый;
- ∠ABD — прямой;
- ∠BCD — острый.
207. От пристани отправился теплоход со скоростью 18 км/ч. Через 3 ч после этого от пристани в том же направлении отправился второй теплоход, который догнал первый через 9 ч после своего выхода.
Найдите скорость второго теплохода.
1) 9 + 3 = 12 (ч) — двигался от пристани до места встречи первый теплоход.
2) 18 • 12 = 216 (км) — расстояние между пристанью и точкой встречи.
3) 216 : 9 = 24 (км/ч) — скорость второго теплохода.
Ответ: 24 км/ч.
208. Из одного города в другой со скоростью 60 км/ч выехал автомобиль. Через 3 ч из другого города навстречу ему выехал второй автомобиль. Они встретились через 7 ч после начала движения первого автомобиля. Найдите скорость второго автомобиля, если расстояние между городами равно 700 км.
1) 60 • 7 = 420 (км) — проехал до встречи первый автомобиль.
2) 700 — 420 = 280 (км) — проехал до встречи второй автомобиль.
3) 7 — 3 = 4 (ч) — находился в пути второй автомобиль.
4) 280 : 4 = 70 (км/ч) — скорость второго автомобиля.
Ответ: 70 км/ч.
Задача от мудрой совы
209. Па поле размером 10 х 10 клеток для игры в «Морской бой» поставили корабль в прямоугольник размером 1 х 3 клетки.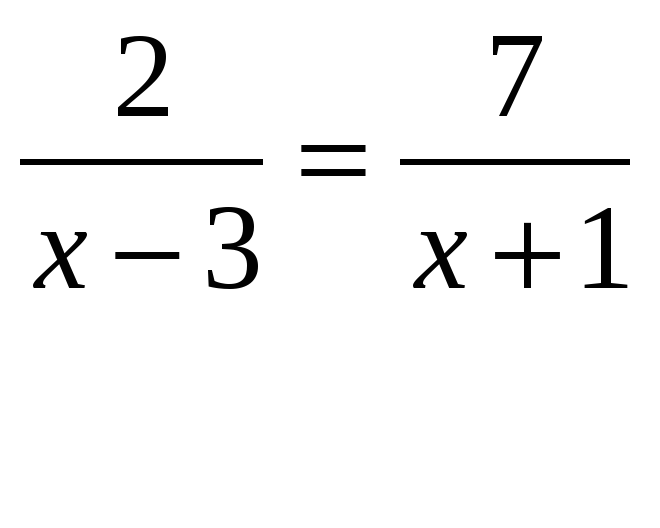
1) 10 • 10 = 100 ( шт) — всего клеток на поле.
2) 100 — 3 = 97 (шт) — клеток не занято кораблём.
3) 3 • 33 = 99 (шт) — клеток — максимальное количество клеток, которое можно поразить за 33 хода (стрелять надо в каждую третью клетку, а не подряд в каждую).
4) 99 > 97 — значит в течении 33 ходов можно наверняка попасть корабль размером в 3 клетки.
Ответ: да, можно.
- Ответы к учебнику для 6 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Wolfram|Alpha Примеры: Common Core Math: 6 класс
О-о! Wolfram|Alpha не работает без JavaScript.
Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.
Примеры для
В шестом классе учащиеся работают с алгебраическими выражениями, включающими показатели степени и переменные. Учащиеся работают с выражениями, проверяют решения уравнений и неравенств и алгебраически решают одношаговые уравнения. Учащиеся исследуют отношения между двумя величинами, различая независимые и зависимые переменные. Учащиеся собирают данные, задавая статистические вопросы, и обобщают полученные распределения данных, сообщая показатели центра и разброса и отображая данные на графиках. Учащиеся выполняют арифметические действия с дробями и отрицательными числами, визуализируя свою работу с помощью числовых линий, ленточных диаграмм и графиков. Студенты также работают с отношениями, чтобы описать пропорциональные отношения и проценты.
Стандарты Common Core
Получить информацию об Стандартах Common Core.
Поиск конкретного стандарта:
CCSS.Math.Content.6.NS.A.1Общий базовый стандарт для шестого класса RP.A.3Поиск всех стандартов для шестого класса:
общий базовый стандарт в 6-м классеВыражения и уравнения Запись , оценивайте выражения и управляйте ими, решайте уравнения и неравенства.
Напишите выражение, представляющее словесное описание (CCSS.Math.Content.6.EE.A.2a):
вычесть x из 10Вычислить выражение (CCSS.Math.Content.6.EE.A.2c):
если x = 4, сколько будет 3x + 50?Напишите эквивалентные выражения (CCSS.Math.Content.6.EE.A.3):
распределите 9 (y + 2) на коэффициент 28x + 18Решите уравнение (CCSS.Math.Content.6.EE.B.7 ):
решить x + 1/2 = 3/4Проверить решения уравнений и неравенств (CCSS.Math.Content.6.EE.B.5):
равно 5 решению 1/2x + 2 > 3/ 4?Больше примеровГеометрияВычисление площади, объема и площади поверхности. Нанесите точки на координатную плоскость.
Найдите площадь прямоугольника или треугольника (CCSS.Math.Content.6.G.A.1):
площадь прямоугольника 4,3 x 8,2площадь треугольника с основанием 5 и высотой 6Найдите объем прямоугольной призмы (CCSS.Math .Content.6.G.A.2):
объем прямоугольной призмы 1/3 на 2/3 на 5/3Найти расстояние между двумя точками (CCSS.Math.Content.
6.G.A.3): расстояние между (5 , 4) и (5, -2)Другие примерыСистема счисленияВыполнять арифметические действия с помощью, изучать свойства и строить рациональные числа.
Деление с дробями (CCSS.Math.Content.6.NS.A.1):
(2/5) / (1/6)Выполнение арифметических действий с десятичными дробями (CCSS.Math.Content.6.NS.B .3):
238,87 — 23,65Вычисление наибольшего общего делителя (CCSS.Math.Content.6.NS.B.4):
наибольшего общего делителя 24 и 88Представление чисел на числовой прямой (CCSS.Math.Content .6.NS.C.6c):
-7 и 7 на числовой прямойПостройте упорядоченные пары в виде точек (CCSS.Math.Content.6.NS.C.6b):
постройте (-3, 1)Найдите расстояние между двумя точками (CCSS.Math.Content.6.NS.C.8):
расстояние между (2, -4 1/2) и (2, 1 1/2)Больше примеровСоотношения и пропорцииОпределение и вычисление с использованием процентов и соотношений.
Определение удельной стоимости, связанной с коэффициентом (CCSS.
Math.Content.6.RP.A.2): 80 долларов США за 10 элементовВычисление процента от числа (CCSS.Math.Content.6.RP.A .3c):
48% от 50Преобразование дроби в проценты (CCSS.Math.Content.6.RP.A.3c):
сколько процентов составляет 15 из 60?Больше примеровДАЛЬШЕ
Шаг- Пошаговые решения по алгебре
Pre-Algebra Web App
Бесплатная неограниченная алгебра. Проблемы практики
Связанные примеры
Анализ и отображение наборов данных.
Расчет мер центра (CCSS.Math.Content.6.SP.B.5c):
среднее {2, 4, 4, 6, 6, 8, 8, 8, 8, 10}медиана {19, 20 , 14, 18, 19, 21, 17}Расчет показателей вариации (CCSS.Math.Content.6.SP.B.5c):
диапазон {81, 100, 92, 97, 88, 97}межквартильный диапазон {10, 9, 8, 4, 7, 11 , 12, 15, 10}Создание графиков для отображения данных (CCSS.Math.Content.6.SP.B.4):
блок-график {19, 20, 27, 13, 16, 27, 14, 22}Дополнительно примеры6 класс – Center for Mathematics and Teaching Inc.
Образцы пакетов учащихся. Нажмите «Просмотр», чтобы просмотреть документы.
Нажмите ЗДЕСЬ, чтобы просмотреть выбранные компоненты.
| Пакет | Урок 1 | Урок 2 | Урок 3 | Стандартные корреляции |
|---|---|---|---|---|
| 1 Вид | Применение свойств арифметики | Деление с остатком | Умножение и деление: стандартные алгоритмы | 4НБТ.5,6 5.НБТ.2,5,6 6.НС.2 |
| 2 Вид | Факторы и множители | GCF и LCM | Числовые выражения | 6.НС4М 6.EE.1, 2b, 3, 4 |
| 3 Вид | Дробные полоски | Упорядочивание дробей в числовой строке | Переименование дробей | 3.NF1, 2, 3 4.NF.1, 2 |
| 4 Вид | Дроби и десятичные дроби | Десятичное разрядное значение и числовые строки | Сады дробей, десятичных чисел и процентов | 3. NF.3; 4.NF.6 5.NBT.1, 3ab |
| 5 Вид | Имя Очки | Дисплеи данных | Обзоры данных | 6.СП.1, 2, 3, 4, 5abcd |
| 6 Вид | Эквивалентные дроби | Добавление дроби | Вычитание дроби | 4.NF.1, 2 5.NF.1, 2 |
| 7 Вид | Умножение дроби | Фракция Раздел 1 | Фракция Раздел 2 | 5.NF4ab, 6, 7abc 6.НС.1 |
| 8 Вид | Расчетный счет | Десятичное умножение | Десятичное деление | 5.НБТ.1, 2, 3а 5.НБТ. 4-7 6.НС.2, 3 |
| 9 Вид | Введение в переменные и выражения | Уравнения | Неравенства | 6.NS.3 6.EE.2abc, 3-8 |
| 10 Вид | Числовые и переменные выражения | Стратегии решения уравнений | Решение уравнений с дробями и десятичными знаками | 6. НС.3 6.EE.1, 2аб, 3-7 |
| 11 Вид | Соотношения | Удельные ставки | Проблемы соотношения и удельной стоимости | 6.РП.1, 2, 3аб |
| 12 Вид | Преобразование измерений | Понимание процентов чисел | Процент проблем | 6.RP.3cd |
| 13 Вид | Площади полигонов | Том | Площадь поверхности | 6.ЕЕ.2а, 4 6.Г. 1, 2, 4 |
| 14 Вид | Целые числа | Противоположности и абсолютная ценность | Рациональные числа | 6.НС.5, 6а, 7абкд |
| 15 Вид | Графические точки с целочисленными координатами | Графические точки с рациональными координатами | Отражения | 6.NS.6abc, 8 6.G.3 |
| 16 Вид | Накопление на покупку | Проблемы с лучшей покупкой | Покраска комнаты | 6. |