Приведение определителя к треугольному виду
Для того что бы вычислить определитель матрицы четвертого порядка или выше можно разложить определитель по строке или столбцу или применить метод Гаусса и привести определитель к треугольному виду. Рассмотрим приведение определителя матрицы к треугольному виду.
Для того чтобы привести матрицу к треугольному используйте свойства определителя для элементарных преобразований над строками и столбцами. Для нахождения определителя нужно умножить все элементы на главной диагонали.
Пример
Найдем определитель матрицы четвертого порядка.
Сделаем элемент a2,1 равный нулю.
Из строки №2 вычтем строку №1, умноженную на 1 элемент строки №2, т.
Сделаем элемент a3,1 равный нулю.
Из строки №3 вычтем строку №1, умноженную на 1 элемент строки №3, т.е. на 8
Сделаем элемент a4,1 равный нулю.
Из строки №4 вычтем строку №1, умноженную на 1 элемент строки №4, т.е. на 6
Сделаем элемент a3,2 равный нулю.
Из строки №3 вычитаем строку №2, умноженную на 5
Сделаем элемент a4,2 равный нулю.
Из строки №4 вычитаем строку №2, умноженную на 2
Сделаем элемент a4,3 равный нулю.Из строки №4 вычтем строку №3, умноженную на 9/21.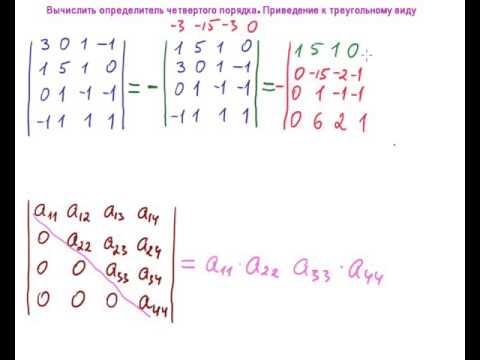
Умножим элементы матрицы находящиеся на диагонали.
Приведение матрицы к треугольному виду
Ниже два калькулятора для приведения матриц к треугольному, или ступенчатому, виду. Первый использует для этого метод Гаусса, второй — метод Барейса. Описание методов и немного теории — под калькуляторами.
Приведение матрицы к треугольному виду (метод Гаусса)
3 2 3 4 4 4 3 2 1 4 4 3 2 3 1 1Точность вычисленияЗнаков после запятой: 4
Треугольная матрица (метод Гаусса)
Треугольная матрица (метод Гаусса с выбором максимума в столбце)
Треугольная матрица (метод Гаусса с выбором максимума по всей матрице)
content_copy Ссылка save Сохранить extension Виджет
Приведение матрицы к треугольному виду (метод Барейса)
3 2 3 4 4 4 3 2 1 4 4 3 2 3 1 1Точность вычисленияТреугольная матрица (метод Барейса)
Треугольная матрица (метод Барейса с выбором максимума в столбце)
Треугольная матрица (метод Барейса с выбором максимума по всей матрице)
content_copy Ссылка save Сохранить extension Виджет
Итак, для начала определимся с понятием треугольной, или ступенчатой матрицы:
Матрица имеет ступенчатый вид, если:
- Все нулевые строки матрицы стоят последними
- Первый ненулевой элемент строки всегда находится строго правее первого ненулевого элемента предыдущей строки
- Все элементы столбца под первым ненулевым элементом строки равны нулю (это впрочем следует из первых двух пунктов)
Пример ступенчатой матрицы:
1 0 2 5
0 3 0 0
0 0 0 4
Понятие треугольной матрицы более узкое, оно используется только для квадратных матриц (хотя я думаю, что это не строго), и формулируется проще: треугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.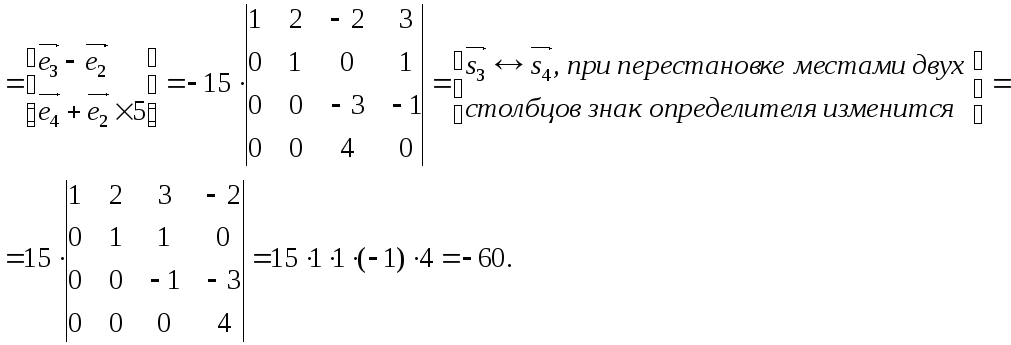
Пример треугольной (верхнетреугольной) матрицы:
1 0 2 5
0 3 1 3
0 0 4 2
0 0 0 3
Кстати, определитель треугольной матрицы вычисляется простым перемножением ее диагональных элементов.
Чем же так интересны ступенчатые (и треугольные) матрицы, что к ним надо приводить все остальные? — спросите вы.
У них есть замечательной свойство, а именно, любую прямоугольную матрицу можно с помощью элементарных преобразований привести к ступенчатой форме.
Что же такое элементарные преобразования? — спросите вы.
Элементарными преобразованиями матрицы называют следующие операции:
- перестановка любых двух строк (столбцов) матрицы
- умножение любой строки (столбца) на призвольное, отличное от нуля, число
- сложение любой строки (столбца) с другой строкой (столбцом), умноженной (умноженным) на произвольное, отличное от нуля, число.

И что? — спросите вы.
А то, что элементарные преобразования матрицы сохраняют эквивалентность матриц. А если вспомнить, что системы линейных алгебраический уравнений (СЛАУ) записывают как раз в матричной форме, то это означает, что элементарные преобразования матрицы не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
Приведя матрицу системы линейных уравнений AX=B к треугольной форме A’X = B’, то есть, с соответствующими преобразованиями столбца B, можно найти решение этой системы так называемым «обратным ходом».
Чтобы было понятно, используем треугольную матрицу выше и перепишем систему уравнений в более привычной форме (столбец B я придумал сам):
Понятно, что сначала мы найдем , потом, подставив его в предыдущее уравнение, найдем и так далее — двигаясь от последнего уравнения к первому. Это и есть обратный ход.
Алгоритм приведения матрицы к ступенчатой форме с помощью элементарных преобразований называют методом Гаусса. Метод Гаусса — классический метод решения систем линейных алгебраических уравнений. Также его еще называют Гауссовым исключением, так как это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к эквивалентной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Метод Гаусса — классический метод решения систем линейных алгебраических уравнений. Также его еще называют Гауссовым исключением, так как это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к эквивалентной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Теперь про сам метод.
Собственно, как можно занулить переменную во втором уравнении? Вычтя из него первое, домноженное на коэффициент
Зануляем во втором уравнении:
Во втором уравнении больше не содержится
Обобщенно алгоритм метода Гаусса можно представить следующим образом:
где N — число строк,
— i-тая строка,
— элемент, находящийся в i-той строке, j-том столбце
И все бы ничего, да и метод отличный, но. Дело все в делении на , присутствующем в формуле. Во-первых, если диагональный элемент будет равен нулю, то метод работать не будет. Во-вторых, в процессе вычисления будет накапливаться погрешность, и чем дальше, тем больше. Результат будет отличаться от точного.
Во-вторых, в процессе вычисления будет накапливаться погрешность, и чем дальше, тем больше. Результат будет отличаться от точного.
Для уменьшения погрешности используют модификации метода Гаусса, которые основаны на том, что погрешность тем меньше, чем больше знаменатель дроби. Эти модификации — метод Гаусса с выбором максимума в столбце и метод Гаусса с выбором максимума по всей матрице. Как следует из названия, перед каждым шагом исключения переменной по столбцу (всей матрице) ищется элемент с максимальным значением и проводится перестановка строк (строк и столбцов), таким образом, чтобы он оказался на месте .
Но есть еще более радикальная модификация метода Гаусса, которая называется методом Барейса (Bareiss).
Как можно избавиться от деления? Например, умножив перед вычитанием строку на . Тогда вычитать надо будет строку , домноженную только на , без всякого деления.
.
Уже хорошо, но возникает проблема с ростом значений элементов матрицы в ходе вычисления.
Барейс предложил делить выражение выше на и показал, что если исходные элементы матрицы — целые числа, то результатом вычисления такого выражения тоже будет целое число. При этом принимается, что для нулевой строки .
Кстати, то, что в случае целочисленных элементов исходной матрицы алгоритм Барейса приводит к треугольной матрице с целочисленными элементами, то есть без накопления погрешности вычислений — довольно важное свойство с точки зрения машинной арифметики.
Алгоритм Барейса можно представить следующим образом:
Алгоритм, аналогично методу Гаусса, также можно улучшить поиском максимума по столбцу(всей матрице) и перестановкой соответствующих строк (строк и столбцов).
Страница не найдена — ПриМат
© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Денис Стехун (8), Елизавета Савицкая (8), Игорь Любинский (8), Юлия Стерлянко (8), Александр Базан (7), Валентин Малявко (7), Анна Чалапчий (7), Константин Берков (7), Олег Шпинарев (7), Максим Швандт (6), Людмила Рыбальченко (6), Кирилл Волков (6), Татьяна Корнилова (6), Влад Радзивил (6), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2),
Метод приведения матрицы к треугольному виду
При помощи элементарных преобразований любую матрицу можно привести к верхнему (или нижнему) треугольному виду (метод Гаусса).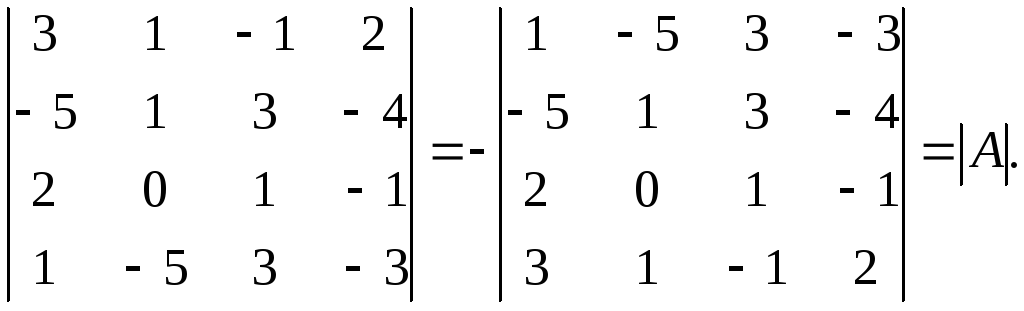 Отсюда следует, что любой определитель, используя перечисленные выше элементарные преобразования, можно привести к треугольному виду, а затем вычислить согласно п.3 замечаний 2.2.
Отсюда следует, что любой определитель, используя перечисленные выше элементарные преобразования, можно привести к треугольному виду, а затем вычислить согласно п.3 замечаний 2.2.
Итак, метод состоит из двух шагов.
1. При помощи элементарных преобразований привести определитель к треугольному виду.
2. Вычислить определитель треугольного вида, перемножая его элементы, стоящие на главной диагонали.
Пример 2.12. Вычислить определитель четвёртого порядка
приводя его к треугольному виду.
Решение. 1. При помощи элементарных преобразований приведем матрицу к треугольному виду. Взяв элемент первой строки в качестве ведущего, все остальные элементы первого столбца сделаем равными нулю. Для этого ко второй строке прибавим первую, умноженную на (-2), к третьей строке прибавим первую, умноженную на (-3), а к четвертой строке прибавим первую, умноженную на (-4):
Заметим, что при использовании этих элементарных преобразований III типа определитель не изменяется.
Умножим элементы второй строки на (-1), а элементы третьей строки — на 0,5, при этом, чтобы не нарушить равенство, надо полученный определитель разделить на , т.е. умножить на (-2):
В полученной матрице нужно сделать равными нулю элементы и второго столбца, стоящие ниже главной диагонали. Для этого берем в качестве ведущего элемента и прибавляем к третьей и четвертой строкам вторую строку, умноженную на 1 и на 7 соответственно:
Осталось сделать равным нулю элемент . К четвертой строке прибавим третью, умноженную на 2 (определитель при этом не изменится):
Получили определитель треугольного вида.
2. Вычислим определитель верхней треугольной матрицы, перемножая элементы, стоящие на главной диагонали:
Не нашли то, что искали? Воспользуйтесь поиском:
Метод сведения определителя к треугольному виду использует те же преобразования, что и метод эффективного понижения порядка. Только при вычислении определителя методом эффективного понижения порядка мы постепенно уменьшаем порядок определителя, а для метода сведения к треугольному виду порядок определителя остаётся неизменным до конца процесса решения.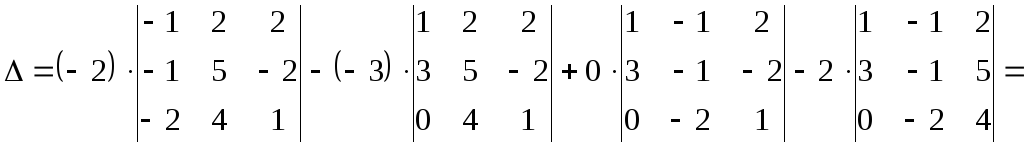 Суть метода сведения к треугольному виду такова: с помощью действий со строками (или столбцами) преобразовать определитель к виду, когда все элементы, лежащие ниже (или выше) главной диагонали равны нулю. Т.е. после преобразований определитель должен принять одну из двух форм (элементы на главной диагонали выделены синим цветом):
Суть метода сведения к треугольному виду такова: с помощью действий со строками (или столбцами) преобразовать определитель к виду, когда все элементы, лежащие ниже (или выше) главной диагонали равны нулю. Т.е. после преобразований определитель должен принять одну из двух форм (элементы на главной диагонали выделены синим цветом):
Хотя разницы и нет, обычно приводят к первому случаю, когда нули расположены под главной диагональю. После преобразований определитель вычисляется простым умножением элементов, расположенных на главной диагонали. Для того, чтобы обнулить требуемые элементы и вычислить определитель, нам пригодятся несколько свойств определителей, которые указаны в теме «Некоторые свойства определителей». Я запишу ниже несколько свойств, которые нам пригодятся при решении. В примечании после каждого свойства будет указан пример его применения.
- Если поменять местами две строки (столбца) определителя, то знак определителя изменится на противоположный.
Пример применения этого свойства: показатьскрыть
Рассмотрим определитель $left| egin 2 & 5 \ 9 & 4 end
ight|$. Найдём его значение, используя формулу №1 из темы вычисления определителей второго и третьего порядков:
Найдём его значение, используя формулу №1 из темы вычисления определителей второго и третьего порядков:
$$left| egin 2 & 5 \ 9 & 4 end
ight|=2cdot 4-5cdot 9=-37.$$
Теперь поменяем местами первую и вторую строки. Получим определитель $left| egin 9 & 4 \ 2 & 5 end
ight|$. Вычислим полученный определитель: $left| egin9 & 4 \ 2 & 5 end
ight|=9cdot 5-4cdot 2=37$. Итак, значение исходного определителя равнялось (-37), а у определителя с изменённым порядком строк значение равно $-(-37)=37$. Знак определителя изменился на противоположный.
Пример применения этого свойства: показатьскрыть
Рассмотрим определитель $left| egin -7 & 10 & 0\ -9 & 21 & 4 \ 2 & -3 & 1 end
ight|$. Прибавим к элементам второй строки соответствующие элементы третьей строки, умноженные на 5. Записывают это действие так: $r_2+5cdot$. Вторая строка будет изменена, остальные строки останутся без изменений.
$$ left| egin -7 & 10 & 0\ -9 & 21 & 4 \ 2 & -3 & 1 end
ight| eginphantom<0>\ r_2+5cdot\ phantom <0>end= left| egin-7 & 10 & 0\ -9+5cdot 2 & 21+5cdot (-3) & 4+5cdot 1 \ 2 & -3 & 1 end
ight|= left| egin-7 & 10 & 0\ 1 & 6 & 9 \ 2 & -3 & 1 end
ight|.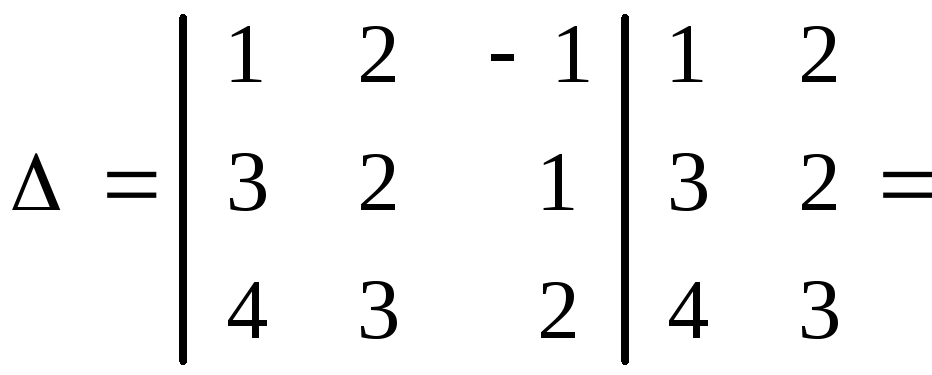 $$
$$
Пример применения этого свойства: показатьскрыть
Рассмотрим определитель $left| egin -7 & 10 \ -9 & 21 end
ight|$. Заметьте, что все элементы второй строки делятся на 3:
$$left| egin -7 & 10 \ -9 & 21 end
ight|=left| egin-7 & 10 \ 3cdot(-3) & 3cdot 7 end
ight|$$
Число 3 и есть общий множитель всех элементов второй строки. Вынесем тройку за знак определителя:
$$ left| egin -7 & 10 \ -9 & 21 end
ight|=left| egin-7 & 10 \ 3cdot(-3) & 3cdot 7 end
ight|= 3cdot left| egin-7 & 10 \ -3 & 7 end
ight| $$
Пример применения этого свойства: показатьскрыть
Буквами $r$ (от слова «row») станем обозначать строки: $r_1$ – первая строка, $r_2$ – вторая строка и так далее. Буквами $c$ (от слова «column») станем обозначать столбцы: $c_1$ – первый столбец, $c_2$ – второй столбец и так далее.
Найти определитель $Delta = left|egin -8 & 2 & 9 & 17\ -3 & 1 & 2 & 6\ 13 & -3 & -7 & -26\ 11 & 1 & 23 & 6end
ight|$.
В принципе, начинать решение можно и не преобразовывая определитель. Однако очень удобно, когда первым элементом первой строки является единица (ну, или (-1) на крайний случай). Единицы есть во втором столбце нашего определителя. Сделаем так, чтобы второй столбец стал первым. Для этого просто поменяем местами первый и второй столбцы, используя свойство (1). Не забываем, что при смене мест двух столбцов перед определителем появится знак «минус»:
$$Delta = left|egin -8 & 2 & 9 & 17\ -3 & 1 & 2 & 6\ 13 & -3 & -7 & -26\ 11 & 1 & 23 & 6end
ight|=-left|egin2 & -8 & 9 & 17\ 1 & -3 & 2 & 6\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6end
ight|.$$
Итак, столбцы поменяли, однако единица покамест не вышла на первое место в первой строке, – но это дело поправимое. Поменяем местами первую и вторую строки, при этом перед определителем вновь возникнет знак «минус». Ну, а так как «минус» на «минус» даёт «плюс», то получим мы следующее:
$$Delta =-left|egin 2 & -8 & 9 & 17\ 1 & -3 & 2 & 6\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6end
ight|=-left( -left|egin1 & -3 & 2 & 6\ 2 & -8 & 9 & 17\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6end
ight|
ight)= left|egin1 & -3 & 2 & 6\ 2 & -8 & 9 & 17\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6end
ight|.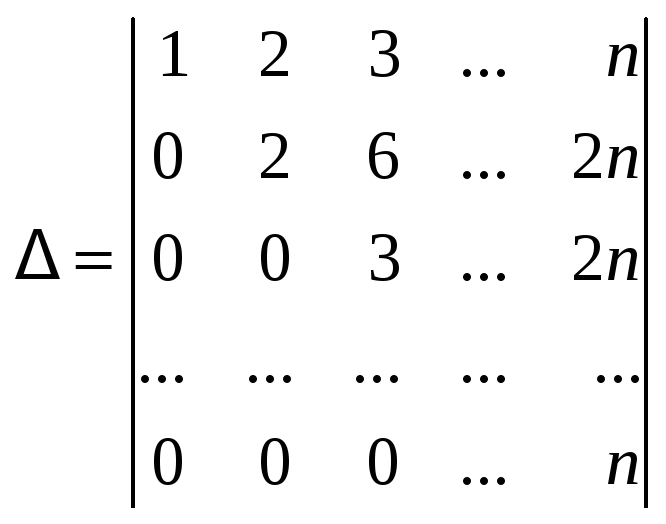 $$
$$
Начнём решение. Нам нужно получить нули под главной диагональю. Для этого придётся осуществить несколько шагов, на которых будем изменять строки нашего определителя. На первом шаге мы должны сделать так, чтобы все элементы первого столбца стали нулями – кроме элемента на главной диагонали, выделенного красным цветом:
$$ left|egin oldred <1>& -3 & 2 & 6\
ormgreen <2>& -8 & 9 & 17\
ormblue <-3>& 13 & -7 & -26\
ormpurple <1>& 11 & 23 & 6end
ight| $$
Преобразования со строками, которые нужно выполнить, чтобы обнулить «серые» элементы, получаются так:
Запись $r_2-2r_1$ означает, что от элементов второй строки вычли соответствующие элементы первой строки, умноженные на два. Полученный результат записали вместо прежней второй строки. Остальные записи расшифровываются аналогично. Согласно свойству (2) значение определителя от таких действий не изменится. Для наглядности я запишу это действие отдельно:
После выполнения всех требуемых операций со строками, мы получим новый определитель. Записывается это так:
Записывается это так:
$$ Delta=left|egin 1 & -3 & 2 & 6\ 2 & -8 & 9 & 17\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6end
ight| eginphantom <0>\ r_2-2r_1 \ r_3+3r_1 \ r_4-r_1 end= left|egin1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 14 & 21 & 0end
ight|. $$
Перед тем, как мы пойдём дальше, обратим внимание на то, что все элементы четвёртой строки делятся на 7. Согласно свойству (3) число 7 можно вынести за знак определителя:
$$ left|egin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 14 & 21 & 0end
ight|=7cdot left|egin1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 2 & 3 & 0end
ight| $$
Теперь нам нужно обнулить элементы во втором столбце (под главной диагональю). Т.е., обнулению подлежат элементы, выделенные зелёным и синим цветом. Элемент на главной диагонали, который останется без изменений, выделен красным цветом:
$$ left|egin 1 & -3 & 2 & 6\ 0 & oldred <-2>& 5 & 5\ 0 &
ormblue <4>& -1 & -8 \ 0 &
ormblue <2>& 3 & 0end
ight| $$
А если бы вместо числа -2 возник ноль? показатьскрыть
Если бы вместо числа -2 получился ноль, мы бы поменяли местами строки или столбцы. Например, вот так:
Например, вот так:
$$ left|egin 1 & -3 & 2 & 6\ 0 & 0 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 2 & 3 & 0end
ight| =[r_2leftrightarrow] =-left|egin1 & -3 & 2 & 6\ 0 & 2 & 3 & 0\ 0 & 4 & -1 & -8 \ 0 & 0 & 5 & 5 end
ight| $$
Или же может возникнуть иная ситуация: когда обнулятся все элементы во втором столбце под первой строкой. Вот так:
$$ left|egin 1 & -3 & 2 & 6\ 0 & 0 & 5 & 5\ 0 & 0 & -1 & -8 \ 0 & 0 & 3 & 0end
ight| $$
В этом случае имеем пропорциональность столбцов, т.е. $c_2=-3c_1$, а это означает, что определитель равен 0.
В принципе, мы можем получить (-1) на месте диагонального «красного элемента». Для этого достаточно поменять местами второй и третий столбцы, а затем поменять местами вторую и третью строки. Однако в нашем случае этого можно и не делать, так как все «синие элементы» нацело делятся на «красный элемент», т.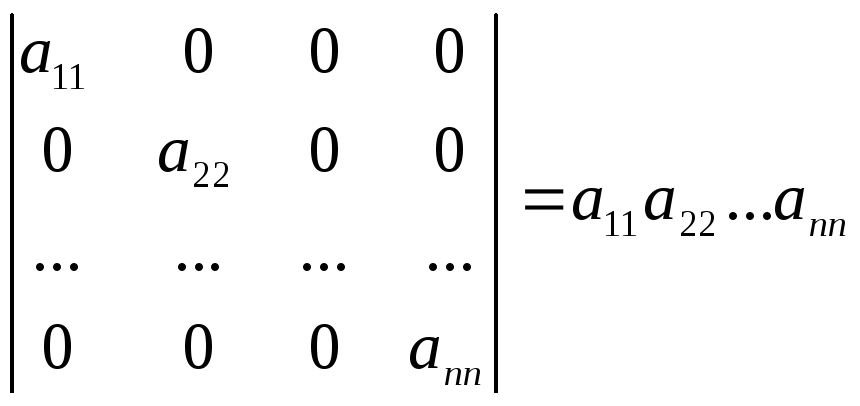 е. на (-2). Следовательно, никакой работы с дробями не предвидится. Впрочем, тут дело вкуса: можете попробовать для тренировки продолжить решение, поменяв местами строки и столбцы, чтобы «красным элементом» стала (-1). Выполним такие операции со строками:
е. на (-2). Следовательно, никакой работы с дробями не предвидится. Впрочем, тут дело вкуса: можете попробовать для тренировки продолжить решение, поменяв местами строки и столбцы, чтобы «красным элементом» стала (-1). Выполним такие операции со строками:
Отдельно выписывать действия со строками не станем, так как они полностью аналогичны рассмотренным ранее. Наш определитель станет таким:
$$ Delta=7cdot left|egin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 2 & 3 & 0end
ight| eginphantom <0>\ phantom <0>\ r_3+2r_2 \ r_4+r_2end= 7cdot left|egin1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & 8 & 5end
ight|. $$
Осталось последнее действие. Нужно обнулить элемент 8 под главной диагональю:
$$ left|egin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & oldred <8>& 5end
ight| $$
Тут уже придется поработать с дробями. Обычно такой работы стараются избегать – и до этого момента нам это удавалось – но теперь уже деваться некуда:
Обычно такой работы стараются избегать – и до этого момента нам это удавалось – но теперь уже деваться некуда:
$$ Delta = 7cdot left|egin 1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & 8 & 5end
ight| eginphantom <0>\ phantom <0>\ phantom <0>\ r_4-frac<8><9>r_3 end= 7cdot left|egin1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & 0 & frac<29><9>end
ight|. $$
Преобразования окончены. Осталось лишь использовать свойство (4) и переменожить элементы, расположенные на главной диагонали:
$$ Delta=7cdot 1cdot (-2)cdot 9 cdot frac<29><9>=-406. $$
Ответ получен. Полное решение без пояснений выглядит так:
$$ Delta = left|egin -8 & 2 & 9 & 17\ -3 & 1 & 2 & 6\ 13 & -3 & -7 & -26\ 11 & 1 & 23 & 6end
ight| =[c_1leftrightarrow] =left|egin2 & -8 & 9 & 17\ 1 & -3 & 2 & 6\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6end
ight| =[r_1leftrightarrow]=\ =left|egin1 & -3 & 2 & 6\ 2 & -8 & 9 & 17\ -3 & 13 & -7 & -26\ 1 & 11 & 23 & 6end
ight| eginphantom <0>\ r_2-2r_1 \ r_3+3r_1 \ r_4-r_1 end= 7cdot left|egin1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 4 & -1 & -8 \ 0 & 2 & 3 & 0end
ight| eginphantom <0>\ phantom <0>\ r_3+2r_2 \ r_4+r_2 end=\ =7cdot left|egin1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & 8 & 5end
ight| eginphantom <0>\ phantom <0>\ phantom <0>\ r_4-frac<8><9>r_3end=7cdot left|egin1 & -3 & 2 & 6\ 0 & -2 & 5 & 5\ 0 & 0 & 9 & 2 \ 0 & 0 & 0 & frac<29><9>end
ight| =7cdot 1cdot (-2)cdot 9 cdot frac<29><9>=-406. $$
$$
В принципе, преобразования метода сведения к треугольному виду просты, однако стоит иметь в виду свойства определителей, изложенные соответствующей теме. Например, на каком-то шаге может обнулиться строка или столбец, или же окажется, что некие строки или столбцы пропорциональны. Это будет означать, что рассматриваемый определитель равен 0.
Для того что бы вычислить определитель матрицы четвертого порядка или выше можно разложить определитель по строке или столбцу или применить метод Гаусса и привести определитель к треугольному виду. Рассмотрим приведение определителя матрицы к треугольному виду.
Для того чтобы привести матрицу к треугольному используйте свойства определителя для элементарных преобразований над строками и столбцами. Для нахождения определителя нужно умножить все элементы на главной диагонали.
Пример
Найдем определитель матрицы четвертого порядка.
Сделаем элемент a2,1 равный нулю.
Из строки №2 вычтем строку №1, умноженную на 1 элемент строки №2, т.е. на 3
Сделаем элемент a3,1 равный нулю.
Из строки №3 вычтем строку №1, умноженную на 1 элемент строки №3, т.е. на 8
Сделаем элемент a4,1 равный нулю.
Из строки №4 вычтем строку №1, умноженную на 1 элемент строки №4, т.е. на 6
Сделаем элемент a3,2 равный нулю.
Из строки №3 вычитаем строку №2, умноженную на 5
Сделаем элемент a4,2 равный нулю.
Из строки №4 вычитаем строку №2, умноженную на 2
Сделаем элемент a4,3 равный нулю.
Из строки №4 вычтем строку №3, умноженную на 9/21.
Умножим элементы матрицы находящиеся на диагонали.
Методы вычисления определителей n го порядка. 1. Метод приведения к треугольному виду
3. Определители высших порядков
Определители высших порядков Понятие определителя п-го порядка и его основные свойства Понятие определителя п-го порядка вводится на основе изучения структуры определителей -го и -го порядков Так например
ПодробнееТема 1-7: Определители
Тема 1-7: Определители А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для механиков (1 семестр) Перестановки
Подробнее1.
 Определители. a11 a12. a21 a22
Определители. a11 a12. a21 a22. Определители. Определитель второго порядка Пусть задана таблица четырех чисел, расположенных в две строки и в два столбца 2 () 2 22 Элементы а, а 2 образуют первую строку, элементы а 2, а 22 образуют
ПодробнееУПРАЖНЕНИЯ ПО ЛИНЕЙНОЙ АЛГЕБРЕ
УПРАЖНЕНИЯ ПО ЛИНЕЙНОЙ АЛГЕБРЕ Как изменится произведение B матриц и B если: а переставить -ю и j -ю строки матрицы? б переставить -й и j -й столбцы матрицы B? в к -й строке матрицы прибавить ее j -ю строку
ПодробнееПЕРЕСТАНОВКИ. Определение 1. Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,…, n в строчку одно за другим.
ПЕРЕСТАНОВКИ Определение 1 Перестановкой степени n называется любая упорядоченная запись натуральных чисел 1, 2, 3,, n в строчку одно за другим Например, 2, 4, 3, 1, 5 Это перестановка пятой степени Вообще
ПодробнееТема 3: Определители
Тема 3: Определители А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для физиков-инженеров Начало
Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для физиков-инженеров Начало
2 5 8 A = a) A = 2 3. ; b) B =
Занятие 1 Определители 11 Матричные обозначения Основные определения Матрицей размера m n, или m n-матрицей, называется таблица чисел (или других математических выражений с m строками и n столбцами Матрица
Подробнее0.5 setgray0 0.5 setgray1
0.5 setgray0 0.5 setgray1 1 Лекция 1 ОПРЕДЕЛИТЕЛИ. СИСТЕМЫ УРАВНЕНИЙ 0. План лекции 1. Определитель второго порядка. 1.1 Система двух уравнений. 1.2. Метод исключения переменных. 1.3. Матрица 2 2. 1.4.
ПодробнееГлава 3. Определители
Глава Определители Перестановки Q Рассмотрим множество первых натуральных чисел которое обозначим как Определение Перестановкой P множества элементов из Q назовем любое расположение этих элементов в некотором
ПодробнееГлава 1.
 Начала линейной алгебры
Начала линейной алгебрыГлава Начала линейной алгебры Системы линейных уравнений Систему m линейных уравнений с n неизвестными будем записывать в следующем виде: + + + + n n = + + + + nn = m + m + m + + mnn = m () Здесь n неизвестные
ПодробнееМАТЕМАТИКА ЛИНЕЙНАЯ АЛГЕБРА
ООО «Резольвента», wwwresolventru, resolvent@listru, (95) 509-8-0 Учебный центр «Резольвента» Доктор физико-математических наук, профессор К Л САМАРОВ МАТЕМАТИКА Учебно-методическое пособие по разделу
ПодробнееЭлементы линейной алгебры
Элементы линейной алгебры Линейная алгебра часть алгебры, изучающая линейные пространства и подпространства, линейные операторы, линейные, билинейные и квадратичные функции на линейных пространствах Литература
ПодробнееРешение уравнений в целых числах
Решение уравнений в целых числах Линейные уравнения. Метод прямого перебора Пример. В клетке сидят кролики и фазаны. Всего у них 8 ног. Узнать сколько в клетке тех и других. Укажите все решения. Решение.
Метод прямого перебора Пример. В клетке сидят кролики и фазаны. Всего у них 8 ног. Узнать сколько в клетке тех и других. Укажите все решения. Решение.
Тема 2-19: Билинейные и квадратичные формы
Тема 2-19: Билинейные и квадратичные формы А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной математики алгебра и геометрия для механиков
ПодробнееЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Государственное образовательное учреждение высшего профессионального образования «Московский авиационный институт (национальный исследовательский университет)» Кафедра «Высшая математика» ЛИНЕЙНАЯ АЛГЕБРА
Подробнее0.5 setgray0 0.5 setgray1
05 setgray0 05 setgray Лекция 4 ОПРЕДЕЛИТЕЛИ Определители порядка > Пусть A K a a a a 2 a 2 2 a 2 A = a a2 a a a a 2 A =, A a 2 2 2 = a a2 = A,A 2,,A,,, A = a a 2 ṇ a Определение Определителем, или детерминантом
ПодробнееДробно-рациональные выражения
Дробно-рациональные выражения Выражения содержащие деление на выражение с переменными называются дробными (дробно-рациональными) выражениями Дробные выражения при некоторых значениях переменных не имеют
ПодробнееМатематика 8 класс Многочлены
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СПЕЦИАЛИЗИРОВАННЫЙ УЧЕБНО-НАУЧНЫЙ ЦЕНТР Математика 8 класс Многочлены Новосибирск Многочлены Рациональными
ПодробнееISBN К 22.
 14я721 ISBN
14я721 ISBNДК 373:512 К 22.14721 49 49 аа, аьяа Маа.. 7 9 /.М.. М : Э, 2018. 128. (. ). ISBN 978-5-04-093533-8, 7 9-. П ё -. П,. П 7 9-,, -. ДК 373:512 К 22.14я721 ISBN 978-5-04-093533-8 аа.м., 2018 О. ООО «Иаь «Э»,
ПодробнееСИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ После изучения данной темы вы сможете: проводить численное решение задач линейной алгебры. К решению систем линейных уравнений сводятся многочисленные практические задачи, решение
ПодробнееМАТЕМАТИЧЕСКИЙ ПРАКТИКУМ
МАТЕМАТИЧЕСКИЙ ПРАКТИКУМ Ю.Л.Калиновский Введение Решение квадратных уравнений Решение квадратных уравнений c помощью разложения на множители. Решение квадратных уравнений c помощью дополнения до полного
ПодробнееАЛГЕБРА И ГЕОМЕТРИЯ. АЛГЕБРА МАТРИЦ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ
ПодробнееКонспект лекции 8 ОПРЕДЕЛИТЕЛИ II
Конспект лекции 8 ОПРЕДЕЛИТЕЛИ II 0 План лекции Лекция Определители II 4 Существование и единственность определителя Продолжение 44 Теорема о равенстве deta = deta T Определители специального вида 5 Лемма
Подробнее1.
 Линейная алгебра. a21x1 a12 x2 a13 x3 b2
Линейная алгебра. a21x1 a12 x2 a13 x3 b21. Линейная алгебра 1.1. В 1 представлены задачи на решение линейных алгебраических крамеровских систем с определителем, отличным от нуля, вычисление определителей и действий с матрицами. Линейные алгебраические
ПодробнееГлава 4. Матрицы. Лекция Основные понятия.
Лекция 0. Глава 4. Матрицы. В этой главе мы рассмотрим основные виды матриц, операции над ними, понятие ранга матрицы и их приложения к решению систем линейных алгебраических уравнений. 4.. Основные понятия.
ПодробнееКонспект лекции 7 ОПРЕДЕЛИТЕЛИ I
Конспект лекции 7 ОПРЕДЕЛИТЕЛИ I План лекции Лекция Определители Определители второго порядка Система линейных уравнений; 2 Определение определителя второго порядка; 3 Запись через определители; 4 Свойства
ПодробнееАлгебра и теория чисел
Московский международный институт эконометрики информатики финансов и права Балюкевич ЭЛ Романников АН Алгебра и теория чисел Москва УДК ББК А Балюкевич ЭЛ Романников АН Алгебра и теория чисел // Московский
Подробнее0.
 5 setgray0 0.5 setgray1
5 setgray0 0.5 setgray15 setgry 5 setgry Лекция 2 ОПРЕДЕЛИТЕЛИ СВОЙСТВА План лекции Свойство определителей Определение транспонированной матрицы 2 Свойство : A t = A 3 Свойство 2: A, B, C = A, C, B 4 Свойство 3: тоже для перестановки
Подробнее13. Билинейные и квадратичные функции
95 Билинейные и квадратичные функции Билинейная функция Определение Билинейной функцией (билинейной формой) на линейном пространстве L называется функция от двух векторов из L линейная по каждому из своих
ПодробнееВведение в линейную алгебру
Введение в линейную алгебру Матрицы. Определение. Таблица m n чисел вида m m n n mn состоящая из m строк и n столбцов называется матрицей. Элементы матрицы нумеруются аналогично элементам определителя
ПодробнееМатрицы.
 Операции над матрицами. Элементарные преобразования. Приведение к ступенчатому виду. Ранг матрицы
Операции над матрицами. Элементарные преобразования. Приведение к ступенчатому виду. Ранг матрицы1. Матрицы. Операции над матрицами. Элементарные преобразования. Приведение к ступенчатому виду. Ранг матрицы. Решение систем
Тема 4Матрицы. Операции над матрицами.
Элементарные преобразования.
Приведение к ступенчатому виду. Ранг
матрицы. Решение систем линейных
алгебраических уравнений методом
Гаусса
Калабухова Галина Валентиновна,
к.социол.н., доцент
2. Вопросы темы:
Матрицы: терминология и обозначения.Операции над матрицами: сложение, умножение матрицы
на число. Умножение матриц. Транспонирование матрицы.
Элементарные преобразования матрицы. Приведение к
ступенчатому виду.
Ранг матрицы.
Решение систем линейных алгебраических уравнений
методом Гаусса.
Матрицы:
терминология и обозначения
4. Определение
Матрицей размера m x n называется прямоугольнаятаблица, состоящая из m строк и n столбцов, заполненная
некоторыми элементами
a11
a
21
.
 ..
..a i1
…
a m1
a12
… a1 j
a 22
… a 2 j
ai 2
…
am 2
… a mj
aij
a1n
… a 2 n
… ain
… a mn
…
Обозначения:
Amxn – матрица
aij – элемент матрицы,
расположенный на
пересечении i-той строки и
j-ого столбца
m x n – размер матрицы
5. Применение матриц
Матрицы широко применяются в математике для компактнойзаписи систем линейных алгебраических уравнений или систем
дифференциальных уравнений. Тогда количество строк матрицы
соответствует количеству уравнений системы, а количество
столбцов равно количеству неизвестных
6. Другие определения
Если n = m, то матрицаназывается квадратной,
а n – порядком
матрицы.
Если все элементы
матрицы равны нулю, то
матрица называется
нулевой. Обозначается: Θ
7. Другие определения
Строка (столбец) матрицы называется нулевой, если все ее(его)элементы равны нулю.

Если хотя бы один из элементов строки (столбца) не равен
нулю, то строка (столбец) называется ненулевой
Пример:
нулевой
столбец
нулевая строка
ненулевая строка
ненулевой
столбец
8. Другие определения
Главной диагональю матрицы называется диагональ,проведённая из левого верхнего угла матрицы в правый
нижний.
Побочной диагональю матрицы называется диагональ,
проведённая из левого нижнего угла матрицы в правый
верхний.
побочная диагональ
Пример:
главная диагональ
9. Другие определения
Матрица, состоящая из одной строки, называется векторстрокой, а матрица, состоящая из одного столбца, вектор-столбцом.Примеры:
вектор-строка
вектор-столбец
10. Другие определения
Квадратная матрицаназывается
диагональной, если
все ее элементы,
стоящие вне главной
диагонали, равны нулю.
Скалярной называется диагональная матрица S, у которой все
диагональные элементы равны между собой.

Единичной матрицей En называется скалярная матрица
порядка n, диагональные элементы которой равны 1.
11. Другие определения
Матрица называется верхней треугольной матрицей, есливсе элементы ниже главной диагонали равны нулю.
Матрица называется нижней треугольной матрицей, если
все элементы выше главной диагонали равны нулю.
Примеры:
верхнетреугольная
матрица
12. Другие определения
Ступенчатойназывается матрица,
которая содержит m
строк и у которой
первые r ≤ m
диагональных
элементов ненулевые,
а элементы, лежащие
ниже главной
диагонали и элементы
последних (m — r) строк
равны нулю, то есть
это матрица вида:
Главным элементом некоторой
строки матрицы A называется ее
первый ненулевой элемент
13. Другие определения
Матрица А называется ступенчатой, если:все ее нулевые строки стоят после ненулевых;
в каждой ненулевой строке, начиная со второй, ее главный
элемент стоит правее (в столбце с большим номером)
главного элемента предыдущей строки.

Примеры ступенчатых матриц:
НЕ ЯВЛЯЕТСЯ
СТУПЕНЧАТОЙ:
14. Другие определения
Две матрицы называются равными, если они имеютодинаковые размеры и их соответствующие элементы
равны:
Anxm = Bnxm aij = bij, i = 1,n, j = 1,m
Операции над матрицами
16. Произведением матрицы на число
называется матрица, полученная из исходной умножениемкаждого ее элемента на заданное число
B = λA, bij = λaij, i = 1,n, j = 1,m
17. Суммой матриц
A и B одного размера называется матрица C = A + B, такогоже размера, получаемая из исходных путем сложения
соответствующих элементов
C = A + B, cij = aij+bij, i = 1,n, j = 1,m
18. Свойства линейных операций
Умножение матрицы на числоСумма матриц
— линейные операции
1. Ассоциативность: (A + B) + C = A + (B + C)
2. A + Θ = Θ + A, где Θ – нулевая матрица
3. A – A = Θ
4. Коммуникативность: A + B = B + A
5. Дистрибутивность: λ * (A + B) = λ * A + λ * B
6.
 (λ + μ) * A = λ * A + μ * A
(λ + μ) * A = λ * A + μ * A7. (λ * μ) * A = λ * (μ * A)
19. Произведением матриц
Amxn на матрицу Bnxk называется матрица Cmxk такая, чтоэлемент матрицы С, стоящий в i-той строке и j-том столбце
(т.е. элемент cij) равен сумме произведений элементов i-той
строки матрицы A на соответствующие элементы j-го
столбца матрицы B
C = A * B, cij = Σail*blj, l = 1,n
20. Свойства произведения матриц
1. Ассоциативность: (A * B) * C = A * (B * C)2. Ассоциативность по умножению: (μ * A) * B = μ * (A * B)
3. Дистрибутивность: A * (B + C) = A * B + A * C;
(A + B) * C = A * C + B * C
4. Умножение на единичную матрицу: E * A = A * E = A
5. Некоммуникативно: A * B ≠ B * A
21. Транспонирование матрицы
это операция над матрицей, когда ее строки становятсястолбцами с теми же номерами.
Обозначается AT
22. Свойства операции транспонирования матриц
1. (AT)T = A2. (λ * A)T = λ * AT
3. (A + B)T = AT + BT
4.
 (A * B)T = BT * AT
(A * B)T = BT * ATЭлементарные преобразования
матрицы
24. Эквивалентные преобразования над строками матрицы
называют следующие преобразования строк:умножение строки на ненулевое число;
перестановка двух строк;
прибавление к одной строке матрицы другой ее строки,
умноженной на некоторое ненулевое число.
Если от матрицы к матрице перешли с помощью
эквивалентных преобразований над строками, то такие
матрицы называются эквивалентными и обозначают
A ~ B.
Ранг матрицы
26. Определения
Линейной комбинацией (ЛК) строк s1, s2, …, sm матрицы Aназывается выражение λ1s1 + λ2s2 +…+λmsm.
ЛК называется тривиальной, если все коэффициенты λi
равны нулю одновременно.
ЛК называется нетривиальной, если хотя бы один из
коэффициентов λi отличен от нуля.
Система строк называется линейно зависимой (ЛЗ), если
существует их нетривиальная ЛК, равная нулевой строке
Система строк называется линейно независимой (ЛНЗ), если
только тривиальная ЛК равна нулевой строке
27.
 Рангом системы строк называется
Рангом системы строк называетсямаксимальное
независимых строк этой системы
количество
линейно
В каждой матрице может быть два ранга: строчный ранг (ранг
системы строк) и столбцовый ранг (ранг системы столбцов).
Теорема: Строчный ранг матрицы равен её столбцовому рангу
28. Рангом матрицы
называется ранг её системы строк или столбцовОбозначается: rang A.
Элементарные преобразования над строками (столбцами)
матрицы не меняют её ранга.
Ранг ступенчатой матрицы равен количеству её ненулевых
строк.
На практике для нахождения ранга матрицы используют
следующее утверждение: ранг матрицы равен количеству
ненулевых строк после приведения матрицы к ступенчатому
виду.
Решение систем линейных
алгебраических уравнений
методом Гаусса
30. Системой линейных алгебраических уравнений (СЛАУ)
называется система вида:Упорядоченный набор значений {x01, x02, …, x0n} называется
решением системы, если при подстановке в уравнения
все уравнения превращаются в тождество
31.
 Определения СЛАУ называется совместной, если она имеет хотя бы одно
Определения СЛАУ называется совместной, если она имеет хотя бы однорешение.
В противном случае система называется несовместной.
Система называется определённой, если она совместна и
имеет единственное решение.
В противном случае (т.е. если система совместна и имеет
более одного решения) система называется
неопределённой.
Система называется однородной, если все правые части
уравнений, входящих в нее, равны нулю одновременно.
Система называется квадратной, если количество уравнений
равно количеству неизвестных.
32. Определения
Расширенной матрицей системы A = (A|B) называетсяматрица, полученная из матрицы системы A, дописыванием
справа после вертикальной черты столбца свободных
членов B.
33. Принцип метода Гаусса
Метод Гаусса включает в себя прямой (приведениерасширенной матрицы к ступенчатому виду) и обратный
(получение нулей над главной диагональю расширенной
матрицы) ходы.
 Прямой ход и называется методом
Прямой ход и называется методомГаусса, обратный — методом Гаусса-Жордана, который
отличается от первого только последовательностью
исключения переменных.
Метод Гаусса идеально подходит для решения систем
содержащих больше трех линейных уравнений, для
решения систем уравнений, которые не являются
квадратными, т.о. метод Гаусса — наиболее универсальный
метод для нахождения решения любой системы линейных
уравнений, он работает в случае, когда система имеет
бесконечно много решений или несовместна
Приведение матрицы к диагональному виду
Приведение матрицы к диагональному виду [c.317]А-5д. Приведение матриц к диагональному виду. В структурных задачах часто встречаются матрицы разного типа, например матрица энергии. Обычно они эрмитовы, но не обязательно [c.437]
Если С — матрица поворота двумерной системы координат [эта матрица унитарна, см. уравнение (А-48)], то можно развить общий метод приведения к диагональному виду любой матрицы [c. 440]
440]
ПРИВЕДЕНИЕ МАТРИЦЫ СТАТИСТИЧЕСКИХ ВЕСОВ К ДИАГОНАЛЬНОМУ ВИДУ [c.198]
В методе Якоби для приведения матрицы А к диагональному виду с помощью преобразования подобия (10—100) используется ортогональная матрица С, для которой имеет место равенство где транспонированная матрица. Ортогональная матрица С в этом методе определяется как предел последовательности элементарных преобразований, осуществляемых над элементами матрицы А с помощью ортогональных матриц вида [c.286]
Этот метод приведения к диагональному виду эрмитовой матрицы (в данном случае она симметрична) с помощью унитарной матрицы и матрицы, обратной ей, имеет общее значение для любых эрмитовых матриц. В этой книге чаще всего встречаются примеры диагонализации матриц гамильтониана (гл. 10—12 и приложение В), а также диагонализации матриц —тензора и тензора СТВ (гл. 7). [c.440]
Итак, задачу о нахождении собственных значений оператора, заданного в форме матрицы, можно рассматривать как задачу о приведении этой матрицы к диагональному виду. В курсах математики доказывается, что эрмитовы матрицы всегда могут быть приведены к диагональному виду. [c.140]
В курсах математики доказывается, что эрмитовы матрицы всегда могут быть приведены к диагональному виду. [c.140]
Способы экспериментального нахождения матрицы Тш, приведение ее к диагональному виду и определение ориентации молекулярной системы координат относительно осей ориентации кристалла рассмотрены в работе [8]. Не будем здесь касаться этих вопросов, а остановимся на расчете компонент тензора Т. [c.15]
Квадратичная форма (VH.60) положительно определенная. Матрицы и Р действительные и симметрические. Они одинакового порядка г. Поэтому в соответствии с теоремой об одновременном приведении к диагональному виду двух симметрических матриц можно потребовать, чтобы X L X и Х РХ были диагональными матрицами. [c.247]
Если матрица О порядка / имеет кратные собственные числа, то необходимым и достаточным условием приведения ее преобразованием подобия к диагональному виду является равенство ранга матрицы О —11 величине / — где — кратность корня векового уравнения (т. е. среди миноров порядка / — матрицы [c.149]
е. среди миноров порядка / — матрицы [c.149]
Приведенную аргументацию можно изложить гораздо короче все указанные преимущества суть следствие использования ортогональных функций, которые приводят матрицу нормальных уравнений к диагональному виду. Но такое объяснение требует знакомства с соответствующим математическим аппаратом, и мы надеемся, что статья показывает настоятельную практическую необходимость его освоения. [c.163]
Для верхней треугольной матрицы получим тот же результат. Поэтому в целом пет необходимости приводить матрицу определителя к диагональному виду, достаточно привести ее к нижнему или верхнему треугольному виду. Если на каком-то шаге приведения один или несколько столбцов (строк) матрицы обратятся в нуль, то процедура заканчивается, ибо в этом случае определитель равен нулю. [c.38]
Указанные уравнения образуют систему линейных уравнений, и их можно решать как таковые обычным способом. Кроме того, для решения и исследования уравнений (30), (31) можно применять метод приведения матрицы к диагональному виду. [c.358]
[c.358]
Матрица коэффициентов системы (6-12) является трехдиаго» нальной. Для решения такой системы уравнений используется спе» циальный метод, основанный на приведении матрицы к диагональному виду с помощью элементарных преобразований по рекуррентным соотношениям [17] [c.386]
Следовательно, путем приведения матрицы к диагональному виду можно значительно упростить вычисление статистической суммы. Единственная операция, которую необходимо выполнить, — это нахождение собственных чисел матрицы М и построение матриц Т и Т по соответствующим собственным векторам. [c.199]
Матрицы коэффициентов системы (7.203) являются трехдиагональными. Для решения таких систем можно воспользоваться специальным методом, основанном на приведении к диагональному виду с помош ью элементарных преобразований по рекуррентным формулам [c.340]
Эти формулы позволят вычислить матрицы Ь и 8 для антисимметричных состояний при уу-связи при помощи неантисимметричных величин (12. 16). Приведение этих матриц к диагональному виду в случае двухэлектронных состояний вплоть до йй дает ряд матриц преобразования, приведенных в табл. 24. Слева от матриц приведены значения у и у для состояний уу-связи, значение J помещено сверху в рессел-саундерсовских обозначениях. От М преобразования не зависят. [c.290]
16). Приведение этих матриц к диагональному виду в случае двухэлектронных состояний вплоть до йй дает ряд матриц преобразования, приведенных в табл. 24. Слева от матриц приведены значения у и у для состояний уу-связи, значение J помещено сверху в рессел-саундерсовских обозначениях. От М преобразования не зависят. [c.290]
Найти определитель с помощью сокращения строк
\ (\) \ (\) \ (\) \ (\)Приведены примеры и вопросы с их решениями о том, как найти определитель квадратной матрицы с помощью формы эшелона строк. Основная идея состоит в том, чтобы привести данную матрицу к треугольной форме, а затем вычислить ее определитель. Определитель данной матрицы вычисляется из определителя треугольной с учетом свойств, перечисленных ниже.
Детерминантные свойства и сокращение строк
Приведем заданную матрицу в виде эшелона строк (верхний треугольник или нижний треугольник) с учетом следующих свойств определителей:Свойство 1: Если линейная комбинация строк данной квадратной матрицы добавляется к другой строке той же квадратной матрицы, то определители полученной матрицы равны определителю исходной матрицы.

Свойство 2: Если две строки данной матрицы поменять местами, то определитель полученной матрицы равен определителю исходной матрицы, умноженному на -1.
Свойство 3: Если строка данной матрицы умножается на скаляр k, то определитель полученной матрицы равен определителю исходной матрицы, умноженному на k.
Примеры поиска определителя с использованием сокращения строк
Пример 1Объедините строки и используйте указанные выше свойства, чтобы переписать приведенную ниже матрицу 3 3 в треугольной форме и вычислить ее определитель.\ [A = \ begin {bmatrix} 2 и -1 и 3 \\ -2 и 5 и 6 \\ 4 и 6 и 7 \ end {bmatrix} \]
| Решение примера 1 Пусть D будет определителем данной матрицы.  шаг 1: добавить строку (1) в строку (2) — см. Свойство (1) выше — определитель не меняет D \ [ \ color {red} {\ begin {matrix} \\ R_2 = R_2 + R_1 \\ \\ \ end {matrix}} \ begin {bmatrix} 2 и -1 и 3 \\ 0 и 4 и 9 \\ 4 и 6 и 7 \ end {bmatrix} \] шаг 2: вычтите 2 раза строку (1) из строки (3) — см. Свойство (1) выше — определитель не изменит D \ [ \ color {red} {\ begin {matrix} \\ \\ R_3 -2 \ раз R_1 \\ \ end {matrix}} \ begin {bmatrix} 2 и -1 и 3 \\ 0 и 4 и 9 \\ 0 и 8 и 1 \ end {bmatrix} \] шаг 3: вычтите 2 раза строку (2) из строки (3) — см. Свойство (1) выше — определитель не изменит D \ [ \ color {red} {\ begin {matrix} \\ \\ R_3 — 2 \ раза R_2 \ \ end {matrix}} \ begin {bmatrix} 2 и -1 и 3 \\ 0 и 4 и 9 \\ 0 & 0 & -17 \ end {bmatrix} \] Теперь, когда матрица имеет треугольную форму, определитель данной матрицы вычисляется как произведение элементов на главной диагонали (вверху слева направо вниз). Определитель треугольной матрицы = (2) (4) (- 17) = — 136 = D = Det (A) Пример 2 вычислить определитель матрицы \ [A = \ begin {bmatrix} -1 и 2 и 4 и 6 \\ 0 & 0 & 1 & 7 \\ -1 и 2 и 4 и 14 \\ 0 и 2, 4 и 6 \ end {bmatrix} \] Решение примера 3 Пусть D будет определителем данной матрицы. 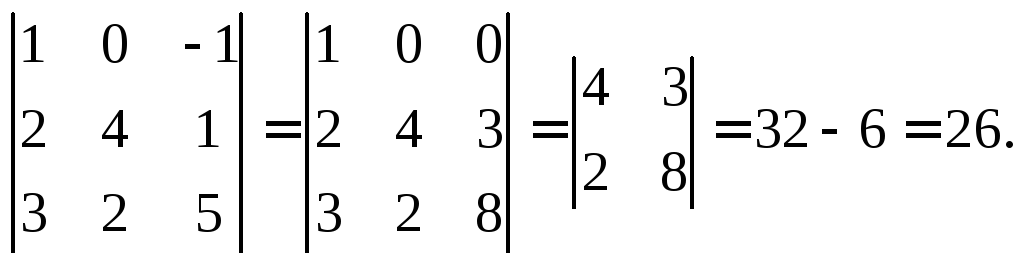 Шаг 1: вычтите строку (1) из строки (3), и согласно свойству (1) определитель не изменится. \ [\ color {красный} {\ begin {matrix} \\ \\ R_3 — R_1 \\ \\ \ end {matrix}} \ begin {bmatrix} -1 и 2 и 4 и 6 \\ 0 & 0 & 1 & 7 \\ 0 & 0 & 0 & 8 \\ 0 и 2, 4 и 6 \ end {bmatrix} \] Шаг 2: поменять местами строки (3) и (4) и согласно свойству (2) знак определителя поменять знак на — D \ [\ color {красный} {\ begin {matrix} \\ \\ \ text {from} R_4 \\ \ text {from} R_3 \\ \ end {matrix}} \ begin {bmatrix} -1 и 2 и 4 и 6 \\ 0 & 0 & 1 & 7 \\ 0 и 2 и 4 и 6 \\ 0 и 0 и 0 и 8 \ end {bmatrix} \] Шаг 3: поменять местами строки (2) и (3) и согласно свойству (2) знак определителя поменять знак на — (- D) \ [\ color {красный} {\ begin {matrix} \\ \ text {from} R_3 \\ \ text {from} R_2 \\ \\ \ end {matrix}} \ begin {bmatrix} -1 и 2 и 4 и 6 \\ 0 и 2 и 4 и 6 \\ 0 & 0 & 1 & 7 \\ 0 и 0 и 0 и 8 \ end {bmatrix} \] Теперь матрица имеет треугольную форму, а ее определитель определяется произведением элементов на главной диагонали.  Определитель треугольной матрицы = (-1) (2) (1) (8) = — 16 = — (- D) = D = Det (A) Вопросы по определителю и редукции строкЧасть 1Используйте метод эшелонированной формы строк для вычисления определителя матриц. \ (A = \ begin {bmatrix} 1 & -1 & -3 & 0 & 1 \\ -1 & 0 & 0 & 1 & 5 \\ 1 и -1 и 1 и 4 и 5 \\ 0 & 0 & 1 & 0 & -1 \\ 1 и 0 и 1 и 2 и 2 \ end {bmatrix} \) Часть 2 Определитель матрицы \ (A = \ begin {bmatrix} а & б & с \\ d & e & f \\ g & h & k \ end {bmatrix} \) равно D. Найдите детермиант в терминах D следующих матриц а) \ (\ begin {bmatrix} 2a и 2b и 2c \\ d & e & f \\ -3g, -3h и -3k \ end {bmatrix} \), б) \ (\ begin {bmatrix} d & e & f \\ а & b & c \\ 7g, 7h и 7k \ end {bmatrix} \) Решения вышеуказанных вопросов Часть 2 Дополнительные ссылки и ссылкиДополнительные ссылки и ссылки |
Онлайн-калькулятор: Калькуляторы матричной триангуляции
Ниже представлены два калькулятора для матричной триангуляции.
Первый использует метод Гаусса, второй — метод Барейсса. Описание методов и их теории приведено ниже.
Матричная триангуляция (метод Гаусса)
3 2 3 4 4 4 3 2 1 4 4 3 2 3 1 1 Точность вычисленияЦифры после десятичной точки: 4
Треугольная матрица (метод Гаусса)
Треугольная матрица (метод Гаусса с максимальным выбором в столбце):
Треугольная матрица (метод Гаусса с максимальным выбор во всей матрице):
content_copy Ссылка сохранить Сохранить расширение Виджет
Матричная триангуляция (метод Барейса)
3 2 3 4 4 4 3 2 1 4 4 3 2 3 1 1 Точность вычисленияЦифры после десятичной точки: 4
Треугольная матрица (метод Барейса)
Треугольная матрица (метод Барейса с максимальным выбором в столбце)
Треугольная матрица (метод Барейса с максимальным выбором во всей матрице)
content_copy Ссылка сохранить Сохранить расширение Виджет
Сначала мы дадим понятие треугольной или строчной эшелонирующей матрице:
Матрица имеет вид строкового эшелона, если:
- все нулевые строки, если таковые имеются, принадлежат нижней части матрицы
- Старший коэффициент (первое ненулевое число слева, также называемое опорной точкой) ненулевой строки всегда находится строго справа от ведущего коэффициента строки над ней
- Все ненулевые строки (строки с хотя бы одним ненулевым элементом) находятся над любыми строками со всеми нулями
Пример матрицы эшелона строк:
1 0 2 5
0 3 0 0
0 0 0 4
Понятие треугольной матрицы более узкое и используется только для квадратных матриц.Это выглядит так: треугольная матрица — это квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.
Пример верхней треугольной матрицы:
1 0 2 5
0 3 1 3
0 0 4 2
0 0 0 3
Кстати, определитель треугольной матрицы вычисляется простым умножением всех ее диагональных элементов.
Вы спросите, чем же интересны эти строковые (и треугольные) матрицы? Что ж, у них есть удивительное свойство — любую прямоугольную матрицу можно свести к матрице эшелона строк с помощью элементарных преобразований.
Итак, что за элементарные преобразования, спросите вы?
Преобразования элементарной матрицы — это следующие операции:
- Переключение строк (строка в матрице может быть заменена другой строкой)
- Умножение строк (каждый элемент в строке можно умножить на ненулевую константу)
- Сложение строк (строка может быть заменена суммой этой строки и кратной другой строке)
Что теперь?
Элементарные преобразования матриц сохраняют эквивалентность матриц.И, если вы помните, что системы линейных алгебраических уравнений записываются только в матричной форме, это означает, что преобразование элементарных матриц не меняет множества решений системы линейных алгебраических уравнений, которые эта матрица представляет.
Триангулируя матрицу линейного уравнения AX = B до A’X = B ‘, т.е. с соответствующим преобразованием столбца B, вы можете выполнить так называемую «обратную подстановку».
Чтобы объяснить, мы будем использовать треугольную матрицу выше и перепишем систему уравнений в более общей форме (я составил столбец B):
Понятно, что сначала найдем, потом подставим в предыдущее уравнение, найдем и так далее — переходя от последнего уравнения к первому.Это то, что называется обратной заменой.
Этот алгоритм сокращения строк называется методом Гаусса. Метод Гаусса — классический метод решения систем линейных уравнений. Его также называют методом исключения Гаусса, так как это метод последовательного исключения переменных, когда с помощью элементарных преобразований системы уравнений приводятся к эшелонированной (или треугольной) форме, в которой размещаются все остальные переменные (начиная с последний).
Теперь несколько мыслей об этом методе.
Как можно обнулить переменную во втором уравнении?
Путем вычитания из него первого, умноженного на коэффициент
Вот пример:
Ноль в первом уравнении
Во втором уравнении нет
В обобщенном смысле метод Гаусса можно представить следующим образом:
где N — размер строки,
— i-й ряд,
— элемент i-го ряда, j-й столбец
Вроде бы отличный метод, но есть один нюанс — его деление на встречающееся в формуле.Во-первых, если диагональный элемент равен нулю, этот метод не сработает. Во-вторых, при расчете отклонение будет расти и чем дальше, тем больше. Так что результат не будет точным.
Для уменьшения отклонения используются модификации метода Гаусса. Они основаны на том, что чем больше знаменатель, тем меньше отклонение. Эти модификации представляют собой метод Гаусса с максимальным выбором по столбцу и метод Гаусса с максимальным выбором по всей матрице. Как следует из названия, перед каждой основой исключения переменной ищется элемент с максимальным значением в строке (всей матрице) и выполняется перестановка строк, поэтому он будет меняться местами с.
Однако существует радикальная модификация метода Гаусса — метод Барейсса.
Как можно избавиться от разделения? Умножив строку на перед вычитанием. Затем вам нужно вычесть, умножить на без деления.
.
Вроде бы хорошо, но при расчетах возникает проблема увеличения значения элемента
Bareiss предложил разделить приведенное выше выражение на и показал, что если исходные элементы матрицы являются целыми числами, то результирующее число будет целым.Также предполагается, что для нулевой строки.
Кстати, то, что алгоритм Барейсса сводит целые элементы исходной матрицы к треугольной матрице с целыми элементами, т.е. без накопления отклонений, это довольно важная особенность с точки зрения машинной арифметики.
Алгоритм Барейса можно представить как:
Этот алгоритм может быть усовершенствован, как и алгоритм Гаусса, с максимальным выбором в столбце (всей матрице) и перестановкой соответствующих строк (строк и столбцов).
Вычислите определитель каждой матрицы, приведя его к верхней треугольной форме. (а) $$ \ left [\ begin {array} {rrr} {1} & {- 1} & {2} \\ {3} & {1} & {1} \\ {2} & {- 1 } & {3} \ end {array} \ right] $$, (b) $$ \ left [\ begin {array} {rrr} {- 1} & {3} & {1} \\ {2} & {5} & {3} \\ {1} & {- 2} & {1} \ end {array} \ right] $$, (c) $$ \ left [\ begin {array} {rrrr} {- 1} & {- 1} & {1} & {0} \\ {2} & {1} & {1} & {3} \\ {0} & {1} & {1} & {2} \ \ {1} & {3} & {- 1} & {2} \ end {array} \ right] $$, (d) $$ \ left [\ begin {array} {llll} {2} & {3 } & {1} & {1} \\ {0} & {2} & {
[математика] \ sinh [/ математика][математика] \ sinh [/ математика]
[math] \ ch [/ math]
[math] \ tanh [/ math]
[math] \ operatorname {sech} [/ math]
[math] \ operatorname {csch} [/ math]
[math] \ coth [/ math]
[математика] \ in [/ математика][математика] \ notin [/ математика]
[математика] \ подмножество [/ математика]
[математика] \ substeq [/ математика]
[математика] \ cap [/ математика]
[математика] \ чашка [/ математика]
[математика] \ существует [/ математика]
[математика] \ forall [/ математика]
[математика] \ грех [/ математика][математика] \ sin [/ математика]
[математика] \ cos [/ математика]
[math] \ tan [/ math]
[математика] \ сек [/ математика]
[математика] \ csc [/ математика]
[математика] \ cot [/ математика]
[математика] \ arcsin [/ математика][математика] \ arcsin [/ математика]
[математика] \ arccos [/ математика]
[математика] \ arctan [/ математика]
[math] \ operatorname {arcsec} [/ math]
[math] \ operatorname {arccsc} [/ math]
[math] \ operatorname {arccot} [/ math]
[math] \ theta [/ math]
[математика] \ phi [/ математика]
[математика] \ varphi [/ математика]
[математика] \ int_ {a} ^ {b} f (x) \, dx [/ math]
[математика] \ bigg | _ {a} ^ {b} [/ math]
[математика] \ left [\ right] _ {a} ^ {b} [/ math]
Верхняя треугольная форма — обзор
1.7 LU Decomposition
Обращение матриц элементарных матриц лежит в основе еще одного популярного метода, известного как разложение LU , для решения одновременных уравнений в матричной форме Ax = b . Способ основан на факторизации невырожденной матрицы коэффициентов A в произведение нижней треугольной матрицы L на верхнюю треугольную матрицу U . Как правило, существует множество таких факторизаций. Если требуется, чтобы L имел все диагональные элементы, равные 1, тогда разложение, если оно существует, уникально, и мы можем записать
(1.33) A = LU
с
L = 100 ⋯ 0l2110 ⋯ 0l31l321 ⋯ 0 ⋮⋮⋮ ⋱ ⋮ ln1ln2ln3 ⋯ 1
U = u11u12u13 ⋯ u1n0u22u23 ⋯ u2n00u23 ⋯ u30003 n A в форму (1.33), мы сначала преобразуем A в верхнюю треугольную форму, используя только операцию третьей элементарной строки R 3 . Это похоже на преобразование матрицы в форму с сокращенной строкой, за исключением того, что мы больше не используем первые две элементарные операции со строками. Мы не меняем местами строки и не умножаем строки на ненулевые константы.Следовательно, мы больше не требуем, чтобы первый ненулевой элемент каждой ненулевой строки был равен 1, и если какая-либо из опорных точек равнялась 0, что указывало бы на обмен строк при преобразовании в форму с сокращенной строкой, тогда искомая нами схема декомпозиции не может быть Выполнено.
Пример 1 Используйте операцию третьей элементарной строки для преобразования матрицы
A = 2−13421−6−12
в верхнюю треугольную форму.
Решение:
| A = 2−13421−6−12 → 2−1304−5−6−12 | путем прибавления ко второй строке — 2 раза к первой строке |
| → 2−1304−50−411 | , прибавив к третьей строке 3 раза первую строку |
| → 2−1304−5006 | , прибавив к третьей строке 1 раз вторую строку |
Если квадратная матрица A может быть приведена к верхней треугольной форме U последовательностью операций с элементарной строкой третьего типа, тогда существует последовательность элементарных матриц E 21 , E 31 , E 41 ,…, E n, n — 1 так, что
(1.34) En, n – 1… E41E31E21A = U
, где E 21 обозначает элементарную матрицу, которая помещает 0 в позицию 2-1, E 31 обозначает элементарную матрицу, которая помещает 0 в позиция 3-1, E 41 обозначает элементарную матрицу, которая помещает 0 в позицию 4-1 и так далее. Поскольку элементарные матрицы имеют обратные, мы можем записать уравнение (1.29) как
(1.35) A = E21−1E31−1E41−1… En, n − 1−1U
Каждая элементарная матрица в уравнении (1.34) имеет нижнюю треугольную форму. Из теоремы 4 раздела 1.5 следует, что каждая из обратных точек в уравнении (1.35) является нижнетреугольной, а затем из теоремы 2 раздела 1.3, что произведение этих обратных нижних треугольников является нижним треугольником. Если мы установим
L = E21−1E31−1E41−1… En, n − 1−1
, тогда L будет нижним треугольником и уравнение (1.35) может быть переписано как A = LU , что разложение, которое мы ищем.
Квадратная матрица A имеет разложение LU , если A можно преобразовать в верхнюю треугольную форму, используя только операцию третьей элементарной строки.
Пример 2 Постройте разложение LU для матрицы, приведенной в Примере 1.
Решение: Элементарные матрицы, связанные с операциями элементарной строки, описанными в Примере 1, равны
E21 = 100−210001, E31 = 100010-301, и E32 = 1000100-11
с инверсиями, соответственно
E21-1 = 100210001, E31-1 = 100010-301 и E32-1 = 1000100-11.
Тогда
2−13421−6−12 = 100210001100010−3011000100−112−1304−5006
или, после умножения обратных элементарных матриц,
2−13421−6−12 = 100210−3 −112−1304−5006.
Пример 2 предлагает важное упрощение процесса разложения. Обратите внимание, что элементы в L , расположенные ниже главной диагонали, являются отрицательными значениями скаляров , используемых в элементарных операциях со строками в Примере 1, чтобы уменьшить A до верхней треугольной формы! Это не случайно.
▸Наблюдение 1
Если при преобразовании квадратной матрицы A в верхнюю треугольную форму ноль помещается в позицию ij путем добавления к строке i скаляра k раз строки j , то элемент ij из L в разложении LU из A равен — k. ◂
Мы резюмируем процесс разложения следующим образом: Используйте только операцию третьей элементарной строки, чтобы преобразовать квадратную матрицу A в верхнюю треугольную форму. Если это невозможно из-за нулевого поворота, остановитесь. В противном случае, разложение LU находится путем определения результирующей верхней треугольной матрицы как U и построения нижней треугольной матрицы L в соответствии с наблюдением 1.
Пример 3 Построение разложения LU для матрицы
A = 212362481−10401−3−4
Решение: Преобразовывая A в верхнюю треугольную форму, мы получаем
| 212362481−10401−3−4 → 21230−1−2−11−10401− 3−4 | прибавив ко второй строке — 3 раза первую строку |
| → 21230−1−2−10−32−15201−3−4 | прибавив к третьей строке — 1/2 раза первая строка |
| → 21230−1−2−1002401−3−4 | путем прибавления к третьей строке — 3/2 раза вторая строка |
| → 21230−1−2−1002400−5− 5 | прибавив к четвертой строке 1 раз второй ряд |
| → 21230−1−2−100240005 | на добавив к четвертой строке 5/2 раза третью строку |
Теперь у нас есть верхняя треугольная матрица U .Чтобы получить нижнюю треугольную матрицу L в разложении, отметим, что мы использовали скаляр — 3, чтобы поместить 0 в позицию 2-1, поэтому его отрицательный — (- 3) = 3 переходит в позицию 2-1. из Л . Мы использовали скаляр — 1/2, чтобы разместить 0 в позиции 3-1 на втором этапе предыдущего процесса триангуляции, так что его отрицательное значение 1/2 становится элементом 3-1 в L ; мы использовали скаляр 5/2, чтобы поместить 0 в позицию 4-3 на последнем этапе процесса триангуляции, так что его отрицательное значение — 5/2 становится элементом 4-3 в L .Продолжая таким же образом, мы генерируем разложение
212362481-10401-3-4 = 100031001232100-1-52121230-1-2-100240005
LU разложения, когда они существуют, используются для решения систем одновременных линейных уравнений . Если квадратную матрицу A можно разложить на A = LU , то система уравнений Ax = b может быть записана как L (Ux) = b . Чтобы найти x , мы сначала решаем систему
(1.36) Ly = b
для y , а затем, как только y определено, мы решаем систему
(1,37) Ux = y
для x . Обе системы (1.36) и (1.37) легко решаются, первая — прямой заменой, а вторая — обратной заменой.
Если A = LU для квадратной матрицы A , то уравнение Ax = b решается сначала путем решения уравнения Ly = b для y , а затем решения уравнение Ux = y для x .
Пример 4 Решите систему уравнений:
2x – y + 3z = 94x + 2y + z = 9–6x – y + 2z = 12
Решение: Эта система имеет матричную форму
2−13421−6−12xyz = 9912
Разложение LU для матрицы коэффициентов A приведено в примере 2. Если мы определим компоненты y как α, β и γ, соответственно , матричная система Ly = b равна
100210−3−11αβγ = 9912
, что эквивалентно системе уравнений
α = 92α + β = 9−3α − β + γ = 12
Решая эту систему сверху вниз, получаем α = 9, β = — 9 и γ = 30.Следовательно, матричная система Ux = y равна
2−1304−5006xyz = 9−930
, что эквивалентно системе уравнений
2x – y + 3z = 94y – 5z = –96z = 30
Решая эту систему снизу вверх, мы получаем окончательное решение x = — 1, y = 4 и z = 5.
Пример 5 Решите систему
2a + b + 2c + 3d = 56a + 2b + 4c + 8d = 8a – b + 4d = –4b – 3c – 4d = –3
Решение: Матричное представление для этой системы имеет в качестве матрицы коэффициентов матрицу A Пример 3.Определим
y = αβγδT
Затем, используя разложение, определенное в примере 3, мы можем записать матричную систему Ly = b как систему уравнений
α = 53α + β = 812α + 32β + γ = −4 − β − 52γ + δ = −3
, которое имеет своим решением α = 5, β = — 7, γ = 4 и δ = 0. Таким образом, матричная система Ux = y эквивалентен системе уравнений
2a + b + 2c + 3d = 5 – b – 2c – d = –72c + 4d = 45d = 0
Решая этот набор снизу вверх, мы вычисляем окончательное решение как a = — 1, b = 3, c = 2 и d = 0.
Задачи 1,7
В задачах с 1 по 14 даны A и b . Постройте разложение LU для матрицы A и затем используйте его для решения системы Ax = b для x .
- (1)
A = 1134, b = 1-6.
- (2)
A = 2112, b = 11-2.
- (3)
A = 8352, b = 625550.
- (4)
A = 110101011, b = 41-1.
- (5)
A = −1201−312−23, b = −1−23.
- (6)
A = 213410−2−1−2, b = 10−400.
- (7)
A = 321401392, b = 508020.
- (8)
A = 12-1201-113, b = 80159-75.
- (9)
A = 12-1021001, b = 8-15.
- (10)
A = 100320112, b = 242.
- (11)
A = 1011110111100111, b = 4−3−2−2.
- (12)
A = 21−13142100−110111, b = 1000200100100.
- (13)
A = 1211112111120111, b = 30301010.
- (14)
A = 20202206-43111031, b = −2494.
- (15)
- (a)
Используйте разложение LU для решения системы
–x + 2y = –92x + 3y = 4
- (b)
Используйте разложение для решения предыдущей системы при замене правых частей уравнений на 1 и — 1 соответственно.
- (16)
- (a)
Используйте разложение LU для решения системы
x + 3y – z = –12x + 5y + z = 42x + 7y – 4z = –6
- (b)
Используйте разложение для решения предыдущей системы, когда правая часть каждого уравнения заменяется на 10, 10 и 10 соответственно.
- (17)
Решите систему Ax = b для следующих векторов b , когда A задан как в Задаче 4:
- (a)
57− 4,
- (b)
220,
- (c)
405020,
- (d)
113.
- (18)
Solo Ax = b для следующих векторов b , когда A задано как в Задаче 13:
- (a)
−1111,
- (b)
0000,
- (в)
116060,
- (г)
1111.
- (19)
Покажите, что разложение LU нельзя использовать для решения системы
2y + z = –1x + y + 3z = 82x – y – z = 1
, но это разложение можно использовать, если поменять местами первые два уравнения.
- (20)
Покажите, что разложение LU нельзя использовать для решения системы
x + 2y + z = 22x + 4y – z = 7x + y + 2z = 2
, но это разложение может использоваться, если поменять местами первое и третье уравнения.
- (21)
- (a)
Покажите, что процедура декомпозиции LU , приведенная в этом разделе, не может быть применена к
A = 0209
- (b)
Убедитесь, что A = LU , когда
L = 1011andU = 0207
- (c)
Убедитесь, что A = LU , когда
L = 1031andU = 0203
- (d) Как вы думаете, почему процедура разложения LU не работает для этого A ? Чем можно объяснить тот факт, что A имеет более одного разложения LU ?
Объяснение урока: операции с элементарными строками
В этом пояснении мы узнаем, как выполнять элементарные операции со строками в матрице и как представлять систему линейных уравнений в виде расширенной матрицы.
Одна из роскоши при работе с линейной алгеброй — это огромное разнообразие методов, которые часто доступны для решения проблема или завершение расчета. Возможно, наиболее показательным из них является метод исключения Гаусса – Жордана, где любая комбинация допустимых строковых операций может использоваться для приведения матрицы к форме сокращенного эшелона, который часто используется для решения системы линейных уравнений. Метод исключения Гаусса – Жордана также можно использовать для вычислить обратную квадратную матрицу (если она существует), как и сопряженный метод.Принципы присоединения также можно использовать для вычисления определителя матрицы, который в качестве альтернативы можно найти с помощью расширение по любой строке или столбцу и объединение с соответствующими минорами матрицы. Это смешение эквивалентных идеи — прекрасная особенность линейной алгебры, которая вознаграждает за долгое изучение и исследование. Неизбежно, однако люди в конечном итоге останавливаются на своих любимых методах работы с линейной алгеброй, часто забывая или полностью игнорируя другие, эквивалентные идеи, которые могут быть существенно более полезными.
Часто при вычислении определителя матрицы мы использовали один из двух методов, упомянутых выше. Однако есть один метод, который для сравнения используется нечасто, несмотря на то, что он универсален и якобы аналогично процессу исключения Гаусса – Жордана. Наша цель будет заключаться в использовании элементарных операций со строками для управления матрицу в верхнетреугольную форму, отслеживая любое влияние на определитель, а затем используйте эту форму для быстрого вычислить окончательный ответ.Для этого нам нужно сначала повторить операции с элементарными строками для матриц.
Определение: элементарные операции со строками
Рассмотрим матрицу 𝐴 порядка 𝑚 × 𝑛 со строками, помеченными 𝑟, 𝑟,…, 𝑟. Затем мы можем выполнить следующие три элементарные операции со строками:
- Переключение строки 𝑖 со строкой 𝑗, обозначенной 𝑟↔𝑟;
- Масштабирование строки 𝑖 ненулевой константой 𝑐, обозначаемой 𝑟 → 𝑐𝑟;
- Добавление масштабированной версии строки 𝑗 в строку 𝑖, обозначенную 𝑟 → 𝑟 + 𝑐𝑟.
Если операция элементарной строки используется для преобразования матрицы 𝐴 в новую матрицу 𝐴, то мы должны сказать, что эти две матрицы «эквивалентны по строкам».
Чтобы продемонстрировать эффект этих операций со строками, рассмотрим матрицу 𝐴 = 12610301102−2012.
Операцию с первой элементарной строкой проще всего описать, поскольку она включает в себя переключение только двух строк, без изменений в их записях. Например, строковая операция 𝑟↔𝑟 меняет местами первую и третью строки, оставляя все остальные строки без изменений: 2−20123011012610.
Мы также можем взять целую строку и умножить ее на ненулевую константу. Предположим, что мы хотели умножьте каждую запись во второй строке этой новой матрицы на коэффициент масштабирования 3. Мы бы использовали элементарная операция со строкой 𝑟 → 3𝑟 на матрице непосредственно выше, давая 2−201212610.
Как видим, изменение коснулось только второй строки. Чтобы продемонстрировать третий тип операции элементарной строки выбираем пример 𝑟 → 𝑟 − 2𝑟. Это требует каждого элемент в первой строке, удваивает его, а затем вычитает его из записи в том же столбце третий ряд.Это изменяет только третью строку матрицы, давая 2−2012−366−1−4.
Все вышеперечисленные матрицы эквивалентны строкам, потому что мы можем преобразовывать одну в другую, только с использованием элементарных операций со строками. Если бы мы работали с квадратной матрицей, мы могли бы Интересует, как определитель изменяется между сериями матриц, эквивалентных строкам. Со строкой операции настолько полезны при работе с матрицами, что понятно, что мы могли бы классифицируйте влияние на концепцию, которая столь же распространена, как и детерминант.Результаты приятно простой, как описано в следующей теореме.
Теорема: элементарные операции со строками и определитель
Рассмотрим квадратную матрицу 𝐴 порядка 𝑛 × 𝑛. Тогда предположим, что элементарный Строчная операция используется для создания эквивалентной строки матрицы 𝐴. Тогда эффект от каждой элементарной операции со строкой будет следующим:
- Для 𝑟↔𝑟, где 𝑖 ≠ 𝑗, имеем | 𝐴 | = — | 𝐴 |.
- Для 𝑟 → 𝑐𝑟, где 𝑐 ≠ 0, имеем | 𝐴 | = 𝑐 | 𝐴 |.
- При 𝑟 → 𝑟 + 𝑐𝑟 имеем | 𝐴 | = | 𝐴 |.
Операция с первой элементарной строкой просто влияет на определитель, вводя только изменение знака. Операция второй строки включает масштабирование всей строки ненулевой константой, что соответствует масштабированию определитель тем же номером. Операция третьего элементарного ряда является самой сложной и, тем не менее, нет общего влияния на детерминант. Последний результат особенно удобен, потому что мы будем использовать элементарные операции со строками, чтобы привести квадратные матрицы к верхнетреугольной форме.Если мы будем использовать третий тип операции с элементарной строкой, тогда не будет необходимости изменять детерминант вообще, что, безусловно, будет преимуществом. В следующих двух примерах мы будем продемонстрировать, как реализовать элементарные операции со строками, и отследить общее влияние на определитель.
Пример 1: Элементарные операции со строками и определитель матрицы 2 × 2
Рассмотрим матрицу 𝐴 = 263−1.
После получения эквивалентной строки матрицы 𝐴 путем выполнения следующих элементарных операций со строками по порядку: 𝑟 → 12𝑟, 𝑟↔𝑟, 𝑟 → 𝑟 − 2𝑟, и 𝑟 → 𝑟 − 𝑟, каков определитель матрицы в терминах определителя эквивалентной строки матрицы?
Ответ
Применяем первую строчную операцию 𝑟 → 12𝑟, чтобы получить эквивалентную по строке матрицу. 𝐴 = 133−1.
Учитывая, что мы использовали операцию элементарной строки, мы должны отслеживать влияние на определитель. Мы реализовали 𝑟 → 12𝑟, что означает, что определитель должен масштабироваться на то же число. Другими словами, | 𝐴 | = 12 | 𝐴 |. Далее мы выполняем операцию замены строк 𝑟↔𝑟, присвоение этой матрицы предыдущей переменной 𝐴, давая 𝐴 = 3−113.
(Хотя перезапись переменной, подобная этой, является несколько неправильной записью, она очень удобна для отслеживания общего воздействия на определитель, поэтому мы допускаем его в данной ситуации.)
Мы использовали операцию перестановки строк, и это означает, что есть изменение знака в определителе, давая | 𝐴 | = −12 | 𝐴 |. Операция элементарной строки 𝑟 → 𝑟 − 2𝑟 не влечет за собой никаких изменений в определителе. Следовательно, матрица 𝐴 = 1−713 имеет предыдущее детерминантное соотношение 𝐴 = −12 | 𝐴 |. Так же, операция элементарной строки 𝑟 → 𝑟 − 𝑟 также не действует на определителе, несмотря на то, что возвращает матрицу 𝐴 = 1−7010.
В целом связь между определителями двух матриц | 𝐴 | = −12 | 𝐴 |. Преобразование этого уравнения дает | 𝐴 | = −2 | 𝐴 |.
Мы можем проверить правильность ответа в предыдущем примере, исследуя детерминанты обеих матриц: 𝐴 = 263−1, 𝐴 = 1−7010.
Для исходной матрицы 𝐴 мы могли бы использовать стандартную формулу для определителя матрицы 2 × 2 для вычисления | 𝐴 | = || 263−1 || = 2 × (−1) −6 × 3 = −20.
Применение того же метода к эквивалентной строке матрицы 𝐴 дает | 𝐴 | = || 1−7010 || = 1 × 10 — (- 7) × 0 = 10.
Это подтверждает обнаруженную в предыдущем примере взаимосвязь между детерминантами: | 𝐴 | = −2 | 𝐴 |.
Пример 2: Элементарные операции со строками и определитель матрицы 3 × 3
Рассмотрим матрицу 𝐴 = 15−2201−120.
После получения эквивалентной строки матрицы 𝐴 путем выполнения следующих элементарных операций со строками по порядку: 𝑟 → 3𝑟, 𝑟 → −2𝑟, 𝑟 → 𝑟 + 𝑟, 𝑟↔𝑟, и 𝑟 → 𝑟 − 2𝑟, каков определитель в терминах определитель эквивалентной строки матрицы 𝐴?
Ответ
Первой операцией со строкой, которую нам нужно выполнить, является масштабирование строки 𝑟 → 3𝑟.Это дает эквивалентную строку матрицу 𝐴 = 15−2603−120.
Учитывая, что мы масштабировали одну из строк на константу 3, мы должны помнить, что | 𝐴 | = 3 | 𝐴 |. Затем нас просят выполнить еще одно масштабирование строки операция: 𝑟 → −2𝑟. Новая матрица 𝐴 = − 2−104603−120 и мы должны обновить взаимосвязь между детерминантами, в данном случае | 𝐴 | = (- 2) × 3 | 𝐴 | = −6 | 𝐴 |. Следующая элементарная строковая операция: 𝑟 → 𝑟 + 𝑟, который относится к третьему типу строковой операции и поэтому не влияет на определитель.Строка эквивалентная матрица 𝐴 = − 2−104603523 поэтому сохраняет определяющее соотношение | 𝐴 | = −6 | 𝐴 |. Операция перестановки строк влечет изменение знака определителя. Используя 𝑟↔𝑟, чтобы получить матрицу 𝐴 = 523603−2−104 означает, что детерминантное отношение должно быть изменено, чтобы включить изменение знака, означает, что | 𝐴 | = 6 | 𝐴 |. Последняя строчная операция 𝑟 → 𝑟 − 2𝑟 снова относится к типу, который не меняет определителя.Следовательно, эквивалентная строка матрица 𝐴 = 523−4−4−3−2−104 имеет определяющее отношение | 𝐴 | = 6 | 𝐴 |. Преобразование уравнения дает | 𝐴 | = 16 | 𝐴 |.
Как и в предыдущем вопросе относительно матрицы 2 × 2, мы также можем проверить пример выше, вручную вычислив определитель. Для этого мы используем правило Сарруса для обеих матриц: 𝐴 = 15−2201−120, 𝐴 = 523−4−4−3−2−104.
Для исходной матрицы 𝐴 находим | 𝐴 | = (1) × || 0120 || — (5) × || 21−10 || + (- 2) × || 20−12 || = + (1) × (−2) — ( 5) × (1) + (- 2) × (4) = — 15.
Тогда для эквивалентной строки матрицы 𝐴 правило Сарруса дает | 𝐴 | = (5) × || −4−3−104 || — (2) × || −4−3−24 || + (3) × || −4−4−2−10 | | = + (5) × (−46) — (2) × (−22) + (3) × (32) = — 90.
Как и ожидалось, мы подтвердили связь, указанную в конце предыдущего вопроса, а именно, что | 𝐴 | = 16 | 𝐴 |.
Наша работа до сих пор была полезной тем, что позволяла нам использовать строковые операции (одна из наиболее распространенных использованные инструменты линейной алгебры), чтобы упростить вычисление определителей (один из наиболее распространенных вычисляемые величины в линейной алгебре).Несмотря на очевидные преимущества такого инструментария, у нас есть еще не использовали это в полной мере. В приведенных выше примерах для создания отношения между эквивалентными строками матрицами, что позволит оптимизировать подход к вычисление определителя. Однако мы еще не показали, как этот метод может быть использован на самом деле вычислить определитель матрицы автономным способом. Для этого нам понадобится еще один результат поразительной элегантности, которая связывает верхнетреугольные матрицы с определителем.
Теорема: верхнетреугольная форма и определитель
Для квадратной матрицы 𝐴 в верхнетреугольной форме определитель | 𝐴 | — произведение диагональных элементов.
Эту теорему можно объединить с нашим пониманием того, как элементарные операции со строками будут влияет на детерминант матрицы, и это в равной степени относится к нижнетреугольным матрицам (которые здесь бесполезны, но встречаются во многих контекстах, таких как разложение LU и PLU). Еще более полезно то, что этот подход использует почти идентичные методы и тактики для при выполнении исключения Гаусса – Жордана найти эшелонированную форму матрицы.Как мы будем см. следующие примеры, можно радикально сократить расчет детерминант, если операции со строками могут быть быстро использованы для преобразования матрицы в эквивалентную по строке матрицу, которая также имеет верхнюю треугольную форму. Любую матрицу в таком виде можно вычислить по приведенной выше теореме.
Пример 3: Вычисление определителя матрицы 2 × 2 с использованием элементарных операций со строками
Рассмотрим матрицу 𝐴 = 243−1.
- Используйте элементарные операции со строками, чтобы привести матрицу к верхнетреугольной форме.
- Вычислить определитель матрицы 𝐴.
Ответ
Перед тем, как использовать какие-либо операции со строками, мы выделяем опорные точки в каждой строке, которые являются первыми ненулевыми записями: 𝐴 = 243−1.
Существует бесконечно много способов преобразовать эту матрицу в верхнетреугольную форму. форма с использованием элементарных операций со строками. Ниже приводится один из таких методов. при этом мы стремимся удалить опорную точку во второй строке с помощью строковых операций, тем самым помещая матрицу в верхнетреугольную форму.Подберем подход который использует строковые операции для присвоения поворотным точкам одинакового значения. Операция масштабирования строки 𝑟 → 3𝑟 возвращает эквивалентную строку матрицу 𝐴 = 6123−1.
Масштабируя каждую запись в одной из строк ненулевой константой, мы повлияли на детерминант матрицы такая, что | 𝐴 | = 3 | 𝐴 |. Теперь мы будем использовать строковую операцию 𝑟 → 2𝑟, чтобы убедиться, что два поворота имеют одинаковое значение: 𝐴 = 6126−2.
Мы снова изменили определитель так, что | 𝐴 | = 2 × 3 | 𝐴 | = 6 | 𝐴 |.Теперь легко превратить эту матрицу в верхнетреугольную форму с строчная операция 𝑟 → 𝑟 − 𝑟. Этот тип строковой операции не изменяется определитель, означающий, что выводимая матрица 𝐴 = 6120−14 и нет изменений в определяющем соотношении | 𝐴 | = 6 | 𝐴 |. В качестве альтернативы (и с большей пользой) мы можем эквивалентно сказать, что | 𝐴 | = 16 | 𝐴 |.
Теперь, когда 𝐴 — верхнетреугольная матрица, определитель | 𝐴 | просто произведение диагональных элементов.Другими словами, мы имеем | 𝐴 | = 6 × (−14) = — 84. Учитывая, что | 𝐴 | = 16 | 𝐴 |, имеем | 𝐴 | = 16 × (−84) = — 14. Это можно проверить, напрямую вычислив определитель любым допустимым методом.
Мы не можем утверждать, что описанный выше метод был проще, чем стандартный метод вычисления определителя. матрицы 2 × 2. Трудно представить себе ситуацию, когда использование строковых операций было бы предпочтительнее для вычисления определителя матриц с таким порядком, хотя достоинства быстро становятся снимается при работе с матрицами порядка 3 × 3 и более.Это определенно не так что метод, представленный в этом пояснении, лучше в любой ситуации, хотя в следующих примеры ясно, что использование строковых операций даст быстрый ответ по сравнению с более грубым инструментом такие как правило Сарруса. Как показывает практика, чем ближе матрица к верхнетреугольной форме, тем полезнее будет наш метод.
Также стоит иметь в виду, что третий тип строковой операции 𝑟 → 𝑟 + 𝑐𝑟 не влияет на детерминант.Обычно мы выбираем эту строковую операцию, если она не работает. приводит к получению слишком большого количества фракций (что может загрязнить последующую работу с распространяющиеся ошибки). Ключевой навык работы с этим методом — умение понимать ситуации. в котором метод, который мы представили, является наиболее подходящим, с принципом работы, заключающимся в том, что по возможности следует использовать третий тип строковой операции.
Пример 4: Вычисление определителя матрицы 3 × 3 с использованием элементарных операций со строками
Рассмотрим матрицу 𝐴 = 13−6021142.
- Используйте элементарные операции со строками, чтобы привести матрицу к верхнетреугольной форме.
- Вычислить определитель матрицы 𝐴.
Ответ
Сначала мы выделяем опорную точку в каждой из строк. Это первые ненулевые записи каждой строки: 𝐴 = 13−6021142.
Чтобы получить верхнетреугольную форму, сначала необходимо заменить стержень в третьем ряду. с нулевой записью. Один из вариантов достижения этого — строчная операция 𝑟 → 𝑟 − 𝑟, что дает эквивалентную строку матрицу 𝐴 = 13−6021018.
Мы использовали третий тип строковой операции, которая не изменяет определитель и, следовательно, | 𝐴 | = | 𝐴 |. Получим верхнетреугольную форму форму, если стержень в третьей строке можно переместить вправо, заменив эта запись с нуля. Операция 𝑟 → 𝑟 − 12𝑟 предоставляет эквивалентную строку матрицу 𝐴 = ⎛⎜⎜⎝13−602100152⎞⎟⎟⎠.
Этот тип строковой операции не изменил определитель 𝐴. Теперь, когда 𝐴 находится в верхней треугольной форме, определитель вычисляется взяв произведение диагональных элементов.Это дает | 𝐴 | = 1 × 2 × 152 = 15. Поскольку | 𝐴 | = | 𝐴 |, заключаем, что | 𝐴 | = 15. Этот результат можно проверить по правилу Сарруса или любым другим допустимым методом.
В примерах, с которыми мы работали до сих пор, все детерминанты были ненулевыми, что означает, что матрица будет обратимой. Мы видели, что определитель верхнетреугольная матрица вычисляется как произведение диагональных элементов. Если какой-либо из этих элементов равны нулю, определитель матрицы также будет равен нулю.В следующем примере мы будем использовать элементарные операции со строками для управления квадратом. матрицу в верхнетреугольную форму, после чего мы обнаружим, что один из диагональных элементов равно нулю, что означает, что определитель будет равен нулю и, следовательно, матрица не будет обратимой.
Пример 5: Вычисление определителя матрицы 3 × 3 с использованием элементарных операций со строками
Рассмотрим матрицу 𝐴 = − 26−1−13−1−26−7.
- Используйте элементарные операции со строками, чтобы привести матрицу к верхнетреугольной форме.
- Вычислить определитель матрицы 𝐴.
Ответ
Сначала выделим все сводные записи в матрице 𝐴: 𝐴 = − 26−1−13−1−26−7.
Чтобы преобразовать эту матрицу в верхнетреугольную форму с помощью операций со строками, обычно выгодно указывать значение «1» в левом верхнем углу. матрицы, так что оставшиеся записи в этом столбце может быть легче удаленный. Один из способов добиться этого — использовать сводную запись во второй строке, поместив это в первую строку с помощью операции обмена 𝑟↔𝑟.Это дает эквивалентную строку матрицу 𝐴 = − 13−1−26−1−26−7.
Учитывая, что мы однажды использовали операцию перестановки строк, мы изменили знак определителя, означает, что | 𝐴 | = — | 𝐴 |. Теперь поворотной точке в левом верхнем углу можно присвоить значение 1 с помощью операции масштабирования строки. 𝑟 → −𝑟, что дает 𝐴 = 1−31−26−1−26−7.
Мы увеличили одну из строк в матрице константой, в данном случае константой -1. Мы просто корректируем знак определителя, а это значит, что | 𝐴 | = — (- | 𝐴 |) = | 𝐴 |.Теперь мы можем использовать третий тип строковой операции, чтобы начать переходя к верхнетреугольной форме. Сводные записи во втором и третьи строки могут быть превращены в нулевые записи с помощью параллельных операций со строками 𝑟 → 𝑟 + 2𝑟 и 𝑟 → 𝑟 + 2𝑟. Это дает матрицу 𝐴 = 1−3100100−5.
Третий тип операции со строкой не вызывает никаких изменений в определителе, что означает, что мы поддерживаем связь | 𝐴 | = | 𝐴 |. Также можно заметить, что теперь матрица 𝐴 на самом деле имеет форму верхнего треугольника, что означает, что определитель — это просто произведение диагональных входов.Учитывая, что один из этих элементов равен нулю, мы находим, что | 𝐴 | = | 𝐴 | = 0 × 0 × (−5) = 0.
Преимущества этого метода могут быть дополнительно оценены при работе с матрицами даже больших порядков. Для таких матриц стандартный метод вычисления определителя учитывает элемент выбора, чтобы упростить расчеты. Однако чаще всего невозможно избежать большое количество вычислений при использовании стандартного метода, поэтому мы должны быть открыты для альтернативный подход, который мы разработали в этом объяснителе.Как и в предыдущем примере, в следующем вопросе мы должны быть заинтересованы в использовании третьего типа строковых операций, чтобы преобразовать матрицу в верхнетреугольную форму.
Пример 6: Вычисление определителя матрицы 4 × 4 с использованием элементарных операций со строками
Рассмотрим матрицу 𝐴 = ⎛⎜⎜⎝10360−105203−20241⎞⎟⎟⎠.
- Используйте элементарные операции со строками, чтобы привести матрицу к верхнетреугольной форме.
- Вычислить определитель матрицы 𝐴.
Ответ
Сначала выделим опорные точки в каждой из строк: 𝐴 = ⎛⎜⎜⎝10360−105203−20241⎞⎟⎟⎠.
Наша цель будет заключаться в использовании строковых операций для преобразования этой матрицы в верхнетреугольную форму. Во-первых, мы должны удалить ненулевую запись в третьей строке. Сделать это, мы можем использовать первую строку следующим образом: 𝑟 → 𝑟 − 2𝑟. Это дает эквивалентную строку матрицу 𝐴 = ⎛⎜⎜⎝10360−10500−3−140241⎞⎟⎟⎠.
На определитель не повлиял из-за типа строковой операции, которую мы использовали.Следовательно, | 𝐴 | = | 𝐴 |. Теперь мы должны удалить опорную точку в четвертой строке, поэтому мы выбираем строковую операцию 𝑟 → 𝑟 + 2𝑟, что дает 𝐴 = ⎛⎜⎜⎝10360−10500−3−1400411⎞⎟⎟⎠.
Опять же, мы не меняли определитель и, следовательно, | 𝐴 | = | 𝐴 |. Для приведения матрицы к верхнетреугольной форме требуется одна последняя строковая операция: 𝑟 → 𝑟 + 43𝑟. Результат 𝐴 = ⎛⎜⎜⎜⎝10360−10500−3−14000−233⎞⎟⎟⎟⎠.
Матрица 𝐴 теперь имеет верхнетреугольную форму и, следовательно, определитель является произведением всех диагональных элементов.Это значит, что | 𝐴 | = | 𝐴 | = 1 × (−1) × (−3) × − 233 = −23.
Этот метод использования операций со строками очень напоминает метод исключения Гаусса – Жордана, где мы бы стремились достичь упрощенной формы матрицы. Фактически, многие из те же стратегии применимы к нашему методу вычисления определителя с использованием операций со строками для получения эквивалентной по строке верхнетреугольной матрицы. Эти две техники не идентичны, и метод, продемонстрированный в этом объяснении, более тесно связан с идеей LU или Декомпозиция PLU, при которой матрицы определенной формы используются для упрощения сложных вычислений. и служат основой многих разносторонних и проницательных теорем.Хотя бывает много ситуаций (например, те, что мы привели в этом объяснении), где использование строковых операций явно является оптимальным метод расчета определителя, не менее важно быть знакомым с другими доступными методы, поскольку всегда будут ситуации, в которых они более применимы.
Ключевые моменты
- Три элементарных операции со строками можно использовать для вычисления определителя квадратной матрицы путем преобразования его в эквивалентная строка верхнетреугольная матрица.
- Первый тип строковой операции (𝑟↔𝑟) изменяет знак определителя.
- Второй тип строковой операции (𝑟 → 𝑐𝑟𝑐 ≠ 0, где) умножает определитель на 𝑐.
- Третий тип строковой операции (𝑟 → 𝑟 + 𝑐𝑟) предпочтительнее, поскольку он не влияет на определитель.
- Чем ближе квадратная матрица к верхнетреугольной форме, тем больше вероятность, что этот метод будет оптимальным.
4×4 Определитель | Суперпроф
Что такое детерминанты?
Определитель — это скалярное значение, полученное из элементов квадратной матрицы.Другими словами, мы можем сказать, что при вычислении определителя входными данными является квадратная матрица, а выходными данными — скалярное число. В квадратной матрице количество строк и столбцов равно. Определитель матрицы обозначен двумя вертикальными линиями ||. Например, определитель матрицы A обозначим как | A |.
Определитель матрицы — важное понятие в линейной алгебре, поскольку он весьма полезен при решении линейных уравнений, изменении переменных в интегралах и сообщении нам, как линейные преобразования изменяют площадь или объем.Они также полезны при вычислении обратной матрицы и имеют некоторые приложения в исчислении.
Определителем матрицы 1×1 является само число. Например, определитель матрицы
.Определитель матрицы 2×2 приведен ниже:
По мере того, как мы получаем матрицы более высокого порядка, вычисление определителей становится все более и более сложным. Например, просто посмотрите на следующую формулу для вычисления определителя матрицы 3×3.
Для этой матрицы вам необходимо разбить большую матрицу на меньшие матрицы 2×2. В следующем разделе мы увидим, как вычислить определитель матрицы 4×4.
Лучшие преподаватели по математике
Первый урок бесплатноВычисление определителя матрицы 4×4
Матрица 4×4 состоит из 4 строк и 4 столбцов. Было бы очень трудоемко и сложно найти определитель матрицы 4×4, используя элементы в первой строке и разбивая матрицу на более мелкие подматрицы 3×3.
В этом разделе мы увидим, как вычислить определитель матрицы 4×4, используя метод исключения Гаусса и свойства матрицы. Но прежде чем переходить к примерам, вы должны знать, что такое метод исключения Гаусса и различные виды треугольных матриц.
Исключение по Гауссу
Исключение по Гауссу также называется сокращением строки. В линейной алгебре алгоритм Гаусса используется для решения системы линейных уравнений. По сути, это серия операций, применяемых к элементам матрицы.Этот метод полезен при нахождении рангов, вычислении определителей и обратных матриц.
Для сокращения строк мы применяем ряд арифметических операций с матрицей, так что каждый элемент ниже главной диагонали матрицы становится нулевым. Этот метод включает в себя три вида операций со строками:
- Перестановка двух строк. Значение определителя меняет знак, т.е. если оно было отрицательным, становится положительным и наоборот.
- Умножение строки на ненулевую константу.Определитель остается неизменным.
- Добавление или вычитание одной строки из другой. Это не влияет на значение определителя.
Треугольное свойство матрицы
Вспомните треугольное свойство определителя, которое гласит, что если каждый элемент в матрице выше или ниже главной диагонали равен нулю, определитель равен произведению элементов на диагонали. . Существует три вида треугольных матриц:
Верхняя треугольная матрица
Матрицы, в которых все, что ниже диагонали, равно нулю.Все ненулевые элементы находятся выше главной диагонали. Например, рассмотрим следующую матрицу, которая имеет верхнюю треугольную форму:
Нижняя треугольная матрица
Матрицы, в которых все элементы над главной диагональю равны нулю. Все ненулевые элементы присутствуют под главной диагональю. Например, рассмотрим следующую матрицу, имеющую форму нижнего треугольника:
Диагональная матрица
На главной диагонали присутствуют все ненулевые элементы.Все, что находится выше или ниже главной диагонали, равно нулю. Например, рассмотрим следующую диагональную матрицу, в которой все элементы, кроме главной диагонали, равны нулю.
Определители таких матриц являются произведением элементов на их диагоналях.
При нахождении определителя матрицы 4×4 целесообразно преобразовать матрицу в треугольную форму, применяя операции со строками в свете метода исключения Гаусса. После того, как мы преобразовали матрицу в треугольную форму, мы можем просто умножить элементы по диагонали, чтобы получить определитель матрицы.
Пример 1
Найдите определитель следующей матрицы 4×4.
Решение
При нахождении определителей матриц мы можем добавлять строки и столбцы к другим строкам и столбцам. Это не повлияет на определитель матрицы. Давайте применим эти операции к матрице выше, чтобы преобразовать ее в треугольную форму:
Результирующий определитель будет выглядеть так:
Вы можете видеть, что все элементы ниже главной диагонали — нули, поэтому эта матрица имеет верхнюю треугольную форму.Умножим элементы по диагонали, чтобы получить определитель.
Пример 2
Найдите определитель следующей матрицы 4×4.
Решение
Давайте применим эти операции к матрице выше, чтобы преобразовать ее в треугольную форму:
Результирующий определитель будет выглядеть так:
Вы можете видеть, что все элементы ниже главной диагонали находятся нули, поэтому эта матрица имеет верхнюю треугольную форму.Чтобы получить определитель, умножим элементы на главной диагонали.
Пример 3
Найдите определитель следующей матрицы 4×4.
Решение
Давайте применим эти операции к матрице выше, чтобы преобразовать ее в треугольную форму:
Результирующий определитель будет выглядеть так:
Вы можете видеть, что все элементы ниже главной диагонали находятся нули, поэтому эта матрица имеет верхнюю треугольную форму.Вы можете видеть ниже, что мы умножили все элементы на главной диагонали друг на друга, чтобы получить определитель.
Экономичный подход к выбору гибкой оси для оценки детерминанта и инверсии матрицы
PLoS One. 2014; 9 (2): e87219.
, 1 , * , 1 , 1 , 2 и 3Хафса Атхар Джафри
1 Кафедра математических наук, Университет Карачи, Карачи, Пакистан,
Мухаммад Имтиаз
1 Кафедра математических наук, Университет Карачи, Карачи, Пакистан,
Сайед Инаятулла
1 Кафедра математических наук, Университет Карачи, Карачи, Пакистан,
Фозия Ханиф Хан
2 Департамент математики Инженерно-технологического университета сэра Сайда, Карачи, Пакистан,
Таджуддин Низами
3 Департамент математики, Университет Икра, Карачи, Пакистан,
Херардо Адессо, редактор
1 Кафедра математических наук, Университет Карачи, Карачи, Пакистан,
2 Департамент математики Инженерно-технологического университета сэра Сайда, Карачи, Пакистан,
3 Департамент математики, Университет Икра, Карачи, Пакистан,
Ноттингемский университет, Соединенное Королевство,
Конкурирующие интересы: Авторы заявили, что никаких конкурирующих интересов не существует.
Задумал и спроектировал эксперименты: SI. Проведены эксперименты: ФХК ТН. Написал газету: HAJ. Формулировка модели: HAJ. Разработка алгоритмов: HAJ MI SI.
Поступила 26.07.2013; Принято 25 декабря 2013 г.
Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего указания автора и источника.
Эта статья цитируется в других статьях в PMC.Abstract
В этой статье представлены новые простые подходы к вычислению определителя и инверсии матрицы. Выбор оси вращения оставлен произвольным, поэтому они уменьшают ошибку при решении плохо подготовленной системы. Вычисление определителя матрицы стало более эффективным за счет экономии ненужных данных, а также за счет уменьшения порядка матрицы на каждой итерации, в то время как словарная нотация [1] была включена для вычисления обратной матрицы, что позволило сэкономить ненужные вычисления.Эти алгоритмы ориентированы на аудиторию, просты в использовании и реализуются студентами. Воспользовавшись гибкостью при выборе стержня, можно легко избежать развития фракций большинством. В отличие от метода обращения матриц [2] и [3], представленные алгоритмы исключают использование перестановок и обратных перестановок.
Введение
Термин определитель изначально ассоциировался с системой линейных уравнений. Это дает нам возможность предвидеть характер решения данной системы линейных уравнений.
Маклорен [4] опубликовал первый результат по определителю системы и, который был обобщен для систем Крамером [5]. Позже Лапласом было предложено хорошо известное разложение Лапласа для оценки определителя, но он тогда использовал термин «результирующий» вместо определителя. Первое использование термина определитель в современном контексте было сделано Коши [6]. В 1866 году Доджсон представил другой метод нахождения определителя систем, который он назвал «методом конденсации» [7].Для более крупных систем наиболее предпочтительным методом оценки определителя до сих пор является метод Гаусса [8]. Он решает проблему путем преобразования матрицы коэффициентов в ее эквивалентную верхнюю / нижнюю треугольную форму. Произведение поворотных элементов дает определитель.
Существование обратной матрицы также зависит от ее определителя. Метод нахождения обратного по методу Гаусса обсуждается далее в этой статье. Ахмед и Хан [2] и Хан, Шах и Ахмад [3] предложили алгоритмы для вычисления обратной матрицы, которые являются упрощенными формами метода Гаусса и также требуют перестановок и обратных перестановок.В этой статье мы представили два новых алгоритма, связанных с вычислением определителя и обратной матрицы. Первый представленный алгоритм оценивает определитель и более эффективен, чем метод Гаусса, поскольку он уменьшает порядок матрицы на каждой итерации, тем самым экономя ненужные вычисления. Во втором алгоритме мы представили еще один простой способ вычисления обратной матрицы, построив словарь данной системы и, таким образом, исключив необходимость перестановок и обратных перестановок.
Определитель матрицы: краткий обзор
Определитель квадратной матрицы A , обозначенный как det ( A ), в основном является функцией с действительным знаком. Из-за его полезной связи с матрицей A и решением системы уравнений вида A x = b , становится важным иметь знания о детерминантах при изучении матриц. Оценка детерминанта через расширение его кофактора (также известное как разложение Лапласа) известна для матриц более низкого порядка.
Позвольте быть второстепенным элементом записи, который является определителем подматрицы, полученной после удаления строки и столбца A .
Если столбец A выбран для расширения кофактора, тогда
где, — кофактор ввода такой, что.
Точно так же расширение кофактора по строке будет
Для матрицы порядка n оценка определителя с помощью вышеуказанного расширения кофактора требует вычисления n определителей матриц порядка ( n -1).Поэтому его можно легко реализовать для поиска определителя матрицы 2-го или 3-го порядка, но для более высоких порядков это становится утомительной работой. Чтобы уменьшить вычислительные затраты, обычно используются следующие три основные операции со строками матриц для оценки определителя [9], метод известен как оценка определителя путем сокращения строк (также известный как метод Гаусса).
Операции с элементарной строкой
Пусть A будет матрицей, могут применяться следующие операции с элементарной строкой
Умножить строку на ненулевую константу.
Поменять местами два ряда.
Добавить одну строку в другую, кратное одному.
Влияние операций со строками на значение определителя: [9]
Пусть A будет матрицей, тогда
Если B — это матрица, которая получается, когда одна строка или один столбец A умножается на скаляр k, тогда det ( B ) = k det ( А ).
Если B — это матрица, которая получается, когда две строки или два столбца A меняются местами, тогда det ( B ) = −det ( A ).
Если B — это матрица, которая получается, когда число, кратное одной строке A , добавляется к другой строке или когда кратное одному столбцу добавляется к другому столбцу, тогда det ( B ) = det ( А ).
Лемма: [9]
Если A — треугольная матрица (верхняя треугольная, нижняя треугольная или диагональная), то det ( A ) является произведением элементов на главной диагонали матрицы; это, .
Вычисление определителя редукцией строки
Суть метода заключается в преобразовании заданной матрицы в ее верхнюю / нижнюю треугольную форму путем применения элементарных операций со строками. Затем определитель может быть вычислен путем включения свойств, определенных выше в разделе «Эффект строковых операций» и лемме.
Новый метод
Подход к сокращению строк может включать в себя все элементарные операции со строками, как показано в примере выше. Здесь мы определяем операцию (скажем, поворотную операцию для оценки определителя), которая состоит из ( n −1) приложений только строковой операции (c) и может использоваться для оценки определителей, избегая участия строковых операций (a) и (б).
Например, рассмотрим следующую матрицу,
Выбрав ненулевой элемент поворота, расположенный в любом произвольном месте ( i, j ), скажем, и выполнив операцию строки (c), чтобы сделать оставшиеся элементы столбца равными нулю, мы get
Здесь мы видим, что сводная строка остается неизменной, в то время как элемент матрицы,, где и — элементы, соответствующие сводному элементу в сводном столбце и сводной строке соответственно.
Расширение кофактора по столбцу даст
Вышеупомянутая процедура приводит к вычислению определителя матрицы с уменьшенным порядком ( n −1).Повторение описанной выше процедуры в конечном итоге даст определитель. Для матрицы должно быть n ненулевых сводных элементов. Произведение соответствующих элементов поворота дает значение определителя. Однако, если на любом этапе не существует ненулевой точки поворота, мы можем сделать вывод, что определитель данной матрицы равен 0.
Задача 1
Найти определитель матрицы A = порядка.
Пример
Итерация 1:
P : = {1,2,3,4}, здесь мы берем p = 1, поэтому L : = {1,2,3,4}.Принимая k = 1
Итерация 2:
P : = {1,2,3}, здесь мы берем p = 1, поэтому L : = {2,3}. Принимая k = 2
Итерация 3:
P : = {1,2}, здесь мы берем p = 1, поэтому L : = {1,2}. Принимая k = 1
Итерация 4:
P : = {1}, здесь мы берем p = 1, поэтому L : = {1}.Принимая k = 1
Следовательно, определитель данной матрицы равен 12.
Сравнение с методом сокращения строк
Приведенный выше пример иллюстрирует эффективность алгоритма с точки зрения хранения в памяти и количества вычисленных элементов. Если матрица порядка 4 решается методом сокращения строк, количество вычисленных элементов будет 12, 6 и 2 в первой, второй и третьей итерациях соответственно. Однако мы вычислили 9, 4 и 1 элемент в соответствующих итерациях.Таким образом, общее количество вычислений элементов, необходимых для метода сокращения строк, составляет 20, но нашему методу требуется только 14 вычислений элементов. Также на каждой итерации размер матрицы уменьшался. Метод сокращения строк должен хранить 16 элементов для каждой итерации, следовательно, в целом метод требует хранения в памяти 48 элементов, в то время как наш алгоритм, напротив, хранит 16 + 9 + 4 + 1 = 30 элементов, что является заметным сокращением условия хранения.
Сравнение числа вычисленных и сохраненных элементов для оценки определителя различных порядков путем сокращения строк и нашего алгоритма показано на.
Таблица 1
Сравнение метода сокращения строк с алгоритмом 1 для вычисления определителя матрицы.
| Заказ | Метод сокращения строк | Алгоритм 1 | ||||||
| Количество вычислений элементов | Требования к хранению (количество элементов) | Количество вычислений элементов | 917 элементов)||||||
| 2 | 2 | 8 | 1 | 5 | ||||
| 4 | 20 | 48 | 14 | 3016104 | 40105 | 900 125 | 30 | 55 |
| 7 | 112 | 343 | 94 | 140 | ||||
| 10 | 330 | 1000 | 285 | 91741728 | 506 | 650 | ||
Новый подход, основанный на словарной нотации
Сейчас снова рассмотрим уравнение (1) в развернутой форме,
Обычно для решения указанной выше системы используется следующая расширенная матрица:
Здесь мы используем концепцию словарной записи, разработанную [1].Теперь основные переменные — это переменные, коэффициенты которых представлены в виде любого столбца единичной матрицы, а базис — это совокупность всех основных переменных. Мы видим эту основу для указанной выше матрицы и можем рассматривать ее как неоснову текущей матрицы. Цель состоит в том, чтобы преобразовать базовые переменные в неосновные переменные и наоборот, используя операции поворота. Используя концепцию словаря, определенную в [1], мы можем удалить базовые столбцы из матрицы и построить следующую словарную форму с базисом B и неосновным N : (Обратите внимание, что основные переменные показаны в крайнем левом столбце, а не базовые переменные переменные в верхнем ряду словаря).
Операция поворота для оценки инверсии
Следующие операции поворота [1] могут применяться для ввода x i в базис B и y j в неосновной N ,
Разделите сводную строку на сводный элемент, а сводный столбец — на отрицательный элемент сводного элемента (кроме сводного элемента).
Остальные ( n -1) 2 элементов определяются по формуле, как определено в новом методе определителя.
Поверните шарнирный элемент назад.
Если количество опорных элементов равно порядку матрицы, результирующая матрица дает обратное, в противном случае мы можем сделать вывод, что обратного не существует.
Задача 2
Найти обратную матрицу A = порядка.
Алгоритм 2
Шаг 1: Установить H : = {1,2,3, ……, n }, B : = и N : =,.Построить словарь матрицы A , т.е. D ( A ).
Шаг 2: Установить P : = { p :}
Шаг 3: Если P =, перейдите к шагу 6.
В противном случае L : = { k :, x k N }
Шаг 4: Если L =, то инверсия не существует. Выход
В противном случае для любого
Шаг 5: а также .Обновите D ( A ) и перейдите к шагу 2.
Шаг 6: Inv ( A ) = Выход.
Пример
Здесь N : = {}, B : = {}
Итерация 1:
H : = {1,2,3,4}, P : = {1,2,3,4}, принимая p = 1, получаем L : = {1,2,3, 4}. Принимая k = 1
N : = {}, B : = {}
Итерация 2:
P : = {2,3,4}, беря p = 2, получаем L : = {3,4}.Принимая k = 3
N : = {}, B : = {}
Итерация 3:
P : = {3,4}, беря p = 3, получаем L : = {2,4}. Принимая k = 2
N : = {}, B : = {}
Итерация 4:
P : = {4}, беря p = 4, получаем L : = {4}. Принимая k = 4
N : = {}, B : = {}
Теперь разместите элементы относительно индексов переменных в B и N .
Например Здесь H : = {1,2,3,4}, Так и, подразумевает. Также и подразумевается. Аналогичным образом размещая остальные элементы, получаем
Сравнение с методом Гаусса
Приведенный выше пример иллюстрирует эффективность алгоритма с точки зрения хранения в памяти и количества вычисленных элементов. Если матрица порядка 4 решается методом Гаусса, количество вычисляемых элементов будет равно 20 на каждой итерации. Однако наш метод требует вычисления 16 элементов на каждой итерации.Таким образом, общее количество вычислений элементов, необходимых для метода Гаусса, равно 80, с другой стороны, для нашего метода — 64. Также метод Гаусса должен хранить 32 элемента для каждой итерации, следовательно, для всего метода Гаусса требуется сохранить 128 элементов. в памяти, в то время как наш алгоритм, напротив, хранит 64 элемента, что является заметным сокращением требований к хранилищу.
Сравнение количества элементов, вычисленных и сохраненных для оценки обратного метода Гаусса и нашего алгоритма, показано на.
Таблица 2
Сравнение метода Гаусса с алгоритмом 2 для вычисления обратной матрицы.
| Порядок | Метод Гаусса | Алгоритм 2 | ||||||
| Количество вычислений элементов | Требования к хранилищу (количество элементов) | Количество вычислений элементов | элементов) | |||||
| 2 | 12 | 8 | 8 | 4 | ||||
| 4 | 80 | 32 | 64 | 16 | 9017 925 5010416 | 925 25|||
| 125 | 25 | |||||||
| 7 | 392 | 98 | 343 | 49 | ||||
| 10 | 1100 | 200 | 1000 | 288 | 1728 | 144 | ||
Приложения
Определитель матрицы и инверсия имеют ap Работы в различных областях, таких как математика, экономика, физика, биология и т. д.Решение различных моделей, таких как рост населения, предполагает использование матричного детерминанта и обратного. Обратная матрица и определитель также используются в криптографии [10]. Линейные преобразования (вращение, отражение, перенос и т. Д.) Включают вычисление инверсии матрицы. Обратная матрица и определитель также используются в исследовании операций при решении линейных программ, переработанном симплекс-методе и цепях Маркова. Определители порядка 3 используются для определения площади треугольников и проверки коллинеарности точек.Анализ данных методом наименьших квадратов требует оценки обратной матрицы [11]. p -мерный объем параллелепипеда в определяется расчетным определителем [12].
Заключение
В данной статье представлены простые алгоритмы вычисления определителя и обратной матрицы. Поскольку порядок данной матрицы уменьшался на каждом шаге при вычислении ее определителя, алгоритм снижает требования к памяти (как показано в примере). Вычисление инверсии было выполнено с использованием словарной нотации, что исключает использование перестановок и упрощает обучение в классе.Плохо подготовленная система также может обрабатываться, поскольку выбор шарниров оставлен произвольным, что улучшает числовую точность системы.
Заявление о финансировании
У авторов нет поддержки или финансирования, о которых можно было бы сообщить.
Ссылки
1. Чватал В. (1983) Линейное программирование. Соединенные Штаты Америки: W.H. Фримен и компания. [Google Scholar] 2. Ахмад Ф, Хан Х (2010) Эффективный и простой алгоритм обращения матриц. Международный журнал распространения технологий 20–27.[Google Scholar] 3. Хан Х., Шах И.А., Ахмад Ф. (2010) Эффективный универсальный алгоритм обращения матриц. Международный журнал распространения технологий 36–41. [Google Scholar] 4. Маклорен C (1748) Трактат по алгебре. Лондон: А. Миллар и Дж. Норс. [Google Scholar] 5. Крамер Г. (1750) Введение в анализ алгебраических кривых. [Google Scholar]6. Огюстен К.Л. (1815) Мемуары о функциях, которые несут в себе двойные валентные ценности и знаки, противоположные номинальным перестановкам, оперирующим во время перестановки переменных.de l’École polytechnique.
7. Райс А., Торренс Э. (2006) Метод конденсации Льюиса Кэролла для оценки детерминантов. Математические горизонты 12–15. [Google Scholar] 8. Хайэм, штат Нью-Джерси (2011), исключение по Гауссу. John Wiley & Sons, Inc., 230–238. [Google Scholar] 9. Антон Х, Роррес С (2005) Элементарная линейная алгебра. John, Wiley & Sons, Inc. [Google Scholar] 10. Веллаиканнан Б., Мохан Д.В., Гнанарадж В. (2010) Заметка о применении квадратичных форм в теории кодирования с примечанием о безопасности. Int J Comp Tech Appl 78–87.[Google Scholar] 11. Гринберг Г., Сархан А. Е. (1959) Обращение матриц, ее интерес и применение в анализе данных. Журнал Американской статистической ассоциации 755–766. [Google Scholar] .
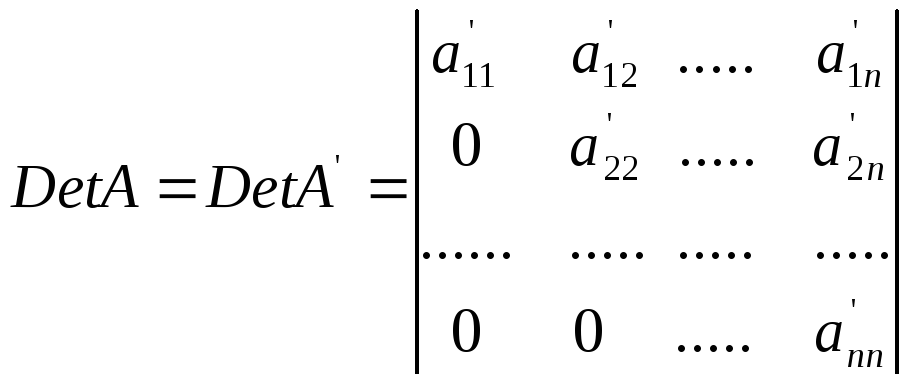
 \ [A = \ begin {bmatrix}
-1 и 0 и -1 и 3 и 6 \\
1 и 1 и -1 и 0 и 4 \\
1 и -3 и 0 и -2 и 2 \\
-1 и 2 и 2 и 1 и -3 \\
0 и -1 и 2 и 0 и 2
\ end {bmatrix} \] Решение примера 2
\ [A = \ begin {bmatrix}
-1 и 0 и -1 и 3 и 6 \\
1 и 1 и -1 и 0 и 4 \\
1 и -3 и 0 и -2 и 2 \\
-1 и 2 и 2 и 1 и -3 \\
0 и -1 и 2 и 0 и 2
\ end {bmatrix} \] Решение примера 2 

