Сравнение смешанных чисел. Онлайн калькулятор
Для сравнения смешанных чисел, когда дробные части – правильные дроби используют следующее правило:
При сравнении смешанных чисел больше то смешанное число, целая часть которого больше, если же целые части равны, то больше то смешанное число, дробная часть которого больше.
Если попадаются примеры, в которых целые части разные и одна или обе дробные части представляют собой неправильные дроби, сравнение смешанных чисел можно свести к сравнению обыкновенных дробей. Для этого нужно представить смешанные числа в виде неправильных дробей.
Сравним два смешанных числа и :
- Переводим смешанные числа в неправильные дроби:
- Приводим неправильные дроби к общему знаменателю:
- Сравниваем:
, значит
Смешанные числа равны, если соответственно равны их целые и дробные части.
Правило сравнения смешанного числа с натуральным числом:
Если целая часть смешанного числа больше или равна данному натуральному числу, то смешанное число больше данного натурального числа, а если целая часть смешанного числа меньше данного натурального числа, то смешанное число меньше данного натурального числа.
Если целая часть смешанного числа меньше данного натурального числа, а дробная часть является неправильной дробью, то сравнение можно свести к сравнению обыкновенных дробей.
Сравним смешанное число с натуральным числом 6:
- Переводим числа в неправильные дроби:
- Приводим неправильные дроби к общему знаменателю:
- Сравниваем:
, значит
Любое смешанное число больше любой правильной дроби.
Сравнение смешанного числа c неправильной дробью можно свести к сравнению двух неправильных дробей. Для этого смешанное число нужно представить в виде неправильной дроби.
Сравним смешанное число с неправильной дробью :
- Переводим смешанное число в неправильную дробь:
- Приводим неправильные дроби к общему знаменателю:
- Сравниваем:
, значит
Калькулятор сравнения смешанных чисел
Данный калькулятор поможет вам сравнить смешанные числа. Просто введите два числа и нажмите кнопку Сравнить
. Данный калькулятор позволяет также сравнивать: натуральное число с дробью, смешанное число с дробью и натуральное число со смешанным.
Сравнение обыкновенных дробей. Онлайн калькулятор
Сравнить две дроби – значит определить, какая из дробей больше, какая меньше или установить, что дроби равны.
Сравнение дробей с одинаковыми числителями
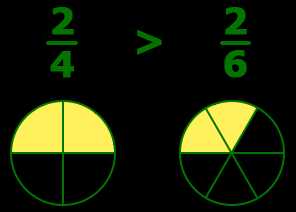
При сравнении двух дробей, у которых одинаковые числители, больше будет та дробь, у которой знаменатель меньше.
Например, больше , так как количество взятых долей в обеих дробях одинаковое, но первая дробь содержит более крупные доли, чем вторая:
Сравнение дробей с одинаковыми знаменателями
При сравнении двух дробей, у которых одинаковые знаменатели, больше будет та дробь, у которой числитель больше.
Например, меньше , так как первая дробь содержит меньше взятых долей, чем вторая:
Сравнение дробей с разными знаменателями
Чтобы сравнить дроби, у которых разные числители и знаменатели, нужно привести их к общему знаменателю. После приведения дробей к общему знаменателю, их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.
Например, сравним две дроби: и . Приводим их к общему знаменателю:
Теперь сравниваем их:
так как , значит
Равенство дробей
Две обыкновенные дроби считаются равными, если равны их числители и знаменатели или, если они выражают одну и ту же часть единицы.
Сравнение дроби с натуральным числом
Правильная дробь меньше любого натурального числа.
Чтобы сравнить неправильную дробь с натуральным числом, нужно натуральное число представить в виде неправильной дроби, затем привести дроби к общему знаменателю. После приведения дробей к общему знаменателю, их сравнивают по правилу сравнения дробей с одинаковыми знаменателями.
Пример. Сравним неправильную дробь с числом 5.
1. Переводим натуральное число в неправильную дробь:
3. Сравниваем:
так как , значит
Онлайн калькулятор сравнения дробей
Данный калькулятор поможет вам сравнить обыкновенные дроби. Просто введите две дроби и нажмите кнопку Сравнить
.
naobumium.info
Онлайн калькуляторы для сравнения десятичных дробей

Одной из задач в области арифметики является сравнение десятичных дробей. Сам процесс обычно не вызывает никаких сложностей, однако иногда над решением нужно подумать. Если нет желания самостоятельно проводить расчеты или нужно сверить результат, за помощью можно обратиться к специальным онлайн-сервисам. Именно о них мы и расскажем в этой статье.
Читайте также: Конвертеры величин онлайн
Сравниваем десятичные дроби онлайн
На просторах интернета есть множество практически идентичных по реализации веб-ресурсов. Они функционируют примерно по одному и тому же алгоритму и одинаково хорошо справляются со своей главной задачей. Поэтому мы решили рассмотреть только два подобных сайта, а вы, исходя из представленных инструкций, сможете понять принцип работы на таких сервисах.
Способ 1: Calc
Одним из самых популярных сборников различных калькуляторов и конвертеров является сайт Calc. На нем вам доступно проведение самых разнообразных расчетов в совершенно любых областях науки, строительства, бизнеса, одежды и многого другого. Здесь присутствует инструмент, позволяющий провести необходимое нам сравнение. Произвести процедуру не составит труда, просто следуйте следующему руководству:
Перейти на сайт Calc
- Откройте калькулятор, перейдя по указанной выше ссылке с помощью любого удобного браузера.
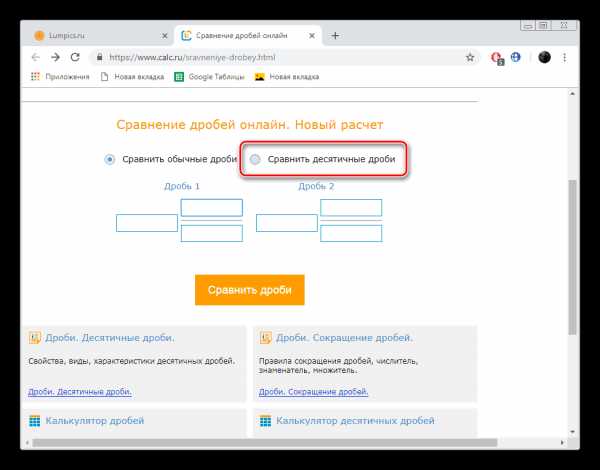
- Здесь отметьте маркером пункт «Сравнить десятичные дроби».
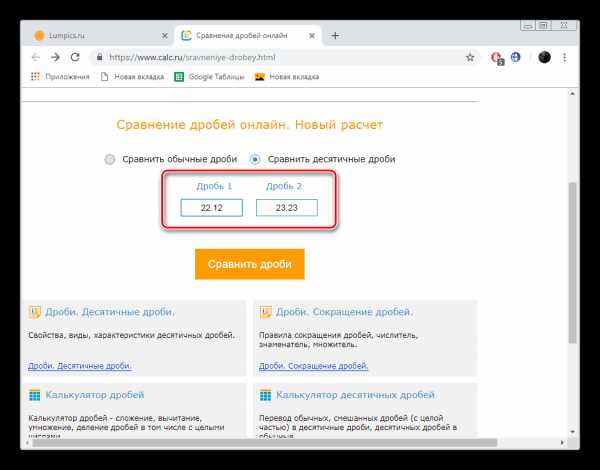
- Заполните отобразившиеся поля, введя в каждое необходимое для сравнения число.
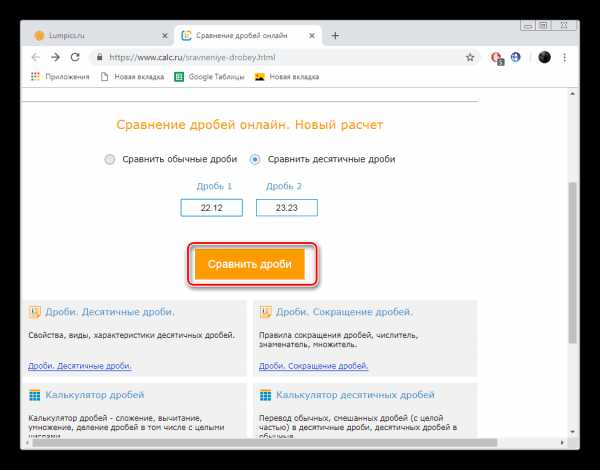
- Щелкните левой кнопкой мыши по плитке с надписью «Сравнить».
- Ознакомьтесь с полученным результатом и можете переходить к проведению других расчетов.
- Кроме этого доступна отправка в печать открывшегося документа и рассылка решения друзьям через социальные сети.
- Опуститесь вниз по вкладке. Там вы найдете другие материалы по теме десятичных дробей.
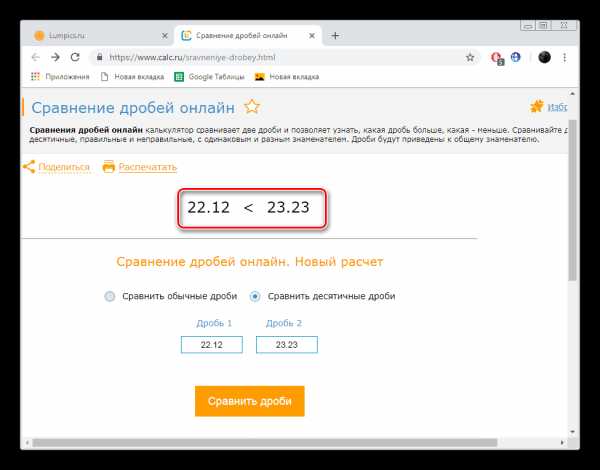
На этом проведение сравнения завершено, оно заняло буквально несколько минут, а решения не пришлось долго ждать. Надеемся, вопросов по работе с этим сайтом у вас не осталось, поэтому рекомендуем перейти к рассмотрению следующего.
Способ 2: Naobumium
Интернет-ресурс под названием Naobumium не только собрал в себе математические калькуляторы и правила, но и предоставляет информацию в сфере русского языка. Однако сегодня нас интересует только один инструмент. Давайте скорее ознакомимся с ним.
Перейти на сайт Naobumium
- Перейдите на главную страницу Naobumium, где на верхней панели выберите категорию «Арифметика».
- Обратите внимание на панель слева. Отыщите там раздел «Десятичные дроби» и разверните его.
- Кликните левой кнопкой мыши на надписи «Сравнение».
- Ознакомьтесь с представленными правилами, чтобы разобраться в принципе решения поставленной задачи.
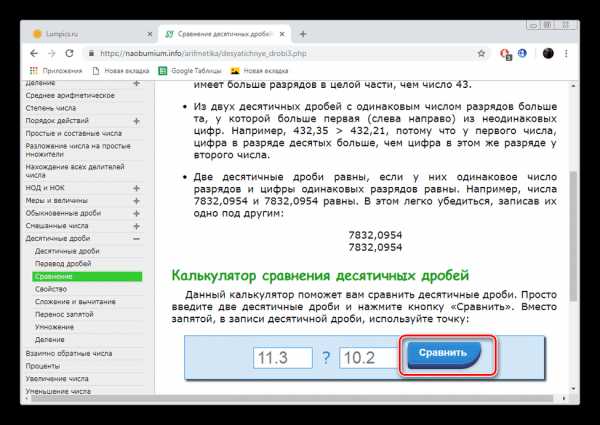
- Опуститесь вниз по вкладке, где в соответствующие поля введите два необходимых для сравнения числа.
- Нажмите на кнопку «Сравнить».
- Ознакомьтесь с полученным результатом и переходите к решению следующих примеров.
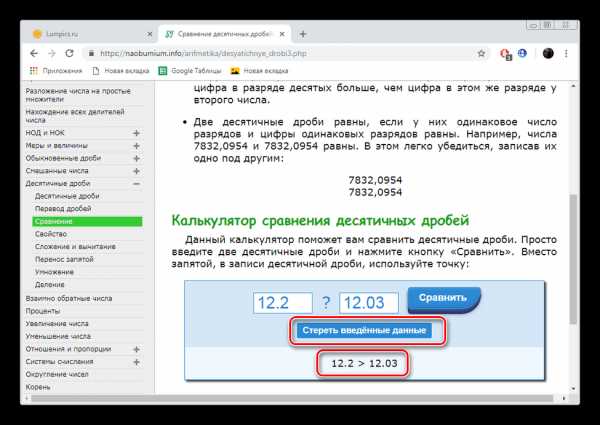
Читайте также:
Перевод в систему СИ онлайн
Перевод из десятичной в шестнадцатеричную систему онлайн
Перевод из восьмеричной в десятичную онлайн
Сложение систем счисления онлайн
Как видите, два рассмотренных сегодня сервиса мало чем отличаются друг от друга, разве что общая функциональность сайтов и оформление сразу бросаются в глаза. Поэтому мы не можем дать рекомендации по поводу выбора конкретного веб-ресурса. Подбирайте оптимальный вариант, исходя из собственных предпочтений.
Мы рады, что смогли помочь Вам в решении проблемы.Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТlumpics.ru
Калькулятор сравнения дробей с разными знаменателями, сортировка чисел онлайн
Сравнение обыкновенных дробей
Сравнить две дроби – значит определить, какая из дробей больше, какая меньше или установить, что дроби равны.
Сравнение дробей с одинаковыми числителями
При сравнении двух дробей, у которых одинаковые числители, больше будет та дробь, у которой знаменатель меньше.
Например, больше , так как количество взятых долей в обеих дробях одинаковое, но первая дробь содержит более крупные доли, чем вторая:
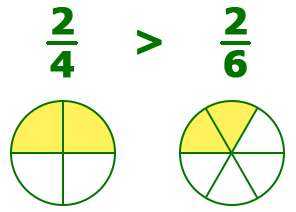
Сравнение дробей с одинаковыми знаменателями
При сравнении двух дробей, у которых одинаковые знаменатели, больше будет та дробь, у которой числитель больше.
Например, меньше , так как первая дробь содержит меньше взятых долей, чем вторая:
Сравнение дробей с разными знаменателями
Чтобы сравнить дроби, у которых разные числители и знаменатели, нужно привести их к общему знаменателю. После приведения дробей к общему знаменателю, их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.
Например, сравним две дроби: и . Приводим их к общему знаменателю:
Теперь сравниваем их:
так как , значит
Равенство дробей
Две обыкновенные дроби считаются равными, если равны их числители и знаменатели или, если они выражают одну и ту же часть единицы.
Сравнение дроби с натуральным числом
Правильная дробь меньше любого натурального числа.
Чтобы сравнить неправильную дробь с натуральным числом, нужно натуральное число представить в виде неправильной дроби, затем привести дроби к общему знаменателю. После приведения дробей к общему знаменателю, их сравнивают по правилу сравнения дробей с одинаковыми знаменателями.
Пример. Сравним неправильную дробь с числом 5.
1. Переводим натуральное число в неправильную дробь:
2. Приводим дроби к общему знаменателю:
3. Сравниваем:
так как , значит
Онлайн калькулятор сравнения дробей
Данный калькулятор поможет вам сравнить обыкновенные дроби. Просто введите две дроби и нажмите кнопку .
описание
Вам не нужно иметь навыки программирования для написания сложных сценариев или тратить время на классифицирование классифицированных программ — Excel или Word.
Как сравнить фракции
Теперь вы можете использовать готовые решения в повседневной работе.
Алгоритм поможет сразу отсортировать значения в алфавитном и обратном порядке, чтобы строить данные по количеству символов в слове или любому значению символа.
инструкции
Инструмент отлично справляется с добавленной стоимостью в столбце и отдельными словами, заданными запятой или пробелом.
Скопируйте данные, необходимые для сортировки в левом окне, укажите одну из четырех функций и нажмите кнопку Сортировать по.
По умолчанию он доступен Алфавитный порядок (A — R / 0 — 9).
По выбору Обратный порядок (H — A / 9 — 0), алгоритм сразу отображает матрицу в обратном направлении.
черты Значения на длину (от малого до большого) и Значения по длине (от более высокой до нижней) работайте по аналогичному принципу, но сортировка основана на количестве символов в строке.
Написать комментарий
Для меня важно знать, как работает служба и как ее можно улучшить. Написать комментарий по почте [email protected] или в нижней форме.
Добавьте ссылку на этот и другие полезные инструменты в свои закладки и поделитесь ими с коллегами.
Как работать с калькулятором регулярных фракций?
Калькулятор предназначен для спасения простые фракции и фракции с целыми числами (смешанный). Функция десятичных дробей запланирована в будущем, но в настоящее время она недоступна.
Чтобы начать работу с частичным калькулятором, вам нужно понять очень простой принцип ввод данных.
Все целые числа вводятся с помощью больших кнопок слева. Все счетчики вводятся с маленькими белыми кнопками, расположенными в верхней правой части цифр. Все символы вводятся нажатием кнопки в правом нижнем углу. Метод ввода данных является своего рода инновационным, поскольку он четко описывает весь числитель и знаменатель, который позволяет проводить расчеты, экономит время и позволяет более эффективно взаимодействовать с использованием.
Скажи это, вы должны добавить квадратный корень из двух пятых и один двадцать два на шестом шаге.
Начните вводить пример из корневой кнопки. Затем нажмите на номер 2 в области измерителя и номер пять в знаменателе. Первый термин готов. Теперь щелкните знак «+» — это надстройка. Затем введите целое число в основную клавиатуру, затем номер 2 в области счетчика и девять в знаменателе. Затем нажмите кнопку «^», а затем на номер шесть на главной клавиатуре.
В результате мы получаем готовый пример:
в настоящее время Нажмите эквивалентную кнопку и перейдите стоимость результата.
В приведенном выше примере показан почти весь арсенал дробных калькуляторов. Вы можете сделать то же самое так же размножение, деление и вычитание фракций, так же просто, как алгебраические, с одинаковыми и разными знаменателями, целыми числами и т. д.
Калькулятор также может рассчитывать фракции из фракций, что не часто требуется, но тем не менее очень важно решить ряд неотложных проблем.
Чтобы получить положительное отрицательное число, сначала введите номер и нажмите кнопку «+/-».
После этого число или часть автоматически завертываются в скобки с отрицательным значением или наоборот (в зависимости от начального состояния номера). Чтобы удалить число, счетчик или знаменатель, используйте соответствующую стрелку возврат на одну позицию, который находится в блоке как числителя, так и знаменателя.
Стрелки работают одинаково, а затем удаляют номера или символы на экране компьютера.
Управляйте частичным калькулятором с клавиатуры.
Используйте его Калькулятор веб-фракций не только с компьютерной мышью, но и с клавиатурой.
Логика очень проста:
- Все вводится как обычно, нажимая цифровые клавиши.
- Все счетчики вводятся путем добавления клавиши CTRL (например, CTRL + 1).
- Все знаменатели вводятся путем добавления клавиши ALT (например, ALT + 2).
Меры умножения, деления, добавления и вычитания, а также запуска соответствующих клавиш на клавиатуре, если они есть (обычно расположены с правой стороны, так называемая область Numpad).
Удаление выполняется нажатием клавиши Backspace. Очистка (красная кнопка «C») запускается нажатием клавиши «C». Квадратный корень — нажатием соседней клавиши «V».
Удаление выполняется нажатием клавиши Backspace.
Зачем вам нужен онлайн-калькулятор?

Дробный калькулятор онлайн предназначен для обработки гладкий и смешанный дробей (с целым числом).
Решение фракций часто необходимо для студентов и студентов, а также для инженеров и выпускников. Наш калькулятор позволяет создавать следующие действия с частицами: расщепление фракций, умножение фракций, добавление фракций и вычитание фракций. Калькулятор также может работать с корнями и ставками, а также с отрицательными числами, что делает его несколько раз превышает аналогичные веб-приложения.
Простой калькулятор фракционной дроби онлайн поможет вам решить дела с фракциями, поэтому вам не нужно беспокоиться о том, как противодействовать фракции.
Он становится здесь автоматически, поскольку само приложение вычисляет общий знаменатель и, наконец, показывает конечный результат.
Каковы преимущества этого метода для решения фракций?
калькулятор поддерживает работу с скобками, что позволяет решать фракции, даже в сложных математических случаях. Кампании часто необходимы для скобок алгебраические дроби или отрицательные фракции, над которыми мы должны постоянно избегать всех учащихся средних школ.
Калькулятор для сравнения фракций
Кроме того, вы можете использовать этот калькулятор сокращение фракций или дробные растворы с разными знаменателями. Кроме того, этот калькулятор, в отличие от многих других бесплатных сервисов, может работать с двумя, тремя, четырьмя и вообще с любым количеством дробей и чисел.
Калькулятор регулярных фракций абсолютно бесплатно и не требует регистрации.
Вы можете использовать его в любое время дня и ночи. Вы можете сделать это с помощью мыши или непосредственно с клавиатуры (это относится к числу и действиям). Мы попытались реализовать максимум удобный интерфейс частичные вычисления, которые делают сложные математические расчеты меняющимися в одно удовольствие!
🙂
Сравнение обыкновенных дробей
Удобный и простой онлайн-калькулятор фракций с точным решением вы можете:
- Складывайте, вычитайте, размножайте и размещайте фрагменты в Интернете,
- Получите частичное решение изображения и просто загрузите его.
Результат фракций будет здесь …
Наш калькулятор онлайн-калькуляторов имеет быстрый ввод.
Например, если вы хотите получить частичное решение , просто введите 1/2 + 2/7 в калькулятор и нажмите кнопку «Rescue Faction».
Калькулятор напишет вам детальное решение фракций и вопросы легко скопировать изображение.
Персонажи, используемые для записи в калькуляторе
| знак | замечание | Пример записи |
| / | Частичный символ (не используется для разделения) | Фракция 1/3 1/3 |
| + | Знак плюса для добавления фракций | 1/2 + 3/5 |
| — | Минус для вычитания фракций | 3 / 5-2 / 7 |
| * или × | Умножение фракций | 2/3 * 5/8 |
| : или ÷ | Фракция фракций (частичная «/» не используется!) | 1/3: 7/8 |
Вы можете ввести пример решения с клавиатуры или с помощью кнопки.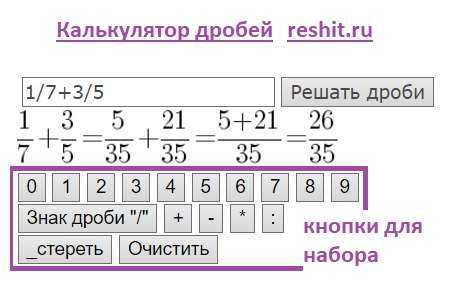
Характеристики калькулятора веб-фракций
Калькулятор фракций может выполнять операции только с двумя простыми фракциями.
Они могут быть правильными (счетчик меньше знаменателя) или неверны (счетчик больше знаменателя). Числа в числителе и знаменателе не должны быть отрицательными и больше 999.
Наш онлайн-калькулятор принимает решения по фракциям и направляет ответ на правильный формат — уменьшает долю и, при необходимости, назначает всю часть.
Просто используйте свойства минус, чтобы сохранить отрицательные части. При умножении и делении отрицательных дробей знак плюс добавляет плюс. Это означает, что продукт и распределение отрицательных дробей идентичны произведению и распределению того же положительного. Если фракция отрицательная, если вы ее умножаете или делите, удалите минус и добавьте ее в ответ. При добавлении отрицательных фракций результат будет таким же, как добавление одинаковых положительных пропорций.
Если вы добавите одну отрицательную долю, то это то же самое, что и вычесть тот же самый положительный результат.
При вычитании отрицательных дробей результат будет таким же, как если бы они были изменены в местах и стали положительными.
Сравнение фракций
Это означает, что минус минус в этом случае дает плюс, и сумма не изменяется от суммы. Те же правила, которые мы используем при подсчете фракций, один из которых отрицателен.
Чтобы решить смешанные фракции (фракции, в которых размещена вся часть), просто заполните всю фракцию во фракцию.
Чтобы сделать это, умножьте всю часть на знаменатель и добавьте его в счетчик.
Если вы хотите сохранить 3 или более акций в Интернете, они должны быть приняты. Во-первых, подсчитайте первые две фракции, затем с полученным ответом определите следующую долю и так далее. Выполните операции на линии 2 фракций, и в конце вы получите правильный ответ.
Зачем принимать решения в калькуляторе
Решения в калькуляторе должны узнать, как сохранить дроби.
Калькулятор не имеет намерения решать фракции для вас.
Это не универсальный резак, это инструмент обучения. Это поможет вам понять решение, так что вы можете легко решить фракции самостоятельно. В дополнение к учебному калькулятору мы также рекомендуем изучить наши материалы: «Как разрешить фракции». Решение фракций. «
Если вы заметили какие-либо ошибки или неудобства при использовании калькулятора, пожалуйста, свяжитесь с нами в комментариях. Насколько это возможно, мы закончим калькулятор!
Онлайн калькулятор. Сравнение фракций.
Студент видит на экране несколько номеров с интересной цветовой схемой. Эти числа расположены в случайном порядке. Ребенок, который знает правильный порядок учетной записи, должен отредактировать от малого до большого. Проблема с упражнением заключается в том, что цифры, показанные на рисунке, не обязательно идут один за другим.
Фактически, промежутки между ними могут быть важными. Но студент, который выполняет эту задачу, должен помнить, какой из чисел больше и меньше. Когда ребенок создает последовательность, он немедленно переходит на следующий уровень (если ответ правильный) или после просмотра правильной опции — если он совершает ошибку.
Это упражнение не только развивает логическое мышление, оно учит вас анализировать и готовить последовательные выводы из образа, но также помнить о правильной последовательности чисел при подсчете.
Порядок увеличения является естественным для многих партий, поэтому ребенок может легко обнаружить его.
vipstylelife.ru
Сравнение чисел | Формулы с примерами
Сравнение рациональных чисел в математике
Определение
При сравнении чисел в математике, большим является то,
которое на координатной прямой находится правее.
Соответственно меньшее то, которое левее.
Сравнение целых чисел в пределах 10
Пример| — 5 | 1 > — 4; | 6 > — 5; | — 4 | — 1 > — 5. |
Сравнение двузначных чисел на координатной прямой
Пример| — 15 | 12 > — 14; | 16 > — 15; | — 14 | — 11 > — 15. |
Правила сравнения чисел
Правило ! Любое положительно число больше нуля.| 1 > 0; | 11 > 0; | 0, 002 > 0; | 10, 3231 > 0 | 235, 0902 > 0. |
! Любое отрицательное число меньше нуля.
| — 1 | — 13 | — 0, 0321 | — 310, 3231 | — 1235, 1235 |
! Любое отрицательное число меньше положительного.
Правило
! Из двух отрицательных чисел больше то, модуль которого, меньше.
| — 700 | — 4 > — 20,5; | — 66 > — 22; | — 1,43 |
! Направления возрастания чисел при движении по координатной
прямой — слева направо.
formula-xyz.ru
Сравнение рациональных чисел
Продолжаем изучать рациональные числа. В данном уроке мы научимся сравнивать их.
Из предыдущих уроков мы узнали, что чем правее число располагается на координатной прямой, тем оно больше. И соответственно, чем левее располагается число на координатной прямой, тем оно меньше.
Например, если сравнивать числа 4 и 1, то можно сразу ответить, что 4 больше чем 1. Это вполне логичное утверждение и каждый с этим согласится.
В качестве доказательства можно привести координатную прямую. На ней видно, что четвёрка лежит правее единицы
4 > 1
Для этого случая есть и правило, которое при желании можно использовать. Выглядит оно следующим образом:
Из двух положительных чисел больше то число, модуль которого больше.
Чтобы ответить на вопрос какое число больше, а какое меньше, сначала нужно найти модули этих чисел, сравнить эти модули, а потом уже ответить на вопрос.
Например, сравним те же числа 4 и 1, применяя вышеприведенное правило
Находим модули чисел:
|4| = 4
|1| = 1
Сравниваем найденные модули:
4 > 1
Отвечаем на вопрос:
4 > 1
Для отрицательных чисел существует другое правило, выглядит оно следующим образом:
Из двух отрицательных чисел больше то число, модуль которого меньше.
Например, сравним числа −3 и −1
Находим модули чисел
|−3| = 3
|−1| = 1
Сравниваем найденные модули:
3 > 1
Отвечаем на вопрос:
−3 < −1
Нельзя путать модуль числа с самим числом. Частая ошибка многих новичков. К примеру, если модуль числа −3 больше, чем модуль числа −1, это не означает, что число −3 больше, чем число −1.
Число −3 меньше, чем число −1. Это можно понять, если воспользоваться координатной прямой
Видно, что число −3 лежит левее, чем −1. А мы знаем, что чем левее, тем меньше.
Если сравнивать отрицательное число с положительным, то ответ будет напрашиваться сам. Любое отрицательное число будет меньше любого положительного числа. Например, −4 меньше, чем 2
−4 < 2
Видно, что −4 лежит левее, чем 2. А мы знаем, что «чем левее, тем меньше».
Здесь в первую очередь нужно смотреть на знаки чисел. Минус перед числом будет говорить о том, что число отрицательное. Если знак числа отсутствует, то число положительное, но вы можете записать его для наглядности. Напомним, что это знак плюса
−4 < +2
Мы рассмотрели в качестве примера целые числа, вида −4, −3 −1, 2. Сравнить такие числа, а также изобразить на координатной прямой не составляет особого труда.
Намного сложнее сравнивать другие виды чисел, такие как обыкновенные дроби, смешанные числа и десятичные дроби, некоторые из которых являются отрицательными. Здесь уже в основном придётся применять правила, потому что точно изобразить такие числа на координатной прямой не всегда возможно. В некоторых случаях, число надо будет видоизменять, чтобы сделать его более простым для сравнения и восприятия.
Пример 1. Сравнить рациональные числа
Итак, требуется сравнить отрицательное число с положительным. Любое отрицательное число меньше любого положительного числа. Поэтому не теряя времени отвечаем, что меньше, чем
Пример 2. Сравнить рациональные числа и
Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то, модуль которого меньше.
Находим модули чисел:
Сравниваем найденные модули:
Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа
Пример 3. Сравнить числа 2,34 и
Требуется сравнить положительное число с отрицательным. Любое положительное число больше любого отрицательного числа. Поэтому не теряя времени отвечаем, что 2,34 больше, чем
2,35 >
Пример 4. Сравнить рациональные числа и
Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше.
Находим модули чисел:
Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно переведём в неправильные дроби и приведём к общему знаменателю
Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа
Пример 5. Сравнить рациональные числа 0 и
Требуется сравнить ноль с отрицательным числом. Ноль больше любого отрицательного числа, поэтому не теряя времени отвечаем, что 0 больше, чем
Пример 6. Сравнить рациональные числа 0 и
Требуется сравнить ноль с положительным числом. Ноль меньше любого положительного числа, поэтому не теряя времени отвечаем, что 0 меньше, чем
Пример 7. Сравнить рациональные числа 4,53 и 4,403
Требуется сравнить два положительных числа. Из двух положительных чисел больше то число, модуль которого больше.
Сделаем в обеих дробях количество цифр после запятой одинаковым. Для этого в дроби 4,53 припишем в конце один ноль
4,530
Далее применим правило сравнения положительных чисел.
Находим модули чисел
|4,530| = 4,530
|4,403| = 4,403
Сравниваем найденные модули:
Согласно правилу, из двух положительных чисел больше то число, модуль которого больше. Значит рациональное число 4,53 больше, чем 4,403 потому что модуль числа 4,53 больше, чем модуль числа 4,403
4,53 > 4,403
Пример 8. Сравнить рациональные числа и
Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше.
Находим модули чисел:
Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно переведём смешанное число в неправильную дробь, затем приведём обе дроби к общему знаменателю:
Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа
Сравнивать десятичные дроби намного проще, чем обыкновенные дроби и смешанные числа. В некоторых случаях, посмотрев на целую часть такой дроби, можно сразу ответить на вопрос какая дробь больше, а какая меньше.
Чтобы сделать это, нужно сравнить модули целых частей. Это позволит быстро ответить на вопрос в задаче. Ведь как известно, целые части в десятичных дробях имеют вес больший, чем дробные.
Пример 9. Сравнить рациональные числа 15,4 и 2,1256
Модуль целой части дроби 15,4 больше, чем модуль целой части дроби 2,1256
|15| = 15
|2| = 2
15 > 2
поэтому и дробь 15,4 больше, чем дробь 2,1256
15,4 > 2,1256
Другими словами, нам не пришлось тратить время на дописывание нулей дроби 15,4 и сравнивать получившиеся дроби, как обычные числа
15,4000 2,1256
154000 > 21256
Правила сравнения остаются всё теми же. В нашем случае мы сравнивали положительные числа.
Пример 10. Сравнить рациональные числа −15,2 и −0,152
Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей
|−15| = 15
|−0| = 0
15 > 0
Видим, что модуль целой части дроби −15,2 больше, чем модуль целой части дроби −0,152.
А значит рациональное −0,152 больше, чем −15,2 потому что модуль целой части числа −0,152 меньше, чем модуль целой части числа −15,2
−0,152 > −15,2
Пример 11. Сравнить рациональные числа −3,4 и −3,7
Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей. Но проблема в том, что модули целых чисел равны:
|−3| = 3
|−3| = 3
3 = 3
В этом случае придётся пользоваться старым методом: найти модули рациональных чисел и сравнить эти модули
|−3,4| = 3,4
|−3,7| = 3,7
Сравниваем найденные модули:
Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное −3,4 больше, чем −3,7 потому что модуль числа −3,4 меньше, чем модуль числа −3,7
−3,4 > −3,7
Пример 12. Сравнить рациональные числа 0,(3) и
Требуется сравнить два положительных числа. Причем сравнить периодическую дробь с простой дробью.
Переведём периодическую дробь 0,(3) в обыкновенную дробь и сравним её с дробью . После перевода периодической дроби 0,(3) в обыкновенную, она обращается в дробь
Находим модули чисел:
Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно приведём к общему знаменателю: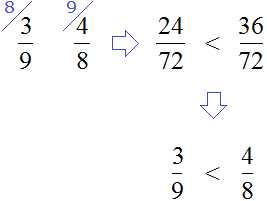
Согласно правилу, из двух положительных чисел больше то число, модуль которого больше. Значит рациональное число больше, чем 0,(3) потому что модуль числа больше, чем модуль числа 0,(3)
0,(3) <
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Навигация по записям
spacemath.xyz
