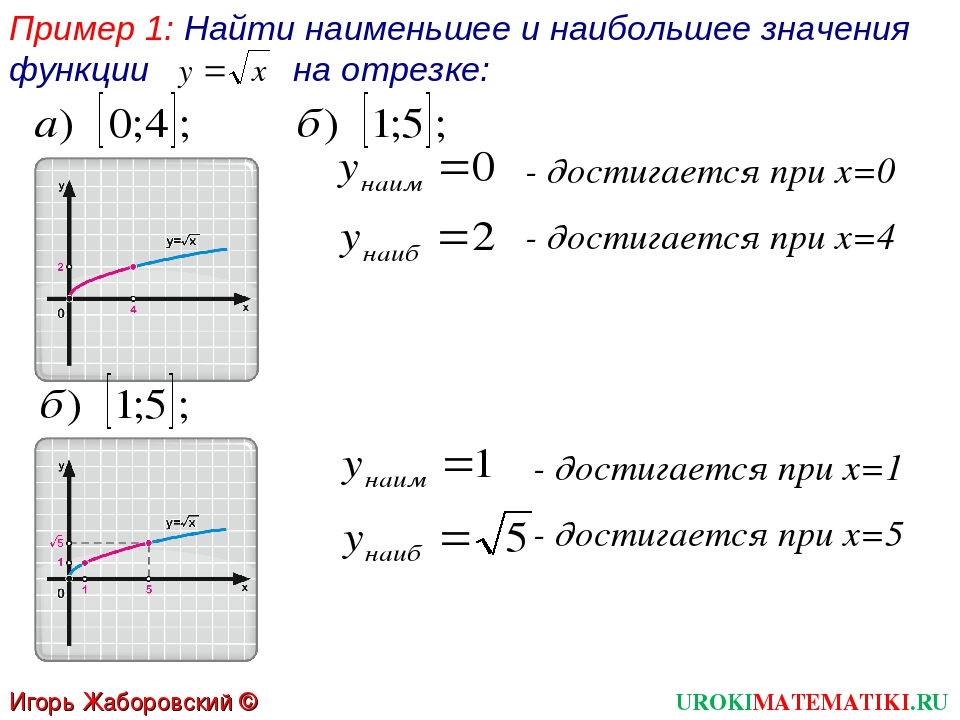
Наименьшее и наибольшее значения функции на отрезке
На рисунках ниже показано, где функция может достигать наименьшего и наибольшего значения. На левом рисунке наименьшее и наибольшее значения зафиксированы в точках локального минимума и максимума функции. На правом рисунке — на концах отрезка.
Если функция y = f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке наименьшего и наибольшего значений. Это, как уже говорилось, может произойти либо в точках экстремума, либо на концах отрезка. Поэтому для нахождения наименьшего и наибольшего значений функции, непрерывной на отрезке [a, b], нужно вычислить её значения во всех критических точках и на концах отрезка, а затем выбрать из них наименьшее и наибольшее.
Пусть, например, требуется определить наибольшее значение функции
 Для этого следует найти все её критические точки, лежащие на [a, b].
Для этого следует найти все её критические точки, лежащие на [a, b].
Критической точкой называется точка, в которой функция определена, а её производная либо равна нулю, либо не существует. Затем следует вычислить значения функции в критических точках. И, наконец, следует сравнить между собой по величине значения функции в критических точках и на концах отрезка (f(a) и f(b)). Наибольшее из этих чисел и будет наибольшим значением функции на отрезке [a, b].
Аналогично решаются и задачи на нахождение наименьших значений функции.
Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.
Пример 1. Найти наименьшее и наибольшее значения функции на отрезке [-1, 2].
Решение. Находим производную данной функции . Приравняем производную нулю () и получим две критические точки: и . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на концах отрезка и в точке , так как точка не принадлежит отрезку [-1, 2]. Эти значения функции — следующие: , , . Из этого следует, что наименьшее значение функции (на графике ниже обозначено красным), равное -7, достигается на правом конце отрезка — в точке , а наибольшее (тоже красное на графике), равно 9, — в критической точке .
Если функция непрерывна в некотором промежутке и этот промежуток не является отрезком
(а является, например, интервалом; разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок),
то среди значений функции может и не быть наименьшего и наибольшего. Так, например, функция, изображённая
на рисунке ниже, непрерывна на ]-∞, +∞[ и не имеет
наибольшего значения.
Так, например, функция, изображённая
на рисунке ниже, непрерывна на ]-∞, +∞[ и не имеет
наибольшего значения.
Однако для любого промежутка (закрытого, открытого или бесконечного) справедливо следующее свойство непрерывных функций.
Если функция непрерывна в промежутке и имеет единственный экстремум, то он является наименьшим значением в случае минимума и наибольшим — в случае максимума.
Как наименьшее значение функции, так и её наибольшее значение, могут быть найдены не только в одной точке, принадлежащей заданного интервала, а, как, например, далее — в двух.
Нередки случаи, когда уравнение, полученное от приравнивания производной функции нулю, не имеет действительных решений. Тогда наименьшее и наибольшее значения функции можно найти только на концах отрезка. Таков следующий пример.
Неплохо было бы взять и случаи, когда производная функции вычисляется не одним махом,
как в предыдущих примерах. Это мы сейчас и сделаем, решив пример, где требуется найти
производную частного.
Это мы сейчас и сделаем, решив пример, где требуется найти
производную частного.
Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.
Есть преподаватели, которые по теме нахождения наименьшего и наибольшего значений функции не дают студентам для решения примеры сложнее только что рассмотренных, то есть таких, в которых функция — многочлен либо дробь, числитель и знаменатель которой — многочлены. Но мы не ограничимся такими примерами, поскольку среди преподавателей бывают любители заставить студентов думать по полной (таблице производных). Поэтому в ход пойдут логарифм и тригонометрическая функция.
Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.
В прикладных экстремальных задачах нахождение наименьшего (наибольшего) значений
функции, как правило, сводится к нахождению минимума (максимума). Но больший практический интерес имеют
не сами минимумы или максимумы, а те значения аргумента, при которых они достигаются. При решении
прикладных задач возникает дополнительная трудность — составление функций, описывающих рассматриваемое
явление или процесс.
Но больший практический интерес имеют
не сами минимумы или максимумы, а те значения аргумента, при которых они достигаются. При решении
прикладных задач возникает дополнительная трудность — составление функций, описывающих рассматриваемое
явление или процесс.
Пример 10. Резервуар ёмкостью 4 , имеющий форму параллелепипеда с квадратным основанием и открытый сверху, нужно вылудить оловом. Каковы должны быть размеры резервуара, чтобы на его покрытие ушло наименьшее количество материала?
Решение. Пусть x — сторона основания, h — высота резервуара, S — площадь его поверхности без крышки, V — его объём. Площадь поверхности резервуара выражается формулой , т.е. является функцией двух переменных . Чтобы выразить S как функцию одной переменной, воспользуемся тем, что , откуда . Подставив найденное выражение h в формулу для S:
или
.
Исследуем эту функцию на экстремум. Она определена и дифференцируема всюду в ]0, +∞[, причём
.
Приравниваем производную нулю () и находим критическую точку . Кроме того, при производная не существует, но это значение не входит в область определения и поэтому не может быть точкой экстремума. Итак, — единственная критическая точка. Проверим её на наличие экстремума, используя второй достаточный признак. Найдём вторую производную . При вторая производная больше нуля (). Значит, при функция достигает минимума . Поскольку этот минимум — единственный экстремум данной функции, он и является её наименьшим значением. Итак, сторона основания резервуара должна быть равна 2 м, а его высота .
Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.
Пример 11. Из пункта A, находящегося на линии железной
дороги, в пункт С, отстоящий от неё на расстоянии l, должны переправляться грузы.
Стоимость провоза весовой единицы на единицу расстояния по железной дороге равна ,
а по шоссе она равна . К
какой точке М линии железной дороги следует провести шоссе, чтобы транспортировка груза из
А в С была наиболее экономичной (участок АВ железной дороги предполагается
прямолинейным)?
Из пункта A, находящегося на линии железной
дороги, в пункт С, отстоящий от неё на расстоянии l, должны переправляться грузы.
Стоимость провоза весовой единицы на единицу расстояния по железной дороге равна ,
а по шоссе она равна . К
какой точке М линии железной дороги следует провести шоссе, чтобы транспортировка груза из
А в С была наиболее экономичной (участок АВ железной дороги предполагается
прямолинейным)?Пусть , , (см. рисунок ниже).
Тогда , , . Стоимость провоза p единиц груза по шоссе СМ составит , а по железной дороге МА она составит . Общая стоимость провоза груза по пути СМА выражается функцией
,
где .
Нужно найти наименьшее значение этой функции. Она дифференцируема при всех значениях x, причём
.
Приравняв производную нулю, получим иррациональное уравнение , решение которого даёт единственную критическую точку (так как точка не входит в область определения функции).
Взяв контрольные точки и слева и справа от критической точки, убедимся, что производная меняет знак с минуса на плюс. Следовательно, при стоимость провоза груза из А и С является наименьшей, если . Если же , т. е. , то шоссе должно пройти по прямой АС (см. рисунок ниже).
Весь блок «Производная»
Наибольшее и наименьшее значение функции, формулы и примеры
Если функция $y=f(x)$ определена и
непрерывна на отрезке
$[a ; b]$ , то она на этом отрезке достигает своих наибольшего
и наименьшего значений. Если свое наибольшее значение $M$
функция $f(x)$ принимает в точке
$x_{0} \in[a ; b]$, то
$M=f\left(x_{0}\right)$ будет локальным максимумом функции
$f(x)$, так как в этом случае существует окрестность точки
$x_{0}$, такая, что
$f(x) \leq f\left(x_{0}\right)$ .
Из полученных значений нам надо оставить лишь те, которые принадлежат заданному промежутку $[0 ; 5]$ . Оба значения лежат в этом промежутке.
Находим значения функции в полученных стационарных точках из промежутка и на концах промежутка:
$y(0)=4 ; \quad y\left(\frac{1}{3}\right)=\frac{106}{27} \approx 3,92 ; y(5)=454$
Таким образом,
Ответ.
Читать дальше: выпуклость функции, точки перегиба.
Слишком сложно?
Наибольшее и наименьшее значение функции, непрерывной на отрезке не по зубам? Тебе ответит эксперт через 10 минут!
Наибольшее и наименьшее значение функции
На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др.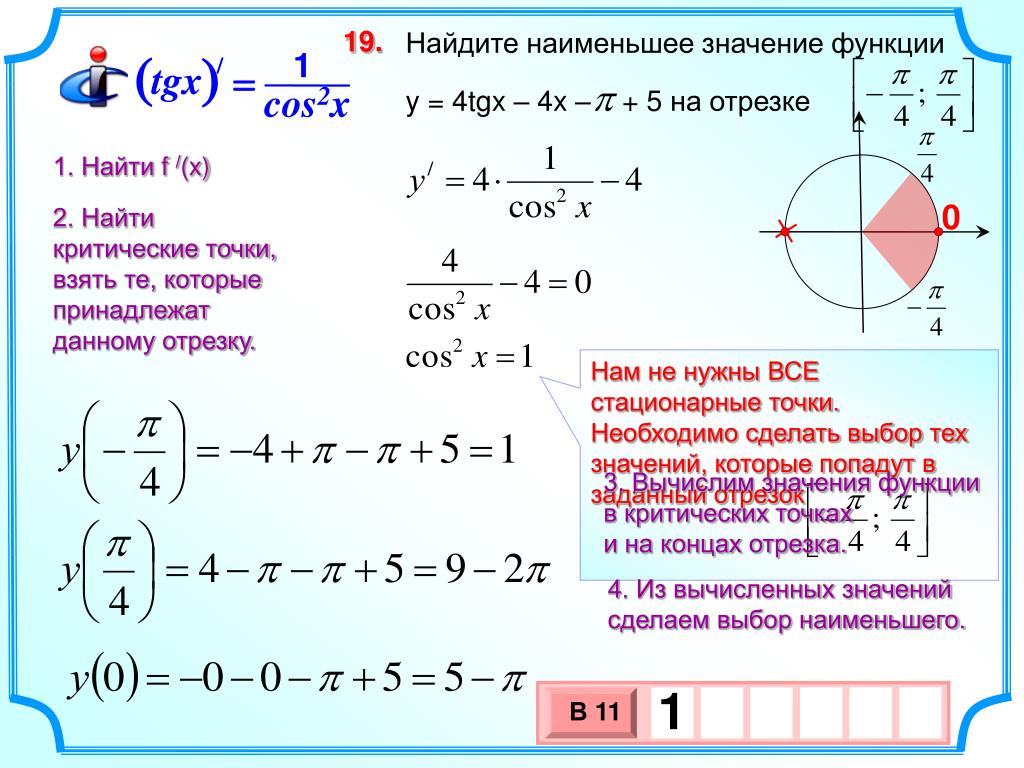 , то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
, то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
Обычно мы определяем эти значения в рамках некоторого интервала x, который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [a; b], так и открытый интервал (a; b), (a; b], [a; b), бесконечный интервал (a; b), (a; b], [a; b) либо бесконечный промежуток -∞; a, (-∞; a], [a; +∞), (-∞; +∞).
В этом материале мы расскажем, как вычисляется наибольшее и наименьшее значение явно заданной функции с одной переменной y=f(x)y=f(x).
Основные определения
Начнем, как всегда, с формулировки основных определений.
Определение 1Наибольшее значение функции y=f(x) на некотором промежутке x – это значение max y=f(x0)x∈X, которое при любом значении xx∈X, x≠x0 делает справедливым неравенство f(x)≤f(x0).
Определение 2Наименьшее значение функции y=f(x) на некотором промежутке x– это значение minx∈Xy=f(x0), которое при любом значении x∈X, x≠x0 делает справедливым неравенство f(Xf(x)≥f(x0).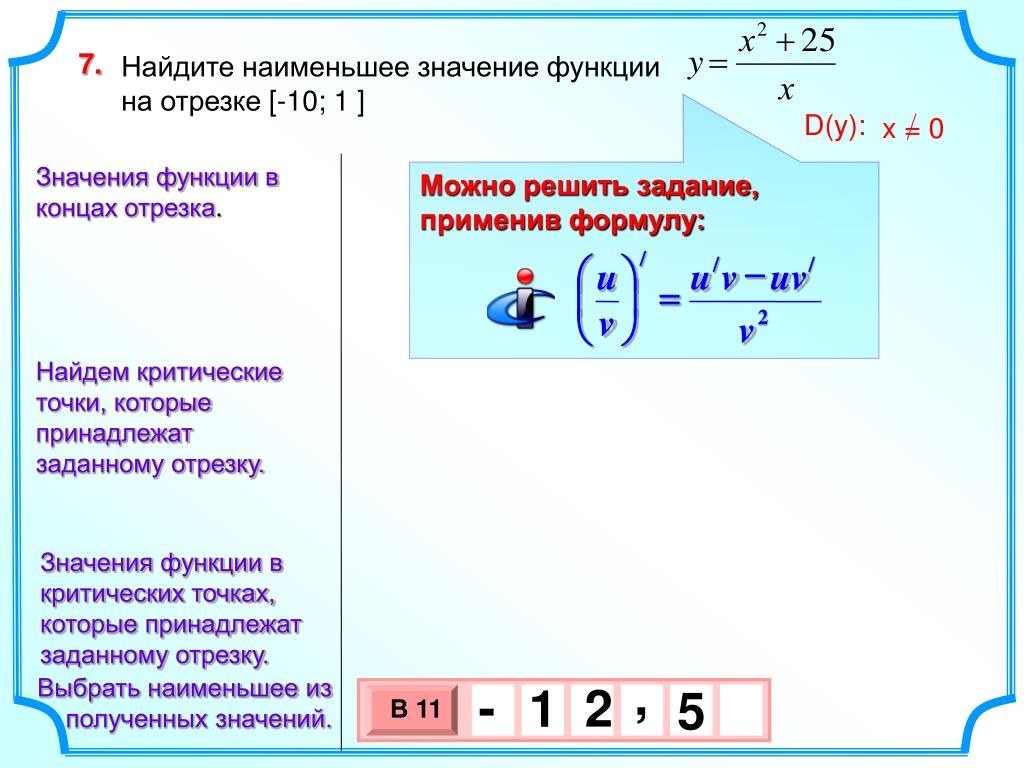
Данные определения являются достаточно очевидными. Еще проще можно сказать так: наибольшее значение функции – это ее самое большое значение на известном интервале при абсциссе x0, а наименьшее – это самое маленькое принимаемое значение на том же интервале при x0.
Определение 3Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0.
Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.
Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.
Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы может определить наибольшее или наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с бесконечным интервалом. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.
Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.
Более понятными эти моменты станут после изображения на графиках:
Наибольшее и наименьшее значение функции на отрезке
Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения (max y и min y) в стационарных точках, расположенных на отрезке [-6;6].
Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [1;6] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.
На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [-3;2]. Они соответствуют наибольшему и наименьшему значению заданной функции.
Наибольшее и наименьшее значение функции на открытом интервале
Теперь посмотрим на четвертый рисунок. В нем функция принимает max y (наибольшее значение) и min y (наименьшее значение) в стационарных точках на открытом интервале (-6;6).
В нем функция принимает max y (наибольшее значение) и min y (наименьшее значение) в стационарных точках на открытом интервале (-6;6).
Если мы возьмем интервал [1;6), то можно сказать, что наименьшее значение функции на нем будет достигнуто в стационарной точке. Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x, равном 6, если бы x=6 принадлежала интервалу. Именно этот случай нарисован на графике 5.
На графике 6 наименьшее значение данная функция приобретает в правой границе интервала (-3;2], а о наибольшем значении мы не можем сделать определенных выводов.
Наибольшее и наименьшее значение функции на бесконечности
На рисунке 7 мы видим, что функция будет иметь max y в стационарной точке, имеющей абсциссу, равную 1. Наименьшего значения функция достигнет на границе интервала с правой стороны. На минус бесконечности значения функции будут асимптотически приближаться к y=3.
Если мы возьмем интервал x∈2; +∞, то увидим, что заданная функция не будет принимать на нем ни наименьшего, ни наибольшего значения. Если x стремится к 2, то значения функции будут стремиться к минус бесконечности, поскольку прямая x=2 – это вертикальная асимптота. Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y=3. Именно этот случай изображен на рисунке 8.
Если x стремится к 2, то значения функции будут стремиться к минус бесконечности, поскольку прямая x=2 – это вертикальная асимптота. Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y=3. Именно этот случай изображен на рисунке 8.
Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке
В этом пункте мы приведем последовательность действий, которую нужно выполнить для нахождения наибольшего или наименьшего значения функции на некотором отрезке.
- Для начала найдем область определения функции. Проверим, входит ли в нее заданный в условии отрезок.
- Теперь вычислим точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего их можно встретить у функций, аргумент которых записан под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом.
- Далее выясним, какие стационарные точки попадут в заданный отрезок.
 Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу. - Определим, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычисляем значения для x=a и x=b.
- 5. У нас получился ряд значений функции, из которых теперь нужно выбрать самое больше и самое маленькое. Это и будут наибольшее и наименьшее значения функции, которые нам нужно найти.
Посмотрим, как правильно применить этот алгоритм при решении задач.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 1Условие: задана функция y=x3+4×2. Определите ее наибольшее и наименьшее значение на отрезках [1;4] и [-4;-1].
Решение:
Начнем с нахождения области определения данной функции. В этом случае ей будет множество всех действительных чисел, кроме 0. Иными словами, D(y): x∈(-∞; 0)∪0; +∞. Оба отрезка, заданных в условии, будут находиться внутри области определения.
Теперь вычисляем производную функции согласно правилу дифференцирования дроби:
y’=x3+4×2’=x3+4’·x2-x3+4·x2’x4==3×2·x2-(x3-4)·2xx4=x3-8×3
Мы узнали, что производная функции будет существовать во всех точках отрезков [1;4] и [-4;-1].
Теперь нам надо определить стационарные точки функции. Сделаем это с помощью уравнения x3-8×3=0. У него есть только один действительный корень, равный 2. Он будет стационарной точкой функции и попадет в первый отрезок [1;4].
Вычислим значения функции на концах первого отрезка и в данной точке, т.е. для x=1, x=2 и x=4:
y(1)=13+412=5y(2)=23+422=3y(4)=43+442=414
Мы получили, что наибольшее значение функции max yx∈[1; 4]=y(2)=3 будет достигнуто при x=1, а наименьшее min yx∈[1; 4]=y(2)=3 – при x=2.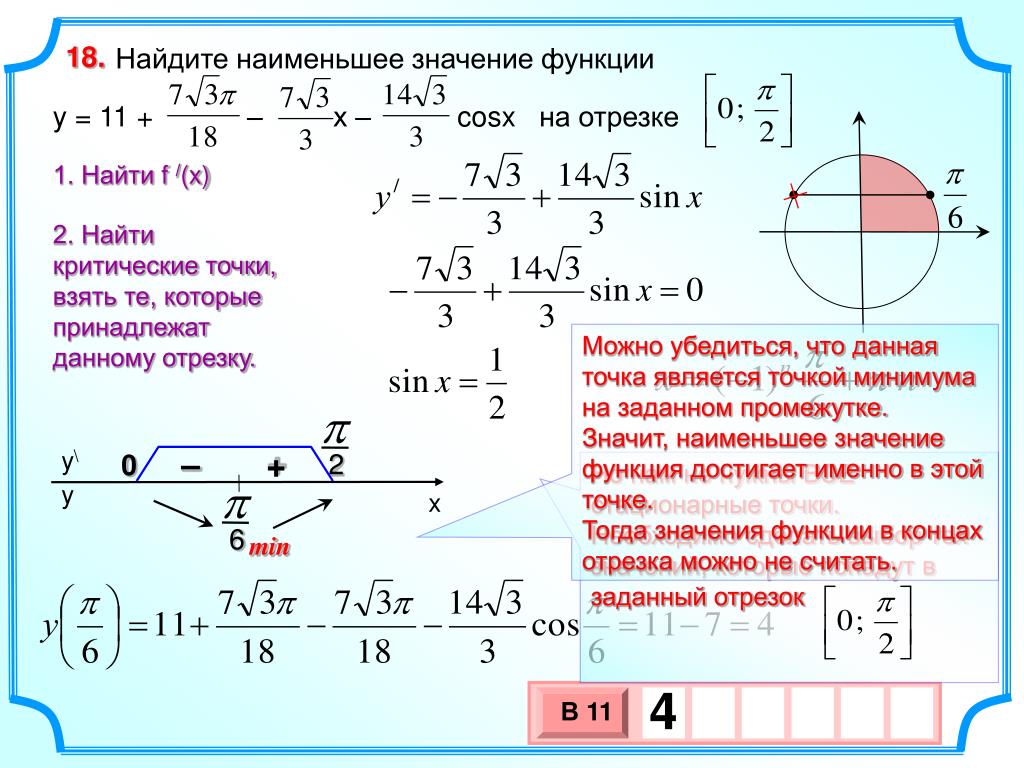
Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:
y(-1)=(-1)3+4(-1)2=3
Значит, max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.
Ответ: Для отрезка [1;4] — max yx∈[1; 4]=y(2)=3, min yx∈[1; 4]=y(2)=3, для отрезка [-4;-1] — max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.
См. на рисунке:
Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале
Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
- Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.

- Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
- Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0, решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям. Их определяет вид интервала.
- Если интервал имеет вид [a;b), то нам надо вычислить значение функции в точке x=a и односторонний предел limx→b-0f(x).
- Если интервал имеет вид (a;b], то нам надо вычислить значение функции в точке x=b и односторонний предел limx→a+0f(x).
- Если интервал имеет вид (a;b), то нам надо вычислить односторонние пределы limx→b-0f(x),limx→a+0f(x).

- Если интервал имеет вид [a; +∞), то надо вычислить значение в точке x=a и предел на плюс бесконечности limx→+∞f(x).
- Если интервал выглядит как (-∞; b], вычисляем значение в точке x=b и предел на минус бесконечности limx→-∞f(x).
- Если -∞; b, то считаем односторонний предел limx→b-0f(x) и предел на минус бесконечности limx→-∞f(x)
- Если же -∞; +∞, то считаем пределы на минус и плюс бесконечности limx→+∞f(x), limx→-∞f(x).
- В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4-8 в первой части материала.
Условие: дана функция y=3e1x2+x-6-4. Вычислите ее наибольшее и наименьшее значение в интервалах -∞; -4, -∞; -3, (-3;1], (-3;2), [1;2), 2; +∞, [4; +∞).
Решение
Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в 0:
x2+x-6=0D=12-4·1·(-6)=25×1=-1-52=-3×2=-1+52=2⇒D(y): x∈(-∞; -3)∪(-3; 2)∪(2; +∞)
Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.
Теперь выполним дифференцирование функции и получим:
y’=3e1x2+x-6-4’=3·e1x2+x-6’=3·e1x2+x-6·1×2+x-6’==3·e1x2+x-6·1’·x2+x-6-1·x2+x-6′(x2+x-6)2=-3·(2x+1)·e1x2+x-6×2+x-62
Следовательно, производные функции существуют на всей области ее определения.
Перейдем к нахождению стационарных точек. Производная функции обращается в 0 при x=-12. Это стационарная точка, которая находится в интервалах (-3;1] и (-3;2).
Вычислим значение функции при x=-4 для промежутка (-∞; -4], а также предел на минус бесконечности:
y(-4)=3e1(-4)2+(-4)-6-4=3e16-4≈-0.456limx→-∞3e1x2+x-6=3e0-4=-1
Поскольку 3e16-4>-1, значит, max yx∈(-∞; -4]=y(-4)=3e16-4. Это не дает нам возможности однозначно определить наименьшее значение функции. Мы можем только сделать вывод, что внизу есть ограничение -1, поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.
Это не дает нам возможности однозначно определить наименьшее значение функции. Мы можем только сделать вывод, что внизу есть ограничение -1, поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.
Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы. Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к -3 с левой стороны, мы получим только интервал значений:
limx→-3-03e1x2+x-6-4=limx→-3-03e1(x+3)(x-3)-4=3e1(-3-0+3)(-3-0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→-∞3e1x2+x-6-4=3e0-4=-1
Значит, значения функции будут расположены в интервале -1; +∞
Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке x=-12, если x=1. Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к -3 с правой стороны:
y-12=3e1-122+-12-6-4=3e425-4≈-1. 444y(1)=3e112+1-6-4≈-1.644limx→-3+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1-3+0+3(-3+0-2)-4==3e1(-0)-4=3e-∞-4=3·0-4=-4
444y(1)=3e112+1-6-4≈-1.644limx→-3+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1-3+0+3(-3+0-2)-4==3e1(-0)-4=3e-∞-4=3·0-4=-4
У нас получилось, что наибольшее значение функция примет в стационарной точке max yx∈(3; 1]=y-12=3e-425-4. Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до -4.
Для интервала (-3;2) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:
y-12=3e1-122+-12-6-4=3e-425-4≈-1.444limx→-3+03e1x2+x-6-4=-4limx→2-03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2-0+3)(2-0-2)-4==3e1-0-4=3e-∞-4=3·0-4=-4
Значит, max yx∈(-3; 2)=y-12=3e-425-4, а наименьшее значение определить невозможно, и значения функции ограничены снизу числом -4.
Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [1;2) наибольшее значение функция примет при x=1, а найти наименьшее невозможно.
На промежутке (2; +∞) функция не достигнет ни наибольшего, ни наименьшего значения, т.е. она будет принимать значения из промежутка -1; +∞.
limx→2+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2+0+3)(2+0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→+∞3e1x2+x-6-4=3e0-4=-1
Вычислив, чему будет равно значение функции при x=4, выясним, что max yx∈[4; +∞)=y(4)=3e114-4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y=-1.
Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.
Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.
Урок 17. наибольшее и наименьшее значения функций — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №17. Наибольшее и наименьшее значения функции.
Перечень вопросов, рассматриваемых в теме
1) Нахождение наибольшего и наименьшего значения функции,
2)Определение алгоритма нахождения наибольшего и наименьшего значений функции на отрезке,
3) Рассмотреть прикладные задачи на нахождение наибольшего и наименьшего значений
Глоссарий по теме
Алгоритм нахождения наибольшего и наименьшего значений функции y = f(x) на отрезке [a; b]:
- Найти область определения функции D(f).
- Найти производную f‘ (x).
- Найти стационарные и критические точки функции, принадлежащие интервалу (a; b).
- Найти f(a), f(b) и значения функции в стационарных точках, принадлежащих интервалу (а; b).

- Среди полученных значений выбрать наибольшее и наименьшее.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Нахождение наибольшего и наименьшего значений функции на отрезке.
- Если функция непрерывна на отрезке, то она достигает на нем своего наибольшего и своего наименьшего значения.
- Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
- Если наибольшее (наименьшее) значение функции достигается внутри отрезка, то только в стационарной или критической точке.

Алгоритм нахождения наибольшего и наименьшего значений функции y = f(x) на отрезке [a; b]:
- Найти производную f‘ (x) стационарные и критические точки функции, принадлежащие интервалу (a; b).
- Найти f(a), f(b) и значения функции в стационарных точках, принадлежащих интервалу (а; b)и среди полученных значений выбрать наибольшее и наименьшее
Примеры и разбор решения заданий тренировочного модуля
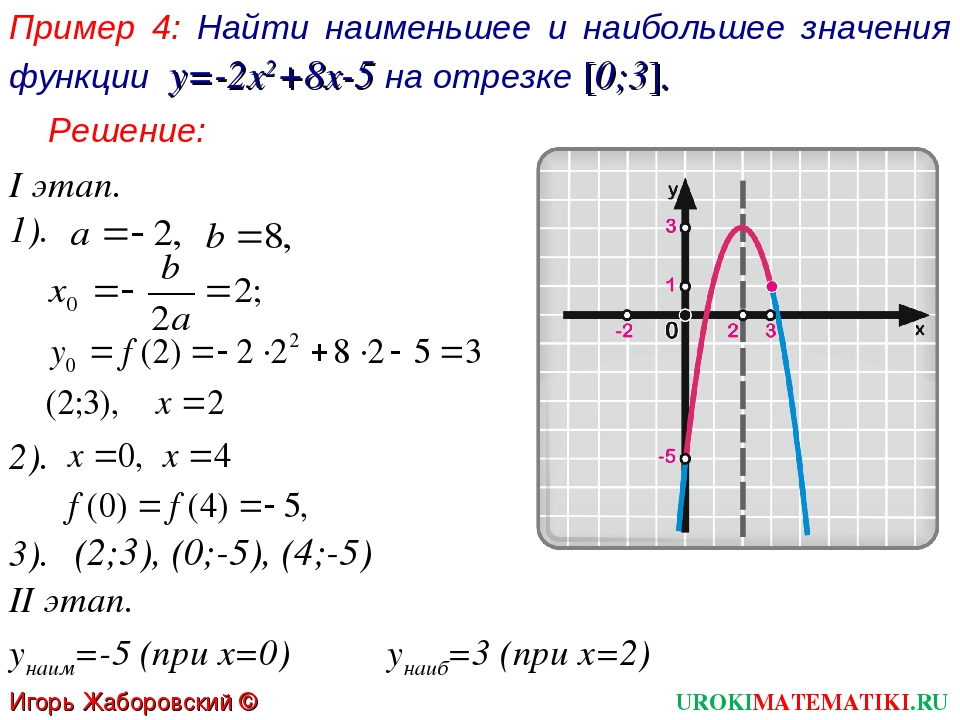
№1.Найти наибольшее и наименьшее значения функции f (x) = 2x3 – 9x2 + 12x – 2 на отрезке [0; 3]
Решение. Действуем в соответствии с алгоритмом.
1) D(f) = (-∞; +∞).
2) f (x) = 6x2 – 18x + 12
3) Стационарные точки: х = 1; х = 2.
4) f(0) = -2
f(3) = 7
f(1) = 3
f(2) = 2
5) fнаим.=f(0) = -2
fнаиб.=f(3) = 7.
Ответ: fнаим= -2
fнаиб.= 7.
№2.Найдите два положительных числа, сумма которых равна 16, а произведение наибольшее.
Решение.
Пусть первое число равно х,
Тогда второе число —
Следовательно,
Произведение этих чисел равно х(16 – х).
Составим функцию:
f(x) = x(16 – x)
x = 8 – единственная стационарная точка на интервале (0; 16), она является точкой максимума.
Следовательно, в этой точке функция F(x) = x(16 – x) принимает наибольшее значение.
Следовательно, два положительных числа, сумма которых равна 16, а произведение наибольшее, это 8 и 8.
Ответ: 8 и 8
Найти наименьшее общее кратное (НОК)
Общее кратное для двух целых чисел — это такое целое число, которое делится нацело без остатка на оба заданных числа.Наименьшее общее кратное для двух целых чисел — это наименьшее из всех целых чисел, которое делится нацело и без остатка на оба заданных числа.
Способ 1. Найти НОК можно, по очереди, для каждого из заданных чисел, выписывая в порядке возрастания все числа, которые получаются путем их умножения на 1, 2, 3, 4 и так далее.
Пример для чисел 6 и 9.
Умножаем число 6, последовательно, на 1, 2, 3, 4, 5.
Получаем: 6, 12, 18, 24, 30
Умножаем число 9, последовательно, на 1, 2, 3, 4, 5.
Получаем: 9, 18, 27, 36, 45
Как видно, НОК для чисел 6 и 9 будет равно 18.
Данный способ удобен, когда оба числа небольшие и их несложно умножать на последовательность целых чисел. Однако, бывают случаи, когда нужно найти НОК для двузначных или трехзначных чисел, а также, когда исходных чисел три или даже больше.
Способ 2. Найти НОК можно, разложив исходные числа на простые множители.
После разложения необходимо вычеркнуть из получившихся рядов простых множителей одинаковые числа. Оставшиеся числа первого числа будут множителем для второго, а оставшиеся числа второго — множителем для первого.
Пример для числе 75 и 60.
Наименьшее общее кратное чисел 75 и 60 можно найти и не выписывая подряд кратные этих чисел. Для этого разложим 75 и 60 на простые множители:
Для этого разложим 75 и 60 на простые множители:
75 = 3 * 5 * 5, а
60 = 2 * 2 * 3 * 5.
Как видно, множители 3 и 5 встречаются в обоих строках. Мысленно их «зачеркиваем».
Выпишем оставшиеся множители, входящие в разложение каждого из этих чисел. При разложении числа 75 у нас осталось число 5, а при разложении числа 60 — остались 2 * 2
Значит, чтобы определить НОК для чисел 75 и 60, нам нужно оставшиеся числа от разложения 75 (это 5) умножить на 60, а числа, оставшиеся от разложения числа 60 (это 2 * 2 ) умножить на 75. То есть, для простоты понимания, мы говорим, что умножаем «накрест».
75 * 2 * 2 = 300
60 * 5 = 300
Таким образом мы и нашли НОК для чисел 60 и 75. Это — число 300.
Пример. Определить НОК для чисел 12, 16, 24
В данном случае, наши действия будут несколько сложнее. Но, сначала, как всегда, разложим все числа на простые множители
12 = 2 * 2 * 3
16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3
Чтобы правильно определить НОК, выбираем наименьшее из всех чисел (это число 12) и последовательно проходим по его множителям, вычеркивая их, если хотя бы в одном из других рядов чисел встретился такой же, еще не зачеркнутый множитель.
Шаг 1 . Мы видим, что 2 * 2 встречаются во всех рядах чисел. Зачеркиваем их.
12 = 2 * 2 * 3
16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3
Шаг 2. В простых множителях числа 12 осталось только число 3. Но оно присутствует в простых множителях числа 24. Вычеркиваем число 3 из обоих рядов, при этом для числа 16 никаких действий не предполагается.
12 = 2 * 2 * 3
16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3
Как видим, при разложении числа 12 мы «вычеркнули» все числа. Значит нахождение НОК завершено. Осталось только вычислить его значение.
Для числа 12 берем оставшиеся множители у числа 16 (ближайшего по возрастанию)
12 * 2 * 2 = 48
Это и есть НОК
Как видим, в данном случае, нахождение НОК было несколько сложнее, но когда нужно его найти для трех и более чисел, данный способ позволяет сделать это быстрее. Впрочем, оба способа нахождения НОК являются правильными.
Впрочем, оба способа нахождения НОК являются правильными.
Наибольшее и наименьшее значение функции | ЕГЭ по математике (профильной)
Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.
Чтобы найти наибольшее или наименьшее значение функции необходимо:
- Найти производную функции $f'(х)$
- Найти стационарные точки, решив уравнение $f'(х)=0$
- Проверить, какие стационарные точки входят в заданный отрезок.
- Вычислить значение функции на концах отрезка и в стационарных точках из п.3
- Выбрать из полученных результатов наибольшее или наименьшее значение.
Чтобы найти точки максимума или минимума необходимо:
- Найти производную функции $f'(х)$
- Найти стационарные точки, решив уравнение $f'(х)=0$
- Разложить производную функции на множители.
 2}$
2}$4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции
$f(g(x))′=f′(g(x))∙g′(x)$
Пример:
$f(x)= cos(5x)$
$f′(x)=cos′(5x)∙(5x)′= — sin(5x)∙5= -5sin(5x)$
Пример:
Найдите точку минимума функции $y=2x-ln(x+11)+4$
Решение:
1. Найдем ОДЗ функции: $х+11>0; х>-11$
2. Найдем производную функции $y’=2-{1}/{x+11}={2x+22-1}/{x+11}={2x+21}/{x+11}$
3. Найдем стационарные точки, приравняв производную к нулю
${2x+21}/{x+11}=0$
Дробь равна нулю если числитель равен нулю, а знаменатель не равен нулю
$2x+21=0; x≠-11$
$2х=-21$
$х=-10,5$
4. Начертим координатную прямую, расставим на ней стационарные точки и определим знаки производной в полученных интервалах. Для этого подставим в производную любое число из крайней правой области, например, нуль.
$y'(0)={2∙0+21}/{0+11}={21}/{11}>0$
5. В точке минимума производная меняет знак с минуса на плюс, следовательно, точка $-10,5$ — это точка минимума.
 3-5=6-90-5= -89$
3-5=6-90-5= -89$Наибольшее значение равно $967$
Ответ: $967$
Как найти и выделить минимальное значение в Excel?
В этой статье вы узнаете, как использовать функцию МИН в Excel 2007-2019, найти минимальное значение, наименьшее значение по условию и выделить самое маленькое число в вашем диапазоне.
Сегодня мы расскажем вам, как использовать базовую, но очень важную функцию МИН в Excel. Вы увидите способы найти минимальное значение, в том числе исключая нули, абсолютный минимум и наименьшее значение с учётом условий. Кроме того, я покажу вам пошагово, как выделить цветом наименьшее число, а также подскажу, что делать, если ваша функция МИН возвращает ошибку вместо нужного результата.
Итак, начнем 🙂
Функция Excel МИН — синтаксис
Функция МИН проверяет ваш диапазон данных и возвращает минимальное значение в этом наборе.
Синтаксис для Excel МИН следующий:
МИН (число 1; [число 2]; .
 ..)
..)число1, [число2],… — это серия чисел, откуда вы хотите получить минимум. Число1 — обязательный аргумент, в то время как [число 2] и следующие являются необязательными. В одной формуле МИН допускается до 255 аргументов. Аргументы могут быть числами, ссылками на ячейки и диапазонами.
Функция МИН является одной из самых простых в применении. Вот пару примеров, доказывающих это:
1. Нахождение наименьшего значения
Допустим, у вас есть фрукты на складе. Ваша задача — проверить, какие из них заканчиваются. Есть несколько способов это сделать:
1: Ввести каждое значение из столбца «Количество на складе» в формулу:
= МИН(366;476;398;982;354;534;408)
2: Сделать ссылки на каждую ячейку столбца Количество:
= МИН(В2; В3; В4; В5; В6; В7; В8)
3: Или просто сослаться на весь диапазон ячеек:
= МИН(В2:В8)
4: в качестве альтернативы вы можете создать именованный диапазон и использовать его вместо этого, чтобы избежать любых прямых ссылок:
2.
 Как найти самую раннюю дату
Как найти самую раннюю датуПредставьте, что вы ждете несколько доставок и хотели бы быть готовыми к самой ближайшей. Как узнать самую раннюю дату в Excel? Легко! Используйте функцию МИН, следуя логике из примера 1:
Примените МИН и выберите даты, ссылаясь непосредственно на ячейки:
= МИН(В2:В8)
или на именованный диапазон:
= МИН(дата_поставки)
3. Поиск абсолютного минимума в Excel
Предположим, что у вас есть диапазон чисел, и вам нужно определить не просто самое маленькое из них, но найти абсолютный минимум или минимум по абсолютному значению (по модулю). Одна только МИН функция не сможет справиться с этим, поскольку она просто будет искать минимальное число. Здесь вам нужна вспомогательная функция, которая может конвертировать все отрицательные числа в положительные.
Есть ли готовое решение для этого случая? Вопрос был риторическим, в Excel есть решение любой задачи.
 Если у вас есть какие-либо сомнения, просто просмотрите наш блог. 🙂
Если у вас есть какие-либо сомнения, просто просмотрите наш блог. 🙂Но вернемся к нашей задаче. Готовое решение для этого конкретного случая называется функцией ABS, которая возвращает абсолютное значение заданных вами чисел. Таким образом, комбинация функций МИН и ABS сделает свое дело. Просто введите следующую формулу в любую пустую ячейку:
{= МИН(ABS(А1:Е12))}
Важно! Вы заметили фигурные скобки вокруг формулы? Это признак того, что это формула массива, и ее нужно вводить с помощью комбинации клавиш
Ctrl + Shift + Enter, а не простоEnter.Как найти самое маленькое значение в Excel, исключая нули
Вам кажется, что вы уже знаете все о поиске минимальных значений в Excel? Не спешите с выводами, всегда есть чему поучиться. Например, как бы вы определили наименьшее ненулевое значение? Есть идеи? Не обманывай и не гугли, просто продолжай читать;)
Дело в том, что Excel МИН работает не только с положительными и отрицательными числами, но и с нулями.
 Если вы не хотите, чтобы нули были таким минимумом, вам нужна помощь функции ЕСЛИ (IF). Как только вы добавите ограничение, что ваш диапазон должен быть больше нуля, ожидаемый результат не заставит себя ждать. Вот пример формулы для использования:
Если вы не хотите, чтобы нули были таким минимумом, вам нужна помощь функции ЕСЛИ (IF). Как только вы добавите ограничение, что ваш диапазон должен быть больше нуля, ожидаемый результат не заставит себя ждать. Вот пример формулы для использования:{= МИН(ЕСЛИ(В2: В15>0,В2:В15))}
Вы, наверное, заметили фигурные скобки вокруг формулы массива. Просто помните, что вы не вводите их вручную. Они появляются в тот момент, когда вы нажимаете
Ctrl + Shift + Enterна клавиатуре.Нахождение минимума на основе условия
Предположим, вам нужно найти наименьшее количество продаж определенного фрукта в списке. Другими словами, ваша задача — определить минимальное значение на основе некоторого критерия. В Excel условия обычно требуют использования функции ЕСЛИ. Все, что вам нужно сделать, это создать идеальную комбинацию МИН и ЕСЛИ для решения этой задачи:
Нажмите Ctrl + Shift + Enter, чтобы эта функция массива работала, и наслаждайтесь результатом.

Выглядит довольно легко, правда? И как вы определите минимум на основе 2 или более условий? Может быть, есть более простая формула для этой задачи, доступная в Excel? Читайте дальше, чтобы узнать ответ. 😉
Как подсветить наименьшее число в Excel
А что, если вам не нужно возвращать минимальное значение, а вы просто хотите найти его в своей таблице? Самый простой способ найти ячейку — выделить ее. И самый простой способ сделать это — применить условное форматирование. Это даже проще, чем создать формулу:
1 Создайте новое правило условного форматирования, щелкнув Условное форматирование -> Создать правило
2 Когда откроется диалоговое окно «Создание правила форматирования», выберите тип правила «Форматировать только первые или последние значения».
3 Поскольку задача состоит в том, чтобы найти одно-единственное наименьшее значение, выберите опцию «последним» в раскрывающемся списке и укажите 1 в качестве количества ячеек, которые нужно выделить.

Но что делать, если в вашей таблице снова есть ноль? Как игнорировать нули при выделении минимального значения? Не беспокойтесь, для этого случая тоже есть маленькая хитрость:
1. Создайте новое правило условного форматирования, выбрав опцию «Использовать формулу для определения форматируемых ячеек».
2. Введите это выражение в поле «Значения формата» для проверки условия:
=B2=МИН(ЕСЛИ($B$2:$B$15>0,$B$2:$B$15))
Где B2 — первая ячейка диапазона, в которой будет найдено самое маленькое значение
3. Выберите цвет ( Формат… -> Заливка) и нажмите ОК.
4. Наслаждайтесь 🙂
Почему не работает функция МИН?
В идеальном мире все формулы будут работать как часы и возвращать правильные результаты, когда вы нажмете
Enter. Но в мире, в котором мы живем, формулы иногда возвращают ошибку, а не результат, который нам нужен. Не беспокойтесь, сама ошибка всегда намекает на ее возможную причину. Вам просто нужно всмотреться в вашу формулу.
Вам просто нужно всмотреться в вашу формулу.Исправление ошибки #ЗНАЧ! в формуле МИН
Как правило, вы получаете #ЗНАЧ! сообщение об ошибке, когда хотя бы одно из значений, использованных в формуле, неверно. Что касается МИН, это может произойти, когда один из аргументов поврежден, например, что-то не так с ячейками, которые использует формула.
Например, #ЗНАЧ! может появиться, если один из аргументов является ячейкой с ошибкой или в ссылке на ячейку есть опечатка.
Что может вызвать ошибку #ЧИСЛО! ?
Excel показывает ошибку #ЧИСЛО!, когда невозможно рассчитать вашу формулу. Обычно это происходит, когда числовое значение слишком велико или мало для отображения в Excel. В Excel допустимы номера от -2,2251E-308 до 2,2251E-308. Если один из ваших аргументов находится вне этого диапазона, функция вернет #ЧИСЛО!
Я получаю сообщение #ДЕЛ/0!, что делать?
Исправление #ДЕЛ/0! — это легко. Не делите на ноль! 🙂 Не шучу, это единственное решение этой проблемы.
 Проверьте диапазон ваших данных, исправьте ошибку #ДЕЛ/0!, и формула незамедлительно вернет правильный результат.
Проверьте диапазон ваших данных, исправьте ошибку #ДЕЛ/0!, и формула незамедлительно вернет правильный результат.Ищете минимум, но получаете #ИМЯ?
Сообщение #ИМЯ? означает, что Excel не может распознать формулу или ее аргументы. Наиболее вероятная причина этого результата — опечатка. Вы можете либо неправильно написать формулу, либо указать неверные аргументы для получения такого результата.
Другая возможная причина этой проблемы лежит в именованном диапазоне. Итак, если вы ссылаетесь на несуществующий диапазон или в нем есть опечатка, вы увидите #ИМЯ? в ячейке с результатом.
Это были некоторые из способов найти минимум в Microsoft Excel с помощью функции МИН. Для вас я рассмотрел различные подходы, чтобы найти самое маленькое значение в Excel и найти абсолютный минимум. Вы можете считать эту статью своей шпаргалкой и использовать всякий раз, когда вам нужно найти минимальное число в зависимости от условия, чтобы предотвратить и исправить возможные ошибки.

Вот и все на сегодня. Пожалуйста, не стесняйтесь делиться своими мыслями и вопросами в разделе комментариев, я буду рад получить от вас обратную связь! 🙂
Еще полезная дополнительная информация:
Функция МАКС в Excel: как найти максимальное значение — В этой статье объясняется функция МАКС с множеством примеров формул, которые показывают, как найти наибольшее значение в Excel и выделить наибольшее число на листе. МАКС — одна из самых простых и простых в использовании функций Excel. Тем не менее, у нее… Как сделать зависимый выпадающий список в Excel? — Одной из наиболее полезных функций проверки данных является возможность создания выпадающего списка, который позволяет выбирать значение из предварительно определенного перечня. Но как только вы начнете применять это в своих таблицах, то неизбежно столкнетесь с проблемой: нужно сделать один выпадающий список… Создаем выпадающий список в Excel при помощи формул — Задача: Создать выпадающий список в Excel таким образом, чтобы в него автоматически попадали все новые значения. Сделаем это при помощи формул, чтобы этот способ можно было использовать не только в Excel 2007 и старше, но и в Excel 2003. Как… 5 способов создания выпадающего списка в ячейке Excel — Одной из наиболее полезных функций при вводе данных является возможность использовать выпадающий список. Он позволяет выбирать значение из предварительно определенного перечня и разрешает вводить только те данные, которые соответствуют вашим требованиям. Мы предложим вам несколько простых способов, как создавать выпадающие…
Сделаем это при помощи формул, чтобы этот способ можно было использовать не только в Excel 2007 и старше, но и в Excel 2003. Как… 5 способов создания выпадающего списка в ячейке Excel — Одной из наиболее полезных функций при вводе данных является возможность использовать выпадающий список. Он позволяет выбирать значение из предварительно определенного перечня и разрешает вводить только те данные, которые соответствуют вашим требованиям. Мы предложим вам несколько простых способов, как создавать выпадающие…0 0 голоса
Рейтинг статьи
Q10 Найдите наименьшее квадратное число, которое делится на eac
.Решение:
L.C.M. из 8, 15 и 20 — 120.
Простые множители 120 = 2 x 2 x 2 x 3 x 5
Здесь простые множители 2, 3 и 5 не имеют пары.
 Следовательно, 120 нужно умножить на 2 x 3 x 5, чтобы получился полный квадрат.
Следовательно, 120 нужно умножить на 2 x 3 x 5, чтобы получился полный квадрат.\ поэтому 120 \ times2 \ times3 \ times5 = 3600
Следовательно, наименьшее квадратное число, которое делится на 8, 15 и 20, равно 3600.
привет, дети, добро пожаловать в Lido Homework в этом видео мы собираемся решить эту проблему Вопрос, в котором говорится найти наименьшее квадратное число, которое делится на каждое из чисел 8, 15 и 20. чтобы найти наименьшее квадратное число Делится на 8, 15 и 20 Давайте узнаем lcm данные числа 8 15 и 20. хорошо так что давайте запишем это 8 15 20. два четверки восемь-пятнадцать два десятка две двойки четыре пятнадцать как два пятерки — десять два — два пятнадцать и пять, как это, следующее число будет три три пятерки пятнадцать и пять как есть и следующим числом будет пять, хорошо так что lcm равно 2 в 2 в 2 в 3 в 5 это 8 в 3 на 5, что даст вам 120, так что lcm 8 15 и 20 — 120.
 Теперь обратите внимание на
слово
квадрат, который упоминается здесь, вы
просто не найти ни одного наименьшего числа
это не самое маленькое число, которое
там, но вы найдете самый маленький квадрат
номер
поэтому для этого нам нужно выяснить, 120
идеальный квадрат или нет для этого
мы должны проверить это с праймом
факторизация давайте разложим на множители 120
два шесть — ноль
две тройки
два два пятерки
три пятерки и пять
Итак, множители в простых множителях
120
2 в 2 в
2 на 3 на 5.так что когда тебе нужно найти идеальный
квадрат мы сначала группируем числа и
видеть
сколько номеров не имеют группы и
мы умножаем на эти числа прямо так
вы можете увидеть здесь
У 2 есть отличная группа, теперь 2 одиночки
3 — холост, а 5 — не замужем, они этого не делают.
иметь группу
так что мне нужно сделать, мне придется
умножать
120 на еще один два
еще один три и еще один пять ну и что
Я собираюсь добавить
еще два здесь, еще три здесь.
и еще пять здесь, чтобы я получил
полный
группы вправо, а затем число, которое я
получать
будет идеальным квадратом, поэтому 120 на 2
в 3 в 5 даст мне 3
6 двойных 0.
Теперь обратите внимание на
слово
квадрат, который упоминается здесь, вы
просто не найти ни одного наименьшего числа
это не самое маленькое число, которое
там, но вы найдете самый маленький квадрат
номер
поэтому для этого нам нужно выяснить, 120
идеальный квадрат или нет для этого
мы должны проверить это с праймом
факторизация давайте разложим на множители 120
два шесть — ноль
две тройки
два два пятерки
три пятерки и пять
Итак, множители в простых множителях
120
2 в 2 в
2 на 3 на 5.так что когда тебе нужно найти идеальный
квадрат мы сначала группируем числа и
видеть
сколько номеров не имеют группы и
мы умножаем на эти числа прямо так
вы можете увидеть здесь
У 2 есть отличная группа, теперь 2 одиночки
3 — холост, а 5 — не замужем, они этого не делают.
иметь группу
так что мне нужно сделать, мне придется
умножать
120 на еще один два
еще один три и еще один пять ну и что
Я собираюсь добавить
еще два здесь, еще три здесь.
и еще пять здесь, чтобы я получил
полный
группы вправо, а затем число, которое я
получать
будет идеальным квадратом, поэтому 120 на 2
в 3 в 5 даст мне 3
6 двойных 0. так что самый маленький
квадратное число, которое делится на 8 15
и 20
шестьсот
Надеюсь, я смог разрешить твои сомнения
с этим конкретным видео
пожалуйста, не стесняйтесь делиться и
комментарий и увидимся в другом
видео
Спасибо.
так что самый маленький
квадратное число, которое делится на 8 15
и 20
шестьсот
Надеюсь, я смог разрешить твои сомнения
с этим конкретным видео
пожалуйста, не стесняйтесь делиться и
комментарий и увидимся в другом
видео
Спасибо.Q9 Найдите наименьшее квадратное число, которое делится на
Решение:
L.C.M. из 4, 9 и 10 — 180.
Простые множители 180 = 2 x 2 x 3 x 3 x 5
Здесь у простого множителя 5 нет пары.Следовательно, 180 нужно умножить на 5, чтобы получился полный квадрат.
\ следовательно180 \ times5 = 900
Следовательно, наименьшее квадратное число, которое делится на 4, 9 и 10, равно 900.
«В этом видео мы собираемся решить этот вопрос: найти наименьшее квадратное число, которое делится на каждое из чисел 9, и найти наименьшее число, которое делится на 4, 9 и 10.
Программа Python Нам нужно найти НОК 4. минус 10.Итак, начнем с этого. Итак, давайте найдем НОК для 9 и 10. Это идет двумя двумя двойками — четырьмя 925 Сартен Снова по нашему мнению и пятеркам. Следующее число — 3 3 3 za Скажите, что самые грустные — три — три фута. Огонь остается, так как следующая цифра — 5 wanzer. Таким образом, НОК будет умножением всех этих множителей 2 на 2, 3, 3, 5, 2, 2, 4, 3, 3, 9, 5. Мы получаем ответ: 1 TT отлично. Итак, 180 — это число, но если вы разделите 4 9 и 10, вы получите полностью делимое число.Но здесь вопрос говорит, что нам нужно найти. Квадратный номер, верно? Итак, для этого давайте проверим, является ли 180 идеальным квадратом или нет. Так что давайте сделаем это тоже девять, сэр. И тогда ноль две пятерки несут одну две пятерки — 10:45. Это будет три, три, три пятерки, три пятерки и пять единиц, так что просто чтобы проверить, является ли 180 идеальным квадратом, верно? Итак, мы просто запишем Просто легкость, это запишет факторы. Итак, 2 на 2 на 3 на 3 на 5.
Нам нужно найти НОК 4. минус 10.Итак, начнем с этого. Итак, давайте найдем НОК для 9 и 10. Это идет двумя двумя двойками — четырьмя 925 Сартен Снова по нашему мнению и пятеркам. Следующее число — 3 3 3 za Скажите, что самые грустные — три — три фута. Огонь остается, так как следующая цифра — 5 wanzer. Таким образом, НОК будет умножением всех этих множителей 2 на 2, 3, 3, 5, 2, 2, 4, 3, 3, 9, 5. Мы получаем ответ: 1 TT отлично. Итак, 180 — это число, но если вы разделите 4 9 и 10, вы получите полностью делимое число.Но здесь вопрос говорит, что нам нужно найти. Квадратный номер, верно? Итак, для этого давайте проверим, является ли 180 идеальным квадратом или нет. Так что давайте сделаем это тоже девять, сэр. И тогда ноль две пятерки несут одну две пятерки — 10:45. Это будет три, три, три пятерки, три пятерки и пять единиц, так что просто чтобы проверить, является ли 180 идеальным квадратом, верно? Итак, мы просто запишем Просто легкость, это запишет факторы. Итак, 2 на 2 на 3 на 3 на 5. Хорошо, давайте сгруппируем их и посмотрим, есть ли у нас полные группы.У нас есть группа, чтобы у нас была группа из трех человек, а группа из пяти человек отсутствует. Итак, чтобы получить 180 или полный квадрат. Я умножу его на 5, чтобы сформировать группу. Так что же мне делать? Я умножу 180 на 5, что даст 900, поэтому наименьшее квадратное число, которое делится на 4, 9 и 10, равно 900, пожалуйста, обратите внимание на число для словесного квадрата, которое упомянуто. Хорошо, если вы пропустите это конкретное слово, вы можете даже остановиться на ответе, в котором говорится, что 180 делится на 4, 9 и 10, но здесь упоминается загвоздка.Что ему нужно наименьшее квадратное число. Это все в этом видео. Большое спасибо. Пожалуйста, не стесняйтесь делиться и комментировать, и увидимся в другом видео. «
Хорошо, давайте сгруппируем их и посмотрим, есть ли у нас полные группы.У нас есть группа, чтобы у нас была группа из трех человек, а группа из пяти человек отсутствует. Итак, чтобы получить 180 или полный квадрат. Я умножу его на 5, чтобы сформировать группу. Так что же мне делать? Я умножу 180 на 5, что даст 900, поэтому наименьшее квадратное число, которое делится на 4, 9 и 10, равно 900, пожалуйста, обратите внимание на число для словесного квадрата, которое упомянуто. Хорошо, если вы пропустите это конкретное слово, вы можете даже остановиться на ответе, в котором говорится, что 180 делится на 4, 9 и 10, но здесь упоминается загвоздка.Что ему нужно наименьшее квадратное число. Это все в этом видео. Большое спасибо. Пожалуйста, не стесняйтесь делиться и комментировать, и увидимся в другом видео. «для поиска наименьшего числа в списке
В этом руководстве мы увидим различные программы Python для поиска наименьшего числа в списке .
 Например, если список — [15, 20, 10, 16], тогда программа должна отображать число 10 в качестве вывода (наименьшее число в данном списке).
Например, если список — [15, 20, 10, 16], тогда программа должна отображать число 10 в качестве вывода (наименьшее число в данном списке).Пример 1: Поиск наименьшего числа в списке с помощью метода sort ()
В следующей программе мы находим наименьшее число в данном списке с помощью функции sort () . Функция sort () сортирует данный список в порядке возрастания . Затем мы отображаем первый элемент списка , который является наименьшим номером отсортированного списка .
# Программа на Python для поиска наименьшего числа в списке # Данный список чисел lis = [89, 100, 35, 16, 99] # сортируем данный список "lis" # Функция sort () сортирует список в порядке возрастания Лис.Сортировать() # Отображение первого элемента списка # наименьшее число в отсортированном списке print ("Наименьшее число в списке:", lis [0])Выход:
Пример 2: Поиск наименьшего числа в списке с помощью метода min ()
В следующей программе мы находим наименьший номер списка с помощью метода min () .
 Метод min () возвращает наименьший элемент списка .
Метод min () возвращает наименьший элемент списка .# Программа Python для поиска наименьшего числа в # данный список с использованием метода min () # Данный список чисел lis = [9, 100, 3, 16, 60] # Метод min () возвращает наименьший элемент списка print ("Наименьшее число в списке:", min (lis))Выход:
Пример 3: Поиск наименьшего числа в списке, где список предоставляется пользователем
В следующей программе мы находим наименьшее число в предоставленном пользователем списке , пользователю предлагается ввести количество элементов для добавления в список.Затем пользователь вводит элементы списка один за другим, каждый элемент ввода добавляется к списку с помощью метода append (). В конце программы отображается наименьший номер списка с использованием метода min () .
# создание пустого списка lis = [] # пользователь вводит количество элементов для добавления в список count = int (input ('Сколько чисел?')) # итерация до count для добавления всех входных элементов в список для n в диапазоне (количество): число = int (input ('Введите число:')) Лис. добавить (число)
# отображение наименьшего элемента
print ("Наименьший элемент списка:", min (lis))
добавить (число)
# отображение наименьшего элемента
print ("Наименьший элемент списка:", min (lis)) Выход:
Связанные примеры Python
- Программа Python для поиска наибольшего числа в списке
- Программа Python для поиска наибольшего из трех чисел
- Программа Python для преобразования десятичного числа в шестнадцатеричное
- Программа Python для замены двух чисел
Как найти наименьшее значение (MIN) — SurveyMonkey Apply
Используя Advanced Expression Piping в ваших формах, вы можете создавать математические формулы для вычисления значения.Используя функцию MIN, вы можете вернуть наименьшее значение из списка значений, предоставленного вашими кандидатами.
В этой статье …
Что такое функция MIN?
Функция MIN принимает список значений с плавающей запятой или целых чисел и возвращает наименьшее из них.
 Это можно использовать для отдельной строки или столбца в вопросе сетки, для таблицы в целом или для списка переменных в форме.
Это можно использовать для отдельной строки или столбца в вопросе сетки, для таблицы в целом или для списка переменных в форме.Вернуться к началу
Правильное форматирование для выражений MIN
Настройка и форматирование выражения MIN являются обязательными для предотвращения появления сообщения об ошибке в вашей форме там, где обычно отображается результат вашего выражения. Первая строка выражения MIN должна иметь следующий вид:
{{МИН (переменная1, переменная2)}} - Каждое выражение всегда заключено в пару двойных «фигурных» скобок {{}}
- Между первым экземпляром MIN и последней скобкой должен быть пробел.
- Используемые переменные чувствительны к регистру
- Всегда закрывайте каждую операцию MIN скобками ()
- Может содержать (,) для разделения значений.
 Не может содержать операторов, таких как (+), (-), (*) и т. Д.
Не может содержать операторов, таких как (+), (-), (*) и т. Д.
МИН. Выбранных ячеек {{МИН (q1 [0], q1 [2], [q1 [3])}} На основе индексации сетки это даст вам наименьшее значение для 1-й, 3-й и 4-й ячеек.
МИН столбца {{MIN (q1 [: 0])}} На основе индексации сетки найдется наименьшее значение в столбце 1.
МИН ряда {{MIN (q2 [1:])}} На основе индексации сетки найдется наименьшее значение в строке 2.
МИН диапазона {{MIN (q1 [0: 4])}} На основе индексации сетки это даст вам наименьшее значение из первых 4 ячеек.
МИН. Оценок рецензента {{МИН (q1.score, q2.score, q3.score)}} Значение самого низкого балла, полученного за один из перечисленных вопросов.

Вернуться к началу
Ограничения функции MIN
Функция MIN не сможет выполнять какие-либо операции с использованием такого выражения, как сложение (+), а также невозможно иметь другие функции в одном выражении MIN, такие как SUM, для вычисления различных переменных вместе, чтобы затем найти наименьшее значение.
Лучший способ извлечь наименьшее значение из этой информации — это иметь операции SUM на одной странице и передавать итоги на следующую страницу, используя выражение MIN.
Вернуться к началу
Поиск наименьшего и наибольшего элемента в массиве
Программа для поиска наименьших и наибольших элементов в массиве обсуждается здесь. Для данного массива задача состоит в том, чтобы найти наибольший и наименьший элементы массива.
Метод 1: Обходите массив итеративно и отслеживайте наименьший и наибольший элемент до конца массива.

Метод 2: Рекурсивно обойти массив и отслеживать наименьший и наибольший элемент до конца массива.
Метод 3: Отсортируйте массив с помощью STL и верните первый элемент как наименьший элемент, а последний элемент как наибольший элемент.
Например, рассмотрим массив.
arr = {1, 2, 3, 4, 5}
Наименьший элемент: 1
Самый большой элемент: 5
Алгоритм поиска наименьшего и наибольшего чисел в массиве- Введите элементы массива.
- Инициализировать small = large = arr [0]
- Повторить от i = 2 до n
- if (arr [i]> large)
- large = arr [i]
- if (arr [i]
- small = arr [i]
- Печатайте мелким и крупным шрифтом.
Выход
Введите количество элементов: 5
Введите элементы массива: 1 2 3 4 5
Наименьший элемент — 1
Самый большой элемент — 5Выход
Введите количество элементов: 5
Введите элементы массива: 1 2 3 4 5
Наименьший элемент — 1
Самый большой элемент — 5Выход
Самый маленький элемент — 1
Самый большой элемент — 5Выход
Сколько чисел: 5
Введите числа: 1 2 3 4 5
Максимальный элемент: 5
Минимальный элемент: 1Временная сложность: O (n)
Рекурсивная программа для поиска наименьшего и наибольшего элемента в массивеВыход
Введите размер массива: 5
Введите элементы массива: 1 2 3 4 5
Наименьший элемент в массиве — 1
Наибольший элемент в массиве — 5Выход
Введите размер массива: 5
Введите элементы массива: 1 2 3 4 5
Наименьший элемент в массиве — 1
Наибольший элемент в массиве — 5Выход
Наименьший элемент в массиве — 1
Наибольший элемент в массиве — 5Временная сложность: O (n)
Программа для поиска наименьшего и наибольшего элемента в массиве с использованием STL?
Выход
Введите размер массива: 5
Введите элементы массива: 1 2 3 4 5
Наименьший элемент в массиве — 1
Наибольший элемент в массиве — 5Выход
Минимальное количество массивов: 1
Максимальное количество массивов: 5Сложность времени: O (n log n)
Рекомендуемые программы
Если у вас есть отзывы об этом статью и хотите улучшить ее, напишите на запрос @ faceprep.
 в
в Безопасность | Стеклянная дверь
Мы получаем подозрительную активность от вас или кого-то, кто пользуется вашей интернет-сетью. Подождите, пока мы подтвердим, что вы настоящий человек. Ваш контент появится в ближайшее время. Если вы продолжаете видеть это сообщение, напишите нам чтобы сообщить нам, что у вас возникли проблемы.
Nous aider à garder Glassdoor sécurisée
Nous avons reçu des activités suspectes venant de quelqu’un utilisant votre réseau internet.Подвеска Veuillez Patient que nous vérifions que vous êtes une vraie personne. Вотре содержание apparaîtra bientôt. Si vous continuez à voir ce message, veuillez envoyer un электронная почта à pour nous informer du désagrément.
Unterstützen Sie uns beim Schutz von Glassdoor
Wir haben einige verdächtige Aktivitäten von Ihnen oder von jemandem, der in ihrem Интернет-Netzwerk angemeldet ist, festgestellt. Bitte warten Sie, während wir überprüfen, ob Sie ein Mensch und kein Bot sind.
 Ihr Inhalt wird в Kürze angezeigt.
Wenn Sie weiterhin diese Meldung erhalten, informieren Sie uns darüber bitte по электронной почте:
.
Ihr Inhalt wird в Kürze angezeigt.
Wenn Sie weiterhin diese Meldung erhalten, informieren Sie uns darüber bitte по электронной почте:
.We hebben verdachte activiteiten waargenomen op Glassdoor van iemand of iemand die uw internet netwerk deelt. Een momentje geduld totdat, мы выяснили, что u daadwerkelijk een persoon bent. Uw bijdrage zal spoedig te zien zijn. Als u deze melding blijft zien, электронная почта: om ons te laten weten dat uw проблема zich nog steeds voordoet.
Hemos estado detectando actividad sospechosa tuya o de alguien con quien compare tu red de Internet. Эспера mientras verificamos que eres una persona real. Tu contenido se mostrará en breve. Si Continúas recibiendo este mensaje, envía un correo electrónico a para informarnos de que tienes problemas.
Hemos estado percibiendo actividad sospechosa de ti o de alguien con quien compare tu red de Internet. Эспера mientras verificamos que eres una persona real.Tu contenido se mostrará en breve.
 Si Continúas recibiendo este
mensaje, envía un correo electrónico a
para hacernos saber que
estás teniendo problemas.
Si Continúas recibiendo este
mensaje, envía un correo electrónico a
para hacernos saber que
estás teniendo problemas.Temos Recebido algumas atividades suspeitas de voiceê ou de alguém que esteja usando a mesma rede. Aguarde enquanto confirmamos que Você é Uma Pessoa de Verdade. Сеу контексто апаресера эм бреве. Caso продолжить Recebendo esta mensagem, envie um email para пункт нет informar sobre o проблема.
Abbiamo notato alcune attività sospette da parte tua o di una persona che condivide la tua rete Internet.Attendi mentre verifichiamo Che sei una persona reale. Il tuo contenuto verrà visualizzato a breve. Secontini visualizzare questo messaggio, invia un’e-mail all’indirizzo per informarci del проблема.
Пожалуйста, включите куки и перезагрузите страницу.
Это автоматический процесс. Ваш браузер в ближайшее время перенаправит вас на запрошенный контент.

Подождите до 5 секунд…
Перенаправление…
Заводское обозначение: CF-102 / 65a651e2ff29325c.
Поиск наибольшего или наименьшего числа с помощью Excel — Office Mastery
Найти наибольшее число в диапазоне ячеек Excel очень просто.
То же самое для выбора наименьшего числа.
Есть много ситуаций, когда вам нужно найти наибольшее / наименьшее, наибольшее / наименьшее, наибольшее / наименьшее значение в наборе данных. Например,
- Какой сотрудник брал больше всего больничных дней в этом году?
- Какие самые большие расходы в этом году?
- Какая самая низкая стоимость лида в наших рекламных кампаниях?
Возьмите контрольный список :
7 шагов к совершенствованию формул1.
 Как найти наибольшее число в Excel
Как найти наибольшее число в ExcelИспользуйте функцию МАКС, чтобы найти наибольшее число в списке (или самое высокое, самое длинное, наибольшее и т. Д.)
= МАКС (число1, число 2…)
= MAX (A1, A2, A3)
= MAX (A1: A10)
= MAX (TestScores)
2. Как найти наименьшее число в Excel
Используйте функцию MIN для найти наименьшее число в списке (или наименьшее, наименьшее, наименьшее и т. д.))
= МИН (число1, число 2…)
= МИН (B1, B2, B3)
= МИН (B1: B10)
= МИН (Расходы отдела)
Функции MAX и MIN можно выбрать в раскрывающемся меню Автосумма или введя их непосредственно в ячейку.
Допустим, у вас есть значения в ячейках от A1 до A10,
Чтобы использовать инструмент автосуммирования:
1. Выделите 10 ячеек.
2.


 Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.



 2}$
2}$ 3-5=6-90-5= -89$
3-5=6-90-5= -89$ ..)
..) Как найти самую раннюю дату
Как найти самую раннюю дату Если у вас есть какие-либо сомнения, просто просмотрите наш блог. 🙂
Если у вас есть какие-либо сомнения, просто просмотрите наш блог. 🙂 Если вы не хотите, чтобы нули были таким минимумом, вам нужна помощь функции ЕСЛИ (IF). Как только вы добавите ограничение, что ваш диапазон должен быть больше нуля, ожидаемый результат не заставит себя ждать. Вот пример формулы для использования:
Если вы не хотите, чтобы нули были таким минимумом, вам нужна помощь функции ЕСЛИ (IF). Как только вы добавите ограничение, что ваш диапазон должен быть больше нуля, ожидаемый результат не заставит себя ждать. Вот пример формулы для использования:

 Вам просто нужно всмотреться в вашу формулу.
Вам просто нужно всмотреться в вашу формулу. Проверьте диапазон ваших данных, исправьте ошибку #ДЕЛ/0!, и формула незамедлительно вернет правильный результат.
Проверьте диапазон ваших данных, исправьте ошибку #ДЕЛ/0!, и формула незамедлительно вернет правильный результат.
 Сделаем это при помощи формул, чтобы этот способ можно было использовать не только в Excel 2007 и старше, но и в Excel 2003. Как… 5 способов создания выпадающего списка в ячейке Excel — Одной из наиболее полезных функций при вводе данных является возможность использовать выпадающий список. Он позволяет выбирать значение из предварительно определенного перечня и разрешает вводить только те данные, которые соответствуют вашим требованиям. Мы предложим вам несколько простых способов, как создавать выпадающие…
Сделаем это при помощи формул, чтобы этот способ можно было использовать не только в Excel 2007 и старше, но и в Excel 2003. Как… 5 способов создания выпадающего списка в ячейке Excel — Одной из наиболее полезных функций при вводе данных является возможность использовать выпадающий список. Он позволяет выбирать значение из предварительно определенного перечня и разрешает вводить только те данные, которые соответствуют вашим требованиям. Мы предложим вам несколько простых способов, как создавать выпадающие… Следовательно, 120 нужно умножить на 2 x 3 x 5, чтобы получился полный квадрат.
Следовательно, 120 нужно умножить на 2 x 3 x 5, чтобы получился полный квадрат. Теперь обратите внимание на
слово
квадрат, который упоминается здесь, вы
просто не найти ни одного наименьшего числа
это не самое маленькое число, которое
там, но вы найдете самый маленький квадрат
номер
поэтому для этого нам нужно выяснить, 120
идеальный квадрат или нет для этого
мы должны проверить это с праймом
факторизация давайте разложим на множители 120
два шесть — ноль
две тройки
два два пятерки
три пятерки и пять
Итак, множители в простых множителях
120
2 в 2 в
2 на 3 на 5.так что когда тебе нужно найти идеальный
квадрат мы сначала группируем числа и
видеть
сколько номеров не имеют группы и
мы умножаем на эти числа прямо так
вы можете увидеть здесь
У 2 есть отличная группа, теперь 2 одиночки
3 — холост, а 5 — не замужем, они этого не делают.
иметь группу
так что мне нужно сделать, мне придется
умножать
120 на еще один два
еще один три и еще один пять ну и что
Я собираюсь добавить
еще два здесь, еще три здесь.
и еще пять здесь, чтобы я получил
полный
группы вправо, а затем число, которое я
получать
будет идеальным квадратом, поэтому 120 на 2
в 3 в 5 даст мне 3
6 двойных 0.
Теперь обратите внимание на
слово
квадрат, который упоминается здесь, вы
просто не найти ни одного наименьшего числа
это не самое маленькое число, которое
там, но вы найдете самый маленький квадрат
номер
поэтому для этого нам нужно выяснить, 120
идеальный квадрат или нет для этого
мы должны проверить это с праймом
факторизация давайте разложим на множители 120
два шесть — ноль
две тройки
два два пятерки
три пятерки и пять
Итак, множители в простых множителях
120
2 в 2 в
2 на 3 на 5.так что когда тебе нужно найти идеальный
квадрат мы сначала группируем числа и
видеть
сколько номеров не имеют группы и
мы умножаем на эти числа прямо так
вы можете увидеть здесь
У 2 есть отличная группа, теперь 2 одиночки
3 — холост, а 5 — не замужем, они этого не делают.
иметь группу
так что мне нужно сделать, мне придется
умножать
120 на еще один два
еще один три и еще один пять ну и что
Я собираюсь добавить
еще два здесь, еще три здесь.
и еще пять здесь, чтобы я получил
полный
группы вправо, а затем число, которое я
получать
будет идеальным квадратом, поэтому 120 на 2
в 3 в 5 даст мне 3
6 двойных 0. так что самый маленький
квадратное число, которое делится на 8 15
и 20
шестьсот
Надеюсь, я смог разрешить твои сомнения
с этим конкретным видео
пожалуйста, не стесняйтесь делиться и
комментарий и увидимся в другом
видео
Спасибо.
так что самый маленький
квадратное число, которое делится на 8 15
и 20
шестьсот
Надеюсь, я смог разрешить твои сомнения
с этим конкретным видео
пожалуйста, не стесняйтесь делиться и
комментарий и увидимся в другом
видео
Спасибо. Нам нужно найти НОК 4. минус 10.Итак, начнем с этого. Итак, давайте найдем НОК для 9 и 10. Это идет двумя двумя двойками — четырьмя 925 Сартен Снова по нашему мнению и пятеркам. Следующее число — 3 3 3 za Скажите, что самые грустные — три — три фута. Огонь остается, так как следующая цифра — 5 wanzer. Таким образом, НОК будет умножением всех этих множителей 2 на 2, 3, 3, 5, 2, 2, 4, 3, 3, 9, 5. Мы получаем ответ: 1 TT отлично. Итак, 180 — это число, но если вы разделите 4 9 и 10, вы получите полностью делимое число.Но здесь вопрос говорит, что нам нужно найти. Квадратный номер, верно? Итак, для этого давайте проверим, является ли 180 идеальным квадратом или нет. Так что давайте сделаем это тоже девять, сэр. И тогда ноль две пятерки несут одну две пятерки — 10:45. Это будет три, три, три пятерки, три пятерки и пять единиц, так что просто чтобы проверить, является ли 180 идеальным квадратом, верно? Итак, мы просто запишем Просто легкость, это запишет факторы. Итак, 2 на 2 на 3 на 3 на 5.
Нам нужно найти НОК 4. минус 10.Итак, начнем с этого. Итак, давайте найдем НОК для 9 и 10. Это идет двумя двумя двойками — четырьмя 925 Сартен Снова по нашему мнению и пятеркам. Следующее число — 3 3 3 za Скажите, что самые грустные — три — три фута. Огонь остается, так как следующая цифра — 5 wanzer. Таким образом, НОК будет умножением всех этих множителей 2 на 2, 3, 3, 5, 2, 2, 4, 3, 3, 9, 5. Мы получаем ответ: 1 TT отлично. Итак, 180 — это число, но если вы разделите 4 9 и 10, вы получите полностью делимое число.Но здесь вопрос говорит, что нам нужно найти. Квадратный номер, верно? Итак, для этого давайте проверим, является ли 180 идеальным квадратом или нет. Так что давайте сделаем это тоже девять, сэр. И тогда ноль две пятерки несут одну две пятерки — 10:45. Это будет три, три, три пятерки, три пятерки и пять единиц, так что просто чтобы проверить, является ли 180 идеальным квадратом, верно? Итак, мы просто запишем Просто легкость, это запишет факторы. Итак, 2 на 2 на 3 на 3 на 5.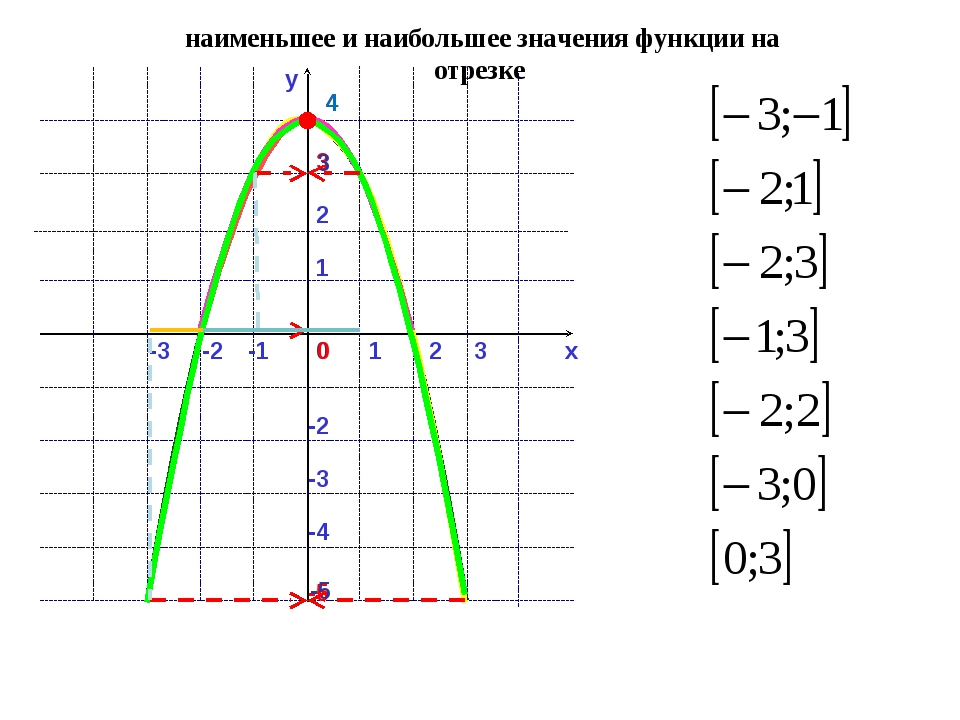 Хорошо, давайте сгруппируем их и посмотрим, есть ли у нас полные группы.У нас есть группа, чтобы у нас была группа из трех человек, а группа из пяти человек отсутствует. Итак, чтобы получить 180 или полный квадрат. Я умножу его на 5, чтобы сформировать группу. Так что же мне делать? Я умножу 180 на 5, что даст 900, поэтому наименьшее квадратное число, которое делится на 4, 9 и 10, равно 900, пожалуйста, обратите внимание на число для словесного квадрата, которое упомянуто. Хорошо, если вы пропустите это конкретное слово, вы можете даже остановиться на ответе, в котором говорится, что 180 делится на 4, 9 и 10, но здесь упоминается загвоздка.Что ему нужно наименьшее квадратное число. Это все в этом видео. Большое спасибо. Пожалуйста, не стесняйтесь делиться и комментировать, и увидимся в другом видео. «
Хорошо, давайте сгруппируем их и посмотрим, есть ли у нас полные группы.У нас есть группа, чтобы у нас была группа из трех человек, а группа из пяти человек отсутствует. Итак, чтобы получить 180 или полный квадрат. Я умножу его на 5, чтобы сформировать группу. Так что же мне делать? Я умножу 180 на 5, что даст 900, поэтому наименьшее квадратное число, которое делится на 4, 9 и 10, равно 900, пожалуйста, обратите внимание на число для словесного квадрата, которое упомянуто. Хорошо, если вы пропустите это конкретное слово, вы можете даже остановиться на ответе, в котором говорится, что 180 делится на 4, 9 и 10, но здесь упоминается загвоздка.Что ему нужно наименьшее квадратное число. Это все в этом видео. Большое спасибо. Пожалуйста, не стесняйтесь делиться и комментировать, и увидимся в другом видео. « Например, если список — [15, 20, 10, 16], тогда программа должна отображать число 10 в качестве вывода (наименьшее число в данном списке).
Например, если список — [15, 20, 10, 16], тогда программа должна отображать число 10 в качестве вывода (наименьшее число в данном списке). Метод min () возвращает наименьший элемент списка .
Метод min () возвращает наименьший элемент списка . добавить (число)
# отображение наименьшего элемента
print ("Наименьший элемент списка:", min (lis))
добавить (число)
# отображение наименьшего элемента
print ("Наименьший элемент списка:", min (lis))  Это можно использовать для отдельной строки или столбца в вопросе сетки, для таблицы в целом или для списка переменных в форме.
Это можно использовать для отдельной строки или столбца в вопросе сетки, для таблицы в целом или для списка переменных в форме. Не может содержать операторов, таких как (+), (-), (*) и т. Д.
Не может содержать операторов, таких как (+), (-), (*) и т. Д. 

 в
в  Ihr Inhalt wird в Kürze angezeigt.
Wenn Sie weiterhin diese Meldung erhalten, informieren Sie uns darüber bitte по электронной почте:
.
Ihr Inhalt wird в Kürze angezeigt.
Wenn Sie weiterhin diese Meldung erhalten, informieren Sie uns darüber bitte по электронной почте:
. Si Continúas recibiendo este
mensaje, envía un correo electrónico a
para hacernos saber que
estás teniendo problemas.
Si Continúas recibiendo este
mensaje, envía un correo electrónico a
para hacernos saber que
estás teniendo problemas.
 Как найти наибольшее число в Excel
Как найти наибольшее число в Excel