Комплексные числа | Формулы и расчеты онлайн
Определение комплексного числа
Комплексное число имеет вид
\[a+ib\]
здесь a и b – действительные числа, а i – число нового рода, называемое мнимой единицей.
Мнимые числа – представляют собой частный вид комплексных чисел (когда a = 0). С другой стороны, и действительные (т.е. положительные и отрицательные) числа, являются частным видом комплексных чисел (когда b = 0).
Действительное число a называется абсциссой комплексного числа. Действительное число b называется ординатой комплексного числа. Основное свойство числа i состоит в том, что произведение i · i равно –1
\[i^2 = -1\]
Долгое время не удавалось найти такие физические величины, над которыми можно выполнять действия, подчиненные тем же правилам, что и действия над комплексными числами – в частности правилу 2. Отсюда произошли названия: Мнимая единица, мнимое число и т.п.
В настоящее время известен целый ряд таких физических величин, и комплексные числа широко применяются не только в математике, но также в физике и технике (теория упругости, электротехника, аэродинамика и другие).
Великие математики,
открывшие комплексные числа и их свойства
История комплексных чисел
В связи с развитием алгебры, математикам потребовалось ввести сверх прежде известных положительных и отрицательных чисел, числа нового рода. Комплексные числа.
Итальянский математик Кардано в середине 16-ого века для решения кубических уравнений ввел квадратные корни из отрицательных чисел. Квадратные корни из отрицательных чисел он назвал софистическими, т.е. мудреными.
Решения уравнений третьей степени по формулам Кардано исследовал итальянский математик Бомбелли. Он обнаружил некоторые свойства комплексных чисел.
Французкий математик Декарт в 30-х годах 17-ого века ввел наименование мнимые числа, которое применяется по сей день.
В противоположность мнимым числам прежде известные числа (положительные и отрицательные, в том числе иррациональные) стали называть действительными или вещественными.
Сумма действительного и мнимого чисел и называется комплексным числом. Это термин впервые ввел немецкий математик и астроном Гаусс в 1831-ом году.
В 18-ом веке крупнейшие математики мира спорили о том, как находить логарифмы комплексных чисел. Хотя с помощью комплексных чисел удалось получить много важных фактов, относящихся к действительным числам, но само существование комплексных чисел многим казалось сомнительным.
В 1707-ом году Муавр открыл формулу Муавра для возведения в степень (и извлечения корней) комплексных чисел, заданных в тригонометрической форме.
Исчерпывающие правила действий с комплексными числами дал в середине 18-ого века русский академик Эйлер.
На рубеже 18 и 19 веков было указано Весселем (Дания) и Арганом (Франция) геометрическое изображение комплексных чисел. Но на работы Весселя и Аргана не обратили внимания, и лишь в 1831г., когда тот же способ был развит великим математиком Гауссом, он стал всеобщим достоянием.
В помощь студенту
Комплексные числа |
стр. 67 |
|---|
www.fxyz.ru
§1. Комплексные числа: основные определения

Лекция 22
Символ  вводят соотношением
вводят соотношением 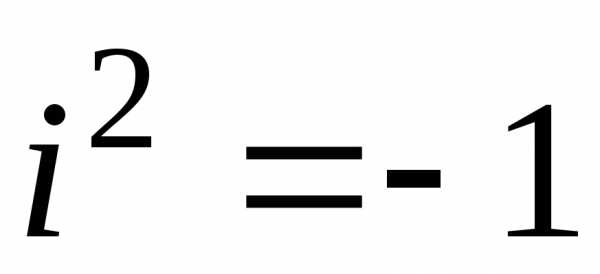 и называют мнимой единицей. Другими
словами,
и называют мнимой единицей. Другими
словами,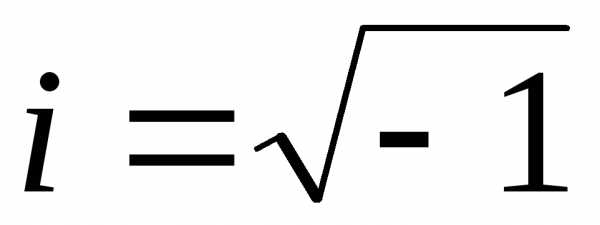 .
.
Определение. Выражение вида
,
где,
называется комплексным числом, при этом
число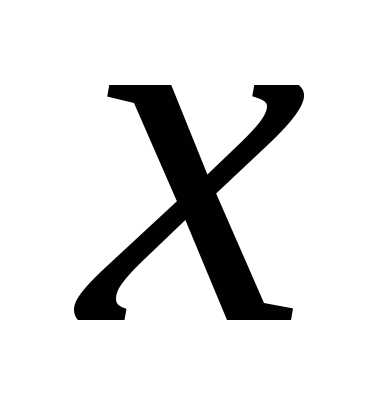 называют вещественной частью комплексного
числа
называют вещественной частью комплексного
числа и обозначают,
число
и обозначают,
число – мнимой частью
– мнимой частью и обозначают
и обозначают
Из такого определения следует, что действительные числа – это те комплексные числа, мнимая часть которых равна нулю.
Комплексные числа
удобно изображать точками плоскости,
на которой задана декартова прямоугольная
система координат, а именно: комплексному
числу
соответствует точка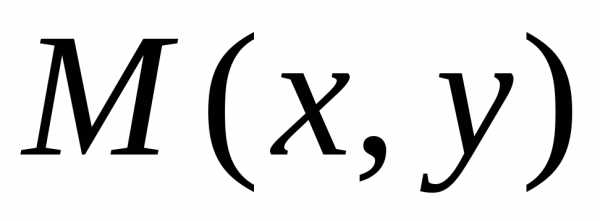 и наоборот. На оси
и наоборот. На оси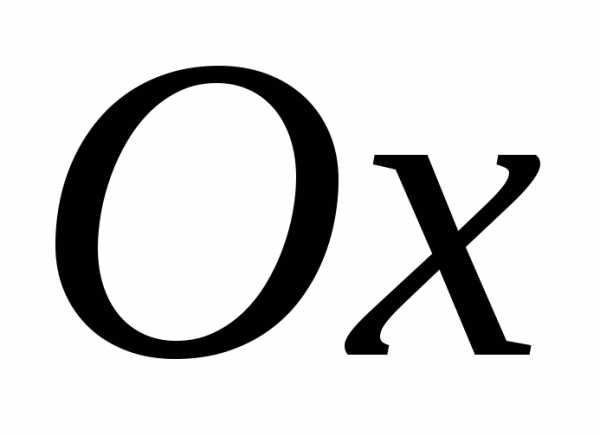 изображаются вещественные числа и её
называют вещественной осью. Комплексные
числа вида
изображаются вещественные числа и её
называют вещественной осью. Комплексные
числа вида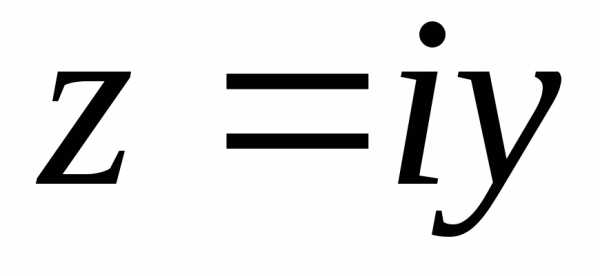 называют чисто мнимыми. Они изображаются
точками на оси
называют чисто мнимыми. Они изображаются
точками на оси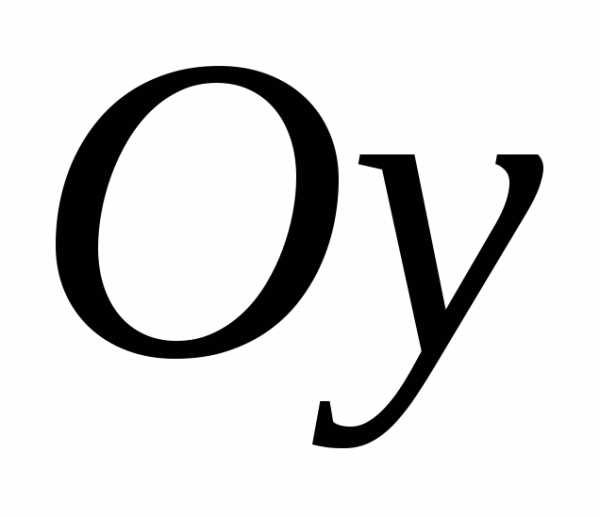 ,
которую называют мнимой осью. Эту
плоскость, служащую для изображения
комплексных чисел, называют комплексной
плоскостью. Комплексное число, не
являющееся действительным, т.е. такое,
что,
иногда называют мнимым.
,
которую называют мнимой осью. Эту
плоскость, служащую для изображения
комплексных чисел, называют комплексной
плоскостью. Комплексное число, не
являющееся действительным, т.е. такое,
что,
иногда называют мнимым.
Сложение, вычитание
и умножение комплексных чисел производится
по обычным правилам алгебры многочленов
с учётом того, что 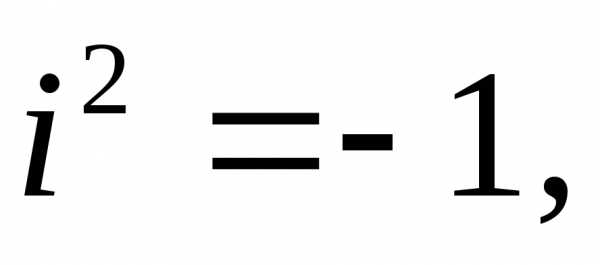 . Операцию деления можно определить как
обратную к операции умножения и доказать
единственность результата (если делитель
отличен от нуля). Однако на практике
используется другой подход.
. Операцию деления можно определить как
обратную к операции умножения и доказать
единственность результата (если делитель
отличен от нуля). Однако на практике
используется другой подход.
Комплексные числа
и называют сопряжёнными, на комплексной
плоскости они изображаются точками,
симметричными относительно вещественной
оси. Очевидно, что:
называют сопряжёнными, на комплексной
плоскости они изображаются точками,
симметричными относительно вещественной
оси. Очевидно, что:
1) 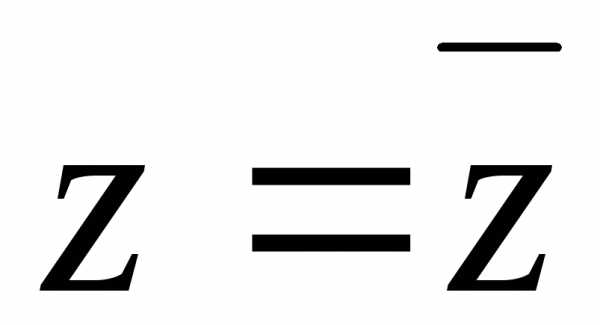 ;
;
2) ;
3) .
Теперь разделить 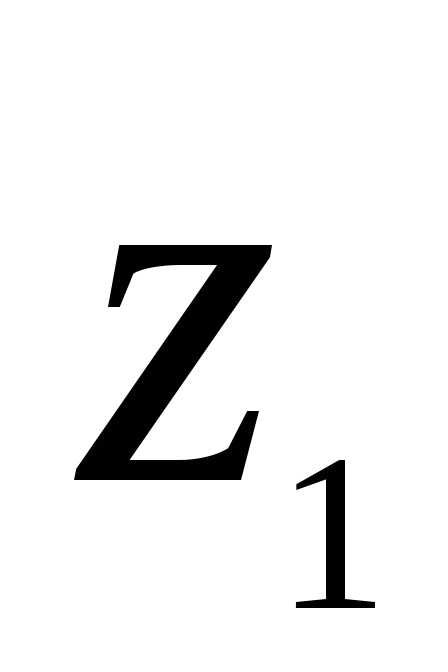
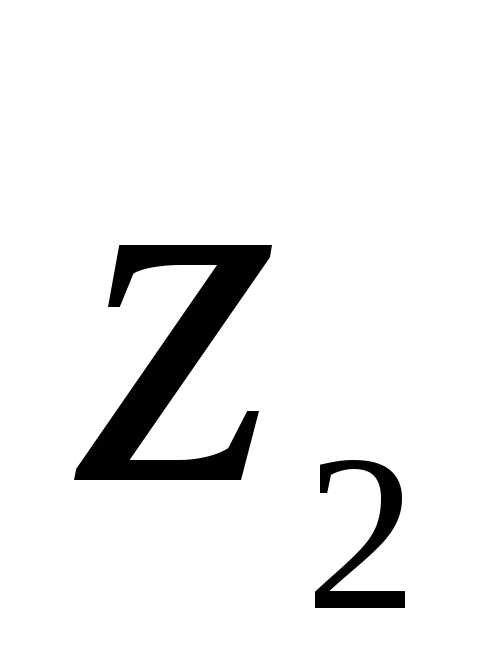 можно следующим образом:
можно следующим образом:.
Не трудно показать, что
,
где символ  обозначает любую
арифметическую операцию.
обозначает любую
арифметическую операцию.
Пусть некоторое мнимое
число, а 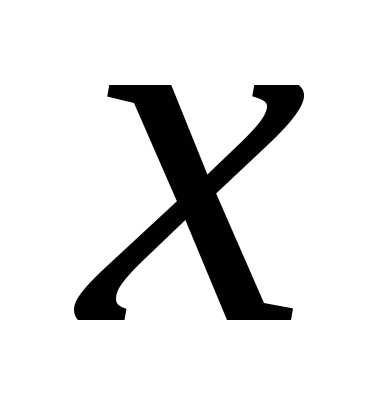 – вещественная переменная. Произведение
двух биномов
– вещественная переменная. Произведение
двух биномов
есть квадратный трёхчлен с действительными коэффициентами.
Теперь, имея в распоряжении комплексные числа, мы сможем решить любое квадратное уравнение .Если , то
и уравнение имеет два комплексных сопряжённых корня
.
Если 
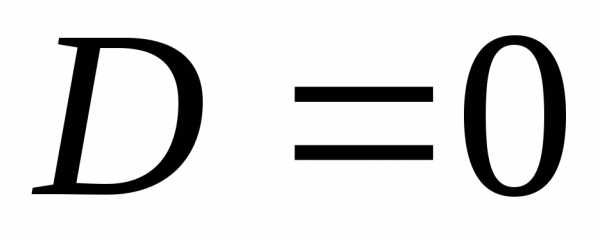 ,
то уравнение имеет два одинаковых корня.
,
то уравнение имеет два одинаковых корня.§2. Тригонометрическая форма комплексного числа
Как говорилось
выше, комплексное число
удобно изображать точкой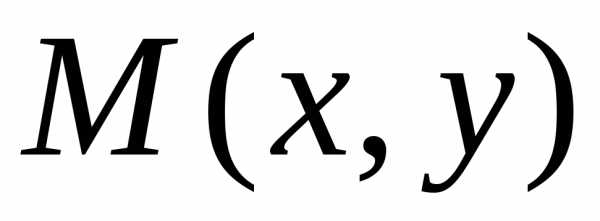 .
Можно также такое число отождествлять
с радиус-вектором этой точки.
При такой интерпретации сложение и
вычитание комплексных чисел производится
по правилам сложения и вычитания
векторов. Для умножения и деления
комплексных чисел более удобной
оказывается другая форма.
.
Можно также такое число отождествлять
с радиус-вектором этой точки.
При такой интерпретации сложение и
вычитание комплексных чисел производится
по правилам сложения и вычитания
векторов. Для умножения и деления
комплексных чисел более удобной
оказывается другая форма.
Введём на комплексной
плоскости 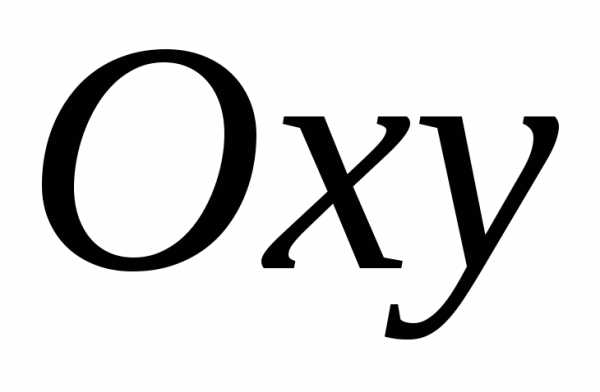 полярную систему координат. Тогда,
где,и комплексное числоможно записать в виде:
полярную систему координат. Тогда,
где,и комплексное числоможно записать в виде:
.
Эту форму записи
называют тригонометрической (в отличие
от алгебраической формы
).
В этой форме число
 – аргументом комплексного числа
– аргументом комплексного числа .
Они обозначаются:
.
Они обозначаются: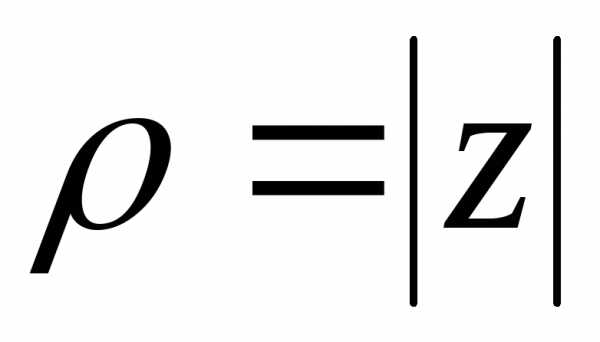 ,
,
 .
Для модуля имеем формулу
.
Для модуля имеем формулу
Аргумент числа
определён неоднозначно, а с точностью
до слагаемого 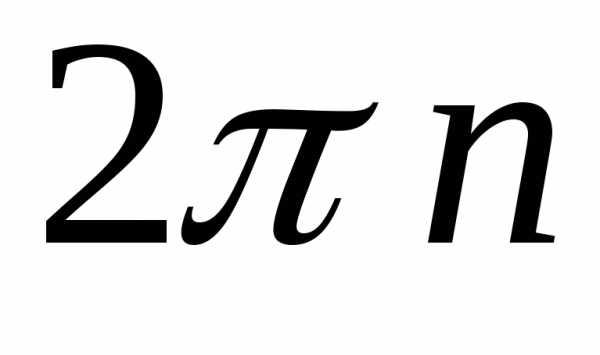 ,
, .
Значение
аргумента, удовлетворяющего неравенствам
,
называется главным и обозначается
.
Значение
аргумента, удовлетворяющего неравенствам
,
называется главным и обозначается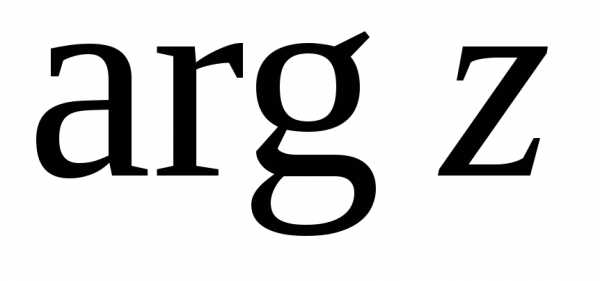
 .
Для главного значения аргумента можно
получить такие выражения:
.
Для главного значения аргумента можно
получить такие выражения: 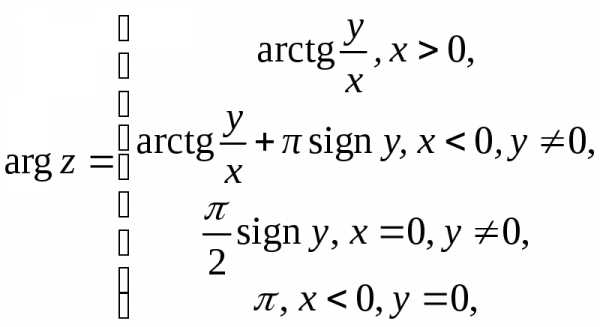 ,
,
аргумент числа  считается неопределённым.
считается неопределённым.
Условие равенства
двух комплексных чисел в тригонометрической
форме имеет вид: модули чисел равны, а
аргументы отличаются на число кратное 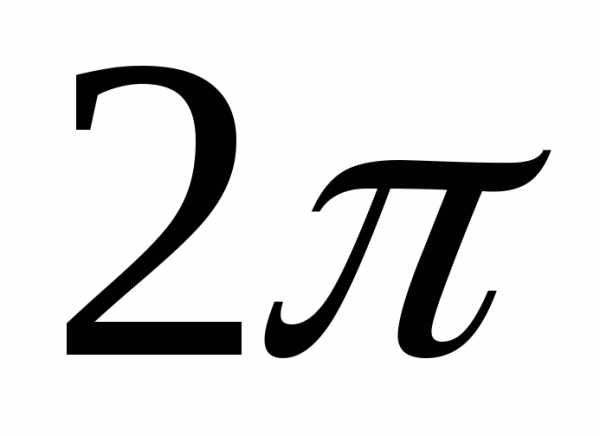 .
.
Найдём произведение двух комплексных чисел в тригонометрической форме:
Итак, при умножении чисел их модули умножаются, а аргументы складываются.
Аналогичным образом можно установить, что при делении модули чисел делятся, а аргументы вычитаются.
Понимая возведение в степень как многократное умножение, можно получить формулу возведения комплексного числа в степень:
.
Выведем формулу
для 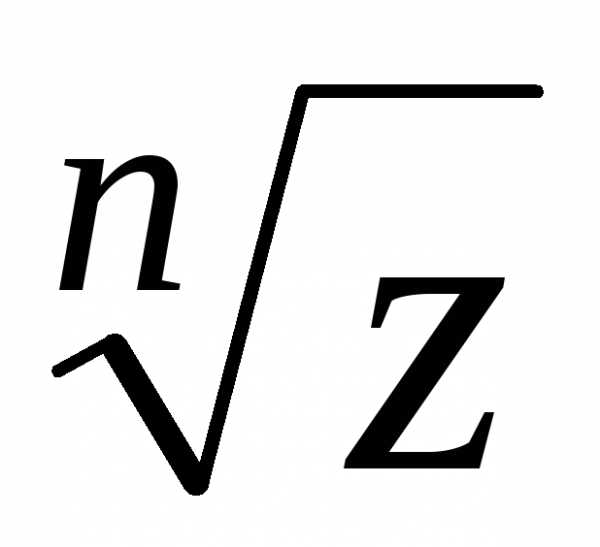 – корня
– корня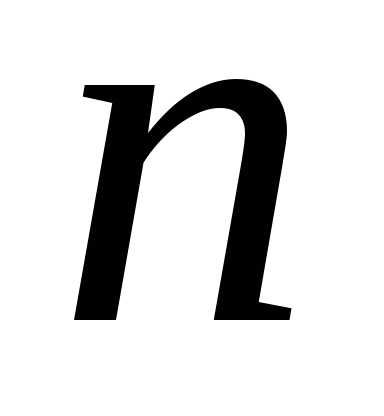 -ой
степени из комплексного числа
-ой
степени из комплексного числа (не путать с арифметическим корнем из
действительного числа!). Операция
извлечения корня является обратной по
отношению к операции возведения в
степень. Поэтому
(не путать с арифметическим корнем из
действительного числа!). Операция
извлечения корня является обратной по
отношению к операции возведения в
степень. Поэтому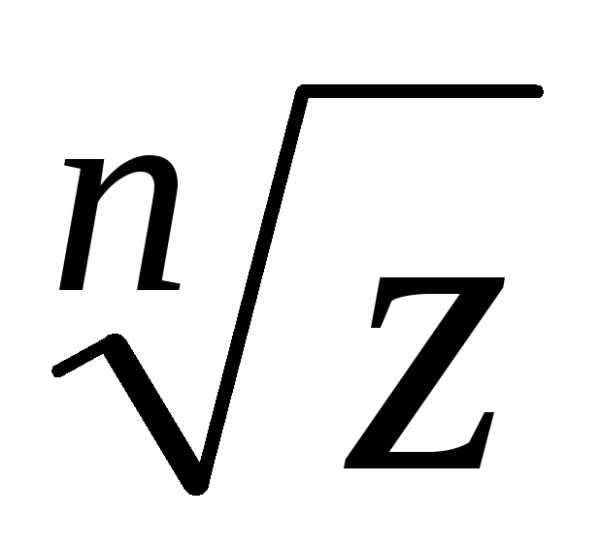 – это комплексное число
– это комплексное число такое, что
такое, что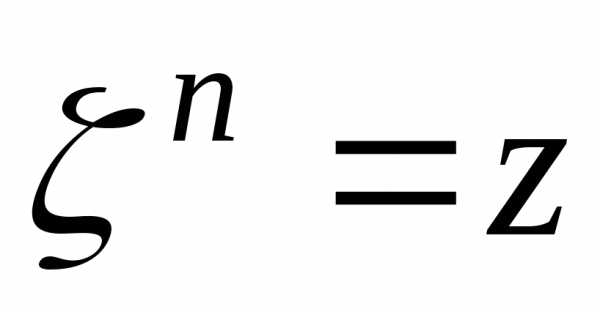 .
.
Пусть известно, атребуется найти. Тогда
.
Из равенства двух комплексных чисел в тригонометрической форме следует, что
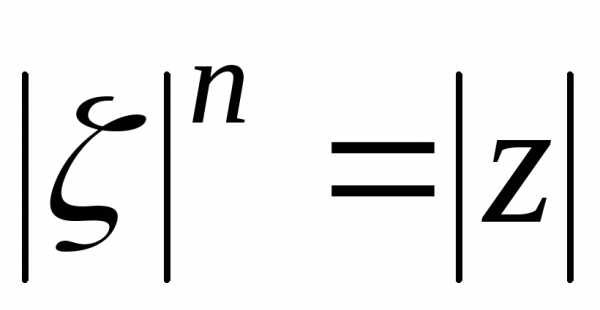 ,
,
,
,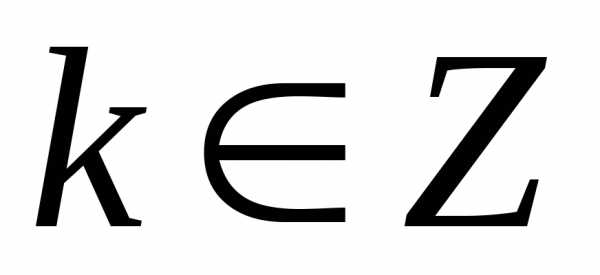 .
.
Отсюда 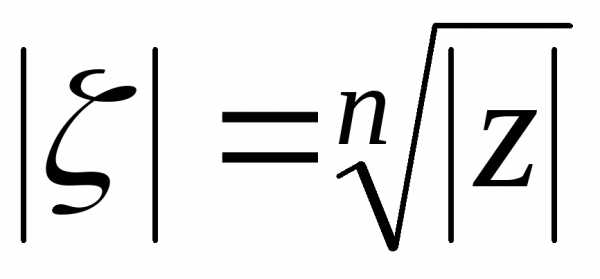 (это арифметический корень!),
(это арифметический корень!),
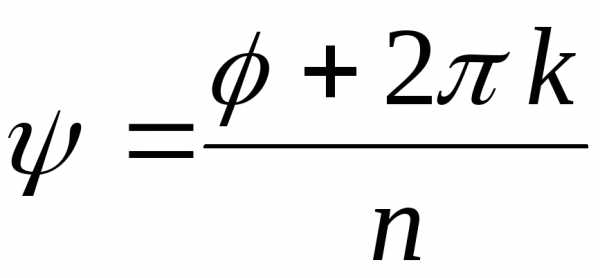 ,
, 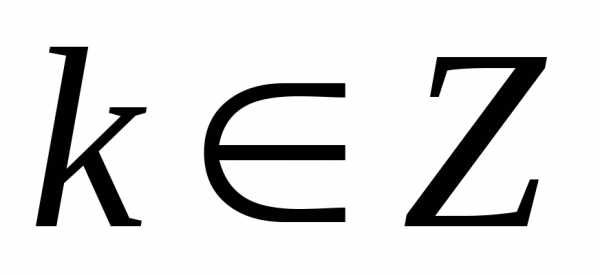 .
.
Нетрудно убедиться,
что  может принимать лишь
может принимать лишь различных по существу значений, например,
при.
Окончательно имеем формулу:
различных по существу значений, например,
при.
Окончательно имеем формулу:
, .
Итак, корень 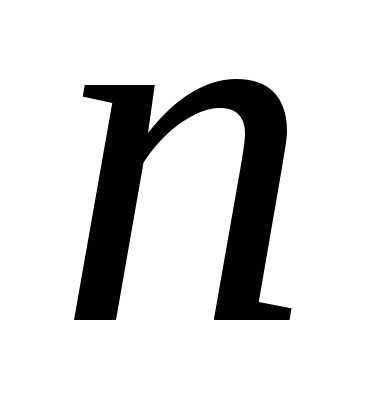 -ой
степени из комплексного числа имеет
-ой
степени из комплексного числа имеет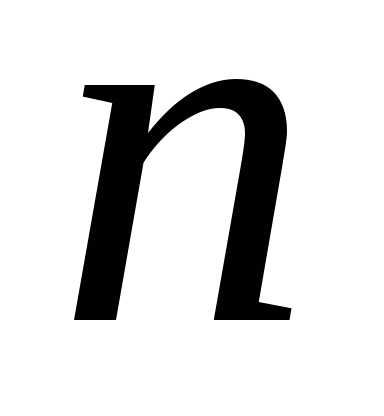 различных значений. На комплексной
плоскости эти значения располагаются
в вершинах правильно
различных значений. На комплексной
плоскости эти значения располагаются
в вершинах правильно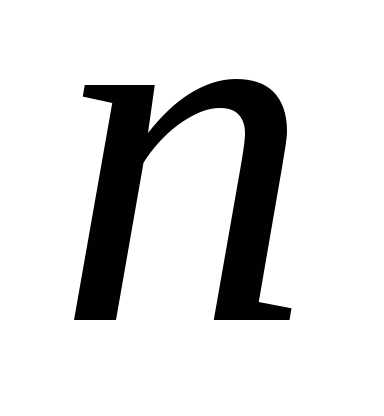 -угольника,
вписанного в окружность радиуса
-угольника,
вписанного в окружность радиуса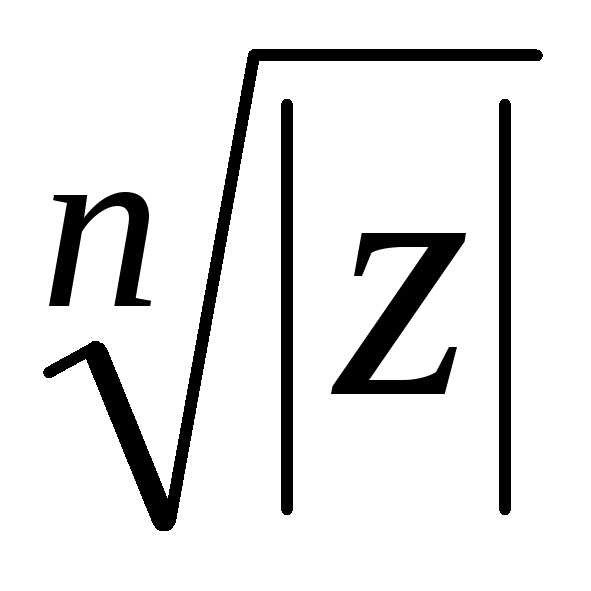 с центром в начале координат. “Первый”
корень имеет аргумент
с центром в начале координат. “Первый”
корень имеет аргумент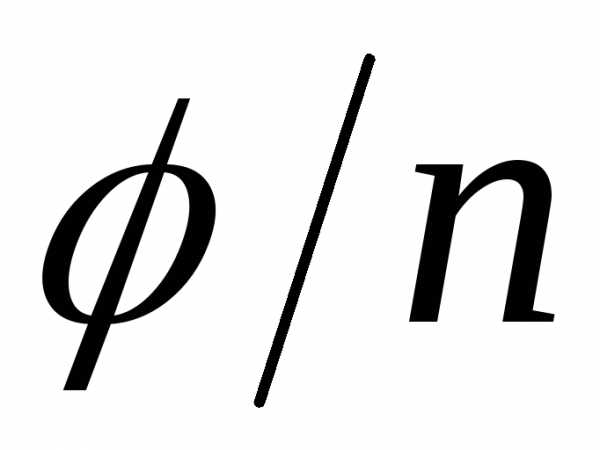 ,
аргументы двух “соседних” корней
отличаются на
,
аргументы двух “соседних” корней
отличаются на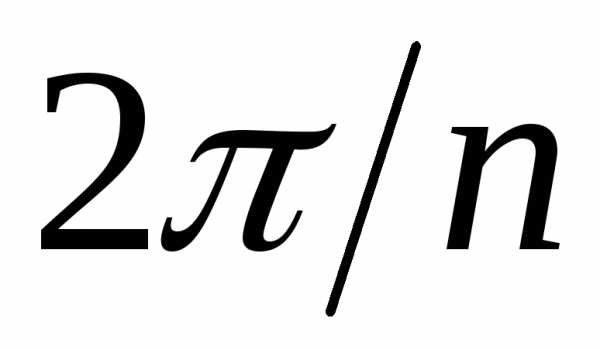 .
.
Пример.Извлечём корень кубический из мнимой
единицы: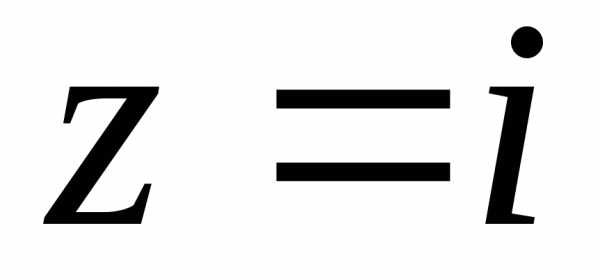 ,
,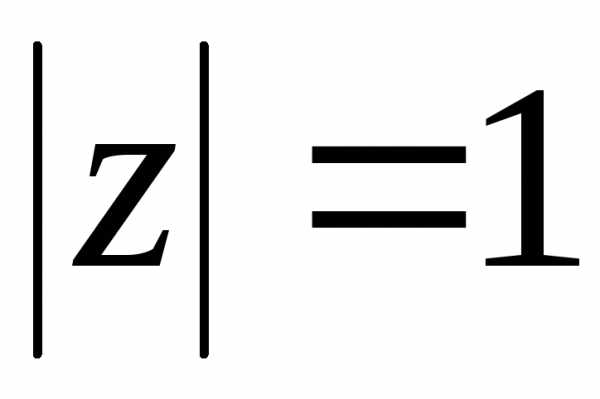 ,.
Тогда:
,.
Тогда:
,
,
.
studfiles.net
§1. Комплексные числа: основные определения
 Тема Комплексные числа и многочлены
Тема Комплексные числа и многочлены
Лекция 22
Символ 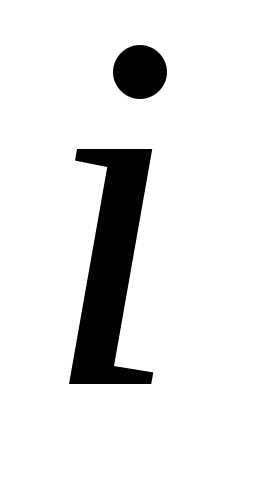 вводят соотношением
вводят соотношением 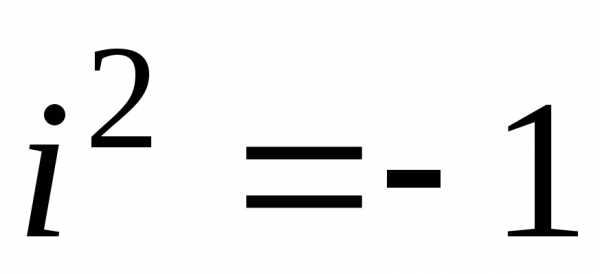 и называют мнимой единицей. Другими
словами,
и называют мнимой единицей. Другими
словами,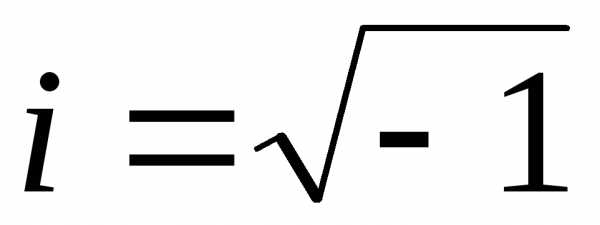 .
.
Определение. Выражение вида
,
где,
называется комплексным числом, при этом
число называют вещественной частью комплексного
числаи обозначают,
число
называют вещественной частью комплексного
числаи обозначают,
число – мнимой частью
– мнимой частью и обозначают
и обозначают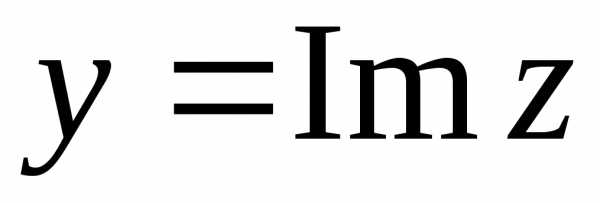 .
.
Из такого определения следует, что действительные числа – это те комплексные числа, мнимая часть которых равна нулю.
Комплексные числа
удобно изображать точками плоскости,
на которой задана декартова прямоугольная
система координат, а именно: комплексному
числу
соответствует точка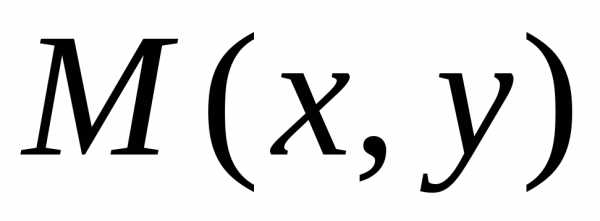 и наоборот. На оси
и наоборот. На оси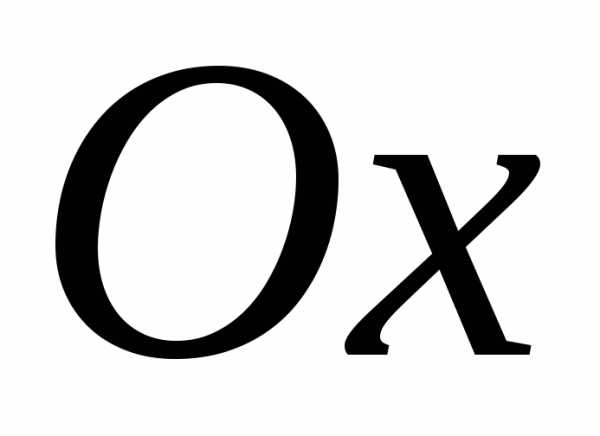 изображаются вещественные числа и её
называют вещественной осью. Комплексные
числа вида
изображаются вещественные числа и её
называют вещественной осью. Комплексные
числа вида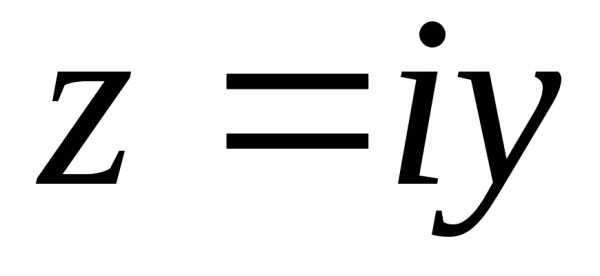 называют чисто мнимыми. Они изображаются
точками на оси
называют чисто мнимыми. Они изображаются
точками на оси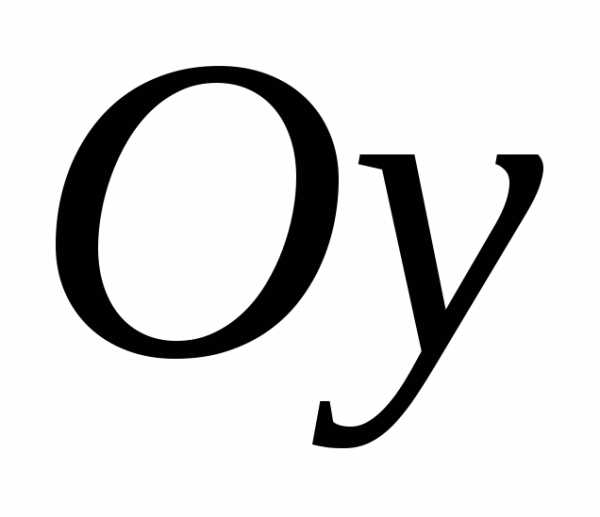 ,
которую называют мнимой осью. Эту
плоскость, служащую для изображения
комплексных чисел, называют комплексной
плоскостью. Комплексное число, не
являющееся действительным, т.е. такое,
что,
иногда называют мнимым.
,
которую называют мнимой осью. Эту
плоскость, служащую для изображения
комплексных чисел, называют комплексной
плоскостью. Комплексное число, не
являющееся действительным, т.е. такое,
что,
иногда называют мнимым.
Два комплексных числа называют равными тогда и только тогда, когда у них совпадают как вещественные, так и мнимые части.
Сложение, вычитание
и умножение комплексных чисел производится
по обычным правилам алгебры многочленов
с учётом того, что 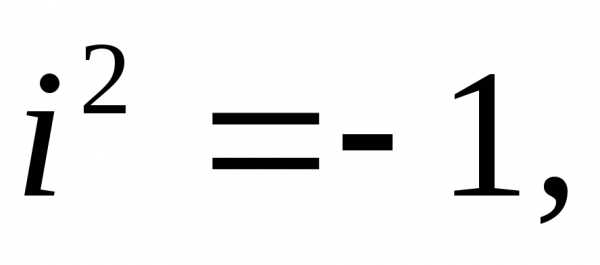 . Операцию деления можно определить как
обратную к операции умножения и доказать
единственность результата (если делитель
отличен от нуля). Однако на практике
используется другой подход.
. Операцию деления можно определить как
обратную к операции умножения и доказать
единственность результата (если делитель
отличен от нуля). Однако на практике
используется другой подход.
Комплексные числа
и называют сопряжёнными, на комплексной
плоскости они изображаются точками,
симметричными относительно вещественной
оси. Очевидно, что:
называют сопряжёнными, на комплексной
плоскости они изображаются точками,
симметричными относительно вещественной
оси. Очевидно, что:
1) 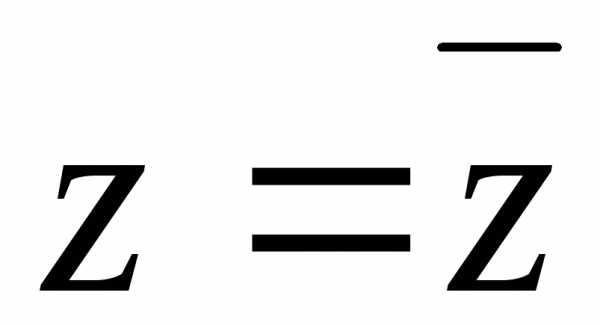 ;
;
2) ;
3) .
Теперь разделить  на
на можно следующим образом:
можно следующим образом:
.
Не трудно показать, что
,
где символ  обозначает любую
арифметическую операцию.
обозначает любую
арифметическую операцию.
Пусть некоторое мнимое
число, а 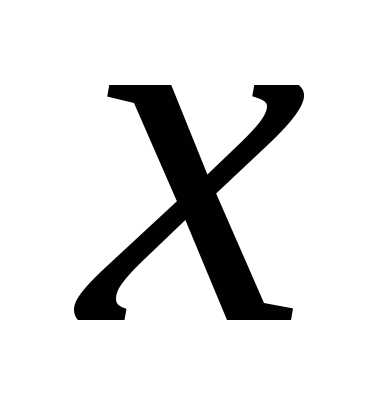 – вещественная переменная. Произведение
двух биномов
– вещественная переменная. Произведение
двух биномов
есть квадратный трёхчлен с действительными коэффициентами.
Теперь, имея в распоряжении комплексные числа, мы сможем решить любое квадратное уравнение .Если , то
и уравнение имеет два комплексных сопряжённых корня
.
Если  ,
то уравнение имеет два различных
вещественных корня. Если
,
то уравнение имеет два различных
вещественных корня. Если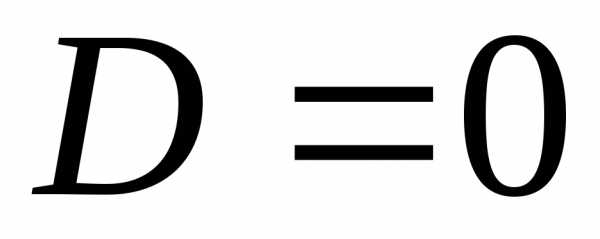 ,
то уравнение имеет два одинаковых корня.
,
то уравнение имеет два одинаковых корня.
§2. Тригонометрическая форма комплексного числа
Как говорилось
выше, комплексное число
удобно изображать точкой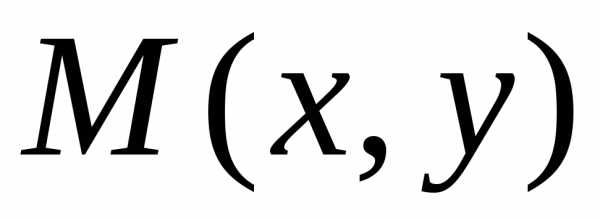 .
Можно также такое число отождествлять
с радиус-вектором этой точки.
При такой интерпретации сложение и
вычитание комплексных чисел производится
по правилам сложения и вычитания
векторов. Для умножения и деления
комплексных чисел более удобной
оказывается другая форма.
.
Можно также такое число отождествлять
с радиус-вектором этой точки.
При такой интерпретации сложение и
вычитание комплексных чисел производится
по правилам сложения и вычитания
векторов. Для умножения и деления
комплексных чисел более удобной
оказывается другая форма.
Введём на комплексной
плоскости 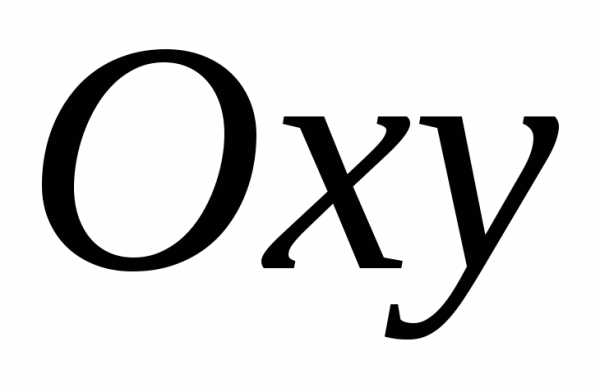 полярную систему координат. Тогда,
где,и комплексное числоможно записать в виде:
полярную систему координат. Тогда,
где,и комплексное числоможно записать в виде:
.
Эту форму записи
называют тригонометрической (в отличие
от алгебраической формы
).
В этой форме число называют модулем, а
называют модулем, а – аргументом комплексного числа
– аргументом комплексного числа .
Они обозначаются:
.
Они обозначаются: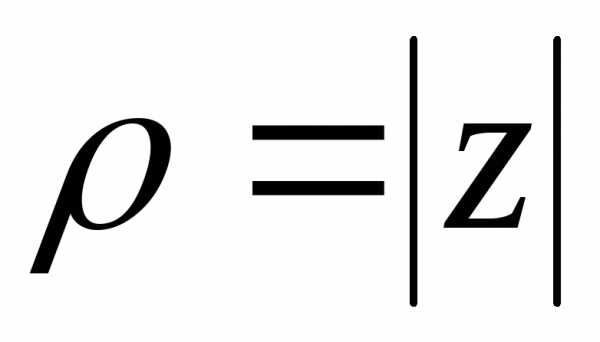 ,
,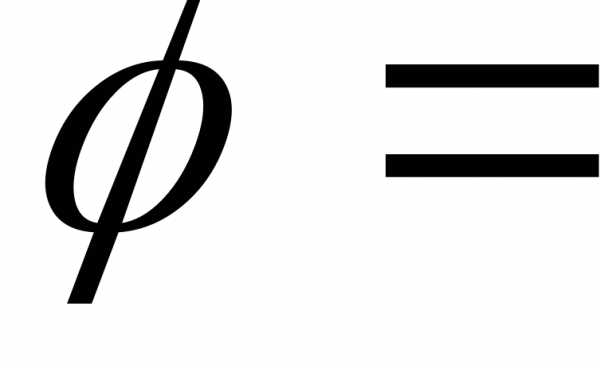
 .
Для модуля имеем формулу
.
Для модуля имеем формулу
Аргумент числа
определён неоднозначно, а с точностью
до слагаемого  ,
,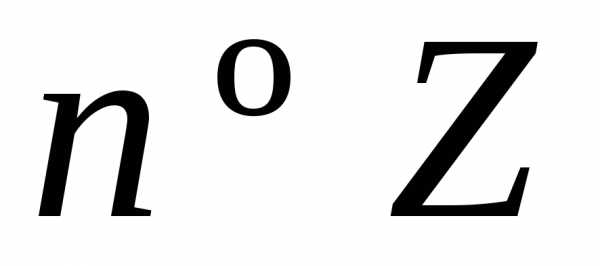 .
Значение
аргумента, удовлетворяющего неравенствам
,
называется главным и обозначается
.
Значение
аргумента, удовлетворяющего неравенствам
,
называется главным и обозначается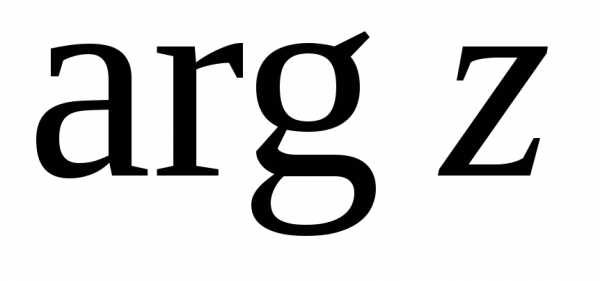 .
Тогда,
.
Тогда,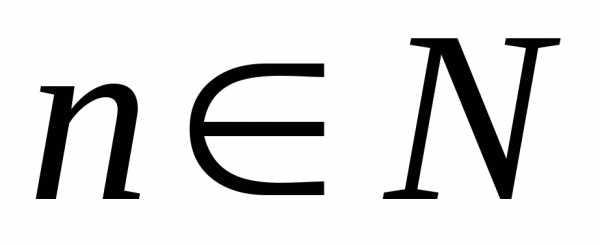 .
Для главного значения аргумента можно
получить такие выражения:
.
Для главного значения аргумента можно
получить такие выражения:
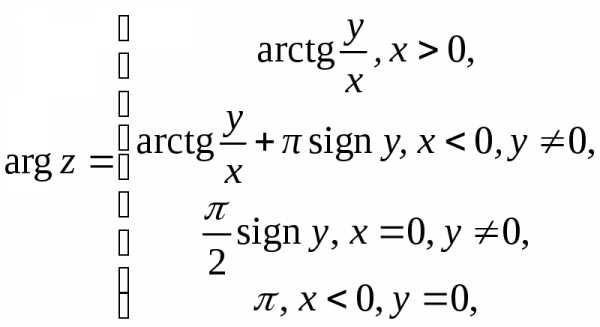 ,
,
аргумент числа 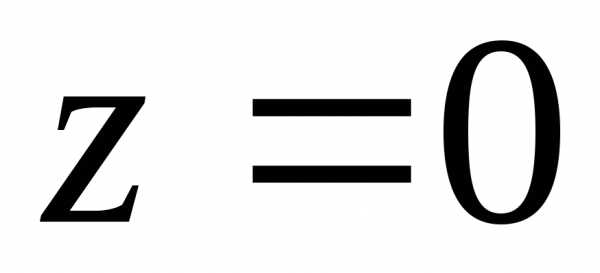 считается неопределённым.
считается неопределённым.
Условие равенства
двух комплексных чисел в тригонометрической
форме имеет вид: модули чисел равны, а
аргументы отличаются на число кратное 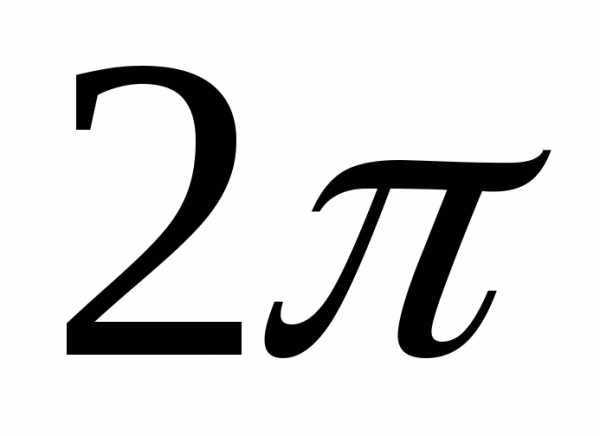 .
.
Найдём произведение двух комплексных чисел в тригонометрической форме:
Итак, при умножении чисел их модули умножаются, а аргументы складываются.
Аналогичным образом можно установить, что при делении модули чисел делятся, а аргументы вычитаются.
Понимая возведение в степень как многократное умножение, можно получить формулу возведения комплексного числа в степень:
.
Выведем формулу
для 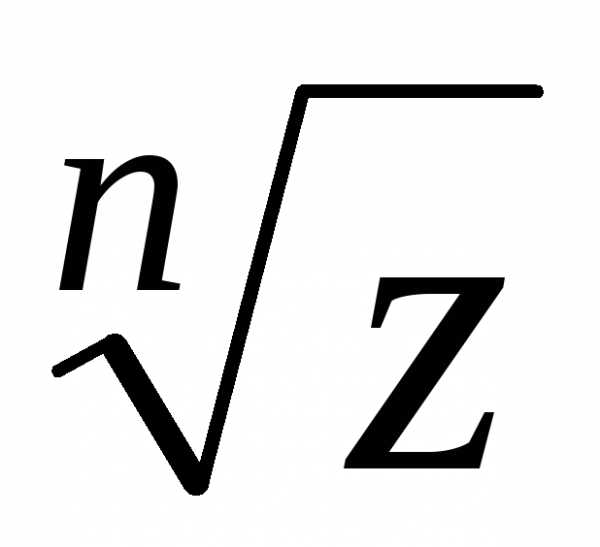 – корня
– корня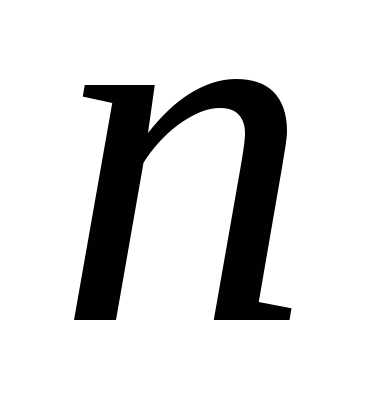 -ой
степени из комплексного числа
-ой
степени из комплексного числа (не путать с арифметическим корнем из
действительного числа!). Операция
извлечения корня является обратной по
отношению к операции возведения в
степень. Поэтому
(не путать с арифметическим корнем из
действительного числа!). Операция
извлечения корня является обратной по
отношению к операции возведения в
степень. Поэтому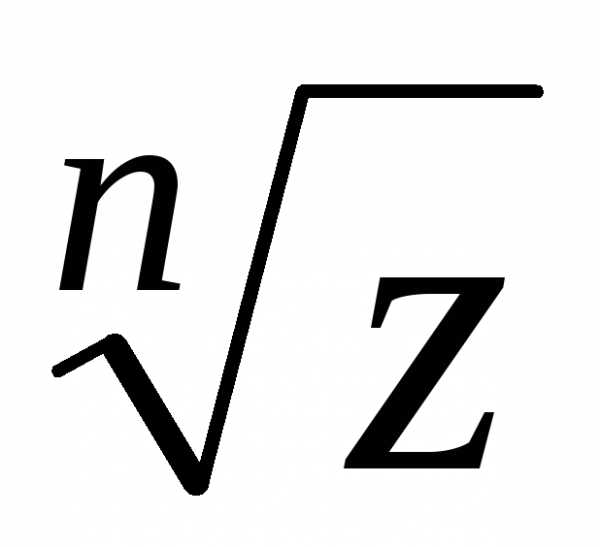 – это комплексное число
– это комплексное число такое, что
такое, что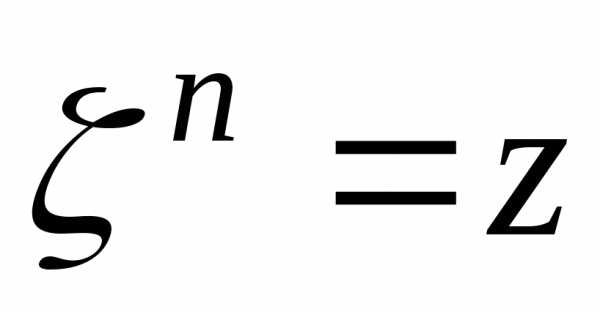 .
.
Пусть известно, атребуется найти. Тогда
.
Из равенства двух комплексных чисел в тригонометрической форме следует, что
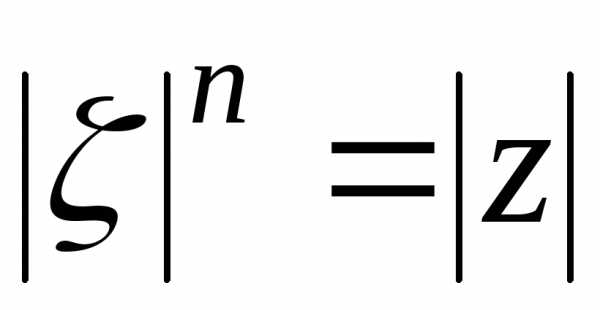 ,
,
,
,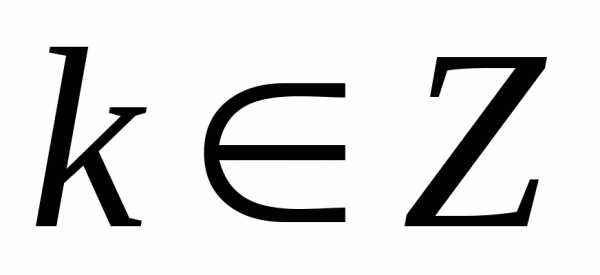 .
.
Отсюда 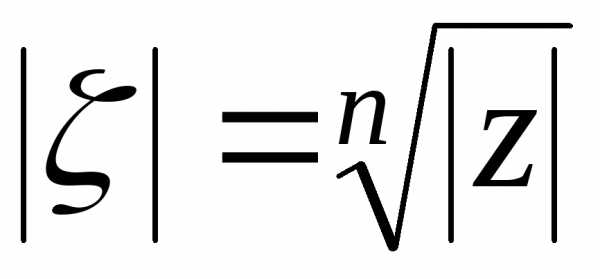 (это арифметический корень!),
(это арифметический корень!),
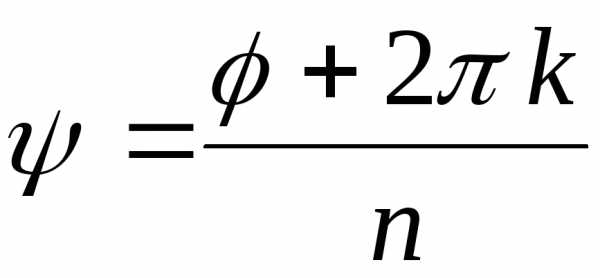 ,
, 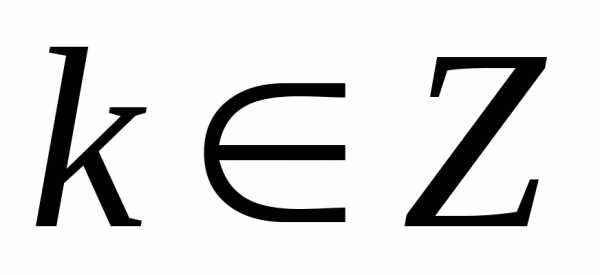 .
.
Нетрудно убедиться,
что 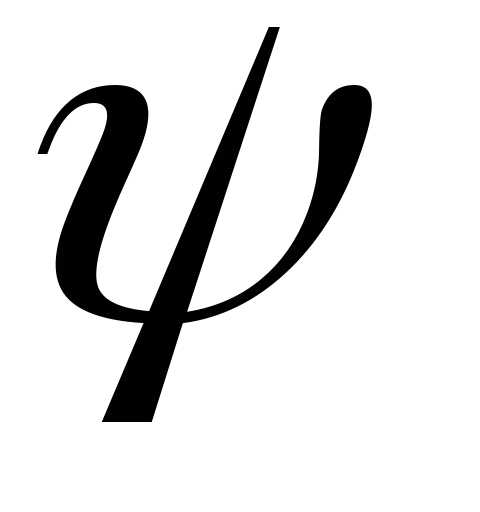 может принимать лишь
может принимать лишь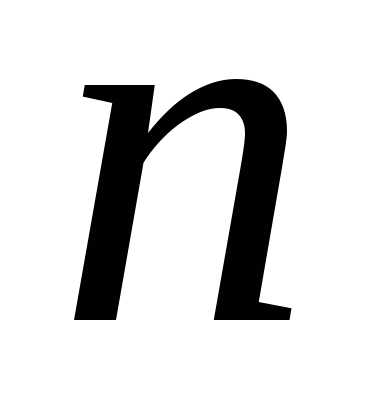 различных по существу значений, например,
при.
Окончательно имеем формулу:
различных по существу значений, например,
при.
Окончательно имеем формулу:
, .
Итак, корень 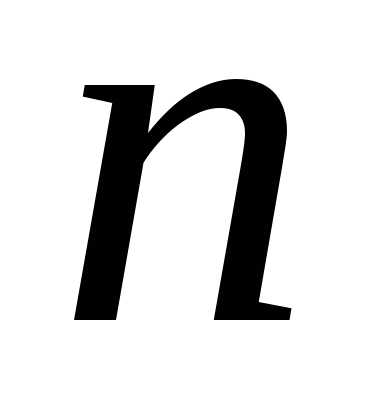 -ой
степени из комплексного числа имеет
-ой
степени из комплексного числа имеет различных значений. На комплексной
плоскости эти значения располагаются
в вершинах правильно
различных значений. На комплексной
плоскости эти значения располагаются
в вершинах правильно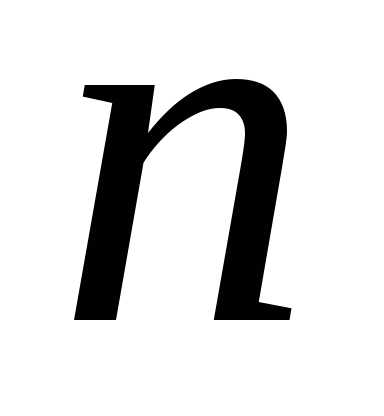 -угольника,
вписанного в окружность радиуса
-угольника,
вписанного в окружность радиуса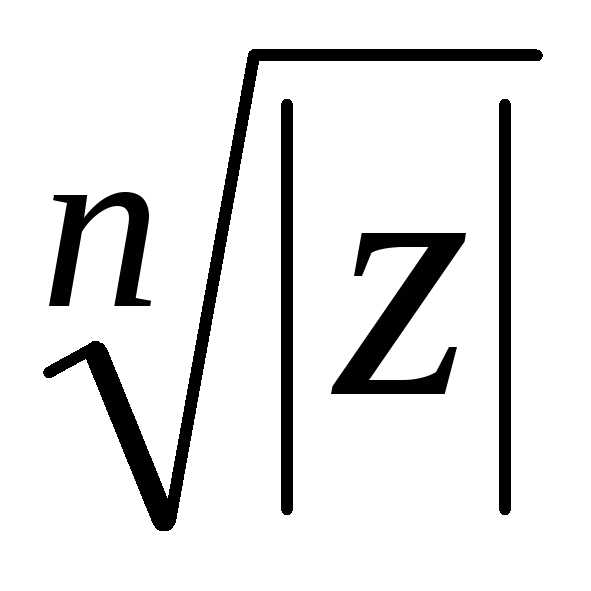 с центром в начале координат. “Первый”
корень имеет аргумент
с центром в начале координат. “Первый”
корень имеет аргумент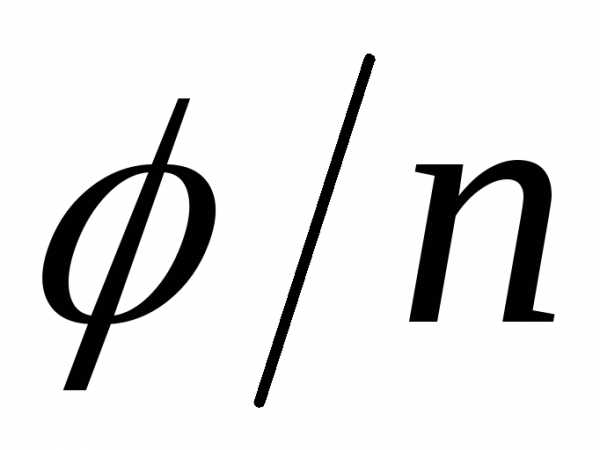 ,
аргументы двух “соседних” корней
отличаются на
,
аргументы двух “соседних” корней
отличаются на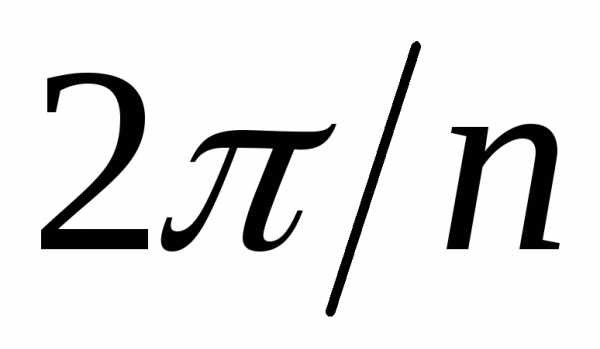 .
.
Пример.Извлечём корень кубический из мнимой
единицы: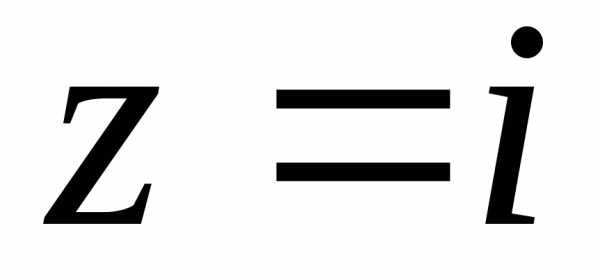 ,
,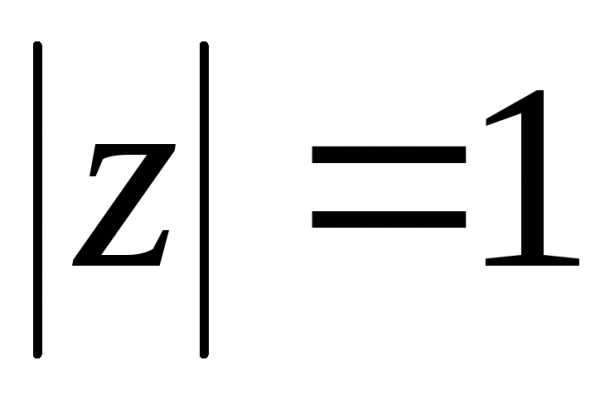 ,.
Тогда:
,.
Тогда:
,
,
.
studfiles.net
Комплексные числа и операции с ними
Введение
При решении квадратных уравнений часто возникает ситуация, когда дискриминант отрицательный. В этом случае это означает что парабола не пересекает прямую абсцисс ни в одной точке. Другими словами, корни квадратного уравнения не существуют среди вещественных значений и их также надо искать за пределами вещественных чисел.
Комплексная плоскость и мнимая единица
Естественным расширением числовой прямой является плоскость, которую называют комплексной плоскостью. Числовая прямая вещественных чисел и ее расширение до комплексной плоскости показано на рисунке 1. Любая точка на комплексной плоскости определяет одно комплексное число. Например на рисунке 1 показано числоРисунок 1. Расширение множества вещественных чисел до множества комплексных числел.
Для того чтобы отделить одну координату от другой (реальную и мнимую части) вводят число , называемое мнимой единицей. Это так раз то число, которого не существует на множестве действительных чисел. Оно обладает особым свойством: . Тогда комплексное число может не только перемещаться по вещественной прямой вправо и влево, но и двигаться по комплексной плоскости потому что мы добавили ему слагаемое с мнимой единицей . Мнимую единицу в математической литературе принято обозначать как но в технике буква уже закреплена за обозначением электрического тока, поэтому чтобы избежать путаницы мы будем обозначать мнимую единицу буквой . Если и , тогда число является действительным и располагается на реальной оси . Если и , тогда число является чисто мнимым и располагается на мнимой оси . Если и , тогда число располагается в одной из четвертей комплексной плоскости.Модуль и фаза комплексного числа
Представление комплексного числа как называют алгебраической формой записи. Если из начала координат комплексной плоскости к точке восстановить вектор (смотри рисунок 1), то можно вычислить длину этого вектора как(1)
Связь реальной и мнимой частей комплексного числа с его амплитудой и фазой представлено следующим выражением:
(2)
Тогда комплексное число можно представить в тригонометрической форме:(3)
Связь угла поворота вектора комплексного числа с реальной и мнимой частью комплексного числа, представленного в алгебраической форме:
(4)
тогда
(5)
где учитывает четверть комплексной плоскости в которой расположено число :(6)
На рисунке 2 показаны значения параметра , в зависимости от того в какой четверти комплексной плоскости расположено число.Рисунок 2. Значение поправки фазы комплексного числа в зависимости от расположения на комплексной плоскости.
На рисунке 2а исходное комплексное число расположено в первой четверти комплексной плоскости и . Тогда и значение фазы комплексного числа равно:(7)
(8)
(9)
(10)
Функция которая позволяет получить фазу комплексного числа c учетом четверти комплексной плоскости в которой расположено комплексное число называется функция арктангенс-2 и обозначается . Функция арктангенс-2 присутствует во всех математических приложениях и может быть использована для расчета верного угла поворота вектора комплексного числа.Показательная форма комплексного числа. Формула Эйлера
Мы уже рассмотрели алгебраическую и тригонометрическую формы записи комплексного числа. Помимо алгебраической и тригонометрической формы существует также показательная форма комплексного числа:
(11)
связанная с тригонометрической формой формулой Эйлера:
(12)
Cоотношение (12) легко доказать, если произвести разложение экспоненты в ряд Тейлора:
(13)
Представим ряд (13) в виде суммы четных и нечетных членов последовательности:
(14)
(15)
В выражении (15) первая сумма по четным степеням дает разложение в ряд Тейлора функции , а вторая сумма по нечетным степеням дает разложение в ряд Тейлора функции . Таким образом, получено доказательство справедливости формулы Эйлера (12). Необходимо отметить, что формула Эйлера является одной из важнейших в теории функций комплексного переменного. Так например при помощи формулы Эйлера можно связать математические константы и с использованием мнимой единицы :(16)
Операции над комплексными числами. Комплексно-сопряженные числа
В данном параграфе мы кратко рассмотрим операции над комплексными числами. Сумма двух комплексных чисел и представляет собой комплексное число(17)
При сложении реальные и мнимые части комплексного числа также складываются. На комплексной плоскости операцию сложения можно реализовать как сложение векторов комплексных чисел по правилу параллелограмма (рисунок 3а).
Рисунок 3. Операции над комплексными числами.
Разность двух комплексных чисел и представляет собой комплексное число(18)
При вычитании реальные и мнимые части комплексного числа также вычитаются. На комплексной плоскости операцию вычитания можно реализовать как вычитание векторов по правилу параллелограмма (рисунок 3б). На первом шаге из вектора формируется вектор (обозначенный пунктирной линией на рисунке 3б), после чего вектор складывается с вектором по правилу параллелограмма.Для того чтобы получить формулу для умножения комплексных числен необходимо перемножить два комплексных числа по правилу умножения многочленов:
(19)
Умножение комплексных проще выполнять если числа представлены в показательной форме:
(20)
При перемножении в показательной форме модули комплексных чисел перемножаются а фазы складываются. Операция произведения комплексных чисел показано на рисунке 3в.
Введем понятие комплексно-сопряженного числа. Число является комплексно-сопряженным числу . Комплексно-сопряженные числа отличаются знаком перед мнимой частью. Графически комплексно-сопряженные числа показаны на рисунке 3г. При этом можно заметить, что модули комплексно-сопряженных чисел равны а фазы имеют противоположные знаки. Произведение комплексно-сопряженных чисел(21)
представляет собой действительное число равное квадрату модуля этих чисел.
Из элементарных операций нам осталось рассмотреть лишь деление комплексных чисел. Рассмотрим результат деления комплексных чисел в показательной форме:
(22)
Таким образом, при делении комплексных чисел модуль частного равен частному модулей исходных чисел, а фаза равна разности фаз исходных чисел. При этом необходимо потребовать, чтобы был не равен нулю, иначе у нас появится деление на ноль при расчете модуля частного.Рассмотрим теперь деление комплексных чисел в алгебраической форме:
(23)
Домножим и числитель и знаменатель на число, комплексно-сопряженное знаменателю:
(24)
Выводы
В данной статье введено понятие комплексного числа и рассмотрены основные его свойства. Введено понятие мнимой единицы.
Подробно рассмотрена комплексная плоскость и представление комплексных чисел в алгебраической, тригонометрической и показательной формах. Введены понятия модуля и фазы комплексного числа.
Рассмотрены основные арифметические операции над комплексными числами. Показано как выполнять операции сложения, вычитания в алгебраической форме, введено понятие комплексно-сопряженных чисел, а также операции умножения и деления в показательной и алгебраической формах.
Список литературы
[1] Пантелеев А.В., Якимова А.С. Теория функций комплексного переменного и операционное исчисление в примерах и задачах. М: Высшая школа, 2011.
[2] Дубровин В.Т. Теория функций комплексного переменного. Теория и практика Казань: Казанский государственный университет, 2010. [PDF]
ru.dsplib.org
| Главная > Учебные материалы > Математика: Комплексные числа | ||||
|
1.Понятие комплексного числа. 2.Тригонометрическая форма комплексного числа.
|
||||
| 19 20 21 22 23 24 25 26 27 | ||||
1.Понятие комплексного числа.Выражение вида z = x + iy называется комплексным числом. Число х называется действительной частью комплексного числа z и обозначается Re(z), число y — мнимой частью комплексного числа z и обозначается Im(z). Числа z = x + iy и z1 = x — iy называются сопряженными. Если равны действительные и мнимые части комплексного числа, то они называются равными т.е. z1 = z2 или x1 + iy1 = x2 + iy2. Операции над комплексными числами. |
||||
1. Сумма (разность) комплексных чисел. z1+z2 = x1+x2+i(y1+y2). 2. Произведение комплексных чисел. z1z2 = (x1x2 — y1y2) + i(x1y2 + x2y1). отсюда i² = (0 + i1)(0 + i1) = (0 -1) + i(0 + 0) = -1. 3. Деление двух комплексных чисел. |
 |
|||
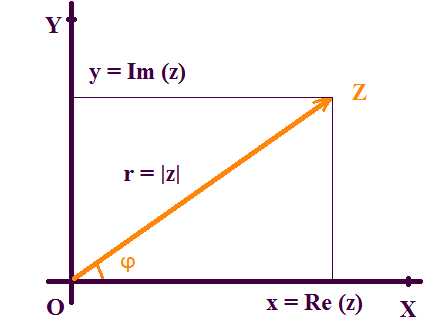
Рассмотрим на плоскости декартову прямоугольную систему координат Oxy. Каждому комплексному числу Z = x + iy ставится в соответствие единственная точка плоскости z(xy). Плоскость Oxy, где каждая точка отождествлена с комплексным числом, называется комплексной. Координатные оси Ox и Oy, на которых расположены действительные и мнимые числа, называются действительной и мнимой осями. |
 |
|||
2.Тригонометрическая форма комплексного числа.До любой точки комплексной плоскости из начала координат можно провести вектор определенной длины r. Число r называется модулем комплексного числа z и обозначается |z|. |
||||
Угол ϕ, образованный между вектором и осью Ox, называется аргументом комплексного числа z и обозначается Arg z. Из значения ϕ = Arg z выделяется главное значение arg z, которое кратно 2π. ϕ = Arg z = arg z + 2kπ где 0≤ argz < 2π Таким образом: x = r cos ϕ, y = r sin ϕ. Следовательно, комплексное число z = x + iy можно представить как: |
||||
Представление комплексного числа в такой форме, где r = |z| ≥ 0, ϕ = Arg z, называется тригонометрической формой комплексного числа. |
||||
 |
||||
| Пример. | ||||
 |
||||
| 19 20 21 22 23 24 25 26 27 | ||||
www.mathtask.ru
Комплексные числа
Глава 6
§ 28. Что такое комплексные числа
Повторить: § 17: векторы на плоскости.
В этой главе мы познакомимся с комплексными числами, о которых уже неоднократно упоминали. Итак, что же это такое?
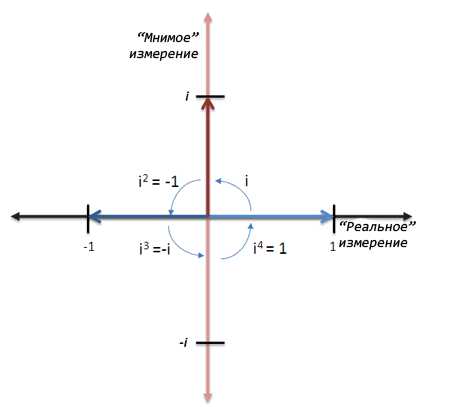
Как известно, из отрицательного числа извлечь квадратный корень невозможно: квадраты всех чисел неотрицательны. Давайте, однако, вообразим, что нашлось такое необычное число i, квадрат которого равняется −1. Посмотрим, что получится, если это число i добавить к обычным числам.
Для начала поумножаем i на само себя: i2 = −1 (как мы и
договаривались), тогда i3 = (i2) · i = (−1) · i = −i; i4 = i3i = = (−i) · i = −i2 = −(−1) = 1 и т. д.
Задача 28.1. Чему равно i5? i6? i2003?
Теперь давайте умножать число i на обычные числа и складывать его с обычными числами. При этом будут получаться выражения наподобие 1 − i, −4i, 2 + 5i и т.д. Раскрывая скобки
иприводя подобные члены, такие выражения можно складывать
иперемножать; поскольку i2 всякий раз можно заменять на −1,

в выражения, получающиеся после упрощений, i будет входить не более чем в первой степени:
(2 + 5i) + (3 − i) = 2 + 3 + 5i − i = 5 + 4i;
(2 + 5i)(3 − i) = 6 + 15i − 2i − 5i2 = 6 + 13i − 5(−1) = 11 + 13i.
Задача 28.2. Упростите выражения: а) √3 + i3; б) (1 + i)20.
Имея в распоряжении число i, мы можем извлечь корень не
только из −1, но и из любого отрицательного числа. Например, в | |||||||||||||||
√ |
|
|
| √ |
|
| √ |
|
| 2 | = i | 2 | ·2 = −2. | ||
качестве −2 подойдет число i 2, поскольку (i | 2) |
|
| ||||||||||||
| √ |
|
|
|
|
|
|
|
|
| √ |
|
| мы тоже | |
Впрочем, −i | 2 также даст в квадрате −2; число −i | 2 |
| ||||||||||||
будем называть квадратным корнем из −2. Выделять из этих двух квадратных корней один «арифметический корень» мы не будем: для чисел, в записи которых участвует i, не удается разумным образом определить, какие из них следует считать положительными, а какие — отрицательными.
Задача 28.3. Пользуясь формулой для корней квадратного уравнения, найдите корни уравнения x2 − 4x + 5 = 0 (дискриминант этого уравнения отрицателен, так что в их записи будет участвовать i). Проверьте найденные значения x, подставив их в уравнение.
А если выражение с i стоит в знаменателе? Сейчас мы увидим, что всякую дробь, в знаменателе которой присутствует i, можно преобразовать так, чтобы в знаменателе были только обычные числа. Покажем это на примере.
Пусть требуется упростить выражение 2 +1 3i. Поступим так
же, как мы делали, когда в школьных примерах избавлялись от иррациональности в знаменателе: домножим числитель и знаменатель на «сопряженное выражение» 2 − 3i:
| 1 |
| = | 2 − 3i |
| = | 2 − 3i | = |
| 2 |
| + | 3 | i. | |||
| 2 + 3i |
|
|
|
| 13 |
|
| |||||||||
|
| (2 + 3i)(2 − 3i) | 4 − (−9) |
|
|
|
| 13 | |||||||||
Задача 28.4. Упростите выражения: а) | 7 − 11i | ; б) |
| 1 | . |
|
| ||||||||||
3 + i |
|
|
| ||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| i |
|
| |||
|
|
|
|
| 165 |
|
|
|
|
|
|
|
|
|
|
| |

Теперь можно ответить на вопрос, стоящий в заглавии этого параграфа: комплексные числа — это те самые выражения с участием i, которыми мы до сих пор занимались. Точнее говоря:
Комплексным числом называется выражение вида a + bi, где a и b — обычные (действительные, или вещественные) числа. Комплексные числа a + bi и c + di считаются равными, если a = c и b = d. Чтобы сложить или перемножить два комплексных числа, надо раскрыть скобки и привести подобные члены, заменяя i2 на −1.
Если провести это приведение подобных в общем виде, получится вот что:
(a + bi) + (c + di) = (a + c) + (b + d)i;
(a + bi)(c + di) = (ac − bd) + (ad + bc)i.
Чтобы поделить одно комплексное число на другое, надо «домножить на сопряженные»:
a + bi | = | (a + bi)(c − di) | = | ac + bd | + i | bc − ad | . | |
c + di |
| (c + di)(c − di) | c2 + d2 |
| ||||
|
|
| c2 + d2 | |||||
Задача 28.5. Умножьте ac ++ dibi, вычисленное по вышеприведенной
формуле, на c+di и убедитесь, что действительно получится a+bi (то есть что деление комплексных чисел действительно является действием, обратным к умножению).
Комплексное число a+bi удобно изображать точкой на плоскости с координатами (a; b) (рис. 28.1). Абсцисса этой точки, то есть a, называется вещественной (или действительной) частью числа a+bi, а ордината этой точки, то есть b, называется мнимой частью числа a + bi. Плоскость с системой координат, на которой изображаются комплексные числа, называется комплексной плоскостью.
Комплексные числа, мнимая часть которых равна нулю, располагаются при таком изображении на оси абсцисс (когда речь
Рис. 28.1. Комплексная плоскость.
идет о таком изображении комплексных чисел, ось абсцисс принято называть вещественной, или действительной, осью, а ось ординат — мнимой осью). Комплексные числа, лежащие на действительной оси, складываются и умножаются так же, как обычные действительные числа: ведь в их записи i не участвует. Поэтому можно считать, что действительные числа — частный случай комплексных, а действительная ось, которую они заполняют, — это знакомая нам с младших классов числовая прямая.
Задача 28.6. Докажите, что уравнение z2 = −1 не имеет (в комплексных числах) других решений, кроме i и −i.
Указание. Пусть z = x + iy. Тогда z2 = x2 − y2 + i · 2xy. По условию, z2 = −1. Так как комплексные числа равны тогда и только тогда, когда равны их действительные и мнимые части, получаем:
(
x2 − y2 = 1;
2xy = 0.
Решите эту систему уравнений.
Задача 28.7. Найдите все комплексные решения уравнения z3 = 1 и изобразите их на комплексной плоскости.
Указание. Решений три; на комплексной плоскости они окажутся вершинами правильного треугольника.
Задача 28.8. Найдите все комплексные решения уравнения z2 = = 5 − 12i.

Задача 28.9. Докажите, что для всякого отличного от нуля ком-
плексного числа a + bi существуют ровно два решения уравнения z2 = a + bi.
Результат задачи 28.9 показывает, что, имея в своем распоряжении комплексные числа, можно извлекать квадратные корни не только из отрицательных, но и вообще из любых комплексных чисел.
Если дано комплексное число z = a + bi, то сопряженным к нему называется число a − bi. Мы уже сталкивались с сопряженными комплексными числами, когда обсуждали деление комплексных чисел. Число, сопряженное к комплексному числу z, обозначается z¯. Говорят еще, что числа z и z¯ сопряжены друг другу. Сопряженные числа изображаются на комплексной плоскости точками, симметричными относительно действительной оси.
Задача 28.10. Докажите тождества:
¯
а) (¯)z = z; б) (z + w) = z¯ + w¯; в) (zw) = z¯ + w¯.
Задача 28.11. Пусть z и w — комплексные числа, не являющиеся действительными. Докажите, что z и w сопряжены тогда и только тогда, когда z + w и zw — действительные числа.
Задача 28.12. Докажите, что всякое квадратное уравнение с действительными коэффициентами и отрицательным дискриминантом имеет два комплексных корня, сопряженных друг с другом. Верна ли для таких уравнений теорема Виета?
Если изобразить комплексные числа точками на плоскости, то оказывается, что у действий над комплексными числами есть геометрический смысл. Давайте выясним, какой геометрический операции соответствует сложение комплексных чисел.
Соединим начало координат 0 (соответствующее числу нуль) с точкой на плоскости, соответствующей комплексному числу z = x + iy — получится вектор OZ, имеющий координаты (x; y). Так как при сложении векторов их координаты складываются, то равенство z1 + z2 = z3 равносильно равенству OZ1 + OZ2 = OZ3 (рис.28.2). Итак, сложить комплексные числа — все равно что сложить соответствующие векторы.
studfiles.net
Просто о сложном: комплексные числа
Комплексные числа всегда меня занимали. Как и с понятием экспоненты, большинство определений подпадали под одну из двух категорий:
- это математическая абстракция, всё упирается в формулы. Смиритесь.
- это используется в продвинутой физике, поверьте. Просто дождитесь университета.
Какой хороший способ привлечь деток к математике! Сегодня мы возьмем эту тему штурмом, используя наши любимые инструменты:
- Будем основываться на связях, а не на механических формулах.
- Рассмотрим комплексные числа как дополнение к нашей системе счисления, такому же, как ноль, дробные или отрицательные числа.
- Визуализируем идеи в графиках, чтобы лучше понять суть, а не просто изложим сухим текстом.
И наше секретное оружие: изучение по аналогии. Мы доберемся до комплексных чисел, начав с их предков, отрицательных чисел. Вот вам небольшое руководство:
Пока что смысла в этой таблице мало, но пусть она будет рядом. К концу статьи всё станет на свои места.
Давайте действительно поймем, что такое отрицательные числа
Отрицательные числа не так просты. Представьте, что вы — европейский математик в XVIII веке. У вас есть 3 и 4, и вы можете написать 4 – 3 = 1. Всё просто.
Но сколько будет 3 – 4? Что, собственно, это означает? Как можно отнять 4 коровы от 3? Как можно иметь меньше, чем ничего?
Отрицательные числа рассматривались как полная чушь, что-то, что «бросало тень на всю теорию уравнений» (Фрэнсис Масерес, 1759). Сегодня было бы полной чушью думать об отрицательных числах, как о чем-то нелогичном и неполезном. Спросите вашего учителя, нарушают ли отрицательные числа основы математики.
Что же произошло? Мы изобрели теоретическое число, которое обладало полезными свойствами. Отрицательные числа нельзя потрогать или ощутить, но они хорошо описывают определенные связи (как задолженность, например). Это очень полезная выдумка.
Вместо того, чтобы сказать «Я должен вам 30», и читать слова, чтобы понять в плюсе я или в минусе, я могу просто записать «-30», и знать, что это означает. Если я заработаю деньги и оплачу свои долги (-30 + 100 = 70), я смогу легко записать эту транзакцию несколькими символами. У меня останется +70.
Знаки плюса и минуса автоматически фиксируют направление — вам не нужно целое предложение, чтобы описать изменения после каждой транзакции. Математика стала проще, элегантнее. Стало не важно, являются ли отрицательные числа «осязаемыми» — у них есть полезные свойства, и мы пользовались ими, пока они крепко не вошли в наш обиход. Если кто-то из ваших знакомых еще не понял суть отрицательных чисел, теперь вы ему поможете.
Но не будем умалять человеческие страдания: отрицательные числа были настоящим сдвигом в сознании. Даже Эйлер, гений, открывший число е и много еще чего, не понимал отрицательные числа так же хорошо, как мы сегодня. Они рассматривались как «бессмысленные» результаты вычислений.
Странно требовать от детей, чтобы они спокойно понимали идеи, которые когда-то смущали даже самых лучших математиков.
Ввод мнимых чисел
С мнимыми числами та же история. Мы можем решать уравнения вроде этого целыми днями:
Ответами будут 3 и -3. Но представим, что какой-то умник приписал сюда минус:
Ну и ну. Такой вопрос заставляет людей съеживаться, первый раз видя его. Вы хотите вычислить квадратный корень из числа, меньшего, чем ноль? Это немыслимо! (Исторически реально существовали подобные вопросы, но мне удобнее представлять какого-то безликого умника, чтобы не вгонять в краску ученых прошлого).
Выглядит безумно, как в свое время выглядели и отрицательные числа, ноль и иррациональные числа (неповторяющиеся числа). В этом вопросе нет «реального» смысла, правда?
Нет, не правда. Так называемые «мнимые числа» нормальны настолько же, как и все другие (или настолько же ненормальные): они являются инструментом для описания мира. В том же духе, как мы представляем, что -1, 0.3 и 0 «существуют», давайте предположим, что существует некое число i, где:
Другими словами, вы умножаете i на себя же, чтобы получить -1. Что сейчас происходит?
Ну, сначала у нас конечно болит голова. Но, играя в игру «Давайте представим, что i существует», мы действительно делаем математику проще и элегантнее. Появляются новые связи, которые мы с легкостью можем описать.
Вы не поверите в i, как и те старые математики-ворчуны не верили в существовании -1. Все новые, сворачивающие мозг в трубочку понятия сложны для восприятия, и их смысл вырисовывается не сразу, даже для гениального Эйлера. Но, как показали нам отрицательные числа, странные новые идеи могут быть чрезвычайно полезными.
Я не люблю сам термин «мнимые числа» — такое чувство, что он был выбран специально, чтобы оскорбить чувства i. Число i такое же нормальное, как и другие, но за ним закрепилась кличка «мнимое», так что мы тоже будем ей пользоваться.
Визуальное понимание отрицательных и комплексных чисел
Уравнение x^2 = 9 на самом деле означает следующее:
или
Какое преобразование x, применяемое дважды, превращает 1 в 9?
Есть два ответа: «x = 3» и «x = -3». То есть, вы можете «масштабировать в» 3 раза или «масштабировать в 3 раза и перевернуть» (переворачивание или взятие обратного результата — всё это интерпретации умножения на отрицательную единицу).
А теперь давайте подумаем об уравнении x^2 = -1, которое можно записать так:
Какое преобразование x, применяемое дважды, превращает 1 в -1? Хм.
- Мы не можем умножить дважды положительное число, потому что результат будет положительным.
- Мы не можем умножить дважды отрицательное число, потому что результат опять будет положительным.
А как насчёт… вращения! Звучит, конечно, необычно, но что если представить х как «поворот 90 градусов», тогда применив х дважды, мы совершим поворот на 180 градусов на координатной оси, и 1 обернется в -1!
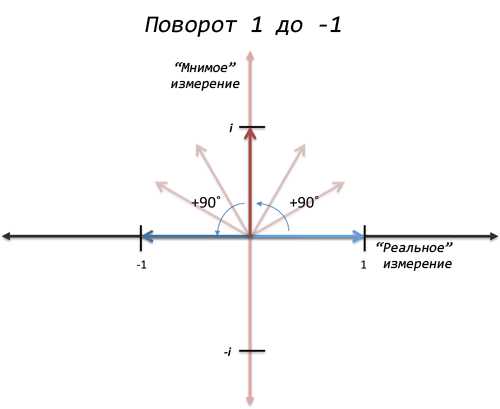
Вот это да! И если мы еще немного над этим поразмышляем, то мы можем совершить два оборота в противоположном направлении, и также перейти с 1 на -1. Это «отрицательное» вращение или умножение на -i:
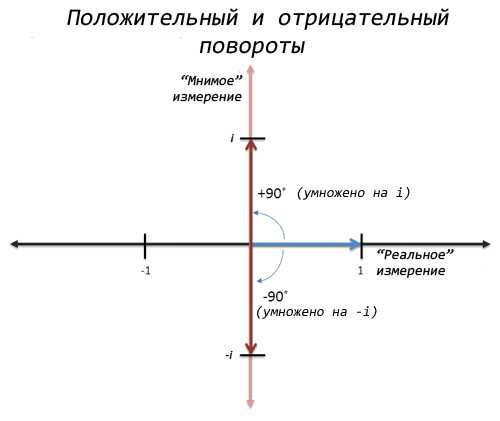
Если мы дважды умножим на-i, то при первом умножении получим -i из 1, а при втором -1 из -i. Так что на самом деле существует два квадратных корня -1: i и -i.
Это довольно круто! У нас есть что-то вроде решения, но что оно означает?
- i — это «новая мнимая размерность» для измерения числа
- i (или -i) — это то, чем «становятся» числа при вращении
- Умножение на i — это вращение на 90 градусов против часовой стрелки
- Умножение на -i — это вращение на 90 градусов по часовой стрелке.
- Двойное вращение в любом из направлений дает -1: оно опять возвращает нас к «обычной» размерности положительных и отрицательных чисел (ось x).
Все числа 2-мерные. Да, это трудно принять, но древним римлянам было бы также трудно принять десятичные дроби или деление в столбик. (Как это так, между 1 и 2 есть еще числа?). Выглядит странно, как и любой новый способ мыслить в математике.
Мы спросили «Как превратить 1 в -1 в два действия?» и нашли ответ: повернуть 1 на 90 градусов дважды. Довольно странный, новый способ мыслить в математике. Но очень полезный. (Между прочим, эта геометрическая интерпретация комплексных чисел появилась только десятилетия спустя после открытия самого числа i).
Также, не забывайте, что принятие оборота против часовой стрелки за положительный результат — это сугубо человеческая условность, и всё могло бы быть совсем по-другому.
Поиск множеств
Давайте углубимся немного в детали. При умножении отрицательных чисел (как -1), вы получаете множество:
- 1, -1, 1, -1, 1, -1, 1, -1
Поскольку -1 не меняет размер числа, а только знак, вы получаете одно и то же число то со знаком «+», то со знаком «-». Для числа х у вас получится:
Это очень полезная мысль. Число «х» может представлять хорошие и плохие недели. Представим, что хорошая неделя сменяет плохую; это хорошая неделя; а какой будет 47-я неделя?
-x означает, что неделя выдастся плохой. Видите, как отрицательные числа «следят за знаком» — мы можем просто ввести (-1)^47 в калькуляторе вместо того, чтобы считать («Неделя 1 хорошая, неделя 2 плохая… неделя 3 хорошая…»). Вещи, которые постоянно чередуются можно отлично смоделировать, используя отрицательные числа.
Хорошо, а что будет, если мы продолжим умножать на i?
Очень смешно, давайте немного это всё упростим:
Вот всё то же представлено графически:
Мы повторяем цикл каждый 4-й поворот. В этом определенно есть смысл, да? Любой ребенок скажет вам, что 4 поворота влево — это всё равно, что не поворачиваться вовсе. А теперь оторвитесь от мнимых чисел (i, i^2)и посмотрите на общее множество:
- X, Y, -X, -Y, X, Y, -X, -Y…
Точно, как отрицательные числа моделируют зеркальное отражение чисел, мнимые числа могут моделировать что угодно, что вращается между двумя измерениями «Х» и «Y». Или что угодно с циклической, круговой зависимостью — есть что-нибудь на примете?
Понимание комплексных чисел
Есть еще одна деталь для рассмотрения: может ли число быть и «реальным», и «мнимым»?
Даже не сомневайтесь. Кто сказал, что нам обязательно нужно поворачивать строго на 90 градусов? Если мы одной ногой станем на «реальную» размерность, а другой — на «мнимую», то будет выглядеть примерно так:
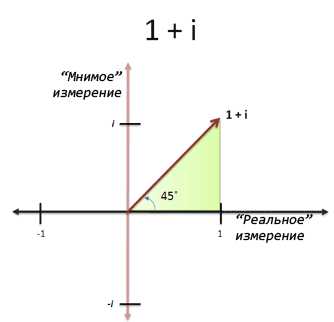
Мы находимся на отметке в 45 градусов, где вещественная и мнимая части одинаковы, и само число равно «1 + i». Это как хот-дог, где есть и кетчуп, и горчица — кто сказал, что нужно обязательно выбирать что-то одно?
По сути, мы можем выбрать любую комбинацию вещественной и мнимой части и сделать из всего этого треугольник. Угол становится «углом вращения». Комплексное число — это заумное название для чисел, в которых есть вещественная и мнимая части. Они пишутся, как «a + bi», где:
- a — вещественная часть
- b — мнимая часть
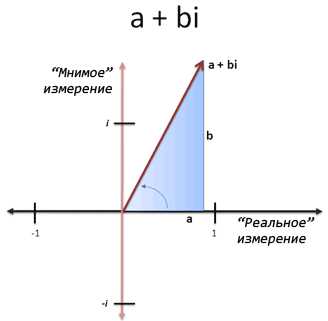
Неплохо. Но остается один последний вопрос: как «велико» комплексное число? Мы не можем измерить вещественную часть или мнимую отдельно, потому что мы упустим общую картину.
Давайте сделаем шаг назад. Размер отрицательного числа — это расстояние от нуля:
Это другой способ найти абсолютную величину. Но как измерить оба компонента на 90 градусах для комплексных чисел?
Это птица в небе… или самолет… Пифагор спешит на помощь!
Эта теорема выскакивает, где только можно, даже в числах, придуманных через 2000 лет после самой теоремы. Да, мы делаем треугольник, и его гипотенуза и будет равна расстоянию от нуля:
Хоть измерить комплексное число не так просто, как «просто опустить знак -», у комплексных чисел есть очень полезные применения. Давайте рассмотрим некоторые из них.
Реальный пример: Вращения
Мы не будем дожидаться университетского курса физики, чтобы попрактиковаться с комплексными числами. Мы займемся этим уже сегодня. Много можно рассказать на тему умножения комплексных чисел, но пока нужно понять главное:
- Умножение на комплексное число совершает вращение на его угол
Давайте посмотрим, как это работает. Представьте, что я на лодке, движусь с курсом 3 единицы на Восток каждые 4 единицы на Север. Я хочу изменить свой курс на 45 градусов против часовой стрелки. Каким будет мой новый курс?
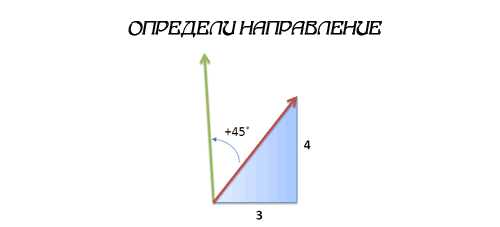
Кто-то может сказать «Это просто! Вычислите синус, косинус, погуглите значение по тангенсу…и тогда…» Кажется, я сломал свой калькулятор…
Давайте пойдем более простым путем: мы идем по курсу 3 + 4i (не важно, какой тут угол, нам всё равно пока) и хотим повернуться на 45 градусов. Ну, 45 градусов это 1 + i (идеальная диагональ). Так что мы можем умножить наш курс на это число!
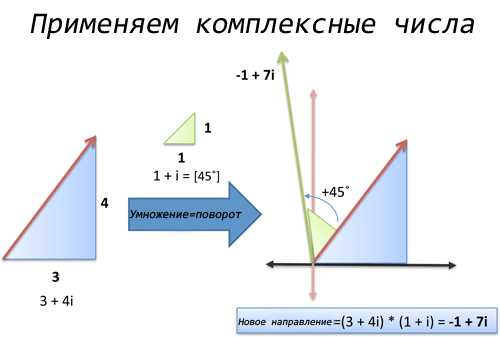
Вот в чем суть:
- Исходный курс: 3 единицы на Восток, 4 единицы на Север = 3 + 4i
- Вращение против часовой стрелки на 45 градусов = умножение на 1 + i
При умножении мы получаем:
Наш новый ориентир — 1 единица на Запад (-1 на Восток) и 7 единиц на Север, можете нарисовать координаты на графике и следовать им.
Но! Мы нашли ответ за 10 секунд, без всяких синусов и косинусов. Не было векторов, матриц, отслеживания, в каком квадранте мы находимся. Это была простая арифметика и немного алгебры для приведения уравнения. Мнимые числа отлично справляются с вращением!
Более того, результат такого вычисления очень полезен. У нас есть курс (-1, 7) вместо угла (atan(7/-1) = 98.13, и сразу ясно, что мы во втором квадранте. Как, собственно, вы планировали нарисовать и следовать указанному углу? Используя транспортир под рукой?
Нет, вы бы конвертировали угол в косинус и синус (-0.14 и 0.99), нашли бы примерное соотношение между ними (около 1 к 7) и набросали бы треугольник. И тут комплексные числа несомненно выигрывают — аккуратно, молниеносно, и без калькулятора!
Если вы похожи на меня, то это открытие покажется вам сногсшибательным. Если нет, боюсь, что математика вас совсем не зажигает. Уж извините!
Тригонометрия хороша, но комплексные числа значительно упрощают вычисления (вроде поиска cos(a + b)). Это только маленький анонс; в следующих статьях я предоставлю вам полное меню.
Лирическое отступление: некоторые люди думают примерно так: «Эй, ну не удобно же иметь курс Север/Восток вместо простого угла для следования судна!»
Правда? Ну хорошо, посмотрите на свою правую руку. Какой угол между основанием вашего мизинца и кончиком указательного пальца? Удачи с вашим способом вычисления.
А можно просто ответить «Ну, кончик находится на Х дюймов вправо и Y дюймов вверх» и с этим уже можно что-то сделать.
Комплексные числа стали ближе?
Мы пронеслись смерчем по моим базовым открытиям в области комплексных чисел. Посмотрите на самую первую иллюстрацию, теперь он должен стать более понятным.
Есть еще столько всего интересного в этих красивых, чудных числах, но мой мозг уже устал. Моя цель была проста:
- Убедить вас в том, что комплексные числа только рассматривались как «сумасшествие», а на деле они могут быть очень полезными (точно как и отрицательные числа)
- Показать, как комплексные числа могут упростить некоторые задачи вроде вращения.
Если я кажусь слишком озабоченным этой темой, то для этого есть причина. Мнимые числа годами были моей навязчивой идеей — недостаток понимания меня раздражал.
Сейчас я наконец-то дошел до этого долгожданного понимания, и мне не терпелось поделиться с вами. Но меня по-прежнему злит, что вы знакомитесь с этими замечательными, несложными приемами понимания в блоге какого-то безумного лунатика, а не в классе на уроке математики. Мы душим в себе вопросы и «пыхтим» над непонятными вещами, потому что не хотим искать, находить и делиться чистыми, абсолютно логичными объяснениями.
Но зажечь свечу лучше, чем пробираться сквозь кромешную тьму: вот мои мысли, и я уверен, что огонек зажжется и в умах моих читателей.
Эпилог: Но они по-прежнему довольно странные!
Я знаю, они и для меня всё еще выглядят странными. Я пытаюсь мыслить, как мыслил первый человек, открывший ноль.
Ноль — это такая странная идея, «что-то» представляет «ничего», и это никак не могли понять в Древнем Риме. То же самое и с комплексными числами — это новый способ мышления. Но и ноль, и комплексные числа значительно упрощают математику. Если бы мы никогда не внедряли странности вроде новых систем счисления, мы бы до сих пор считали всё на пальцах.
Я повторяю эту аналогию, потому что так легко начать думать, что комплексные числа «не нормальные». Давайте быть открытыми к новшествам: в будущем люди будут только шутить над тем, как кто-то вплоть до XXI века не верил в комплексные числа.
Перевод статьи «A Visual, Intuitive Guide to Imaginary Numbers»
zero2hero.org
