Что такое Угол? Определение, виды, как обозначают? Примеры
Определение угла
Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.
Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.
Если нам дана прямая a на плоскости, и на ней есть некоторая точку O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.
Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:
Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.
В математике существует специальный символ для обозначения угла, вот он: ∠.
Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.
Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре.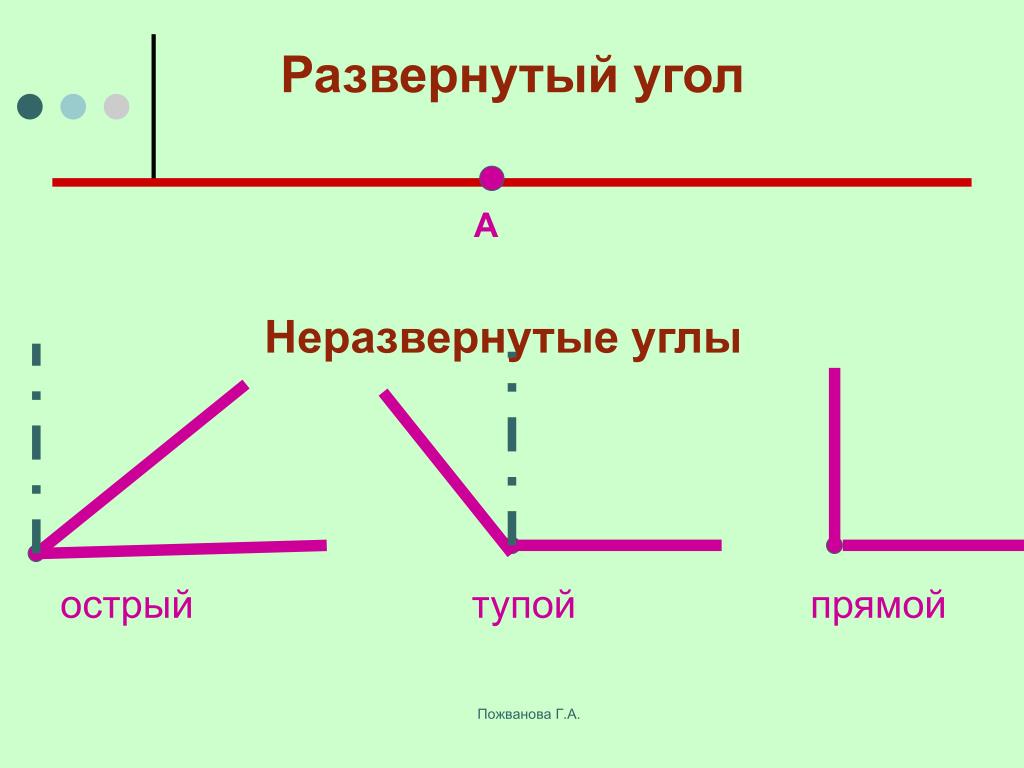
Иногда можно встретить обозначение в виде цифр — так тоже можно.
Для наглядности — все способы обозначения углов:
Что такое вершина и стороны угла:
- Стороны угла — лучи, из которых состоит угол.
- Вершина угла — общее начало сторон угла.
Биссектриса — это луч, который исходит из вершины угла и делит его на два равных угла.
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Единица измерения углов — градусы. Символ для обозначения градуса угла: °.
Определение смежных и вертикальных углов
Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Таким образом два смежных угла составляют развернутый угол. Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны, при условии, что смежные углы не равны.
Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны, при условии, что смежные углы не равны.
Вертикальные углы — это пара углов, у которых есть общая вершина, при этом стороны одного угла составляют продолжение сторон другого угла.
При пересечении прямых получается четыре пары смежных и две пары вертикальных углов. Вот как это выглядит:
Виды углов
Есть разные типы углов и у каждого своё название:
- острый
- прямой
- тупой
- развернутый
- выпуклый
- полный
Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.
Острый угол
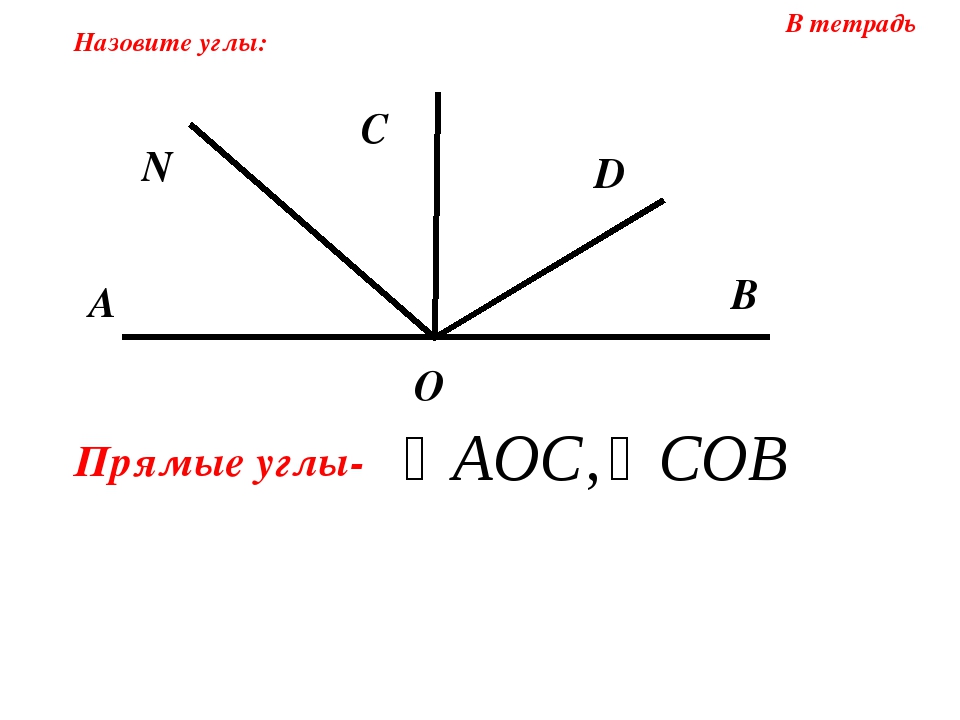
Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен половине развернутого угла, то есть = 90°.
Если два смежных угла равны между собой, то каждый из них является прямым.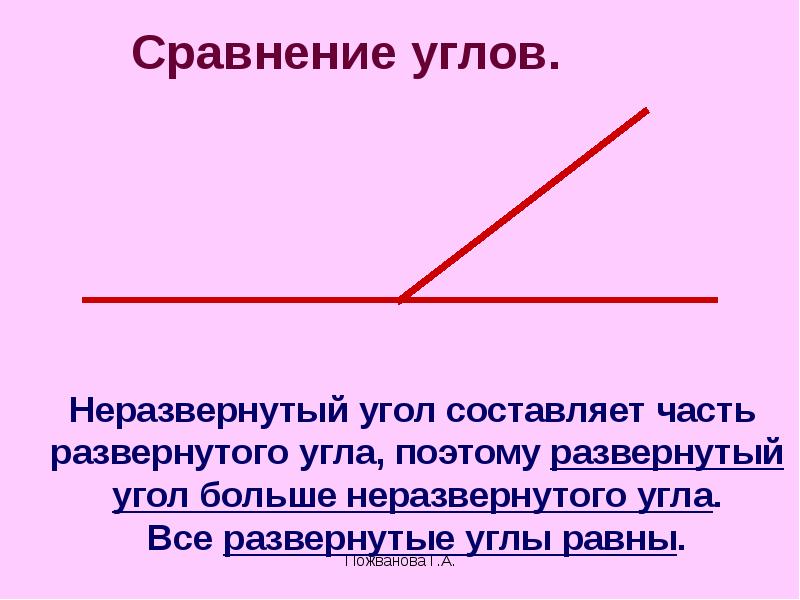 Для удобства прямой угол обозначается уголком. Вот так:
Для удобства прямой угол обозначается уголком. Вот так:
На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.
Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол показано на первой картинке.
Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.
Тупой угол — это угол, который больше прямого угла, но меньше развернутого:
Выпуклый угол — это угол, который больше развернутого угла, но меньше полного:
180° < выпуклый угол < 360°.
Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.
Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.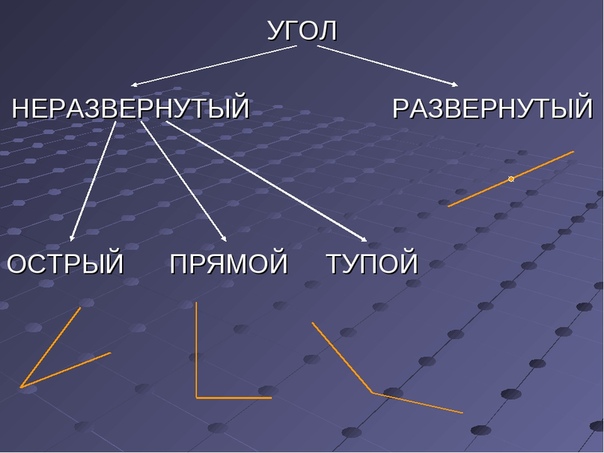
На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.
Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.
Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:
- ∠AOC = ∠AOB — ∠COB,
- ∠COB = ∠AOB — ∠AOC.
Сравнение углов
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:
При этом развернутые углы всегда являются равными.
Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:
- Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.

- Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.
Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶<∠𝑀𝑁𝐾.
Сравнить углы можно также, измерив их величины. Для этого понадобится специальный инструмент для построения и измерения углов — транспортир. Вот, как он выглядит:
Как правильно измерять углы
Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Обозначается — 0.
Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.
Минута — 1/60 часть градуса. Обозначается — ´.
Секунда — 1/60 часть минуты. Обозначается — ´´.
Градус состоит из 3600 секунд, то есть: 1° = 60′ = 3600′.
Как происходит измерение угла: сначала измеряются стороны угла, а после его внутренняя область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.
Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠ A O B = ∠ A O C + ∠ D O B = 45° + 30° + 60° = 135 °.
Угол называется прямым, если он равен 90°, а острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол имеет 180°.
Равные углы имеют равную градусную меру.
Обозначение углов на чертеже
Чертеж помогает решать задачки по геометрии в разы быстрее.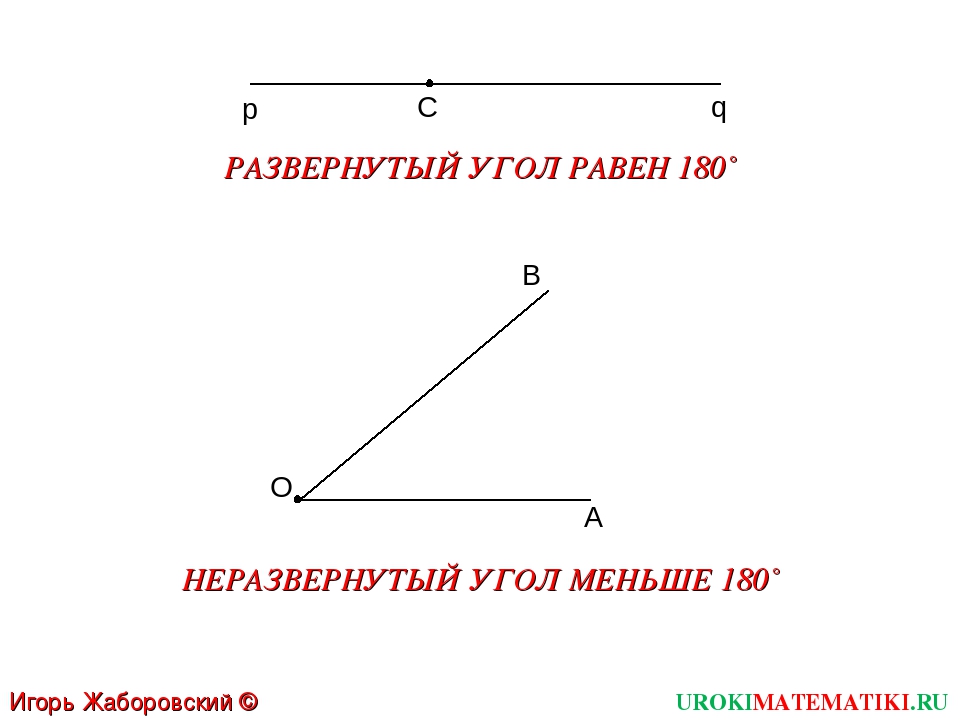 Чтобы наглядно изображать дуги, углы и прочие фигурки, придумали даже отдельное направление — геометрический чертеж.
Чтобы наглядно изображать дуги, углы и прочие фигурки, придумали даже отдельное направление — геометрический чертеж.
Задачи с углами могут быть разными и не всегда есть возможность правильно изобразить и отметить угол. Вот, что важно запомнить при обозначении лучей и углов:
- Равные углы обозначают одинаковым количеством дуг.
- Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.
- Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.
На чертеже отмечены острые, равные и неравные углы.
Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом необязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.
Вникать во все тонкости математической вселенной комфортнее с внимательным наставником. Наши учителя объяснят сложную тему, ответят на неловкие вопросы и вдохновят ребенка учиться. А красочная платформа с увлекательными заданиями поможет заниматься современно и в удовольствие.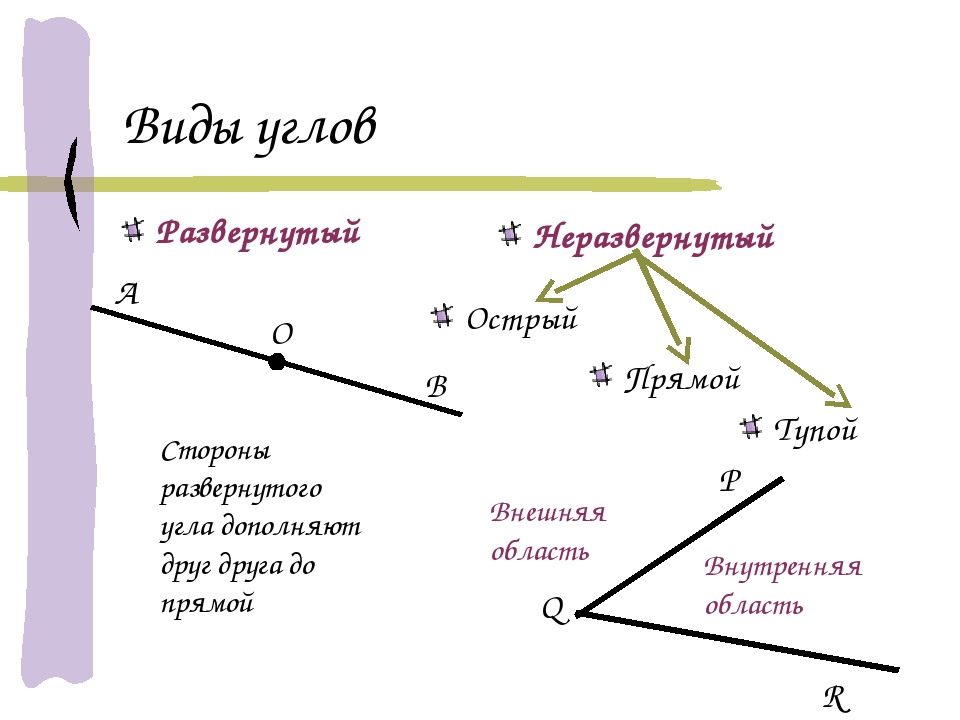
понятие, определение и виды углов на рисунках
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О, и сторонами k и m.
На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.
Развернутый и неразвернутый угол
Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла.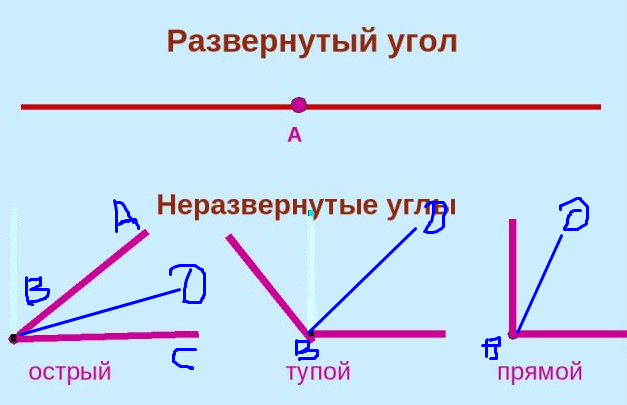 На рисунке нижк представлен развернутый угол О.
На рисунке нижк представлен развернутый угол О.
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.
Измерение углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус. Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
1. Острый угол — градусная мера от 0 до 90 градусов.
2. Прямой угол — градусная мера 90 градусов.
3. Тупой угол — градусная мера больше 90 градусов.
Нужна помощь в учебе?
Предыдущая тема: Луч: понятие, сущность, примеры и задача
Следующая тема:   Равенство геометрических фигур: определение и примеры
Чему равен открытый угол. Развернутый, тупой, вертикальный и неразвернутый: виды углов геометрии
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L , в радианах — отношение длины дуги s к радиусу r ; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.
1 оборот = 2π радианам = 360° = 400 градам .
В морской терминологии углы обозначаются румбами .
Типы углов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation . 2010 .
Смотреть что такое «Развернутый угол» в других словарях:
Угол, равный двум прямым. *РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. Развертка кривой см. Эвольвента … Большой Энциклопедический словарь
угол — ▲ разность направление (в пространстве) угол протяженность поворота от одного направления к другому; разность направлений; часть полного оборота (# наклона. образовывать #). наклон. наклонный. отклонение. уклониться (дорога уклонилась вправо).… …
Угол — Углы: 1 общего вида; 2 смежные; 3 прилежащие; 4 вертикальные; 5 развернутый; 6 прямой, острый и тупой; 7 между кривыми; 8 между прямой и плоскостью; 9 между скрещивающимися прямыми (не лежащими в одной плоскостью) прямыми. УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь
УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь
Геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У. Фигура делит плоскость… … Математическая энциклопедия
Угол, равный двум прямым. * * * РАЗВЕРНУТЫЙ УГОЛ РАЗВЕРНУТЫЙ УГОЛ, угол, равный двум прямым … Энциклопедический словарь
Раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
1) Замкнутая ломаная линия, именно: если различные точки, никакие последовательные три из к рых не лежат на одной прямой, то совокупность отрезков наз. многоугольником (см. рис. 1). М. могут быть пространственными или плоскими (ниже… … Математическая энциклопедия
поперек — ▲ под углом максимум, косой угол поперечный. поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка
поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка
градус — а, м. 1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка
Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Очень важной с практической точки зрения является проблема о конформном… … Википедия
Что такое угол?
Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160).
Лучи, образующие угол , называют сторонами угла, а точку, из которой они выходят, — вершиной угла.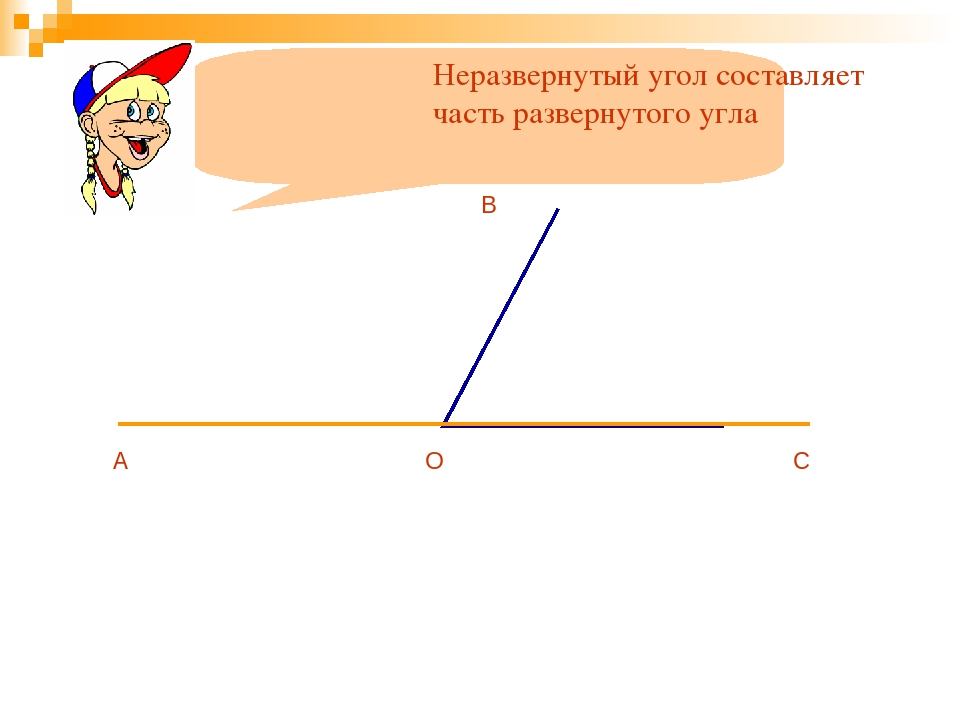
На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.
При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины.
Например, вместо «угол АОВ» пишут короче: «угол О».
Вместо слова «угол» пишут знак .
Например, AОВ, O.
На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки М и Н — на сторонах угла.
Как и все геометрические фигуры, углы сравниваются с помощью наложения.
Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.
Например, на рисунке 162 ABC = MNK.
Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК.
Пишут: COP
Прямой и развернутый угол
Два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. 164).
164).
Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165).
Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166).
Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми.
Прямым углом называют половину развернутого угла.
Чертежный треугольник
Для построения прямого угла пользуются чертежным треугольником (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо:
а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА;
б) провести вдоль второй стороны треугольника луч ОВ.
В результате получим прямой угол АОВ.
Вопросы к теме
1.Что такое угол?
2.Какой угол называют развернутым?
3.Какие углы называют равными?
4.Какой угол называют прямым?
5.Как строят прямой угол с помощью чертежного треугольника?
Нам с вами уже известно, что любой угол делит плоскость на две части. Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О.
Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных.
Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла.
А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым.
Свойства развернутого угла
Развернутый угол обладает такими свойствами:
Во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую;
во-вторых, развернутый угол равен 180°;
в-третьих, два смежных угла образуют развернутый угол;
в-четвертых, развернутый угол составляет половину полного угла;
в-пятых, полный угол будет равен сумме двух развёрнутых углов;
в-шестых, половина развернутого угла составляет прямой угол.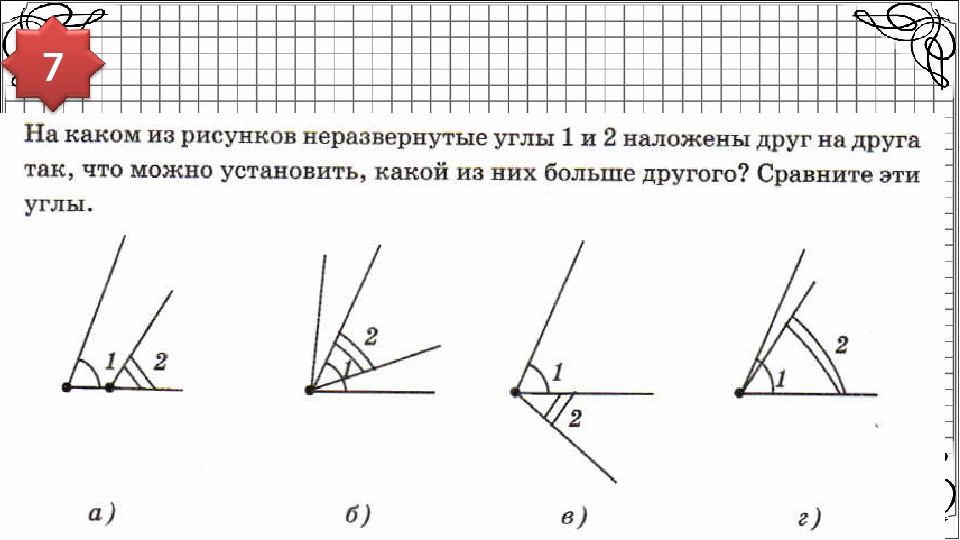
Измерение углов
Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам.
То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид: « ° ».
Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным.
А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360: 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°. Это и есть развернутый угол.
Мы с вами получили угол, который равен полуплоскости круга и имеет 180°. Это и есть развернутый угол.
Практическое задание
1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения.
1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость ?
1615. Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
1616. Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD.
1617. Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а еще за 15 мин — на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170).
1618. Изобразите с помощью чертежного треугольника 4 прямых угла в разных положениях.
1619. С помощью чертежного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения.
Запишите их обозначения.
1620. Укажите прямые углы в классной комнате.
а) 0,09 200; б) 208 0,4; в) 130 0,1 + 80 0,1.
1629. Сколько процентов от 400 составляет число 200; 100; 4; 40; 80; 400; 600?
1630. Найдите пропущенное число:
а) 2 5 3 б) 2 3 5
13 6 12 1
2 3? 42?
1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года?
1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?
1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
1635. Найдите с помощью микрокалькулятора:
а) 4,5% от 168; в) 28,3% от 569,8;
б) 147,6% от 2500; г) 0,09% от 456 800.
1636. Решите задачу:
1) Площадь огорода 6,4 а. В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось?
1637. Выполните действия:
1) ((23,79: 7,8 — 6,8: 17) 3,04 — 2,04) 0,85;
2) (3,42: 0,57 9,5 — 6,6) : ((4,8 — 1,6) (3,1 + 0,05)).
1638. Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла.
1639. Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК.Какая точка лежит внутри угла АМВ> но вне угла АМК.Какие точки лежат на сторонах угла АМК?
1640. Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь.
1642. Найдите значение выражения:
а) 14,791: а + 160,961: b, если а = 100, b = 10;
б) 361,62с + 1848: d, если с = 100, d =100.
1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий во второй день?
1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке?
1645. Грузовики в первый день проехали 24% намеченного пути, во второй день — 46% пути, а в третий — остальные 450 км. Сколько километров проехали эти грузовики?
1646. Найдите, сколько составляют:
а) 1% от тонны; в) 5% от 7 т;
б) 1% от литра; г) 6% от 80 км.
1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т?
1648.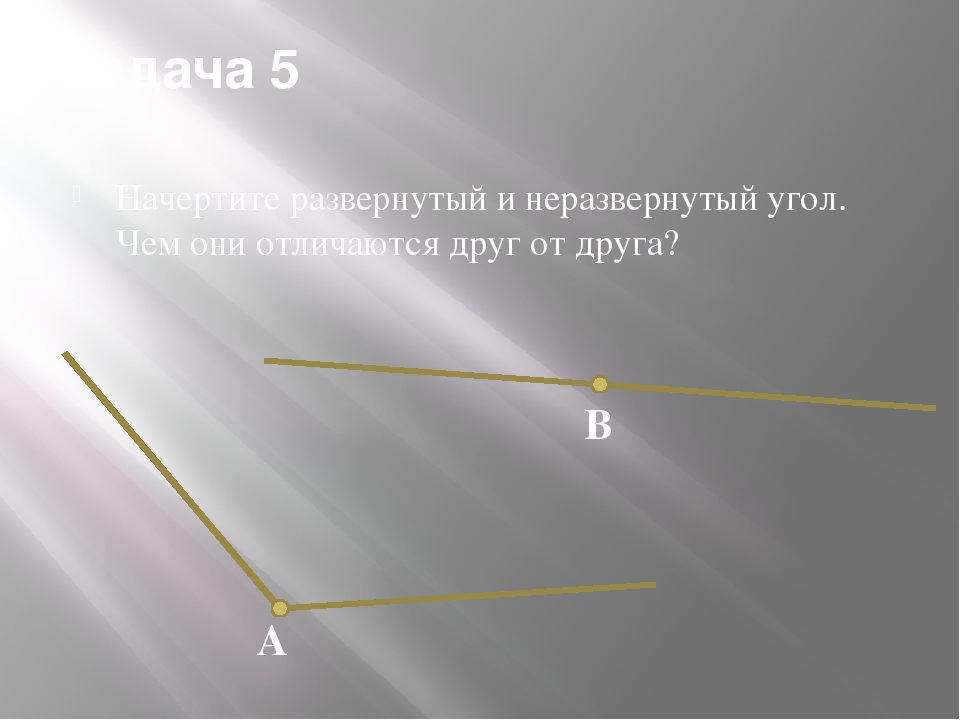 Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m .
На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.
Развернутый и неразвернутый угол
Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.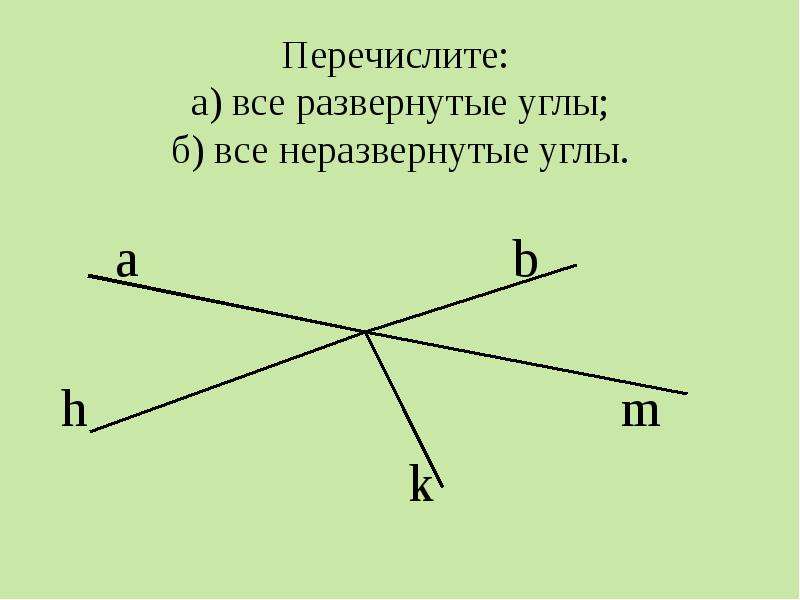
Измерение углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус . Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L , в радианах — отношение длины дуги s к радиусу r ; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.
1 оборот = 2π радианам = 360° = 400 градам .
В морской терминологии углы обозначаются румбами .
Типы углов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation
. 2010
.
2010
.
Смотреть что такое «Полный угол» в других словарях:
Неузаконенная внесистемная ед. плоского угла. 1 П. у.= 2ПИ рад 6.283 185 рад (см. Радиан) … Большой энциклопедический политехнический словарь
Угол вертикальной наводки ствола орудия при стрельбе с учетом углов качки корабля. Определяется приборами центрального артиллерийского поста. EdwART. Толковый Военно морской Словарь, 2010 … Морской словарь
Угол горизонтальной наводки ствола орудия при стрельбе с учетом углов качки корабля. Определяется ߑؐѐޑАܐؠцентрального артиллерийского поста. EdwART. Толковый Военно морской Словарь, 2010 … Морской словарь
полный механический угол поворота подвижной системы переменного резистора — полный механический угол поворота Полный угол поворота подвижной системы переменного резистора от упора до упора. Примечание Для резисторов, не имеющих упоров, полный механический угол равен максимальному углу между двумя положениями подвижной… … Справочник технического переводчика
Полный механический угол поворота подвижной системы переменного резистора — 52. Полный механический угол поворота подвижной системы переменного резистора Полный механический угол поворота D. Mechanischer Drehwinkel E. Total mechanical rotation F. Course mécanique totale Полный угол поворота подвижной системы переменного… … Словарь-справочник терминов нормативно-технической документации
Полный механический угол поворота подвижной системы переменного резистора Полный механический угол поворота D. Mechanischer Drehwinkel E. Total mechanical rotation F. Course mécanique totale Полный угол поворота подвижной системы переменного… … Словарь-справочник терминов нормативно-технической документации
УГОЛ — (1) атаки угол между направлением воздушного потока, набегающего на крыло самолёта, и хордой сечения крыла. От этого угла зависит значение подъёмной силы. Угол, при котором подъёмная сила максимальна, называется критическим углом атаки. У… … Большая политехническая энциклопедия
УГОЛ, мера наклона между двумя прямыми линиями или плоскостями, а также величины вращательного движения. Полный круг делится на 360° (градусов) иди на 2p радиан. Прямой угол составляет 90° или p/2 радиан. Один градус подразделяется на 60 (минут) … Научно-технический энциклопедический словарь
Элементы: Drop прыжок с высоты, выполняется с места или из позиции cat leap. Амортизировать падение можно только ногами, или ногами и руками (ну или одной рукой). Spring прыжок через какое либо препятствие, не касаясь его. Например, перелёт через … Википедия
Spring прыжок через какое либо препятствие, не касаясь его. Например, перелёт через … Википедия
Идти в полную. Жарг. угол. Признаваться в совершении преступления. Балдаев 1, 169. Два полных, третий не целый. Новг. Ирон. О небольшом количестве людей где л. НОС 2, 76 …
Жарг. угол. Одобр. Всё в порядке, дела идут хорошо. Б., 159; Быков, 202. /i> Вероятно, из идиш или иврита, где слово является оценкой высшего качества. Елистратов 1994, 537 … Большой словарь русских поговорок
С понятием угол учащиеся знакомятся еще в начальной школе. Но как геометрическую фигуру, имеющую определенные свойства, начинают изучать его с 7-го класса в геометрии. Кажется, довольно простая фигура , что о ней можно сказать. Но, приобретая новые знания, школьники всё больше понимают, что можно узнать о ней довольно интересные факты.
Вконтакте
Когда изучаются
Школьный курс геометрии разделён на два раздела: планиметрию и стереометрию. В каждом из них немалое внимание уделяется углам :
- В планиметрии дается их основное понятие, происходит знакомство с их видами по величине.
 Более подробно изучаются свойства каждого вида треугольников. Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей.
Более подробно изучаются свойства каждого вида треугольников. Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей. - В стереометрии изучаются пространственные углы – двугранные и трехгранные.
Внимание! В данной статье рассматриваются все виды и свойства углов именно в планиметрии.
Определение и измерение
Приступая к изучению, первоначально определяют, что такое угол в планиметрии.
Если на плоскости взять определённую точку и провести от нее два произвольных луча, то получим геометрическую фигуру – угол, состоящую из следующих элементов:
- вершина – та точка, из которой и проводились лучи, обозначается заглавной буквой латинского алфавита;
- стороны – полупрямые, проведенные из вершины.
Все элементы, образующие рассматриваемую нами фигуру, разбивают плоскость на две части :
- внутренняя — в планиметрии не превышает 180 градусов;
- внешняя.

Принцип измерения углов в планиметрии объясняют на интуитивной основе. Для начала знакомят учащихся с понятием развернутый угол.
Важно! Угол называется развернутым, если полупрямые, выходящие из его вершины, образуют прямую линию. Неразвернутый угол это все остальные случаи.
Если его разделить на 180 равных частей, то принято считать меру одной части равной 10. В таком случае говорят, что измерение производится в градусах, а градусная мера такой фигуры составляет 180 градусов.
Основные виды
Виды углов подразделяются по таким критериям, как градусная мера, характер их образования и представленные ниже категории.
По величине
Учитывая величину, углы разделяют на:
- развернутый;
- прямой;
- тупой;
- острый.
Какой угол называется развернутым, было представлено выше. Определимся с понятием прямого.
Его можно получить при делении развернутого на две равные части. В этом случае легко ответить на вопрос: прямой угол, сколько градусов составляет?
180 градусов развернутого делим на 2 и получаем, что прямой угол равен 90 градусам . Это замечательная фигура, так как многие факты в геометрии связаны именно с ней.
Это замечательная фигура, так как многие факты в геометрии связаны именно с ней.
Имеет она и свои особенности в обозначении. Чтобы на рисунке показать прямой угол, его обозначают не дугой, а квадратиком.
Углы, которые получаются при делении произвольным лучом прямого, называют острыми. По логике вещей следует, что острый угол меньше прямого, но его мера отлична от 0 градусов. То есть, он имеет величину от 0 до 90 градусов.
Тупой угол больше прямого, но меньше развернутого. Его градусная мера варьируется в интервале от 90 до 180 градусов.
Данный элемент можно разбить на разные виды рассматриваемых фигур, исключая развёрнутый.
Вне зависимости от того, как разбивается неразвернутый угол, всегда пользуются базовой аксиомой планиметрии — «основное свойство измерения».
При разделении угла одним лучом или несколькими, градусная мера данной фигуры равна сумме мер углов, на которые она разбита.
На уровне 7-го класса виды углов по их величине на этом заканчиваются. Но для повышения эрудиции можно добавить, что существуют и другие разновидности, которые обладают градусной мерой больше 180 градусов.Их называют выпуклыми.
Но для повышения эрудиции можно добавить, что существуют и другие разновидности, которые обладают градусной мерой больше 180 градусов.Их называют выпуклыми.
Фигуры при пересечении прямых
Следующие типы углов, с которыми знакомятся учащиеся – элементы, образованные при пересечении двух прямых. Фигуры, которые размещаются друг напротив друга, называют вертикальными. Их отличительное свойство – они равны.
Элементы, которые прилегают к одной и той же прямой, называют смежными. Теорема, отображающая их свойство, говорит о том, что смежные углы в сумме дают 180 градусов .
Элементы в треугольнике
Если рассматривать фигуру как элемент в треугольнике, то углы подразделяют на внутренний и внешний. Треугольник ограничен тремя отрезками и состоит из трёх вершин. Углы, расположенные внутри треугольника при каждой вершине, называют внутренними .
Если взять любой внутренний элемент при любой вершине и продлить любую сторону, то угол, который образовался и является смежным с внутренним, называется внешним.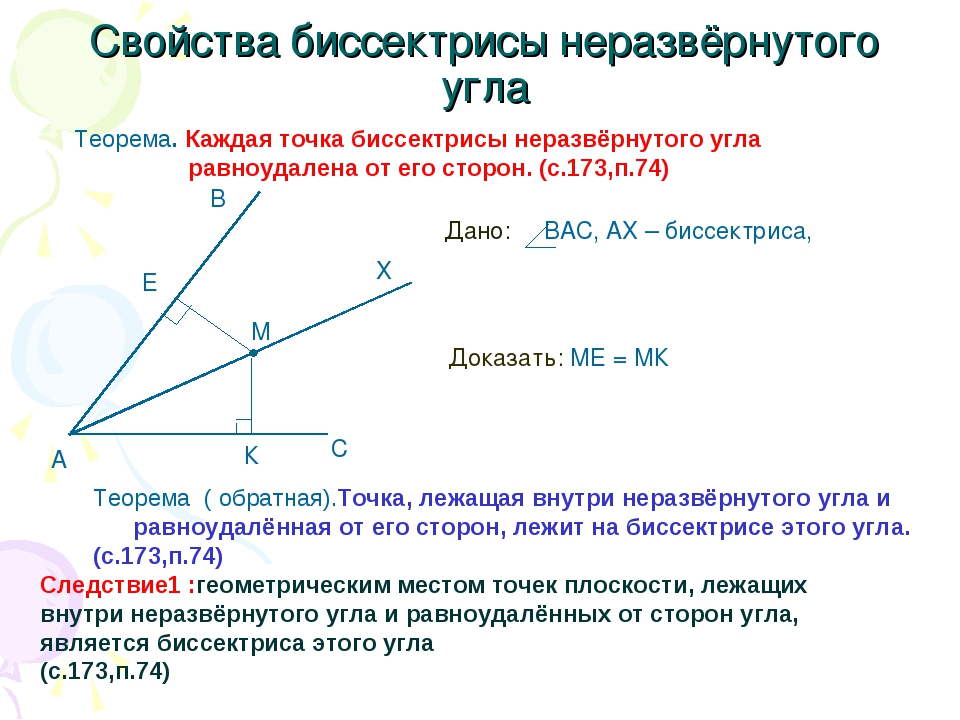 Эта пара элементов имеет следующее свойство: их сумма равна 180 градусам.
Эта пара элементов имеет следующее свойство: их сумма равна 180 градусам.
Пересечение двух прямых секущей
Пересечение прямых
При пересечении двух прямых секущей также образуются углы , которые принято распределять по парам. Каждая пара элементов имеет свое название. Выглядит это следующим образом:
- внутренние накрест лежащие:∟4 и ∟6, ∟3 и ∟5;
- внутренние односторонние: ∟4 и ∟5, ∟3 и ∟6;
- соответствующие: ∟1 и ∟5, ∟2 и ∟6, ∟4 и ∟8, ∟3 и ∟7.
В том случае, когда секущая пересекает две
Три неразвернутых угла и один развернутый. Развернутый, тупой, вертикальный и неразвернутый: виды углов геометрии
С понятием угол учащиеся знакомятся еще в начальной школе. Но как геометрическую фигуру, имеющую определенные свойства, начинают изучать его с 7-го класса в геометрии. Кажется, довольно простая фигура , что о ней можно сказать. Но, приобретая новые знания, школьники всё больше понимают, что можно узнать о ней довольно интересные факты.
Вконтакте
Когда изучаются
Школьный курс геометрии разделён на два раздела: планиметрию и стереометрию. В каждом из них немалое внимание уделяется углам :
- В планиметрии дается их основное понятие, происходит знакомство с их видами по величине. Более подробно изучаются свойства каждого вида треугольников. Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей.
- В стереометрии изучаются пространственные углы – двугранные и трехгранные.
Внимание! В данной статье рассматриваются все виды и свойства углов именно в планиметрии.
Определение и измерение
Приступая к изучению, первоначально определяют, что такое угол в планиметрии.
Если на плоскости взять определённую точку и провести от нее два произвольных луча, то получим геометрическую фигуру – угол, состоящую из следующих элементов:
- вершина – та точка, из которой и проводились лучи, обозначается заглавной буквой латинского алфавита;
- стороны – полупрямые, проведенные из вершины.

Все элементы, образующие рассматриваемую нами фигуру, разбивают плоскость на две части :
- внутренняя — в планиметрии не превышает 180 градусов;
- внешняя.
Принцип измерения углов в планиметрии объясняют на интуитивной основе. Для начала знакомят учащихся с понятием развернутый угол.
Важно! Угол называется развернутым, если полупрямые, выходящие из его вершины, образуют прямую линию. Неразвернутый угол это все остальные случаи.
Если его разделить на 180 равных частей, то принято считать меру одной части равной 10. В таком случае говорят, что измерение производится в градусах, а градусная мера такой фигуры составляет 180 градусов.
Основные виды
Виды углов подразделяются по таким критериям, как градусная мера, характер их образования и представленные ниже категории.
По величине
Учитывая величину, углы разделяют на:
- развернутый;
- прямой;
- тупой;
- острый.

Какой угол называется развернутым, было представлено выше. Определимся с понятием прямого.
Его можно получить при делении развернутого на две равные части. В этом случае легко ответить на вопрос: прямой угол, сколько градусов составляет?
180 градусов развернутого делим на 2 и получаем, что прямой угол равен 90 градусам . Это замечательная фигура, так как многие факты в геометрии связаны именно с ней.
Имеет она и свои особенности в обозначении. Чтобы на рисунке показать прямой угол, его обозначают не дугой, а квадратиком.
Углы, которые получаются при делении произвольным лучом прямого, называют острыми. По логике вещей следует, что острый угол меньше прямого, но его мера отлична от 0 градусов. То есть, он имеет величину от 0 до 90 градусов.
Тупой угол больше прямого, но меньше развернутого. Его градусная мера варьируется в интервале от 90 до 180 градусов.
Данный элемент можно разбить на разные виды рассматриваемых фигур, исключая развёрнутый.
Вне зависимости от того, как разбивается неразвернутый угол, всегда пользуются базовой аксиомой планиметрии — «основное свойство измерения».
При разделении угла одним лучом или несколькими, градусная мера данной фигуры равна сумме мер углов, на которые она разбита.
На уровне 7-го класса виды углов по их величине на этом заканчиваются. Но для повышения эрудиции можно добавить, что существуют и другие разновидности, которые обладают градусной мерой больше 180 градусов.Их называют выпуклыми.
Фигуры при пересечении прямых
Следующие типы углов, с которыми знакомятся учащиеся – элементы, образованные при пересечении двух прямых. Фигуры, которые размещаются друг напротив друга, называют вертикальными. Их отличительное свойство – они равны.
Элементы, которые прилегают к одной и той же прямой, называют смежными. Теорема, отображающая их свойство, говорит о том, что смежные углы в сумме дают 180 градусов .
Элементы в треугольнике
Если рассматривать фигуру как элемент в треугольнике, то углы подразделяют на внутренний и внешний.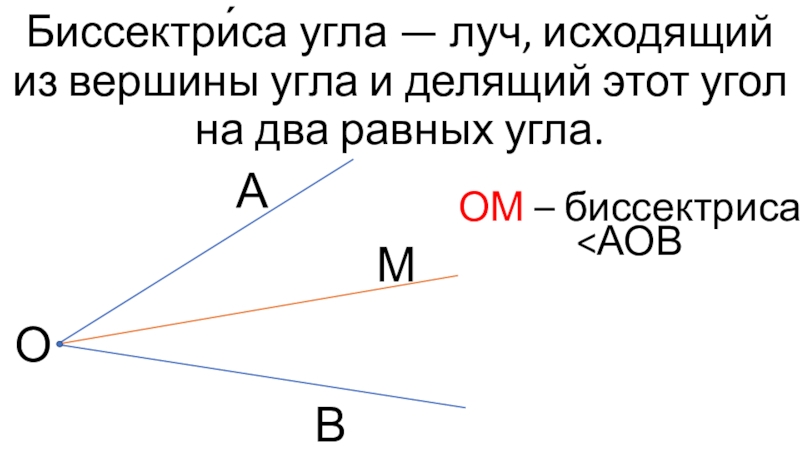 Треугольник ограничен тремя отрезками и состоит из трёх вершин. Углы, расположенные внутри треугольника при каждой вершине, называют внутренними .
Треугольник ограничен тремя отрезками и состоит из трёх вершин. Углы, расположенные внутри треугольника при каждой вершине, называют внутренними .
Если взять любой внутренний элемент при любой вершине и продлить любую сторону, то угол, который образовался и является смежным с внутренним, называется внешним. Эта пара элементов имеет следующее свойство: их сумма равна 180 градусам.
Пересечение двух прямых секущей
Пересечение прямых
При пересечении двух прямых секущей также образуются углы , которые принято распределять по парам. Каждая пара элементов имеет свое название. Выглядит это следующим образом:
- внутренние накрест лежащие:∟4 и ∟6, ∟3 и ∟5;
- внутренние односторонние: ∟4 и ∟5, ∟3 и ∟6;
- соответствующие: ∟1 и ∟5, ∟2 и ∟6, ∟4 и ∟8, ∟3 и ∟7.
В том случае, когда секущая пересекает две прямые, все эти пары углов имеют определённые свойства:
- Внутренние накрест лежащие и соответственные фигуры между собой равны.

- Внутренние односторонние элементы в сумме дают 180 градусов.
Изучаем углы в геометрии, их свойства
Виды углов в математике
Вывод
В этой статье представлены все основные виды углов, которые встречаются в планиметрии и изучаются в седьмом классе. Во всех последующих курсах свойства, касающихся всех рассмотренных элементов, являются основой для дальнейшего изучения геометрии. К примеру, изучая , необходимо будет вспомнить все свойства углов, образованных при пересечении двух параллельных прямых секущей. При изучении особенностей треугольников, необходимо вспомнить, что такое смежные углы. Перейдя в стереометрию, все объёмные фигуры будут изучаться и строиться, опираясь на планиметрические фигуры.
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m .
На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.
Развернутый и неразвернутый угол
Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.
Измерение углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус . Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
Давайте начнем с определения того, что такое угол. Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:
Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:
Градусная мера всегда больше 90 о, но меньше 180 о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:
Градусная мера острого угла всегда меньше 90 о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Развернутый
Развернутый угол имеет такой вид:
В многоугольниках он не встречается, но не менее важен, чем все остальные.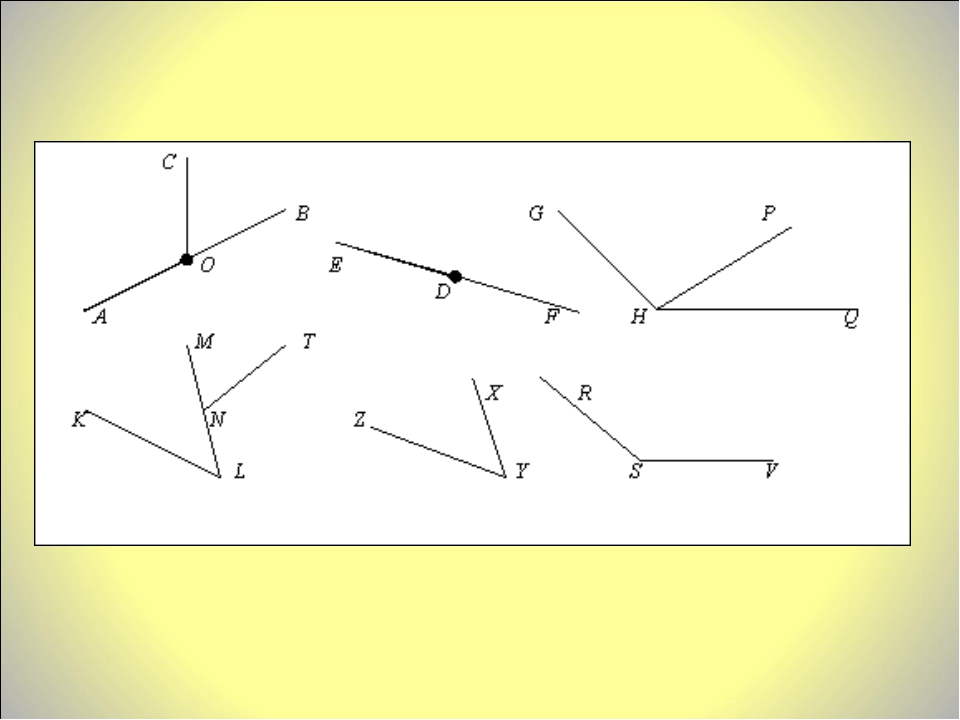 Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Он выглядит так:
Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о, 90 о, 180 о, 270 о.
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о.
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно.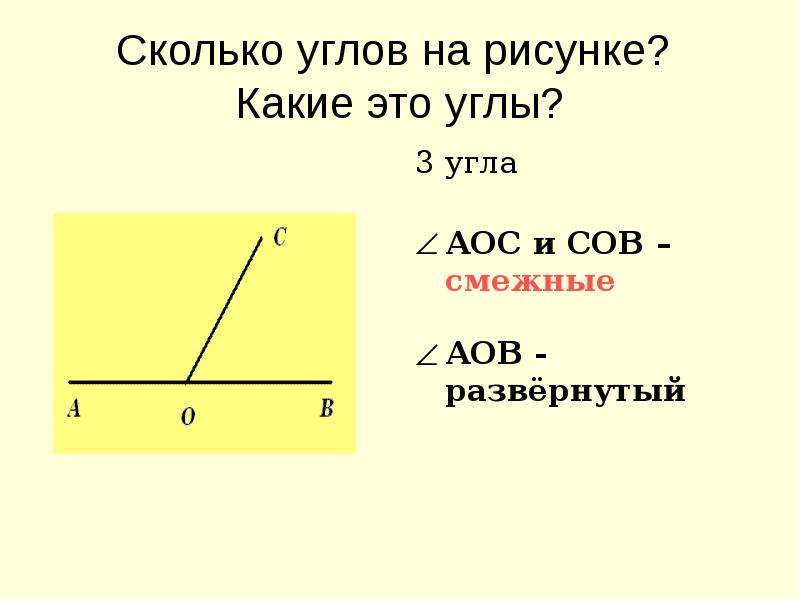
5. Полный
Полным является угол с градусной мерой 360 о.
Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные
Это два острых угла, образовывающие один прямой, т.е. их сумма 90 о.
2. Смежные
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о.
3. Вертикальные
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный
Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.
2. Вписанный
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
В этой статье будет рассматриваться одна из основных геометрических фигур — угол. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.
Введение в понятие геометрического угла
В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него.
Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии — это точка, прямая на плоскости и собственно сама плоскость. Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца.
Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца.
Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом. Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Виды углов и геометрии
Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии:
- Прямой угол. Он характеризируется величиной в 90 градусов, а значит, его стороны всегда перпендикулярны между собой.
- Острый угол. К таким углам относятся все их представители, имеющие размер меньше 90 градусов.
- Тупой угол. Здесь же могут быть все углы с величиной от 90 до 180 градусов.

- Развернутый угол. Имеет размер строго 180 градусов и внешне его стороны составляют одну прямую.
Понятие развернутого угла
Теперь давайте рассмотрим развернутый угол более подробно. Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.
Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными.
Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов. Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой — тупым.
Свойства развернутых углов
Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке:
- Стороны развернутого угла антипараллельны и составляют прямую.
- Величина развернутого угла всегда составляет 180˚.
- Два смежных угла вместе всегда составляют развернутый угол.
- Полный угол, который составляет 360˚, состоит из двух развернутых и равен их суме.
- Половина развернутого угла — это прямой угол.
Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач.
Задачи с развернутыми углами
Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.
- Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
- Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
- Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
- Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4.
 Вычислите полученные углы.
Вычислите полученные углы.
Решения и ответы:
- Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.
- Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.
- Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
- Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х. Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚.
 Ответ: 36˚ и 144˚.
Ответ: 36˚ и 144˚.
Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.
Угол
Определение угла
Определение 1. Угол − это геометрическая фигура,которая состоит из двух лучей, исходящих из одной точки.
Лучи называются сторонами угла, а их общее начало − вершиной угла.
Обозначение угла
На рисунке 1 изображен угол с вершиной O и сторонами m и n. Данный угол обозначают \( \small ∠mn \) или \( \small ∠O. \) Если на сторонах угла выбрать точки A и B, то угол можно обозачить так: \( \small ∠AOB \) или \( \small ∠BOA. \)
Развернутый угол. Внутренняя и внешняя область угла
Угол называется развернутым, если его стороны находятся на одной прямой. На рисунке 2 изображен развернутый угол с вершиной А и сторонами m и n.
Любой угол разделяет плоскость на две части. Если угол неразвернутый, то меньшая из частей называется внутренней областью, а другая − внешней областью этого угла (Рис.3).
Если угол развернутый, то любую из двух частей, на которые разделяет угол данную плоскось можно считать внутренней областью угла.
Фигуру, состоящую из угла и его внутренней области также называют углом.
На рисунке 4 точки P и Q лежат внутри угла mn (т.е. во внутренней области угла), точки R и S лежат вне угла mn (т.е. во внешней области угла), а точки A и B на сторонах этого угла.
Типы углов
В зависимости от величин, углы бывают следующих типов (Рис.5):
- Нулевой угол (0°). Стороны угла совпадают. Его внутренняя область пустое множество.
- Острый угол (больше 0° и меньше 90°)
- Прямой угол (90°). Стороны прямого угла перпендикулярны друг другу.

- Тупой угол (больше 90° и меньше 180°).
- Развернутый угол (180°).
- Невыпуклый угол (от 0° до 180° включительно).
- Выпуклый угол (больше 180° и меньше 360°).
- Польный угол (360°).
Сравнение углов
Углы можно сравнить, то есть определить равны ли они или какой угол меньше а какой больше. Чтобы определить равны ли углы или нет нужно наложить один угол на другой так, чтобы сторона одного угла совместилась со стороной другого угла а две другие оказались по одну сторону от совместившихся сторон. Если две другие стороны также совместились, то углы полностью совместятся и,следовательно они равны. Если же эти стороны не совместяться, то меньшим считается тот угол, который является частью другой.
На рисунках 6a и 6b представлены два угла: 1 и 2. На рисунке 7 угол 2 является частью угла 1, следовательно угол 2 меньше угла 1. Это пишется так: \( \small ∠2 \lt \angle 1. \)
Градусная мера угла
Измерение углов основана на сравнении их с углом, принятым за единицу измерения. За единицей измерения углов примнимают градус, которая является \( \small \frac {1}{180} \) частью развернутого угла. Положительное число, показывающая, сколько раз градус и его части помещаются в данном угле называвется градусной мерой угла. Для измерения углов используют транспортир (Рис.8).
За единицей измерения углов примнимают градус, которая является \( \small \frac {1}{180} \) частью развернутого угла. Положительное число, показывающая, сколько раз градус и его части помещаются в данном угле называвется градусной мерой угла. Для измерения углов используют транспортир (Рис.8).
Для угла AOB, градусная мера которого равна 120° говорят «угол AOB равен 120° » и пишут: \( \small ∠AOB=120 °. \) Очевидно, что градусная мера развернутого угла равна 180°. \( \small \frac {1}{60} \) часть градуса называется минутой и обозначается так: » ‘ «. \( \small \frac {1}{60} \) часть минуты называется секундой и обозначается так: » » «. Если градусная мера угла AOB равна 56 градусов 6 минут и 43 секунды, то пишут: \( \small \angle AOB=56°6’43». \)
Отметим, что равные углы имеют равные градусные меры. Если углы разные, то меньший угол имеет меньшую градусную меру.
Неразвернутые углы фото
Понятие и виды углов
| На этом сайте вы найдете репетитора! Nado5. Оставьте заявку или позвоните нам. Мы подберем репетитора, учитывая все пожелания. Или найдите репетитора в нашей базе самостоятельно, используя фильтр слева. |
| Получите консультацию по телефону. Мы всегда рады проконсультировать Вас по вопросам образования. Задайте свои вопросы профессионалам. Больше не надо ломать голову, к кому обратиться за помощью — для этого есть Nado5.ru! |
| Наши репетиторы помогут вам. Прислушайтесь к нашим советам, чтобы найти репетитора быстрее: Совет 1. Чтобы значительно упростить процесс поиска, достаточно лишь позвонить нам, и оператор найдет репетитора, который максимально подходит под ваши требования. |
| Мы подберем репетитора бесплатно! Прислушайтесь к нашим советам, чтобы найти репетитора быстрее: Совет 2. |
| Мы найдем репетитора в течение дня! Прислушайтесь к нашим советам, чтобы найти репетитора быстрее: Совет 3. Вопреки сложившемуся мнению, студент-репетитор очень хорошо справляется со своей задачей. Он более мобилен, цена ниже, и он с легкостью найдет общий язык с учеником. |
МАТВОКС ⋆ Виды углов. Неразвернутый угол ⋆ Энциклопедия математики
Перейти к содержаниюВиды углов. Неразвернутый угол
Вы здесь:
- …
- Глава 2. Углы: виды углов…
Неразвернутый угол – это любой угол, который не является развернутым.
Неразвернутый угол – это любой угол, не равный 180°.
Когда в задачах идет речь об углах, и отдельно не оговаривается то, какие именно углы рассматриваются, то подразумеваются неразвернутые углы.
Т.е. в задачах слово «неразвернутый» пропускают.
ВОС – неразвернутый угол
Прямой угол
Угол называют прямым, если он равен 90°.
∠MBC = 90°, значит ∠MBC – прямой угол.
Острый угол
Если угол меньше 90°, то его называют острым углом.
∠AOE = 30°, значит ∠ AOE – острый угол.
Тупой угол
Если угол больше 90°, но меньше 180°, то такой угол называют тупым углом.
∠KNL = 120°, значит ∠ KNL – тупой угол.
Виды неразвернутых углов
Свойство 1
Если угол неразвернутый, то одна из частей называется внутренней, а другая внешней областью этого угла.
Внутренняя область угла выделена голубым.
Внешняя область угла выделена оранжевым
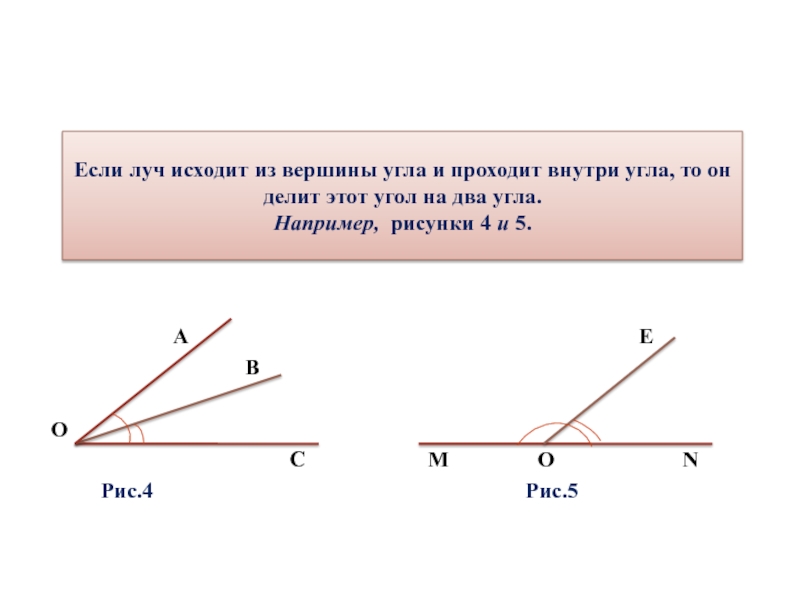
Если луч ОС исходит из вершины (О) неразвернутого угла и проходит внутри угла, то он делит этот угол АОВ на два угла – угол АОС и угол СОВ или ∠АОС и ∠СОВ.
Свойство 2
Go to TopЭтот сайт использует файлы cookies для более комфортной работы пользователя. Продолжая просмотр страниц сайта, вы соглашаетесь с использованием файлов cookies. Если вам нужна дополнительная информация , пожалуйста, посетите страницу Политика Конфиденциальности Принять
Продолжая просмотр страниц сайта, вы соглашаетесь с использованием файлов cookies. Если вам нужна дополнительная информация , пожалуйста, посетите страницу Политика Конфиденциальности Принять
Privacy & Cookies Policy
Виды углов
- Смежные углы
- Вертикальные углы
Каждый угол, в зависимости от его величины, имеет своё название:
| Острый | Меньше 90° | |
| Прямой | Равен 90°. На чертеже прямой угол, обычно обозначают символом , проведённым от одной стороны угла до другой. | |
| Тупой | Больше 90°, но меньше 180° | |
| Развёрнутый | Равен 180° Развёрнутый угол равен сумме двух прямых углов, а прямой угол составляет половину развёрнутого угла. | |
| Выпуклый | Больше 180°, но меньше 360° | |
| Полный | Равен 360° |
Смежные углы
Два угла называются смежными, если у них одна сторона общая, а две другие стороны составляют прямую линию:
Углы MOP и PON смежные, так как луч OP – общая сторона, а две другие стороны – OM и ON составляют прямую.
Общая сторона смежных углов называется наклонной к прямой, на которой лежат две другие стороны, только в том случае, когда смежные углы не равны между собой. Если смежные углы равны, то их общая сторона будет перпендикуляром.
Сумма смежных углов равна 180°.
Два угла называются вертикальными, если стороны одного угла дополняют до прямых линий стороны другого угла:
Углы 1 и 3, а также углы 2 и 4 – вертикальные.
Вертикальные углы равны.
Докажем, что вертикальные углы равны:
Сумма ∠1 и ∠2 составляет развёрнутый угол. И сумма ∠3 и ∠2 составляет развёрнутый угол. Значит, эти две суммы равны:
∠1 + ∠2 = ∠3 + ∠2.
В этом равенстве слева и справа есть по одинаковому слагаемому – ∠2. Равенство не нарушится, если это слагаемое в левой и в правой части опустить. Тогда мы получаем:
∠1 = ∠3.
Развернутый угол
Определение.
Развернутый угол — это угол, стороны которого лежат на одной прямой.
Градусная мера развёрнутого угла равна 180º.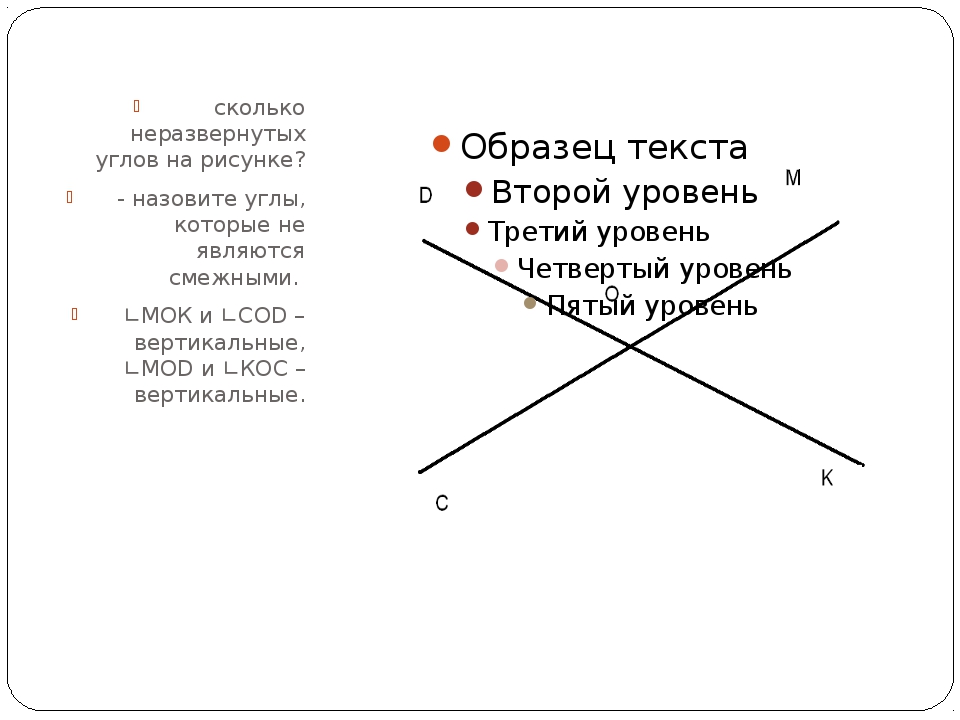
Каждая сторона развернутого угла дополняет другую сторону до прямой, то есть стороны развёрнутого угла являются дополнительными лучами.
Например, ∠CDK — развёрнутый. Точка D — вершина, лучи DK и DC — стороны угла CDK.
Чтобы нарисовать развернутый угол, достаточно провести прямую и отметить на ней точку — вершину угла.
Можно поступить иначе — сначала отметить точку — вершину угла, затем через неё провести прямую:
∠AOB — развернутый угол
Если луч делит развернутый угол на два угла, то эти углы — смежные:
Например, ∠ABD — развернутый, BC — луч,
∠ABС и ∠CBD — смежные углы.
Биссектриса развернутого угла делит его на два прямых угла.
Например, KF — биссектриса развернутого угла MKP,
∠MKF и ∠FKP — прямые углы.
определение угла, измерение углов, обозначения и примеры. Развернутый и неразвернутый угол
Давайте начнем с определения того, что такое угол.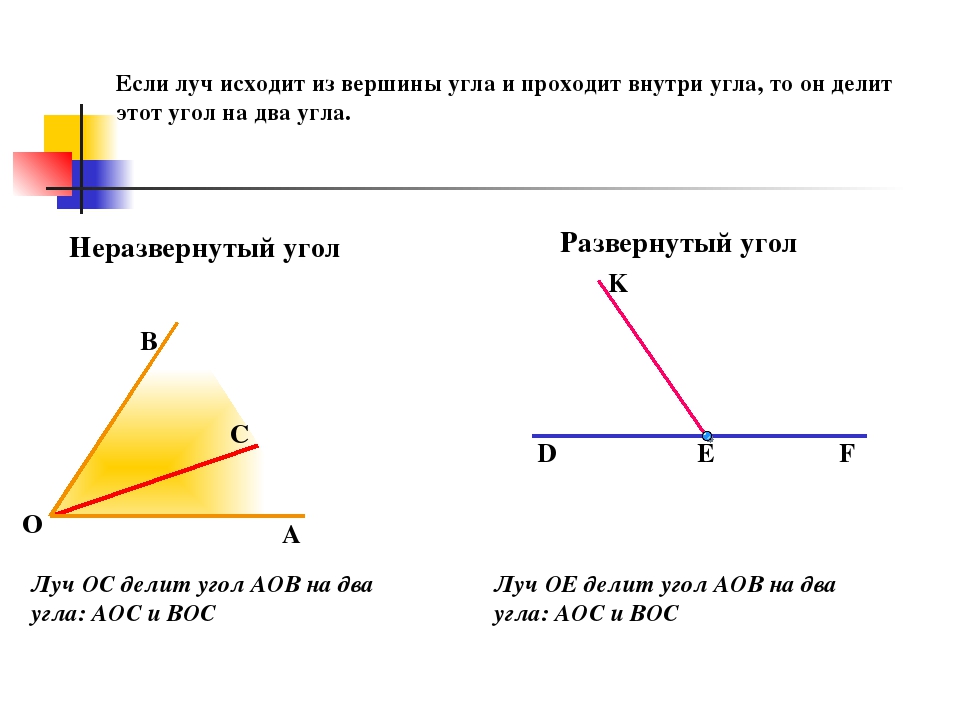 Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:
Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:
Градусная мера всегда больше 90 о, но меньше 180 о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:
Градусная мера острого угла всегда меньше 90 о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.
Развернутый
Развернутый угол имеет такой вид:
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Он выглядит так:
Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о, 90 о, 180 о, 270 о.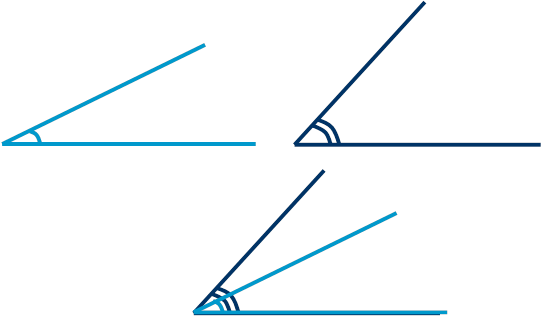
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о.
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно.
5. Полный
Полным является угол с градусной мерой 360 о.
Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные
Это два острых угла, образовывающие один прямой, т.е. их сумма 90 о.
2. Смежные
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о.
3. Вертикальные
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный
Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.
2. Вписанный
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m .
На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.
Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.
Развернутый и неразвернутый угол
Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.
Измерение углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус . Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L , в радианах — отношение длины дуги s к радиусу r ; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.
1 оборот = 2π радианам = 360° = 400 градам .
В морской терминологии углы обозначаются румбами .
Типы углов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation . 2010 .
Смотреть что такое «Развернутый угол» в других словарях:
Угол, равный двум прямым. *РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. Развертка кривой см. Эвольвента … Большой Энциклопедический словарь
угол — ▲ разность направление (в пространстве) угол протяженность поворота от одного направления к другому; разность направлений; часть полного оборота (# наклона. образовывать #). наклон. наклонный. отклонение. уклониться (дорога уклонилась вправо).… …
Угол — Углы: 1 общего вида; 2 смежные; 3 прилежащие; 4 вертикальные; 5 развернутый; 6 прямой, острый и тупой; 7 между кривыми; 8 между прямой и плоскостью; 9 между скрещивающимися прямыми (не лежащими в одной плоскостью) прямыми. УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь
Геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У. Фигура делит плоскость… … Математическая энциклопедия
Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У. Фигура делит плоскость… … Математическая энциклопедия
Угол, равный двум прямым. * * * РАЗВЕРНУТЫЙ УГОЛ РАЗВЕРНУТЫЙ УГОЛ, угол, равный двум прямым … Энциклопедический словарь
Раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
1) Замкнутая ломаная линия, именно: если различные точки, никакие последовательные три из к рых не лежат на одной прямой, то совокупность отрезков наз. многоугольником (см. рис. 1). М. могут быть пространственными или плоскими (ниже… … Математическая энциклопедия
поперек — ▲ под углом максимум, косой угол поперечный. поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка
перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка
градус — а, м. 1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка
Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Очень важной с практической точки зрения является проблема о конформном… … Википедия
«Основные понятия геометрии» — Признак равенства треугольника. Отрезки. Геометрия. Смежные и вертикальные углы. Построение параллельных прямых. Построение треугольника. Выводы. Прямые параллельны. Вершины. Простейшие геометрические фигуры. Какая фигура называется треугольником. Равные отрезки имеют равные длины. Угол – это геометрическая фигура, которая состоит из точки и двух лучей.
Угол – это геометрическая фигура, которая состоит из точки и двух лучей.
«Геометрия в таблицах» — Координаты точки и координаты вектора в пространстве Скалярное произведение векторов в пространстве Движение Цилиндр Конус Сфера и шар Объем прямоугольного параллелепипеда Объем прямой призмы и цилиндра Объем наклонной призмы Объем пирамиды Объем конуса Объем шара и площадь сферы. Таблицы геометрия.
«Геометрия 8 класс» — Каждое утверждение опирается на уже доказанные. У любого здания есть фундамент. Понятие теоремы. Аксиома -утверждение, истинность которых принимается без доказательств. Каждое математическое утверждение, получаемое путем логического доказательства, есть теорема. Так перебирая теоремы, можно добраться до аксиом.
«Геометрия это наука» — Геометрия состоит из двух разделов: планиметрии и стереометрии. Какая геометрическая фигура была отличительным знаком пифагорейцев? Какую форму, по мнению пифагорейцев, имела вся Вселенная? Ответ: 580 – 500 гг. до н. эры. Когда существовала Древняя Греция? Введение. Ответ: «Плоскомерие». Объяснение устройства мира пифагорейцы тесно связывали с геометрией.
Ответ: «Плоскомерие». Объяснение устройства мира пифагорейцы тесно связывали с геометрией.
«Геометрические термины» — Конус. Пирамида. Радиус и центр. Диагональ. Геометрия. Квадрат. Ромб. Куб. Трапеция. Возникновение геометрических терминов. Точка. Линия. Цилиндр. Гипотенуза и катет. Сфера. Призма. Из истории геометрических терминов.
«Что изучает геометрия» — Слово «параллельный» происходит от греческого «параллелос» — идти рядом. История геометрии. Преобразования в основном ограничивались подобием. L=(Р1+Р2)/2 L – длина окружности Р1 — периметр большого квадрата Р2 — периметр малого квадрата. Vпрям. Геометрия в Древней Греции. Муза геометрии, Лувр. Мы узнаем откуда пришла, и какой раньше была геометрия.
Всего в теме 24 презентации
Удерживать и складывать | Математические решения
Урок для первоклассников
Крис Конфер
Этот урок для всего класса адаптирован из раздела «Математика всеми средствами» «Геометрия» для 1–2 классов, написанного Крисом Конфером. Сложив квадрат бумаги несколькими заранее определенными способами, дети исследуют и записывают различные формы, которые они могут сделать.Это задание дает детям ценный опыт в изучении того, как формы соотносятся друг с другом.
Сложив квадрат бумаги несколькими заранее определенными способами, дети исследуют и записывают различные формы, которые они могут сделать.Это задание дает детям ценный опыт в изучении того, как формы соотносятся друг с другом.
Чтобы подготовиться к уроку, Крис вырезал для детей квадраты из копировальной бумаги. (Квадраты были около 4 дюймов со стороны.) Крис также приготовил по одному листу газетной бумаги размером 12 на 18 дюймов для каждой пары детей и большой лист диаграммной бумаги, чтобы использовать его для начертания фигур для записи класса.
Дав каждому ребенку по квадрату, Крис сказал: «Смотрите внимательно и складывайте свою бумагу, как я складываю свою.”
Крис сложила свой квадрат пополам, чтобы получился прямоугольник. Когда дети сложили свои листы, она попросила их пересчитать, чтобы убедиться в наличии четырех сторон и четырех углов. «Какой оно формы?» она спросила. (См. Рисунок 1.)
Рисунок 1.
Большинство детей ответили: «Прямоугольник».
Крис развернул прямоугольник, сложил его в другом направлении и попросил детей сделать то же самое.
«Мы хотим иметь возможность легко складывать бумагу вперед и назад, вперед и назад», — объяснила она, поворачивая складку в соответствии со своими словами.Дети поступили так же. Затем Крис попросил детей развернуть лист до полной квадратной формы.
«Сначала посмотрите, как я складываю два угла вниз, как мы делаем бумажный самолетик», — сказал Крис. (См. Рисунок 2.)
Рисунок 2.
После того, как класс сложил свои листы и посчитал стороны и углы, Крис объяснил: «Когда фигура имеет пять сторон и пять углов, она называется пятиугольником». Она попросила детей негромко произнести «пятиугольник». Затем она посоветовала им несколько раз покачивать новые складки взад и вперед.
Рисунок 3.
Затем Крис показал, как сложить оставшиеся два угла, чтобы получился квадрат меньше исходного, но у детей были свои идеи. «Это воздушный змей!» «Это алмаз». (См. Рисунок 3.)
(См. Рисунок 3.)
Крис повернула сложенный квадрат так, чтобы одна сторона была параллельна полу. «Что это за форма?» она спросила.
«Это квадрат», — ответили студенты. «Но я знаю, что это бриллиант», — настаивал Стив.
«Эта форма может выглядеть как воздушный змей или алмаз, когда я держу ее вот так», — объяснил Крис, поворачивая фигуру так, чтобы угол был направлен вверх.«Но это все равно квадрат, как бы он ни повернулся».
Затем Крис представил исследование. «Сегодня мы собираемся исследовать формы, которые можно сделать, складывая бумагу разными способами. Правило таково: вы можете сложить бумагу на один, два или несколько сгибов, но только на уже сделанных сгибах. Вы не можете делать новые складки. Проследите различные формы, которые вы найдете. Вы будете работать с партнером, обрисовывая свои формы на одном листе газетной бумаги ».
Когда Крис раздавала каждой паре студентов по листу газетной бумаги размером 12 на 18 дюймов, она спросила: «Как вы думаете, сколько форм вы найдете?»
Оценки детей колебались от двух до десяти. (На самом деле существует девять различных форм, если считать исходный квадрат; см. Диаграмму ниже, рисунок 4.)
(На самом деле существует девять различных форм, если считать исходный квадрат; см. Диаграмму ниже, рисунок 4.)
Рисунок 4.
Наблюдая за детьми
Крис распространил, когда дети начали складывать свои листы и обводить найденные формы.
Дэнни спросил: «Можем ли мы написать что-нибудь посередине?» Он указал на начертанный им пятиугольник.
«Как что?» — поинтересовался Крис.
«Супермен», — ответил он. Форма напомнила Дэнни символ на рубашке Супермена.
Другие дети решили украсить свои фигуры. Из пятиугольников выросли дымоходы и кирпичи, а из трапеций выросли колеса и выхлопные трубы, пока дети связывали формы со знакомыми объектами.
Габриэль и Стейси усердно работали и уже нарисовали шесть различных форм. «Посмотрите! Я сделала пятиугольник, — сказала Стейси, пробуя новое слово. «А в перевернутом виде это похоже на кошку», — добавила она.
Адриан также усердно работал, отслеживая свою первую форму. Хотя способности детей сильно различаются, каждый ребенок может добиться успеха в этом исследовании формы.
«Могу я сделать это?» — спросил Дэнни, показывая Крису тощий пятиугольник.
«Он отличается от форм, которые вы уже нашли?» она спросила. Крис и Дэнни посмотрели на очертания, которые он нарисовал.
«Да», — ответил Дэнни, демонстрируя, как он создал два разных пятиугольника, сложив свой квадрат по-разному.
Джози и Франциска нарисовали на своей бумаге два одинаковых квадрата. Крис сказал им: «Мне кажется, вы дважды нарисовали одну и ту же фигуру на своей бумаге.”
«Но мы сделали один квадрат, а другой ромб», — сказала Франциска.
«Мне они кажутся одинаковыми, — сказал Крис. «Они кажутся одинаковыми по размеру и форме, но этот перевернут», — указал Крис на бриллиант. Девочки кивнули и начали стирать одну из фигур.
Стив и Хавьер, казалось, закончили. «Сколько разных форм вы нашли?» — спросил Крис.
«Шесть», — ответил Стив. «Вот сколько их». Стив изначально предсказывал, что будет шесть различных форм.
«Откуда вы знаете, что их всего шесть?» — спросил Крис.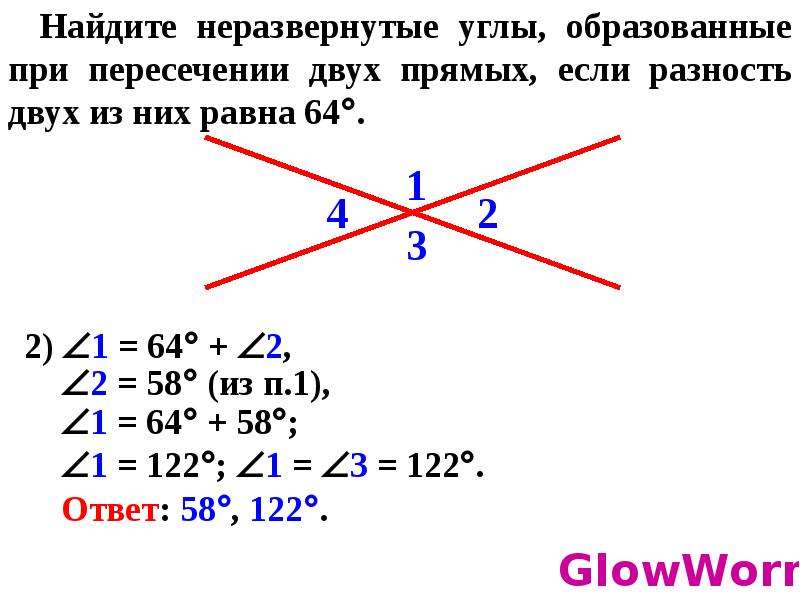
Стив пожал плечами. «Мы смотрели и смотрели, и вот сколько мы нашли», — сказал он. Но затем Хавьер обрел новую форму. Он показал Стиву, как складывать все створки, кроме одного, чтобы получить пятиугольник. (См. Рисунок 5.)
Рис. 5. Стив и Хавьер обрисовали и пометили все девять фигур.
Обсуждение класса
Когда у детей было время поработать над заданием, Крис начал обсуждение в классе. «Кто бы хотел подойти и нарисовать фигуру?» — спросила она, раскладывая диаграмму.Многие дети подняли руку, желая поучаствовать.
Хавьер поднес свой свернутый шестиугольник к карте и осторожно обвел его маркером. Крис и дети вместе сосчитали стороны и углы. «Это бриллиант!» «Это шестиугольник!» «Это трапеция!» — кричали дети.
«Фигура с шестью сторонами и шестью углами называется шестиугольником», — сказал Крис и обозначил фигуру. Крис поднял для сравнения один из желтых шестиугольников из блоков шаблона. Дети заметили, что хотя их шестиугольник также имел шесть сторон, он был длиннее, тоньше и больше походил на алмаз.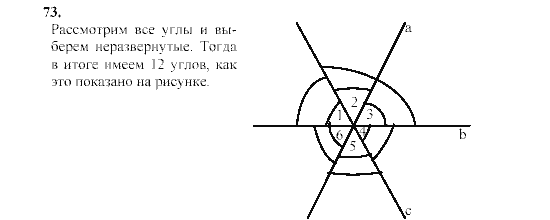 Некоторые говорили, что шестиугольник Pattern Block был толще и больше напоминал круг.
Некоторые говорили, что шестиугольник Pattern Block был толще и больше напоминал круг.
Затем Адриан показал классу пятиугольник. Никто не запомнил это слово. Франциска подошла вплотную. «Ручка . . . ручка . . . »
«Это пятиугольник», — сказал Крис. Детям требуется много опыта, чтобы выучить новую терминологию и научиться ее использовать.
Класс продолжил рисовать фигуры, маркировать их и считать стороны и углы. Габриэль указал на пятиугольник и сказал: «Похоже на лицо клоуна! Вот волосы.Адриан назвал трапецию туфлей. Маркосу показалось, что его сложенный квадрат раскрывается, как конверт. «Послушайте, это письмо, — сказал он.
Затем Крис сказал детям, что для выполнения домашних заданий они должны забрать домой свои квадраты и поработать со своими семьями, чтобы найти все формы. Крис знал, что детям будет полезно снова заняться этим заданием, и им понравится. Кроме того, это была возможность показать родителям геометрию, которую они изучали в школе.
Из печатного информационного бюллетеня, выпуск № 22, осень 1997 г.
8 способов обеспечить раскрытие конструкции из листового металла
Разгрузка изгиба в конструкции из листового металла
В том, что мы строим, есть хитрость.Если вы попытаетесь согнуть эти стороны на листогибочном прессе, окружающий металл деформируется, потому что вы не разработали разгрузку изгиба . Это не что иное, как два небольших разреза, расположенных по обе стороны от изгиба. Помните, что каждая вертикальная сторона коробки, которая скоро станет вертикальной, по сути, представляет собой фланец и должна иметь возможность двигаться независимо от других.
Перед тем, как развернуть деталь в программе дизайна, сделайте небольшие надрезы в углах, где встречаются две стороны. Их должно быть не меньше 0.030 дюймов шириной и расположите их по крайней мере на 0,015 дюйма (0,381 мм) за концом радиуса изгиба по обе стороны от изгиба на вашей стороне. Это позволит металлу свободно сгибаться, а детали правильно формироваться.
Вы, наверное, думаете, что в этом углу образовалась небольшая дыра, и вы правы. Хорошая новость заключается в том, что площадь воздействия очень мала. При необходимости об этом позаботится сварка, чтобы сделать вашу деталь более прочной в этом месте.
Особенности сбоев в конструкциях из листового металла
Это не просто отличное название для панк-группы, это базовый курс физики.Квантовая механика утверждает, что одна и та же частица не может находиться в двух местах одновременно. В нашем примере с коробкой представьте, что мы сделали отверстие на одной стороне с четырьмя фланцами, загнутыми наружу из отверстия. Фланцы того же размера, что и отверстие. Как вы понимаете, это не сработает. После того, как вы спроектировали фланец для определенной области, этот металл больше не будет использоваться где-либо еще. Вместо этого вы захотите создать вторую часть (или несколько частей), составляющую коробку, окружающую отверстие. Он должен быть полностью отделен от вашей основной части.
ВНИМАНИЕ: Некоторые программы проектирования позволяют создавать детали без толщины. Вы должны решить эту проблему на этапе развертывания, или вы можете услышать от производителя, что задерживает вашу деталь.
Остерегайтесь неоднородной толщины
Это звучит довольно разумно, и это потому, что это так. Ваши проекты должны отражать реальность того, что листовой металл имеет одну толщину. Если листовой металл имеет толщину 0,100 дюйма (2,54 мм), вся деталь также должна иметь эту толщину.Обратите внимание на различия, которые могут помешать правильному раскладыванию вашей детали.
Импорт поверхностей для листового металла
Вот хитрый вопрос. Можно спроектировать детали, которые представляют собой все поверхности. Они выглядят как твердые части, но на самом деле они полые, а поверхности не имеют толщины материала. В приведенном здесь примере эта деталь фактически состоит из 10 поверхностей — все шесть кромок плюс четыре плоские стороны — каждая с нулевой толщиной. Итак, это выглядит хорошо визуально, но не раскрывается на листовой металл.Лучшее решение — всегда начинать с твердого тела и поддерживать одинаковую толщину по всей конструкции.
Итак, это выглядит хорошо визуально, но не раскрывается на листовой металл.Лучшее решение — всегда начинать с твердого тела и поддерживать одинаковую толщину по всей конструкции.
Расположение элементов из листового металла
При проектировании всех деталей из листового металла необходимо учитывать, где вы размещаете элементы относительно друг друга. То, что хорошо выглядит как сплошная деталь, может плохо передаваться или даже не может быть развернуто как плоское. Итак, важно визуализировать процесс изготовления в уме, прежде чем предполагать, что ваш дизайн будет иметь смысл. Например, если вы хотите сделать отверстие рядом с изгибом, и расположите эти два элемента слишком близко друг к другу, вы, скорее всего, получите деформированную деталь.Листогибочный пресс не сможет плавно формировать металл, если нет твердой зоны, где используются формовочные инструменты.
Хорошая новость в том, что есть несколько простых и понятных правил, которые вы можете использовать.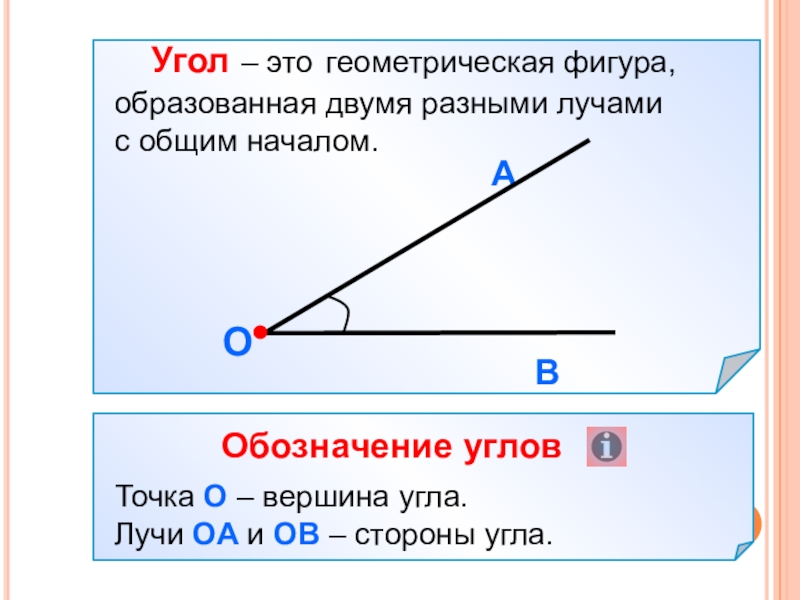 После того, как вы определили толщину материала, всегда старайтесь держать в уме расстояние, в четыре раза превышающее эту толщину, при поиске отверстий. Также убедитесь, что длина всех кромок и фланцев как минимум в четыре раза превышает толщину материала. Используя практическое правило 4T, вы можете избежать поломки детали во время производства.
После того, как вы определили толщину материала, всегда старайтесь держать в уме расстояние, в четыре раза превышающее эту толщину, при поиске отверстий. Также убедитесь, что длина всех кромок и фланцев как минимум в четыре раза превышает толщину материала. Используя практическое правило 4T, вы можете избежать поломки детали во время производства.
В конечном итоге дизайнеры, которым удобнее моделировать твердотельные 3D-объекты, все равно могут создавать конструктивные конструкции из листового металла. Для этого потребуется всего несколько дополнительных шагов и возможность сгладить вашу перспективу. Посетите наш веб-семинар «Как развернуть компоненты из листового металла» для более подробного изучения этой темы.
За дополнительной помощью обращайтесь к инженеру по приложениям Protolabs по телефону 877-479-3680 или [электронная почта защищена]. Чтобы начать свой следующий дизайн-проект сегодня, просто загрузите 3D-модель САПР и получите интерактивное ценовое предложение в течение нескольких часов.
GSMD / AN ОШИБКА ВО ВРЕМЯ РАСПОЛОЖЕННОГО УГЛОВОГО УСТРОЙСТВА №
Статус APAR
Закрыто как невоспроизводимое в следующем выпуске.
Описание ошибки
GSMD / ОШИБКА ПРИ РАЗВЕРТЫВАНИИ ПРОИЗВОДИТСЯ РАСЧЕТ УГЛОВОГО ПОМОЩИ. . Сценарий. . 1. откройте SMD.CATPart. 2.Щелкните значок «Сложить / развернуть». 3.Щелкните значок снятия напряжения в углах 4.Выберите цилиндрический изгиб 1 и 2 в качестве опор. 5.Выберите значок профиля пользователя 6.Выберите Sketch.4 в качестве профиля. 7. Установите 6 мм в качестве радиуса 8. Нажмите OK. Ошибка обновления происходит следующим образом; Произошла ошибка при снятии загнутого угла вычисление. Вы должны изменить ввод параметры. . Ожидаемый результат. . Ошибка НЕ должна возникать. .
Локальное исправление
Описание проблемы
GSMD / ОШИБКА ПРИ ВЫПОЛНЕНИИ РАЗВЕРНУТЫХ УГЛОВЫХ УСТРОЙСТВ Н.
 ПРИ РАЗВЕРТЫВАНИИ ПРОИЗВОДИТСЯ ОШИБКА GSMD / AN
РАСЧЕТ УГЛОВОГО ПОМОЩИ.
.Сценарий.
.
1. откройте SMD.CATPart.
2.Щелкните значок «Сложить / развернуть».
3.Щелкните значок снятия напряжения в углах
4.Выберите цилиндрический изгиб 1 и 2 в качестве опор.
5. выберите значок профиля пользователя.
6.Выберите Sketch.4 в качестве профиля.
7. Установите 6 мм в качестве радиуса
8. Нажмите OK. Ошибка обновления происходит следующим образом;
Произошла ошибка при снятии загнутого угла
вычисление. Вы должны изменить ввод
параметры.
.
Ожидаемый результат.
.
Ошибка НЕ должна возникать.
.
ПРИ РАЗВЕРТЫВАНИИ ПРОИЗВОДИТСЯ ОШИБКА GSMD / AN
РАСЧЕТ УГЛОВОГО ПОМОЩИ.
.Сценарий.
.
1. откройте SMD.CATPart.
2.Щелкните значок «Сложить / развернуть».
3.Щелкните значок снятия напряжения в углах
4.Выберите цилиндрический изгиб 1 и 2 в качестве опор.
5. выберите значок профиля пользователя.
6.Выберите Sketch.4 в качестве профиля.
7. Установите 6 мм в качестве радиуса
8. Нажмите OK. Ошибка обновления происходит следующим образом;
Произошла ошибка при снятии загнутого угла
вычисление. Вы должны изменить ввод
параметры.
.
Ожидаемый результат.
.
Ошибка НЕ должна возникать.
.
Вывод проблемы
Временное исправление
Комментарии
Информация APAR
Номер APAR
HD51817
Сообщаемое имя компонента
CATIA V5 NT> XP
Идентификатор зарегистрированного компонента
569151000
Зарегистрированный выпуск
515
Статус
ЗАКРЫТО UR1
ЧП
НОПЭ
HIPER
NoHIPER
Особое внимание
NoSpecatt
Дата отправки
19.
 04.2006
04.2006Дата закрытия
05.05.2006
Дата последнего изменения
08.06.2006
APAR настроен через систему от одного или нескольких из следующих:
APAR настроен на одну или несколько из следующих систем:
Имя фиксированного компонента
CATIA V5 NT> XP
Идентификатор фиксированного компонента
569151000
Применимые уровни компонентов
R515 PSN
UP
R516 PSN SP51605
UP06 / 06/08 I 1000
[{«Подразделение»: {«код»: «BU048», «ярлык»: «Программное обеспечение IBM»}, «Продукт»: {«код»: «SSVJ2K», «ярлык»: «CATIA V5″}, » Компонент «:» «,» Категория ARM «: [],» Платформа «: [{» код «:» PF025 «,» метка «:» Независимая платформа «}],» Версия «:» 515 «,» Издание » : «», «Направление деятельности»: {«code»: «», «label»: «»}}]
УГОЛ ОТСУТСТВУЕТ В РАЗЛОЖЕННОМ ВИДЕ
Статус APAR
Описание ошибки
ASMD: УГОЛ ОТСУТСТВУЕТ В РАЗЛОЖЕННОМ ВИДЕ Сценарий: 1.
 запустить CATIA
2. Workbench Aerospace проектирование листового металла.
3. Откройте Corner_R18.CATPart.
4. См. Отмеченный желтым цветом радиус края (угол) на
часть.
5. Переключитесь в развернутый вид.
Результат: в развернутом виде вы видите желтый
отмеченный угол отсутствует.
Ожидаемый результат: если угол создан, он также должен
отражаться в развернутом виде.
.
.
запустить CATIA
2. Workbench Aerospace проектирование листового металла.
3. Откройте Corner_R18.CATPart.
4. См. Отмеченный желтым цветом радиус края (угол) на
часть.
5. Переключитесь в развернутый вид.
Результат: в развернутом виде вы видите желтый
отмеченный угол отсутствует.
Ожидаемый результат: если угол создан, он также должен
отражаться в развернутом виде.
.
.
Локальное исправление
Описание проблемы
ASMD: УГОЛ ОТСУТСТВУЕТ В РАЗЛОЖЕННОМ ВИДЕ ASMD: В развернутом виде отсутствует угол Сценарий: 1.запустить CATIA 2. Workbench Aerospace проектирование листового металла. 3. Откройте Corner_R18.CATPart. 4. См. Отмеченный желтым цветом радиус края (угол) на часть. 5. Переключитесь в развернутый вид. Результат: в развернутом виде вы видите желтый отмеченный угол отсутствует. Ожидаемый результат: если угол создан, он также должен отражаться в развернутом виде. . .
Вывод проблемы
ЭТА ПРОБЛЕМА БУДЕТ УСТРАНЕНО В ВЕРСИИ CATIA 5 ВЫПУСК 19 GA LEVEL.
 Диагностика инцидента: ASMD: УГОЛ ОТСУТСТВУЕТ В
В развернутом виде
Объяснение исправления:
Невозможно проецировать угол в развернутом виде
из-за одного из выбранных ребер, следовательно, ошибка
было добавлено сообщение, которое указывает
ситуации и попросите пользователя выбрать края индивидуально
.
Диагностика инцидента: ASMD: УГОЛ ОТСУТСТВУЕТ В
В развернутом виде
Объяснение исправления:
Невозможно проецировать угол в развернутом виде
из-за одного из выбранных ребер, следовательно, ошибка
было добавлено сообщение, которое указывает
ситуации и попросите пользователя выбрать края индивидуально
.
Временное исправление
Комментарии
Информация APAR
Номер APAR
HD72020
Сообщаемое название компонента
CATIA V5 HP-UX
Зарегистрированный идентификатор компонента
56
00Зарегистрированный выпуск
518
Статус
ЗАКРЫТО ПО
ЧП
НОПЭ
HIPER
NoHIPER
Особое внимание
NoSpecatt
Дата отправки
2008-03-03
Дата закрытия
19.03.2008
Дата последнего изменения
19.
 03.2008
03.2008
APAR настроен через систему от одного или нескольких из следующих:
APAR настроен на одну или несколько из следующих систем:
Имя фиксированного компонента
CATIA V5 HP-UX
Идентификатор фиксированного компонента
56
00
Применимые уровни компонентов
[{«Подразделение»: {«код»: «BU048», «ярлык»: «Программное обеспечение IBM»}, «Продукт»: {«код»: «SSVJ2K», «ярлык»: «CATIA V5″}, » Компонент «:» «,» Категория ARM «: [],» Платформа «: [{» код «:» PF025 «,» метка «:» Независимая платформа «}],» Версия «:» 518 «,» Издание » : «», «Направление деятельности»: {«code»: «», «label»: «»}}]
NIMH »Улавливатель стресса
Жизнь иногда бывает сложной, и детям (и взрослым!) Важно выработать стратегии, позволяющие справляться со стрессом или тревогой. Эта «гадалка» для снятия стресса предлагает несколько стратегий, которые дети могут применять и использовать, чтобы справиться со стрессом и другими тяжелыми эмоциями.
Эта «гадалка» для снятия стресса предлагает несколько стратегий, которые дети могут применять и использовать, чтобы справиться со стрессом и другими тяжелыми эмоциями.
Загрузите PDF-файл с инструкциями и шаблоном для снятия стресса, чтобы создать веселый и интерактивный способ для детей практиковать стратегии выживания.
Посмотрите это видео, чтобы увидеть, как сделать и использовать средство для снятия стресса.
Создайте свой ловец стресса
Загрузите и распечатайте шаблон PDF, а затем выполните следующие действия, чтобы создать свой собственный ловец стресса.
- Шаг 1. Раскрасьте датчик напряжения (на странице 2) и вырежьте квадрат.
- Шаг 2. Поместите датчик напряжения лицевой стороной вниз. Сложите каждый угол к противоположному углу, а затем разверните, чтобы создать две диагональные складки в квадрате.
- Шаг 3. Загните каждый угол к центру квадрата так, чтобы числа и цвета были обращены к вам.
 Переверните квадрат и снова загните каждый угол в центр, чтобы были видны названия цветов.
Переверните квадрат и снова загните каждый угол в центр, чтобы были видны названия цветов. - Шаг 4. Сложите квадрат пополам так, чтобы названия цветов соприкасались, а числа были снаружи. Теперь откройте его и сложите пополам.
- Шаг 5. Вставьте большой и указательный пальцы каждой руки (зажимающее движение) под щитки с цифрами.
- Шаг 6. Закройте датчик напряжения, чтобы отображались только числа.
Используйте ловушку для стресса
- Выберите номер, а затем открывайте и закрывайте датчик напряжения это количество раз.
- Затем выберите цвет и произнесите название цвета, открывая и закрывая улавливатель ударения для каждой буквы.
- Затем выберите цвет, который виден, и откройте клапан.
- Прочтите, что в нем говорится, и практикуйте стратегию выживания.
- В эту игру можно играть с одним или двумя игроками, и это способ отработать стратегии преодоления трудностей.

Дополнительные ресурсы
5 вещей, которые вы должны знать о стрессе
Мозг подростка: 7 вещей, которые нужно знать
5 шагов, которые помогут человеку, страдающему эмоциональной болью
National Suicide Prevention Lifeline
1-800-273-TALK (8255) для бесплатной круглосуточной помощи
Crisis Text Line
Отправьте сообщение HELLO на номер 741741, чтобы получить бесплатную круглосуточную помощь
Узнайте больше о психическом здоровье на тематических страницах NIMH, посвященных психическому здоровью, и найдите информацию по широкому кругу вопросов, связанных со здоровьем, в службе MedlinePlus Национальной медицинской библиотеки.
Министерство здравоохранения и социальных служб США
Национальные институты здравоохранения
Публикация NIH № 20-MH-8121
Функции разгрузки изгиба и разгрузки углов — Центр поддержки и поддержки Bricsys
Команды : SMFLANGEEDGE, SMRELIEFCREATE, SMJUNCTIONSWITCH, SMRELIEFSWITCH
Рельефы необходимы в деталях из листового металла, чтобы избежать разрыва материала при изгибе при разрыве пресса.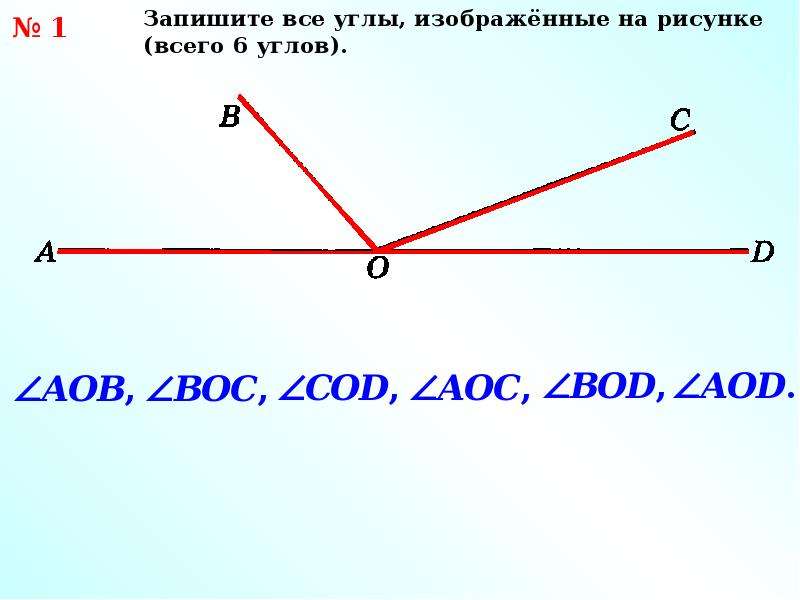 По сути, вам не нужно заботиться о рельефах, потому что BricsCAD автоматически создает все необходимые рельефы, когда вы создаете изгиб (неявно или явно).Однако, если вы переделываете плохие детали из листового металла, вам может быть полезно создать разгрузку углов и сгибов с помощью специальных инструментов.
По сути, вам не нужно заботиться о рельефах, потому что BricsCAD автоматически создает все необходимые рельефы, когда вы создаете изгиб (неявно или явно).Однако, если вы переделываете плохие детали из листового металла, вам может быть полезно создать разгрузку углов и сгибов с помощью специальных инструментов.
Угловые разгрузки и стыки
При создании фланца с помощью команды SmFlangeEdge рядом с кромкой сгиба автоматически создается разгрузка угла в углу, где встречаются три фланца. Кроме того, между двумя фланцами создается стык, который не соединен с коленом.
Учебное пособие: проектирование с нуля в BricsCAD Sheet Metal
Нажмите здесь, чтобы посмотреть
Создание недостающих рельефов
Выполните одно из следующих действий:
- Нажмите кнопку инструмента Создать рельеф () на вкладке ленты Листовой металл .
- Выберите Создать рельеф в меню Листовой металл .

- Введите smreliefcreate в командной строке.
Появится запрос: Выберите твердую кромку, грань сгиба, грань фланца или трехмерное тело [Вся модель]:
Выберите элемент (см. Примечание ниже).
Введите размер разгрузки по коэффициенту радиуса сгиба или [усилие разгрузки сгиба / Авто] <Авто>:Выполните одно из следующих действий:
- Нажмите Enter или щелкните правой кнопкой мыши, чтобы принять коэффициент радиуса изгиба по умолчанию.
- Введите значение в командной строке и нажмите Enter.
Рельеф создан.
Выбранные грани сгиба | Созданные рельефы |
ПРИМЕЧАНИЕ |
|
Опция усилие Разгрузка изгиба принудительно создает разгрузку изгиба, даже если нет необходимости создавать разгрузку изгиба.Как показано на изображении ниже, нет необходимости создавать разгрузку изгиба, но геометрия отличается от прямоугольного среза.
Разгрузка изгиба не требуется из-за плавного перехода геометрии. | Прямоугольная разгрузка изгиба создается, только если включена опция усилие Разгрузка изгиба . |
Переключение типа разгрузки от изгиба
Тип разгрузки от изгиба можно переключать между четырьмя типами:
прямоугольный | Гладкий | Круглый | Рип |
ПРИМЕЧАНИЯ |
|
Использование ленты, меню или панели инструментов
Чтобы выбрать желаемый тип разгрузки, выполните одно из следующих действий:
- Нажмите кнопку раскрывающегося списка Relief на панели Листовой металл / Изменить на ленте и выберите Перейти на прямоугольную , Перейти на гладкую , Перейти на круглую или Перейти на Rip .

- Нажмите кнопку инструмента на панели инструментов SM Relief : Переключиться на прямоугольный снимок (), Переключиться на плавный сброс (), Переключиться на скругленный сброс () или Переключиться на снятие разрыва ().
- Выберите тип снятия напряжения в меню Листовой металл / Снятие напряжения .
Вам будет предложено: Выберите грани, трехмерные тела для переключения рельефа на V-образный [прямоугольный / круглый / V-образный / SMooth / RIp / ROund / рельефное расширение / вся модель] <Вся модель>:
- Нажмите кнопку раскрывающегося списка Relief на панели Листовой металл / Изменить на ленте и выберите Перейти на прямоугольную , Перейти на гладкую , Перейти на круглую или Перейти на Rip .
Выполните одно из следующих действий:
- Нажмите Enter, чтобы применить выбранный тип рельефа ко всей модели.
- Щелкните соседний фланец, сгиб или грань разгрузки сгиба.
Разгрузка при изгибе преобразована.
Если команда была вызвана с ленты, команда повторяет главную подсказку до тех пор, пока вы не нажмете клавишу ESC для остановки.

Использование Quad
Наведите указатель мыши на соседний фланец, изгиб или грань разгрузки изгиба.
Если выбран параметр Выбрать грани системной переменной SELECTIONMODES, фланец или грань выделяются; в противном случае удерживайте клавишу CTRL при наведении курсора, пока лицо не выделится.Выберите требуемый тип разгрузки на вкладке Листовой металл в квадрате.
Смена типа разгрузки угла
Тип разгрузки угла может быть переключен между тремя типами:
прямоугольный | Циркуляр | V-образный |
Используя ленту, меню или панель инструментов:
Чтобы выбрать желаемый тип разгрузки, выполните одно из следующих действий:
- Нажмите кнопку раскрывающегося списка Рельеф на панели Листовой металл / Изменить на ленте и выберите тип рельефа.

- Нажмите кнопку инструмента на панели инструментов SM Relief .
- Выберите тип снятия напряжения в меню Листовой металл / Снятие напряжения .
Вам будет предложено: Выберите грани, трехмерные тела для переключения рельефа на V-образный [прямоугольный / круглый / V-образный / SMooth / RIp / ROund / рельефное расширение / вся модель] <Вся модель>:
- Нажмите кнопку раскрывающегося списка Рельеф на панели Листовой металл / Изменить на ленте и выберите тип рельефа.
Выполните одно из следующих действий:
- Нажмите Enter, чтобы применить выбранный тип рельефа ко всей модели.
- Щелкните соседний фланец, сгиб или грань углового выреза.
Разгрузка угла преобразована.
Если команда была вызвана с ленты, команда повторяет главную подсказку до тех пор, пока вы не нажмете клавишу ESC для остановки.
Использование Quad:
Убедитесь, что выбран параметр Select Faces системной переменной SELECTIONMODES.

Наведите указатель мыши на соседний фланец, изгиб или грань углового выреза.
Выберите требуемый тип разгрузки в группе команд Sheet Metal в Quad.
Оригами Magic Rose Cube: 17 шагов (с изображениями)
Введение: Оригами Magic Rose Cube
Это куб, который может превращаться в розу с небольшой вашей помощью!
Добавить TipAsk QuestionDownload
Шаг 1: Материалы
Какие материалы вам понадобятся для изготовления Оригами Волшебный кубик розы:
Добавить TipAsk QuestionDownload
Шаг 2:
Возьмите красный или розовый лист бумаги и сложите его. половина.Затем снова пополам в том же направлении, в котором вы сложили его в первый раз, а затем разверните. Затем вы согнете верхний правый угол бумаги под углом 45 градусов, чтобы выровняться с первой линией слева. Затем проделайте то же самое с нижним левым углом.
Добавить TipAsk QuestionDownload
Шаг 3:
Вам нужно будет взять верхний угол треугольника, который вы только что сложили, и сделать сгиб по направлению к вам на линии. Затем возьмите верхний левый угол бумаги и согните его вправо по линии.Наконец, хорошо разровняйте бумагу и переверните ее.
Затем возьмите верхний левый угол бумаги и согните его вправо по линии.Наконец, хорошо разровняйте бумагу и переверните ее.
Добавить TipAsk QuestionDownload
Шаг 4:
Вам нужно будет поднять клапан в правом нижнем углу и загнуть нижний левый угол в клапан. Затем вам нужно будет сложить к себе на линии угол того, что раньше было левым нижним углом. Затем загните верхний левый угол вправо, а затем разгладьте его.
Добавить TipAsk QuestionDownload
Шаг 5:
Вам нужно будет перевернуть бумагу вверх дном и сложить треугольники сверху и снизу.Затем согните верхний правый угол бумаги к верхнему левому углу бумаги. Затем согните нижний левый угол бумаги к нижнему правому углу бумаги. Затем разверните последние четыре складки, которые вы сделали. Наконец, повторите шаги 2–5, пока не получите три фигуры.
Добавить TipAsk QuestionDownload
Шаг 6:
Возьмите зеленый лист бумаги и сложите его пополам. Затем снова пополам в том же направлении, в котором вы сложили его в первый раз, а затем разверните.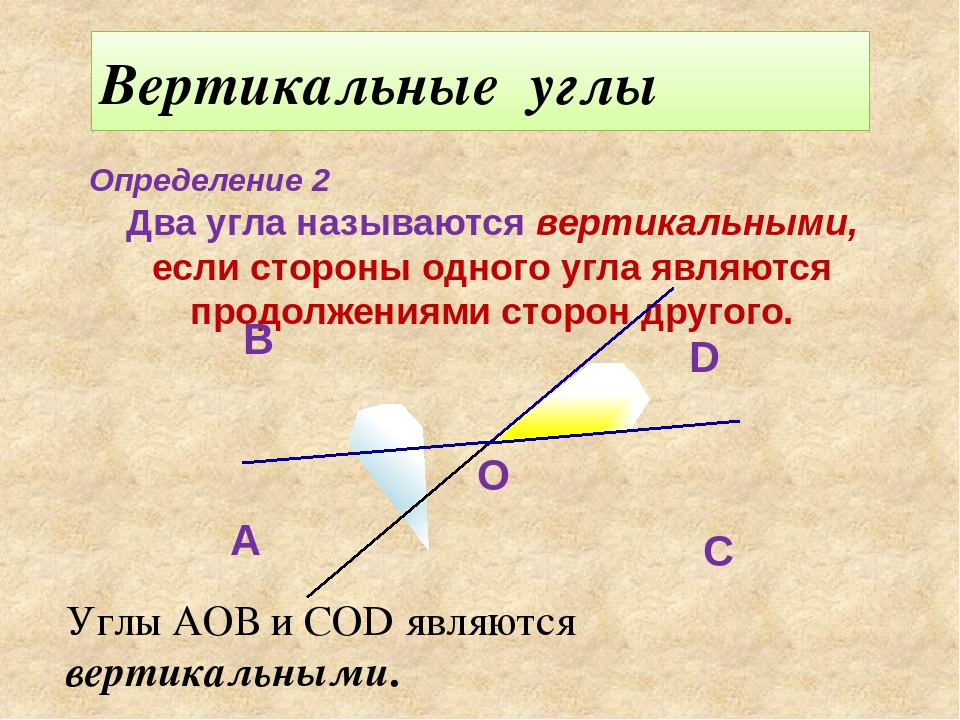 Затем вы согнете верхний правый угол бумаги под углом 45 градусов, чтобы выровняться с первой линией слева.Затем проделайте то же самое с нижним левым углом.
Затем вы согнете верхний правый угол бумаги под углом 45 градусов, чтобы выровняться с первой линией слева.Затем проделайте то же самое с нижним левым углом.
Добавить TipAsk QuestionDownload
Шаг 7:
Вам нужно будет взять верхний угол треугольника, который вы только что сложили, и сделать сгиб по направлению к вам на линии. Затем возьмите верхний левый угол бумаги и согните его вправо по линии и, наконец, хорошо распрямите бумагу.
Добавить TipAsk QuestionDownload
Шаг 8:
Вам нужно будет взять нижний правый угол и сложить его под углом 45 градусов, чтобы он был на той же стороне, что и треугольник рядом с ним.Затем вам нужно будет сложить треугольник внизу вверх, а затем сложить нижний правый угол под углом 45 градусов, чтобы он оказался рядом с клапаном слева. Наконец, разверните последнюю сделанную вами складку.
Добавить TipAsk QuestionDownload
Шаг 9:
Вам нужно будет перевернуть бумагу и загнуть нижний левый угол бумаги по линии в правый клапан. Затем вам нужно будет сложить то, что раньше было левым нижним углом к себе. Затем вам нужно будет сложить треугольник в верхнем левом углу пополам и расправить бумагу.
Затем вам нужно будет сложить то, что раньше было левым нижним углом к себе. Затем вам нужно будет сложить треугольник в верхнем левом углу пополам и расправить бумагу.
Добавить TipAsk QuestionDownload
Шаг 10:
Вам нужно будет сложить маленький треугольник в правом нижнем углу. Затем вам нужно будет сложить нижний угол в средний правый угол. Затем разверните два последних сгиба и переверните бумагу вверх дном. Наконец, повторите шаги 6-10, пока не получите три фигурки.
Добавить TipAsk QuestionDownload
Шаг 11:
На этом этапе у вас должно быть по три каждой из фигур.
Добавить TipAsk QuestionDownload
Шаг 12:
Теперь вы соберете красные или розовые фигуры вместе.Сначала вам нужно будет засунуть одну из отворотов фигурки в правый карман другой. Затем положите один из отворотов фигурки в правый карман одной из двух фигур, которые находятся вместе. Наконец, вам нужно будет засунуть последний клапан в карман фигурки, а без клапанов ни в один из карманов. Этот шаг сложен, не торопитесь, иначе вы все испортите. В конце этого шага у вас должна получиться трехсторонняя фигура, похожая на половину куба, и с каждой стороны выступают откидные створки.
Этот шаг сложен, не торопитесь, иначе вы все испортите. В конце этого шага у вас должна получиться трехсторонняя фигура, похожая на половину куба, и с каждой стороны выступают откидные створки.
Добавить TipAsk QuestionDownload
Шаг 13:
Теперь вы соберете зеленые фигуры вместе. Сначала вам нужно будет засунуть одну из отворотов фигурки в правый карман другой. Затем положите один из отворотов фигурки в правый карман одной из двух фигур, которые находятся вместе. Наконец, вам нужно будет положить последний клапан в карман фигурки, а без клапанов ни в один из ее карманов. Этот шаг сложен, не торопитесь, иначе вы все испортите.В конце этого шага у вас должна получиться трехсторонняя фигура, которая выглядит как половина куба и три треугольника, которые выступают с каждой поверхности.
Добавить TipAsk QuestionDownload
Шаг 14:
Теперь вы соберете две фигурки, которые вы собрали на шагах 12 и 13, вместе. Сначала вам нужно будет засунуть одну из лоскутов красной или розовой фигурки в карман зеленой фигурки. Затем сложите две фигурки вместе, чтобы они образовали куб. Затем положите один из зеленых клапанов зеленой фигурки в карман рядом с первым клапаном, который вы положили.Затем вам нужно будет положить еще один красный клапан в один из зеленых карманов. Эти шаги сложны, не торопитесь, иначе вы все испортите.
Затем сложите две фигурки вместе, чтобы они образовали куб. Затем положите один из зеленых клапанов зеленой фигурки в карман рядом с первым клапаном, который вы положили.Затем вам нужно будет положить еще один красный клапан в один из зеленых карманов. Эти шаги сложны, не торопитесь, иначе вы все испортите.
Добавить TipAsk QuestionDownload
Шаг 15:
Затем вам нужно будет положить один из зеленых клапанов в один из красных карманов рядом с последним клапаном, который вы положили. Затем вставьте последний красный клапан в последний зеленый карман. и, наконец, засунул зеленый клапан в последний красный карман. Последние две заслонки сложнее всего надеть, так что будьте язычниками и не торопитесь.После этого у вас должен получиться куб с тремя зелеными сторонами и тремя красными или розовыми сторонами.
Добавить TipAsk QuestionDownload
Шаг 16:
Чтобы цветок появился, вам нужна магия. Шучу, вам нужно будет схватить каждый из красных или розовых карманов с внешней стороны и осторожно протолкнуть их примерно на полдюйма.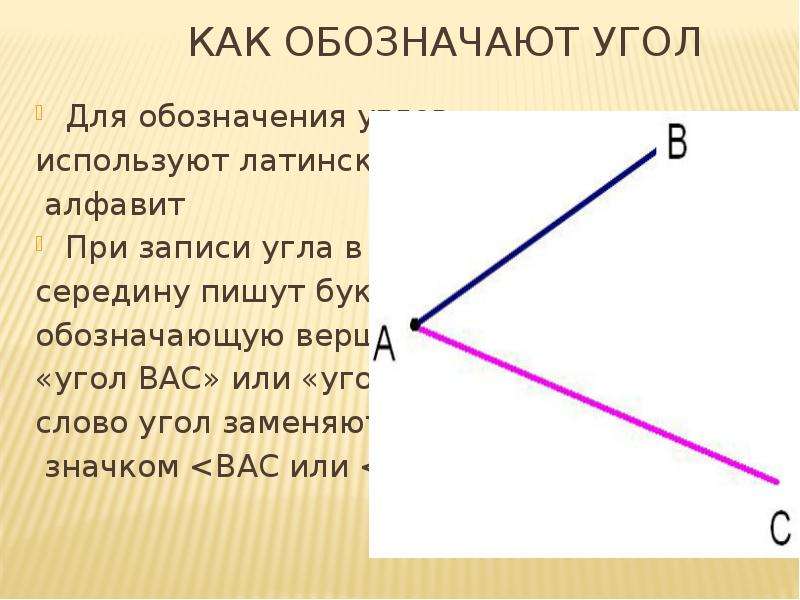


 Более подробно изучаются свойства каждого вида треугольников. Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей.
Более подробно изучаются свойства каждого вида треугольников. Появляются новые определения для учащихся – это геометрические фигуры, образованные при пересечении двух прямых между собой и пересечении нескольких прямых секущей.
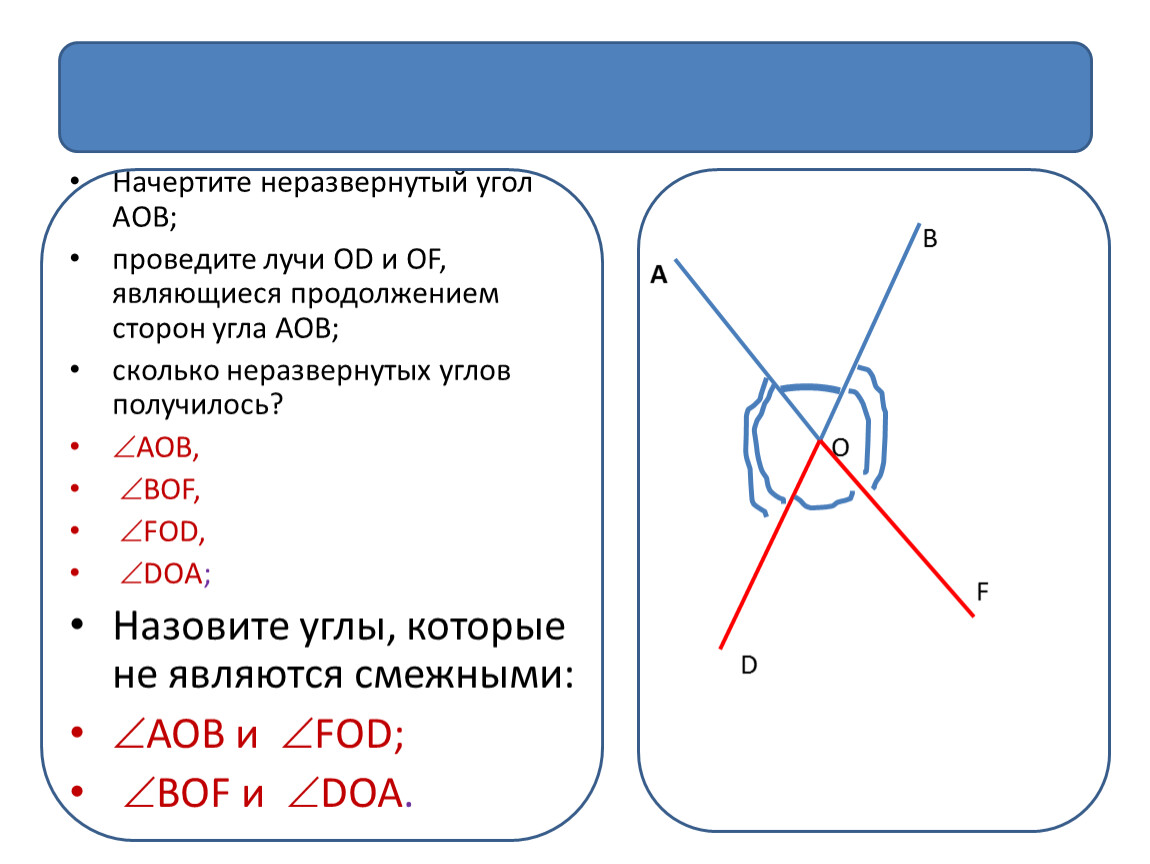


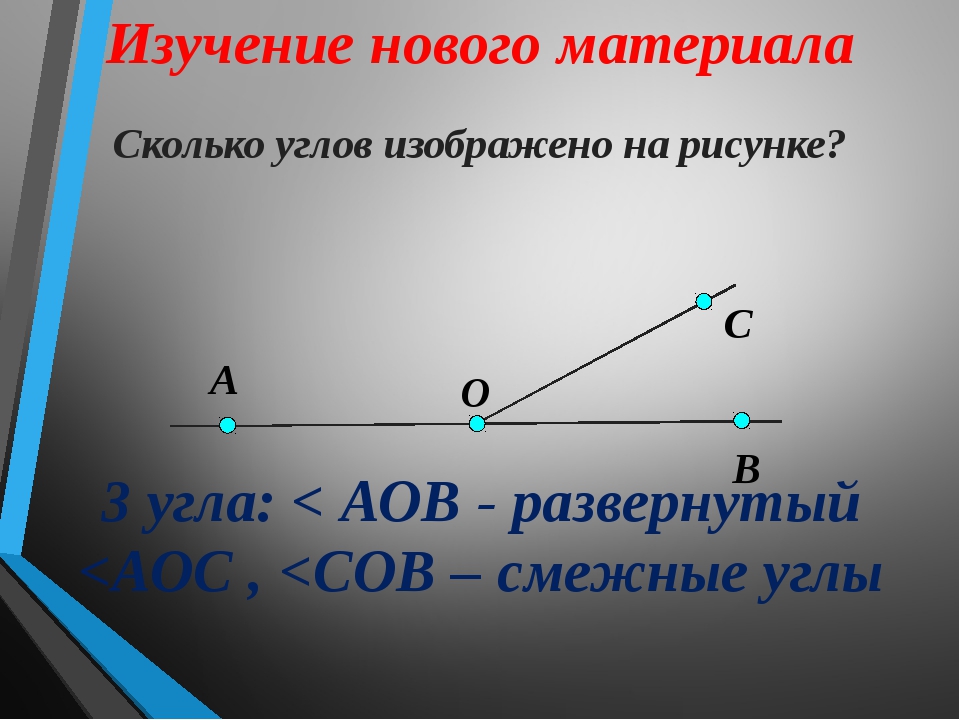
 Вычислите полученные углы.
Вычислите полученные углы.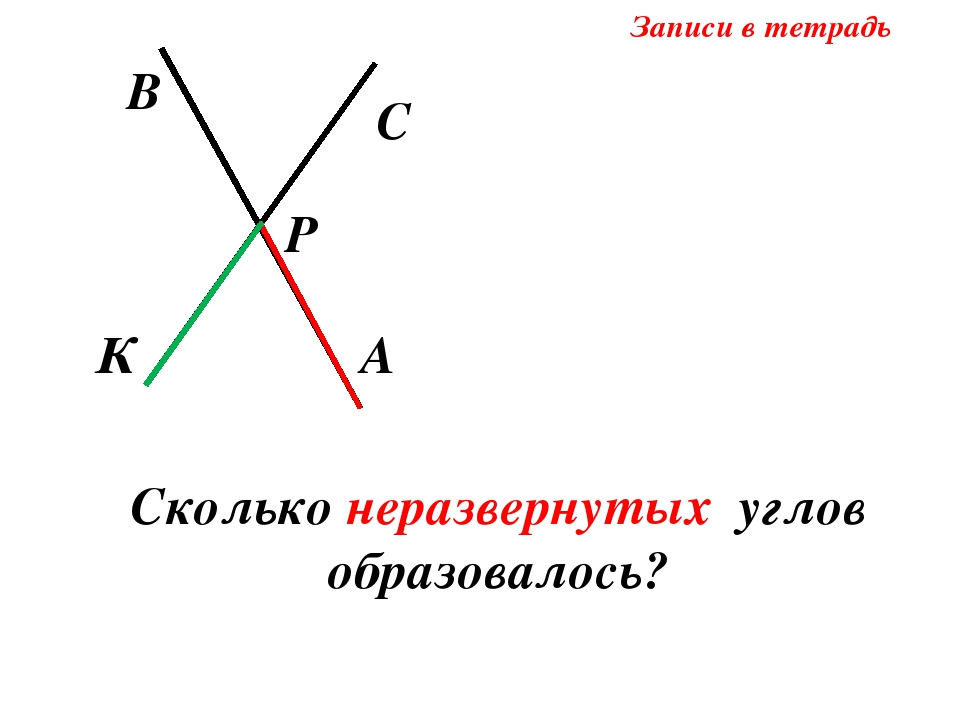 Ответ: 36˚ и 144˚.
Ответ: 36˚ и 144˚.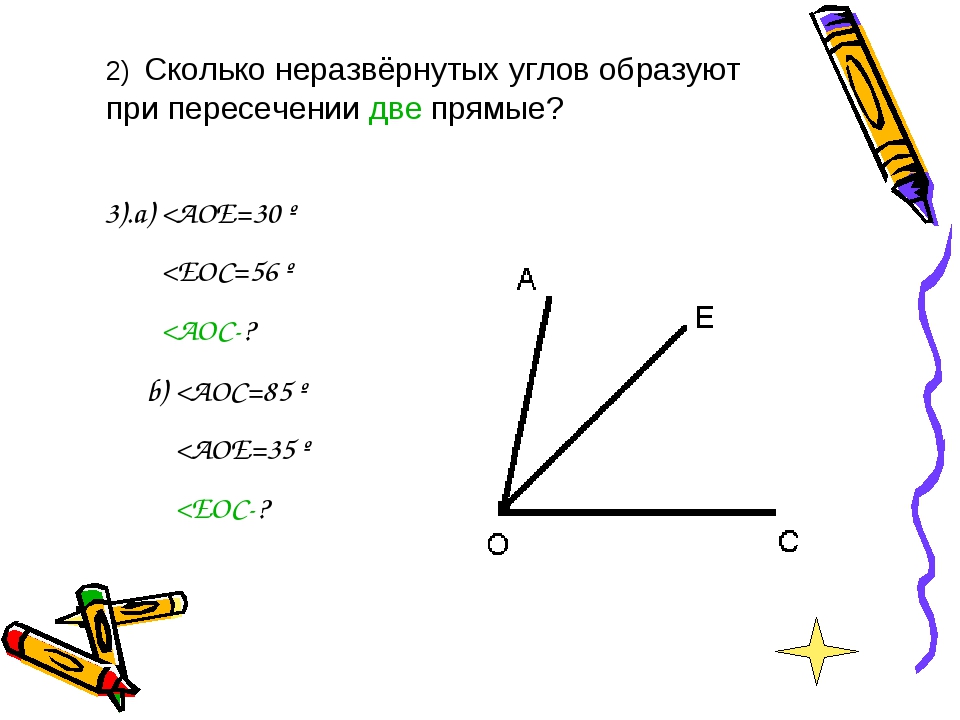
 ru — профессиональный инструмент для поиска репетитора.Здесь вы найдете подходящего репетитора быстро, удобно и бесплатно.
ru — профессиональный инструмент для поиска репетитора.Здесь вы найдете подходящего репетитора быстро, удобно и бесплатно.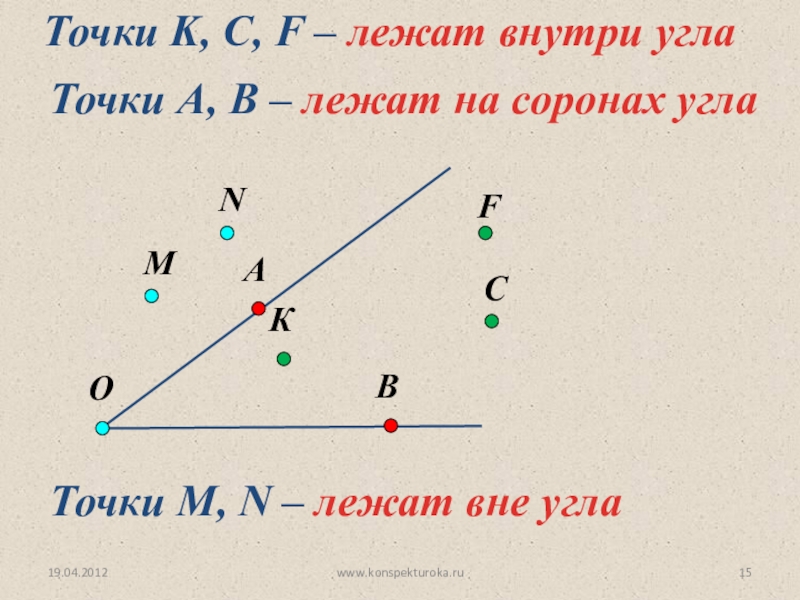 Если вы оставляете заявку на подбор репетитора, то в поле «ваши пожелания» укажите как можно больше подробностей и требований, чтобы мы могли найти самого подходящего вам репетитора.
Если вы оставляете заявку на подбор репетитора, то в поле «ваши пожелания» укажите как можно больше подробностей и требований, чтобы мы могли найти самого подходящего вам репетитора. ПРИ РАЗВЕРТЫВАНИИ ПРОИЗВОДИТСЯ ОШИБКА GSMD / AN
РАСЧЕТ УГЛОВОГО ПОМОЩИ.
.Сценарий.
.
1. откройте SMD.CATPart.
2.Щелкните значок «Сложить / развернуть».
3.Щелкните значок снятия напряжения в углах
4.Выберите цилиндрический изгиб 1 и 2 в качестве опор.
5. выберите значок профиля пользователя.
6.Выберите Sketch.4 в качестве профиля.
7. Установите 6 мм в качестве радиуса
8. Нажмите OK. Ошибка обновления происходит следующим образом;
Произошла ошибка при снятии загнутого угла
вычисление. Вы должны изменить ввод
параметры.
.
Ожидаемый результат.
.
Ошибка НЕ должна возникать.
.
ПРИ РАЗВЕРТЫВАНИИ ПРОИЗВОДИТСЯ ОШИБКА GSMD / AN
РАСЧЕТ УГЛОВОГО ПОМОЩИ.
.Сценарий.
.
1. откройте SMD.CATPart.
2.Щелкните значок «Сложить / развернуть».
3.Щелкните значок снятия напряжения в углах
4.Выберите цилиндрический изгиб 1 и 2 в качестве опор.
5. выберите значок профиля пользователя.
6.Выберите Sketch.4 в качестве профиля.
7. Установите 6 мм в качестве радиуса
8. Нажмите OK. Ошибка обновления происходит следующим образом;
Произошла ошибка при снятии загнутого угла
вычисление. Вы должны изменить ввод
параметры.
.
Ожидаемый результат.
.
Ошибка НЕ должна возникать.
.
 04.2006
04.2006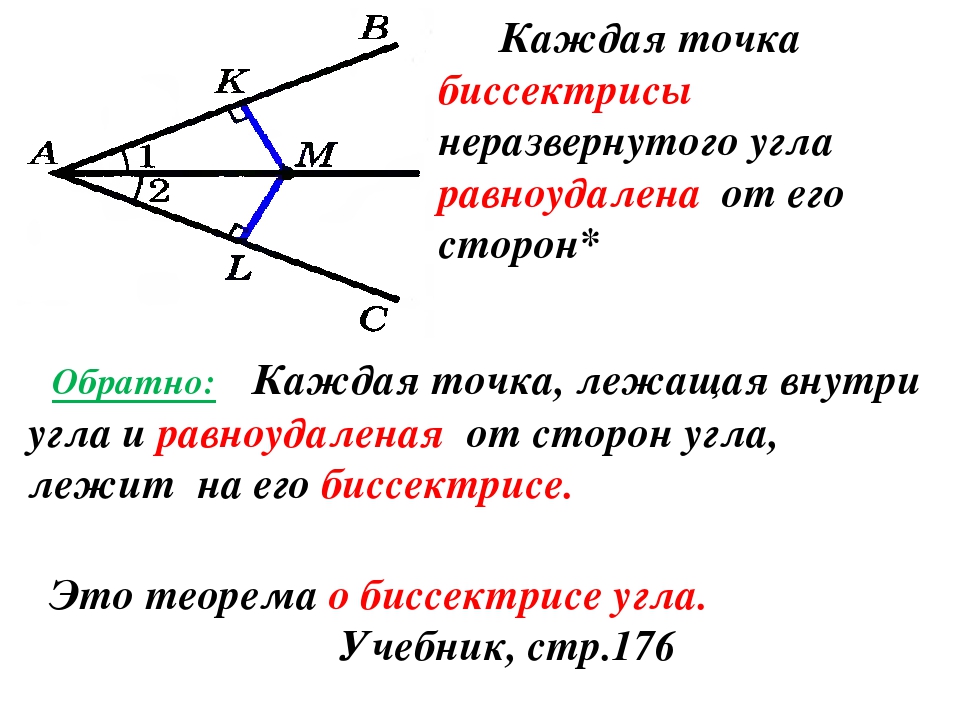 запустить CATIA
2. Workbench Aerospace проектирование листового металла.
3. Откройте Corner_R18.CATPart.
4. См. Отмеченный желтым цветом радиус края (угол) на
часть.
5. Переключитесь в развернутый вид.
Результат: в развернутом виде вы видите желтый
отмеченный угол отсутствует.
Ожидаемый результат: если угол создан, он также должен
отражаться в развернутом виде.
.
.
запустить CATIA
2. Workbench Aerospace проектирование листового металла.
3. Откройте Corner_R18.CATPart.
4. См. Отмеченный желтым цветом радиус края (угол) на
часть.
5. Переключитесь в развернутый вид.
Результат: в развернутом виде вы видите желтый
отмеченный угол отсутствует.
Ожидаемый результат: если угол создан, он также должен
отражаться в развернутом виде.
.
.
 Диагностика инцидента: ASMD: УГОЛ ОТСУТСТВУЕТ В
В развернутом виде
Объяснение исправления:
Невозможно проецировать угол в развернутом виде
из-за одного из выбранных ребер, следовательно, ошибка
было добавлено сообщение, которое указывает
ситуации и попросите пользователя выбрать края индивидуально
.
Диагностика инцидента: ASMD: УГОЛ ОТСУТСТВУЕТ В
В развернутом виде
Объяснение исправления:
Невозможно проецировать угол в развернутом виде
из-за одного из выбранных ребер, следовательно, ошибка
было добавлено сообщение, которое указывает
ситуации и попросите пользователя выбрать края индивидуально
. 03.2008
03.2008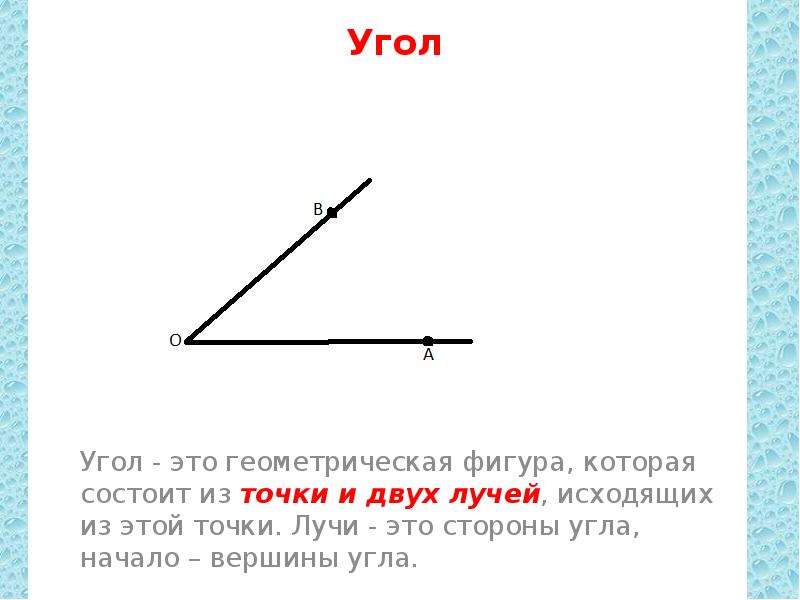 Переверните квадрат и снова загните каждый угол в центр, чтобы были видны названия цветов.
Переверните квадрат и снова загните каждый угол в центр, чтобы были видны названия цветов.