6 класс. Математика. Признаки делимости на 10, на 5 и на 2 — Признаки делимости на 10, на 5 и на 2
Комментарии преподавателяУвидев очень высокого человека, мы можем предположить, что он баскетболист.
Глядя на очень большой камень, мы поймем, что нам не удастся его поднять, он слишком тяжелый. Глядя на число 252, мы понимаем, что оно делится на 2.
Во всех этих примерах мы не проверяли, а делали вывод на основе внешних признаков. Причем в первых двух случаях мы могли ошибиться, но про число 252 мы знаем точно. Последняя цифра делится на 2, значит, и все число делится. Просто в математике есть точные признаки делимости на разные числа. Легко понять, что 12 делится на 2 или что 100 делится на 10.
Но, оказывается, можно быстро понять, делится ли на 3 числа 16547984622, 45758554963. Первое делится, а второе – нет. Просто сумма цифр первого числа делится на 3, а у второго – нет.
Это и указывает, делится ли само число на 3.
Признаки делимости на разные числа устроены по-разному. Но есть похожие, одного типа. Сегодня мы начнем с признаков делимости на 10, 5 и 2. Они устроены одинаково: смотрим на последнюю цифру и понимаем, делится или нет.
Начнем с самого главного вопроса: что значит «одно число делится на другое»? Например, что значит, что число 15 делится на 5? Это означает, что число 15 можно представить в виде произведения двух натуральных чисел, и одно из них будет 5.
15 содержит еще и множитель 3, это означает, что 15 делится и на 3 тоже.
Тот факт, что делится на (), мы можем записать или словами, или указать, что содержит множитель . Второй множитель , это результат деления на .
Теперь рассмотрим числа, которые оканчиваются нулем. Если число оканчивается нулем, то в его разложение на множители входит множитель 10.
Например, . Мы знаем, что 10 мы можем представить как , тогда . Мы получили, что фразы «в разложении содержится множитель 10» и «в разложении содержатся множители 5 и 2» эквиваленты. Таким образом, можем утверждать, что если число оканчивается нулем, то оно делится на 10, на 5 и на 2.
Разложим на множители: . Получили эквивалентную запись числа 60. Видим, что число 30 также раскладывается на множители, получим ещё одну эквивалентную запись: . Продолжим до тех пор, пока можем раскладывать на множители: .
Полученные числа разложить на множители уже не получается – они не делятся ни на одно число, кроме 1 и себя. Такие числа называются простыми. Остальные числа (например, 60, 30, 15 называются составными). 1 считается единственным числом, которое не является ни простым, ни составным.
Понятно, что, используя наш алгоритм (представляя любой составной множитель в виде произведения), для любого числа рано или поздно можно получить его эквивалентное представление в виде произведения простых множителей.
Но мы могли пойти по-другому: .
Как видим, получилось то же эквивалентное представление (с точностью до порядка множителей). Всегда ли так будет? Оказывается, да. Можно доказать, что любое число единственным образом представляется в виде произведения простых множителей. Этот результат называется основной теоремой арифметики.
Получается, что как бы мы ни раскладывали число на простые множители, в итоге мы получим одно и то же разложение (с точностью до порядка).
Если провести аналогию, то простые множители – это буквы, из которых состоят числа – слова. Добавь или убери букву – смысл слова изменится. Так же и с простыми множителями: любое изменение в наборе простых множителей даст нам другое число.
Таким образом, простые числа –такие числа, которые нельзя разложить на множители, например, 2, 3, 5. Составные числа – такие числа, которые можно разложить на множители.
А любое число можно представить в виде произведения простых множителей единственным образом.
Число делится на число тогда и только тогда, когда а содержит bкак множитель.
Обратим внимание на число 0. Это число можно представить как произведение нуля и любого другого числа: . Таким образом, ноль делится на любое число. Результатом будет второй множитель – 0.
А что с делением на ноль? Если бы некоторое число можно было поделить на ноль, то был бы ответ: . Тогда вспомним о том, что деление – это операция обратная умножению: . Но всегда будет равно 0, а мы это число выбирали произвольно. Так мы пришли к противоречию.
На самом деле без деления на ноль можно обойтись, поэтому данная операция нам не нужна.
Таким образом, ноль можно делить на любое число, не равное нулю, и получать ноль. При этом никакое число на ноль делить нельзя.
Рассмотрим два равенства.
В первом равенстве: слагаемое 16 делится на 4, слагаемое 1 не делится на 4, и сумма 17 не делится на 4.
Во втором равенстве: слагаемые 16 и 4 делятся на 4, и сумма 20 также делится на 4.
Таким образом мы получаем правило: если каждое из слагаемых делится на заданное число, то и сумма тоже делится на это число. Если одно из слагаемых делится на заданное число, а второе – нет, то сумма не делится на это число.
Возьмем очень большое число, например, 31419265358979323846. Постараемся определить, на какие числа оно делится.
Представим наше число в виде суммы: .
Первое слагаемое оканчивается нулем, а значит, оно делится на 10, на 5 и на 2.
Второе слагаемое 6 не делится на 10 (а первое делится), а значит, согласно правилу, и сумма не делится на 10.
Второе слагаемое 6 не делится на 5 (а первое делится), а значит, согласно правилу, и сумма не делится на 5.
Второе слагаемое 6 делится на 2 (и первое делится), а значит, согласно правилу, и сумма делится на 2.
Итак, сделаем вывод в виде теоремы.
Если каждое слагаемое суммы делится на одно число, то и вся сумма делится на это число. Например, делится на 3, так как и 3, и 12, и 9, и 6 делятся на 3.
Если все слагаемые делятся, а одно слагаемое не делится на число, то сумма не будет делиться на это число. Например, не делится на 5, так как все слагаемые, кроме одного (4), делятся на 5.
Если два и больше слагаемых не делятся на число, то результат может быть различным. Например, делится на 4, а при этом только слагаемое 4 делится на 4, а остальные два (5 и 3) на 4 не делятся.
Или не делится на 4, хотя ситуация не изменилась: одно слагаемое делится на 4, а остальные два (3 и 6) не делятся.
Теорема (признак делимости на 2, 5 и 10): число делится на 2, на 5 или 10 тогда и только тогда, когда последняя цифра этого числа делится на 2, на 5 или на 10 соответственно.
Доказательство
Пусть задано число . Представим его в виде суммы двух слагаемых:
Слагаемое оканчивается нулем, а значит, делится на 10, на 5, на 2. Но тогда делимость на 10, 5 и 2 всей суммы зависит от второго слагаемого, которое является последней цифрой нашего числа.
Таким образом, если последняя цифра числа делится на 10, 5 или 2, то и все число делится на 10, 5 или 2 соответственно. Теорема доказана.
Определить, делится ли число на 10, 5 и 2.
1)
Так как число оканчивается нулем, то оно делится на 10, 5 и 2.
2) 12687
Данное число оканчивается 7, 7 не делится ни на 2, ни на 5, ни на 10, а значит, и число 12687 на них не делится.
3) 1256
Данное число оканчивается 6, 6 делится на 2, но не делится на 5 и на 10, значит, число 1256 делится на 2, но не делится на 5 и на 10.
4) 258585
Последняя цифра 5, 5 делится на 5, но не делится на 2 и 10, значит, 258585 делится на 5, но не делится на 2 и 10.
5) 520000
Число оканчивается нулем, а значит, оно делится на 2, 5 и 10.
Обратите внимание: по последней цифре мы можем судить только о делимости на 2, на 5 и на 10. Для делимости на другие числа нельзя использовать этот признак. Например, число 13 не делится на 3, хотя и оканчивается 3, которое на 3 делится. Или 17 не делится 7, хотя и последняя цифра 7 на 7 делится.
источник конспекта — http://interneturok.ru/ru/school/matematika/6-klass/delimost-chisel/priznaki-delimosti-na-10-na-5-i-na-2
источник видео — http://www.youtube.com/watch?v=DJHdBicHi8s
источник видео — http://www.youtube.com/watch?v=8B0MazGfwvs
источник видео — http://www.youtube.com/watch?v=lOcNTfRCeac
источник презентации — http://ppt4web.ru/matematika/priznaki-delimosti-na-0.html
источник теста — http://testedu.ru/test/matematika/6-klass/priznaki-delimosti-na-2-5-10.html
ГИПР — Делится ли число на экране на 18 нацело признак делимости на 18 видеотест 30 мин средний темп смотреть онлайн видео от ГИПР
12+
1 год и 1 неделю назад
ГИПР — Говорит и показывает репетитор24 подписчика
Категория 12+.
Этот видеоролик — основа эпизода игры в репетитора и ученика и позволяет тренироваться применять признак делимости на 18 нацело (без остатка).
ВНИМАНИЕ: продолжительность видеоролика 30 минут, но это не означает, что нужно играть все полчаса. При появлении первых признаков усталости ПРЕКРАЩАЙТЕ ИГРУ!
Правила игры в этом эпизоде такие: после запуска видео репетитор-компьютер (планшет, смартфон, телевизор) показывает (отображает) на экране число, а вопрос репетитора следующий: «Делится ли изображенное число на 18 нацело?». Игрок-ученик должен дать ответ (вслух или про себя). Через некоторое время на экране появляется правильный ответ, с которым нужно сравнить свой собственный. Затем показывается следующее число и т. д.
Цель игрока-ученика — дать как можно больше правильных ответов.
Я рекомендую это видео в первую очередь детям, осваивающим тему «Признаки делимости нацело».
Таким образом, ролик представляет собой игровой видеотест, имеющий общие черты с программой-тренажером, дающей онлайн примеры и ответы на них.
Поскольку предлагаемая игра подразумевает развитие навыков, применяемых в образовательном процессе ребенка, ролик отнесён к категории «Образование». Но я подчеркиваю — ролик не создавался как образовательный материал, соответствующий государственным стандартам в сфере образования, методическим указаниям и рекомендациям для образовательного процесса, т. е. образовательным материалом он не является.
Также, по моему мнению и отзывам некоторых моих подписчиков, результат моей работы оказался полностью или частично подходящим ответом на такие популярные поисковые запросы, как:
— признак делимости на 18;
— признак делимости чисел на восемнадцать;
— математика признаки делимости;
— упражнения на признаки делимости;
— признаки делимости натуральных чисел.
Я выкладываю этот видеоролик на всеобщее обозрение руководствуясь следующими соображениями. Для каждого ребенка, обращавшегося ко мне за помощью по математике и с которым я общался вживую, видеотест способствовал освоению темы; фактов негативного влияния не было.
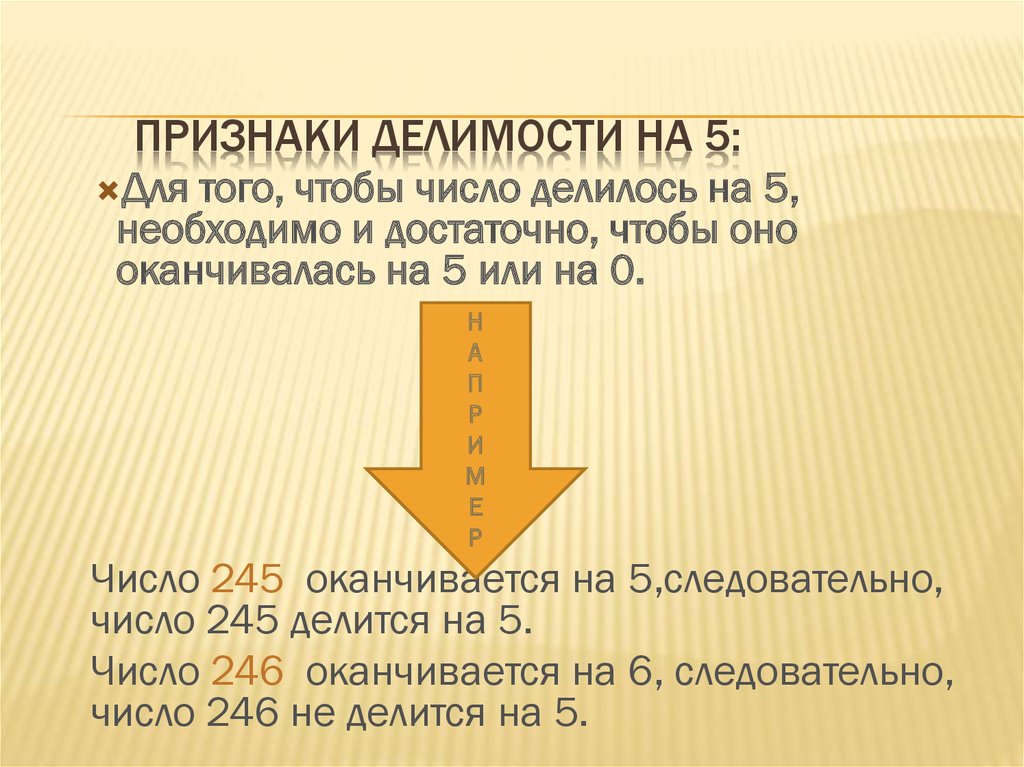
ru/channel/23724933/playlists/
Адрес моей группы: https://ok.ru/giprgovorit
Мои каналы на других ресурсах: https://zen.yandex.ru/giprgovorit и https://yarus.ru/u/5776747Задавать вопрос
спросил
Изменено 8 лет назад
Просмотрено 27 тысяч раз
$\begingroup$
95-н,30)=30$$ Подробности, пожалуйста, потому что прохожу Теорию чисел первый раз. В третьем семестре дипломного курса по математике Какова идея решить эту проблему с помощью Greatest Common? Эта проблема в этом раздаточном материале НОД?
- теория элементарных чисел
- простые числа
$\endgroup$
3
$\begingroup$
Попробуйте факторинг: 95-n}{30} = 4\binom{n}{5} + 8\binom{n}{4} + 5\binom{n}{3} + \binom{n}{2} -n $$
(На самом деле каждый многочлен, который принимает значения в $\mathbf{Z}$, может быть выражен как сумма биномиальных коэффициентов с целыми коэффициентами, как указано выше, так что это не было волшебством.
