Как решать задачи на проценты 7 класс: Как решать задачи с процентами? Примеры решений задач

Кружок 7 класса: задачи про Карлсона на проценты: klarissa45 — LiveJournal

?

Categories:

• Дети
• Спорт
• Путешествия
• Cancel

Почти подведены итоги школьного этапа ВОШ по математике, началась подготовка к муниципальному ( окружному) туру.
Тур будет проходить для 7-11 классов.
У меня в этом году геометрический кружок для 7 класса, однако вчера мы успели порешать ещё задачи на проценты.
Я совершенно случайно раздала ребятам варианты, у которых оказались похожи не только задачи на углы, но и задачи на проценты, где фигурировали Малыш и Карлсон.

Показываю варианты и ответы-решения.
Выводы делайте сами.

Решения и ответы

Решения и ответы

С учениками 5-6 классов я предпочитаю решать задачи арифметическими методами, а с 7 классами можно и с помощью уравнений.
Вчерашнее занятие показало, что у нынешних семиклассников проблемы с выбором неизвестного ( а сейчас такие задачи, например на движение, накручивают на ОГЭ, что нужен достаточный опыт в их решении).

https://oge.sdamgia.ru/problem?id=353092

Ещё хочу написать вот про что: как учить детей проверять себя и искать ошибки в решении?
Я вчера нечаянно допустила ошибки в решениях обоих задач про Карлсона. Дети их не заметили. Однако заметили, что ответы не сошлись.
Ошибки были разные. В одном случае я неправильно умножила 0.16 на 5, в во втором неверно записала увеличение на 150 процентов ( коэффициент 1.5 вместо 2.5)
Я на собственном примере показала детям, как снова внимательно перечитать условие задачи.

Как проверить составленное уравнение и его решение.
Потом мы обсудили сколько баллов я бы потеряла на олимпиаде при таких ошибках ( в ответах и решениях есть критерии проверки).
Арифметическая ошибка — это не очень страшно на олимпиаде( 3 балла вместо 4), а вот понимание условия — это большая потеря баллов( получаешь 1 балл из 4 за задачу).

Tags: 7 класс, 9 класс, ОГЭ, кружок, олимпиады, проценты

Subscribe

• MathEdu — общедоступная электронная библиотека по вопросам преподавания математики

  Я уже давала несколько ссылок на книжки из этой электронной библиотеки. Про неё либо забывают, либо вообще не знают. «Математическое…

• Решаем задачи с помощью геогебры

  В одном из предыдущих постов писала, что пересматривала свою видеолекцию. В конце я рассказала о том, что меня вдохновляет. Одним из вдохновляющих…

• Когда опускаются руки, и нет сил вести кружки

  Надо включить свою собственную лекцию, записанную в конце сентября 2020 года, в последнюю-препоследнюю 89 минуту и посмотреть на…

• Задания отборочного тура IХ Санкт-Петербургской математической олимпиады начальной школы

  12 февраля 2023 состоится олимпиада начальной школы 2х2. http://mathbaby.ru/olympiads/olimpiada-nachalnoy-shkoly/2023 Наша школа подаёт заявку в…

• Кружок по лингвистике: задачи конкурса «Русский медвежонок-2022»

  На сайте конкурса задачи в zip-файлах. Поэтому выложу их сюда в нормальном виде. Собираюсь на математическом кружке с 3 классом порешать. Зачем? Я…

• Константин Кноп: как и зачем обучать математике

  https://youtu.be/x7rfyqTDJys PS Константин Кноп пишет в чате Телеграм-канала «Я веду кружок» Я все же хотел бы защитить позицию…

• Кружок 3 класса: носки-перчатки и рыбаки-судаки

  Иногда полезно давать детям задачи «на вырост». В 5-6 классе такие задачи называют «в худшем случае»,…

• 2023 и расстановка знаков и скобок

  Нашла прошлогодний пост про 2022. https://klarissa45.livejournal.com/386677.html Посмотрела по ссылке. А там теперь про 2023…

• Кружок 3-4 класса: разрезаем циферблат на части

  Я уже писала про эту книжку, когда мы в ковидные времена решали задачи на взвешивания и переливания https://klarissa45. livejournal.com/217328.html…

Photo

Hint http://pics.livejournal.com/igrick/pic/000r1edq

Как решать задачи на проценты в 6 классе — Математика для школьников

40 комментариев / От Светлана Михайловна / 02.01.2013 18.03.2018

Предлагаю вашему вниманию легкий способ разобраться, как решать задачи на проценты в 6 классе.

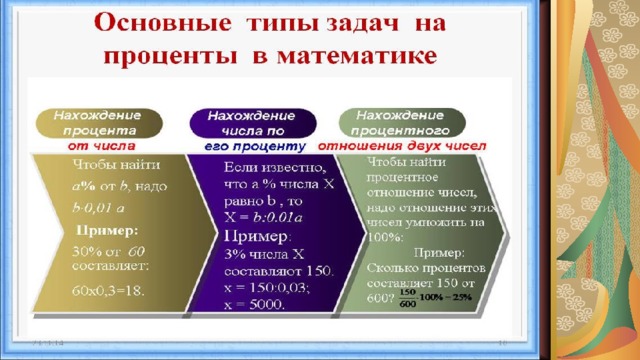
При решении задачи на проценты первым делом нужно определить вид задачи. Задачи на проценты в 6 классе можно подразделить на  три вида:

1) Нахождение процентов от числа.

2) Нахождение числа по его процентам.

3) Нахождение процентного отношения двух чисел.

Определить вид задачи на проценты можно по записи ее условия. Если напротив 100% стоит число, то это — задача на нахождение процентов от числа. Если число напротив 100% неизвестно, то это — задача на нахождение числа по его процентам. Если же неизвестное значение стоит в колонке процентов, то это — задача на нахождение процентного отношения двух чисел.

Рассмотрим на примерах, как научиться определять вид задачи на проценты.

1. Из картофеля выходит 20% крахмала. Сколько крахмала выйдет из 45 т картофеля?

	тонны	%
Картофель	45т	100%
Крахмал	?	20%

 

Это задача на нахождение процентов от числа (так как напротив 100% стоит число).

2. Руда содержит 67% железа. Сколько нужно руды для получения 13,4 т железа?

	тонны	%
Руда	?	100%
Железо	13,4т	67%

Это задача на нахождение числа по его процентам (так как напротив 100% стоит ?)

3. Из 400 зерен пшеницы взошло 360. Определить процент всхожести семян.

	Зерна	%
Всего посеяли	400	100%
Взошло	360	?

Это задача на процентное отношение (так как в колонке процентов стоит ?). 

Знакомство с процентами. Рабочие листы по математике для 7-го класса, учебные пособия и ключи к ответам.

Числа и операции (NCTM)

Понимать числа, способы представления чисел, отношения между числами и системы счисления.

Гибкая работа с дробями, десятичными знаками и процентами для решения задач.

Развитие значения процентов больше 100 и меньше 1.

Координаторы учебной программы 7 класса (NCTM)

Числа и операции, алгебра и геометрия: развитие понимания и применение пропорциональности, включая сходство

Учащиеся расширяют свою работу с отношениями, чтобы развить понимание пропорциональности, которое они применяют для решения одношаговых и многошаговых задач в различных контекстах. Они используют отношение и пропорциональность для решения самых разных процентных задач, включая задачи, связанные со скидками, процентами, налогами, чаевыми и процентным увеличением или уменьшением. Они также решают задачи о подобных объектах (включая фигуры), используя масштабные коэффициенты, которые связывают соответствующие длины объектов, или используя тот факт, что отношения длин внутри объекта сохраняются в подобных объектах. Учащиеся изображают пропорциональные отношения и определяют удельную норму как наклон связанной линии. Они отличают пропорциональные отношения (y/x = k или y = kx) от других отношений, в том числе обратно пропорциональных (xy = k или y = k/x).

Числа и операции и алгебра: развитие понимания операций над всеми рациональными числами и решение линейных уравнений

Учащиеся расширяют понимание сложения, вычитания, умножения и деления вместе с их свойствами на все рациональные числа, включая отрицательные целые числа. Применяя свойства арифметики и рассматривая отрицательные числа в повседневных контекстах (например, ситуации, когда вы должны денег или измеряете высоту над и под уровнем моря), учащиеся объясняют, почему правила сложения, вычитания, умножения и деления с отрицательными числами имеют смысл. Они используют арифметику рациональных чисел, когда формулируют и решают линейные уравнения с одной переменной и используют эти уравнения для решения задач. Учащиеся делают стратегический выбор процедур для решения линейных уравнений с одной переменной и эффективно их реализуют, понимая, что когда они используют свойства равенства для выражения уравнения по-новому, решения, которые они получают для нового уравнения, также решают исходное уравнение.

Связи с координационными центрами 7-го класса (NCTM)

Числа и операции: В 4-м классе учащиеся использовали эквивалентные дроби для определения десятичных представлений дробей, которые они могли представить с конечными десятичными знаками. Учащиеся теперь используют деление, чтобы выразить любую дробь в виде десятичной дроби, включая дроби, которые они должны представлять с помощью бесконечных десятичных знаков. Они находят этот метод полезным при работе с пропорциями, особенно с процентами. Свою работу с делением дробей учащиеся связывают с решением уравнений вида ах = b, где а и b — дроби. Учащиеся продолжают развивать свое понимание умножения и деления, а также структуры чисел, определяя, является ли счетное число больше 1 простым, а если нет, разлагая его на произведение простых чисел.

Математика 7 класс | Проценты и масштабирование

Учащиеся расширяют и применяют свое понимание процентов, изучая увеличение и уменьшение процентов, приложения процентов, такие как налоги и простые проценты, а также геометрические чертежи в масштабе.

Раздел 5

7-й класс

Fishtank Plus для математики

Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.

Подробнее

Оценка

---

Следующие тесты сопровождают Единицу 5.

Предварительная часть

Предложите учащимся выполнить Предварительную оценку и Предварительную самооценку учащегося перед началом модуля. Используйте Руководство по анализу предварительной оценки, чтобы определить пробелы в фундаментальном понимании и наметить план ускорения обучения на протяжении всего модуля.

Промежуточный блок

Предложите учащимся пройти промежуточный этап оценки.

Post-Unit

Используйте приведенные ниже ресурсы для оценки усвоения учащимися содержания модуля и плана действий для будущих модулей.

• Постмодальная оценка

• Ключ к ответам после модульной оценки

• Руководство по анализу послемодульной оценки

  92F25A3F-8529-4314-9899-6EE68694E3D0

• Самооценка студентов после окончания обучения

Расширенный пакет оценивания

Используйте данные учащихся для управления планированием с помощью расширенного набора модульных оценок, помогающих оценить способности учащихся с базовыми навыками и понятиями, а также их прогресс в изучении содержания модуля.

Скачать образец

Подготовка блока

---

Интеллектуальная подготовка

Рекомендации по подготовке к изучению этого модуля

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

Запуск модуля

Подготовьтесь к преподаванию этого модуля, погрузившись в стандарты, большие идеи и связи с предыдущим и будущим содержанием. Запуск модулей включает в себя серию коротких видеороликов, целевую литературу и возможности для планирования действий.

Обновление до Плюс

Интернализация стандартов посредством итоговой оценки

• Пройдите заключительную оценку. Аннотировать для:
  • Стандарты, которым соответствует каждый вопрос
  • Стратегии и представления, используемые на ежедневных уроках
  • Связь с основными вопросами раздела
  • Уроки, на которые Оценка указывает

Интернализация траектории отряда

• Прочитайте и аннотируйте сводку отряда.
• Обратите внимание на последовательность понятий в модуле, используя карту урока.
• Выполнить все целевые задачи. Аннотируйте целевые задачи для:
  • Основные понятия
  • Связь с вопросами послемодульной оценки
• Определите ключевые возможности для вовлечения учащихся в академический дискурс. Прочтите наш Инструмент для учителя на Академический дискурс и ссылайтесь на него на протяжении всего модуля.

Интеллектуальная подготовка для конкретного модуля

• Прочтите следующие последовательности для общепринятых базовых государственных стандартов по математике для стандартов, относящихся к этому разделу.
  • Геометрия, 7-8, средняя школа
  • 6-7, Соотношения и пропорциональные отношения
  • Система счисления, 6-8
  • 6–8, Выражения и уравнения 
• Прочтите следующую таблицу, в которой указаны модели, используемые во всем устройстве

Модель	Пример
Стол	280 учеников посещают карнавал, что составляет 80% школы.
Схема ленты	280 учеников посещают карнавал, что составляет 80% школы.
Двойная числовая строка	280 учеников посещают карнавал, что составляет 80% школы.
Доля	280 учеников посещают карнавал, что составляет 80% школы. $$\frac{280}{x}=\frac{80}{100}$$ $$x=350$$
Уравнение процентов	280 учеников посещают карнавал, что составляет 80% школы. $280=0,80x$ $$x=280/0,80$$ $$x=350$$

Основные понятия

Основные математические понятия, которые учащиеся должны понять в этом разделе

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

• Проценты можно использовать для понимания связи между частями количества и целым количеством. Проценты также можно использовать для понимания того, как величины изменяются по отношению к их начальным значениям.
  В результате мы можем использовать проценты для моделирования многих реальных приложений, таких как изменение цен и простой процент.
• Чертежи в масштабе пропорциональны друг другу по показателю, называемому коэффициентом масштабирования.
• Масштабы, такие как «1 дюйм соответствует 10 милям», позволяют нам рисовать и работать с большими или маленькими объектами и мерами в масштабе, например, с картами и планами этажей.

Словарный запас

Условия и обозначения, которые учащиеся изучают или используют в блоке

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

Комиссия

Соответствующие

Дисконтирование

Markup/Markdown

Измерение

%. процентная ошибка

коэффициент масштабирования

масштаб

масштаб изображения/чертежа

простые проценты

налог

чаевые

Чтобы увидеть весь словарный запас для модуля 5, просмотрите наш глоссарий лексики для 7-го класса.

Материалы

Материалы, иллюстрации и инструменты, которые потребуются учителям и учащимся для работы с этим модулем

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

• Веревка (1 на учащегося) — здесь также работает другой гибкий измерительный инструмент.
• Миллиметровая бумага (2-3 листа на учащегося)
• Чистый лист бумаги (2-3 листа на учащегося)
• Линейка (1 на ученика)

Чтобы ознакомиться со всеми материалами, необходимыми для этого курса, ознакомьтесь с нашим Обзором материалов курса для 7-го класса.

Карта урока

---

Тема A: проценты, части и целое

Определение процентов и преобразование между дробями, десятичными знаками и процентами. Решайте процентные задачи в уме с эталонными процентами.

7.РП.А.3

Найти процент от числа, если заданы проценты и целое.

7.NS.A.3 7.РП.А.3

Найдите целое по части и процентам.

7.NS.A.3 7.РП.А.3

Найдите процент от данных части и целого.

7.NS.A.3 7.РП.А.3

Создайте бесплатную учетную запись, чтобы получить доступ к тысячам планов уроков.

Уже есть учетная запись? Войти

Тема B: Процентное увеличение и уменьшение

Найдите новую сумму, учитывая исходную и процентное увеличение или уменьшение.

7.EE.A.2 7.РП.А.3

Найдите исходную сумму, учитывая новую сумму после увеличения или уменьшения на заданный процент.

7.EE.A.2 7.РП.А.3

Найдите процент увеличения или уменьшения исходной и новой сумм.

7.РП.А.3

Быстро решайте процентные задачи, включая процентное увеличение и уменьшение.

7.EE.A.2 7.РП.А.3

Создайте бесплатную учетную запись, чтобы получить доступ к тысячам планов уроков.

Уже есть учетная запись? Войти

Тема C: Процент приложений

Решение процентных приложений, включая скидки, налоги и чаевые.

7.EE.B.3 7.РП.А.3

Решение процентных приложений, включающих простые проценты, комиссионные и другие сборы.

7.EE.B.3 7.РП.А.3

Решите процентные приложения, включающие измерение и процентную ошибку.

7.EE.B.3 7.РП.А.3

Создайте бесплатную учетную запись, чтобы получить доступ к тысячам планов уроков.

Уже есть учетная запись? Войти

Тема D: Чертежи в масштабе

Определение и идентификация масштабных изображений.

7.G.A.1

Определите и определите масштабный коэффициент между двумя изображениями в масштабе. Используйте коэффициент масштабирования для рисования масштабных изображений.

7.G.A.1 7.РП.А.3

Используйте весы для определения фактических размеров.

7.G.A.1 7.РП.А.3

Используйте масштабы на картах, чтобы найти фактические расстояния между локациями.

7.G.A.1 7.РП.А.3

Используйте масштабы на планах этажей, чтобы найти фактические измерения и размеры.

7.G.A.1 7.РП.А.3

Расчет фактических площадей по чертежам в масштабе.

7. G.A.1 7.РП.А.3

Рисовать чертежи в разных масштабах.

7.G.A.1 7.РП.А.3

Создайте масштабный план этажа (необязательно).

7.G.A.1 7.РП.А.3

Создайте бесплатную учетную запись, чтобы получить доступ к тысячам планов уроков.

Уже есть учетная запись? Войти

Общие базовые стандарты

---

Ключ

Основной кластер

Вспомогательный кластер

Дополнительный кластер

Основные стандарты

Стандарты содержания, рассматриваемые в этом модуле

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

Выражения и уравнения

• 7.EE.A.2 — Поймите, что переписывание выражения в разных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней величины. Например, a + 0,05a = 1,05a означает, что «увеличение на 5%» равносильно «умножению на 1,05».

• 7. EE.B.3 — Решайте многоэтапные задачи из реальной жизни и математические задачи, связанные с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), стратегически используя инструменты. Применять свойства операций для вычисления с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает надбавку на 10%, она будет получать дополнительную 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить перекладину для полотенец длиной 9 3/4 дюйма в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить перекладину примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.

Геометрия

• 7. Г.А.1 — Решать задачи, связанные с чертежами геометрических фигур в масштабе, включая вычисление фактических длин и площадей по чертежу в масштабе и воспроизведение чертежа в масштабе в другом масштабе.

Соотношения и отношения пропорциональности

• 7.РП.А.3 — Используйте пропорциональные отношения для решения многошаговых задач на соотношение и проценты. Примеры: простой процент, налог, надбавки и уценки, чаевые и комиссионные, сборы, процентное увеличение и уменьшение, процентная ошибка.

Система счисления

• 7.НС.А.3 — Решайте реальные и математические задачи, связанные с четырьмя операциями с рациональными числами. Вычисления с рациональными числами распространяют правила работы с дробями на сложные дроби.

Основополагающие стандарты

Стандарты, рассмотренные в предыдущих разделах или классах, которые важны для текущего раздела

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

Геометрия

• 6. Г.А.1

Число и операции — дроби

• 5.NF.B.5

• 5.НФ.Б.5.А

• 5.НФ.Б.5.Б

Соотношения и отношения пропорциональности

• 6.РП.А.3

• 6.РП.А.3.С

• 7.РП.А.2

Будущие стандарты

Стандарты будущих классов или разделов, которые связаны с содержанием данного раздела

A628D5C3-5B97-4E03-B1EC-5AD5C66D8950

Геометрия

• 8.Г.А.2

• 8.Г.А.4

Стандарты математической практики

• CCSS.

  No related posts.