Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Треугольники |
| Типы треугольников |
| Признаки равенства треугольников |
| Признаки равенства прямоугольных треугольников |
Типы треугольников
Рассмотрим три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки (рис. 1).
Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника, а концы отрезков (три точки, не лежащие на одной прямой) – вершинами треугольника.
Рис.1
В таблице 1 перечислены все возможные типы треугольников в зависимости от величины их углов.
Таблица 1 – Типы треугольников в зависимости от величины углов
| Рисунок | Тип треугольника | Определение |
| Остроугольный треугольник | Треугольник, у которого все углы острые, называют остроугольным | |
| Прямоугольный треугольник | Треугольник, у которого один из углов прямой, называют прямоугольным | |
| Тупоугольный треугольник | Треугольник, у которого один из углов тупой, называют тупоугольным |
| Остроугольный треугольник |
Определение: Треугольник, у которого все углы острые, называют остроугольным |
| Прямоугольный треугольник |
Определение: Треугольник, у которого один из углов прямой, называют прямоугольным |
| Тупоугольный треугольник |
Определение: Треугольник, у которого один из углов тупой, называют тупоугольным |
В зависимости от длин сторон выделяют два важных типа треугольников.
Таблица 2 – Равнобедренный и равносторонний треугольники
| Рисунок | Тип треугольника | Определение |
| Равнобедренный треугольник | Треугольник, у которого две стороны равны, называют равнобедренным треугольником. В этом случае две равные стороны называют боковыми сторонами, а третью сторону называют основанием равнобедренного треугольника | |
| Равносторонний (правильный) треугольник | Треугольник, у которого все три стороны равны, называют равносторонним или правильным треугольником |
| Равнобедренный треугольник |
Определение: Треугольник, у которого две стороны равны, называют равнобедренным треугольником. В этом случае две равные стороны называют боковыми сторонами, а третью сторону называют основанием равнобедренного треугольника |
| Равносторонний (правильный) треугольник |
Определение: Треугольник, у которого все три стороны равны, называют равносторонним или правильным треугольником |
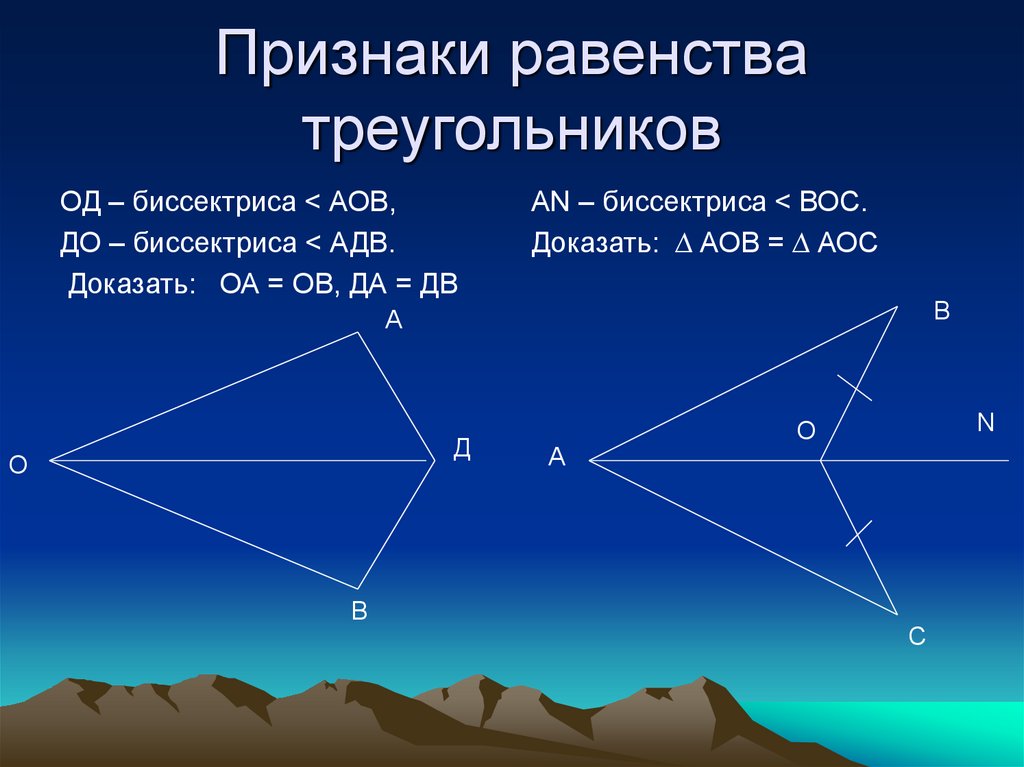
Признаки равенства треугольников
Треугольники называют равными, если их можно совместить наложением.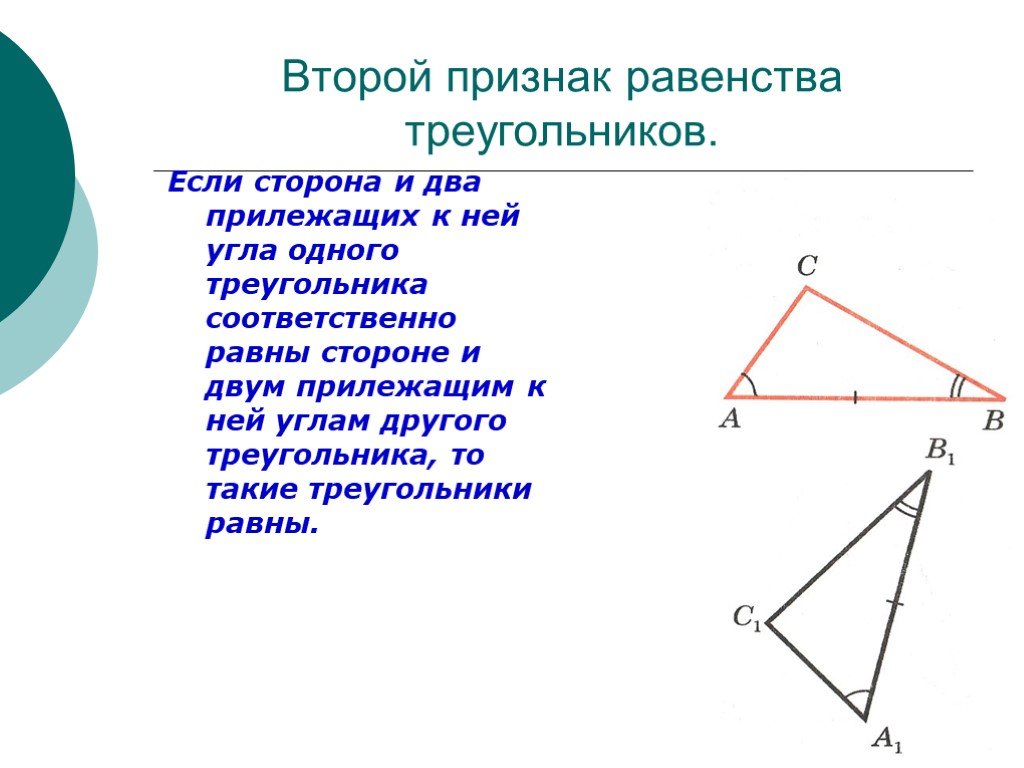
В таблице 3 приведены признаки равенства треугольников.
Таблица 3 – Признаки равенства треугольников
| Рисунок | Название признака | Формулировка признака |
| Признак равенства треугольников по двум сторонам и углу между ними | Если две стороны одного треугольника и угол между ними соответственно равны двум сторонам другого треугольника и углу между ними, то такие треугольники равны | |
| Признак равенства треугольников по стороне и двум прилежащим к ней углам | Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны | |
| Признак равенства треугольников по трём сторонам | Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны |
| Признак равенства треугольников по двум сторонам и углу между ними |
Формулировка признака.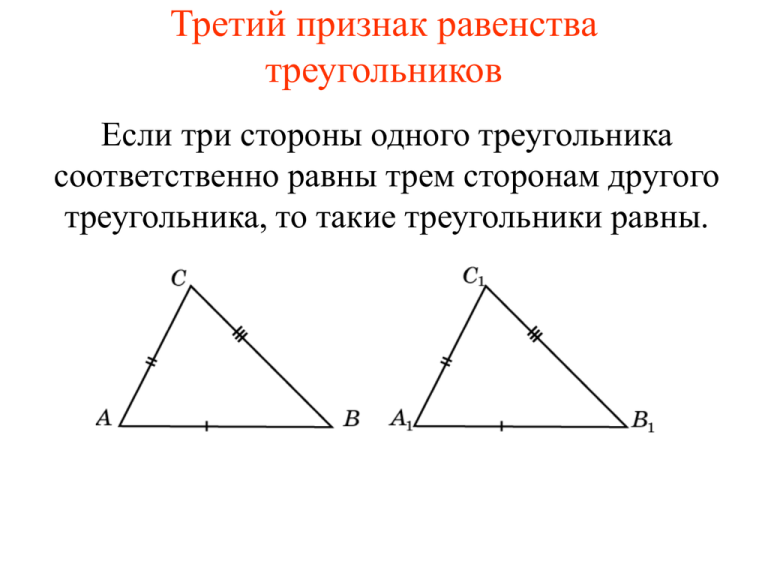 Если две стороны одного треугольника и угол между ними соответственно равны двум сторонам другого треугольника и углу между ними, то такие треугольники равны |
| Признак равенства треугольников по стороне и двум прилежащим к ней углам |
| Формулировка признака. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны |
| Признак равенства треугольников по трём сторонам |
| Формулировка признака. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны |
Признаки равенства прямоугольных треугольников
Для сторон прямоугольных треугольников принято использовать следующие названия.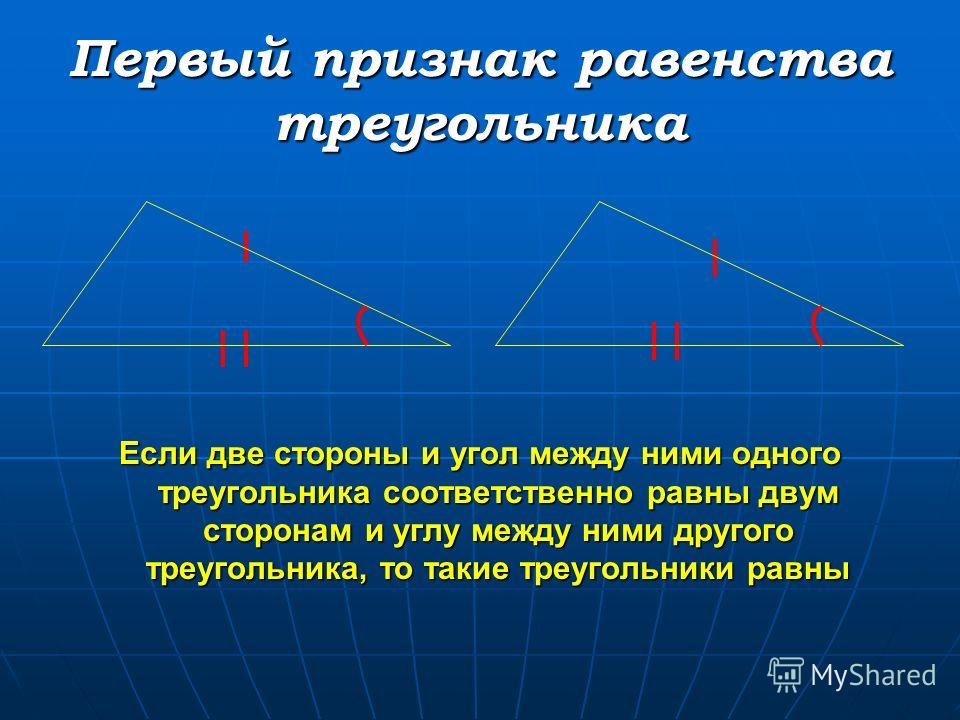
Гипотенузой называют сторону прямоугольного треугольника, лежащую против прямого угла (рис. 2), две другие стороны называют катетами.
Рис.2
Таблица 4 – Признаки равенства прямоугольных треугольников
| Рисунок | Название признака | Формулировка признака |
| Признак равенства прямоугольных треугольников по двум катетам | Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники равны | |
| Признак равенства прямоугольных треугольников по катету и прилежащему острому углу | Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны | |
| Признак равенства прямоугольных треугольников по катету и противолежащему острому углу | Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны | |
| Признак равенства прямоугольных треугольников по гипотенузе и острому углу | Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны | |
| Признак равенства прямоугольных треугольников по катету и гипотенузе | Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие прямоугольные треугольники равны |
| Признак равенства прямоугольных треугольников по двум катетам |
Формулировка признака.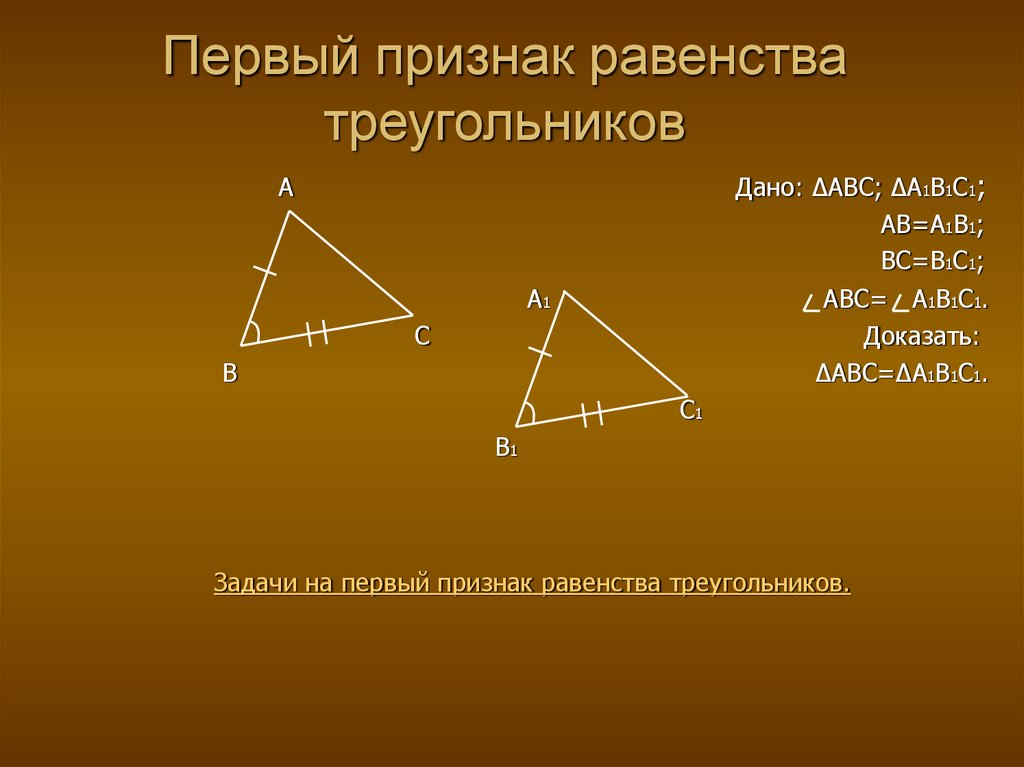 Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники равны |
| Признак равенства прямоугольных треугольников по катету и прилежащему острому углу |
| Формулировка признака. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны |
| Признак равенства прямоугольных треугольников по катету и противолежащему острому углу |
| Формулировка признака. Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны |
| Признак равенства прямоугольных треугольников по гипотенузе и острому углу |
Формулировка признака.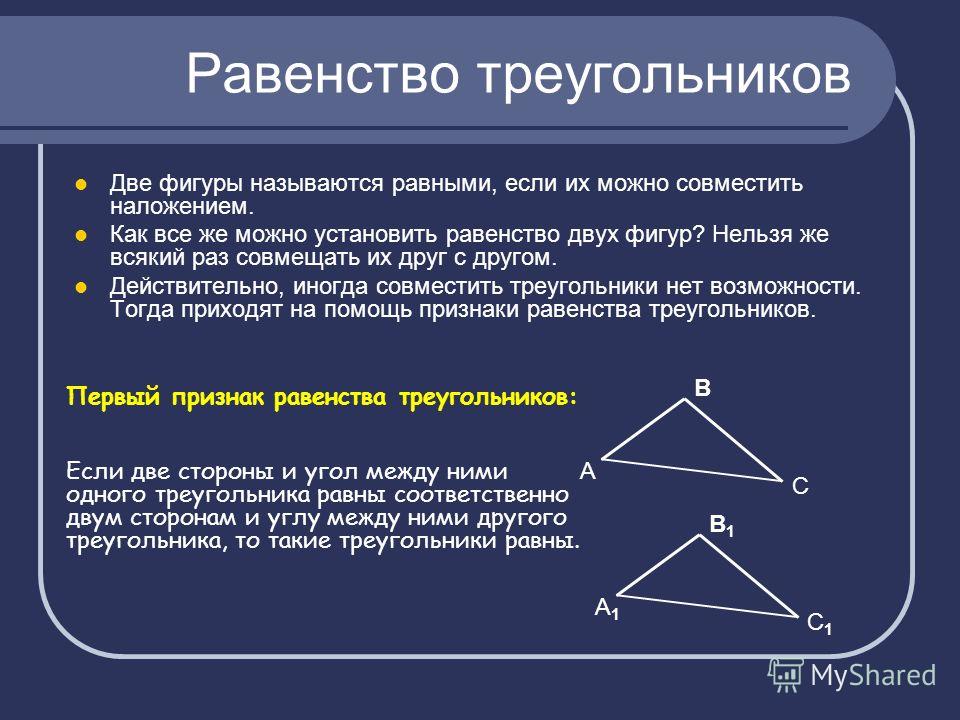 Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники равны |
| Признак равенства прямоугольных треугольников по катету и гипотенузе |
| Формулировка признака. Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие прямоугольные треугольники равны |
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
формулировка и доказательство (7 класс)
В этой статье мы расскажем, как можно сформулировать и доказать первый признак равенства треугольников, который проходят в 7 классе.
Формулировка первого признака равенства треугольников
«Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.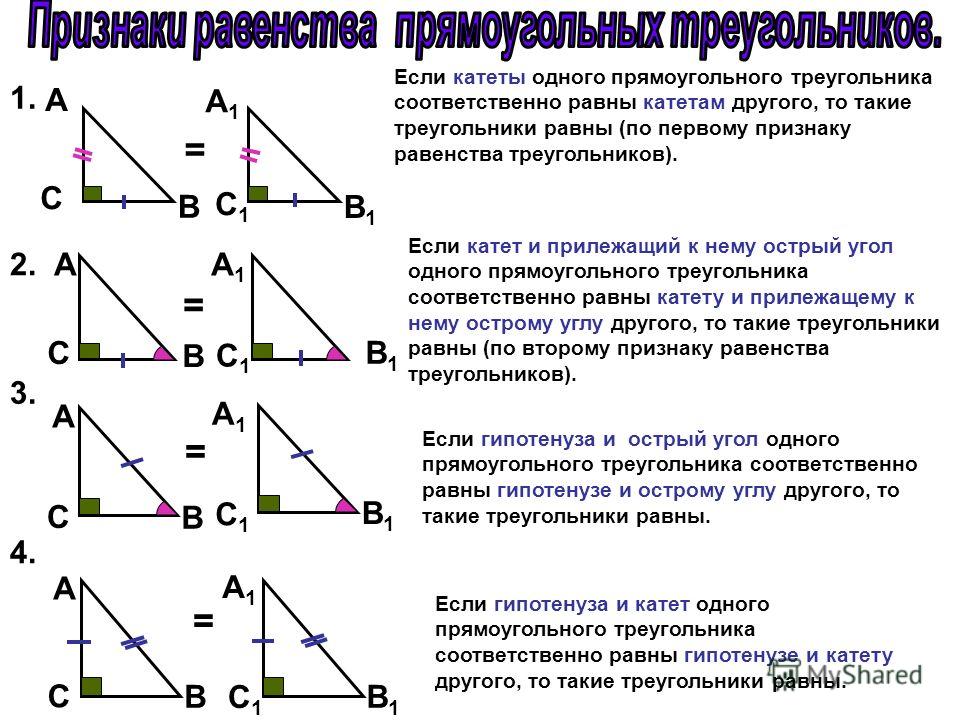
»
Сокращенно его называют равенство «по двум сторонам и углу между ними».
Прежде чем перейти к доказательству теоремы необходимо вспомнить, что называют треугольником и в каком случае можно утверждать, что два треугольника равны.
Что такое треугольник и когда они считаются равными?
Треугольник – это геометрическая фигура из трёх отрезков, соединяющих три точки (при условии, что они не лежат на одной прямой. Эти точки считаются вершинами треугольника. А соединяющие их отрезки – сторонами).
На рисунке 1 представлен треугольник ABС. Который имеет три вершины (А, В и С). И стороны – АВ, АС и ВС.
Рисунок 1
Треугольники считаются равными, когда все их стороны и углы соответственно равны друг другу (в случае, когда равны лишь углы, а стороны пропорциональны, треугольники называются подобными). Таким образом очевидно, что равные треугольники можно наложить друг на друга – и они полностью совпадут.
Доказательство первого признака равенства треугольников
Дано:
Два треугольника: ABC и DEF (рисунок 2).
Рисунок 2
По условию теоремы две пары отрезков этих треугольников равны между собой (АС = FD и СВ = EF). Углы между отрезками также равны (т.е. ∠АСВ = ∠EFD).
Доказать, что треугольник ABC равен треугольнику DEF.
Доказательство:
- Поскольку имеется равенство углов (∠АСВ = ∠EFD), треугольники можно наложить друг на друга, так чтобы вершина С совпадала с вершиной F.
- При этом отрезки СА и СВ наложатся на отрезки FE и FD.
- А поскольку отрезки двух треугольников равны между собой (АС = FD и СВ = EF по условию), то отрезок АВ также совпадёт со стороной ED.
- Это в свою очередь даст совмещение вершин А и D, В и Е.
- Следовательно, треугольники полностью совместятся, а значит, они равны.
Теорема доказана.
Скорее всего, Вам будет интересно:
- Третий признак равенства треугольников формулировка и доказательство
- Свойства вписанной в треугольник окружности
- Средняя линия трапеции: чему равна, свойства, доказательство теоремы
- Свойства медианы в прямоугольном треугольнике с доказательствами
- Таблица прямых и обратных тригонометрических функций, онлайн калькулятор
- Свойства прямоугольной трапеции
- Как найти область определения функции онлайн
- Состав служебного программного обеспечения
- Основные положения молекулярно-кинетической теории (МКТ), формулы МКТ
- Уравнение состояния идеального газа Менделеева-Клапейрона с выводом
конгруэнтных треугольников
конгруэнтных треугольниковПоказать рекламу
Скрыть рекламу
О рекламе
Треугольники конгруэнтны, если они имеют
ровно одинаковых трех сторон и ровно одинаковых трех углов .
Что такое «Конгруэнтность» … ?
Это означает, что одна форма может стать другой с помощью поворотов, переворотов и/или скольжений:
| Повернись! | ||
|---|---|---|
| Отражение | Переверни! | |
| Перевод | Слайд! |
(дополнительную информацию см. в разделе Конгруэнтность)
Конгруэнтные треугольники
Когда два треугольника конгруэнтны, они будут иметь ровно одинаковых трех сторон и ровно одинаковых трех углов .
Равные стороны и углы могут не находиться в одном и том же положении (если есть поворот или флип), но они есть.
Одинаковые стороны
Если стороны одинаковы, треугольники конгруэнтны.
Например:
| соответствует: | |||
| , а также на: |
потому что все они имеют одинаковые стороны .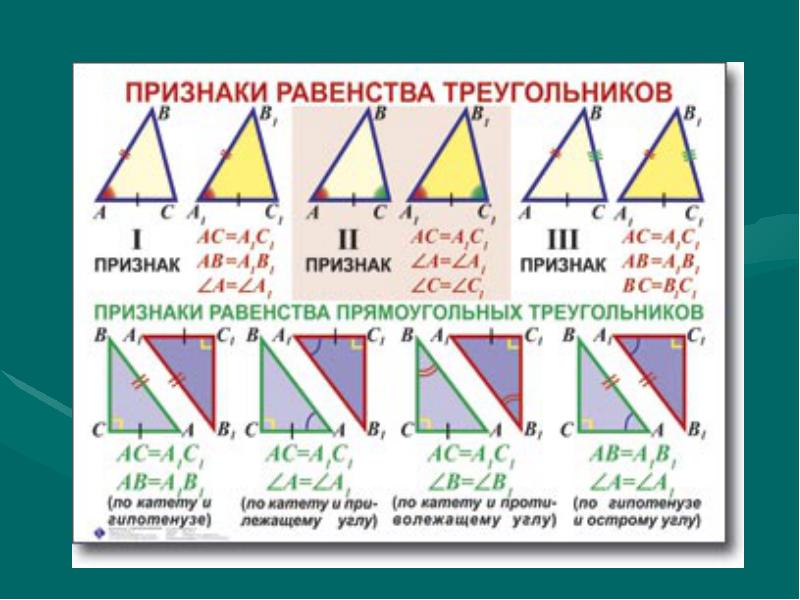
Но:
| это НЕ соответствует: |
, потому что у двух треугольников стороны не совпадают.
Одинаковые углы
Это также работает с углами? Не всегда!
Два треугольника с одинаковыми углами могут быть равны на :
| соответствует: |
только потому, что они одинакового размера
Но они могут НЕ быть конгруэнтными из-за разных размеров :
| равно , НЕ соответствует: |
потому что, хотя все углы совпадают, один больше другого .
Таким образом, просто наличие одинаковых углов не гарантирует их конгруэнтность.
Другие комбинации
Существуют другие комбинации сторон и углов, которые могут работать .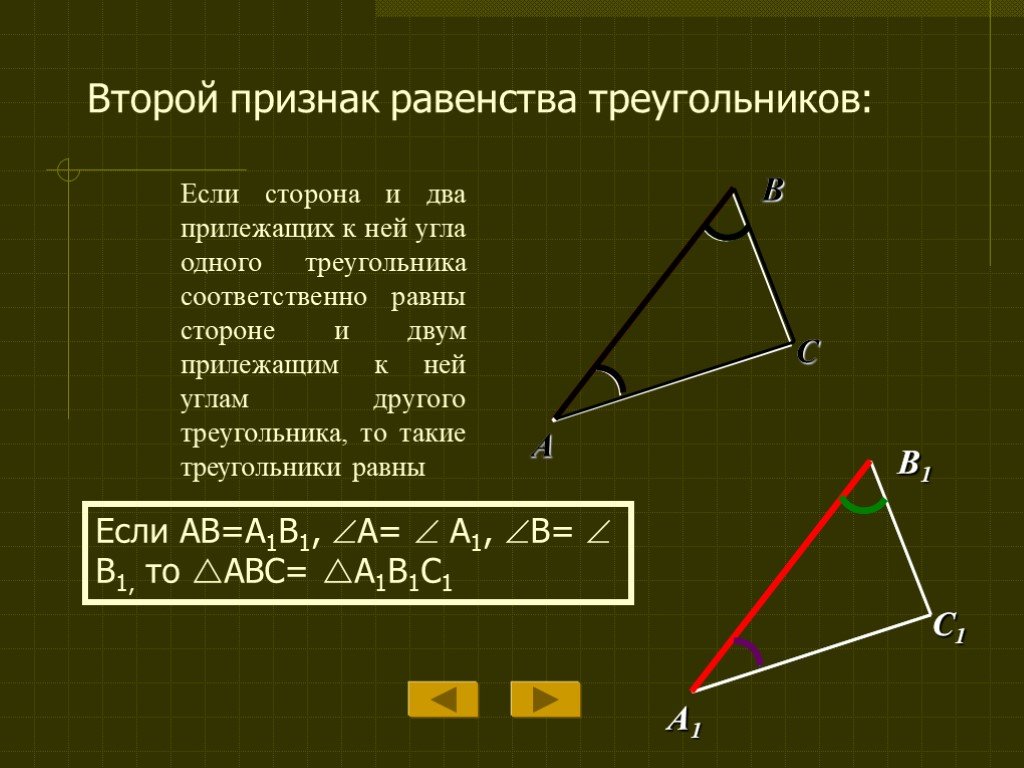
..
… подробнее см. Как определить, конгруэнтны ли треугольники
Маркировка
Когда два треугольника конгруэнтны, мы часто помечаем соответствующие стороны и углы следующим образом:
| соответствует: |
Стороны, отмеченные одной линией, имеют одинаковую длину. Аналогично для сторон, отмеченных двумя линиями. Также для сторон отмечены тремя линиями.
Углы, отмеченные одной дугой, равны по величине. Аналогично для углов, отмеченных двумя дугами. Также для углов, отмеченных тремя дугами.
Copyright © 2017 MathsIsFun.com
постулатов конгруэнтности треугольников | SAS, ASA, SSS, AAS, HL
Конгруэнтные треугольники — это треугольники с одинаковыми сторонами и углами. Три стороны одного точно равны трем сторонам другого. Каждый из трех углов одного равен углу другого.
Содержание
- Постулаты о конгруэнтности треугольников
- Детали в комплекте
- Сторона Сторона Сторона Постулат
- Боковой угол Боковой постулат
- Угол Боковой угол Постулат
- Угол Угол Сторона Теорема
- HL Постулат
- Доказательство с использованием конгруэнтности
Постулаты о конгруэнтности треугольников
Существует пять способов нахождения конгруэнтности двух треугольников:
- SSS или Side Side Side
- SAS или боковая угловая сторона
- ASA или угловая боковая сторона
- AAS, или угловая боковая сторона
- HL, или катет гипотенузы, только для прямоугольных треугольников
Входящие в комплект детали
Уголок , включенный в комплект поставки , расположен между двумя названными сторонами.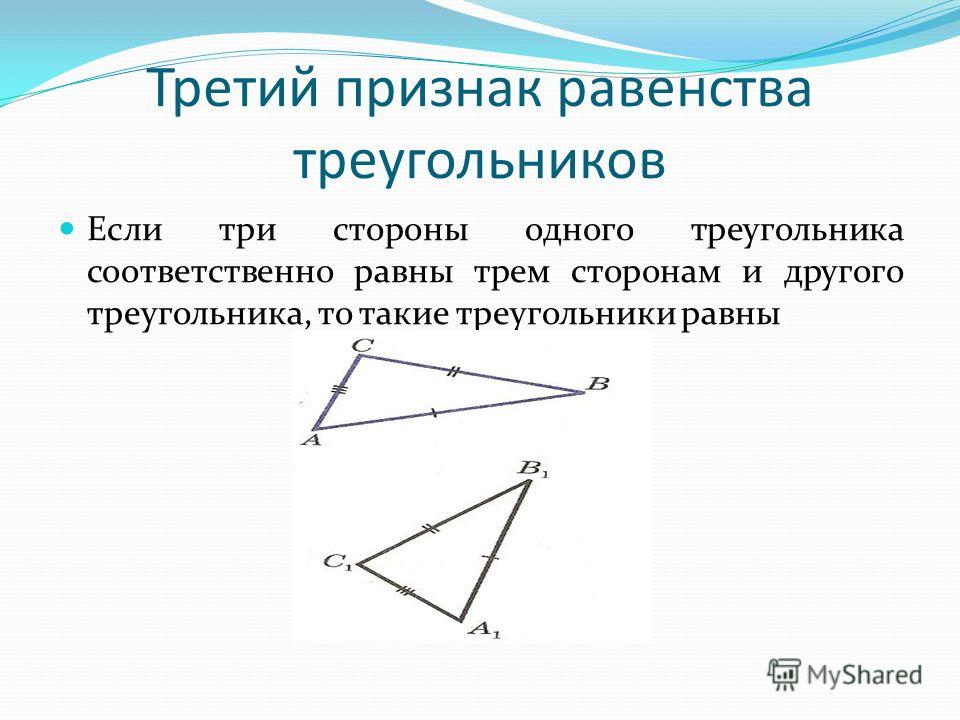
В △CAT ниже включенная ∠A находится между сторонами t и c:
Включенная сторона лежит между двумя именованными углами треугольника.
Сторона Сторона Сторона Постулат
Постулат – это утверждение, принимаемое за истинное без доказательства. Постулат SSS говорит нам:
Если три стороны одного треугольника конгруэнтны трем сторонам другого треугольника, то эти два треугольника конгруэнтны.
Совпадение сторон показано штриховкой, например: ∥. Для двух треугольников стороны могут быть отмечены одной, двумя и тремя штрихами.
Если △ACE имеет стороны, равные по размеру трем сторонам △HUM, то два треугольника конгруэнтны по SSS: прилежащий угол треугольника соответственно равен двум сторонам и прилежащему к нему углу другого треугольника, то эти треугольники равны.
△HUG и △LAB имеют по одному углу, равному ровно 63°. Соответствующие стороны g и b равны. Стороны h и l равны.
Сторона, прилежащий угол и сторона на △HUG и на △LAB равны.
Итак, согласно SAS, два треугольника конгруэнтны.
Угол Сторона Постулат угла
Этот постулат гласит:
Если два угла и прилежащая к ним сторона треугольника конгруэнтны двум углам и прилежащей к ним стороне другого треугольника, то эти два треугольника конгруэнтны.
У нас есть △MAC и △CHZ, сторона m которых равна стороне c. ∠A конгруэнтно ∠H, а ∠C конгруэнтно ∠Z. По постулату ASA эти два треугольника конгруэнтны.
Угол Угол Сторона Теорема
Нам даны два угла и не включенная сторона, сторона, противоположная одному из углов. Теорема об угле и стороне гласит:
Если два угла и не включенная в них сторона одного треугольника конгруэнтны соответствующим частям другого треугольника, то треугольники конгруэнтны.
Вот конгруэнтные △POT и △LID с двумя измеренными углами 56° и 52° и не включенной стороной 13 сантиметров: эти два треугольника равны.
Постулат HL
Исключительно для прямоугольных треугольников, как говорит нам постулат HL,
Два прямоугольных треугольника, которые имеют конгруэнтную гипотенузу и соответствующий конгруэнтный катет, конгруэнтны.