Признаки делимости чисел – таблица с примерами
4
Средняя оценка: 4
Всего получено оценок: 240.
4
Средняя оценка: 4
Всего получено оценок: 240.
Признаки делимости чисел сложно применять, поскольку их достаточно много. Зато знание таких признаков существенно экономит время, поскольку позволяет без деления узнать, делиться одно число на другое или нет. Разберемся в теме подробнее.
Что такое делимость?
Признаки делимости позволяют просто и быстро определить, возможно ли полностью поделить одно число на другое. А делимость это и есть возможность поделить одно число на друге без остатка.
Признаки делимости
Признаки делимости удобнее изучать, разбив возможные делители на группы. Поступим так же и рассмотрим делимость на каждую из групп в отдельности.
На 2,4,8
Эти числа в рассматриваемом вопросе сгруппированы, так как их признаки очень похожи друг на друга.
- Число делится на 2 только если является четным.
- Число делится на 4, если последние две цифры числа делятся на 4 или последние две цифры 00. Например, число 130 не делится на 4, так как 30 не делится на 4. А вот уже число 1400 можно поделить на 4.
- Число делится на 8, если последние две цифры числа нули или делятся на 8
На 3 и 9
Число делится на 3, если сумма цифр этого числа делится на 3. Рассмотрим число: 804. Оно делится на 3, поскольку сумма цифр 8+0+4=12 – делится на 3.
Число делится на 9, если сумма цифр числа делится на 9. Признак похож на признак делимости на число 3.
Интересно: Если число делится на 9, то оно делится и на 3. При этом, число, которое делится на 3 не всегда делится на 9.
На 5
Число делится на 5, если последняя цифра числа равняется 5 или нулю. Это наиболее известный признак делимости, наряду с делимостью на 2.
На 6
Чтобы число делилось на 6, оно должно делиться на 2 и 3, так как 2*3=6. Поэтому признак делимости на 6 это объединение признаков деления на 2 и на 3.
То есть: число делится на 6, если оно четное и сумма всех его цифр делится на 3
На 7
Самые сложные в восприятии признаки делимости на 7 и на 11. Число делится на 7, если разность сумм четных цифр числа и нечетных цифр чисел делится на 7.
Приведем пример: число 469 делится на 7. Почему? Сумма цифр на нечетных позициях 4+9=13. Сумма чисел на четных позициях 6. Разность получившихся сумм: 13-6=7, а это число делится на 7. Поэтому все число 469 делится на 7
На 10
Число делится на 10 только если последней цифрой числа является 0
По тому же принципу определяют делимость числа на 100, 1000 и так далее. Если у числа два нуля на конце, то оно делится на 100, если три нуля на конце, число делится на 1000 и так далее.
На 11
Число делится на 11 только, если разность сумм четных и нечетных цифр числа делится на 11 или равняется нулю Приведем пример:
Число 2035 делится на 11. Сумма цифр, стоящих на четных позициях: 2+3=5. Сумма нечетных цифр: 0+5=5.
Разность полученных выражений:5-5=0, значит число делится на 11.
Нельзя путать понятия четной позиции и четного числа. Цифра это знак, который используется для записи чисел. Число это набор цифр, каждая из которых стоит на своей позиции. В числе 127 всего три цифры. Цифра 1 стоит на первой позиции, цифра 2 на второй и так далее. На четной позиции находится цифра 2. На нечетных позициях цифры 1 и 7.
Чтобы быстрее запомнить все группы можно свести в таблицу признаков делимости чисел.
Признаки | Запомни |
Признак делимости на 2 | Число делится на 2, если его последняя цифра делится на 2 или является нулём. |
Признак делимости на 4 | Число делится на 4, если две его последние цифры нули или образуют число, делящееся на 4. |
Признак делимости на 8 | Число делится на 8, если три последние его цифры нули или образуют число, делящееся на 8. |
Признак делимости на 3 | Число делится на 3, если сумма всех его цифр делится на 3. |
Признак делимости на 6 | Число делится на 6, если оно делится одновременно на 2 и на 3. |
Признак делимости на 9 | Число делится на 9, если сумма всех его цифр делится на 9. |
Признак делимости на 5 | Число делится на 5, если его последняя цифра 5 или 0. |
Признак делимости на 25 | Число делится на 25, если его две последние цифры нули или образуют число, которое делится на 25. |
Признак делимости на 10,100 и 1000. | 10 делятся нацело только те числа, последняя цифра которых нуль. На 100 делятся нацело только те числа, две последние цифры которых нули. На 1000 делятся нацело только те числа, три последние цифры нули. |
Признак делимости на 11 | Число делится на 11, если сумма цифр, которые стоят на четных местах равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на 11. |
Что мы узнали?
Мы поговорили о признаках делимости. Расписали все существующие признаки по группам. В особо сложных ситуациях привели примеры.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Елена Сергеевна
5/5
Елена Фарафонова
5/5
Ольга Гребенева
4/5
Оценка статьи
4
Средняя оценка: 4
Всего получено оценок: 240.
А какая ваша оценка?
Признаки делимости чисел | umath.ru
Содержание
- Таблица признаков делимости чисел
- Доказательство признаков делимости чисел
- Признаки делимости по последним цифрам [2, 4, 5, 8, 10, 25]
- Признаки делимости по сумме цифр [3, 9, 11]
- Признаки делимости по сумме граней [7, 11, 13, 37]
Признаки делимости — особенности чисел, которые помогают быстро определить, делится ли данное число на другое.
Знание этих признаков необходимо при решении многих арифметических задач. Кроме того, умение пользоваться признаками делимости часто пригождается при решении задач ЕГЭ, особенно задания С6.
Таблица признаков делимости чисел
| Число | Число делится на число тогда и только тогда, когда |
| 2 | Последняя цифра числа делится на 2 |
| 3 | Сумма цифр числа делится на 3 |
| 4 | Число, составленное из двух последних цифр числа , делится на 4 |
| 5 | Число оканчивается цифрой 0 или 5 |
| 6 | Число делится на 2 и на 3 |
| 7 | Знакочередующаяся сумма трёхзначных граней* числа делится на 7 |
| 8 | Число, составленное из трёх последних цифр числа , делится на 8 |
| 9 | Сумма цифр числа делится на 9 |
| 10 | Число оканчивается цифрой 0 |
| 11 | Знакочередующаяся сумма цифр числа делится на 11 |
| 12 | Число делится на 3 и на 4 |
| 13 | Знакочередующаяся сумма трёхзначных граней* делится на 13 |
| 25 | Число, составленное из двух последних цифр числа , делится на 25 |
*Грани числа – числа, полученные при разбиении исходного числа на двузначные или трёхзначные числа, взятые справа налево.
Например, разбиение числа 1234567 на двузначные грани выглядит так: 1|23|45|67, а на трёхзначные так: 1|234|567.
Признаки делимости чисел и их доказательство
Пусть натуральное число имеет десятичную запись
где — цифры этого числа,
Разобьём признаки делимости на три группы. Доказательства признаков делимости в каждой группе основаны на одной и той же идее.
Признаки делимости по последним цифрам
| Если | то делится на |
| (последняя цифра числа) делится на 2 или 5 | 2 или 5 соответственно |
| (число, составленное из двух последних цифр числа ) делится на 4 или 25 | 4 или 25 соответственно |
| (число, составленное из трёх последних цифр числа ) делится на 8 | 8 |
| равно 0 | 10 |
Приведём её на примере признака делимости на 25. Распишем число так:
Число 100 делится на 25, поэтому если число делится на 25, то и делится на 25. Заметим, что обратное утверждение тоже верно.
Признаки делимости по сумме цифр
| Если | то делится на |
| Сумма цифр числа делится на 3 или 9 | 3 или 9 соответственно |
| Знакочередующаяся сумма цифр числа делится на 11 | 11 |
Выражение под первыми скобками делится на 9. Поэтому число делится на 3 или 9 тогда и только тогда, когда число делится на 3 или 9 соответственно.
Докажем признак делимости на 11. Для этого прежде заметим, что все числа вида , то есть числа 11, 1001, 100001 и т.д., делятся на 11. Покажем это на примере числа 100001:
Число распишем следующим образом:
Все слагаемые в первых скобках делятся на 11, поэтому число делится на 11 тогда и только тогда, когда на 11 делится знакопеременная сумма цифр числа .
Признаки делимости по сумме граней
Введём следующее определение.
Определение.Двузначные грани числа — это числа, которые получены разбиением исходного числа на двузначные числа. Например, разбиение числа 123456789 на двузначные грани выглядит так: 1|23|45|67|89 (разбиение числа начинается с его конца). Числа 1, 23, 45, 67, 89 являются двузначными гранями числа 123456789.
Трёхзначные грани числа — это числа, полученные разбиением исходного числа на трёхзначные числа. Например, разбиение числа 1234567890 на трёхзначные грани выглядит так: 1|234|567|890. Числа 1, 234, 567, 890 являются трёхзначными гранями числа 1234567890.
Перейдём к признакам делимости.
| Если | то делится на |
| Сумма двузначных граней делится на 11 | 11 |
| Сумма трёхзначных граней делится на 37 | 37 |
| Знакочередующаяся сумма трёхзначных граней делится на 7, 11, 13 | 7, 11, 13 соответственно |
В левых скобках все числа делятся на 11, поэтому число делится на 11 тогда и только тогда, когда сумма его двузначных граней делится на 11.
Остальные признаки доказываются аналогично.
Признаки делимости чисел на 2, 3, 4, 5, 9,10, 11, 25
Главная » Задания » Домашка
Автор Admin На чтение 3 мин. Просмотров 7.4k. Обновлено
Признаки делимости — это такие признаки, благодаря которым мы можем определить без расчетов, делится ли число на другое нацело (без остатка) или нет, т.е. является ли число (делимое) кратно другому (делителю).
Рассмотрим конкретные признаки делимости на числа 2, 3, 4, 5, 9,10, 11, 25 и приведем примеры. Для наглядности выбран вид изложения материала — табличный. Внизу статьи вы сможете скачать наглядные материалы для лучшего усвоения данной темы, а также шпаргалку по данной теме.
Содержание
- Таблица
- Признаки делимости на составное число
- Шпаргалка
- Задача
Таблица
Признак делимости | Примеры |
Число делится на 2. | 18 : 2 = 9 364 : 2 = 182 7395610 : 2 = 3697805 8356489634 : 2 = 4178244817 |
Число делится на 3, если сумма чисел, входящих в состав числа делится на 3 без остатка. | 192 : 3 = 64 (1 + 9 + 2 = 12; 12 делится на 3), 768 : 3 = 256 (7 + 6 + 8 = 21; 21 делится на 3) |
Число делится на 4, если число оканчивается на два нуля или две последние цифры составляют число, которое делится на 4 нацело. | 5700 : 4 = 1425 6324 : 4 = 1581 (24 делится на 4) 648616 : 4 = 162154 (16 делится на 4) 100 : 4 = 25 |
Число делится на 5, если оканчивается на 0 или 5. | 635 : 5 = 127 867420 : 5 = 173484 5765 : 5 = 1153 6140 : 5 = 1228 |
Число делится на 6, если оно делится без остатка и на 2, и на 3 | 3144 : 6 = 524 (3144 делится на 2, так как заканчивается на 4 – признак делимости на 2; 3 + 1 + 4 + 4 = 12; 12 делится на 3) Соответственно 3144 делится на 6. |
Число делится на 7, если разность между делимым без последней цифры и удвоенным числом единиц, делится на 7 | 287 : 7 = 41 (28 – 7×2=28-14=14; 14 делится на7) |
Число делится на 8, если делимое заканчивается на 3 нуля или три последних числа, составляющих делимое делятся на 8. | 456000 : 8 = 57000 87000 : 8 = 10875 1432 : 8 = 179 (т.к. 432 делится на 8; 432 : 8 = 54). |
Число делится на 9, если сумма цифр, входящих в состав числа делится на 9. | 603 : 9 = 67 ( 6 + 0 + 3 = 9, 9 делится на 9). Поменяем местами цифры в делимом и проверим снова кратность числа 96 630 : 9 = 70 (6 + 3 + 0 = 9), 5832 : 9 = 648 (5 + 8 + 3 + 2 = 18; 18 делится на 9) |
Число делится на 10, если делимое заканчивается на 0. Чтобы разделить число на 10, нужно убрать о из разряда единиц. | 8510 : 10 = 851 546700 : 10 = 54670 750 : 10 = 75 6340 : 10 = 634 |
Число делится на 11, если суммы цифр, которые занимают четные позиции в числе равны сумме цифр, занимающих нечетные позиции или отличаются на 11. | 2695 : 11 = 245 (2 + 9 = 6 + 5 = 11) 1232 : 11 = 112 (1 + 3 = 2 + 2 = 4) 3641 : 11 = 331 (3 + 4 = 6 + 1 = 7) |
Число делится на 25, если оно заканчивается на 00, 25, 50, 75, т.е. последние 2 цифры, входящие в состав числа делятся на 25. | 75600 : 25 = 3024 75625 : 25 = 3025 75650 : 25 = 3026 75675 : 25 = 3027 |
Такое число называют чётным, если число разряда единиц делится на 2, т.е. число должно оканчиваться на цифры 0, 2, 4, 6, 8.
Признаки делимости на составное число
Если нам нужно узнать делится ли число на какое-нибудь составное, то нам нужно разложить делитель на два множителя, признаки делимости которых известны.
Посмотрите делится ли исходное число (делимое) на каждый из этих множителей. Если ответ положительный, то число делится на составное.
Примеры:
- Признак делимости на 15. Число должно делится на 3 и на 5 без остатка (15 = 3 x 5). Число 345 делится на 15, так как имеет признаки делимости на 3 (3 + 4 + 5 = 12; 12 делится на 3) и на 5 (число 345 оканчивается на 5). 345 : 15 = 23
- Признак делимости на 18. Исходное число должно делится на 2 и на 9. Пример, 990 делится на 18, так как оно делится на 2 (990 оканчивается на 0) и на 9 (9 + 9 + 0 = 18; 18 делится на 9). 990 : 18 = 55
- Признак делимости на 12. Число должно делится на 3 и на 4. Пример, 324 делится на 12, так как делится на 3 (3 + 2 + 4 = 9; 9 делится на 3) и на 4 (последние две цифры, входящие в состав числа делятся на 4). 324 : 12 = 27
- Признак делимости на 22. Число должно делится на 11 и на 2 (быть чётным). 3454 делится на 11 (т. к. 3 + 5 = 4 + 4) и на 2 (число чётное, оканчивается на 4). 3454 : 22 = 157
к. 3 + 5 = 4 + 4) и на 2 (число чётное, оканчивается на 4). 3454 : 22 = 157Шпаргалка
Эту таблицу вы можете распечатать, чтобы повесить на стену для лучшего запоминания.
Скачать в PNG или PDF (рекомендуется для печати)
И шпаргалка маленького размера ( 10 на 6 см) в виде таблицы
Скачать и распечатать в ворде
Задача
Пользуясь признаками делимости, из данных чисел 1368,2121,2178,4356,5635,7221,8484. Выберете числа кратные
- 5
- 2
- 9
- 3
Ответ: Числа, которые делятся на 5: 5635
Числа с признаками делимости 2: 1268, 2178, 4356, 8484
Числа, кратные 9: 1368, 2178, 4356
Числа, кратные 3: 1368, 2121, 2178, 4356, 7221, 8484
Признаки делимости чисел
Признаки делимости чисел Для удобства пользования, признаки делимости чисел на 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 представлены в таблице.
Кроме этих признаков делимости чисел, существуют признаки делимости и на другие числа. Примеры проверки делимости целых чисел с применением правил, приведенных в таблице делимости чисел, находятся под таблицей делимости чисел.
На 2 (два) делятся все числа, у которых последней цифрой является 0 (ноль), 2 (два), 4 (четыре), 6 (шесть), 8 (восемь). Другими словами, если число оканчивается на ноль, два, четыре, шесть, восемь, то оно делится на два. Например: числа 120 (сто двадцать), 52 (пятьдесят два), 274 (двести семьдесят четыре), 16 (шестнадцать), 2 098 (две тысячи девяносто восемь) делятся на 2 (два). Числа 101 (сто один), 13 (тринадцать), 7 565 (семь тысяч пятьсот шестьдесят пять), 7 (семь), 19 (девятнадцать) не делятся на 2 (два), поскольку при делении этих чисел в остатке остается одна 1 (единица).
Если число делится на 2 (два), то его называют четным числом.
Если же число не делится на 2 (два), то такое число называют нечетным. Все четные числа оканчиваются на одну из следующих цифр: 0, 2, 4, 6, 8. Все нечетные числа оканчиваются цифрой 1, 3, 5, 7, 9. Понятие четные и нечетные числа — одно из основных понятий математики. Примером применения четных и нечетных чисел в повседневной жизни могут служить расписания движения поездов, когда поезда отправляются только по четным или только по нечетным числам.
На 3 (три) делятся числа, у которых сумма цифр делится на 3 (три). Число 159 (сто пятьдесят девять) делится на 3 (три), поскольку сумма его цифр
1 + 5 + 9 = 15
(пятнадцать) делится на 3 (три)
15 : 3 = 5
и дает в результате 5 (пять). Если разделить на 3 (три) взятое нами число
159 : 3 = 53
получится пятьдесят три.
Признак делимости на 3 (три) распространяется и на сумму цифр любого числа.
Проверим делимость на 3 числа 1 234 567 890 (один триллион двести тридцать четыре миллиона пятьсот шестьдесят тысяч восемьсот девяносто). Находим сумму цифр этого числа
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 0 = 45
Еще раз находим сумму цифр для числа 45 (сорок пять):
4 + 5 = 9
Число 9 (девять)делится на 3 и дает в результате число 3. Следовательно, число 1 234 567 890 делится на 3:
1 234 567 890 : 3 = 411 522 630
в результате получится четыреста одиннадцать миллионов пятьсот двадцать две тысячи шестьсот тридцать.
Рассмотрим еще один пример. Проверим делимость на 3 числа 29 443 680 100 259 (двадцать девять триллионов четыреста сорок три миллиарда шестьсот восемьдесят миллионов сто тысяч двести пятьдесят девять). Находим сумму цифр:
2 + 9 + 4 + 4 + 3 + 6 + 8 + 0 + 1 + 0 + 0 + 2 + 5 + 9 = 53
Теперь находим сумму цифр числа 53 (пятьдесят три):
5 + 3 = 8
Число 8 не делится на число 3, следовательно число 29 443 680 100 259 не может быть поделено на число 3 без остатка:
29 443 680 100 259 : 3 = 9 814 560 033 419 и 2 в остатке
(девять триллионов восемьсот четырнадцать миллиардов пятьсот шестьдесят миллионов тридцать три тысячи четыреста девятнадцать и два в остатке).
На 4 (четыре) делятся числа, у которых две последние цифры нули или образуют число, делящееся на 4 (четыре). Специально для проверки делимости чисел на 4 на отдельной странице размещена таблица умножения на 4 первых тридцати натуральных чисел. На этой же странице приведены математические примеры определения делимости чисел на 4 (четыре).
Признаки делимости целых чисел: на 5 (пять) делятся числа, которые оканчиваются цифровой 0 (нуль) или 5 (пять). Число 590 (пятьсот девяносто) делится на 5 (пять), поскольку оно оканчивается на цифру 0 (ноль):
590 : 5 = 118
в результате деления получается сто восемнадцать.
Число 1 375 (тысяча триста семьдесят пять) так же делится на 5 (пять), так как оно оканчивается цифрой 5 (пять):
1 375 : 5 = 275
в математическом результате деления частное составит двести семьдесят пять.
На 6 (шесть) делятся числа, если одновременно соблюдаются признаки делимости на 2 (два) и на 3 (три).
Другими словами, на 6 делятся все четные числа, сумма цифр которых делится на 3 (три). Например, число 948 (девятьсот сорок восемь) делится на 6 (шесть), поскольку оно является четным и сумма его цифр делится на 3 (три):
9 + 4 + 8 = 21
Снова находим сумму цифр числа 21 (двадцать один):
2 + 1 = 3
В математике деление взятого нами числа 948 (девятьсот сорок восемь) на 6 (шесть) можно записать так:
948 : 6 = 158
в результате получается число сто пятьдесят восемь.
На 7 (семь) делятся числа, у которых разность между числом десятков и удвоенной цифрой единиц делится на 7 (семь). Для начала рассмотрим число 14 (четырнадцать). В этом числе 1 (один) десяток и 4 (четыре) единицы. Проверим его делимость по математическим правилам, соблюдая порядок выполнения математических действий:
1 — 4 х 2 = 1 — 8 = -7
Число -7 (минус семь) делится на 7 (семь) и дает в результате -1 (минус единицу).
Следовательно, число 14 (четырнадцать) так же делится на 7 (семь):
14 : 7 = 2
в результате получается два.
Теперь рассмотрим делимость числа 21 (двадцать один). Здесь мы имеем 2 (два) десятка и 1 (одну) единицу. Проверяем делимость этого числа на 7 (семь): 2 — 1 х 2 = 2 — 2 = 0
Число 0 (нуль)делится не только на 7 (семь), но и на все числа, и дает в результате 0 (нуль). Таким образом, число 21 (двадцать один) делится на 7 (семь):
21 : 7 = 3
частное равняется трем.
В заключение рассмотрим более сложный пример признака делимости на 7 (семь). Проверим делимость числа 86 576 (восемьдесят шесть тысяч пятьсот семьдесят шесть). В этом числе 8 657 (восемь тысяч шестьсот пятьдесят семь) десятков и 6 (шесть) единиц. Приступаем к проверке делимости этого числа на 7 (семь):
8657 — 6 х 2 = 8657 — 12 = 8645
Снова проверяем делимость на 7 (семь), теперь уже полученного нами числа 8 645 (восемь тысяч шестьсот сорок пять).
Теперь у нас 864 (восемь шестьдесят четыре) десятка и 5 (пять) единиц:
864 — 5 х 2 = 864 — 10 = 854
Опять повторяем наши действия для числа 854 (восемьсот пятьдесят четыре), в котором 85 (восемьдесят пять) десятков и 4 (четыре) единицы:
85 — 4 х 2 = 85 — 8 = 77
В принципе, уже невооруженным глазом видно, что число 77 (семьдесят семь) делится на 7 (семь) и в результате получается 11 (одиннадцать). Для не верящих сделаем последний шаг, с 7 (семью) десятками и 7 (семью) единицами:
7 — 7 х 2 = 7 — 14 = -7
Подобный результат мы уже рассматривали выше.
После длительного математического исследования нам удалось установить, что число 86 576 (восемьдесят шесть тысяч пятьсот семьдесят шесть) делится на на 7 (семь):
86576 : 7 = 12368
в результате деления получаем двенадцать тысяч триста шестьдесят восемь.
На 8 (восемь) делятся числа, у которых три последние цифры нули или образуют число, делящееся на 8 (восемь).
Проверить делимость чисел на 8 можно, воспользовавшись таблицей умножения на 8, составленной для первых ста пятидесяти натуральных чисел. Математическая таблица умножения охватывает все трехзначные результаты умножения чисел на 8. Примеры определения делимости чисел на 8 (восемь) приведены на этой же странице.
Простые числа до 2803, которые делятся только на единицу и сами на себя представлены в таблице простых чисел на отдельной странице.
23 октября 2009 года — 22 сентября 2019 года.
© 2006 — 2021 Николай Хижняк. Все права защищены.
| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник/ / Математика для самых маленьких.
| |||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||
TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||
Детский сад — 7 класс. / / Признаки делимости на 2, 3, 4, 5, 6, 8, 9, 10 без остатка. + Признаки делимости на 11,13,25,36.
Примеры: а)78 536 делится на 4, так как 36 делится на 4; б)8422 не делится на 4, так как 22 не делится на 4.
Примеры: а)625 делится на 25; б)18900 делится на 25;Признаки делимости правило и примеры
Число, которое делится на 2 называется четным, а если не делится — нечетным.
Число делится на 2, если его последняя цифра оканчивается на нуль или число чётное.
Пример
Число 7774 делится на 2, так как последняя цифра 4 — чётная.
Число 7775 не делится на 2, так как последняя цифра 5 — нечётная.
На 3 делятся только те числа, у которых сумма всех цифр делится на 3.
Пример
777 делится на 3, так как сумма равна 7+7+7=21, а 21 делится на 3.
Число делится на 4 в том случае, если две последние его цифры нули или делятся на 4.
Пример
788 делится на 4, так как последние его цифры 88 делятся на 4.
700 делится на 4, так как последние его цифры нули.
Число делится на 5, если последняя цифра оканчивается на 0 или 5.
Пример
775 делится на 5, так как последняя цифра равна 5.
Число делится на 6, если оно делится как на 2, так и на 3.
Пример
786 делится на 6, так как оно делится и на 2 и на 3 одновременно.
Число делится на 7, когда утроенное число десятков, сложенное с числом единиц делится на 7.
Пример
189 делится на 7, так как 18*3+9=63 делится на 7.
Число делится на 7, когда разность числа десятков и удвоенного числа единиц, взятая по модулю, делится на 7.
Пример
539 делится на 7, так как 53-9*2=35 делится на 7.
Число делится на 7, когда знакочередующаяся сумма трехзначных граней числа делится на 7.
Пример
147700259 делится на 7, так как 147-700+259=-294, а 294 делится на 7.
Число делится на 8, если три последние цифры его нули или делятся на 8.
Пример
7000 делится на 8, так как три нуля в конце.
7648 делится на 8, так как последние его цифры делятся на 8.
На 9 делятся только те числа, у которых сумма цифр делится на 9.
Пример
774 делится на 9, так как 7+7+4=18, а 18 делится на 9.
Последняя цифра числа 0.
Пример
1500 делится на 0, так как последняя цифра 0.
На 11 делятся только те числа, у которых сумма цифр с чередующимися знаками по модулю делится на 11
Пример
Число 292919 делится на 11, так как 2-9+2-9+1-9=-22 делится на 11.
Число делится на 12, если оно делится как на 3, так и на 4.
Пример
924 делится на 12, так как оно делится и на 3 и на 4 одновременно.
Число делится на 13, если число десятков, сложенное с учетверенным числом единиц, делится 13.
Пример
572 делится 13, так как 72-4*5=52 делится на 13.
Число делится на 14, если оно делится и на 2 и и на 7.
Пример
56 делится на 14, так как делится и на 2 и на 7.
Число делится на 15, если оно делится и на 3 и и на 5.
Пример
615 делится на 15, так как делится и на 3 и на 5.
На 25 делятся те числа, у которых две последние цифры нули или образуют число, которое делится на 25 (т. е. числа, которые оканчиваются на 00, 25, 50, 75).
Пример
7775 делится на 25, так как оканчивается на 75
На 10 делятся только те числа, последняя цифра которых оканчивается на нуль, на 100 делятся только те числа, у которых две последние цифры нули, на 1000 — только те, у которых три последние цифры нули.
Пример
777 000 делится на 10,100,1000.
Правила делимости – методы и примеры
Деление – это одна из четырех основных операций, которая делит число на равные части.
Это математический метод, при котором число делится на более мелкие группы, или метод распределения количества на равные части. Обозначается несколькими символами: косой чертой, горизонтальной чертой и знаком деления.
Деление — это операция, обратная умножению. Например, умножение 5 на 2 дает 10. Вы можете получить любой из множителей 2 и 5, разделив 10 на любое из чисел.
Что такое правило делимости?
Правила делимости были разработаны, чтобы упростить и ускорить процесс деления . Понимание правил делимости от 1 до 20 — важный навык в математике, поскольку он позволяет лучше решать задачи.
Например, правило делимости числа 9 определенно скажет нам, делится ли это число на 9, каким бы большим оно ни казалось.
Вы можете легко запомнить правила делимости для таких чисел, как 2, 3, 4 и 5. Но правила делимости для 7, 11 и 13 немного сложны, и по этой причине их необходимо тщательно понимать .
Правила делимости
Как следует из названия, правила делимости или тесты — это процедуры, используемые для проверки того, делится ли число на другое число, без обязательного выполнения фактического деления.
Число делится на другое число, если результат или частное является целым числом, а остаток равен нулю.
Поскольку не все числа полностью делятся на другие числа, правила делимости на самом деле являются кратчайшим путем определения фактического делителя числа, просто исследуя цифры, из которых состоит число.
Давайте теперь рассмотрим эти правила делимости для разных чисел.
- Правило делимости на 1
Признак делимости на 1 не имеет никаких условий для чисел. Все числа делятся на 1, независимо от того, насколько они велики. Когда любое число делится на 1, результатом является само число. Например, 5/1=5 и 100000/1=100000.
- Признак делимости на 2
Число делится на 2, если последняя цифра числа 2, 4, 6, 8 или 0.
Например: 102/2 = 51, 54/2 = 27, 66/2 = 33, 28/2 = 14 и 20/2 = 10
- Правила делимости на 3 3 утверждает, что число полностью делится на 3, если цифры числа делятся на 3 или кратны 3.
Например, рассмотрим два числа, 308 и 207:
Чтобы проверить, делится ли 308 на 3 или нет , найти сумму цифр.
3+0+8= 11. Так как сумма равна 11, что не делится на 3, то 308 тоже не делится на 3.
Проверить число 207, суммируя его цифры: 2 + 0 + 7 = 9, так как 9 кратно 3, то 207 также делится на 3.
- Признак делимости на 4 утверждает, что число делится на 4, если последние две цифры числа делятся на 4,
Например: Рассмотрим два числа, 2508 и 2506.
Последние цифры числа 2508 равны 08. Так как 08 делится на 4, то число 2508 тоже делится на 4.
2506 не делится на 4, потому что две последние цифры, 06, не делятся на 4.
- Признак делимости на 5 Например, 100/5 = 20, 205/5 = 41.
- Признак делимости на 6
Число делится на 6, если его последняя цифра четное число или ноль, а сумма цифр равна кратно 3.
Например, 270 делится на 2, потому что последняя цифра 0.
Сумма цифр: 2 + 7 + 0 = 9, что также делится на 3.
Следовательно, 270 делится на 6.
- объясняется в следующем алгоритме
Рассмотрим число 1073. Проверить, делится ли число на 7 или нет?
Исключите число 3 и умножьте его на 2, что станет 6. Вычтите 6 из оставшегося числа 107, поэтому 107 – 6 = 101.
Повторите процесс. Имеем 1 x 2 = 2, а оставшееся число 10 – 2 = 8. Так как 8 не делится на 7, то и число 1073 не делится на 7.
- Делимость на 8 Признак делимости на 8 утверждает, что число делится на 8, если его последние три цифры делятся на 8.
- Признак делимости на 9
сумма цифр числа делится на 9, то число также делится на 9.
Пример: В таком числе, как 78532, сумма его цифр равна: 7+8+5+3+2 = 25. Поскольку 25 не делится на 9, 78532 равно также не делится на 9. Рассматривая другой случай числа: 686997, сумма цифр равна: 6 + 8 + 6 + 9 + 9 + 7 = 45. Поскольку сумма делится на 9, то число 686997 делится на 9
- Признак делимости на 10
Правило делимости на 10 гласит, что любое число, последняя цифра которого равна нулю, тогда число I делится на 10.
Например, числа: 30, 50, 8000, 20 33000 делятся на 10.
- Правила делимости 11 альтернативные цифры делятся на 11.
Например, чтобы проверить, делится ли число 2143 на 11 или нет, процедура такова:
Сумма альтернативных цифр каждой группы: 2 + 4 = 6 и 1+ 3 = 4
Следовательно, 6-4 = 2, поэтому число не делится на 11. Следовательно, 2143 не делится на 11.
- Правила делимости на 13
Чтобы проверить, делится ли число на 13, к оставшемуся числу прибавляют 4 раза последнюю цифру, пока не получится двузначное число. Если двузначное число делится на 13, то и целое число делится на 13.
Например:
2795 → 279 + (5 x 4) → 279 + (20) → 299 → 29 + (9 х 4) → 29 + 36 → 65.
В этом случае двузначное число оказывается равным 65, которое делится на 13, следовательно, число 2795 также делится на 13.
Правила делимости | По 2,3,4,5,6,7,8,9,10 и Примеры
Примечание: эта страница содержит устаревшие ресурсы, которые больше не поддерживаются.
Вы можете продолжать использовать эти материалы, но мы можем поддерживать только наши текущие рабочие листы, доступные как часть нашего членского предложения.Говорят, что число «а» полностью делится на другое число «b», если «а» при делении на число «b» не оставляет остатка. Это означает, что «a» делится на «b», если a ÷ b оставляет остаток 0. Можно ли определить, делится ли одно число на другое число, не разделив его на самом деле?
Здесь у нас есть несколько правил, также известных как правила делимости, которые помогут вам определить делимость числа, фактически не проходя весь процесс деления. Эти правила также можно назвать ярлыками для проверки делимости числа.
Правило делимости – Все четные числа делятся на 2. Это означает, что числа, оканчивающиеся на 0, 2, 4, 6 и 8, делятся на 2.
Например,
Давайте проверим, делится ли следующие цифры на 2:
202, 305, 638, 7894, 519
Номер 9 № 99 999 93 1010101010101010101010101010101010101010101010101093 1010101010101010101010101093 Divisible by 2 202 2 Yes 305 5 No 638 8 Yes 7894 4 Yes 519 9 No Divisibility Rule – Add the digits of the number whose divisibility на 3 надо проверить.
Если сумма этих цифр делится на 3, то и число будет делиться на 3. Например,
Проверим, делятся ли на 3 следующие числа:
345, 796, 6125, 321, 506
Number Sum of the Digits Sum Divisible by 3 Number Divisible by 3 345 12 Yes Yes 796 22 No No 6125 14 No No 321 6 Yes Yes 506 11 No No Divisibility Rule – Check the last two digits of число.
Если число, состоящее из этих двух цифр, делится на 4 или две последние цифры равны 00, то полное число также будет делиться на 4. Например,
Let us check whether the following numbers are divisible by 4:
488, 564, 3128, 6431, 9147
Number Last Two Digits Last Two digits Divisible by 4 Number Divisible by 4 488 88 Yes Yes 500 00 Yes Yes 3128 28 Yes Yes 6431 31 No No 9147 47 No No Правило делимости – проверьте разрядность числа.
Число, оканчивающееся на 0 или 5, будет делиться на 5. Например,
Проверим, делятся ли на 5 следующие числа:
185, 269, 7846, 490, 355
Number Number at unit’s place Number Divisible by 5 185 5 Yes 269 9 No 7846 6 No 490 0 Yes 355 5 Да Правило делимости – Проверить, делится ли данное число на 2, а также делится ли оно на 2 и на 3.
by 6. For example,
Let us check whether the following numbers are divisible by 6:
618, 948, 4536, 4172, 6541
Number Number Divisible by 2 Number divisible by 3 Number Divisible by 6 618 Yes Yes Yes 948 Yes Yes Yes 4536 Yes Yes Yes 4172 Yes No № 6541 № № № Правило делимости по месту данного числа единицы.
Вычтите дважды эту цифру из остальных цифр. Если полученное таким образом число делится на 7, исходное число также будет делиться на 7. Например,
Проверим, делятся ли на 7 следующие числа:
749, 357, 5125, 648, 321
Номер Дважды с цифровым номером . Number Divisible by 7 749 9 x 2 = 18 74 – 18 = 56 Yes Yes 357 7 x 2 = 14 35 — 14 = 21 Да Да 5125 5 x 2 = 10 - 0
5 x 2 = 10 - 0
. 648 8 x 2 = 16 64 — 16 = 48 № NO 321 321 321 321 321 321 . Да Правило делимости – проверяйте последние три цифры числа. Если число, состоящее из этих трех цифр, делится на 8 или последние три цифры равны 000, то полное число также будет делиться на 8.
Например,
Проверим, делятся ли на 8 следующие числа:
161, 25000, 648, 488, 368
2
Number Last Three Digits Last Three digits Divisible by 8 Number Divisible by 8 1610 610 No No 25000 000 Yes Yes 20648 648 Yes Yes 72488 488 Yes Yes 13368 368 Yes Yes Divisibility Rule – Add the digits of the number whose divisibility by 9 is to be checked.
Если сумма этих цифр делится на 9, то и число будет делиться на 9. Например,
Проверим, делятся ли на 9 следующие числа:
649, 327, 127, 7120, 3025
Number Sum of the Digits Sum Divisible by 9 Number Divisible by 9 649 19 No No 333 18 Yes Yes 129 12 No No 7128 18 Yes Yes 3025 10 No No Divisibility Rule – Check the digit at the unit’s place данного числа.
Если на месте единицы стоит 0, то число делится на 10. Проверим, делятся ли на 10 следующие числа:
640, 545, 329, 2148, 9410
Number Number at unit’s place Number Divisible by 10 640 0 Yes 545 5 No 329 9 No 2148 8 No 9410 0 Да Важно отметить, что помимо приведенных выше правил число делится на определенное число, если оно делится на свои множители.
Например, число, которое делится на 2 и 4, также будет делиться на 8. Точно так же число, которое делится на 2 и 3, также будет делиться на 6. Вот еще примеры, которые помогут вам наглядно визуализировать приведенные выше объяснения правил делимости и лучше понять эти короткие, но важные темы математики.
Правила делимости помогают нам определить, делится ли число точно на другие числа (то есть нет остатка).
Эти правила позволяют быстро определить, делятся ли числа точно без выполнения вычислений деления. Некоторые из этих правил вместе с примерами проиллюстрированы ниже:
Делится на 2?Правило: Если оно заканчивается на 0, 2, 4, 6 или 8
Делится на 3?Число Делимый? Почему? 456 Да Последняя цифра 6 68 Да Последняя цифра 8 25 № Последняя цифра – 5 (, а не , 2,4,6 или 8) 207 № Последняя цифра – 7 (, а не , 2,4,6 или 8) Правило: Если сумма цифр кратна 3
Номер Делимый? Почему? 405 Да 4 + 0 + 5 = 9 (9 кратно 3) 381 Да 3 + 8 + 1 = 12 (12 кратно 3) 928 № 9 + 2 + 8 = 19 (19 — это , а не , кратное 3) 4 616 № 4 + 6 + 1 + 6 = 17 (17 равно вместо кратно 3)
Делится на 4?Помощник: числа, кратные 3, включают… 3 6 9 12 15 18 21 24 27 30 33 36 39 42 45 Правило: если последние две цифры кратны 4
(или если последние две цифры 00)Номер Делимый? Почему? 348 Да 48 кратно 4 27 616 Да 16 кратно 4 8 514 № 14 — это , а не , кратное 4 722 № 22 — это , а не , кратное 4 1 200 Да Последние две цифры 00
200 кратно 4
Делится на 5?Помощник: числа, кратные 4, включают… 4 8 12 16 20 24 28 32 36 40 44 48 52 56 60 Правило: Если оно заканчивается на 5 или 0
Делится на 6?Число Делимый? Почему? 3 425 Да Последняя цифра 5 750 Да Последняя цифра 0 8 551 № Последняя цифра – 1 (, а не – 0 или 5) 394 № Последняя цифра – 4 (, а не – 0 или 5) Правило: Если делится на 2 и на 3
Делится на 9?Число Делимый? Почему? 5 106 Да Последняя цифра 2 (кратно 2 ) и… 5 + 1 + 0 + 6 = 12 (12 кратно 3) 636 Да Последняя цифра 6 (кратно 2) и… 6 + 3 + 6 = 15 (15 кратно 3) 5 912 № Последняя цифра — 2 (кратно 2) , но … 5 + 9 + 1 + 2 = 17 (17 — это , а не , кратное 3) 508 № Последняя цифра — 8 (кратно 2) , но … 5 + 0 + 8 = 13 (13 — это , а не кратно 3) Правило: Если сумма цифр кратна 9
Число Делимый? Почему? 7 686 Да 7 + 6 + 8 + 6 = 27 (27 кратно 9) 252 Да 2 + 5 + 2 = 9 (9 кратно 9) 883 № 8 + 8 + 3 = 19 (19 — это , а не , кратное 9) 5 105 № 5 + 1 + 0 + 5 = 11 (11 — это , а не , кратное 9)
Делится ли на 10?Помощник: числа, кратные 9, включают… 9 18 27 36 45 54 63 72 81 90 99 108 117 126 135 Правило: Если последняя цифра 0
Число Делимый? Почему? 880 Да Последняя цифра 0 9 560 Да Последняя цифра 0 312 № Последняя цифра – 2 (, а не – 0) 7 897 № Последняя цифра – 7 (, а не – 0) Мы тратим много времени на изучение и сбор информации на этом сайте.
Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!Правило делимости 6 — методы, примеры
Правило делимости 6 гласит, что число делится на 6, если оно делится и на 2, и на 3. Для этого нам нужно использовать тест делимости на 2 и тест на делимость на 3. Правила делимости помогают легко решать задачи без фактического деления. Давайте узнаем больше о правиле делимости 6 в этой статье.
1. Что такое правило делимости числа 6? 2. Делимость на 6 для больших чисел 3. Правило делимости на 6 и 7 4. Правило делимости на 6 и 9 5. Часто задаваемые вопросы о правиле делимости 6 Что такое правило делимости числа 6?
Говорят, что целое число делится на 6, если оно удовлетворяет двум приведенным ниже условиям.
- Заданное целое число должно делиться на 2. Число делится на 2, если цифра в разряде единиц числа четная, т. е. это 0, 2, 4, 6 и 8.
- Заданное целое число должно делиться на 3. Число делится на 3, если сумма всех цифр числа точно делится на 3.
Оба условия должны применяться к числу при выполнении теста на делимость 6. Если число не удовлетворяет обоим условиям, то данное число не делится на 6. Другими словами, мы можем сказать, что все четные числа, которые входят в таблицу умножения 3 делятся на 6.
Правило делимости на 6 с примерами
Пример: Применить тест на делимость на 6 к числу 9156.
Решение:
Условие 1: данное число должно делиться на 2. Здесь 9156 заканчивается четным числом (6). Следовательно, оно делится на 2 [9156 ÷ 2 = 4578]
Условие 2: Заданное число должно делиться на 3. Сумма цифр числа 9156 равна 21 (9 + 1 + 5 + 6 = 21). Сумма 21 делится на 3. Следовательно, число 9156 делится на 3.
Поскольку 9156 делится и на 2, и на 3, мы можем сказать, что оно делится на 6.Пример: Примените правило делимости 6 к числу 825.
Решение:
Условие 1: данное число должно делиться на 2. Здесь 825 заканчивается нечетным числом (5), что означает, что оно НЕ делится на 2.
Условие 2: Заданное число должно делиться на 3. Сумма цифр числа 825 равна 15 (8+2+5=15). Сумма 15 делится на 3, значит, число 825 делится на 3 (825 ÷ 3 = 275)
Мы видим, что 825 делится на 3, но НЕ делится на 2. Поскольку число не удовлетворяет одному условию, следовательно, 825 НЕ делится на 6.Делимость на 6 для больших чисел
Правило делимости на 6 одинаково для всех чисел, будь то маленькое или большое число. Большое число делится на 6, если оно делится и на 2, и на 3. Другими словами, большое число должно удовлетворять обоим условиям признака делимости 6.
Давайте выполним шаги, указанные ниже, чтобы проверить, делится ли большое число на 6 или нет.
- Шаг 1: Посмотрите, является ли данное число четным или нечетным. Это можно сделать, проверив последнюю цифру заданного числа, которая должна быть четной (0, 2, 4, 6, 8). Если это четное число, оно делится на 2, а если нечетное, оно НЕ делится на 2.
- Шаг 2: Проверьте сумму всех цифр числа. Если сумма делится на 3, то и число делится на 3.
- Шаг 3: Если шаг 1 и шаг 2 говорят, что большое число делится и на 2, и на 3, то говорят, что большое число делится на 6.
Пример: Используйте правило делимости 6 на 145962.
Решение: Давайте применим тест делимости 6 на 145962 с помощью следующих шагов.
- Шаг 1: Число 145962 четное, поэтому оно делится на 2.
- Шаг 2: Сумма всех цифр равна 1 + 4 + 5 + 9+ 6 + 2 = 27. Сумма 27 делится на 3, значит, 145962 тоже делится на 3.
- Шаг 3: Число 145962 делится и на 2, и на 3. Следовательно, число 145962 делится на 6.
Правило делимости на 6 и 7
Правила делимости 6 и 7 совершенно разные.
Правило делимости 6 гласит, что число должно делиться и на 2, и на 3. Если число делится на 2 и 3, говорят, что оно делится на 6. Правило делимости на 7 гласит, что для того, чтобы число делилось на 7, умножьте последнюю цифру числа на 2 и вычтите ее из остальная часть числа слева от него, оставляя цифру на месте единиц. Если результат равен 0 или кратен 7, то число делится на 7. Например, возьмем число 443. Число в последней цифре равно 3. Умножив его на 2, мы получим 6 (3 × 2 = 6). Теперь давайте вычтем это из оставшейся части числа, которая равна 44. Итак, 44 — 6 = 38. Но 38 не делится на 7, поэтому мы можем сказать, что 443 не делится на 7.Правило делимости на 6 и 9
Правила делимости 6 и 9 отличаются друг от друга. В правиле делимости 6 мы проверяем, делится ли число на 2 и 3 или нет, а в признаке делимости 9 мы вычисляем сумму всех цифр числа. Если сумма цифр является числом, которое делится на 9, то данное число также делится на 9. Давайте возьмем пример, чтобы лучше понять его.
Проверим, делится ли 450 на 6 или нет. Для этого сначала проверим его делимость на 2 и 3. Последняя цифра числа 450 0, значит оно делится на 2, а сумма цифр 4+5+0=9, которое делится на 3. Итак, 450 делится на 6. Теперь давайте проверим, делится ли 450 на 9. Правило делимости говорит, что нам нужно найти сумму чисел, которая равна 4 + 5 + 0 = 9, что делится на 9. Следовательно, 450 делится и на 6, и на 9.☛ Похожие темы
- Правило делимости числа 4
- Правило делимости числа 5
- Правило делимости числа 7
- Правило делимости 8
- Правило делимости числа 9
- Правило делимости числа 11
- Правило делимости числа 13
Правило делимости 6 примеров
Пример 1: Проверить делимость следующих чисел на 6, используя правило делимости на 6.
a.) 80
б.) 264Решение: а.) Поскольку 80 — четное число, оно делится на 2, но сумма цифр 8 + 0 = 8 не делится на 3, поэтому 80 не делится на 2.
делится на 3. Таким образом, число 80 не делится на 6, потому что оно делится на 2, но не делится на 3.b.) Поскольку 264 — четное число, оно делится на 2. Кроме того, сумма цифр 2 + 6 + 4 = 12 делится на 3, поэтому число 264 также делится на 3. Таким образом, число 264 делится на 6, потому что оно делится и на 2, и на 3.
Пример 2: Используя правило делимости на 6, выясните, делится ли число 4578 на 6 или нет.
Решение: Мы знаем, что 4578 — четное число, а значит, оно делится на 2. Кроме того, сумма цифр 4 + 5 + 7 + 8 = 24 делится на 3, поэтому число 4578 также делится на 3. Следовательно, число 4578 делится на 6, потому что оно делится на 2 и 3 (4578 ÷ 6 = 763).
Пример 3: Проверьте, делится ли данное число 433788 на 6 или нет, используя признак делимости на 6.
Решение: Данное число 433788 является четным числом, что означает, что оно делится на 2.
Также , сумма цифр 4 + 3 + 3 + 7 + 8 + 8 = 33 делится на 3, поэтому число 433788 также делится на 3. Следовательно, число 433788 делится на 6, потому что оно делится как на 2, так и на 3. (433788 ÷ 6 = 72298).
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.
Часто задаваемые вопросы о правиле делимости 6
Что такое правило делимости на 6?
Правило делимости 6 гласит, что если число делится и на 2, и на 3, то говорят, что число делится на 6. Например, 78 — четное число, поэтому оно делится на 2. сумма 78 равна 15 (7 + 8 = 15), а 15 делится на 3. Следовательно, не производя деления, мы можем сказать, что число 78 делится на 6 (78 ÷ 6 = 13), потому что оно делится на 2 и 3. оба.
Используя правило делимости 6, проверьте, делится ли 225 на 6.
Число 225 не делится на 6. Используя тест делимости 6, во-первых, мы должны проверить, является ли число 225 четным или нечетным. Мы видим, что 225 — нечетное число, что означает, что оно не делится на 2. Поскольку число не делится на 2, оно не может делиться на 6, потому что правило делимости 6 гласит, что число должно делиться на 2 и 3. оба, чтобы оно делилось на 6. Итак, 225 не делится на 6.
Что такое правило делимости 6 и 3?
Правило делимости на 6 гласит, что число делится на 6 только в том случае, если оно полностью делится и на 2, и на 3. С другой стороны, правило делимости на 3 гласит, что если сумма всех цифр числа делится на 3, то это число делится на 3. Мы используем правило делимости на 3 в тесте на делимость на 6, поэтому оно Очень важно выучить правило делимости на 3 до изучения правила делимости на 6.
Как проверить делимость больших чисел на 6?
Если большое число делится и на 2, и на 3, то оно делится и на 6. Для этого сначала нужно проверить, является ли данное число четным или нечетным.
Если это четное число, то оно делится на 2. После этого нам нужно найти сумму всех цифр, и если сумма делится на 3, то число также делится на 3. Как только оба условия выполнены, можно сказать, что число делится на 6.Используя правило делимости 6, проверьте кратность числа 288 на 6.
Согласно правилу делимости 6, число 288 должно делиться и на 2, и на 3. Если это не так, то число не делится на 6. Поскольку 288 — четное число, оно делится на 2. Сумма цифр 2 + 8 + 8 = 18, а 18 делится на 3, поэтому 288 делится на 2. 3. Следовательно, мы можем сказать, что 288 делится на 6, потому что оно делится и на 2, и на 3.
Запишите правило делимости числа 6 с примером.
Правило делимости на 6 гласит, что данное число должно делиться и на 2, и на 3. Например, если мы возьмем число 864, мы увидим, что оно делится на 2, потому что 864 — четное число. Теперь проверим, делится ли оно на 3. Так как 8 + 6 + 4 = 18, а мы знаем, что 18 делится на 3. Следовательно, число 864 делится и на 2, и на 3.
Это означает, что данное число 864 делится на 6.Скачать БЕСПЛАТНЫЕ учебные материалы
Правила делимости Рабочий лист
Правила делимости — 7 – упрощено
В вашем браузере деактивирован JavaScript.
Чтобы получить доступ ко всем функциям нашего веб-сайта,
активируйте JavaScript для вашего браузера.Попробуйте 30 дней бесплатно
Узнайте, почему более 1,2 МИЛЛИОНА студентов выбирают диван-репетитор!
- Математика
- Средняя школа
- Характеристики чисел
- Правила делимости — 7
Рейтинг
Ø 5,0 / 3 балла
Вы должны войти в систему, чтобы иметь возможность дать оценку.
Вау, спасибо!
Оцените нас и в Google! Мы с нетерпением ждем этого!Перейти к Google
Авторы
Сьюзен Сайфан
Основы по теме
Правила делимости — 7Число делится на 7, если при делении на 7 оно имеет нулевой остаток. Примерами чисел, которые делятся на 7, являются 28, 42, 56, 63 и 98. Делимость на 7 можно проверить с помощью деления в большую сторону, хотя этот процесс может занять довольно много времени. Особенно когда сталкиваешься с очень большим количеством. Таким образом, знание правил делимости на 7 может быть очень полезным для быстрого определения, делится ли число на 7 или нет.
Вот два правила, которые можно использовать для проверки делимости на 7: Правило 1: Удалите последнюю цифру, удвойте ее, вычтите ее из усеченного исходного числа и продолжайте делать это, пока не останется только одна цифра. Если это 0 или 7, то исходное число делится на 7. Например, чтобы проверить делимость 12264 на 7, мы просто выполняем следующие манипуляции: 1226 — 8 = 1218 121 — 16 = 105 10 — 10 = 0 Таким образом, 12264 делится на 7,9.
0003Правило 2: Возьмите цифры числа в обратном порядке, то есть справа налево, умножая их последовательно на цифры 1, 3, 2, 6, 4, 5, повторяя с этой последовательностью множителей до тех пор, пока необходимый. Затем добавьте продукты. Если полученная сумма делится на 7, то исходное число делится на 7. Например, чтобы проверить делимость 12264 на 7, мы просто проверяем 4(1) + 6(3) + 2(2) + 2(6) + 1(4) = 4 + 18 + 4 + 12 + 4 = 42, двузначное число, которое делится на 7. Следовательно, 12264 должно также делится на 7,
Познакомьтесь с множителями и множителями.
CCSS.MATH.CONTENT.4.OA.B.4
Стенограмма
Правила делимости — 7Зеркало, зеркало, настенное, кто самый умный из всех? Злая ведьма, Белоснежка или ее 7 друзей Оставайтесь с нами, чтобы узнать, чем закончится эта история У ведьмы есть идея, которую она считает потрясающей сделать зелье, которое также является снотворным. С Белоснежкой в стране грез, злая ведьма может раскрыть свой план.
Есть только один глюк,
заминка для ведьмы
Чтобы избежать билета в один конец на небеса,
Белоснежка опирается на Правила делимости для номера 7 . В попытке обмануть Белоснежку ведьма предлагает ей корзину с 15 аппетитными яблоками. Белоснежка не знает, что яблоки пропитаны снотворным, но все равно отвергает их. Почему? Потому что она не может поровну разделить 15 яблок между 7 гномами и не играет в фаворитов. Ведьма не унывает. Итак, на следующий день она возвращается. На этот раз у нее есть тележка, полная яблок. Ведьма сомневается, что Белоснежка может рассчитает такое большое частное быстро и просто решит принять тележку и ее ядовитое содержимое. Ведьма с гордостью заявляет, что у нее 543 яблока, больше, чем гномы и Белоснежка могут когда-либо съесть. И снова Белоснежка отказывается, потому что она не может разделить количество яблок поровну на группы по 7 штук. Как она так быстро это определила?
Делимость на 7
Белоснежка владеет правилом делимости для номер 7 , так что ей не нужно всегда полагаться на деление в большую сторону.
Чтобы проверить, является ли число делящимся без остатка на 7:
Берем последнюю цифру числа, удваиваем Затем вычесть результат из остального числа
Если полученное число делится без остатка на 7 , исходное число также.
Давайте попробуем проделать трюк с количеством яблок в тележке, 543. Последняя цифра 3, удвоить , чтобы получилось 6, вычесть из 6 из оставшихся цифр . 54 минус 6 равно 48.
48 не делится на 7 без остатка, поэтому 543 также не делится на 7 без остатка.Давайте проверим, просто чтобы убедиться. 7 входит в число 54 семь раз. Вычтите 49 из 54, уменьшите 3, 7 входит в 53 семь раз, вычтите 49 из 53, в результате чего у нас останется 4. Итак, мы были правы! 543 не делится на 7 без остатка!
Опять провал. Что же делать злой ведьме? Неужели Белоснежка просто перехитрил ее?
Злая ведьма не сдается.
! 7 входит в число 24 три раза, из 24 вычитается 21, опускается число 7, 7 входит в число 37 пять раз. Она собирает все яблоки в королевстве, а точнее 2478, и доставляет их Белоснежке.
Посмотрим. Хорошо. Последняя цифра равна 8. Удвойте , и мы получим 16. Вычтите 16 из 247. Разница составит 231. Это все еще большое число, поэтому мы просто проделываем те же шаги еще раз. Double последняя цифра , это равно 2 и 23 минус 2 равно 21.
21 равно , которое делится на 7 без остатка , поэтому огромная куча яблок тоже должна быть без остатка 9.0009 делится на 7 Вычитание из 37 дает нам 2, а 7 входит в 28 ровно 4 раза. Что ты знаешь? Белоснежка была права! 2478 делится на 7 без остатка!
Пока мы были заняты расчетами, 77 пирогов уже готовы и ждут. Приготовлено Белоснежкой с любовью и заботой, ее пироги славятся далеко, широко и повсюду. И поскольку она такая супер милая, она предлагает ведьме бесподобный пирог.
Правила делимости — 7 упражнение
Хотели бы вы применить полученные знания? Вы можете просмотреть и попрактиковаться с заданиями к видео Правила делимости — 7 .
Укажите, как использовать правила делимости числа $7$.
Подсказки
Первый шаг в проверке, делится ли число на $7$, это удвоение последней цифры этого числа.
После удвоения последней цифры проверяемого числа вы вычитаете это новое число из того, что осталось от исходного числа.
Например, имея 827$, вы удваиваете 7$, чтобы получить 14$. Затем вы вычитаете 14 долларов из 82 долларов, чтобы получить 68 долларов. Делится ли 68$ на 7$?
Решение
Вот как Белоснежка может использовать правила делимости числа $7$:
Чтобы проверить, делится ли большое число на $7$, она сначала берет последнюю цифру числа и удваивает ее. В этом случае с яблоками по 543$ она берет 3$ и удваивает их, чтобы получить 6$.
Затем она вычитает новое число из остатка исходного числа. В этом случае она вычитает 6 долларов из 54 долларов и получает 48 долларов.
Если результат делится на $7$, то делится и исходное число. Если оно не делится на $7$, исходное число также не делилось на $7$.
В этом случае $48$ не делится на $7$, потому что $7$ не является множителем $48$. Следовательно, $543$ также не делится на $7$.
Суммируйте правило делимости для $7$.
Подсказки
На каждом из трех шагов есть одна ошибка.
Обратите особое внимание на то, какие операции следует использовать на каждом шаге.
Решение
- Первый шаг — удвоить последнюю цифру, а не утроить ее.
- На втором этапе вы вычитаете результат из оставшихся цифр. Вы не используете дополнение.
- Наконец, если разность равна , кратному 7$, то исходное число также делится на 7$.
Объясните, как использовать правило делимости $7$ с большими числами.
Подсказки
Правило делимости $7$ дает меньшее число. Если это меньшее число делится на $7$, то исходное число также делится на $7$. Если число, которое дает вам правило делимости, все еще очень велико, то вы можете повторять правило делимости снова и снова. В конце концов вы получите достаточно маленькое число, чтобы проверить, делится ли оно на $7$, не прибегая к делению в длину.
Было бы полезно записать этапы правила делимости $7$. Сравнение ваших расчетов с шагами поможет вам проверить наличие ошибок.
Решение
Белоснежка использует правила делимости $7$, чтобы проверить, делится ли $9827$ на $7$.
Она начинает с использования правил кратности $7$ на $9827$, точно так же, как и с меньшим числом. Она убирает последнюю цифру, удваивает ее и вычитает результат из того, что осталось от исходного числа.
Она снимает $7$ с $9827$.
Удваивая $7$, она получает $14$. Затем она вычитает 14 долларов из 982 долларов, чтобы получить 968 долларов.Теперь у Белоснежки число меньше, чем то, с которого она начинала, но все равно очень большое. Она знает, что может повторите те же шаги, чтобы проверить, делится ли это новое число на $7$. Ей не нужна новая техника или калькулятор.
Она берет 8$ из 968$. Удвоив $8$, она получит $16$. Она вычитает 16 долларов из 96 долларов и получает 80 долларов. Затем мы получаем, что 80$ не делятся на 7$, поэтому она знает, что 9827$ также не делятся на 7$.
Определите, какие предложения делятся на $7$.
Подсказки
Вы можете использовать правила делимости числа $7$, чтобы проверить, делится ли предлагаемое количество каждой закуски на $7$.
Если вы получили большое число после использования правила делимости числа $7$, вы можете повторить шаги, чтобы получить меньшее число.
Чтобы проверить, делится ли большое число на $7$, сначала возьмите последнюю цифру числа и удвойте ее.
Затем вычтите новое число из остатка исходного числа.
Если результат делится на $7$, то делится и исходное число.
Решение
Белоснежка проверяет предложенное количество каждой закуски, чтобы убедиться, что оно делится на $7$. Она начинает с арахиса за 1083$.
- Она убирает последнюю цифру, удваивает ее и вычитает результат из того, что осталось от исходного числа. Здесь Белоснежка снимает 3 доллара со 1083 долларов. Удвоив $3$, она получит $6$. Затем она вычитает 6 долларов из 108 долларов, чтобы получить 102 доллара.
- Она не уверена, что $102$ делится на $7$, поэтому повторяет свои шаги. Белоснежка снимает 2 доллара со 102 долларов и удваивает их, чтобы получить 4 доллара. Она вычитает 4 доллара из 10 долларов, чтобы получить 6 долларов.
- Шесть не делится на $7$, поэтому она знает, что $1083$ не делится на $7$. Поэтому она не может купить арахис своим друзьям.
Точно так же она проверяет другие закуски.
- $596$ не делится на $7$, поэтому она не может купить помидоры черри.
- $826$ и $7406$ делятся на $7$, поэтому она может купить миндаль и чернику.
Объясните, что значит, если одно число делится на другое число.
Подсказки
Чтобы два числа можно было назвать делимыми, после их деления не может быть остатка.
Выполнение правил делимости занимает больше времени, чем выполнение деления в длинное число?
Деление — это обратное умножение, а множители — это числа, которые мы можем перемножить, чтобы получить другое число.
Решение
- Даны два числа, если вы можете разделить первое на второе без остатка, первое число делится на второе. ✓ Правда.
- Одно число делится на другое, даже на , если при делении получается остаток . ✗ Ложь. Если вы получаете остаток, число не делится на число, которое вы использовали.
- Если большое количество яблок делится на $6$, вы можете разложить все яблоки на 6 ровных кучек, и яблок не останется. ✓ Правда. Это равносильно высказыванию «если большое число делится на шесть, вы не получите остатка при делении его на 6».
- Правило делимости — это очень долгий путь определения, делится ли данное число на фиксированный делитель без выполнения деления. ✗ Ложь. Правило делимости — это сокращенный или, как правило, более быстрый способ определения делимости без фактического деления.
- Если одно целое число делится на другое число, то второе число является множителем первого числа. ✓ Правда. Факторы — это числа, которые мы можем перемножить, чтобы получить другое число.
Кстати, ноль делится на любое число, потому что ноль, разделенный на любое число, равен нулю. Следовательно, никакого остатка никогда не будет.
Определите, какие числа делятся на $7$.
Подсказки
Вы можете использовать правила делимости числа $7$, чтобы проверить, делится ли предлагаемое количество каждого предложения на $7$.
При использовании правил делимости числа $7$ с большими числами потребуется выполнить действия несколько раз подряд.
Чтобы проверить, делится ли большое число на $7$, сначала возьмите последнюю цифру числа и удвойте ее.
Затем вычтите новое число из остатка исходного числа.
Если результат делится на $7$, то делится и исходное число.
Решение
Гномы начинают с проверки, делятся ли $89273$ гвоздей на $7$.
- Они убирают последнюю цифру, удваивают ее и вычитают результат из того, что осталось от исходного числа. Удваивая $3$, они получают $6$. Вычитая 6$ из 8927$, они получают 8921$.
- Это число все еще довольно велико, поэтому они повторяют процесс, пока не получат одно- или двузначное число. Удваивая $1$, они получают $2$. Вычитая 2$ из 892$, они получают 890$. Удваивая $0$, они получают $0$. Вычитая $0$ из $89$, они получают $89$.
- Они знают, что $89$ не делится на $7$. Итак, 89 долларов273$ также не должны делиться на $7$.
Используя ту же стратегию, они находят:
✓ Винты стоимостью 83489$ делятся на 7$.
✓ Палочки по 39823$ делятся на 7$.
✗ Доски за 72382$ не делятся на 7$.
✓ Болты $29827$ делятся на $7$.
✗ Шайбы стоимостью $19723$ не делятся на $7$.
Еще видео по теме Характеристики номеров
Четные и нечетные числа
Правила делимости — 3, 6, 9
Правила делимости — 7
Правила делимости — 4, 5, 8, 10
Простые числа
Компания
- Наша команда
- Цены
- Вакансии
Платформа
Как это работает
- Обучающие видео
- Упражнения
- Диван-герой
- Рабочие листы
- Чат
Справка
- Часто задаваемые вопросы
- Дайте нам отзыв
Юридический отдел
- Положения и условия
- Право на отзыв
- Политика конфиденциальности
- Свяжитесь с нами
- Не продавать мою личную информацию
Есть вопросы? Свяжитесь с нами!
help@sofatutor.
com- дивантутор.com
- диван-репетитор.ch
- диван-репетитор.ат
- дивантутор.com
- ru.sofatutor.co.uk
Есть вопросы? Свяжитесь с нами!
Полезная математика: Знаки делимости. Я узнал немало из… | У. Ринат
Знаки делимости я выучил, кажется, в 6-м классе, и эти знания остаются одной из тех полезных вещей, которые я до сих пор использую в своей повседневной жизни.
Так что же такое знак делимости? Это признак того, что любое число (независимо от того, насколько оно велико) делится (кратно) другому числу.
Стоит отметить, что термин «знаки делимости» я перевел с русского дословно. Немного погуглив, я не смог найти хороших альтернативных фраз на английском языке, я имею в виду, кроме «правил делимости», но на самом деле это не правила, а маленькие, очень полезные знаки. Пожалуйста, не стесняйтесь исправлять меня.
Так чем может быть полезен знак делимости? Один небольшой пример, ответьте на вопрос: 2013 год високосный? Как мы знаем, год является високосным, если он делится на 4. Можем ли мы определить, делится ли 2013 год на 4, не используя калькулятор? Я точно могу! А сможете после ознакомления со знаками делимости. Другой еще меньший пример: можем ли мы поровну разделить счет в баре между 3 людьми? Ответ: делимость на 3 знака! 🙂 Итак, начнем:
Делимость на 2
Это просто: число делится на 2 только в том случае, если последняя цифра этого числа четная (делится на 2):
Число 3242346 делится на 2, потому что 6 — четное число (делится на 2)
Признак кратности 3
Число делится на 3, только если сумма всех его цифр делится на 3.
Например: число 345 делится на 3, потому что сумма его цифр (3+ 4+5=12) делится на 3.
Делимость на 4
Хорошо. Здесь это начинает немного усложняться.
Числа больше 99:
Число делится на 4, если последние 2 цифры этого числа равны нулю или составляют число, которое делится на 4, например: 14676 делится на 4, потому что это последние 2 цифры 76 составляют число, которое делится на 4 (76/4=19).
Число 345200 также делится на 4, потому что последние 2 цифры — нули.Числа меньше 99:
Число делится на 4 только тогда, когда удвоенное количество десятков, составленное из этого числа, с добавленной последней цифрой делится на 4. Пример: число 64, количество десятков здесь равно 6, мы нужно удвоить это количество и добавить последнюю цифру: 2 * 6 + 4 = 16, 16 делится на 4, таким образом, 64 делится на 4.
Делимость на 5
Это так же просто, как и делимость на 2: число делится на 5 только тогда, когда последняя цифра 0 или 5. Пример: 34565 делится на 5.
Делимость на 6
Есть на самом деле 2 правила:
- Число делится на 6, когда оно делится на 2 и делится на 3.
- Число делится на 6, когда количество десятков, составленное из этого числа, умножается на 4 с добавлением последней цифры, образуя число, которое делится на 6. Пример: 66 делится на 6, потому что 4 * 6 + 6 = 30 делится на 6, таким образом, 66 делится на 6.
Признак кратности 7
Хм здесь 4 знака:
- Число делится на 7, если количество десятков, составленное из этого числа, умноженное на 3, с добавлением последней цифры делится на 7, пример: 91 делится на 7, потому что 9 * 3 + 1 = 28 делится на 7.
- Когда модуль алгебраической суммы чисел, составляющих нечетные группы из трех цифр (начиная с первой цифры), в сочетании со знаком «+» , а четные группы по 3 со знаком «-» делятся на 7. Пример:
Большое число 138689257 делится на 7, потому что |138–689+257|=294 делится на 7. - Число делится на 7, когда вы берете число, составленное из трех последних цифр данного числа, и вычитаете число, составленное из оставшихся цифр (или наоборот, в зависимости от того, какое число больше), и полученное число делится на 7.
- Число делится на 7, если вычесть удвоенную первую цифру из числа, составленного из оставшихся цифр, делимое 7: 784 делится на 7, потому что 78-(2*4) = 70 делится на 7.
Признак кратности 8
Число делится на 8 только тогда, когда последние 3 цифры этого числа составляют число, которое делится на 8.
Трехзначное число делится на 8 только тогда, когда последняя цифра этого числа добавляется к удвоить число десятков и прибавить к числу сотен это число состоит из умножить на 4 составить число которое делится на 8, например число 952 делится на 8 потому что 9*4 + 5 * 2 + 2 = 48 делится на 8
Делимость на 9
Число делится на 9 только тогда, когда сумма всех его цифр делится на 9, например число 12345678 делится на 9, потому что 1+2+3+4+5+6+7+8=36 делится на 9.
Делимость на 10
Самый простой: число делится на 10 только тогда, когда последняя цифра этого числа 0 (ноль).
Заключение.
10 знаков пока должно быть достаточно. Вы не поверите, но мы действительно можем подняться до 99. Если мы можем, это не значит, что мы должны это делать. Я не думаю, что вам действительно будет полезно знать делимость на 79.знак. Это просто причудливо. Но если вам интересно, напишите комментарий, и я расскажу вам, как определить, делится ли число на 79.
Теперь вернемся к нашему вопросу: был ли 2013 год високосным? Ответ — нет. Потому что последние 2 цифры 2013 года не составляют число, делящееся на 4 (13 не делится на 4).
Правила делимости для 13
Ненулевое целое число m делит целое число n при условии, что существует целое число q такое, что n = mq. Мы говорим, что m является делителем n и m является делителем n, и используем обозначение m|n.
Правила делимости в основном предназначены для решения задач, связанных с целочисленным делением, очень простым способом. Правило делимости пришло, чтобы проверить, может ли целое делимое полностью делиться на любой другой целочисленный делитель или нет.
Для того чтобы проверить делимость большого числа на проценты потребуется около времени. Вот почему были введены правила встречной делимости времени. Итак, в этой статье мы собираемся обсудить правила делимости на 13.
Если при четырехкратном прибавлении к числу, образованному остальными цифрами, последняя цифра делится на 13, то число делится на 13. правила для 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и так далее.
Например:
Правило делимости на 4, 48 в числе, которое полностью делится на 4, так как сумма двух последних цифр числа делится на 4. Найдем другое число 47, которое не делится на 4 так как сумма двух последних цифр числа не делится полностью на 4. Используя это простое правило, мы можем найти, делится ли какое-либо число на 4 или нет.
Теперь давайте обсудим правило делимости на 13, используя определения и примеры.
Различные правила делимости для 13
Нам нужно прочитать 4 различных типа правил делимости для 13. Давайте объясним вам на примерах один за другим.
Правило делимости 1:
Для заданного числа сформируйте чередующиеся суммы блоков из трех чисел справа и слева.
Предположим, что (n1, n2, n3, n4, n5, n6…..) есть число N, тогда если число, образованное альтернативной суммой блоков из 3-3 цифр справа налево (n1, n2, n3 , — n4, n5, n6, + …. ) делится на 13, то число N дополнительно делится на 13.Пример: Пусть число равно 2 453 674. Выясните, делится ли оно на 13 или нет.
Решение: Применяя правило 1,674 — 453 + 2 = 223 не делится на 13
Следовательно, 2,453,674 также не делится на 13
Правило делимости 2:
Если дано число N, умножьте последнюю цифру N на 4 и прибавьте ее к усеченной части числа. Если результат делится на 13, то число N дополнительно делится на 13.
Пример: пусть число равно 780. Найдите, делится ли оно на 13.
Решение. Применяя правило 2780: 78 + 0 x 4 = 78 и число 78 делится на 13 и дает делитель 6.
Следовательно, 780 также делится на 13.
Правило делимости 3:
Для числа N, чтобы проверить, делится ли оно на 13 или нет, вычтите две последние цифры числа N из 4-кратного остатка числа.
Пример: Пусть число равно 728. Проверьте, делится ли оно на 13 или нет.
Решение: применяя правило делимости на 13, мы получаем,2197: 21 х 4 — 97 = 97 — 84 = 13, и число 13 делится на 13, что дает результат как 0.
Правило делимости 4:
Умножьте последнюю цифру числа N на 9 и вычтите ее из остальной части числа. Если результат делится на 13, то число N также делится на 13.
Пример: Если число 858, то выяснить, делится ли оно на 13 или нет.
Решение: Применяя правило 4936: 93 — 6 x 9 = 39, а 39 делится на 13. Следовательно, 936 делится на 13.
Вопросы:
Вопрос 1.
(а). 298 делится на 13?
Анс.
Четыре раза от последней цифры = 4 x 8 = 32
Оставшиеся левые 29
Добавление = 29 + 32 = 61
, поскольку 61 не делится на 13
∴ 298 не делится на 13.
(б). 247 делится на 13?
Анс. Четыре раза последней цифры = 4 x 7 = 28
Осталось 24
Сложение = 24 + 28 = 52
Поскольку 52 делится на 13
∴ 247 делится на 1.
(с). 317 делится на 13?
Анс. Четыре раза от последней цифры = 4 x 7 = 28
Оставшиеся левые 31
Сейчас добавление = 28 + 31 = 59
, поскольку 59 не делится на 13
∴317 не делится на 13.
(д). 50661 делится на 13?
Анс.
Четыре раза после последней цифры = 4 x 1 = 4
Оставшиеся левые 5066
Теперь, добавление = 5066 + 4 = 5070
снова, четыре раза от последней цифры = 4 x 0 = 0
Теперь, четыре раза Сложение = 507 + 0 = 507
Опять же, четыре раза последней цифры = 4 x 7 = 28
Теперь, сложение = 50 + 28 = 78
А, 78 делится на 13 при 13 х 6.
Понятие правила делимости вводится в третьем классе. Во-первых, студентов учат о БОДМАС. Понятие умножения и деления разрабатывается в высших классах. Когда ученики переходят в четвертый класс, их учат множителям и кратным, факторизации простых чисел, составным числам и целым числам. Все эти понятия составляют базовую основу математики, и чрезвычайно важно хорошо владеть этими темами, чтобы получить более высокую оценку в классе, и только после понимания этих тем ученик может пойти на высшее образование.
Группа экспертов по математике в Веданту отобрала весь учебный материал, связанный с правилами делимости, и в этой статье в основном рассматриваются правила делимости на 13. Учащиеся могут найти множество других правил делимости для различных чисел в соответствии со своими потребностями. В этой статье подробно объясняется, что такое правило делимости и почему мы используем эти правила. Чтобы получить конкретное представление о концепции, команда Vedantu также предоставила практические вопросы вместе с их решениями, чтобы учащиеся могли учиться и понимать более простым способом.
Зачем изучать правила делимости?
Эти правила делимости представляют собой математические трюки, которые помогают учащимся играть, оперировать числами, а также помогают решать задачи более простым и эффективным способом. Эти правила делимости помогают улучшить математические навыки. Чтобы использовать правила делимости, учащиеся должны хорошо усвоить концепцию делимости, прежде чем они смогут использовать эти приемы или правила делимости в свою пользу. Студенты должны полностью понимать, когда и как использовать эти правила. Правила делимости чрезвычайно важны при изучении математики, поскольку они облегчают решение задач. Студенты должны быть оснащены этой концепцией как можно раньше, так как это только сделает их умственно сильными и, следовательно, позволит им получить преимущество над другими.
Эти правила помогают учащимся развивать чувство числа и эффективно справляться с большими числами, которые обычно пугают учащихся. Цель состоит в том, чтобы помочь учащимся ознакомиться с числами и быть гибкими при работе с ними.
- Делимость на 8 Признак делимости на 8 утверждает, что число делится на 8, если его последние три цифры делятся на 8.
- Признак делимости на 5 Например, 100/5 = 20, 205/5 = 41.
- Признак делимости на 4 утверждает, что число делится на 4, если последние две цифры числа делятся на 4,
Вы можете продолжать использовать эти материалы, но мы можем поддерживать только наши текущие рабочие листы, доступные как часть нашего членского предложения.
Если сумма этих цифр делится на 3, то и число будет делиться на 3. 
Если число, состоящее из этих двух цифр, делится на 4 или две последние цифры равны 00, то полное число также будет делиться на 4. 
Число, оканчивающееся на 0 или 5, будет делиться на 5. 
by 6. 
Вычтите дважды эту цифру из остальных цифр. Если полученное таким образом число делится на 7, исходное число также будет делиться на 7.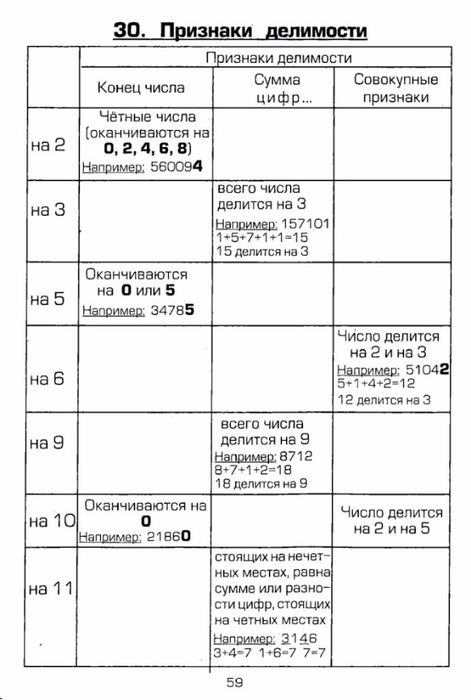 
Если сумма этих цифр делится на 9, то и число будет делиться на 9. 
Если на месте единицы стоит 0, то число делится на 10. 
Например, число, которое делится на 2 и 4, также будет делиться на 8. Точно так же число, которое делится на 2 и 3, также будет делиться на 6. 
Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Правило делимости 6 гласит, что число должно делиться и на 2, и на 3. Если число делится на 2 и 3, говорят, что оно делится на 6. Правило делимости на 7 гласит, что для того, чтобы число делилось на 7, умножьте последнюю цифру числа на 2 и вычтите ее из остальная часть числа слева от него, оставляя цифру на месте единиц. Если результат равен 0 или кратен 7, то число делится на 7. Например, возьмем число 443. Число в последней цифре равно 3. Умножив его на 2, мы получим 6 (3 × 2 = 6). Теперь давайте вычтем это из оставшейся части числа, которая равна 44. Итак, 44 — 6 = 38. Но 38 не делится на 7, поэтому мы можем сказать, что 443 не делится на 7.
Проверим, делится ли 450 на 6 или нет. Для этого сначала проверим его делимость на 2 и 3. Последняя цифра числа 450 0, значит оно делится на 2, а сумма цифр 4+5+0=9, которое делится на 3. Итак, 450 делится на 6. Теперь давайте проверим, делится ли 450 на 9. Правило делимости говорит, что нам нужно найти сумму чисел, которая равна 4 + 5 + 0 = 9, что делится на 9. Следовательно, 450 делится и на 6, и на 9.
делится на 3. Таким образом, число 80 не делится на 6, потому что оно делится на 2, но не делится на 3.
Также , сумма цифр 4 + 3 + 3 + 7 + 8 + 8 = 33 делится на 3, поэтому число 433788 также делится на 3. Следовательно, число 433788 делится на 6, потому что оно делится как на 2, так и на 3. (433788 ÷ 6 = 72298).
Если это четное число, то оно делится на 2. После этого нам нужно найти сумму всех цифр, и если сумма делится на 3, то число также делится на 3. Как только оба условия выполнены, можно сказать, что число делится на 6.
Это означает, что данное число 864 делится на 6.
0003
Есть только один глюк,
заминка для ведьмы
Чтобы избежать билета в один конец на небеса,
Белоснежка опирается на Правила делимости для номера 7 . 
Чтобы проверить, является ли число делящимся без остатка на 7:
Берем последнюю цифру числа, удваиваем Затем вычесть результат из остального числа
Если полученное число делится без остатка на 7 , исходное число также.
Давайте попробуем проделать трюк с количеством яблок в тележке, 543. Последняя цифра 3, удвоить , чтобы получилось 6, вычесть из 6 из оставшихся цифр . 54 минус 6 равно 48.
48 не делится на 7 без остатка, поэтому 543 также не делится на 7 без остатка.
Она собирает все яблоки в королевстве, а точнее 2478, и доставляет их Белоснежке.
Посмотрим. Хорошо. Последняя цифра равна 8. Удвойте , и мы получим 16. Вычтите 16 из 247. Разница составит 231. Это все еще большое число, поэтому мы просто проделываем те же шаги еще раз. Double последняя цифра , это равно 2 и 23 минус 2 равно 21.
21 равно , которое делится на 7 без остатка , поэтому огромная куча яблок тоже должна быть без остатка 9.0009 делится на 7 
Удваивая $7$, она получает $14$. Затем она вычитает 14 долларов из 982 долларов, чтобы получить 968 долларов.
✓ Правда. Это равносильно высказыванию «если большое число делится на шесть, вы не получите остатка при делении его на 6».
