|
Экстраполяция — это метод научного исследования, который основан на распространении прошлых и настоящих тенденций, закономерностей, связей на будущее развитие объекта прогнозирования. К методам экстраполяции относятся метод скользящей средней, метод экспоненциального сглаживания, метод наименьших квадратов. Сущность метода наименьших квадратов состоит в минимизации суммы квадратических отклонений между
наблюдаемыми и расчетными величинами. Расчетные величины находятся по подобранному уравнению – уравнению регрессии. Чем меньше
расстояние между фактическими значениями и расчетными, тем более точен прогноз, построенный на основе уравнения регрессии. Теоретический анализ сущности изучаемого явления, изменение которого отображается временным рядом, служит основой для выбора кривой. Иногда принимаются во внимание соображения о характере роста уровней ряда. Так, если рост выпуска продукции ожидается в арифметической прогрессии, то сглаживание производится по прямой. Если же оказывается, что рост идет в геометрической прогрессии, то сглаживание надо производить по показательной функции. Рабочая формула метода наименьших квадратов: У t+1 = а*Х + b, где t + 1 – прогнозный период; Уt+1 – прогнозируемый показатель; a и b — коэффициенты; Х — условное обозначение времени. Расчет коэффициентов a и b осуществляется по следующим формулам: где, Уф – фактические значения ряда динамики; n – число уровней временного ряда; Сглаживание временных рядов методом наименьших квадратов служит для отражения закономерности развития изучаемого явления. Развитие явления зависит не от того, сколько лет прошло с отправного момента, а от того, какие факторы влияли на его развитие, в каком направлении и с какой интенсивностью. Отсюда ясно, что развитие явления во времени выступает как результат действия этих факторов. Правильно установить тип кривой, тип аналитической зависимости от времени – одна из самых сложных задач
предпрогнозного анализа Подбор вида функции, описывающей тренд, параметры которой определяются методом наименьших квадратов, производится в большинстве случаев эмпирически, путем построения ряда функций и сравнения их между собой по величине среднеквадратической ошибки, вычисляемой по формуле: где Уф – фактические значения ряда динамики; Ур – расчетные (сглаженные) значения ряда динамики; n – число уровней временного
ряда; р – число параметров, определяемых в формулах, описывающих тренд (тенденцию развития). Недостатки метода наименьших квадратов:
Задача. Имеются данные, характеризующие уровень безработицы в регионе, %
Решение методом наименьших квадратов Для решения составим таблицу, в которой будем производить необходимые расчеты: Определим условное обозначение времени как последовательную нумерацию периодов базы прогноза (графа 3). Рассчитаем графы 4 и 5. Расчетные значения ряда Ур определим по формуле У t+1 = а*Х + b, где t + 1 – прогнозный период; Уt+1 – прогнозируемый показатель; a и b — коэффициенты; Х — условное обозначение времени. Коэффициенты a и b определим по следующим формулам: где, Уф – фактические значения ряда динамики; n – число уровней временного ряда. Далее определяем прогнозное значение: Рассчитываем среднюю относительную ошибку по формуле: ε = 28,63/10 = 2,86% точность прогноза высокая. Вывод: Сравнивая результаты, полученные при расчетах
методом скользящей средней, методом экспоненциального сглаживания и методом наименьших квадратов, можно сказать, что средняя относительная ошибка при расчетах методом экспоненциального сглаживания попадает в пределы 20-50%. Это значит, что точность прогноза в данном случае является лишь удовлетворительной. В первом и третьем случае точность прогноза является высокой, поскольку средняя относительная ошибка менее 10%. Но метод скользящих средних позволил получить более достоверные результаты (прогноз на ноябрь – 1,52%, прогноз на декабрь – 1,53%, прогноз на январь – 1,49%), так как средняя относительная ошибка при использовании этого метода наименьшая – 1,13%. Другие статьи по данной теме:
Список использованных источников
|
В аналитическом выражении тренда время рассматривается как независимая переменная, а уровни ряда выступают как функция этой
независимой переменной.
Российский государственный социальный университет. Москва. 2010;Метод наименьших квадратов – Финансовая энциклопедия
Что такое Метод наименьших квадратов?
Метод « наименьших квадратов » – это форма математического регрессионного анализа, используемая для определения линии наилучшего соответствия для набора данных, обеспечивающей визуальную демонстрацию взаимосвязи между точками данных. Каждая точка данных представляет собой отношение между известной независимой переменной и неизвестной зависимой переменной.
Что вам говорит метод наименьших квадратов?
Метод наименьших квадратов дает общее обоснование для размещения линии наилучшего соответствия среди изучаемых точек данных.
Наиболее распространенное применение этого метода, который иногда называют «линейным» или «обычным», направлено на создание прямой линии, которая минимизирует сумму квадратов ошибок, которые генерируются результатами связанных уравнений, таких как в виде квадратов остатков, возникающих в результате различий в наблюдаемом значении, и ожидаемом значении, основанном на этой модели.
Этот метод регрессионного анализа начинается с набора точек данных, которые должны быть нанесены на график по осям x и y. Аналитик, использующий метод наименьших квадратов, сгенерирует линию наилучшего соответствия, которая объясняет потенциальную взаимосвязь между независимыми и зависимыми переменными.
В регрессионном анализе зависимые переменные показаны на вертикальной оси y, а независимые переменные – на горизонтальной оси x. Эти обозначения образуют уравнение для линии наилучшего соответствия, которая определяется методом наименьших квадратов.
В отличие от линейной задачи, нелинейная задача наименьших квадратов не имеет замкнутого решения и обычно решается путем итераций.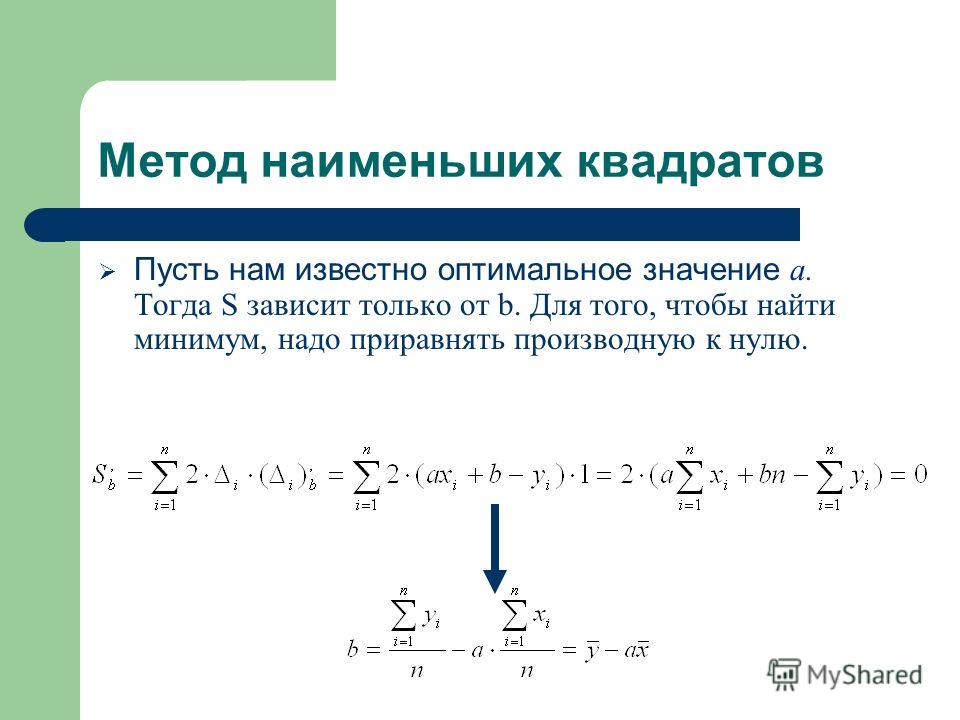
Открытие метода наименьших квадратов приписывают Карлу Фридриху Гауссу, который открыл этот метод в 1795 году.
Ключевые моменты
- Метод наименьших квадратов – это статистическая процедура для поиска наилучшего соответствия для набора точек данных путем минимизации суммы смещений или остатков точек от построенной кривой.
- Регрессия наименьших квадратов используется для прогнозирования поведения зависимых переменных.
Пример метода наименьших квадратов
Примером метода наименьших квадратов является аналитик, желающий проверить взаимосвязь между доходностью акций компании и доходностью индекса, составляющим которого является данная акция. В этом примере аналитик пытается проверить зависимость доходности акций от доходности индекса. Для этого все доходы наносятся на график. Затем доходность индекса обозначается как независимая переменная, а доходность акций – зависимая переменная. Линия наилучшего соответствия предоставляет аналитику коэффициенты, объясняющие уровень зависимости.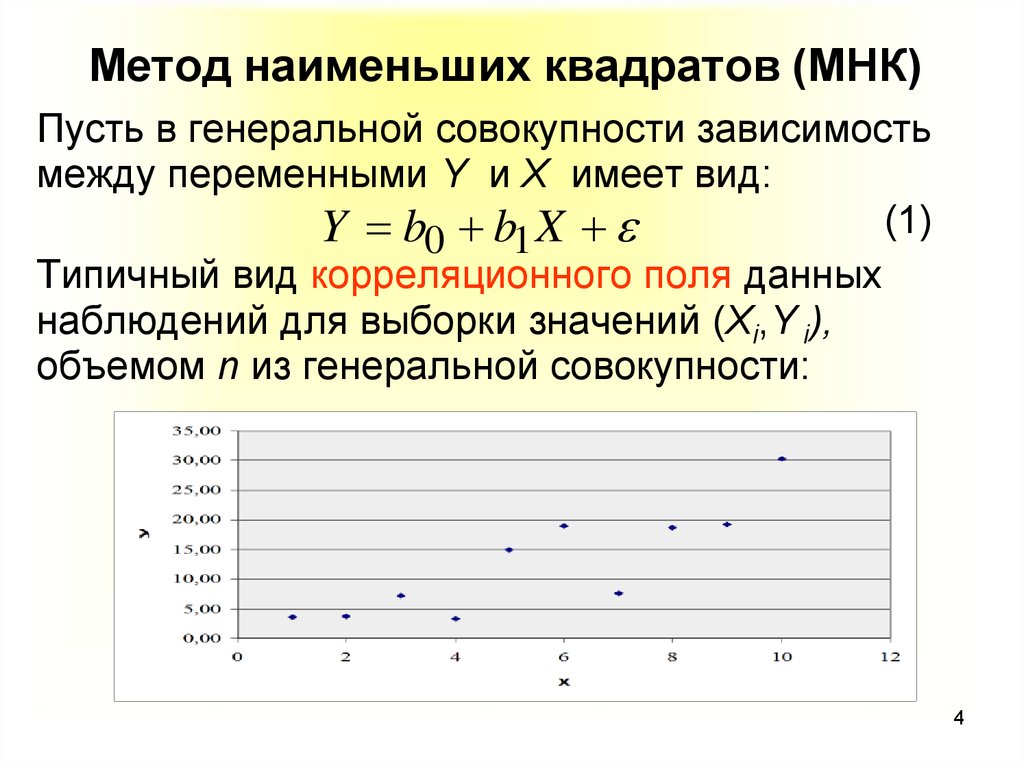
Линия наилучшего соответствия
Линия наилучшего соответствия, определенная методом наименьших квадратов, имеет уравнение, которое описывает взаимосвязь между точками данных. Линия уравнений наилучшего соответствия может быть определена с помощью компьютерных программных моделей, которые включают сводку выходных данных для анализа, где коэффициенты и сводные выходные данные объясняют зависимость проверяемых переменных.
Линия регрессии методом наименьших квадратов
Если данные показывают более тесную связь между двумя переменными, линия, которая лучше всего соответствует этой линейной зависимости, называется линией регрессии наименьших квадратов, которая минимизирует вертикальное расстояние от точек данных до линии регрессии. Термин «наименьшие квадраты» используется потому, что это наименьшая сумма квадратов ошибок, которую также называют «дисперсией».
Что это значит, как использовать, с примерами
Оглавление
Содержание
Что такое метод наименьших квадратов?
Как это работает
Пример
Часто задаваемые вопросы о методе наименьших квадратов
По
Уилл Кентон
Полная биография
Уилл Кентон — эксперт в области экономики и инвестиционного законодательства.
Ранее он занимал руководящие должности редактора в Investopedia и Kapitall Wire, имеет степень магистра экономики Новой школы социальных исследований и степень доктора философии по английской литературе Нью-Йоркского университета.
Узнайте о нашем редакционная политика
Обновлено 28 марта 2022 г.
Рассмотрено
Майкл Дж. Бойл
Рассмотрено Майкл Дж. Бойл
Полная биография
Майкл Бойл — опытный специалист в области финансов, более 10 лет занимающийся финансовым планированием, деривативами, акциями, фиксированным доходом, управлением проектами и аналитикой.
Узнайте о нашем Совет финансового контроля
Факт проверен
Ярилет Перес
Факт проверен Ярилет Перес
Полная биография
Ярилет Перес — опытный мультимедийный журналист и специалист по проверке фактов со степенью магистра журналистики.
Она работала в нескольких городах, освещая последние новости, политику, образование и многое другое. Она специализируется в личных финансах и инвестициях, а также в сфере недвижимости.
Узнайте о нашем редакционная политика
Инвестопедия / Сяоцзе Лю
Что такое метод наименьших квадратов?
Метод наименьших квадратов — это форма математического регрессионного анализа, используемая для определения линии наилучшего соответствия набору данных, обеспечивающая визуальную демонстрацию взаимосвязи между точками данных. Каждая точка данных представляет отношение между известной независимой переменной и неизвестной зависимой переменной.
Ключевые выводы
- Метод наименьших квадратов — это статистическая процедура поиска наилучшего соответствия набору точек данных путем минимизации суммы смещений или невязок точек на построенной кривой.
- Регрессия методом наименьших квадратов используется для прогнозирования поведения зависимых переменных.
- Метод наименьших квадратов обеспечивает общее обоснование размещения линии наилучшего соответствия среди изучаемых точек данных.
Понимание метода наименьших квадратов
Этот метод регрессионного анализа начинается с набора точек данных, которые должны быть нанесены на график по осям x и y. Аналитик, использующий метод наименьших квадратов, создаст линию наилучшего соответствия, которая объясняет возможную взаимосвязь между независимыми и зависимыми переменными.
Метод наименьших квадратов обеспечивает общее обоснование размещения линии наилучшего соответствия среди изучаемых точек данных. Наиболее распространенное применение этого метода, который иногда называют «линейным» или «обычным», направлено на построение прямой линии, которая минимизирует сумму квадратов ошибок, порожденных результатами связанных уравнений, таких как как квадраты остатков, возникающие в результате различий в наблюдаемом значении и ожидаемом значении, основанном на этой модели.
Линия уравнения наилучшего соответствия
Линия наилучшего соответствия, определенная методом наименьших квадратов, имеет уравнение, которое описывает отношения между точками данных. Линия уравнений наилучшего соответствия может быть определена с помощью моделей компьютерного программного обеспечения, которые включают сводку выходных данных для анализа, где коэффициенты и сводные выходные данные объясняют зависимость тестируемых переменных.
Линия регрессии методом наименьших квадратов
Если данные показывают более скудную связь между двумя переменными, линия, которая лучше всего соответствует этой линейной зависимости, называется линией регрессии наименьших квадратов, которая минимизирует расстояние по вертикали от точек данных до линии регрессии. Термин «наименьшие квадраты» используется потому, что это наименьшая сумма квадратов ошибок, которую также называют «дисперсией».
В регрессионном анализе зависимые переменные отображаются на вертикальной оси Y, а независимые переменные — на горизонтальной оси X.
Эти обозначения составят уравнение для линии наилучшего соответствия, которая определяется методом наименьших квадратов.
В отличие от линейной задачи, нелинейная задача наименьших квадратов не имеет закрытого решения и обычно решается путем итерации. Карл Фридрих Гаусс утверждает, что впервые открыл метод наименьших квадратов в 179 г.5, хотя споры о том, кто изобрел этот метод, продолжаются.
Пример метода наименьших квадратов
Примером метода наименьших квадратов является аналитик, который хочет проверить взаимосвязь между доходностью акций компании и доходностью индекса, компонентом которого являются акции. В этом примере аналитик пытается проверить зависимость доходности акций от доходности индекса.
Для этого все доходности наносятся на график. Затем доходность индекса обозначается как независимая переменная, а доходность акций — как зависимая переменная. Линия наилучшего соответствия предоставляет аналитику коэффициенты, объясняющие уровень зависимости.
Что такое метод наименьших квадратов?
Метод наименьших квадратов — это математический метод, который позволяет аналитику определить наилучший способ размещения кривой поверх диаграммы точек данных. Он широко используется для облегчения интерпретации графиков рассеяния и связан с регрессионным анализом. В наши дни метод наименьших квадратов можно использовать как часть большинства статистических программ.
Как метод наименьших квадратов используется в финансах?
Метод наименьших квадратов используется в самых разных областях, включая финансы и инвестиции. Финансовым аналитикам этот метод может помочь количественно оценить взаимосвязь между двумя или более переменными, такими как цена акций и прибыль на акцию (EPS). Выполняя этот тип анализа, инвесторы часто пытаются предсказать будущее поведение цен на акции или других факторов.
Что является примером метода наименьших квадратов?
В качестве иллюстрации рассмотрим случай с инвестором, который рассматривает возможность инвестирования в золотодобывающую компанию.
Инвестор может пожелать узнать, насколько чувствительна цена акций компании к изменениям рыночной цены золота. Чтобы изучить это, инвестор может использовать метод наименьших квадратов, чтобы проследить взаимосвязь между этими двумя переменными во времени на графике рассеяния. Этот анализ может помочь инвестору предсказать, в какой степени цена акций, вероятно, вырастет или упадет при любом заданном повышении или понижении цены на золото.
Источники статей
Investopedia требует, чтобы авторы использовали первоисточники для поддержки своей работы. К ним относятся официальные документы, правительственные данные, оригинальные отчеты и интервью с отраслевыми экспертами. Мы также при необходимости ссылаемся на оригинальные исследования других авторитетных издателей. Вы можете узнать больше о стандартах, которым мы следуем при создании точного и беспристрастного контента, в нашем редакционная политика.
Стиглер М., Стивен. «Гаусс и изобретение метода наименьших квадратов», Статистические анналы , vol.
2.
\]Это называется оценкой наименьших квадратов , поскольку она дает наименьшее значение суммы квадратов ошибок. Поиск наилучших оценок коэффициентов часто называют «подгонкой» модели к данным, а иногда «обучением» или «обучением» модели. Таким образом была получена линия, показанная на рис. 7.3.
Когда мы ссылаемся на предполагаемых коэффициентов, мы будем использовать обозначение \(\hat\beta_0, \dots, \hat\beta_k\). Уравнения для них будут даны в разделе 7.9..
Функция
TSLM()сопоставляет модель линейной регрессии с данными временных рядов. Она аналогична функцииlm(), которая широко используется для линейных моделей, ноTSLM()предоставляет дополнительные возможности для обработки временных рядов.Пример: расходы на потребление в США
Модель множественной линейной регрессии для потребления в США \[ y_t=\beta_0 + \beta_1 x_{1,t}+ \beta_2 x_{2,t}+ \beta_3 x_{3,t}+ \beta_4 x_{4,t}+\varepsilon_t, \] где \(y\) — процентное изменение реальных расходов на личное потребление, \(x_1\) — процентное изменение реального личного располагаемого дохода, \(x_2\) — процентное изменение промышленного производства, \(x_3\) — процентное изменение личных сбережений и \(x_4\) — изменение уровня безработицы.
Следующий вывод предоставляет информацию о установленной модели. В первом столбце таблицы
Коэффициентыдана оценка каждого коэффициента \(\бета\), а во втором столбце указана его стандартная ошибка (т. наборы данных). Стандартная ошибка дает меру неопределенности в оцененном коэффициенте \(\beta\).fit_consMR <- us_change %>% модель (tslm = TSLM (Потребление ~ Доход + Производство + Безработица + Сбережения)) отчет (fit_consMR) #> Серия: Расход #> Модель: TSLM #> #> Остатки: #> Мин. 1 кв. Медиана 3 кв. Макс. #> -0,9055 -0,1582 -0,0361 0,1362 1,1547 #> #> Коэффициенты: #> Оценить стд. Значение ошибки t Pr(>|t|) #> (Перехват) 0,25311 0,03447 7,34 5,7e-12 *** #> Доход 0,74058 0,04012 18,46 < 2e-16 *** #> Производство 0,04717 0,02314 2,04 0,043 * #> Безработица -0,17469 0,09551 -1,83 0,069 . #> Экономия -0,05289 0,00292 -18,09 < 2e-16 *** #> --- #> Обозначение. коды: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 '' 1 #> #> Остаточная стандартная ошибка: 0,31 на 193 степени свободы #> Множественный R-квадрат: 0,768, скорректированный R-квадрат: 0,763 #> F-статистика: 160 на 4 и 193 DF, p-значение: <2e-16В целях прогнозирования последние два столбца представляют ограниченный интерес.
«Значение t» представляет собой отношение оценочного коэффициента \(\бета\) к его стандартной ошибке, а в последнем столбце указано значение p: вероятность того, что оценочный коэффициент \(\бета\) будет настолько большим, насколько это возможно. если бы не было реальной связи между потреблением и соответствующим предиктором. Это полезно при изучении влияния каждого предиктора, но не особенно полезно для прогнозирования.Подобранные значения
Предсказания \(y\) можно получить, используя оценочные коэффициенты в уравнении регрессии и установив член ошибки равным нулю. В общем пишем, \[\начало{уравнение} \hat{y}_t = \hat\beta_{0} + \hat\beta_{1} x_{1,t} + \hat\beta_{2} x_{2,t} + \cdots + \hat\beta_ {к} х_{к, т}. \тег{7.2} \конец{уравнение}\] Подстановка значений \(x_{1,t},\dots,x_{k,t}\) для \(t=1,\dots,T\) возвращает прогнозы \(y_t\) в обучающем наборе , именуемый подогнанными значениями . Обратите внимание, что это прогнозы данных, используемых для оценки модели, а не подлинные прогнозы будущих значений \(y\).
На следующих графиках показаны фактические значения по сравнению с подобранными значениями для процентного изменения в ряду потребительских расходов в США. Временной график на рис. 7.6 показывает, что подогнанные значения довольно точно соответствуют фактическим данным. Это подтверждается сильной положительной взаимосвязью, показанной на диаграмме рассеяния на рис. 7.7.
увеличение (fit_consMR) %>% ggplot (aes (x = четверть)) + geom_line(aes(y = Расход, цвет = "Данные")) + geom_line (aes (y = .fitted, color = "Fitted")) + лаборатории (y = NULL, title = "Процентное изменение потребительских расходов в США" ) + scale_color_manual (значения = c (данные = "черный", встроенный = "# D55E00")) + направляющие (цвет = направляющая_легенда (название = NULL))Рисунок 7.6: График фактических потребительских расходов в США и прогнозируемых потребительских расходов в США во времени.
увеличение (fit_consMR) %>% ggplot(aes(x = потребление, y = .
2.
\]
«Значение t» представляет собой отношение оценочного коэффициента \(\бета\) к его стандартной ошибке, а в последнем столбце указано значение p: вероятность того, что оценочный коэффициент \(\бета\) будет настолько большим, насколько это возможно. если бы не было реальной связи между потреблением и соответствующим предиктором. Это полезно при изучении влияния каждого предиктора, но не особенно полезно для прогнозирования.
