Правило умножения и деления: Порядок действий в Математике

Правила умножения и деления | Дефектология Проф

После того, как выучена таблица умножения, школьникам объясняют правила умножения и деления, учат использовать их при вычислении математических выражений.

ЧТО ТАКОЕ УМНОЖЕНИЕ? ЭТО УМНОЕ СЛОЖЕНИЕ

При сложении и вычитании, умножении и делении чисел в простых выражениях у детей не возникает трудностей:

• 5 × 3 = 15;
• 86 – 9 = 77;
• 81 : 9 = 9.

В таких вычислениях необходимо только знать правила сложения и вычитания и таблицу умножения.
Когда начинаются более сложные упражнения, примеры состоят из двух и более действий, да еще и со скобками, при решении у детей появляются ошибки. И главная из них – неправильный порядок действий.

 

ДА КАКАЯ РАЗНИЦА?

Действительно, настолько ли это важно – какое действие в примере выполнить первым, какое вторым?

• Рассмотрим примеры:

10 – 5 + 2 = ?

Если мы будем выполнять действия по порядку, получим:

1. 10 – 5 = 5;
2. 5 + 2 = 7.

Попробуем иначе:

1. 5 + 2 = 7;
2. 10 – 7 = 3.

Получили два разных ответа. Но так быть не должно, следовательно, порядок выполнения действий имеет значение. Тем более, если в выражении имеются скобки:

25 – (18+2) = ?

Пробуем решить двумя способами:

1. 25 – 18 + 2 = 9;
2. 25 – 20 = 5.

Ответы разные, а для того чтобы определить порядок действий, в выражении стоят скобки – они показывают, какое действие нужно выполнить первым. Значит, правильным будет такое решение:

1. 18 + 2 = 20;
2. 25 – 20 = 5.

Другого решения у ответа у примера быть не должно.

Итак:

ЧТО ВАЖНЕЕ – УМНОЖЕНИЕ ИЛИ СЛОЖЕНИЕ?

При решении примеров
Расставь порядок действий.
Умножить или разделить – на первом месте.

Для выражений, в которых присутствуют не сложение либо вычитание, а умножение или деление, действует то же правило: все действия с числами выполняются по порядку, начиная с левого:

81 : 9 х 2 = ?

1. 81 : 9 = 9;
2. 9 х 2 = 18.

Сложнее случай – когда в одной задаче встречаются умножение или деление со сложением или вычитанием. Каков порядок вычислений тогда?

Рассмотрим пример:

8 : 2 + 2 = ?

Если выполнять все действия по порядку, сначала деление, затем сложение. В итоге получим:

1. 8 : 2 = 4;
2. 4 + 2 = 6.

Значит, пример решен правильно. А если в нем будут скобки?

8 : (2 + 2) = ?

1. 2 + 2 = 4;
2. 8 : 4 = 2.

То, что заключено в скобки, всегда в приоритете. Для того они и стоят в выражении. Поэтому порядок вычислений в подобных выражениях будет следующим:

1. Раскрываем скобки. Если их несколько, делаем вычисления для каждых.
2. Умножение либо деление.
3. Вычисляем конечный результат, выполняя действия слева направо.

Пример:
81 : 9 + (6 – 2) + 3 = ?

1. 6 – 2 = 4;
2. 81 : 9 = 9;
3. 9 + 4 = 13;
4. 13 + 3 = 16.

81 : 9 + (6 – 2) + 3 = 16.

А что будет приоритетным: умножение — или деление, вычитание — или сложение, если оба действия встречаются в задаче? Ничего, они равны, в таком случае действует первое правило – действия производятся одно за другим, начиная слева.

Алгоритм решения выражения:

1. Анализируем задачу – есть ли скобки, какие математические действия нужно будет выполнить.
2. Выполняем вычисления в скобках.
3. Делаем умножение и деление.
4. Выполняем сложение и вычитание.

Пример:

28 : (11 – 4) + 18 – (25 – 8) = ?

Порядок вычисления:

1. 11 – 4 = 7;
2. 25 – 8 = 17;
3. 28 : 7 = 4;
4. 4 + 18 = 22;
5. 22 – 17 = 5.

Ответ: 28 : (11 – 4) + 18 – (25 – 8) = 5.

Важно! Если в выражении есть буквенные обозначения, порядок действий остается прежним.

МАТЕМАТИЧЕСКИЕ ДЕЙСТВИЯ С НУЛЕМ

Круглый нуль такой хорошенький,
Но не значит ничегошеньки.

В примерах нуль как число не встречается, но он может быть результатом какого-либо промежуточного действия, например:

5 × (8 : 2 – 4) = ?

1. 8 : 2 = 4;
2. 4 – 4 = 0;
3. 5 × 0 = ?

При умножении на 0 правило гласит, что в результате всегда получится 0. Почему? Объяснить можно просто: что такое умножение? Это одно и то же число, сложенное с себе подобным несколько раз. Иначе:

0 × 5 = 0 + 0 + 0 + 0 + 0 = 0;

Деление на 0 бессмысленно, а деление нуля на любое число даст в результате всегда 0:

0 : 5 = 0.

Да и как может быть иначе, когда делить-то нечего? Если у вас нет яблок, поделиться с друзьями вам нечем.

Напомним другие арифметические действия с нулем:

УМНОЖЕНИЕ И ДЕЛЕНИЕ НА ЕДИНИЦУ

Математические действия с единицей отличаются от действий с нулем. При умножении или делении числа на 1 получается само первоначальное число:

7 × 1 = 7;

7 : 1 = 7.

Конечно, если у вас есть 7 друзей, и каждый подарил вам по конфете, у вас будет 7 конфет, а если вы их съели в одиночестве, то есть поделились лишь с самим собой, то все они и оказались в вашем желудке.

ВЫЧИСЛЕНИЯ С ДРОБЯМИ, СТЕПЕНЯМИ И СЛОЖНЫМИ ФУНКЦИЯМИ

Это сложные случаи вычислений, которые не рассматриваются в рамках начальной школы.

• Действия с дробями

Умножение простых дробей друг на друга не представляется сложными, достаточно лишь перемножить числитель на числитель, а знаменатель – на знаменатель.
Пример:

25×38 = ?

1. 2 × 3 = 6 — числитель
2. 5 × 8 = 40 — знаменатель

 

Деление простых дробей не так сложно, как кажется на первый взгляд. Достаточно лишь преобразовать задачу – превратить ее в пример с умножением. Сделать это просто – нужно перевернуть дробь так, чтобы знаменатель стал числителем, а числитель – знаменателем.
Пример:

28=25:35=?

28:35=28×53

1. 2 × 5 = 10;
2. 8 × 3 = 24.

28:35=1024=512

• Действия со степенями

Если в задаче встречается число, представленное в виде степени, его значение вычисляется прежде всех остальных (можете представить, что оно заключено в скобки – а действия в скобках выполняются первыми).
Пример:

(5² – 7) : 3 = ?

1. 5² = 5 х 5 = 25;
2. 25 – 7 = 18;
3. 18 : 3 = 6.

(5² – 7) : 3 = 6.

Преобразовав число, представленное в виде степени, в обычное выражение с действием умножения, решить пример оказалось просто: сначала умножение, затем вычитание (потому что в скобках) и деление.

• Действия с корнями, логарифмами, функциями

Поскольку такие функции изучаются только в рамках старшей школы, рассматривать их мы не будем, достаточно только сказать, что они, как и в случае со степенями, имеют приоритет при вычислении: сначала находится значение данного выражения, затем порядок вычислений обычный – скобки, умножение с делением, далее по порядку слева направо.

ГЛАВНЫЕ ПРАВИЛА ПО ТЕМЕ

Говоря о главных и неглавных математических действиях, нужно сказать, что четыре основных действия можно свести к двум: сложение и умножение. Если вычитание и деление представляется для школьников сложным, правила сложения и умножения они запоминают быстрее. Действительно, выражение 5 – 2 можно записать иначе:

2 + х = 5.

Аналогично:

8 : 2 = у × 2 = 8.

В случаях с умножением действуют правила, схожие со свойствами сложения: от перестановки множителей произведение не изменится:

5 × 4 = 4 × 5.

При решении сложных задач первое действие — то, которое выделено скобками, затем — деление или умножение, потом все остальные действия по порядку.
Когда нужно решить примеры без скобок, вначале выполняется умножение или деление, далее — вычитание либо сложение.

  Вся информация взята из открытых источников.
Если вы считаете, что ваши авторские права нарушены, пожалуйста, напишите в чате на этом сайте, приложив скан документа подтверждающего ваше право.

Мы убедимся в этом и сразу снимем публикацию.

Умножение и деление целых чисел. Возведение в степень

• Умножение
• Деление
• Возведение в степень

Умножение

При умножении двух целых чисел умножаются их абсолютные величины. Перед произведением ставится знак плюс, если знаки сомножителей одинаковы, и минус, если они разные

Примеры:

3 · 5 = 15,

3 · (-5) = -15,

-3 · 5 = -15,

-3 · (-5) = 15.

Ниже представлена схема (правило знаков при умножении):

+	·	+	=	+
+	·	—	=	—
—	·	+	=	—
—	·	—	=	+

Из данных примеров следует, что в результате умножения двух чисел с разными знаками получится отрицательное число, а результате умножения двух чисел с одинаковыми знаками – положительное.

При умножении любого числа на  -1  получится число противоположное данному.

Примеры:

-15 · (-1) = 15,

25 · (-1) = -25.

Деление

При делении одного целого числа на другое делят абсолютную величину первого на абсолютную величину второго. Перед частным ставится знак плюс, если знаки делимого и делителя одинаковы, и минус, если они разные.

Примеры:

15 : 5 = 3,

15 : (-5) = -3,

-15 : 5 = -3,

-15 : (-5) = 3.

При делении используется то же правило, что и для умножения. Ниже представлена схема (

правило знаков при делении):

+	:	+	=	+
+	:	—	=	—
—	:	+	=	—
—	:	—	=	+

Из данных примеров следует, что частное двух чисел с разными знаками – отрицательное число, а частное двух чисел с одинаковыми знаками – положительное число.

При делении любого числа на  -1  получится число противоположное данному.

Примеры:

-15 : (-1) = 15,

25 : (-1) = -25.

Возведение в степень

При возведении в степень целого числа в результате может получится как положительное число, так и отрицательное.

Степень положительного числа всегда будет положительным числом.

Примеры:

5² = 5 · 5 = 25,

4³ = 4 · 4 · 4 = 64.

Степень отрицательного числа может быть как положительным, так и отрицательным числом.

Примеры:

Нечётный показатель степени:

(-3)3 =	(-3) · (-3)	· (-3) =
	+

= 9 · (-3) = -27,

то есть   (-3)³ < 0.

Чётный показатель степени:

(-4)4 =	(-4) · (-4)	·	(-4) · (-4)	=
	+		+

= 16 · 16 = 256,

то есть   (-4)⁴ > 0.

следовательно, степень отрицательного числа положительна, если показатель степени чётный, и отрицательна, если показатель степени нечётный.

Умножение и деление

Умножение и деление

Больше практики

Предположим, что население небольшого города составляет примерно 3,0 х 10 ⁴ человек. (это 30 000, но мы написали это таким образом, чтобы подчеркнуть, что мы не уверены в населения во второй цифре числа мы имеем два значащих фигуры). В этом же городе 1,15 х 10 ⁴ (или 11 500 с тремя значащие цифры) дома. Означает ли это, что в среднем 2,608695652174 человека в каждом доме? Это может быть математический ответ, который вы получите разделить количество людей на количество домов, но это не имеет особого смысла отвечать. Где мы должны округлить это?

Этот ответ исходит из правила для значащих цифр, используемых при умножении и подразделение:

Ответ округлить до кратчайшего числа значащих цифры в числах, которые вы умножаете или делите.

Наименьшее количество значащих цифр равно 2 (в 3,0 x 10 4 ). Это означает, что правильный способ сообщить ответ состоит в том, что в среднем 2,6 человека. за дом в этом городе, который тоже имеет 2 значащие цифры. Вот как происходит расчет сделано (цветовая кодировка используется на следующей диаграмме, чтобы проиллюстрировать важные цифры). Необработанный ответ необходимо округлить до двух значащих цифр, поскольку более короткая из числа, которые мы используем (3,0 x 10 4 человек), имеют только две значащие цифры. Обычно рекомендуется выполнять вычисления, как если бы значащих цифр не существовало, то округлить ответ до правильные значащие цифры после завершения всех вычислений.

---

Нажмите здесь, чтобы узнать, почему правило для значащих цифр работает с умножением и делением.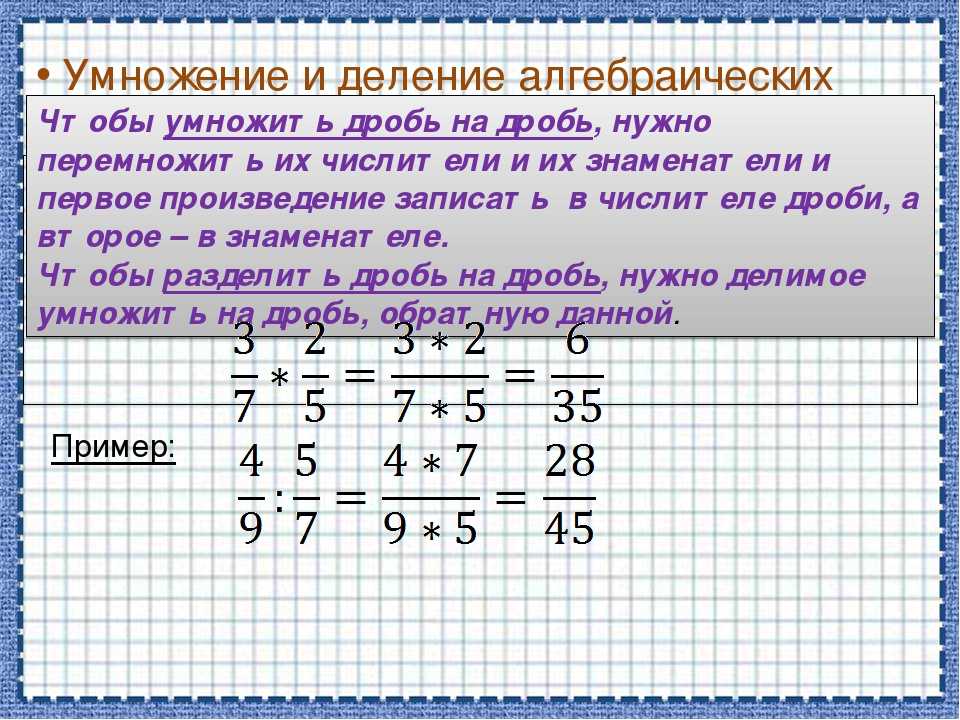

---

Вот еще несколько примеров (синяя подсветка показывает меньшее количество значимых цифры):

Что такое (104,250 x 2,26) / 15,553?

Номер	Номер Значащие цифры	Исходный ответ	Округленный ответ
104.250	6	(235,605)/15,553 = 15,14852440044	15,1
2,26	3
15.553	5

Что такое (0,002450 * 0,1478) / 0,120?

Номер	Количество Значащие цифры	Необработанный ответ	Округленный ответ
0,002450	4	(0,00036211)/0,120 = 0,003017583333333	0,00302
0,1478	4
0,120	3

В каждом случае обратите внимание, что ответ округляется до НАИМЕНЬШЕГО ЧИСЛА значащие цифры.

Как сообщать следующее? Предположим, что каждый число — это экспериментальный результат с правильным количеством значащих цифр.
(32,987 x 0,23) / 5,0000  =	0,10246 х 0,0100 =

Нет никакой разницы в работе с числами, записанными в экспоненциальном представлении. В на самом деле, это проще, потому что никогда не возникает путаницы в том, являются ли нули значительным или нет. Просто посчитайте количество цифр в самом коротком экспериментальном число, умножить (или разделить) числа, а затем округлить ответ до кратчайшего количество цифр.

Что такое (3,125 х 10 ^-6 ) х (2,50 х 10 ^-5 )?

Номер	Количество Значащие цифры	Исходный ответ	Округленный ответ
3,125 x 10 -6	4	7,8125 x 10 -11	7,81 x 10 -11
2,50 x 10 -5	3

Что такое (1,3568 x 10 ^-3 x 2,6554) / 3,266 x 10 ^-7 ?

Номер	Количество Значащие цифры	Исходный ответ	Округленный ответ
1,3568 x 10 -3	5	3,60284672 х 10 -3 = 3,266 х 10 -7 1,103137391304 х 10 4	1,103 x 10 4
2,6554	5
3,266 x 10 -7	4

 

Как сообщать следующее? Предположим, что каждый число — это экспериментальный результат с правильным количеством значащих цифр. Убедиться вы отвечаете в экспоненциальном представлении (например 1.23Е-45).
3,2987 x 10 3   x  2,3 x 10 4 =	1,02467 х 10 -8 / 1,06 х 10 -11 =

---

Сделайте еще несколько примеров для практики

Вероятность правила умножения: определение, примеры

Вероятность и статистика > Вероятность > Вероятность правила умножения

Вероятность правила умножения (общая)

Правило умножения — это способ найти вероятность того, что два события произойдут одновременно (это также одна из формул AP Statistics). Есть два правила умножения. Общая формула правила умножения: P(A ∩ B) = P(A) P(B|A), а конкретное правило умножения: P(A и B) = P(A) * P(B). P(B|A) означает «вероятность того, что A произойдет при условии, что B произошло».

Вероятность правила умножения (конкретная)

Специфическое правило умножения , P(A и B) = P(A) * P(B), допустимо только , если два события независимы. Другими словами, это работает только в том случае, если одно событие не меняет вероятность другого события.
Примеры независимых событий:

• Завести кошку и получать еженедельную зарплату.
• Найти парковочное место и иметь монету для счетчика.
• Покупка книги, а затем покупка кофе.

Вероятность правила умножения: использование специального правила

Использование специальной формулы правила умножения очень просто. Просто умножьте вероятность первого события на второе. Например, если вероятность события А равна 2/9, а вероятность события В равна 3/9, то вероятность того, что оба события произойдут одновременно, равна (2/9)*(3/9) = 6/81. = 2/27.

Вероятность правила умножения: использование общего правила

Это правило можно использовать для любого события (они могут быть независимыми или зависимыми событиями). Вам все еще нужно умножить два числа, но сначала вам нужно использовать немного логики, чтобы вычислить вторую вероятность перед умножением.

Пример задачи: в мешке 6 черных и 4 синих шарика. Из мешка достают два шарика без возврата. Какова вероятность того, что оба шарика синие?

Шаг 1: Обозначьте ваши события A и B. Пусть A будет событием, что шарик 1 станет синим, а B будет событием, что шарик 2 станет синим.
Шаг 2: Рассчитайте вероятность A. В мешке десять шариков, поэтому вероятность вытащить синий шарик равна 4/10.
Шаг 3: Рассчитайте вероятность B. В мешке девять шариков, поэтому вероятность выбрать синий шарик (P B|)A равна 3/9..
Шаг 4: Умножьте шаги 2 и 3 вместе: (4/10)*(3/9) = 2/15.

Посетите наш канал на Youtube, чтобы получить дополнительные советы и помощь по статистике!

Ссылки

Beyer, WH CRC Standard Mathematical Tables, 31st ed. Бока-Ратон, Флорида: CRC Press, стр. 536 и 571, 2002 г.
Гоник, Л.