Производная формулы все: Формулы производных

Таблица всех производных для студентов. Что такое производная

Вычисление производной часто встречается в заданиях ЕГЭ. Данная страница содержит список формул для нахождения производных.

Правила дифференцирования

1. (k⋅ f(x))′=k⋅ f ′(x).
2. (f(x)+g(x))′=f′(x)+g′(x).
3. (f(x)⋅ g(x))′=f′(x)⋅ g(x)+f(x)⋅ g′(x).
4. Производная сложной функции. Если y=F(u), а u=u(x), то функция y=f(x)=F(u(x)) называется сложной функцией от x. Равна y′(x)=Fu′⋅ ux′.
5. Производная неявной функции. Функция y=f(x) называется неявной функцией, заданной соотношением F(x,y)=0, если F(x,f(x))≡0.
6. Производная обратной функции. Если g(f(x))=x, то функция g(x) называется обратной функцией для функции y=f(x).
7. Производная параметрически заданной функции. Пусть x и y заданы как функции от переменной t: x=x(t), y=y(t). Говорят, что y=y(x) параметрически заданная функция на промежутке x∈ (a;b), если на этом промежутке уравнение x=x(t) можно выразить в виде t=t(x) и определить функцию y=y(t(x))=y(x).
8. Производная степенно-показательной функции. Находится путем логарифмирования по основанию натурального логарифма.

Советуем сохранить ссылку, так как эта таблица может понадобиться еще много раз.

На этом занятии мы будем учиться применять формулы и правила дифференцирования.

Примеры. Найти производные функций.

1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Применяем правило I , формулы 4, 2 и 1 . Получаем:

y’=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.

2. y=3x 6 -2x+5. Решаем аналогично, используя те же формулы и формулу 3.

y’=3∙6x 5 -2=18x 5 -2.

Применяем правило I , формулы 3, 5 и 6 и 1.

Применяем правило IV , формулы 5 и 1 .

В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример 4 ), поэтому, будем находить производные 2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.

Дифференцируем 2-ое и 3-е слагаемые по формуле 4 . Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по 4 формуле, находим производные степеней.

Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.

Решим шестой пример и выведем еще одну формулу.

Используем правило IV и формулу 4 . Получившиеся дроби сократим.

Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:

Учим новые формулы!

Примеры.

1. Найти приращение аргумента и приращение функции y=x 2 , если начальное значение аргумента было равно 4 , а новое —4,01 .

Решение.

Новое значение аргумента

х=х 0 +Δx . Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх =4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.е. Δy=f (х 0 +Δх) — f (x 0). Так как у нас функция y=x 2 , то Δу =(х 0 +Δx) 2 — (х 0) 2 =(х 0) 2 +2x 0 · Δx+(Δx) 2 — (х 0) 2 =2x 0 · Δx+(Δx) 2 =

2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.

Ответ: приращение аргумента Δх =0,01; приращение функции Δу =0,0801.

Можно было приращение функции найти по-другому: Δy =y (х 0 +Δx) -y (х 0)=у(4,01) -у(4)=4,01 2 -4 2 =16,0801-16=0,0801.

2. Найти угол наклона касательной к графику функции y=f (x) в точке х 0 , если f «(х 0) = 1 .

Решение.

Значение производной в точке касания

х 0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем: f «(х 0) = tgα = 1 → α = 45°, так как tg45°=1.

Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45° .

3. Вывести формулу производной функции y=x n .

Дифференцирование — это действие нахождения производной функции.

При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (x n)» = nx n-1 .

Вот эти формулы.

Таблицу производных легче будет заучить, проговаривая словесные формулировки:

1. Производная постоянной величины равна нулю.

2. Икс штрих равен единице.

3. Постоянный множитель можно вынести за знак производной.

4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.

5. Производная корня равна единице, деленной на два таких же корня.

6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.

7. Производная синуса равна косинусу.

8. Производная косинуса равна минус синусу.

9. Производная тангенса равна единице, деленной на квадрат косинуса.

10. Производная котангенса равна минус единице, деленной на квадрат синуса.

Учим правила дифференцирования .

1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.

2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.

3. Производная «у», деленного на «вэ» равна дроби, в числителе которой «у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».

4. Частный случай формулы 3.

Учим вместе!

Страница 1 из 1 1

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

Дата: 20.11.2014 Таблица производных. Производная — одно из главных понятий высшей математики. В этом уроке мы познакомимся с этим понятием. Именно познакомимся, без строгих математических формулировок и доказательств. Это знакомство позволит: Понимать суть несложных заданий с производной; Успешно решать эти самые несложные задания; Подготовиться к более серьёзным урокам по производной. Сначала — приятный сюрприз.) Строгое определение производной основано на теории пределов и штука достаточно сложная. Это огорчает. Но практическое применение производной, как правило, не требует таких обширных и глубоких знаний! Для успешного выполнения большинства заданий в школе и ВУЗе достаточно знать всего несколько терминов — чтобы понять задание, и всего несколько правил — чтобы его решить. И всё. Это радует. Приступим к знакомству?) Термины и обозначения. В элементарной математике много всяких математических операций. Сложение, вычитание умножение, возведение в степень, логарифмирование и т.д. Если к этим операциям добавить ещё одну, элементарная математика становится высшей. Эта новая операция называется дифференцирование. Определение и смысл этой операции будут рассмотрены в отдельных уроках. Здесь же важно понять, что дифференцирование — это просто математическая операция над функцией. Берём любую функцию и, по определённым правилам, преобразовываем её. В результате получится новая функция. Вот эта новая функция и называется: производная. Дифференцирование — действие над функцией. Производная — результат этого действия. Так же, как, например, сумма — результат сложения. Или частное — результат деления. Зная термины, можно, как минимум, понимать задания.) Формулировки бывают такие: найти производную функции; взять производную; продифференцировать функцию; вычислить производную и т.п. Это всё одно и то же. Разумеется, бывают и более сложные задания, где нахождение производной (дифференцирование) будет всего лишь одним из шагов решения задания. Обозначается производная с помощью штришка вверху справа над функцией. Вот так: y» или f»(x) или S»(t) и так далее. Читается игрек штрих, эф штрих от икс, эс штрих от тэ, ну вы поняли…) Штрих также может обозначать производную конкретной функции, например: (2х+3)» , (x 3 )» , (sinx)» и т.д. Часто производная обозначается с помощью дифференциалов, но такое обозначение в этом уроке мы рассматривать не будем. Предположим, что понимать задания мы научились. Осталось всего ничего — научиться их решать.) Напомню ещё раз: нахождение производной — это преобразование функции по определённым правилам. Этих правил, на удивление, совсем немного. Чтобы найти производную функции, надо знать всего три вещи. Три кита, на которых стоит всё дифференцирование. Вот они эти три кита: 1. Таблица производных (формулы дифференцирования). 3. Производная сложной функции. Начнём по порядку. В этом уроке рассмотрим таблицу производных. Таблица производных. В мире — бесконечное множество функций. Среди этого множества есть функции, которые наиболее важны для практического применения. Эти функции сидят во всех законах природы. Из этих функций, как из кирпичиков, можно сконструировать все остальные. Этот класс функций называется элементарные функции. Именно эти функции и изучаются в школе — линейная, квадратичная, гипербола и т.п. Дифференцирование функций «с нуля», т.е. исходя из определения производной и теории пределов — штука достаточно трудоёмкая. А математики — тоже люди, да-да!) Вот и упростили себе (и нам) жизнь. Они вычислили производные элементарных функций до нас. Получилась таблица производных, где всё уже готово.) Вот она, эта табличка для самых популярных функций. Слева — элементарная функция, справа — её производная. Функция y Производная функции y y» 1 C (постоянная величина) C» = 0 2 x x» = 1 3 x n (n — любое число) (x n)» = nx n-1 x 2 (n = 2) (x 2)» = 2x 4 sin x (sin x)» = cosx cos x (cos x)» = — sin x tg x ctg x 5 arcsin x arccos x arctg x arcctg x 4 a x e x 5 log a x ln x (a = e ) Рекомендую обратить внимание на третью группу функций в этой таблице производных. Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть. Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!) Найти табличное значение производной, как вы понимаете, задание не самое трудное. Поэтому очень часто в подобных заданиях встречаются дополнительные фишки. Либо в формулировке задания, либо в исходной функции, которой в таблице — вроде и нету… Рассмотрим несколько примеров: 1. Найти производную функции y = x 3 Такой функции в таблице нет. Но есть производная степенной функции в общем виде (третья группа). В нашем случае n=3. Вот и подставляем тройку вместо n и аккуратно записываем результат: (x 3) » = 3·x 3-1 = 3x 2 Вот и все дела. Ответ: y» = 3x 2 2. Найти значение производной функции y = sinx в точке х = 0. Это задание означает, что надо сначала найти производную от синуса, а затем подставить значение х = 0 в эту самую производную. Именно в таком порядке! А то, бывает, сразу подставляют ноль в исходную функцию… Нас же просят найти не значение исходной функции, а значение её производной. Производная, напомню — это уже новая функция. По табличке находим синус и соответствующую производную: y» = (sin x)» = cosx Подставляем ноль в производную: y»(0) = cos 0 = 1 Это и будет ответ. 3. Продифференцировать функцию: Что, внушает?) Такой функции в таблице производных и близко нет. Напомню, что продифференцировать функцию — это просто найти производную этой функции. Если забыть элементарную тригонометрию, искать производную нашей функции достаточно хлопотно. Таблица не помогает… Но если увидеть, что наша функция — это косинус двойного угла , то всё сразу налаживается! Да-да! Запомните, что преобразование исходной функции до дифференцирования вполне допускается! И, случается, здорово облегчает жизнь. По формуле косинуса двойного угла: Т.е. наша хитрая функция есть не что иное, как y = cosx . А это — табличная функция. Сразу получаем: Ответ: y» = — sin x . Пример для продвинутых выпускников и студентов: 4. Найти производную функции: Такой функции в таблице производных нет, разумеется. Но если вспомнить элементарную математику, действия со степенями… То вполне можно упростить эту функцию. Вот так: А икс в степени одна десятая — это уже табличная функция! Третья группа, n=1/10. Прямо по формуле и записываем: Вот и всё. Это будет ответ. Надеюсь, что с первым китом дифференцирования — таблицей производных — всё ясно. Осталось разобраться с двумя оставшимися китами. В следующем уроке освоим правила дифференцирования.

Курс дифференциального и интегрального исчисления. Том 1

Курс дифференциального и интегрального исчисления. Том 1

Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Том 1. Курс дифференциального и интегрального исчисления. Том I Фихтенгольц в 3 томах, Том 1. В книгах представленны все разделы современной высшей матиматеки, правила, задания и примеры их решения, теория и практика. Оглавление ВВЕДЕНИЕ ВЕЩЕСТВЕННЫЕ ЧИСЛА 2. Упорядочение области рациональных чисел. 3. Сложение и вычитание рациональных чисел. 4. Умножение и деление рациональных чисел. 5. Аксиома Архимеда. § 2. Введение иррациональных чисел. Упорядочение области вещественных чисел 7. Упорядочение области вещественных чисел. 8. Вспомогательные предложения. 9. Представление вещественного числа бесконечной десятичной дробью. 10. Непрерывность области вещественных чисел. 11. Границы числовых множеств. § 3. Арифметические действия над вещественными числами 13. Свойства сложения. 14. Определение произведения вещественных чисел. 15. Свойства умножения. 16. Заключение. 17. Абсолютные величины. § 4. Дальнейшие свойства и приложения вещественных чисел 19. Степень с любым вещественным показателем. 20. Логарифмы. 21. Измерение отрезков. ГЛАВА ПЕРВАЯ. ТЕОРИЯ ПРЕДЕЛОВ § 1. Варианта и ее предел 23. Предел варианты. 24. Бесконечно малые величины. 25. Примеры. 26. Некоторые теоремы о варианте, имеющей предел. 27. Бесконечно большие величины. § 2. Теоремы о пределах, облегчающие нахождение пределов 29. Леммы о бесконечно малых. 30. Арифметические операция над переменными. 31. Неопределенные выражения. 32. Примеры на нахождение пределов. 33. Теорема Штольца и ее применения. § 3. Монотонная варианта 35. Примеры. 36. Число е. 37. Приближенное вычисление числа е. 38. Лемма о вложенных промежутках. § 4. Принцип сходимости. Частичные пределы 40. Частичные последовательности и частичные пределы. 41. Лемма Больцано — Вейерштрасса 42. Наибольший и наименьший пределы. ГЛАВА ВТОРАЯ. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ § 1. Понятие функции 44. Функциональная зависимость между переменными. Примеры. 45. Определение понятия функции. 46. Аналитический способ задания функции. 47. График функции. 48. Важнейшие классы функций. 49. Понятие обратной функции. 50. Обратные тригонометрические функции. 51. Суперпозиция функций. Заключительные замечания. § 2. Предел функции 53. Сведение к случаю варианты. 54. Примеры. 55. Распространение теории пределов. 56. Примеры. 57. Предел монотонной функции. 58. Общий признак Больцано—Коши. 59. Наибольший и наименьший пределы функции. § 3. Классификация бесконечно малых и бесконечно больших величин 61. Шкала бесконечно малых. 62. Эквивалентные бесконечно малые. 63. Выделение главной части. 64. Задачи. 65. Классификация бесконечно больших. § 4. Непрерывность (и разрывы) функций 67. Арифметические операции над непрерывными функциями. 68. Примеры непрерывных функций. 69. Односторонняя непрерывность. Классификация разрывов. 70. Примеры разрывных функций. 71. Непрерывность и разрывы монотонной функции. 72. Непрерывность элементарных функций. 73. Суперпозиция непрерывных функций. 74. Решение одного функционального уравнения. 75. Функциональная характеристика показательной, логарифмической и степенной функций. 76. Функциональная характеристика тригонометрического и гиперболического косинусов. 77. Использование непрерывности функций для вычисления пределов. 78. Степенно-показательные выражения. 79. Примеры. § 5. Свойства непрерывных функций 81. Применение к решению уравнений. 82. Теорема о промежуточном значении. 83. Существование обратной функции. 84. Теорема об ограниченности функции. 85. Наибольшее и наименьшее значения функции. 86. Понятие равномерной непрерывности. 87. Теорема Кантора. 88. Лемма Бореля. 89. Новые доказательства основных теорем. ГЛАВА ТРЕТЬЯ. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ § 1. Производная и ее вычисление 91. Задача о проведении касательной к кривой. 92. Определение производной. 93. Примеры вычисления производных. 94. Производная обратной функции. 95. Сводка формул для производных. 96. Формула для превращения функции. 97. Простейшие правила вычисления производных. 98. Производная сложной функции. 100. Односторонние производные. 101. Бесконечные производные. 102. Дальнейшие примеры особых случаев. § 2. Дифференциал 104. Связь между диффереицируемостью и существованием производной. 105. Основные формулы и правила дифференцирования. 106. Инвариантность формы дифференциала. 107. Дифференциалы как источник приближенных формул. 108. Применение дифференциалов при оценке погрешностей. § 3. Основные теоремы дифференциального исчисления 110. Теорема Дарбу 111. Теорема Ролля. 112. Формула Лагранжа. 113. Предел производной. 114. Формула Коши. § 4. Производные и дифференциалы высших порядков 116. Общие формулы для производных любого порядка. 117. Формула Лейбница. 118. Примеры. 119. Дифференциалы высших порядков. 120. Нарушение инвариантности формы для дифференциалов высших порядков. 121. Параметрическое дифференцирование. 122. Конечные разности. § 5. Формула Тейлора 124. Разложение произвольной функции; дополнительный член в форме Пеано. 125. Примеры. 126. Другие формы дополнительного члена. 127. Приближенные формулы. § 6. Интерполирование 129. Дополнительный члеп формулы Лагранжа. 130. Интерполирование с кратными узлами. Формула Эрмита. ГЛАВА ЧЕТВЕРТАЯ. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ § 1. Изучение хода изменения функции 132. Условие монотонности функции. 133. Доказательство неравенств. 134. Максимумы и минимумы; необходимые условия. 136. Достаточные условия. Первое правило. 136. Примеры. 137. Второе правило. 138. Использование высших производных. 139. Разыскание наибольших и наименьших значений. 140. Задачи. § 2. Выпуклые (и вогнутые) функции 142. Простейшие предложения о выпуклых функциях. 143. Условия выпуклости функции. 144. Неравенство Иенсена и его приложения. 145. Точки перегиба. § 3. Построение графиков функций 147. Схема построения графика. Примеры. 148. Бесконечные разрывы, бесконечный промежуток. Асимптоты. 149. Примеры. § 4. Раскрытие неопределенностей 151. 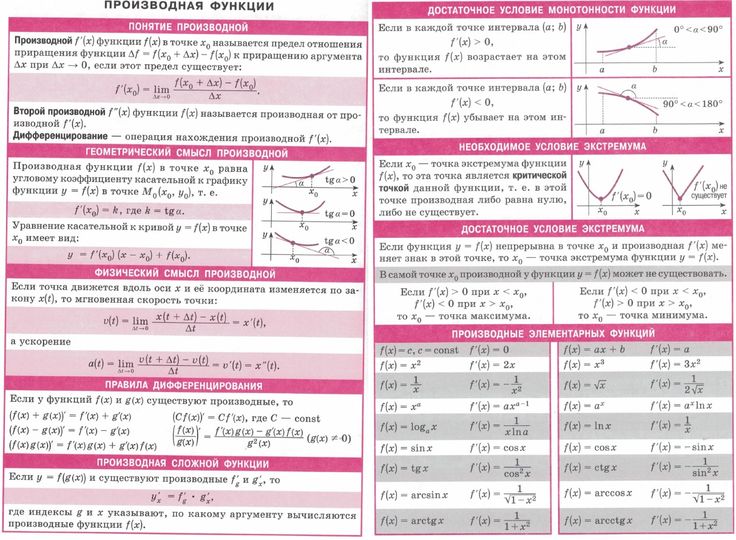Неопределенность вида oo/oo 152. Другие виды неопределенностей. § 5. Приближенное решение уравнений 154. Правило пропорциональных частей (метод хорд). 155. Правило Ньютона (метод касательных). 156. Примеры в упражнения. 157. Комбинированный метод. 158. Примеры и упражнения. ГЛАВА ПЯТАЯ. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 159. Функциональная зависимость между переменными. Примеры. 160. Функции двух переменных и области их определения. 161. Арифметическое n-мерное пространство. 162. Примеры областей в n-мерном пространстве. 163. Общее определение открытой и замкнутой области. 164. Функции n переменных. 165. Предел функции нескольких переменных. 166. Сведение к случаю варианты. 167. Примеры. 168. Повторные пределы. § 2. Непрерывные функции 170. Операции над непрерывными функциями. 171. Функции, непрерывные в области. Теоремы Больцано—Коши. 172. Лемма Больцано—Вейерштрасса. 173. Теоремы Вейерштрасса. 174. Равномерная непрерывность. 175. Лемма Бореля. 176. Новые доказательства основных теорем. § 3. Производные и дифференциалы функций нескольких переменных 178. Полное приращение функции. 179. Полный дифференциал. 180. Геометрическая интерпретация для случая функции двух переменных. 181. Производные от сложных функций. 182. Примеры. 183. Формула конечных приращений. 184. Производная по заданному направлению. 185. Инвариантность формы (первого) дифференциала. 186. Применение полного дифференциала в приближенных вычислениях. 187. Однородные функции. 188. Формула Эйлера. § 4. Производные и дифференциалы высших порядков 190. Теорема о смешанных производных. 191. Обобщение. 192. Производные высших порядков от сложной функции. 193. Дифференциалы высших порядков. 194. Дифференциалы сложных функций. 195. Формула Тейлора. § 5. Экстремумы, наибольшие и наименьшие значения 197. Достаточные условия (случай функции двух переменных). 198. Достаточные условия (общий случай). 199. Условия отсутствия экстремума. 200. Наибольшее и наименьшее значения функции. Примеры. 201. Задачи. ГЛАВА ШЕСТАЯ. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ § 1. Формальные свойства функциональных определителей 203. Умножение якобианов. 204. Умножение функциональных матриц (матриц Якоби). § 2. Неявные функции 206. Существование неявной функции. 207. Дифференцируемость неявной функции. 208. Неявные функции от нескольких переменных. 209. Вычисление производных неявных функций. 210. Примеры. § 3. Некоторые приложения теории неявных функций 212. Метод неопределенных множителей Лагранжа. 213. Достаточные для относительного экстремума условия. 214. Примеры и задачи. 215. Понятие независимости функций. 216. Ранг матрицы Якоби. § 4. Замена переменных 218. Примеры. 219. Функции нескольких переменных. Замена независимых переменных. 220. Метод вычисления дифференциалов. 221. Общий случай замены переменных. 222. Примеры. ГЛАВА СЕДЬМАЯ. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ § 1. Аналитическое представление кривых и поверхностей 224. Примеры. 225. Кривые механического происхождения. 226. Кривые на плоскости (в полярных координатах). Примеры. 227. Поверхности и кривые в пространстве. 228. Параметрическое представление. 229. Примеры. § 2. Касательная и касательная плоскость 231. Примеры. 232. Касательная в полярных координатах. 233. Примеры. 234. Касательная к пространственной кривой. Касательная плоскость к поверхности. 235. Примеры. 236. Особые точки плоских кривых. 237. Случай параметрического задания кривой. § 3. Касание кривых между собой 239. Примеры. 240. Характеристические точки. 241. Порядок касания двух кривых. 242. Случай неявного задания одной из кривых. 243. Соприкасающаяся кривая. 244. Другой подход к соприкасающимся кривым. § 4. Длина плоской кривой 246. Направление на кривой. 247. Длина кривой. Аддитивность длины дуги. 248. Достаточные условия спрямляемости. Дифференциал дуги. 249. Дуга в роли параметра. Положительное направление касательной. § 5. Кривизна плоской кривой 251. Круг кривизны и радиус кривизны. 252. Примеры. 253. Координаты центра кривизны. 254. Определение эволюты и эвольвенты; разыскание эволюты. 255. Свойства эволют и эвольвент. 256. Разыскание эвольвент. ДОПОЛНЕНИЕ. ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ

CBSE Class 12: Mathematics-Formule of Derivatives

Наклон графика функции, или, точнее, наклон касательной в точке, является производной функции. Его вычисление основано на формуле наклона прямой линии, за исключением того, что кривые требуют процесса ограничения. Наклон часто описывается как «увеличение» над «пробегом» или как отношение изменения y к изменению x в декартовых терминах. Формула наклона прямой линии, показанной на рисунке, равна (y1-y0)/(x1-x0). Если h используется для x1-x0, а f(x) для y, другим способом представления этой формулы является

Формулы производных :

 

ddxxn= n.xn-1

ddxk= 0  , где k – константа ложа. где a >0

ddxlog x= 1x

ddxlogae= 1xlogae

ddxx= 12x

Производные

Колебания скорости изменения функции по отношению к независимой переменной называются производными. Когда имеется переменная величина и скорость изменения не постоянна, используется производная. Производная – это инструмент для определения чувствительности одной переменной (зависимой переменной) к другой (независимой переменной).

Derivatives Formula of Trigonometric Functions :

Function	Derivative
sinx	cosx
cosx	-sinx
tanx	sec2x
cotx	0cosec02x00
secx	secx∙tanx
cosec x	-cosecx∙cotx

Derivatives Formula of Trigonometric Functions :

. 1+x2)

Функция	Дериватив
SIN-1X	1/√ (1-x2)
COS-1X 0003	-1/√ (1-x2)
TAN-1X	1/(1+X2)
	77777777
	7777777
9000. 10037777-1
.100377
Sec-1x	1 (| x | ∙ (x2-1))
COSEC-1X	–1 (| X x2-1))

Примеры:

Пример 1:

Пример 2:

Типы производных

Производная первого порядка

Направление функции определяется производными первого порядка, которые указывают, является ли функция возрастающей или убывающей. Первая производная, также известная как производная первого порядка, представляет собой скорость изменения, происходящую мгновенно. Наклон касательной также можно использовать для ее предсказания.

Производная второго порядка

Для понимания формы графика заданной функции используются производные второго порядка. Вогнутость можно использовать для классификации функции.

Свойства производных

Производные можно разбить на более мелкие части, чтобы облегчить вычисление заданных выражений. Термины разделяются на основе оператора, используемого для разделения выражений или функций, например плюс (+), минус (-) или деление (/).

Применение производных:

Производные используются в различных предметах, включая науку, технику, физику и другие, помимо арифметики и реальной жизни. Вы должны были изучить, как найти производную многих функций в более ранних классах, таких как тригонометрические функции, неявные функции, логарифмические функции и так далее. В этом разделе вы узнаете, как применять производные к математическим понятиям и реальным ситуациям. Это также одна из самых важных тем, изучаемых в 12 классе по математике.

Производные используются различными способами в математике, в том числе:

• Минимальные и максимальные значения

• Скорость изменения величины

• Tangent и нормальный к норме

29

• Tangent и нормальный к Curve

29

• .

• Функции возрастания и убывания

Производный инструмент в финансах

Производный инструмент — это финансовый контракт между двумя или более субъектами, стоимость которого определяется согласованным базовым финансовым активом или группой активов, например ценной бумагой или индексом .

Вывод: 

Мы можем найти скорость изменения, используя производные. Это позволяет нам, например, определить скорость изменения скорости по отношению ко времени (которое является ускорением). Это также позволяет нам рассчитать скорость изменения x по отношению к y, которая является градиентом кривой на графике y по отношению к x. Есть несколько простых критериев, которые можно использовать для быстрой дифференциации различных функций.

Производная y (относительно x) записывается как dy/dx, произносится как «dee y by dee x», если y = некоторая функция x (другими словами, если y эквивалентно выражению, включающему целые числа и x) .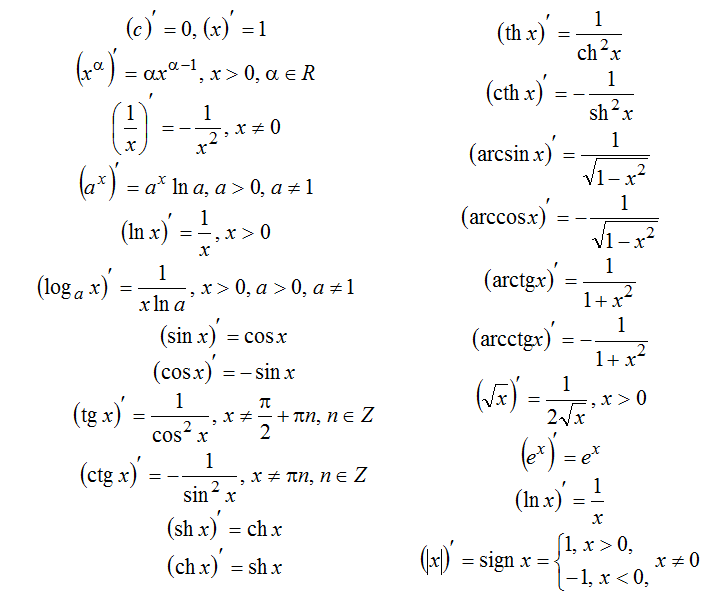

Таблица формул производных для бесплатной печати (PDF)

1 Какие производные правила включены?

2 Бесплатная загрузка таблицы формул деривативов для печати (PDF и WORD)

3 Дополнительные ресурсы для обучения исчислению

Этот пост в блоге содержит партнерские ссылки Amazon. Как партнер Amazon, я получаю небольшую комиссию от соответствующих покупок. Это бесплатно для вас. Спасибо за вашу поддержку Math = Love!

Проблемы с запоминанием всех производных правил? Ознакомьтесь с этой бесплатной печатной таблицей формул производных, которую я создал для своих студентов AP Calculus, чтобы использовать их в качестве справочного материала. Он доступен для скачивания как в формате PDF, так и в формате WORD.

Я хотел создать одностраничную справочную таблицу, чтобы мои студенты, изучающие математику, могли обращаться ко всем нашим модулям по применению дифференцирования.

Прошлым летом я посетил очень информативный Летний институт AP для обучения AP Calculus AB. Нам дали краткое изложение правил дифференциации на одной странице, но я обнаружил, что оно не такое подробное, как хотелось бы.

Естественно, я обратился к Google, чтобы найти идеальную таблицу правил производных, чтобы дать моим студентам AP Calc. Каждый раз, когда я открывал новую диаграмму, я видел несколько вещей, которые мне действительно нравились в диаграмме, и несколько вещей, которые мне не нравились.

Вскоре я понял, что мне просто нужно сделать свою собственную таблицу производных формул для моих студентов, в которой было бы все, что я искал. В процессе создания этой диаграммы я черпал вдохновение из этой диаграммы производных и первообразных правил из Университета Ванкувер-Айленд.

Какие производные правила включены?

Я разбил таблицу формул производных на две части: общие правила производных и правила производных для конкретных функций.

В верхней части диаграммы раздел общих производных правил включает следующие правила дифференцирования: постоянное правило, постоянное кратное правило, правило суммы, правило разности, правило произведения, правило частного и правило цепочки.