Алгебра
Алгебра
Оглавление1. Предисловие2. Перемена мест слагаемых 3. Перемена мест сомножителей 4.  53. Бще одна формула корней квадратного уравнения 54. Квадратное уравнение становится линейным 55. График квадратного трехчлена 56. Квадратные неравенства 57. Максимум и минимум квадратного трехчлена 58. Биквадратные уравнения 59. Возвратные уравнения 60. Как завалить на экзамене. Советы экзаменатору 61. Корни 62. Степень с дробным показателем 63. Доказательства числовых неравенств 64. Среднее арифметическое и среднее геометрическое 65. Среднее геометрическое не больше среднего арифметического 66. Задачи на максимум и минимум 67. Геометрические иллюстрации 68. Средние многих чисел 69. Среднее квадратическое 70. Среднее гармоническое 71. Книги для дальнейшего чтения |
39 глав о математике
Каждая глава необычной книги британского ученого и
популяризатора науки Иэна Стюарта посвящена отдельному числу.
Неудивительно, что и нумерация глав тоже необычная — есть главы
под номером -1, ½ и даже, например, π. Собственно, эти особые
числа и есть главные герои книги, о каждом из них автору есть что
рассказать, да так, чтобы заразить читателя своей страстью.
«Каждое число обладает своей индивидуальностью, — пишет
профессор. — Некоторые особые числа возвышаются над остальными и,
кажется, играют центральную роль во многих областях математики».
Когда вы прочтете книгу, обещает автор, каждое число станет для
вас похожим на старого друга.
Собственно, эти особые
числа и есть главные герои книги, о каждом из них автору есть что
рассказать, да так, чтобы заразить читателя своей страстью.
«Каждое число обладает своей индивидуальностью, — пишет
профессор. — Некоторые особые числа возвышаются над остальными и,
кажется, играют центральную роль во многих областях математики».
Когда вы прочтете книгу, обещает автор, каждое число станет для
вас похожим на старого друга.
Числа, считает профессор, подобны действующим лицам в драме,
каждое из них раскрывает свою историю, приоткрывает двери в
огромный мир математики. Узнавать математику, читая увлекательные
истории профессора Стюарта, не сказать, чтобы очень легко —
временами так и ощущаешь работу собственного мозга — но уж точно
весьма увлекательно. Все мы с десяток лет изучали математику в
школе, но многие ли вспоминают эти уроки как захватывающую
историю? Читая книгу профессора Стюарта, вдруг понимаешь —
почему-то все эти годы ты не задумывался об совершенно
элементарных вещах.
Ну вот, к примеру, что такое число? Допустим, число 7. Не семь коров или семь яблок, просто «семь». Это не символ, ведь в разных языках символы разные, и не слово. Так как тогда определить, что такое число? Если вы никогда об этом не задумывались и сейчас тоже не очень понимаете, как ответить, можно не волноваться — математики тоже основательно задались этим вопросом, только еще в XIX веке. (Строго говоря, древнегреческие математики-философы тоже об этом думали, но их подход все же отличался от парадигмы современной науки, так что это не считается).
«Некоторые логически мыслящие математики вдруг поняли, что, хотя все на свете не одну тысячу лет с удовольствием пользуются числами, никто не знает, что это на самом деле такое», — пишет Стюарт. С тех пор на эту тему написано немало научных работ, поскольку ответить парой слов не получается. Собственно, в книге профессора Стюарта повествование тоже не раз возвращается к этому вопросу.
Или другой вопрос, который автор раскрывает в первой главе книги. Почему 2+2=4? Очевидно? Но на самом деле это теорема, а теорема
требует доказательства. И для этого нам как раз потребуется
понять, что такое число 1. Автор объясняет: это неделимая единица
арифметики, единственное положительное число, которое невозможно
получить путем сложения двух меньших положительных чисел.
Почему 2+2=4? Очевидно? Но на самом деле это теорема, а теорема
требует доказательства. И для этого нам как раз потребуется
понять, что такое число 1. Автор объясняет: это неделимая единица
арифметики, единственное положительное число, которое невозможно
получить путем сложения двух меньших положительных чисел.
Из любого заданного числа можно получить следующее, прибавив к нему единицу. Вот это определение и лежит в основе доказательства нашей теоремы, оно укладывается в одну строчку: нужно просто разложить двойки до единиц и показать их в виде последовательности. Из 1 мы получаем 2, из 2 — 3, из 3 — 4 и т.д. Выглядит это вот так: 2 + 2 = (1 + 1) + (1 + 1) = ( (1 + 1) + 1) + 1 = 4. И это далеко не все, что вы узнаете из главы об единице. Хотя казалось бы…
«Минус на минус дает плюс» — ну кто не знает, что при
перемножении двух отрицательных чисел мы получаем положительное
число. Но почему это так? Ответ на этот вопрос читатель найдет в
главе о числе «-1». Когда математики приняли в семейство чисел и
отрицательные, им пришлось решать, как с ними быть. Если со
сложением и вычитанием все понятно, то с умножением и делением
все намного сложнее. Ведь умножение — это «взять сколько-то раз
по сколько», а что такое «взять минус три раза»? Непонятно. И
математики фактически просто договорились о правилах игры,
правда, собрав целый список аргументов, почему так будет
логичнее. О них и рассказывает профессор Стюарт, и мы видим, как
создавалось то, что сегодня каждый школьник считает само собой
разумеющимся.
Когда математики приняли в семейство чисел и
отрицательные, им пришлось решать, как с ними быть. Если со
сложением и вычитанием все понятно, то с умножением и делением
все намного сложнее. Ведь умножение — это «взять сколько-то раз
по сколько», а что такое «взять минус три раза»? Непонятно. И
математики фактически просто договорились о правилах игры,
правда, собрав целый список аргументов, почему так будет
логичнее. О них и рассказывает профессор Стюарт, и мы видим, как
создавалось то, что сегодня каждый школьник считает само собой
разумеющимся.
Математики, оказалось, вообще, много чего придумали, а вовсе не
описали, что видели. Вот как забавно пишет об этом автор,
предваряя главу о комплексных числах. «Когда математики захотели
разделить число на число там, где разделить нацело невозможно,
они придумали дроби. Когда они захотели вычесть большее число из
меньшего, они придумали отрицательные числа. Всякий раз, когда
чего-то нельзя сделать, математики придумывают что-нибудь новое,
чтобы все-таки сделать это. Так что, когда невозможность извлечь
квадратный корень из отрицательного числа начала серьезно
раздражать, они… догадайтесь, что сделали?»
Так что, когда невозможность извлечь
квадратный корень из отрицательного числа начала серьезно
раздражать, они… догадайтесь, что сделали?»
Но математика, конечно, не замкнута сама на себе. Числа окружают нас. Автор приводит примеры из физики, химии и биологии. Например, вопрос: почему природа создала пчелиные соты именно такими, случайность ли это? Еще древние математики поняли, что нет. На самом деле рисунок сот — это способ разделить плоскость на замкнутые области с минимальным суммарным периметром. Это утверждение много веков оставалось недоказанным, вплоть до 1999 года.
Рассказывая о числах, профессор Стюарт знакомит читателя с
интересными историями из жизни знаменитых математиков,
рассказывает о знаменитых теоремах от теоремы Пифагора до теоремы
о четырех красках и показывает элегантные и красивые
математические закономерности. Даже если вы слышали о каких-то из
них в школе или в вузе, подход, который предлагает автор, вас
удивит. А если не слышали ни разу, то вас ждет огромный мир
математики, прикоснуться к которому удастся, читая увлекательные
истории профессора Стюарта.
Почему умножение двух отрицательных чисел дает положительное?
Лаура ∙ 3 года назад
Делиться
На днях я оказался в сложной ситуации: объяснял умножение двух отрицательных чисел своему 8-летнему ребенку.
Отрицательные числа довольно просто проиллюстрировать при использовании температуры, потому что по обеим сторонам от них четко виден «ноль» градусов Цельсия и числа. Живя в Канаде, мы можем наблюдать резкие колебания температуры за один день.
Но потом мне пришлось объяснять, почему температура вообще должна опускаться ниже нуля… почему бы не начать с более низкого значения? Я рассказал ей о концепции абсолютного нуля и шкале Кельвина и быстро понял это. И я изо всех сил пытался дать очень простое объяснение ее первоначальному вопросу: почему умножение двух отрицательных чисел дает положительное число?
Итак, я посмотрел на информационную супермагистраль, где встретил гораздо лучшую аналогию: деньги.
Найдено на Reddit в сабреддите ELI5 ( Объясните, как будто мне 5 ), на этот вопрос было много ответов. Но тот, кто проголосовал за первое место, был предоставлен пользователем Reddit Zerotan .
Вот объяснение, которое было предоставлено:
Я даю вам три банкноты по 20 долларов: +3 * +20 = +60 для вас
Я даю вам три долга по 20 долларов: +3 * -20 = -60 для вы
Я беру у вас три купюры по 20 долларов: -3 * +20 = -60 для вас
Я беру у вас три долга по 20 долларов: – 3 * -20 = +60 для вас
Результатом является прибыль или убыток от того, с чего вы начали.
Этот ответ был быстро опровергнут другим пользователем, у которого была хорошая мысль: ответ описывает абстракцию , но не лежащие в ее основе корни. Это все равно, что сказать, что Гренландия находится севернее Италии, потому что она выше на карте. Это на самом деле ничего не объясняет.
Если мы сведем математику к подсчету физических вещей, например, крышек от бутылок, то отрицательное число можно рассматривать как долг по пробкам от бутылок. Итак, 5 + 5 — это 10, 5 — 5 — это 0, это очевидно. 5 + -5 равно 0, 5 — -5 равно 10.
-5 означает убрать 5, поэтому 5 – -5 означает убрать 5 единиц на вынос.
Умножение — это просто добавление числа к самому себе некоторое количество раз. 5 умножить на 6 означает прибавить 5 к самому себе 6 раз, или 0 + 5 + 5 + 5 + 5 + 5 + 5 = 30.
Таким же образом, -5 умножить на 6 (0 + -5 + -5 + — 5 + -5 + -5 + -5) равно -30.
Так что насчет 5 раз -6. Что мы имеем в виду, когда умножаем на отрицательное число? Вместо этого мы вычитаем, так что 0 – 5 – 5 – 5 – 5 – 5 – 5 = -30, и -5 раз – 6 : 0 – -5 – -5 – -5 – -5 – -5 – -5 = 30
Короче говоря, » Почему -(-X) = X? ». По той же причине, что противоположность « противоположна up » равна up .
Очевидно.
Источники:
https://mathwithbaddrawings. com/2016/12/14/the-catchy-nonsense-of-two-negatives-make-a-positive/
com/2016/12/14/the-catchy-nonsense-of-two-negatives-make-a-positive/
Что такое целые числа в математике
Главная
Узнать
Базовая математика
- Сравнение целых чисел
- Сложение целых чисел
- Вычитание целых чисел
- Умножение целых чисел
- Деление целых чисел
- Свойства целых чисел
- Проблемы со словами
- Дополнение
- Вычитание
- Умножение
- Подразделение
- Целые числа
- Натуральные числа
- Четное нечетное
множители и множители Ссылки
Предварительная алгебра Ссылки
Целые числа состоят из всех отрицательных и положительных целых чисел. Он также включает ноль. Другими словами, целые числа — это набор целых чисел и их противоположностей — {…,-3,-2,-1,0,1,2,3,…}
Другими словами, целые числа — это набор целых чисел и их противоположностей — {…,-3,-2,-1,0,1,2,3,…}
Числовая строка используется для представления целых чисел. Давайте сначала разберемся с числовой линией.
Эти числа справа от нуля в числовой строке называются .
положительный
целые числа . Это +1, +2, +3…………
Эти числа слева от нуля на числовой прямой называются отрицательные целые числа .
Это -1, — 2, — 3…………
Целое число нулей не имеет ни положительного, ни отрицательного значения и не имеет знака.
Примечание:
Числовая линия идет в обоих направлениях.
Двигаемся вправо, чтобы добавить положительное целое число.
Двигаемся влево, чтобы добавить отрицательное целое число.
Двигаемся влево, чтобы вычесть положительное целое число.
Двигаемся вправо, чтобы вычесть отрицательное целое число.
При сложении двух положительных целых чисел результатом будет положительное целое число.
Пример. 10 + 3 = 13
При сложении двух отрицательных целых чисел результатом будет отрицательное целое число.
Пример. (-1) + (-3) = — 4
При сложении положительного целого числа и отрицательного целого числа результат будет отрицательное или положительное целое число.
Пример. (-3) + 5 = 2 и 3+ (-5) = -2
Берем их разность и ставим знак большего целого числа.
Аддитивные обратные числа — это целое число, противоположное заданному целому.
Скажем число 7.
Аддитивная инверсия целого числа 7 равна (– 7), а аддитивная инверсия (– 7) равна 7.
Пример 1:
В певческом конкурсе за правильное пение начисляются положительные баллы, а за отрицательные баллы начисляются за неправильное пение. Если бы Софья набрала очки в пяти турах, 50, – 15, – 10, 75 и 40, сколько очков она набрала во всех пяти турах?
Всего за все 5 туров София набрала 140 баллов.
Объяснение :
Нам нужно найти общее количество очков во всех пяти раундах.
Набранных Софьей очков в пяти турах было 50, — 15, — 10, 75 и 40
= 50+ (– 15) + (– 10) + 75 + 40
= (50+ 75 + 40) + (– 15 ) + (– 10)
= 165 + (-25)
= 165 – 25
=140
Макс положил на свой банковский счет 5000 рупий. Он снимает с него 3150 рупий за какие-то
цель. Найдите остаток на счету Макса после вывода средств.
Он снимает с него 3150 рупий за какие-то
цель. Найдите остаток на счету Макса после вывода средств.
Остаток на счету Макса после вывода средств составляет рупий. 1850 г.
Объяснение :
Сумма депозита представлена положительным целым числом, потому что она добавляет деньги
на счет.
Снятие суммы со счета представлено отрицательным целым числом
Сумма депозита = 5000 рупий
Сумма снятия = 3150 рупий
Баланс на счету Макса = 5000 + (-3150)
= 5000 – 3150
= 1850
Дженнифер переезжает на пикник из школы, которая находится далеко от школы в 55 км к северу. Ее дом находится в 25 км к югу по той же дороге от места для пикника. Если
она возвращается обратно в дом после пикника прямо, как вы будете представлять
расстояние, которое она должна преодолевать каждый день, чтобы добраться до школы в южном направлении?
Ее дом находится в 25 км к югу по той же дороге от места для пикника. Если
она возвращается обратно в дом после пикника прямо, как вы будете представлять
расстояние, которое она должна преодолевать каждый день, чтобы добраться до школы в южном направлении?
Дженнифер приходится проезжать 30 км каждый день, чтобы добраться до школы на юг.
Объяснение :
Расстояние на север представлено положительным целым числом, а расстояние на
юг представлен отрицательным целым числом.
Место для пикника от школы 55 км к северу
Ее дом находится на расстоянии 25 км к югу от
. Расстояние от дома до школы 55км + (-25км)
Расстояние от дома до школы 55км + (-25км)
55км + (-25км)
= 55 — 25
=30
Что нужно помнить
Если любые два положительных целых числа a и b,
(-a) × (-b) = a × b
Если мы возьмем (-12) × (-5)
Сначала умножьте оба отрицательных числа на целые числа. (-12) × (-5)
Тогда перед полученным произведением поставьте знак плюс .
(-12) × (-5) = 12 × 5 = 60
Примечание:
Если оба числа положительные, произведение положительное.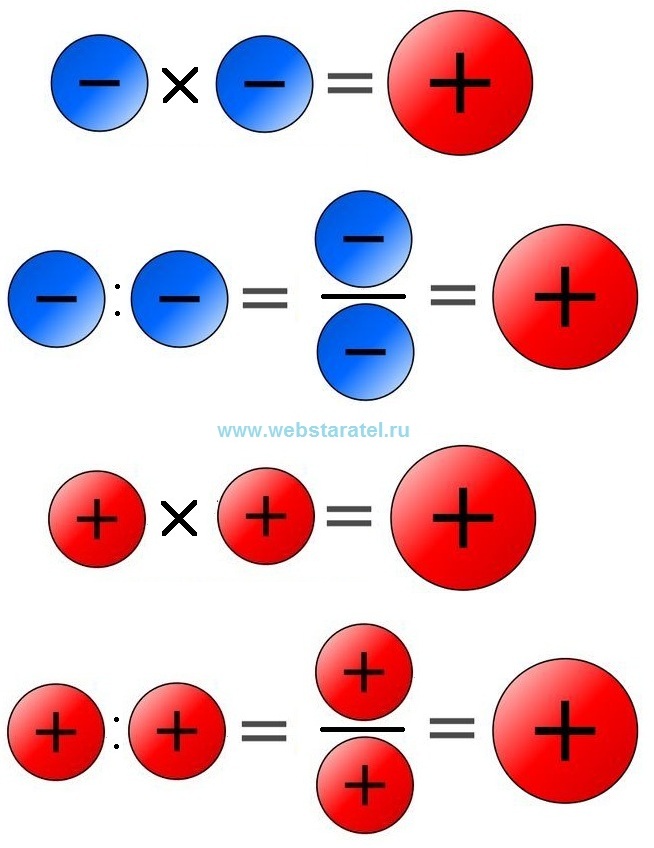
Если оба числа отрицательные, произведение положительное.
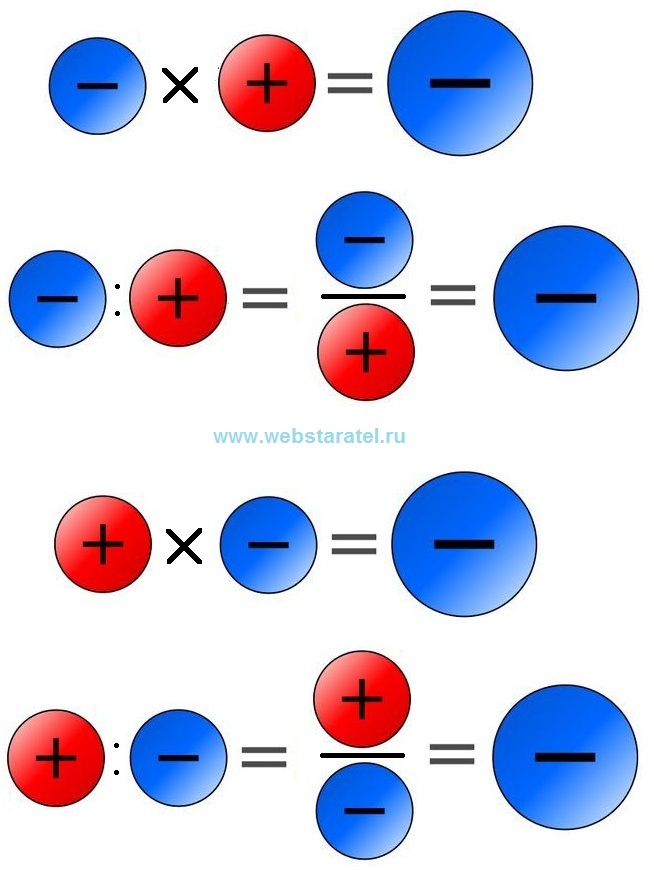
Если любые два положительных целых числа a и b ,
(-a) × b = a × (-b) = — (a×b)
Если мы возьмем (12) × (-5),
Сначала найдите произведение чисел. (12)×(-5)
Поставьте знак минус перед полученным продуктом.
(12) × (-5) = -(12 × 5) = -60
Примечание:
Если одно число положительное, а другое отрицательное, произведение отрицательное.
Если у нас есть одно число отрицательное, а другое положительное, произведение отрицательное.
Например, (-12) × (5) = -(12 × 5) = -60
Пример 1:
245
Объяснение:
Сначала умножьте оба положительных числа
35 × 7
= 245
Пример 2:
-76
Объяснение:
Умножьте оба отрицательных числа на целые числа и поставьте знак минус.
= — ( 38 × 2)
= -( 76)
= -76
Здесь мы заключаем, что если число умноженных отрицательных чисел четно (два, четыре, шесть) произведение будет положительным целым числом, но если число отрицательных целые числа, умноженные на нечетные (три, пять), произведение будет отрицательным целым числом .
Например,
(-3) × (-3) × (-3) = -(3 × 3 × 3) = -27 , но (-3) × (-3) × (-3) × (-3)= (3 × 3 × 3 × 3)= 81
-15
Объяснение:
[(– 3) × (–2)] + [(– 3) × 7]
= (3×2) + (-21)
= 6 + (- 21)
= – (21– 6)
= – 15
16
Объяснение:
(– 4) × [(–3) + (–1)]
= (– 4) × [–(3+ 1)]
= (– 4) × (– 4)
= 16
-104
Объяснение:
[–(8×10)] – [(8×3)]
= –80–24
= – (80 + 24)
= – 104
Например, 18 × 12
Мы можем записать это как 18 × (10 + 2).
Итак, 18 × 12
= 18 × (10 + 2)
= 18 × 10 + 18 × 2
= 180 + 36
= 216
Студентам предлагается классный тест, в котором все 10 вопросов оцениваются в 20 баллов.
За каждый правильный ответ можно получить 2 балла, а за каждый неправильный дается (–1) балл.
отвечать.
1. Елизавета пишет только 5 правильных ответов. Каков будет ее счет?
2. Джессон пишет все 10 ответов правильно. Каков будет ее счет?
Общий балл Элизабет = 5, а общий балл Джессона = 20.

Объяснение :
Для любых двух положительных целых чисел a и b
a ÷ (–b) = (– a) ÷ b где b ? 0
Например,
56 ÷ (–8) = –7 и 40 ÷ (–10) = –4
А также 56 ÷ (–7) = –8 и 40 ÷ (–4) = –10
Для любых двух натуральных чисел а и б
(– a ) ÷ (– b ) = a ÷ b где b ? 0
Например, (–56) ÷ (–8) = 7 и (–40) ÷ (–10) = 4
А также (–56) ÷ (–7) = –8 и (–40) ÷ (–4) = 10
Примечание:
- Когда мы делим положительное целое число на отрицательное целое число, мы сначала делим их
как целые числа, а затем поставить знак минус (-) перед частным.

- Когда мы делим отрицательное целое число на отрицательное целое число, мы сначала делим их как целые числа, а затем поставить знак плюс (+).
Любое целое число, деленное на ноль, не определено, но ноль делится на другое целое число. чем ноль равен нулю.
Например,
0 ÷ и = 0 для и 0
Любое целое число, деленное на 1, дает одно и то же целое число.
Для любого целого числа a, a ÷ 1 = a
Например,
(– 7) ÷ 1 = (– 7), (–12) ÷ 1 = –12, (13) ÷ 1 = 13
Что нужно помнить
Краткие советы
- При умножении целых чисел знак произведения зависит от количества отрицательных целых чисел.



