Производная котангенса: Производная котангенса (ctgx)’

{2} \sqrt{x+1}} \)

Физика

166

Реклама и PR

31

Педагогика

80

Психология

72

Социология

7

Астрономия

9

Биология

30

Культурология

86

Экология

8

Право и юриспруденция

36

Политология

13

Экономика

49

Финансы

9

История

16

Философия

8

Информатика

20

Право

35

Информационные технологии

6

Экономическая теория

7

Менеджент

719

Математика

338

Химия

20

Микро- и макроэкономика

1

Медицина

5

Государственное и муниципальное управление

2

География

542

Информационная безопасность

2

Аудит

11

Безопасность жизнедеятельности

3

Архитектура и строительство

1

Банковское дело

1

Рынок ценных бумаг

6

Менеджмент организации

2

Маркетинг

238

Кредит

3

Инвестиции

2

Журналистика

1

Конфликтология

15

Этика

9

Формулы дифференцирования Производная тангенса Производная косинуса Производная синуса Производная логарифма по основанию a

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю  Политику  конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

10 класс.

Алгебра. Производная. Числовая последовательность. Дифференцирование функций. — Дифференцирование функции y=f(kx+m).

Комментарии преподавателя

Диф­фе­рен­ци­ро­ва­ние функ­ции y=f(kx+m)

Диф­фе­рен­ци­ро­ва­ние функ­ции  

Фи­зи­че­ский смысл про­из­вод­ной – это мгно­вен­ная ско­рость роста функ­ции при дан­ном зна­че­нии ар­гу­мен­та. Мы изу­чи­ли таб­ли­цу про­из­вод­ных от функ­ций, ко­то­рые за­ви­се­ли от ар­гу­мен­та. На­при­мер, , , где  и  – функ­ции, за­ви­ся­щие толь­ко от ар­гу­мен­та . Те­перь вме­сто ар­гу­мен­та  ста­вит­ся ар­гу­мент . На­при­мер, найти про­из­вод­ную  или . Труд­ность за­клю­ча­ет­ся в том, что мы имеем дело со слож­ной функ­ци­ей: функ­ция за­ви­сит не от , а от функ­ции от . В дан­ном слу­чае функ­ция от  — это ли­ней­ная функ­ция.

Без до­ка­за­тель­ства в учеб­ни­ке при­ни­ма­ет­ся сле­ду­ю­щее пра­ви­ло:

.

На­пом­ним, что  

Всю таб­ли­цу про­из­вод­ных и пра­ви­ла диф­фе­рен­ци­ро­ва­ния, ко­то­рые мы знаем, услож­ня­ем на­ли­чи­ем ар­гу­мен­та .

На­учим­ся на­хо­дить такие про­из­вод­ные. На­при­мер, 

.

Рас­смот­рим всю таб­ли­цу про­из­вод­ных, но ар­гу­мен­том будет ли­ней­ная функ­ция от .

1. 

2. 

3. 

4. 

5. .

За­пи­шем кон­крет­ный при­мер:

 .

По­пол­ним таб­ли­цу про­из­вод­ных. Вы­ве­дем про­из­вод­ную , поль­зу­ясь со­от­вет­ству­ю­щи­ми пра­ви­ла­ми. Знаем, что . На­пом­ним, что

Тогда:

Итак, по­лу­чи­ли, что .

Те­перь вме­сто  можем по­ста­вить ли­ней­ную функ­цию от , а имен­но

 .

По­лу­чи­ли еще одну фор­му­лу.

При­ме­ры.

1) .

2) .

Итак, поль­зу­ясь пра­ви­лом, ко­то­рое мы изу­ча­ем, вы­ве­ли до­пол­ни­тель­ную фор­му­лу для про­из­вод­ной тан­ген­са. Сде­ла­ем то же самое от­но­си­тель­но ко­тан­ген­са.

 

Итак, вы­ве­ли еще одну фор­му­лу . Таким об­ра­зом, вы­ве­ли про­из­вод­ную ко­тан­ген­са также как и вы­ве­ли про­из­вод­ную тан­ген­са от про­сто­го ар­гу­мен­та.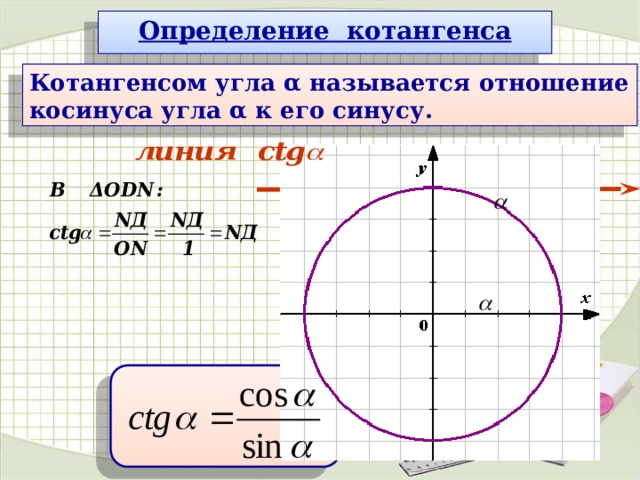 Тогда,

.

При­мер.

Вы­чис­лить про­из­вод­ную . Для на­ча­ла за­пи­шем от­дель­но про­из­вод­ную ар­гу­мен­та , а те­перь за­пи­шем про­из­вод­ную

На уроке изу­че­ны про­из­вод­ные от функ­ций, ар­гу­мен­том ко­то­рых есть ли­ней­ные функ­ции. Для того чтобы найти про­из­вод­ную , нужно взять про­из­вод­ную от самой функ­ции и умно­жить на ко­эф­фи­ци­ент , то есть . Таб­ли­цу про­из­вод­ных, до­пол­ни­ли  про­из­вод­ны­ми тан­ген­са и ко­тан­ген­са.

ИСТОЧНИК

http://interneturok.ru/ru/school/algebra/10-klass/proizvodnaya/differentsirovanie-funktsii-y-f-kx-m

http://www.youtube.com/watch?v=PU08PnahOHA

http://www.youtube.com/watch?v=Qe3lzfV6h58

http://www.webmath.ru/primeri_reshenii/derivative.php

http://11book.ru/images/shcoolbook_ru/10/10_a_mord_baz.pdf

http://u.900igr.net/zip/ea78c638410d04c5280b4e619052fb6d.zip

http://u.900igr.net/zip/ea78c638410d04c5280b4e619052fb6d.zip

http://vseuchebniki.net/uploads/posts/2015-01/1422313744_algebra_10-11_mordkovich_p2_2009. jpg

 

Proof Производная от кроватки x

Proof Производная от кроватки x

Производная от \( \cot (x)\) вычисляется с использованием производной от \(\sin x \) и \(\cos x \) и частного правила дифференцирования. Приведены примеры производных кокасательных составных функций и их решения.

Доказательство производной кроватки x

Тригонометрическое тождество, связывающее \(\cot x \), \(\cos x \) и \(\sin x \), задается выражением \[ \cot x = \dfrac { \cos x }{\sin x } \] Теперь мы используем факторное правило дифференцирования, чтобы найти производную от \( \cot x \) 92 х} \]

График кроватки x и ее производной

Графики \( \cot(x) \) и его производной показаны ниже. Производная cot(x) везде отрицательна, потому что cot(x) — убывающая функция.

Производная составной функции cot (u(x))

Рассмотрим теперь составную функцию, являющуюся функцией ctg другой функции u.