Расстояние между двумя точками. Середина отрезка. Координаты середины отрезка. Тема 4
1. Тема 1-11. Расстояние между двумя точками. Середина отрезка. Координаты середины отрезка. Уравнение прямой на плоскости.
Раздел III. Аналитическая геометрияТема 1-11.
Расстояние между двумя точками. Середина
отрезка. Координаты середины отрезка.
Уравнение прямой на плоскости. Уравнение
прямой в пространстве. Уравнение
плоскости. Расстояние от точки до плоскости.
Расстояние между плоскостями. Расстояние
от точки до прямой на плоскости. Расстояние
от точки до прямой в пространстве. Угол
между плоскостями. Угол между прямой и
плоскостью
2. Расстояние между двумя точками — это длина отрезка, что соединяет эти точки.
Расстояние между двумя точками — этодлина отрезка, что соединяет эти точки.
• Формула вычисления расстояния между двумя
точками A(xa, ya) и B(xb, yb) на плоскости:
AB = √(xb — xa)2 + (yb — ya)2
• Формула вычисления расстояния между двумя
точками A(xa, ya, za) и B(xb, yb, zb) в пространстве:
AB = √(xb — xa)2 + (yb — ya)2 + (zb — za)2
3.
Середина отрезка — это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек.Середина отрезка — это точка, котораялежит на отрезке и находится на равном
расстоянии от конечных точек.
• Формула вычисления координат середины
отрезка с концами A(xa, ya) и B(xb, yb) на
плоскости:
x a + xb
ya + yb
xc =
yc =
2
2
• Формула вычисления координат середины
отрезка с концами A(xa, ya, za) и B(xb, yb, zb) в
пространстве:
xa + xb
ya + yb
za + zb
xc =
yc =
zc =
2
2
2
4. Прямая (прямая линия) — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.
Прямая (прямая линия) — этобесконечная линия, по которой
проходит кратчайший путь между
любыми двумя её точками.
• Любую прямую на плоскости можно
задать уравнением прямой первой степени
вида
A x + B y + C = 0,
где A и B не могут быть одновременно равны
нулю.
5. Уравнение прямой с угловым коэффициентом
• Общее уравнение прямой при B≠0 можнопривести к виду
y = k x + b,
где k — угловой коэффициент равный тангенсу
угла, образованного данной прямой и
положительным направлением оси ОХ.
6. Уравнение прямой в отрезках на осях
• Если прямая пересекает оси OX и OY вточках с координатами (a, 0) и (0, b), то она
может быть найдена используя
формулу уравнения прямой в отрезках
x
a
+
y
b
=1
7. Уравнение прямой, проходящей через две различные точки на плоскости
• Если прямая проходит через две точкиA(x1, y1) и B(x2, y2), такие
что x1 ≠ x2 и y1 ≠ y2 то уравнение
прямой можно найти, используя
следующую формулу
x -x1
x2 -x1
=
y -y1
y2 — y1
8. Параметрическое уравнение прямой на плоскости
• Параметрические уравнения прямой могутбыть записаны следующим образом
x = l t +x0
y = m t + y0
где (x0, y0) — координаты точки лежащей на
прямой,
{l,m} — координаты направляющего вектора
прямой.
9. Каноническое уравнение прямой на плоскости
• Если известны координаты точки A(x0, y0)лежащей на прямой и направляющего
вектора n ={l;m}, то уравнение прямой
можно записать в каноническом виде,
используя следующую формулу
x -x0
l
=
y — y0
m
10. Уравнение прямой, проходящей через две различные точки в пространстве
• Если прямая проходит через две точкиA(x1,y1,z1) и B(x2,y2,z2), такие что
x1 ≠ x2, y1 ≠ y2 и z1 ≠ z2 то уравнение
прямой можно найти используя
следующую формулу
x -x1
x2 -x1
=
y -y1
y2 -y1
=
z -z1
z2 — z1
11. Параметрическое уравнение прямой в пространстве
• Параметрические уравнения прямой могутбыть записаны следующим образом
x = l t +x0
y = m t + y0
z = n t + z0
где (x0, y0, z0) — координаты точки лежащей на
прямой,
{l; m; n} — координаты направляющего вектора
прямой.
12. Каноническое уравнение прямой в пространстве
• Если известны координаты точки A(x0, y0, z0)лежащей на прямой и направляющего
вектора n={l;m;n}, то уравнение прямой
можно записать в каноническом виде,
используя следующую формулу
x -x0
l
=
y -y0
m
=
z -z0
n
13.
Прямая как линия пересечения двух плоскостей• Если прямая является пересечением двухплоскостей, то ее уравнение можно задать
следующей системой уравнений
A1x + B1y + C1z + D1 = 0
A2x + B2y + C2z + D2 = 0
при условии, что не имеет место равенство
A1
A2
=
B1
B2
=
C1
C2
.
14. Плоскость — есть поверхность, полностью содержащая, каждую прямую, соединяющую любые её точки.
Плоскость — есть поверхность, полностьюсодержащая, каждую прямую,
соединяющую любые её точки.
• Любую плоскость можно
задать уравнением плоскости первой
степени вида
Ax+By+Cz+D=0
где A, B и C не могут быть одновременно
равны нулю.
15. Уравнение плоскости в отрезках
• Если плоскость пересекает оси OX, OY и OZ вточках с координатами (a, 0, 0), (0, b, 0) и (0,
0, с), то она может быть найдена, используя
формулу уравнения плоскости в отрезках
x
a
+
y
b
+
z
c
=1
16.
Уравнение плоскости, проходящей через точку, перпендикулярно вектору нормали• Чтобы составить уравнение плоскости, знаякоординаты точки плоскости M(x0, y0, z0) и
вектора нормали плоскости n = {A; B; C} можно
использовать следующую формулу.
A(x — x0) + B(y — y0) + C(z — z0) = 0
17. Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой
• Если заданы координаты трех точекA(x1, y1, z1), B(x2, y2, z2) и C(x3, y3, z3),
лежащих на плоскости, то уравнение
плоскости можно найти по следующей
формуле
x — x1 y — y1 z — z1
x2 — x1 y2 — y1 z2 — z1
x3 — x1 y3 — y1 z3 — z1
=0
18. Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость.
Расстояние от точки до плоскости —равно длине перпендикуляра,
опущенного из точки на плоскость.
• Если задано уравнение плоскости Ax + By +
Cz + D = 0, то расстояние от точки M(Mx, My,
Mz) до плоскости можно найти, используя
следующую формулу:
|A·Mx + B·My + C·Mz + D|
d=
√A2 + B2 + C2
19.
Расстояние между плоскостями — равно длине перпендикуляра, опущенного с одной плоскости на другую.Расстояние между плоскостями — равнодлине перпендикуляра, опущенного с
одной плоскости на другую.
• Если заданы уравнения параллельных
плоскостей Ax + By + Cz + D1 = 0 и
Ax + By + Cz + D2 = 0, то расстояние между
плоскостями можно найти, используя
следующую формулу
|D2 — D1|
d=
√A2 + B2 + C2
20. Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Расстояние от точки до прямой — равнодлине перпендикуляра, опущенного из
точки на прямую.
• Если задано уравнение прямой Ax + By + C = 0,
то расстояние от точки M(Mx, My) до прямой
можно найти, используя следующую формулу
|A·Mx + B·My + C|
d=
√A2 + B2
21. Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Расстояние от точки до прямой —равно длине перпендикуляра,
опущенного из точки на прямую.
• Если s = {m; n; p} — направляющий вектор
прямой l, M1(x1, y1, z1) — точка лежащей на
прямой, тогда расстояние от точки
M0(x0, y0, z0) до прямой l можно найти,
используя формулу
d=
|M0M1×s|
|s|
• Двугранный угол между плоскостями равен углу
образованному нормальными векторами этих
плоскостей.
• Двугранный угол между плоскостями равен углу
образованному прямыми l1 и l2, лежащими в
соответствующих плоскостях и перпендикулярными
линии пересечения плоскостей.
• Если заданы уравнения плоскостей A1x + B1y + C1z +
D1 = 0 и A2x + B2y + C2z + D2 = 0, то угол между
плоскостями можно найти, используя следующую
формулу
|A1·A2 + B1·B2 + C1·C2|
cos α =
√A12 + B12 + C12√A22 + B22 + C22
23. Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
Угол между прямой и плоскостью — это уголмежду прямой и ее проекцией на эту
плоскость.
• Если в пространстве заданы направляющий
вектор прямой L s = {l; m; n} и уравнение
плоскости Ax + By + Cz + D = 0, то угол
между этой прямой и плоскостью можно
найти используя формулу
|A·l+B· m+C· n|
sin φ =
√A2 + B2 + C2 · √l2 + m2 + n2
КООРДИНАТЫ СЕРЕДИНЫ отрезка советы и инструкции 09:59 2023
Некоторые задачки мы с дочкой любим решать вдвоём.
Я неплохо знала когда-то математику и сейчас помогаю ей разобраться с некоторыми темами в ходе учёбы. И хотя она уже в девятом классе и хорошо занимается, приходится иногда вникать в ее проблемы.
Не постоянно конечно- а перед важными контрольными и школьными олимпиадами. И здесь не обходится без помощи интернета и учебников за предыдущие годы учебы. Вот недавно проходили тему векторов и пришлось обратиться к теме координат середины отрезка.
Для начала определение основных понятий
Отрезком называют множество всех точек, лежащих на прямой между двумя точками, включая эти точки.
Проще говоря, если при помощи линейки нарисовать линию от точки А до точки В, это и будет отрезок АВ. А если продлить линию за пределы отрезка в оба конца — то это будет прямая АВ, а отрезок АВ будет лежать на ней, и будет частью её.
Длиной отрезка АВ называют расстояние между точками А и В. Запись отрезка в этом случае обозначается прямыми скобками.
Серединой отрезка называют некоторую точку С, если она лежит на данном отрезке и находится на одинаковом расстоянии от его концов.
Если изобразить отрезок графически и использовать оси координат , то середину отрезка найти легко. Но в школьной программе даются задачи, где нужно найти середину отрезка не прибегая к помощи графических изображений. Здесь на помощь придут формулы.
Начнем с того, что каждая точка имеет свои координаты.
1. Если это одна ось координат Ох и точки отрезка лежат на ней, то у каждой точки будет один параметр обозначающий её координату. Например у точки А — ха Записывают- А(ха)
2.Если точка лежит на плоскости , то её местоположение определяют два параметра относительно двух осей координат Оx и Оy — А(ха, уа)
3. Если точку располагают в пространстве — подключается третья ось координат Оz, и тогда точка будет иметь уже три составляющих её координат — А(ха, уа zа,)
Рассмотрим нахождение середины отрезка |АВ| на одной оси или, как правильно её называют, координатной прямой.
Тогда концы отрезка будут иметь координаты соответственно А(ха) и В(хв) , а точка С, лежащая посередине будет иметь координату С(х с) . Как же найти значение х с?
Допустим , что координата точки А ха = -6, А (-6), а точки В (хв) , В (4) , чтобы найти длину отрезка нужно из координаты его правой конечной точки вычесть координату его левой конечной точки . Тогда длина отрезка АВ по формуле dAB=|4-(-6)| равна 10
Если точка С лежит посередине отрезка |AB|, то |AC|=|CB|. а длина dAC=| х с — ха | и длина dСВ= | х в -хс | а они равны и значит | х с -ха | = | х в — хс | Поскольку применяется модуль, то возможны два варианта:
Первый — из уравнения получается, что х с -ха = х в — хс, следовательно ха+ х в = хс+х с или 2х с = ха+ х в ,
Второй: х с -ха = — (х в — хс), следовательно ха= х в, а этого не может быть , поэтому не учитывается.
Найдём значение х с в нашем примере 2х с = -6+4, х с= -1 середина данного отрезка на координатной прямой находится в точке С(-1). Нужно запомнить формулу
Координаты середины отрезка равны половине суммы координат его концов.
Координаты отрезка на плоскости определяются соответственно, только по каждому параметру и выводятся эти формулы исходя из проекций отрезка на оси координат
По этим формулам можно находить середины отрезков как лежащих наклонно так и лежащих параллельно одной из осей. Например середина отрезка АВ, лежащего параллель но оси Оу с координатами А(3,2) иВ(3, 10) будет вычисляться по той же формуле и будет иметь координаты х с =(3+3):2 и ус= ( 2+10):2 отсюда точка С(3,6). Это доказывает, что точка С лежит на том же отрезке, параллельном к оси Оу и формула к нему применима.
Для нахождения середины отрезка в пространстве третью составляющую находят подобным образом
Видео обзор
| Все(5) |
|---|
 youtube.com/embed/g6w7wEZSFdM» allowfullscreen=»»/> |
| Расстояние между двумя точками. Координаты середины отрезка. | Середина отрезка 6 класс пифагорчик.рф | Декартовы координаты в пространстве. Координаты середины отрезка. Геометрия 10-11 классы. Урок 10 | Построение середины отрезка | Построение середины отрезка |
Пояснение к уроку: Точки, средние точки и расстояния в пространстве
В этом объяснении мы научимся найдите координаты точки в 3D, расстояние между двумя точками в 3D, а также координаты средней и конечной точек в 3D, используя формулу.
Мы уже должны знать, как найти все это в двух измерениях. Любая точка в двух измерениях будет иметь 𝑥- и 𝑦-координату и может быть записана в виде (𝑥,𝑦). Каждое из действительных чисел в упорядоченной паре представляет собой смещение этой точки от начала координат, другими словами, положительное или отрицательное расстояние от точки (0,0).
Если две точки 𝐴 и 𝐵 имеют координаты (𝑥,𝑦) и (𝑥,𝑦) соответственно, то мы можем вычислить их середину по формуле 𝑥+𝑥2,𝑦+𝑦2.
Если две точки 𝐴 и 𝐵 имеют координаты (𝑥,𝑦) и (𝑥,𝑦) соответственно, то мы можем вычислить расстояние между ними, используя формулу расстояния, полученную из теоремы Пифагора, (𝑥−𝑥)+(𝑦−𝑦).
Определение: Координаты точки в трехмерном пространстве
Любая точка в трех измерениях будет иметь 𝑥-, 𝑦-, и 𝑧-координат и может быть записан в виде (𝑥,𝑦,𝑧). Каждое из действительных чисел в упорядоченной тройке дает расстояние от начала координат, измеренное вдоль соответствующей оси.
В нашем первом примере мы рассмотрим, в какой плоскости лежит точка, одна из координат которой равна нулю.
Пример 1. Определение плоскости, в которой находится заданная координата
В какой из следующих координатных плоскостей находится точка (−7,−8,0) ложь?
- 𝑥𝑦
- 𝑥𝑧
- 𝑦𝑧
Ответ
Мы знаем, что точка в 3D будет иметь 𝑥-, 𝑧-.
В этом вопросе 𝑥=−7, 𝑦=−8 и 𝑧=0.
Поскольку 𝑧-координата равна нулю, точка находится на нулевом расстоянии от начала координат в 𝑧-направлении. Это означает, что он будет лежать на 𝑥𝑦-плоскости. В самом деле, любая точка с координаты (𝑥,𝑦,0) будут лежать на этой плоскости.
Таким образом, мы можем заключить, что точка (−7,−8,0) лежит на 𝑥𝑦-плоскости.
Определение: Три координатные плоскости
Любая точка с координатами (𝑥,𝑦,0) будет лежать на 𝑥𝑦-плоскости.
Аналогично, любая точка с координатами (𝑥,0,𝑧) будет лежать на 𝑥𝑧-плоскость, и любая точка с координатами (0,𝑦,𝑧) будет лежать на 𝑦𝑧-плоскости.
В нашем следующем вопросе мы рассмотрим, как мы можем определить координаты точки в трех измерениях.
Пример 2. Нахождение координат заданной точки в 3D
Определить координаты точки 𝐴.
Ответ
Любая точка в трех измерениях будет иметь 𝑥-, 𝑦- и 𝑧-координаты и может быть записана в виде (𝑥,𝑦,𝑧).
Двигаясь от начала координат, мы проходим 3 единицы в положительном 𝑥-направлении,
−3 единицы в 𝑦-направлении и, наконец, 3 единицы в 𝑧-направлении.
Это означает, что 𝑥=3, 𝑦=−3 и 𝑧=3.
Координаты точки 𝐴 равны (3,−3,3).
Напомним, что формула средней точки в двух измерениях просто говорит нам найти среднее значение двух точек. Находим среднее значение 𝑥-координат и среднее значение 𝑦-координат. Теперь мы расширим эту идею до трех измерений, найдя также среднее значение 𝑧-координат.
Чтобы найти среднее любых двух чисел, мы складываем их, а затем делим их сумму на два.
Определение: середина двух точек в трехмерном пространстве
Если две точки 𝐴 и 𝐵 имеют координаты (𝑥,𝑦,𝑧) и (𝑥,𝑦,𝑧) соответственно, то можно вычислить их среднюю точку, используя следующую формулу: 𝑥+𝑥2,𝑦+𝑦2,𝑧+𝑧2.
В нашем следующем примере мы будем использовать эту формулу для определения середины двух точек в пространстве.
Пример 3: Нахождение координат средней точки в 3D
Баллы 𝐴 и 𝐵 имеют координаты (8,−8,−12) и (−8,5,−8) соответственно. Определить координаты середины 𝐴𝐵.
Ответ
Чтобы найти середину двух точек в трех измерениях, мы будем использовать формулу для вычисления середины координат (𝑥,𝑦,𝑧) и (𝑥,𝑦,𝑧): 𝑥+𝑥2,𝑦+𝑦2,𝑧+𝑧2.
Пусть точка 𝐴 имеет координаты (𝑥,𝑦,𝑧), а точка 𝐵 имеет координаты (𝑥,𝑑 ).
Середина между точками 𝐴 и 𝐵 равна =8+(−8)2,−8+52,−12+(−8)2=02,−32,−202=0,−32 ,−10.
Координаты середины 𝐴𝐵 составляют 0,−32,−10.
В нашем следующем примере мы будем использовать формулу средней точки для определения конечной точки по средней точке двух точек в пространстве и другой конечной точке.
Пример 4: Нахождение координат конечной точки отрезка линии по координатам середины и координатам начальной точки
Учитывая, что точка (0,17,−10) является средней точкой 𝐴𝐵 и что 𝐴(−19,7,14), каковы координаты 𝐵?
Ответ
Чтобы найти середину двух точек в трех измерениях, мы будем использовать формулу для вычисления середины координат (𝑥,𝑦,𝑧) и (𝑥,𝑦,𝑧) : 𝑥+𝑥2,𝑦+𝑦2,𝑧+𝑧2.
Мы знаем, что точка 𝐴 имеет координаты (−19,7,14)
и пусть точка 𝐵 имеет координаты (𝑥,𝑦,𝑧). Середина между этими двумя точками имеет координаты (0,17,−10).
Подставив эти значения в формулу, получим (0,17,−10)=−19+𝑥2,7+𝑦2,14+𝑧2.
Затем мы можем приравнять отдельные компоненты, что даст нам решение трех уравнений.
Во-первых, 𝑥-координата дает нам 0=−19+𝑥2.
Умножая обе части уравнения на 2, получаем 0=−19+𝑥.
Итак, 19=𝑥.
Во-вторых, 𝑦-координата дает нам 17=7+𝑦2.
Умножив обе части уравнения на 2, мы получим 34=7+𝑦.
Итак, 27=𝑦.
Наконец, 𝑧-координата дает нам −10=14+𝑧2.
Умножая обе части уравнения на 2, мы получаем −20=14+𝑧.
Итак, −34=𝑧.
Координаты точки 𝐵 равны (19,27,−34).
В двух измерениях мы можем вычислить расстояние между двумя точками, используя адаптацию теоремы Пифагора. Это утверждает, что 𝑎+𝑏=𝑐, где 𝑐 — длина самой длинной стороны, известной как гипотенуза, прямоугольного треугольника.
Если две точки 𝐴 и 𝐵 имеют координаты (𝑥,𝑦) и (𝑥,𝑦) соответственно, то
можно вычислить расстояние между ними по следующей формуле: (𝑥−𝑥)+(𝑦−𝑦).
Теперь мы рассмотрим, как мы можем вычислить расстояние между двумя точками в три измерения.
Рассмотрим трехмерную прямоугольную призму 𝐴𝐵𝐶𝐷𝐸𝐹𝐺𝐻, нарисованную ниже, и предположим, что мы хотим пройти от самого нижнего левого переднего угла, 𝐴, до самого верхнего правого заднего угла, 𝐺.
Сначала рассмотрим треугольник 𝐴𝐵𝐹 в основании призмы. Теорема Пифагора говорит нам, что 𝐴𝐹=𝐴𝐵+𝐵𝐹.
Итак, 𝐴𝐹=√𝑥+𝑦.
Теперь делаем еще один треугольник 𝐴𝐹𝐺, с основанием вдоль 𝐴𝐹 и высотой 𝐹𝐺.
Мы можем снова использовать теорему Пифагора так, чтобы 𝐴𝐺=𝐴𝐹+𝐹𝐺. Подставляя длины 𝐴𝐹 и 𝐹𝐺, мы видим, что 𝐴𝐺=√𝑥+𝑦+𝑧.
Следовательно, 𝐴𝐺=√𝑥+𝑦+𝑧.
Определение: расстояние между двумя точками в трехмерном пространстве
Если две точки 𝐴 и 𝐵
имеют координаты (𝑥,𝑦,𝑧) и (𝑥,𝑦,𝑧),
соответственно, то мы можем рассчитать расстояние между ними по следующей формуле: (𝑥−𝑥)+(𝑦−𝑦)+(𝑧−𝑧). теоремы Пифагора в трех измерениях; мы находим сумму квадратов разницы между каждой координатой и затем квадратный корень этого ответа.
В наших последних двух вопросах мы вычислим кратчайшее расстояние между точкой и одной из осей, а также расстояние между двумя точками в пространстве.
Пример 5. Нахождение расстояния между двумя точками по их координатам в трех измерениях
Нахождение расстояния между двумя точками 𝐴(−7,12,3) и 𝐵(−4,−1,−8).
Ответ
Чтобы вычислить расстояние между двумя точками в трех измерениях, мы будем использовать следующую формулу, где две точки 𝐴 и 𝐵 имеют координаты (𝑥,𝑦,𝑧) и (𝑥,𝑦,𝑧) соответственно: (𝑥−𝑥)+(𝑦−𝑦)+(𝑧−𝑧).
Пусть точка 𝐴 имеет координаты (𝑥,𝑦,𝑧), а точка 𝐵 имеет координаты (𝑥,𝑦,𝑧).
Расстояние между ними равно =√(−4−(−7))+(−1−12)+(−8−3)=√(3)+(−13)+(−11)=√9+169+121=√299 .
Расстояние между двумя точками 𝐴(−7,12,3) и 𝐵(−4,−1,−8) составляет √299 единиц длины.
Пример 6: Нахождение расстояния между точкой и осью в 3D
Каково расстояние между точкой (19,5,5) и осью 𝑥?
Ответ
Мы знаем, что любая точка будет лежать на оси 𝑥, если и ее 𝑦-координата, и ее 𝑧-координата равны нулю.
Это означает, что мы можем определить точку на оси 𝑥 как (𝑥,0,0).
Признаем, что искомое расстояние — это перпендикулярное расстояние от точки до оси 𝑥, что означает проекцию точки на 𝑥-ось будет в точке (19,0,0).
Расстояние между двумя точками можно рассчитать по формуле следующим образом √(19−19)+(5−0)+(5−0)=√0+(5)+(5)=√50=5√2.
Расстояние между точка (19,5,5) и ось 𝑥 составляют 5√2 единиц длины.
Мы закончим это объяснение повторением некоторых ключевых моментов.
Ключевые точки
- Любая точка в трех измерениях имеет координаты, записанные в виде (𝑥,𝑦,𝑧).
- Если 𝑧-координата равна нулю, то мы знаем, что точка лежит в 𝑥𝑦-плоскости; если 𝑦-координата равна нулю, то мы знаем, что точка лежит в 𝑥𝑧-плоскость; а если 𝑥-координата равна нулю, то мы знаем, что точка лежит в 𝑦𝑧-плоскости.
- Если и 𝑦-координата, и 𝑧-координата равны нулю, то точка лежит на 𝑥-оси; если и 𝑥-координата, и
𝑧-координата равна нулю, то точка лежит на 𝑦-оси; и если и 𝑥-координата, и 𝑦-координата равны
равна нулю, то точка лежит на оси 𝑧.
- Середина двух точек с координатами (𝑥,𝑦,𝑧) и (𝑥,𝑦,𝑧) лежит в точке 𝑥+𝑥2,𝑦+𝑦2,𝑧+𝑧2.
- Мы также можем использовать формулу средней точки для вычисления конечной точки отрезка, учитывая среднюю точку и другую конечную точку.
- Расстояние между двумя точками с координатами (𝑥,𝑦,𝑧) и (𝑥,𝑦,𝑧) это равно (𝑥−𝑥)+(𝑦−𝑦)+(𝑧−𝑧).
Как найти середину — математика GCSE
Введение
Как найти середину отрезка
Как найти рабочий лист средней точки
Поиск отсутствующей конечной точки
Распространенные заблуждения
Потренируйтесь находить середину вопросы
Как найти середину вопросов GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Еженедельные онлайн-уроки повторения GCSE по математике теперь доступны
Введение
Как найти середину отрезка
Как найти рабочий лист средней точки
Поиск отсутствующей конечной точки
Распространенные заблуждения
Потренируйтесь находить середину вопросы
Как найти середину вопросов GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем, как найти середину, в том числе найти середину отрезка с использованием декартовых координат и найти отсутствующую конечную точку, когда заданы середина и другая конечная точка.
Существуют также рабочие листы средней точки строки, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные указания о том, что делать дальше, если вы все еще застряли.
Что такое середина линии?
Середина отрезка линии — это точка, которая находится точно посередине между двумя точками. Это одинаковое расстояние от каждой конечной точки отрезка прямой.
Иногда это можно выяснить путем проверки — это проще сделать с положительными целыми числами.
Например, для двух точек (2,2) и (8,6) средняя точка находится ровно посередине между ними и лежит в (5, 4).
Мы видим, что 5 находится посередине между 2 и 8, а 4 — посередине между 2 и 6. В этом может помочь представление числового ряда.
Что такое середина линии?
Середина формулы линии
Если определить середину нелегко или координаты содержат дроби или отрицательные числа, мы можем использовать формулу средней точки.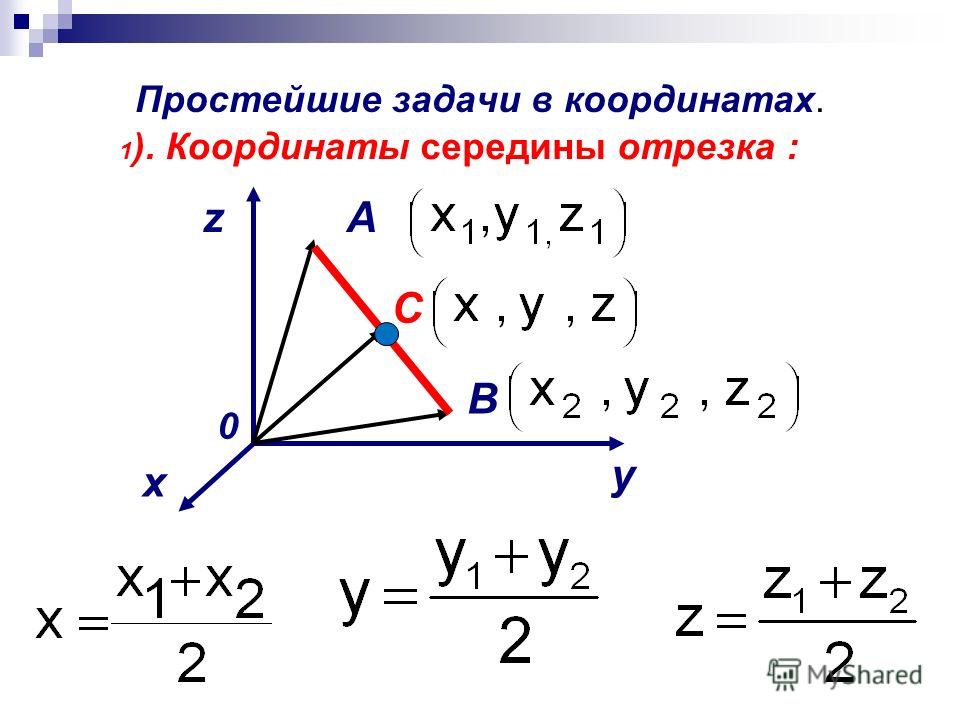
Если точки \mathrm{A}\left(x_{1}, y_{1}\right) и \mathrm{B}\left(x_{2}, y_{2}\right) являются конечными точками отрезок, то середина отрезка, соединяющего точки A и B, равна \left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2} {2}\справа).
Это выглядит сложно, если записать алгебраически, но в основном мы вычисляем (среднее) среднее значение как значений x, так и значений y.
Мы суммируем две координаты x и делим на 2, чтобы найти координату x средней точки, и суммируем две координаты y и делим на 2, чтобы найти координату y средней точки.
Например, если даны две точки A \ (-1,2) и B \ (2,4), средняя точка (M) находится точно посередине между ними и лежит в (0,5, 3). 9{2}}=\sqrt{13} .
Пошаговое руководство: Теорема Пифагора
Если вы продолжите изучение координатной геометрии на уровне A, вы можете встретить общую формулу расстояния,
d=\sqrt{\left(x_{2}- x_{1}\right)+\left(y_{2}-y_{1}\right)}, где (x_{1},y_{1}) и (x_{2},y_{2}) – координаты двух точек, а d — расстояние между ними.
Как найти середину отрезка
Чтобы найти середину отрезка, соединяющего конечные точки A и B:
- Найдите среднее значение \textbf{x} координат двух конечных точек.
- Найдите среднее значение \textbf{y} координат двух конечных точек.
- Запишите координаты точки.
Объясните, как найти середину отрезка
Рабочий лист с прямым графиком (включает в себя, как найти среднюю точку)
Получите бесплатный рабочий лист, как найти среднюю точку из 20+ вопросов и ответов по прямолинейному графику. Включает рассуждения и прикладные вопросы.
СКОРО
ИксРабочий лист с прямым графиком (включает в себя, как найти среднюю точку)
Получите бесплатный рабочий лист, как найти среднюю точку из 20+ вопросов и ответов по прямолинейному графику.
Включает рассуждения и прикладные вопросы.
СКОРО
Как найти середину примеров
Пример 1: две положительные целые конечные точки
Найдите середину отрезка, соединяющего точки (0,6) и (4, 10).
- Найдите среднее значение \textbf{x} координат двух конечных точек.
\frac{0+4}{2}=\frac{4}{2}=2
2 Найдите среднее значение \textbf{y} координат двух конечных точек.
\frac{6+10}{2}=\frac{16}{2}=8
3 Запишите координаты точки.
(2, \ 8)
В этом случае довольно легко увидеть среднюю точку путем осмотра, особенно при работе на графике.
Пример 2: две положительные целые конечные точки с дробным ответом
Найдите середину отрезка, соединяющего точки (1,5) и (6, 0).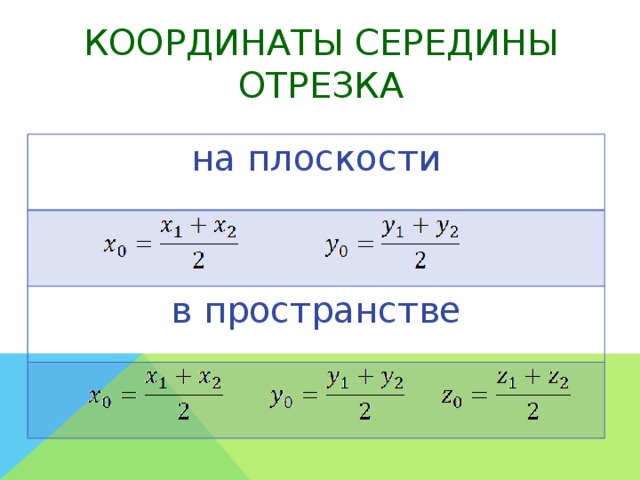
Найдите среднее значение \textbf{x} координат двух конечных точек.
\frac{1+6}{2}=\frac{7}{2}=3,5
Найдите среднее значение \textbf{y} координат двух конечных точек.
\frac{5+0}{2}=\frac{5}{2}=2,5
Запишите координаты точки.
(3.5,\ 2.5)
Обычно можно задавать пары координат в виде коротких десятичных дробей. Любые более длинные или повторяющиеся десятичные дроби следует по возможности указывать в виде дробей, не забывая об упрощении ответа.
Пример 3: пары координат, содержащие отрицательные числа
Найдите середину отрезка, соединяющего точки (-2,7) и (4, 10).
Найдите среднее значение \textbf{x} координат двух конечных точек.
\frac{-2+4}{2}=\frac{2}{2}=1
Найдите среднее значение \textbf{y} координат двух конечных точек.
\frac{7+10}{2}=\frac{17}{2}=8,5
Запишите координаты точки.
(1, \ 8,5)
Графически,
Пример 4: координаты, содержащие десятичные дроби
Найдите середину отрезка, соединяющего точки (0,5, 3) и (4, 2,5).
Найдите среднее значение \textbf{x} координат двух конечных точек.
\frac{0.5+4}{2}=\frac{4.5}{2}=2.25
Найдите среднее значение \textbf{y} координат двух конечных точек.
\frac{3+2.5}{2}=\frac{5.5}{2}=2.75
Запишите координаты точки.
(2,25, \ 2,75)
Графически,
Поиск отсутствующей конечной точки
Иногда вам может быть задана одна конечная точка и средняя точка, и вам придется работать с другой конечной точкой.
Чтобы добраться из первой конечной точки (1,3) в среднюю точку (3,7), мы перемещаем 2 в направлении x и 4 в направлении y.
Поэтому мы просто повторяем это снова из средней точки, чтобы найти координату другой конечной точки, которая в данном случае будет (5,11).
Как найти отсутствующую конечную точку
Чтобы найти отсутствующую конечную точку при наличии одной конечной точки и средней точки:
- Решите, как добраться от заданной конечной точки до средней точки.
- Повторите это, чтобы перейти от средней точки к отсутствующей конечной точке.
- Запишите координаты отсутствующей конечной точки.
Объясните, как найти отсутствующую конечную точку
Пример 5: поиск отсутствующей конечной точки при наличии одной конечной точки и средней точки
Отрезок соединяет точки A и B и имеет середину M.
A имеет координаты (4, 8), а M имеет координаты (6 , 9).
Найдите координаты точки B.
Определите, как добраться из заданной конечной точки в среднюю.
Чтобы добраться из A в M, мы добавляем 2 к координате x точки A и добавляем 1 к координате y точки A.
Повторите это, чтобы добраться от средней точки до недостающей конечной точки.
Чтобы добраться из M в B, мы добавляем 2 к координате x точки M и добавляем 1 к координате y точки M.
Запишите координату отсутствующей конечной точки.
Следовательно, координаты точки B равны (8,10).
Пример 6: поиск отсутствующей конечной точки с отрицательными координатами
Отрезок соединяет точки A и B и имеет середину M.
A имеет координаты (-9, 4), а M имеет координаты (-6, -1 ).
Найдите координаты точки B.
Определите, как добраться из заданной конечной точки в среднюю.
Чтобы перейти от A к M, мы добавляем 3 к координате x точки A и вычитаем 5 из координаты y точки A.
Повторите это, чтобы перейти от средней точки к отсутствующей конечной точке.
Чтобы добраться из M в B, мы добавляем 3 к координате x точки M и вычитаем 5 из координаты y точки M.
Запишите координату отсутствующей конечной точки.
Следовательно, координаты точки B равны (-3,-6).
Распространенные заблуждения
- Нахождение среднего значения каждой точки, а не среднего значения \textbf{x} координат и среднее значение \textbf{y} координат
Например, для точек (2, 3) и (5, 7) убедитесь, что вы не делаете \frac{2+3}{2} и \frac{5+7}{2}.
- Использование формулы средней точки при задании одной конечной точки и средней точки
Если одна конечная точка равна (3, 4), а средняя точка (6, 2), убедитесь, что вы определили, как добраться от конечной точки до средней точки, и повторите это, а не используйте формулу средней точки.
- Ошибки при вычислении отрицательных чисел
Если вы не уверены в своем ответе, нарисуйте схему и посчитайте шаги.
Практика нахождения средней точки вопросы \frac{2+6}{2}=\frac{8}{2}=4, а среднее значение координат y равно \frac{8+12}{2}=\frac{20}{2}=10 .
(1, \ 3)
(6, \ 7.5)
(5.5, \ 7.5)
(6.5, \ 7.5)
Среднее значение координат x равно \frac{4+7}{2}=\frac{11}{ 2}=5,5, а среднее значение координаты Y равно \frac{10+5}{2}=\frac{15}{2}=7,5.
(2, \ 3)
(4, \ 5)
(4, \ 3)
(2, \ 5)
Среднее значение координат x равно \frac{-2+6}{ 2}=\frac{4}{2}=2, а среднее значение координат y равно \frac{8+(-2)}{2}=\frac{6}{2}=3.
(7, \ 7,5)
(7.5, \ 7.25)
(6, \ 8.5)
(7.25, \ 7.25)
Среднее значение координат x равно \frac{3.5+11}{2}=\frac{14.5}{ 2}=7,25, а среднее значение координаты Y равно \frac{6+8,5}{2}=\frac{14,5}{2}=7,5.
(0, \ 7)
(14, \ 6)
(6.5, \ 3)
(5, \ 2)
Чтобы добраться из А в М, прибавьте 5 к координате x и прибавьте 2 к координате у. Повторите это, чтобы перейти от M к B, поэтому координата B равна (14, \ 6).
(1, \ 8.5)
(4, \ 3)
(-3, \ 13)
(-5, \ 13)
Чтобы получить из A в M, вычтите 4 из координаты x и добавьте 3 к координате y. Повторите это, чтобы перейти от M к B, поэтому координата B равна (-5, \ 13).
Как найти середину вопросов GCSE
1. Отрезок соединяет точки A и B и имеет середину M.
A имеет координаты (3, \-12).
B имеет координаты (-5,\10).
Определите координаты точки M.
(2 балла)
Показать ответ
Исправьте координаты x или y или найдите среднюю точку с помощью \frac{3+(-5)}{ 2} или \frac{-12+10}{2} .
(1)
(-1, \-1)
(1)
2.
а) Запишите координаты точки А.
(c) На сетке отметьте крестиком точку (-2, \ 3). Мрака это C.
(3 балла)
Показать ответ
(a) (-2, \ 1)
(1)
(B) (0,2)
(1)
(c)
Точка отмечена в правильном положении.
(1)
3. Отрезок соединяет точки P и Q и имеет середину M.
P имеет координаты (9, \ 5), а M имеет координаты (15, \ 8).
Точка R расположена так, что треугольник PQR является прямоугольным.
Координата y R равна 5. Какова координата x R?
(3 балла)
Показать ответ
Метод определения координат конечной точки, например, +6 к координате x или +3 к координате y.
(1)
Q = (21, \ 11)
(1)
x координата R = 21 .