Производная корень из х 2: Найти производную y’ = f'(x) = sqrt(x/2) (квадратный корень из (х делить на 2))

2

Необходимое условие существования экстремума.

Теорема Ферма. Если внутренняя точка х₀ из области определения непрерывной функции f(х) является точкой экстремума и в этой точке существует производная, то она равна нулю, т. e.f ‘(x₀) = 0.

Чтобы определить, имеет ли функция экстремум в данной точке, необходимо воспользоваться достаточными условиями его существования.

Достаточные условия существования экстремума

Теорема 1. Если существуют такие а и b, что функция f(х), непре­рывная в точке х₀

(а <

х₀ < b), такова, что f(x) > 0 на интервале (а, x₀) и f ‘(х) < 0 на интервале (х₀, b), то точка x₀ является точкой максимума функции f(х).

Теорема 2. Если функция f (х) непрерывна в точке х₀, a f ‘(x)

< 0 на интервале (а, х₀) и f ′(x) > 0 на интервале (х₀, b), то точка х₀ является точкой минимума функции f(x).

Таким образом, чтобы найти экстремумы данной функции у = f(х), необходимо:

1. Найти первую производную f ‘(х).

2. Приравняв первую производную нулю, отыскать действительные корни

х₁, х₂,. . . уравнения f ‘(х) = 0.

Корни этого уравнения являются критическими точками функции.

3. Для каждой критической точки х_k найти окрестность, не содержа­щую других критических точек, подставить в производную любое число, меньшее х_k из этой окрестности, а затем любое число, большее х_k, из этой окрестности; если при этом знак производной:

а) будет меняться с + на –, то функция при х = х₁ имеет максимум;

б) будет меняться с – на +, то функция при х = х₁ имеет минимум;

в) не меняется, то функция при х = х₁ экстремума не имеет;

4.

Найти экстремальные значения функции.

Пример 1. Исследовать функцию , заданную на отрезке [0, 5], на экстремум.

Решение. 1) Находим производную: у’ = х – 3.

2) Находим корень производной: х — 3 = 0 <=> х = 3.

3) Находим значение производной в точке х = 2 интервала (0, 3): y‘(2) = -1 < 0.

4) Находим значение производной в точке х = 4 интервала (3, 5): y‘ (4) = 1 > 0.

Производная у’ в окрестности точки х = 3 меняет знак с – на +, сле­довательно, в точке

х = 3 находится минимум.

5) находим значение функции в критической точке

х = 3: у (3) = — 3∙3 = — 4,5

Таким образом, минимальное значение функции равно -4,5.

Наибольшее и наименьшее значения функции

На рис. 3 изображен график некоторой функции у = f(х), определенной на отрезке

[а, b].

На данном отрезке наша функ­ция в точках х_1, х₂, х₃, х₄, х₅ прини­мает экстремальные значения. Для определения наименьшего и наи­большего значений дифференцируе­мой функции на всем данном отрезке [а, b] следует найти все критические точки функции, лежащие внутри отрезка, вычислить значения функции в этих точках и на концах отрезка и из всех полученных таким образом чисел выбрать наименьшее и наибольшее, т. е., как говорят, найти

глобальные экстремумы функции.

Рис. 3.

Пример 1. Найти наименьшее и наибольшее значение функции на отрезке [-3, 4].

Решение. 1) Находим производную: .

2) Находим корни производной: х₁ = -2 и х₂ = 2.

3) Исследуем значение производной в окрестности критической точки х = -2:

y’(-3) = 1,5 > 0 и y’(-1) = -0,9 < 0. Следовательно, в точке x₁ = -2 данная функция имеет максимум, равный 2,6.

Аналогично находим, что в критической точке х₂ = 2 данная функ­ция имеет минимум, равный – 0,6.

В примере требуется найти наибольшее и наименьшее значение функ­ции в промежутке

[-3, 4], поэтому необходимо найти значение функции и на концах этого промежутка.

Имеем: у(-3) = 1,9 и у(4) = 2,6.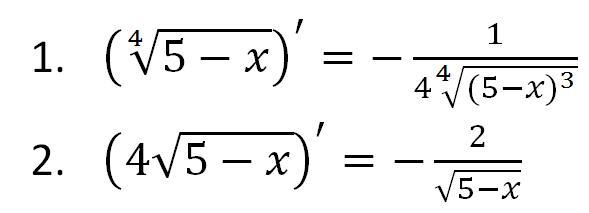 Следователь­но, наименьшее значение, равное — 0,6, данная функция достигает в точке х = 2, а наибольшее значение 2,6 в двух точках: х = — 2 и х = 4.

Пример 2. Каковы должны быть размеры прямоугольной комнаты площадью 25м², чтобы периметр ее был наименьшим?

Решение. Примем длину комнаты равной х (м), тогда ширина равна , а периметр

Периметр у есть функция длины х, определенная для всех положи­тельных значений х. Определим интервалы ее возрастания и убывания. Находим производную: . Так как знаменатель больше нуля и длина х положительна, то знак производной определяется знаком разности (х — 5). Таким образом, периметр прямоугольника имеет наи­меньшее значение (минимум), если длина прямоугольника 5м и ширина т. е. когда комната имеет квадратную форму.

Дифференцировать Ln ( SQRT(x-2))/X² | Wyzant Спросите эксперта

Дифференциация

Санни С.

спросил 12.03.16

Дифференцировать Ln od квадратный корень из x-2, деленный на x в квадрате.

 

Спасибо  

С уважением

Санни

Подписаться І 2

Подробнее

Отчет

3 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Алан Г. ответил 12.03.16

Репетитор

5 (4)

Успешная помощь учащимся в повышении успеваемости по математике!

Смотрите таких репетиторов

Смотрите таких репетиторов

X ² внутри или снаружи ln? Это имеет значение, поэтому я покажу вам оба способа.

 

1)  y = ln {[√(x — 2)]/x ² } = ½ ln (x — 2) — 2 ln x     (расширить, используя свойства логарифмов)

 

900 dy / d x   = ½[1/(x — 2)] — 2(1/x) = 1/[2(x — 2)] — 2/x

 

2) y = [ln (√(x — 2) ]/x ² = [ln (x — 2)]/(2x ² )     (упростить, используя свойства логарифмов)

 

     dy/dx = [2x ² /(x4x — 2) — 2 ln (x — 2)]/(4x ⁴ )    (частное правило)

 

              = [x — (2x — 4) ln (x — 2)]/[2x ³ (x — 2)]    (сокращение дроби)

 

Извините, мне пришлось сделать это дважды, но вы должны быть очень осторожны со скобками при отправке задач, которые можно интерпретировать более чем одним способом.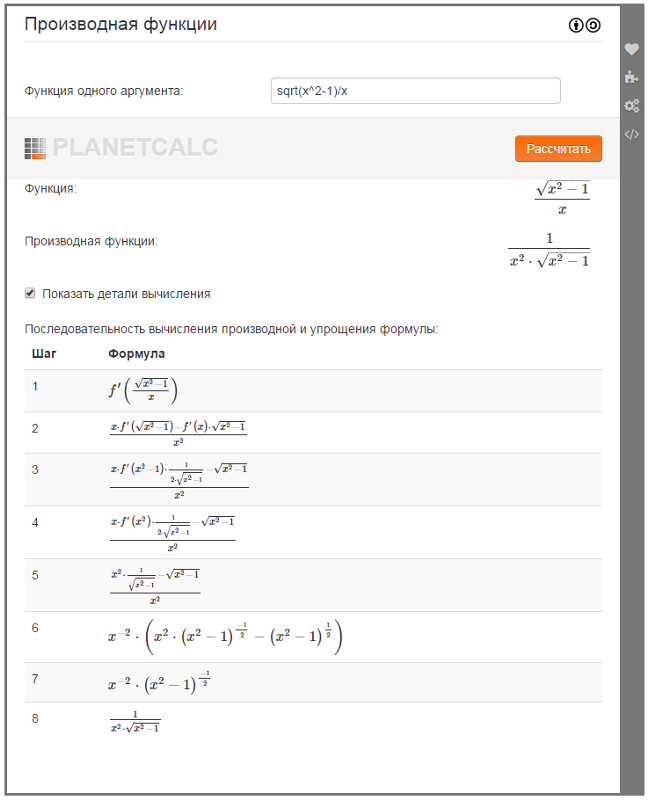 Возможно, я слишком осторожен, но многие студенты забывают это делать.

 

Дайте мне знать, если это поможет вам.

Голосовать за 0 голос против

Подробнее

Отчет

Кеннет С. ответил 12.03.16

Репетитор

4,8 (62)

Экспертная помощь по алгебре/тригонометрии/(пред)исчислению для гарантии успеха в 2018 году

См. таких репетиторов

Смотрите таких репетиторов

    √(x-2)
ln ——— лучше всего упростить как  y = ½ln(x-2) — 2lnx
      x ²

 

, а затем y’ = ½ (1/(x-2)) -2(1/x), и если это поместить в общий знаменатель  2x(x-2), числитель станет

 

x — 2•(x-2)  и я получаю окончательный ответ (4 — x) / [2x(x-2)]

, поэтому я не согласен с ответом Марлен.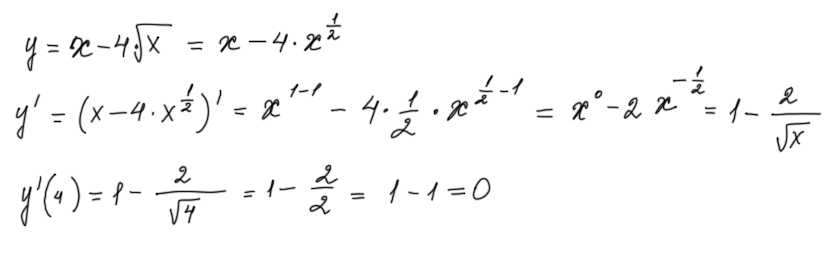

 

Р.С.В.П.

Голосовать за 0 голос против

Подробнее

Отчет

Марлен С. ответил 12.03.16

Репетитор

4.9 (2669)

Актуарии на пенсии Преподаватели математики

Об этом репетиторе ›

Об этом репетиторе ›

Спасибо, Солнышко.

 

ОК. Здесь действует несколько правил дифференциации

 

1) d/dx lnx = 1/x

2) ln x/y = lnx — lny

3) цепная линейка ——

x ²

Давайте переписать, как

LN √ (x-2)-LN x ²

и

LN (X-2) ^1/2. — ln x ²

 

Сначала возьмем производную от ln, которая равна

1/(x-2) ^1/2 d/dx (x-2) ^1/2 — 1/x ² d/dx(x ² )

 

продолжение

 

1/(4x-2/4x-2) 0 1 2) ^-1/2 — 1/x ² (2x)

 

Упрощение

 

Первое слагаемое сокращается до 1/2, а второе сводится к 2/x00 3

3 9, поэтому мы имеем

3 9

1/2 + 2/x

 

(x + 4)/2x

 

 

 

 

Голосовать за 0 голос против

Подробнее

Отчет

Все еще ищете помощь? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

4.2 Линейные аппроксимации и дифференциалы. Расчет, том 1

Цели обучения

• 4.2.1 Описать линейную аппроксимацию функции в точке.
• 4.2.2 Запишите линеаризацию заданной функции.
• 4.2.3 Нарисуйте график, иллюстрирующий использование дифференциалов для аппроксимации изменения величины.
• 4.2.4 Рассчитайте относительную ошибку и процентную ошибку при использовании дифференциального приближения.

Мы только что видели, как производные позволяют нам сравнивать связанные величины, которые изменяются во времени. В этом разделе мы исследуем другое применение производных: возможность локального приближения функций линейными функциями. Линейные функции — это самые простые функции для работы, поэтому они предоставляют полезный инструмент для аппроксимации значений функций. Кроме того, идеи, представленные в этом разделе, обобщаются далее в тексте, когда мы изучаем, как аппроксимировать функции полиномами более высокой степени. Введение в степенные ряды и функции.

Линейная аппроксимация функции в точке

Рассмотрим функцию ff, дифференцируемую в точке x=a.x=a. Напомним, что касательная к графику ff в точке aa задается уравнением

y=f(a)+f′(a)(x−a).y=f(a)+f′(a)(x−a).

Например, рассмотрим функцию f(x)=1xf(x)=1x при a=2.a=2. Поскольку ff дифференцируема при x=2x=2 и f′(x)=−1×2,f′(x)=−1×2, мы видим, что f′(2)=−14.f′(2)=−14. Следовательно, касательная к графику ff при a=2a=2 задается уравнением

у=12-14(х-2).у=12-14(х-2).

На рис. 4.7(a) показан график f(x)=1xf(x)=1x вместе с касательной к ff в точке x=2.x=2. Заметим, что при xx вблизи 2 график касательной близок к графику ф.ф. В результате мы можем использовать уравнение касательной для аппроксимации f(x)f(x) при xx, близком к 2. Например, если x=2,1,x=2,1, значение yy соответствующей точки касательной строка

y=12−14(2,1−2)=0,475.y=12−14(2,1−2)=0,475.

Фактическое значение f(2.1)f(2.1) определяется как

f(2.1)=12.1≈0.47619.f(2.1)=12.1≈0.47619.

Таким образом, касательная дает нам довольно хорошее приближение f(2.1)f(2.1) (рис. 4.7(b)). Однако обратите внимание, что для значений xx, далеких от 2, уравнение касательной не дает нам хорошего приближения. Например, если x=10,x=10, значение yy соответствующей точки на касательной равно

.

y=12−14(10−2)=12−2=−1,5,y=12−14(10−2)=12−2=−1,5,

, тогда как значение функции при x=10x=10 равно f(10)=0,1. f(10)=0,1.

Рисунок 4.7 (a) Касательная к f(x)=1/xf(x)=1/x при x=2x=2 обеспечивает хорошее приближение к ff для xx, близкого к 2. (b) При x=2,1,x=2,1 , значение yy на касательной к f(x)=1/xf(x)=1/x равно 0,475. Фактическое значение f(2.1)f(2.1) равно 1/2.1,1/2.1, что примерно равно 0,47619.

В общем, для дифференцируемой функции f,f уравнение касательной к ff в точке x=ax=a можно использовать для аппроксимации f(x)f(x) для xx вблизи a.a. Следовательно, мы можем написать

f(x)≈f(a)+f′(a)(x−a)дляxneara.f(x)≈f(a)+f′(a)(x−a)дляxneara.

Мы вызываем линейную функцию

L(x)=f(a)+f′(a)(x−a)L(x)=f(a)+f′(a)(x−a)

(4.1)

линейная аппроксимация или аппроксимация касательной линии ff при x=a.x=a. Эта функция LL также известна как линеаризация ff при x=a.x=a.

Чтобы показать, насколько полезной может быть линейная аппроксимация, мы рассмотрим, как найти линейную аппроксимацию для f(x)=xf(x)=x при x=9. x=9.

Пример 4,5

Линейная аппроксимация xx

Найдите линейную аппроксимацию f(x)=xf(x)=x при x=9x=9 и используйте эту аппроксимацию для оценки 9.1.9.1.

Решение

Поскольку мы ищем линейную аппроксимацию при x=9,x=9, используя уравнение 4.1, мы знаем, что линейная аппроксимация дается выражением

L(x)=f(9)+f′(9)(x−9 ).L(x)=f(9)+f′(9)(x−9).

Нам нужно найти f(9)f(9) и f′(9).f′(9).

f(x)=x⇒f(9)=9=3f′(x)=12x⇒f′(9)=129=16f(x)=x⇒f(9)=9=3f′(x )=12x⇒f′(9)=129=16

Таким образом, линейная аппроксимация представлена ​​на рис. 4.8.

L(x)=3+16(x−9)L(x)=3+16(x−9)

Используя линейное приближение, мы можем оценить 9.19.1, записав

9.1=f(9.1 )≈L(9,1)=3+16(9,1−9)≈3,0167,9,1=f(9,1)≈L(9,1)=3+16(9,1−9)≈3,0167.

Рисунок 4,8 Локальное линейное приближение к f(x)=xf(x)=x при x=9x=9 обеспечивает приближение к ff для xx около 9,

Анализ

Используя калькулятор, значение 9. 19.1 с точностью до четырех знаков после запятой равно 3,0166. Значение, данное линейной аппроксимацией, 3,0167, очень близко к значению, полученному с помощью калькулятора, поэтому кажется, что использование этой линейной аппроксимации является хорошим способом оценки x,x, по крайней мере, для xx около 9.9. В то же время может показаться странным использовать линейную аппроксимацию, когда мы можем просто нажать несколько кнопок на калькуляторе, чтобы вычислить 9.1.9.1. Однако как калькулятор вычисляет 9.1?9.1? Калькулятор использует приближение! На самом деле калькуляторы и компьютеры постоянно используют приближения для вычисления математических выражений; они просто используют приближения более высокой степени.

Контрольно-пропускной пункт 4,5

Найдите локальное линейное приближение к f(x)=x3f(x)=x3 при x=8.x=8. Используйте его, чтобы приблизить 8.138.13 к пяти знакам после запятой.

Пример 4.6

Линейная аппроксимация sinxsinx

Найдите линейную аппроксимацию f(x)=sinxf(x)=sinx при x=π3x=π3 и используйте ее для аппроксимации sin(62°). sin(62°).

Решение

Прежде всего отметим, что поскольку π3π3 рад эквивалентно 60°, 60°, использование линейного приближения при x=π/3x=π/3 кажется разумным. Линейное приближение задается выражением

L(x)=f(π3)+f′(π3)(x−π3).L(x)=f(π3)+f′(π3)(x−π3).

Мы видим, что

f(x)=sinx⇒f(π3)=sin(π3)=32f′(x)=cosx⇒f′(π3)=cos(π3)=12f(x)=sinx⇒f(π3)=sin (π3)=32f′(x)=cosx⇒f′(π3)=cos(π3)=12

Таким образом, линейная аппроксимация ff при x=π/3x=π/3 представлена ​​на рис. 4.9.

L(x)=32+12(x−π3)L(x)=32+12(x−π3)

Чтобы оценить sin(62°)sin(62°) с помощью L,L, мы должны сначала преобразовать 62°62° в радианы. У нас есть 62°=62π18062°=62π180 радиан, поэтому оценка для sin(62°)sin(62°) дается как

sin(62°)=f(62π180)≈L(62π180)=32+12( 62π180−π3)=32+12(2π180)=32+π180≈0,88348.sin(62°)=f(62π180)≈L(62π180)=32+12(62π180−π3)=32+12(2π180)= 32+π180≈0,88348.

Рисунок 4.9 Линейное приближение к f(x)=sinxf(x)=sinx при x=π/3x=π/3 обеспечивает приближение к sinxsinx для xx вблизи π/3. π/3.

Контрольно-пропускной пункт 4.6

Найдите линейное приближение для f(x)=cosxf(x)=cosx при x=π2.x=π2.

Линейные аппроксимации могут использоваться при оценке корней и степеней. В следующем примере мы находим линейную аппроксимацию для f(x)=(1+x)nf(x)=(1+x)n при x=0,x=0, которую можно использовать для оценки корней и степеней для действительных чисел около 1. Та же идея может быть распространена на функцию вида f(x)=(m+x)nf(x)=(m+x)n для оценки корней и степеней вблизи другого числа m.m.

Пример 4.7

Аппроксимация корней и степеней

Найдите линейную аппроксимацию f(x)=(1+x)nf(x)=(1+x)n при x=0.x=0. Используйте это приближение для оценки (1.01)3.(1.01)3.

Решение

Линейное приближение при x=0x=0 определяется как

L(x)=f(0)+f′(0)(x−0).L(x)=f(0)+f′(0 )(х−0).

Потому что

f(x)=(1+x)n⇒f(0)=1f′(x)=n(1+x)n−1⇒f′(0)=n,f(x) =(1+x)n⇒f(0)=1f′(x)=n(1+x)n−1⇒f′(0)=n,

линейная аппроксимация представлена ​​на рис. 4.10(a) .

L(x)=1+n(x−0)=1+nxL(x)=1+n(x−0)=1+nx

Мы можем аппроксимировать (1.01)3(1.01)3, оценивая L(0,01)L(0,01) при n=3.n=3. Делаем вывод, что

(1,01)3=f(1,01)≈L(1,01)=1+3(0,01)=1,03.(1,01)3=f(1,01)≈L(1,01)=1+3(0,01) =1,03.

Рисунок 4.10 (a) Линейная аппроксимация f(x)f(x) при x=0x=0 равна L(x).L(x). (b) Фактическое значение 1,0131,013 равно 1,030301. Линейная аппроксимация f(x)f(x) при x=0x=0 оценивает 1,0131,013 как 1,03.

Контрольно-пропускной пункт 4.7

Найдите линейную аппроксимацию f(x)=(1+x)4f(x)=(1+x)4 при x=0x=0, не используя результат предыдущего примера.

Дифференциалы

Мы видели, что для оценки значений функций можно использовать линейные приближения. Их также можно использовать для оценки величины изменения значения функции в результате небольшого изменения входных данных. Чтобы обсудить это более формально, мы определим родственное понятие: дифференциалы. Дифференциалы дают нам способ оценить величину изменения функции в результате небольшого изменения входных значений.

Когда мы впервые рассмотрели производные, мы использовали нотацию Лейбница dy/dxdy/dx для представления производной yy относительно x.x. Хотя в этих обозначениях мы использовали выражения dy и dx , сами по себе они не имели смысла. Здесь мы видим значение выражений dy и dx . Предположим, что y=f(x)y=f(x) — дифференцируемая функция. Пусть dx — независимая переменная, которой можно присвоить любое ненулевое действительное число, и определим зависимую переменную dydy как

dy=f′(x)dx.dy=f′(x)dx.

(4.2)

Важно отметить, что dydy является функцией как xx, так и dx.dx. Выражения dy и dx называются дифференциалами . Мы можем разделить обе части уравнения 4.2 на dx,dx, что дает

dydx=f′(x). dydx=f′(x).

(4.3)

Это известное выражение, которое мы использовали для обозначения производной. Уравнение 4.2 известно как дифференциальная форма уравнения 4.3.

Пример 4,8

Вычисление дифференциалов

Для каждой из следующих функций найдите dy и оцените, когда x=3x=3 и dx=0,1.dx=0,1.

1. у=х2+2ху=х2+2х
2. у=cosxy=cosx

Решение

Ключевым шагом является вычисление производной. Когда у нас это будет, мы сможем получить dy напрямую.

1. Поскольку f(x)=x2+2x,f(x)=x2+2x, мы знаем, что f′(x)=2x+2,f′(x)=2x+2, и, следовательно,

   dy=( 2x+2)dx.dy=(2x+2)dx.

   
   Когда x=3x=3 и dx=0,1,dx=0,1,

   dy=(2·3+2)(0,1)=0,8.dy=(2·3+2)(0,1)=0,8.

2. Поскольку f(x)=cosx,f(x)=cosx,f′(x)=−sin(x).f′(x)=−sin(x). Это дает нам

   dy=-sinxdx.dy=-sinxdx.

   
   Когда x=3x=3 и dx=0,1,dx=0,1,

   dy=-sin(3)(0,1)=-0,1sin(3).dy=-sin(3)(0,1)=-0,1sin (3).

Контрольно-пропускной пункт 4,8

Для y=ex2,y=ex2 найти dy.dy.

Теперь свяжем дифференциалы с линейными приближениями. Дифференциалы можно использовать для оценки изменения значения функции в результате небольшого изменения входных значений. Рассмотрим функцию ff, дифференцируемую в точке п. в. Предположим, что вход xx изменяется на небольшую величину. Нас интересует, насколько изменится выход yy. Если xx меняется с aa на a+dx,a+dx, то изменение xx равно dxdx (также обозначается Δx), Δx), а изменение yy определяется как

Δy=f(a+dx)−f(a).Δy=f(a+dx)−f(a).

Однако вместо того, чтобы вычислять точное изменение y, y, часто бывает проще аппроксимировать изменение yy, используя линейную аппроксимацию. Для xx вблизи a,a,f(x)f(x) можно аппроксимировать линейным приближением

L(x)=f(a)+f′(a)(x−a).L(x)=f(a)+f′(a)(x−a).

Следовательно, если dxdx мал,

f(a+dx)≈L(a+dx)=f(a)+f′(a)(a+dx−a). f(a+dx)≈L(a+dx)=f(a )+f′(a)(a+dx−a).

То есть

f(a+dx)−f(a)≈L(a+dx)−f(a)=f′(a)dx.f(a+dx)−f(a)≈L(a+dx) −f(a)=f′(a)dx.

Другими словами, фактическое изменение функции ff при увеличении xx от aa до a+dxa+dx приблизительно равно разности между L(a+dx)L(a+dx) и f(a),f(a) , где L(x)L(x) — линейная аппроксимация ff в п. в. По определению L(x),L(x) эта разность равна f′(a)dx.f′(a)dx. В общем,

Δy=f(a+dx)−f(a)≈L(a+dx)−f(a)=f′(a)dx=dy.Δy=f(a+dx)−f(a)≈ L(a+dx)−f(a)=f′(a)dx=dy.

Таким образом, мы можем использовать дифференциал dy=f′(a)dxdy=f′(a)dx для аппроксимации изменения yy, если xx увеличивается от x=ax=a до x=a+dx.x=a+dx . Мы можем видеть это на следующем графике.

Рисунок 4.11 Дифференциал dy=f'(a)dxdy=f'(a)dx используется для аппроксимации фактического изменения yy, если xx увеличивается от aa до a+dx.a+dx.

Теперь мы рассмотрим, как использовать дифференциалы для аппроксимации изменения значения функции в результате небольшого изменения значения входных данных. Обратите внимание, что вычисление с дифференциалами намного проще, чем вычисление фактических значений функций, и результат очень близок к тому, что мы получили бы при более точном вычислении.

Пример 4.9

Аппроксимация изменения с помощью дифференциалов

Пусть y=x2+2x.y=x2+2x. Вычислить ΔyΔy и dy при x=3x=3, если dx=0,1.dx=0,1.

Решение

Фактическое изменение yy при изменении xx с x=3x=3 на x=3,1x=3,1 определяется как

Δy=f(3.1)−f(3)=[(3.1)2+2(3.1)] −[32+2(3)]=0,81.Δy=f(3,1)−f(3)=[(3,1)2+2(3,1)]−[32+2(3)]=0,81.

Приблизительное изменение yy определяется выражением dy=f′(3)dx.dy=f′(3)dx. Поскольку f′(x)=2x+2,f′(x)=2x+2, имеем

dy=f′(3)dx=(2(3)+2)(0,1)=0,8.dy=f′(3)dx=(2(3)+2)(0,1)=0,8.

Контрольно-пропускной пункт 4.9

Для y=x2+2x,y=x2+2x найти ΔyΔy и dydy при x=3x=3, если dx=0,2.dx=0,2.

Расчет суммы ошибки

Любой тип измерения подвержен определенной ошибке. Во многих приложениях определенные величины рассчитываются на основе измерений. Например, площадь круга рассчитывается путем измерения радиуса круга. Ошибка в измерении радиуса приводит к ошибке в вычисленном значении площади. Здесь мы исследуем этот тип ошибки и изучим, как можно использовать дифференциалы для оценки ошибки.

Рассмотрим функцию ff с входом, который является измеряемой величиной. Предположим, что точное значение измеренной величины равно a,a, но измеренное значение равно a+dx.a+dx. Мы говорим, что ошибка измерения составляет dx (или Δx).Δx). В результате возникает ошибка в расчетной величине f(x).f(x). Этот тип ошибки известен как распространяемая ошибка и задается как

.

Δy=f(a+dx)−f(a).Δy=f(a+dx)−f(a).

Поскольку все измерения подвержены некоторой ошибке, мы не знаем точного значения измеряемой величины, поэтому мы не можем точно вычислить распространяющуюся ошибку. Однако, учитывая оценку точности измерения, мы можем использовать дифференциалы для аппроксимации распространенной ошибки Δy. Δy. В частности, если ff — дифференцируемая функция в точках a, a, распространяющаяся ошибка равна

Δy≈dy=f′(a)dx.Δy≈dy=f′(a)dx.

К сожалению, мы не знаем точного значения а.е. Однако мы можем использовать измеренное значение a+dx,a+dx и оценить

Δy≈dy≈f′(a+dx)dx.Δy≈dy≈f′(a+dx)dx.

В следующем примере мы рассмотрим, как можно использовать дифференциалы для оценки погрешности вычисления объема коробки, если предположить, что измерение длины стороны выполнено с определенной точностью.

Пример 4.10

Объем куба

Предположим, что длина стороны куба равна 5 см с точностью до 0,1 см.

1. Используйте дифференциалы для оценки ошибки вычисленного объема куба.
2. Вычислите объем куба, если длина стороны равна (i) 4,9 см и (ii) 5,1 см, чтобы сравнить предполагаемую ошибку с фактической потенциальной ошибкой.

Решение

1. Точность измерения длины стороны составляет ±0,1±0,1 см. Следовательно,

   −0,1≤dx≤0,1.−0,1≤dx≤0,1.

   
   Объем куба равен V=x3,V=x3, что дает

   dV=3x2dx.dV=3x2dx.

   
   Используя измеренную длину стороны 5 см, мы можем оценить, что

   −3(5)2(0,1)≤dV≤3(5)2(0,1).−3(5)2(0,1)≤dV≤3 (5)2(0,1).

   
   Следовательно,

   −7,5≤dV≤7,5.−7,5≤dV≤7,5.

2. Если длина стороны равна 4,9 см, то объем куба равен

   V(4,9)=(4,9)3=117,649 см3.V(4,9)=(4,9)3=117,649 см3.

   
   Если длина стороны на самом деле 5,1 см, то объем куба

   V(5,1)=(5,1)3=132,651 см3. V(5,1)=(5,1)3=132,651 см3.

   
   Таким образом, фактический объем куба находится между 117,649 и 132,651. Поскольку длина стороны равна 5 см, вычисленный объем равен V(5)=53=125.V(5)=53=125. Следовательно, ошибка вычисленного объема составляет

   117,649−125≤ΔV≤132,651−125,117,649−125≤ΔV≤132,651−125.

   
   То есть

   −7,351≤ΔV≤7,651.−7,351≤ΔV≤7,651.

   
   Мы видим, что расчетная ошибка dVdV относительно близка к фактической потенциальной ошибке в вычисленном объеме.

Контрольно-пропускной пункт 4.10

Оцените погрешность вычисления объема куба, если длина стороны равна 6 см с точностью 0,2 см.

Ошибка измерения dx (=Δx)(=Δx) и распространяющаяся ошибка ΔyΔy являются абсолютными ошибками. Обычно нас интересует размер ошибки относительно размера измеряемой или вычисляемой величины. Учитывая абсолютную ошибку ΔqΔq для конкретной величины, мы определяем относительную ошибку как Δqq, Δqq, где qq — фактическое значение величины. Процентная ошибка — это относительная ошибка, выраженная в процентах. Например, если мы измеряем высоту лестницы как 63 дюйма, когда фактическая высота составляет 62 дюйма, абсолютная ошибка составляет 1 дюйм, а относительная ошибка составляет 162 = 0,016, 162 = 0,016, или 1,6%.1.6 %. Для сравнения, если мы измеряем ширину куска картона как 8,25 дюйма, когда фактическая ширина составляет 8 дюймов, наша абсолютная ошибка составляет 1414 дюймов, тогда как относительная ошибка составляет 0,258 = 132, 0,258 = 132 или 3,1. %.3.1%. Следовательно, процентная ошибка измерения картона больше, хотя 0,25 дюйма меньше, чем 1 дюйм 9.0003

Пример 4.11

Относительная и процентная погрешность

Астронавт с помощью камеры измеряет радиус Земли как 4000 миль с ошибкой ±80±80 миль. Давайте используем дифференциалы, чтобы оценить относительную и процентную ошибку использования этого измерения радиуса для вычисления объема Земли, предполагая, что планета является идеальной сферой.

Решение

Если измерение радиуса имеет точность в пределах ±80,±80, мы имеем

−80≤dr≤80.−80≤dr≤80.

Поскольку объем сферы определяется как V=(43)πr3,V=(43)πr3, мы имеем

dV=4πr2dr.dV=4πr2dr.

Используя измеренный радиус 4000 миль, мы можем оценить 4000)2(80).

Чтобы оценить относительную ошибку, рассмотрим dVV.dVV. Поскольку мы не знаем точного значения объема V,V, используем измеренный радиус r=4000mir=4000mi для оценки V. V. Получаем V≈(43)π(4000)3.V≈(43)π(4000)3. Поэтому относительная ошибка удовлетворяет

−4π(4000)2(80)4π(4000)3/3≤dVV≤4π(4000)2(80)4π(4000)3/3,−4π(4000)2(80)4π(4000) 3/3≤dVV≤4π(4000)2(80)4π(4000)3/3,

, что упрощается до

−0,06≤dVV≤0,06.−0,06≤dVV≤0,06.

Относительная ошибка составляет 0,06, а процентная ошибка составляет 6%.6%.

Контрольно-пропускной пункт 4.11

Определите процентную ошибку, если радиус Земли измерен как 3950 миль с погрешностью ±100±100 миль.

Раздел 4.2 Упражнения

46.

Какова линейная аппроксимация любой общей линейной функции y=mx+b?y=mx+b?

47.

Определите необходимые условия, чтобы функция линейного приближения была постоянной. Используйте график, чтобы доказать свой результат.

48.

Объясните, почему линейная аппроксимация становится менее точной при увеличении расстояния между xx и a. a. Используйте график, чтобы доказать свой аргумент.

49.

Когда линейное приближение является точным?

Для следующих упражнений найдите линейное приближение L(x)L(x) к y=f(x)y=f(x) вблизи x=ax=a для функции.

50.

f(x)=x+x4,a=0f(x)=x+x4,a=0

51.

f(x)=1x,a=2f(x)=1x,a=2

52.

f(x)=tanx,a=π4f(x)=tanx,a=π4

53.

f(x)=sinx,a=π2f(x)=sinx,a=π2

54.

f(x)=xsinx,a=2πf(x)=xsinx,a=2π

55.

f(x)=sin2x,a=0f(x)=sin2x,a=0

В следующих упражнениях вычислите значения с точностью до 0,01, выбрав соответствующие f(x)f(x) и a,a, и оценив L(x)=f(a)+f′(a)(x− а).L(x)=f(a)+f′(a)(x−a). Проверьте свой ответ с помощью калькулятора.

56.

[Т] (2,001)6(2,001)6

57.

[Т] грех (0,02) грех (0,02)

58.

[Т] cos(0.03)cos(0.03)

59.

[Т] (15,99)1/4(15,99)1/4

60.

[Т] 10.9810.98

61.

[Т] грех (3.14) грех (3.14)

Для следующих упражнений определите соответствующие f(x)f(x) и a,a и оцените L(x)=f(a)+f′(a)(x−a).L(x)= f(a)+f′(a)(x−a). Вычислите числовую ошибку в следующих линейных приближениях.

62.

[Т] (1.01)3(1.01)3

63.

[Т] cos(0.01)cos(0.01)

64.

[T] (sin(0,01))2(sin(0,01))2

65.

[Т] (1,01)−3(1,01)−3

66.

[Т] (1+110)10(1+110)10

67.

[Т] 8.998.99

Для следующих упражнений найдите дифференциал функции.

68.

у=3х4+х2-2х+1у=3х4+х2-2х+1

69.

у=xcosxy=xcosx

70.

у=1+ху=1+х

71.

у=х2+2х-1у=х2+2х-1

В следующих упражнениях найдите дифференциал и оцените данные xx и dx.dx.

72.

y=3×2−x+6,y=3×2−x+6,x=2,x=2,dx=0,1dx=0,1

73.

y=1x+1,y=1x+1,x=1,x=1,dx=0,25dx=0,25

74.

y=tanx,y=tanx,x=0,x=0,dx=π10dx=π10

75.

y=3×2+2x+1,y=3×2+2x+1,x=0,x=0,dx=0,1dx=0,1

76.

y=sin(2x)x,y=sin(2x)x,x=π,x=π,dx=0,25dx=0,25

77.

y=x3+2x+1x,y=x3+2x+1x,x=1,x=1,dx=0,05dx=0,05

Для следующих упражнений найдите изменение объема dVdV или площади поверхности dA.dA.

78.

dVdV, если стороны куба изменяются с 10 на 10,1.

79.

dAdA, если стороны куба меняются с xx на x+dx.x+dx.

80.

dAdA, если радиус сферы изменяется от rr на dr.dr.

81.

dVdV если радиус сферы изменяется от rr на dr.dr.

82.

dVdV, если круглый цилиндр с r=2r=2 меняет высоту с 3 см на 3,05 см. 3,05 см.

83.

dVdV, если круглый цилиндр высотой 3 изменится с r=2r=2 на r=1,9см.