Производная натурального логарифма с примерами решения
Содержание:
- Основные свойства логарифмов
- Примеры с решением
- Натуральные логарифмы
производная натурального логарифма от независимой переменной равна обратной величине этой независимой переменной.
Пусть
где Найдем производную этой функции, пользуясь схемой, изложенной в начале § 2.
Дадим аргументу ( фиксировано) приращение такое, что Тогда функция получит приращение и мы будем иметь следовательно,
или, так как разность логарифмов равна логарифму частного,
Разделив обе части последнего равенства на получим
Полагая здесь находим
или на основании известного свойства логарифма
Пусть тогда, очевидно, и как произведение
бесконечно малой на постоянную величину
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Поэтому
Функция очевидно, непрерывна при Так как логарифмическая функция также непрерывна и
(гл.
VII, § 12), то знаки можно переставить местами (гл. VIII, § 2)1):
Следовательно,
Таким образом, имеем формулу
Пользуясь известным соотношением (гл. VII, §13) формулу (1) можно переписать в виде
Полагая здесь, в частности, и помня, что получаем
т. е. производная натурального логарифма от независимой переменной равна обратной величине этой независимой переменной.
Другой важный частный случай получаем при
где — модуль перехода.
Возможно вам будут полезны данные страницы:
Найти неопределённый интеграл: пример решения |
Таблица интегралов |
Интеграл натурального логарифма |
Интеграл от экспоненты |
Логарифмическая функция определена лишь при Для приложений удобно рассматривать функцию
которая имеет смысл как при положительном, так и при отрицательном, т.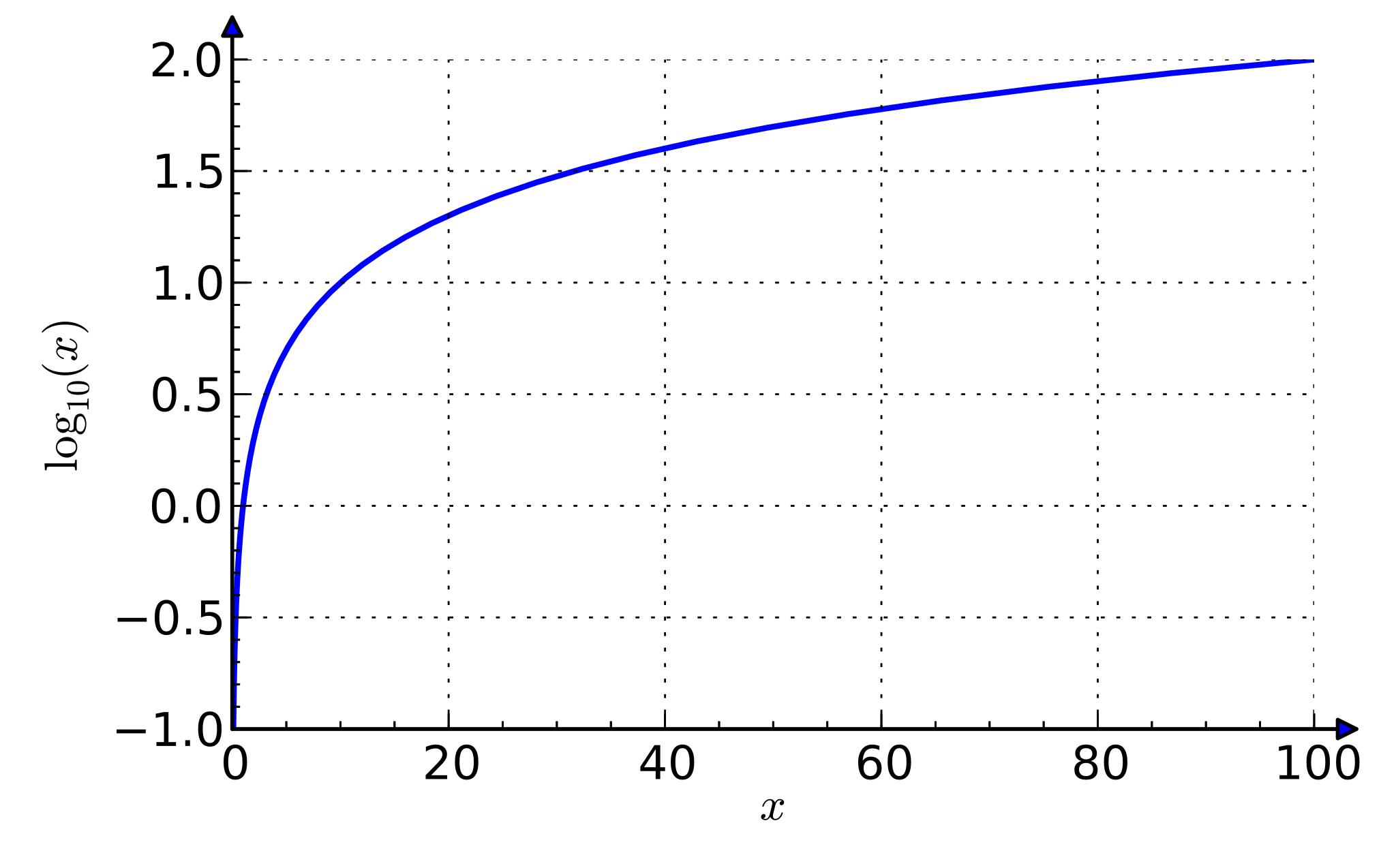 е. определена при (рис. 106). Для нахождения производной этой функции запишем ее с помощью двух равенств:
е. определена при (рис. 106). Для нахождения производной этой функции запишем ее с помощью двух равенств:
Отсюда получаем
Следовательно,
Натуральный логарифм — это логарифм по основанию е (е иррациональное число, приближенное значение которогое~2,7).
Основное логарифмическое тождество Поскольку то подставим вместо к его значение виде логарифма:
где
Например:
Основные свойства логарифмов
При работе с логарифмами применяются следующие их свойства, вытекающие из свойств показательной функции:
При любом и любых положительных и выполняются равенства:
1.
Доказательство:
Вытекает из определения. Действительно
Например,
Доказательство:
Вытекает из определения,
Например,
3. (Логарифм произведения равен сумме логарифмов).
(Логарифм произведения равен сумме логарифмов).
(4) Доказательство:
Воспользуемся основным логарифмическим тождеством:
Перемножая почленно эти равенства, получаем:
т.е. Следовательно, по определению логарифма
Например,
4. (Логарифм частного равен разности логарифмов).
Доказательство:
Снова воспользуемся основным логарифмическим тождеством и получим:
следовательно, но определению
Например,
5. для любого действительного (Логарифм степени равен произведению показателя степени на логарифм основания этой степени). (6)
Доказательство:
Для доказательства воспользуемся тождеством откуда
Следовательно, по определению
Например,
Пример 1. Вычислить
Применяя формулы (4)-(6), находим
Основные свойства логарифмов широко применяются в ходе преобразования выражений, содержащих логарифмы.
Логарифмируя обе части основного логарифмического тождества но основанию получаем
или
где
Эта формула называется формулой перехода от одного основания логарифма к другому. Докажем ее. Доказательство:
Докажем ее. Доказательство:
По правилу логарифмирования и основному логарифмическому тождеству получаем:
Разделив обе части полученного равенства на приходим к формуле (7).
Из формулы (7) при имеем
где
следует, что
Например,
Примеры с решением
Пример 1.
Дано Найти
Решение:
Воспользовавшись формулой (7) перехода к новому основанию, а затем свойствами логарифма, получим:
Теперь рассмотрим логарифмические тождества, знание которых облегчает решение некоторых уравнений.
Натуральными логарифмами называют логарифмы с основанием и обозначают
Функция определена при положительных На рис. 6.5 изображен ее график.
Рассматривают функцию определенную для всех действительных кроме ее график изображен на рис. 6.6.
Экспоненциальной функцией называют функцию употребляется обозначение
Гиперболическими функциями называют функции, определяемые формулами:
(гиперболический синус),
(гиперболический косинус),
(гиперболический тангенс),
(гиперболический котангенс).
Графики гиперболических функций изображены на рис. 6.7.
Натуральные логарифмы
Определение. Логарифм какого-нибудь числа вычисленный по основанию называется натуральным логарифмом этого числа и обозначается через Итак,
Иными словами, натуральный логарифм числа есть показатель степени, в которую надо возвысить чтобы получить
Пример 2.
Решение:
Вероятно, читателя удивит, что в математике, кроме привычных из средней школы десятичных логарифмов, рассматриваются еще и другие логарифмы, да еще по столь .неудобному* основанию, как иррациональное число
По этому поводу следует заметить, что число 10, очень удобное в качестве основания системы логарифмов, когда приходится производить численные расчеты, никаких теоретических достоинств не имеет. В тех случаях, когда приходится вести расчет не численный, а буквенный, многие формулы существенно упрощаются при применении не десятичных, а именно натуральных логарифмов.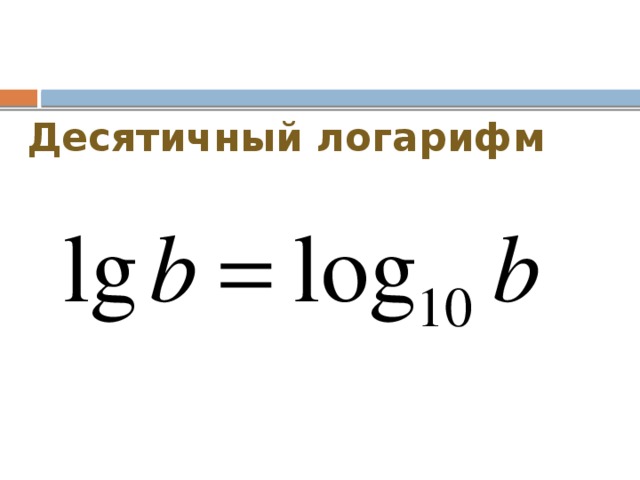
Это обстоятельство, конечно, не понижает вычислительных удобств десятичных логарифмов, которыми всегда пользуются в численных расчетах.
Связь натуральных логарифмов с десятинными. Как уже было отмечено, из самого определения логарифма вытекает равенство
Прологарифмируем это равенство по основанию 10:
Отсюда
Но Пользуясь десятичными таблицами, находим
Значит,
Формула (8) позволяет находить десятичный логарифм числа если известен его натуральный логарифм.
Число называется модулем перехода от натуральных логарифмов к десятичным.
Равенство (8) можно переписать в виде
Но Значит,
По формуле (9) вычисляется натуральный логарифм числа если известен его десятичный логарифм.
Число называется модулем перехода от десятичных логарифмов к натуральным.
Пример 3.
Так как то
| 1 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata — d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) по x | |
| 5 | Trovare la Derivata — d/dx | 1/x | |
| 6 | Trovare la Derivata — d/dx | x^2 | |
| 7 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata — d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x по x | |
| 11 | Вычислим интеграл | интеграл x^2 по x | |
| 12 | Вычислим интеграл | интеграл квадратного корня из x по x | |
| 13 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x по x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 по x | |
| 16 | Trovare la Derivata — d/dx | x^3 | |
| 17 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 по x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 по x | |
| 20 | Trovare la Derivata — d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубический корень из 1+7x по x | |
| 22 | Trovare la Derivata — d/dx | sin(2x) | |
| 23 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) по x | |
| 25 | Trovare la Derivata — d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata — d/dx | cos(2x) | |
| 28 | Trovare la Derivata — d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x по x | |
| 30 | Trovare la Derivata — d/dx | ( натуральный логарифм от x)^2 | |
| 31 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata — d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) по x | |
| 34 | Trovare la Derivata — d/dx | 2e^x | |
| 35 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata — d/dx | -sin(x) | |
| 37 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata — d/dx | y=16 корень четвертой степени из 4x^4+4 | |
| 39 | Trovare la Derivata — d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) по x | |
| 41 | Вычислим интеграл | интеграл cos(2x) по x | |
| 42 | Trovare la Derivata — d/dx | 1/( квадратный корень из x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) по x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata — d/dx | x/2 | |
| 46 | Trovare la Derivata — d/dx | -cos(x) | |
| 47 | Trovare la Derivata — d/dx | sin(3x) | |
| 48 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 по x | |
| 50 | Вычислим интеграл | интеграл 1 по x | |
| 51 | Trovare la Derivata — d/dx | x^x | |
| 52 | Trovare la Derivata — d/dx | x натуральный логарифм от x | |
| 53 | Trovare la Derivata — d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) по x | |
| 59 | Trovare la Derivata — d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x по x | |
| 61 | Trovare la Derivata — d/dx | y=x^2 | |
| 62 | Trovare la Derivata — d/dx | квадратный корень из x^2+1 | |
| 63 | Trovare la Derivata — d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) по x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня из x по x | |
| 66 | Trovare la Derivata — d/dx | e^2 | |
| 67 | Trovare la Derivata — d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) по x | |
| 69 | Trovare la Derivata — d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) по x | |
| 72 | Trovare la Derivata — d/dx | x^5 | |
| 73 | Trovare la Derivata — d/dx | 2/x | |
| 74 | Trovare la Derivata — d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata — d/dx | x^(1/2) | |
| 76 | Trovare la Derivata — d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata — d/dx | cos(x^2) | |
| 78 | Trovare la Derivata — d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata — d/dx | кубический корень из x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) по x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) по x | |
| 82 | Trovare la Derivata — d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 в пределах от 0 до 10 по x | |
| 84 | Вычислим интеграл | интеграл ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata — d/dx | логарифм x | |
| 86 | Trovare la Derivata — d/dx | arctan(x) | |
| 87 | Trovare la Derivata — d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata — d/dx | 5e^x | |
| 89 | Trovare la Derivata — d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 по x | |
| 91 | Вычислим интеграл | интеграл x^2e^x по x | |
| 92 | Trovare la Derivata — d/dx | 16 корень четвертой степени из 4x^4+4 | |
| 93 | Trovare la Derivata — d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) по x | |
| 96 | Trovare la Derivata — d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) по x | |
| 98 | Trovare la Derivata — d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata — d/dx | натуральный логарифм x^2 |
Таблица производных логарифм по основанию x.
 Формулы и примеры производной логарифма. Производная логарифма модуля x
Формулы и примеры производной логарифма. Производная логарифма модуля xПри дифференцировании показательно степенной функции или громоздких дробных выражений удобно пользоваться логарифмической производной. В этой статье мы рассмотрим примеры ее применения с подробными решениями.
Дальнейшее изложение подразумевает умение пользоваться таблицей производных , правилами дифференцирования и знание формулы производной сложной функции .
Вывод формулы логарифмической производной.
Сначала производим логарифмирование по основанию e
, упрощаем вид функции, используя свойства логарифма, и далее находим производную неявно заданной функции:
Для примера найдем производную показательно степенной функции x в степени x .
Логарифмирование дает . По свойствам логарифма . Дифференцирование обеих частей равенства приводит к результату:
Ответ: .
Этот же пример можно решить и без использования логарифмической производной. Можно провести некоторые преобразования и перейти от дифференцирования показательно степенной функции к нахождению производной сложной функции:
Пример.
Найти производную функции .
Решение.
В этом примере функция представляет собой дробь и ее производную можно искать с использованием правил дифференцирования. Но в силу громоздкости выражения это потребует множества преобразований. В таких случаях разумнее использовать формулу логарифмической производной . Почему? Вы сейчас поймете.
Найдем сначала . В преобразованиях будем использовать свойства логарифма (логарифм дроби равен разности логарифмов, а логарифм произведения равен сумме логарифмов, и еще степень у выражения под знаком логарифма можно вынести как коэффициент перед логарифмом):
Эти преобразования привели нас к достаточно простому выражению, производная которого легко находится:
Подставляем полученный результат в формулу логарифмической производной и получаем ответ:
Для закрепления материала приведем еще пару примеров без подробных объяснений.
Пример.
Найдите производную показательно степенной функции
Производная натурального логарифма от x равна единице, деленной на x:
(1) (ln
x)′ =
.
Производная логарифма по основанию a равна единице, деленной на переменную x, умноженную на натуральный логарифм от a
:
(2) (log
a x)′ =
.
Доказательство
Пусть есть некоторое положительное число, не равное единице. Рассмотрим функцию, зависящую от переменной x
,
которая является логарифмом по основанию :
.
Эта функция определена при .
Найдем ее производную по переменной x
.
По определению, производная является следующим пределом:
(3) .
Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам нужно знать следующие факты:
А) Свойства логарифма . Нам понадобятся следующие формулы:
(4) ;
(5) ;
(6) ;
Б) Непрерывность логарифма и свойство пределов для непрерывной функции:
(7) .
Здесь — некоторая функция, у которой существует предел и этот предел положителен.
В) Значение второго замечательного предела:
(8) .
Применяем эти факты к нашему пределу. Сначала преобразуем алгебраическое выражение
.
Для этого применим свойства (4) и (5).
.
Воспользуемся свойством (7) и вторым замечательным пределом (8):
.
И, наконец, применим свойство (6):
.
Логарифм по основанию e называется натуральным логарифмом . Он обозначается так:
.
Тогда ;
.
Тем самым мы получили формулу (2) производной логарифма.
Производная натурального логарифма
Еще раз выпишем формулу производной логарифма по основанию a
:
.
Эта формула имеет наиболее простой вид для натурального логарифма, для которого ,
.
Тогда
(1) .
Из-за такой простоты, натуральный логарифм очень широко используется в математическом анализе и в других разделах математики, связанных с дифференциальным исчислением. Логарифмические функции с другими основаниями можно выразить через натуральный логарифм, используя свойство (6):
.
Производную логарифма по основанию можно найти из формулы (1), если вынести постоянную за знак дифференцирования:
.
Другие способы доказательство производной логарифма
Здесь мы предполагаем, что нам известна формула производной экспоненты:
(9) .
Тогда мы можем вывести формулу производной натурального логарифма, учитывая, что логарифм является обратной функцией к экспоненте.
Докажем формулу производной натурального логарифма, применив формулу производной обратной функции :
.
В нашем случае .
Обратной функцией к натуральному логарифму является экспонента:
.
Ее производная определяется по формуле (9). Переменные можно обозначить любой буквой. В формуле (9), заменим переменную x на y:
.
Поскольку ,
то
.
Тогда
.
Формула доказана.
Теперь докажем формулу производной натурального логарифма с помощью правила дифференцирования сложной функции . Поскольку функции и являются обратными друг к другу, то
.
Дифференцируем это уравнение по переменной x
:
(10) .
Производная от икса равна единице:
Применяем правило дифференцирования сложной функции :
.
Здесь . Подставим в (10):
.
Отсюда
.
Пример
Найти производные от ln 2x, ln 3x и ln nx .
Решение
Исходные функции имеют похожий вид. Поэтому мы найдем производную от функции y = ln nx . Затем подставим n = 2 и n = 3 . И, тем самым, получим формулы для производных от ln 2x и ln 3x .
Итак, ищем производную от функции
y = ln nx .
Представим эту функцию как сложную функцию, состоящую из двух функций:
1) Функции ,
зависящей от переменной :
;
2) Функции ,
зависящей от переменной :
.
Тогда исходная функция составлена из функций и :
.
Найдем производную от функции по переменной x:
.
Найдем производную от функции по переменной :
.
Применяем формулу производной сложной функции .
.
Здесь мы подставили .
Итак, мы нашли:
(11) .
Мы видим, что производная не зависит от n
.
Этот результат вполне естественен, если преобразовать исходную функцию, применяя формулу логарифма от произведения:
.
— это постоянная. Ее производная равна нулю. Тогда по правилу дифференцирования суммы имеем:
.
Ответ
; ; .
Производная логарифма модуля x
Найдем производную от еще одной очень важной функции — натурального логарифма от модуля x
:
(12) .
Рассмотрим случай .
Тогда и функция имеет вид:
.
Ее производная определяется по формуле (1):
.
Теперь рассмотрим случай .
Тогда и функция имеет вид:
,
где .
Но производную этой функции мы также нашли в приведенном выше примере. Она не зависит от n
и равна
.
Тогда
.
Объединяем эти два случая в одну формулу:
.
Соответственно, для логарифма по основанию a
,
имеем:
Производные высших порядков натурального логарифма
Рассмотрим функцию
.
Мы нашли ее производную первого порядка:
(13) .
Найдем производную второго порядка:
.
Найдем производную третьего порядка:
.
Найдем производную четвертого порядка:
.
Можно заметить, что производная n-го порядка имеет вид:
(14) .
Докажем это методом математической индукции.
Доказательство
Подставим в формулу (14) значение n = 1:
.
Поскольку ,
то при n = 1
,
формула (14) справедлива.
Предположим, что формула (14) выполняется при n = k . Докажем, что из этого следует, что формула справедлива при n = k + 1 .
Действительно, при n = k
имеем:
.
Дифференцируем по переменной x
:
.
Итак, мы получили:
.
Эта формула совпадает с формулой (14) при n = k + 1
.
Таким образом, из предположения, что формула (14) справедлива при n = k
следует, что формула (14) справедлива при n = k + 1
.
Поэтому формула (14), для производной n-го порядка, справедлива для любых n
.
Производные высших порядков логарифма по основанию a
Чтобы найти производную n-го порядка от логарифма по основанию a
,
нужно выразить его через натуральный логарифм:
.
Применяя формулу (14), находим n-ю производную:
.
Вам кажется, что до экзамена еще много времени? Это месяц? Два? Год? Практика показывает, что ученик лучше всего справляется с экзаменом в том случае, если начал готовиться к нему заблаговременно. В ЕГЭ немало сложных заданий, который стоят на пути школьника и будущего абитуриента к высшим баллам. Эти преграды нужно научиться преодолевать, к тому же, делать это несложно. Вам необходимо понять принцип работы с различными заданиями из билетов. Тогда и с новыми не возникнет проблем.
Логарифмы на первый взгляд кажутся невероятно сложными, но при детальном разборе ситуация значительно упрощается. Если вы хотите сдать ЕГЭ на высший балл, вам стоит разобраться в рассматриваемом понятии, что мы и предлагаем сделать в этой статье.
Для начала разделим эти определения. Что такое логарифм (log)? Это показатель степени, в которую надо возвести основание, чтобы получить указанное число. Если непонятно, разберем элементарный пример.
Что такое логарифм (log)? Это показатель степени, в которую надо возвести основание, чтобы получить указанное число. Если непонятно, разберем элементарный пример.
В этом случае основание, стоящее внизу, необходимо возвести во вторую степень, чтобы получить число 4.
Теперь разберемся со вторым понятием. Производная функции в любом виде называется понятие, характеризующее изменение функции в приведенной точке. Впрочем, это школьная программа, и если вы испытываете проблемы с данными понятиями по отдельности, стоит повторить тему.
Производная логарифма
В задания ЕГЭ по этой теме можно привести несколько задач в качестве примера. Для начала самая простая логарифмическая производная. Необходимо найти производную следующей функции.
Нам нужно найти следующую производную
Существует специальная формула.
В этом случае x=u, log3x=v. Подставляем значения из нашей функции в формулу.
Производная x будет равняться единице. С логарифмом немного труднее. Но принцип вы поймете, если просто подставите значения. Напомним, что производной lg x называется производная десятичного логарифма, а производная ln х — это производная от натурального логорифма (по основанию e).
С логарифмом немного труднее. Но принцип вы поймете, если просто подставите значения. Напомним, что производной lg x называется производная десятичного логарифма, а производная ln х — это производная от натурального логорифма (по основанию e).
Теперь просто подставьте полученные значения в формулу. Попробуйте сами, далее сверим ответ.
В чем здесь может быть проблема для некоторых? Мы ввели понятие натурального логарифма. Расскажем о нем, а заодно разберемся, как решать задачи с ним. Ничего сложного вы не увидите, особенно, когда поймете принцип его работы. К нему вам стоит привыкнуть, так как он нередко используется в математике (в высших учебных заведениях тем более).
Производная натурального логарифма
По своей сути, это производная логарифма по основанию e (это иррациональное число, которое равняется примерно 2,7). На деле ln очень прост, поэтому часто используется в математике в целом. Собственно, решение задачи с ним тоже не станет проблемой. Стоит запомнить, что производная от натурального логарифма по основанию е будет равно единице поделенной на x. Самым показательным будет решение следующего примера.
Стоит запомнить, что производная от натурального логарифма по основанию е будет равно единице поделенной на x. Самым показательным будет решение следующего примера.
Представим ее как сложную функцию, состоящую из двух простых.
Достаточно преобразовать
Ищем производную от u по x
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения. {\prime}(x)=\frac{2 \ln x}{x}
\)
{\prime}(x)=\frac{2 \ln x}{x}
\)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Производная неявной функции Частные производные Таблица производных сложных функций Таблица производных
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Логарифмическая производная.
 Дифференцирование показательно степенной функции.
Дифференцирование показательно степенной функции.Когда нам нужно выполнить дифференцирование показательно степенной функции вида y=(f(x))g(x) или преобразовать громоздкое выражение с дробями, можно использовать логарифмическую производную. В рамках этого материала мы приведем несколько примеров применения этой формулы.
Чтобы понять эту тему, необходимо знать, как пользоваться таблицей производных, быть знакомым с основными правилами дифференцирования и представлять себе, что такое производная сложной функции.
Как вывести формулу логарифмической производной
Для получения этой формулы нужно сначала произвести логарифмирование по основанию e, а затем упростить получившуюся функцию, применив основные свойства логарифма. После этого надо вычислить производную неявно заданной функции:
y=f(x)ln y=ln(f(x))(ln y)’=(ln(f(x)))’1y·y’=(ln(f(x)))’⇒y’=y·(ln(f(x)))’
Примеры использования формулы
Покажем на примере, как это делается.
Пример 1Вычислить производную показательно степенной функции переменной x в степени x.
Решение
Проводим логарифмирование по указанному основанию и получаем ln y=ln xx. С учетом свойств логарифма это можно выразить как ln y=x·ln x. Теперь дифференцируем левую и правую части равенства и получаем результат:
ln y=x·ln xln y’=x·ln x’1y·y’=x’·ln x+·ln x’⇒y’=y·1·ln x+x·1x=y·(ln x+1)=xx·(ln x+1)
Ответ: xx’=xx·(ln x+1)
Такую задачу можно решить и другим способом, без логарифмической производной. Сначала нам надо преобразовать исходное выражение так, чтобы перейти от дифференцирования показательно степенной функции к вычислению производной сложной функции, например:
y=xx=eln xx=ex·ln x⇒y’=(ex·ln x)’=ex·ln x·x·ln x’=xx·x’·ln x+x·(ln x)’==xx·1·ln x+x·1x=xx·ln x+1
Рассмотрим еще одну задачу.
Пример 2Вычислите производную функции y=x2+13×3·sin x.
Решение
Исходная функция представлена в виде дроби, значит, мы можем решить задачу с помощью дифференцирования. Однако эта функция довольно сложная, значит, преобразований потребуется много. Значит, нам лучше использовать здесь логарифмическую производную y’=y·ln(f(x))’. Поясним, почему такое вычисление удобнее.
Значит, нам лучше использовать здесь логарифмическую производную y’=y·ln(f(x))’. Поясним, почему такое вычисление удобнее.
Начнем с нахождения ln(f(x)). Для дальнейшего преобразования нам потребуются следующие свойства логарифма:
- логарифм дроби можно представить в виде разности логарифмов;
- логарифм произведения можно представить в виде суммы;
- если у выражения под логарифмом есть степень, мы можем вынести ее в качестве коэффициента.
Преобразуем выражение:
ln(f(x))=ln(x2+1)13×3·sin x12=ln(x2+1)13-ln(x3·sin x)12==13ln(x2+1)-32ln x-12ln sin x
В итоге у нас получилось достаточно простое выражение, производную которого вычислить несложно:
(ln(f(x)))’=13ln(x2+1)-32ln x-12ln sin x’==13ln(x2+1)’-32ln x’-12ln sin x’==13(ln(x2+1))’-32(ln x)’-12(ln sin x)’==13·1×2+1·x2+1′-32·1x-12·1sin x·(sin x)’==13·2xx2+1-32x-cos x2 sin x
Теперь то, что у нас получилось, нужно подставить в формулу логарифмической производной.
Ответ: y’=y·ln(f(x))’=x2+13×3·sin x·13·2xx2+1-32x-cos x2 sin x
Чтобы закрепить материал, изучите еще пару следующих примеров. Здесь будут приведены только вычисления с минимумом комментариев.
Здесь будут приведены только вычисления с минимумом комментариев.
Дана показательно степенная функция y=(x2+x+1)x3. Вычислите ее производную.
Решение:
y’=y·(ln(f(x)))’=(x2+x+1)x3·ln(x2+x+1)x3’==(x2+x+1)x3·x3·(x2+x+1)’==(x2+x+1)x3·x3’·ln(x2+x+1)+x3ln(x2+x+1)’==(x2+x+1)x3·3×2·ln(x2+x+1)+x3·1×2+x+1·x2+x+1’==(x2+x+1)x3·3×2·ln(x2+x+1)+x32x+1×2+x+1==(x2+x+1)x3·3×2·ln(x2+x+1)+2×4+x3x2+x+1
Ответ: y’=y·(ln(f(x)))’=(x2+x+1)x3·3×2·ln(x2+x+1)+2×4+x3x2+x+1
Пример 4Вычислите производную выражения y=x2+13·x+1·x3+14×2+2x+2.
Решение
Применяем формулу логарифмической производной.
y’=y·lnx2+13·x+1·x3+14×2+2x+2’==y·lnx2+13+lnx+1+lnx3+14-lnx2+2x+2’==y·13ln(x2+1)+12lnx+1+14ln(x3+1)-12ln(x2+2x+2)’==y·(x2+1)’3(x2+1)+x+1’2(x+1)+(x3+1)’4×3+1-x2+2x+2’2×2+2x+2==x2+13·x+1·x3+14×2+2x+2·2×3(x2+1)+12(x+1)+3×24(x3+1)-2x+22(x2+2x+2)
Ответ:
y’=x2+13·x+1·x3+14×2+2x+2·2×3(x2+1)+12(x+1)+3×24(x3+1)-2x+22(x2+2x+2).
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Производная и ее свойства. Производная функции
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
ПЕРВАЯ ПРОИЗВОДНАЯ
ПЕРВАЯ ПРОИЗВОДНАЯ
(first derivative) Темп прироста значения функции при приросте ее аргумента в какой-либо точке, если сама функция в этой точке определена. На графике первая производная функции показывает угол ее наклона. Если у=f(x), ее первая производная в точке х0 является пределом, к которому стремится f(x0+а)–f(x0)/а по мере того, как а стремится к бесконечно малой величине. Первая производная может обозначаться dy/dx или y´(x). Функция у(х) имеет постоянное значение в точке х0, если dy/dx в точке х0 равно нулю. Равная нулю первая производная является необходимым, но недостаточным условием для того, чтобы функция достигала в данной точке своего максимума или минимума.
Экономика. Толковый словарь. — М.: «ИНФРА-М», Издательство «Весь Мир». Дж. Блэк. Общая редакция: д.э.н. Осадчая И.М. . 2000 .
Экономический словарь . 2000 .
Смотреть что такое «ПЕРВАЯ ПРОИЗВОДНАЯ» в других словарях:
— (derivative) Темп приращения значения функции при приращении ее аргумента в какой либо точке, если сама функция в этой точке определена.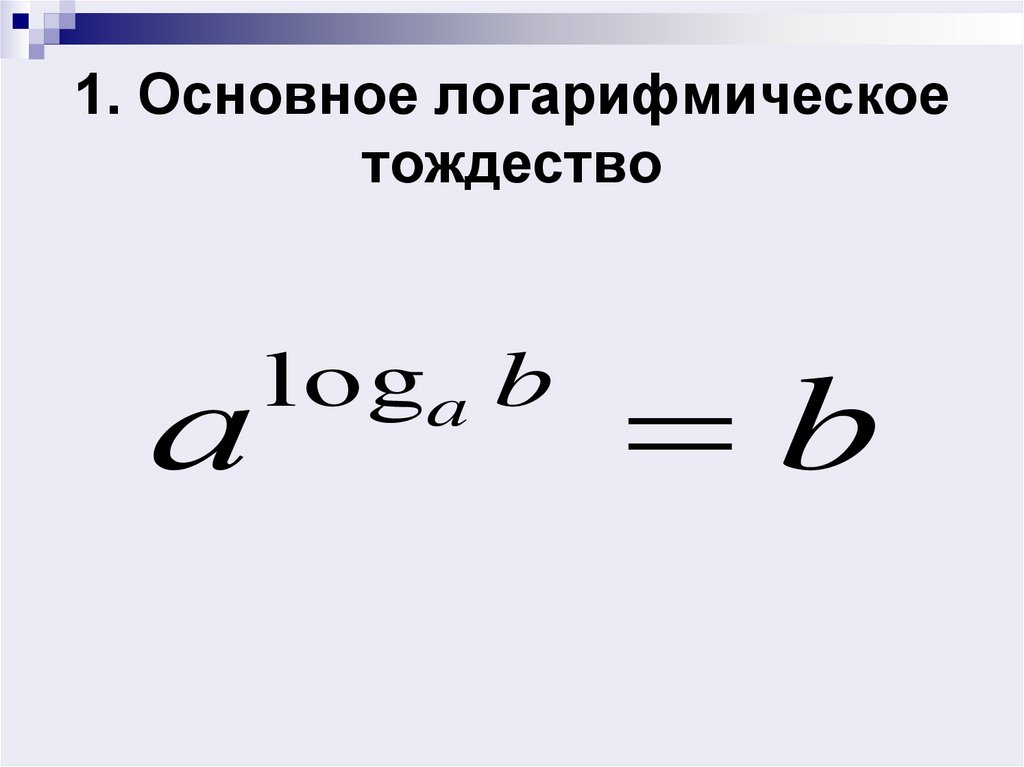 На графике первая производная функции показывает угол ее наклона. Если у=f(x), ее первая производная в точке… … Экономический словарь
На графике первая производная функции показывает угол ее наклона. Если у=f(x), ее первая производная в точке… … Экономический словарь
У этого термина существуют и другие значения, см. Производная. Иллюстрация понятия производной Производная … Википедия
Производная основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел… … Википедия
Краевая задача специального вида; заключается в отыскании в области Dпеременных x=(x1,…, х п).решения дифференциального уравнения (1) четного порядка 2т по заданным значениям всех производных порядка не выше тна границе Sобласти D(или ее части) … Математическая энциклопедия
— (second derivative) Первая производная (first derivative) от первой производной функции. Первая производная измеряет наклон функции; вторая производная измеряет, как изменяется наклон с увеличением аргумента. Вторая производная от y = f(x)… … Экономический словарь
Вторая производная от y = f(x)… … Экономический словарь
Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей. Дробная про … Википедия
— (cross partial derivative) Влияние изменения одного аргумента функции от двух и более переменных на производную данной функции, взятую по другому аргументу. Если y=f(x,z), то ее производная, или первая производная функции у по аргументу х, равна… … Экономический словарь
аналог скорости точки — Первая производная перемещения точки по обобщенной координате механизма …
аналог угловой скорости звена — Первая производная угла поворота звена по обобщенной координате механизма … Политехнический терминологический толковый словарь
обобщённая скорость механизма — Первая производная от обобщенной координаты механизма по времени … Политехнический терминологический толковый словарь
Книги
- Сборник задач по дифференциальной геометрии и топологии , Мищенко А.
 С.. Настоящий сборник задач призван максимально отразить существующие требования к курсам дифференциальной геометрии и топологии как со стороны новых программ, так исо стороны других курсов…
С.. Настоящий сборник задач призван максимально отразить существующие требования к курсам дифференциальной геометрии и топологии как со стороны новых программ, так исо стороны других курсов… - Мои научные статьи. Книга 3. Метод матриц плотности в квантовых теориях лазера, произвольного атома , Бондарев Борис Владимирович. В этой книге рассмотрены опубликованные научные статьи, в которых методом матриц плотности изложены новые квантовые теории лазера, произвольного атома и квантового осциллятора с затуханием.…
Приведем сводную таблицу для удобства и наглядности при изучении темы.
Константа y = C Степенная функция y = x p (x p) » = p · x p — 1 | Показательная функция y = a x (a x) » = a x · ln a В частности, при a = e имеем y = e x (e x) » = e x |
Логарифмическая функция (log a x) » = 1 x · ln a В частности, при a = e имеем y = ln x (ln x) » = 1 x | Тригонометрические функции (sin x) » = cos x (cos x) » = — sin x (t g x) » = 1 cos 2 x (c t g x) » = — 1 sin 2 x |
Обратные тригонометрические функции (a r c sin x) » = 1 1 — x 2 (a r c cos x) » = — 1 1 — x 2 (a r c t g x) » = 1 1 + x 2 (a r c c t g x) » = — 1 1 + x 2 | Гиперболические функции (s h x) » = c h x (c h x) » = s h x (t h x) » = 1 c h 2 x (c t h x) » = — 1 s h 2 x |
Разберем, каким образом были получены формулы указанной таблицы или, иначе говоря, докажем вывод формул производных для каждого вида функций.
Производная постоянной
Доказательство 1
Для того, чтобы вывести данную формулу, возьмем за основу определение производной функции в точке. Используем x 0 = x , где x принимает значение любого действительного числа, или, иначе говоря, x является любым числом из области определения функции f (x) = C . Составим запись предела отношения приращения функции к приращению аргумента при ∆ x → 0:
lim ∆ x → 0 ∆ f (x) ∆ x = lim ∆ x → 0 C — C ∆ x = lim ∆ x → 0 0 ∆ x = 0
Обратите внимание, что под знак предела попадает выражение 0 ∆ x . Оно не есть неопределенность «ноль делить на ноль», поскольку в числителе записана не бесконечно малая величина, а именно нуль. Иначе говоря, приращение постоянной функции всегда есть нуль.
Итак, производная постоянной функции f (x) = C равна нулю на всей области определения.
Пример 1
Даны постоянные функции:
f 1 (x) = 3 , f 2 (x) = a , a ∈ R , f 3 (x) = 4 . 13 7 22 , f 4 (x) = 0 , f 5 (x) = — 8 7
Решение
Опишем заданные условия. В первой функции мы видим производную натурального числа 3 . В следующем примере необходимо брать производную от а , где а — любое действительное число. Третий пример задает нам производную иррационального числа 4 . 13 7 22 , четвертый — производную нуля (нуль – целое число). Наконец, в пятом случае имеем производную рациональной дроби — 8 7 .
В первой функции мы видим производную натурального числа 3 . В следующем примере необходимо брать производную от а , где а — любое действительное число. Третий пример задает нам производную иррационального числа 4 . 13 7 22 , четвертый — производную нуля (нуль – целое число). Наконец, в пятом случае имеем производную рациональной дроби — 8 7 .
Ответ: производные заданных функций есть нуль при любом действительном x (на всей области определения)
f 1 » (x) = (3) » = 0 , f 2 » (x) = (a) » = 0 , a ∈ R , f 3 » (x) = 4 . 13 7 22 » = 0 , f 4 » (x) = 0 » = 0 , f 5 » (x) = — 8 7 » = 0
Производная степенной функции
Переходим к степенной функции и формуле ее производной, имеющей вид: (x p) » = p · x p — 1 , где показатель степени p является любым действительным числом.
Доказательство 2
Приведем доказательство формулы, когда показатель степени – натуральное число: p = 1 , 2 , 3 , …
Вновь опираемся на определение производной. Составим запись предела отношения приращения степенной функции к приращению аргумента:
Составим запись предела отношения приращения степенной функции к приращению аргумента:
(x p) » = lim ∆ x → 0 = ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p — x p ∆ x
Чтобы упростить выражение в числителе, используем формулу бинома Ньютона:
(x + ∆ x) p — x p = C p 0 + x p + C p 1 · x p — 1 · ∆ x + C p 2 · x p — 2 · (∆ x) 2 + . . . + + C p p — 1 · x · (∆ x) p — 1 + C p p · (∆ x) p — x p = = C p 1 · x p — 1 · ∆ x + C p 2 · x p — 2 · (∆ x) 2 + . . . + C p p — 1 · x · (∆ x) p — 1 + C p p · (∆ x) p
Таким образом:
(x p) » = lim ∆ x → 0 ∆ (x p) ∆ x = lim ∆ x → 0 (x + ∆ x) p — x p ∆ x = = lim ∆ x → 0 (C p 1 · x p — 1 · ∆ x + C p 2 · x p — 2 · (∆ x) 2 + . . . + C p p — 1 · x · (∆ x) p — 1 + C p p · (∆ x) p) ∆ x = = lim ∆ x → 0 (C p 1 · x p — 1 + C p 2 · x p — 2 · ∆ x + . . . + C p p — 1 · x · (∆ x) p — 2 + C p p · (∆ x) p — 1) = = C p 1 · x p — 1 + 0 + 0 + . . . + 0 = p ! 1 ! · (p — 1) ! · x p — 1 = p · x p — 1
Так, мы доказали формулу производной степенной функции, когда показатель степени – натуральное число.
Доказательство 3
Чтобы привести доказательство для случая, когда p — любое действительное число, отличное от нуля, используем логарифмическую производную (здесь следует понимать отличие от производной логарифмической функции). Чтобы иметь более полное понимание желательно изучить производную логарифмической функции и дополнительно разобраться с производной неявно заданной функции и производной сложной функции.
Рассмотрим два случая: когда x положительны и когда x отрицательны.
Итак, x > 0 . Тогда: x p > 0 . Логарифмируем равенство y = x p по основанию e и применим свойство логарифма:
y = x p ln y = ln x p ln y = p · ln x
На данном этапе получили неявно заданную функцию. Определим ее производную:
(ln y) » = (p · ln x) 1 y · y » = p · 1 x ⇒ y » = p · y x = p · x p x = p · x p — 1
Теперь рассматриваем случай, когда x – отрицательное число.
Если показатель p есть четное число, то степенная функция определяется и при x
Тогда x p
Если p есть нечетное число, тогда степенная функция определена и при x
y » (x) = (- (- x) p) » = — ((- x) p) » = — p · (- x) p — 1 · (- x) » = = p · (- x) p — 1 = p · x p — 1
Последний переход возможен в силу того, что если p — нечетное число, то p — 1 либо четное число, либо нуль (при p = 1), поэтому, при отрицательных x верно равенство (- x) p — 1 = x p — 1 .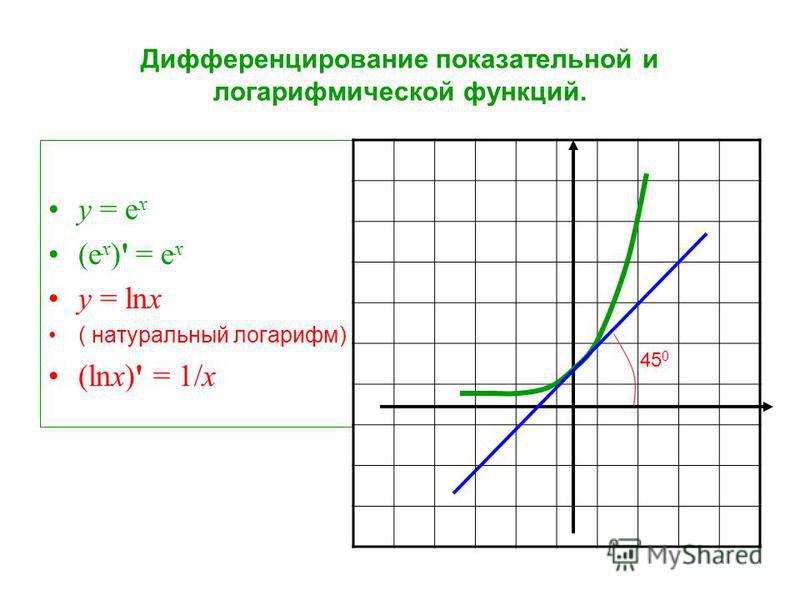
Итак, мы доказали формулу производной степенной функции при любом действительном p .
Пример 2
Даны функции:
f 1 (x) = 1 x 2 3 , f 2 (x) = x 2 — 1 4 , f 3 (x) = 1 x log 7 12
Определите их производные.
Решение
Часть заданных функций преобразуем в табличный вид y = x p , опираясь на свойства степени, а затем используем формулу:
f 1 (x) = 1 x 2 3 = x — 2 3 ⇒ f 1 » (x) = — 2 3 · x — 2 3 — 1 = — 2 3 · x — 5 3 f 2 » (x) = x 2 — 1 4 = 2 — 1 4 · x 2 — 1 4 — 1 = 2 — 1 4 · x 2 — 5 4 f 3 (x) = 1 x log 7 12 = x — log 7 12 ⇒ f 3 » (x) = — log 7 12 · x — log 7 12 — 1 = — log 7 12 · x — log 7 12 — log 7 7 = — log 7 12 · x — log 7 84
Производная показательной функции
Доказательство 4
Выведем формулу производной, взяв за основу определение:
(a x) » = lim ∆ x → 0 a x + ∆ x — a x ∆ x = lim ∆ x → 0 a x (a ∆ x — 1) ∆ x = a x · lim ∆ x → 0 a ∆ x — 1 ∆ x = 0 0
Мы получили неопределенность. Чтобы раскрыть ее, запишем новую переменную z = a ∆ x — 1 (z → 0 при ∆ x → 0). В таком случае a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . Для последнего перехода использована формула перехода к новому основанию логарифма.
Чтобы раскрыть ее, запишем новую переменную z = a ∆ x — 1 (z → 0 при ∆ x → 0). В таком случае a ∆ x = z + 1 ⇒ ∆ x = log a (z + 1) = ln (z + 1) ln a . Для последнего перехода использована формула перехода к новому основанию логарифма.
Осуществим подстановку в исходный предел:
(a x) » = a x · lim ∆ x → 0 a ∆ x — 1 ∆ x = a x · ln a · lim ∆ x → 0 1 1 z · ln (z + 1) = = a x · ln a · lim ∆ x → 0 1 ln (z + 1) 1 z = a x · ln a · 1 ln lim ∆ x → 0 (z + 1) 1 z
Вспомним второй замечательный предел и тогда получим формулу производной показательной функции:
(a x) » = a x · ln a · 1 ln lim z → 0 (z + 1) 1 z = a x · ln a · 1 ln e = a x · ln a
Пример 3
Даны показательные функции:
f 1 (x) = 2 3 x , f 2 (x) = 5 3 x , f 3 (x) = 1 (e) x
Необходимо найти их производные.
Решение
Используем формулу производной показательной функции и свойства логарифма:
f 1 » (x) = 2 3 x » = 2 3 x · ln 2 3 = 2 3 x · (ln 2 — ln 3) f 2 » (x) = 5 3 x » = 5 3 x · ln 5 1 3 = 1 3 · 5 3 x · ln 5 f 3 » (x) = 1 (e) x » = 1 e x » = 1 e x · ln 1 e = 1 e x · ln e — 1 = — 1 e x
Производная логарифмической функции
Доказательство 5
Приведем доказательство формулы производной логарифмической функции для любых x в области определения и любых допустимых значениях основания а логарифма. Опираясь на определение производной, получим:
Опираясь на определение производной, получим:
(log a x) » = lim ∆ x → 0 log a (x + ∆ x) — log a x ∆ x = lim ∆ x → 0 log a x + ∆ x x ∆ x = = lim ∆ x → 0 1 ∆ x · log a 1 + ∆ x x = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x = = lim ∆ x → 0 log a 1 + ∆ x x 1 ∆ x · x x = lim ∆ x → 0 1 x · log a 1 + ∆ x x x ∆ x = = 1 x · log a lim ∆ x → 0 1 + ∆ x x x ∆ x = 1 x · log a e = 1 x · ln e ln a = 1 x · ln a
Из указанной цепочки равенств видно, что преобразования строились на основе свойства логарифма. Равенство lim ∆ x → 0 1 + ∆ x x x ∆ x = e является верным в соответствии со вторым замечательным пределом.
Пример 4
Заданы логарифмические функции:
f 1 (x) = log ln 3 x , f 2 (x) = ln x
Необходимо вычислить их производные.
Решение
Применим выведенную формулу:
f 1 » (x) = (log ln 3 x) » = 1 x · ln (ln 3) ; f 2 » (x) = (ln x) » = 1 x · ln e = 1 x
Итак, производная натурального логарифма есть единица, деленная на x .
Производные тригонометрических функций
Доказательство 6
Используем некоторые тригонометрические формулы и первый замечательный предел, чтобы вывести формулу производной тригонометрической функции.
Согласно определению производной функции синуса, получим:
(sin x) » = lim ∆ x → 0 sin (x + ∆ x) — sin x ∆ x
Формула разности синусов позволит нам произвести следующие действия:
(sin x) » = lim ∆ x → 0 sin (x + ∆ x) — sin x ∆ x = = lim ∆ x → 0 2 · sin x + ∆ x — x 2 · cos x + ∆ x + x 2 ∆ x = = lim ∆ x → 0 sin ∆ x 2 · cos x + ∆ x 2 ∆ x 2 = = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2
Наконец, используем первый замечательный предел:
sin » x = cos x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = cos x
Итак, производной функции sin x будет cos x .
Совершенно также докажем формулу производной косинуса:
cos » x = lim ∆ x → 0 cos (x + ∆ x) — cos x ∆ x = = lim ∆ x → 0 — 2 · sin x + ∆ x — x 2 · sin x + ∆ x + x 2 ∆ x = = — lim ∆ x → 0 sin ∆ x 2 · sin x + ∆ x 2 ∆ x 2 = = — sin x + 0 2 · lim ∆ x → 0 sin ∆ x 2 ∆ x 2 = — sin x
Т.е. производной функции cos x будет – sin x .
Формулы производных тангенса и котангенса выведем на основе правил дифференцирования:
t g » x = sin x cos x » = sin » x · cos x — sin x · cos » x cos 2 x = = cos x · cos x — sin x · (- sin x) cos 2 x = sin 2 x + cos 2 x cos 2 x = 1 cos 2 x c t g » x = cos x sin x » = cos » x · sin x — cos x · sin » x sin 2 x = = — sin x · sin x — cos x · cos x sin 2 x = — sin 2 x + cos 2 x sin 2 x = — 1 sin 2 x
Производные обратных тригонометрических функций
Раздел о производной обратных функций дает исчерпывающую информацию о доказательстве формул производных арксинуса, арккосинуса, арктангенса и арккотангенса, поэтому дублировать материал здесь не будем.
Производные гиперболических функций
Доказательство 7
Вывод формул производных гиперболического синуса, косинуса, тангенса и котангенса осуществим при помощи правила дифференцирования и формулы производной показательной функции:
s h » x = e x — e — x 2 » = 1 2 e x » — e — x » = = 1 2 e x — — e — x = e x + e — x 2 = c h x c h » x = e x + e — x 2 » = 1 2 e x » + e — x » = = 1 2 e x + — e — x = e x — e — x 2 = s h x t h » x = s h x c h x » = s h » x · c h x — s h x · c h » x c h 2 x = c h 2 x — s h 2 x c h 2 x = 1 c h 2 x c t h » x = c h x s h x » = c h » x · s h x — c h x · s h » x s h 2 x = s h 2 x — c h 2 x s h 2 x = — 1 s h 2 x
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Можно выносить за знак производной :
(af(x)» =af » (x).
Например :
Производная алгебраической суммы нескольких функций (взятых в неизменном числе) равна алгебраической сумме их производных :
(f 1 (x) + f 2 (x) — f 3 (x))» = f 1 » (x) + f 2 » (x) — f 3 » (x).
Например :
(0,3 х 2 — 2 х + 0,8)» = (0,3 х 2)» — (2 х)» + (0,8)» = 0,6 х — 2 (производная последнего слагаемого уравнения равна нулю).
Если производная функции g отлична от нуля, то отношение f/g также имеет конечную производную . Данное свойство можно записать в виде:
Данное свойство можно записать в виде:
.
Пусть функции y = f(x) и y = g(x) имеют конечные производные в точке x 0 . Тогда функции f ± g и f · g также имеют конечные производные в этой точке . Тогда получим:
(f ± g) ′ = f ′ ± g ′,
(f · g) ′ = f ′ · g + f · g ′.
Производная сложной функции.
Пусть функция y = f(x) имеет конечную производную в точке x 0 , функция z = s(y) имеет конечную производную в точке y 0 = f(x 0).
Тогда сложная функция z = s (f(x)) также имеет конечную производную в этой точке. Сказанное можно записать в виде:
.
Производная обратной функции.
Пусть функция y = f(x) имеет обратную функцию x = g(y) на некотором интервале (a, b) и существует отличная от нуля конечная производная этой функции в точке x 0 , принадлежащая области определения , т.е. x 0 ∈ (a, b).
Тогда обратная функция имеет производную в точке y 0 = f(x 0):
.
Производная неявной функции.
Если функция y = f(x) задана неявно уравнением F(x, y(x)) = 0, то её производная находится из условия:
.
Говорят, что функция y = f(x) задана неявно , если она тождественно удовлетворяет соотношению:
где F(x, y) — некоторая функция двух аргументов.
Производная функции, заданной параметрически.
Если функция y = f(x) задана параметрическим образом с помощью рассмотренной
Производная от log x — Формула, Доказательство
Прежде чем искать производную от log x, вспомним, что такое «log». «log» — десятичный логарифм. т. е. это логарифм с основанием 10. Если для «журнала» не указано основание, по умолчанию используется основание 10. т. е. log = log₁₀. Мы можем найти производную log x по x следующими методами.
- Использование первого принципа
- Использование неявного дифференцирования
- Использование производной от ln x
Здесь мы не только найдем производную log x (с основанием 10), но также найдем производную log x с любым основанием.
| 1. | Что такое производная log x? |
| 2. | Производные бревна |
| 3. | Производная log x Доказательство по первому принципу |
| 4. | Производная log x Доказательство неявным дифференцированием |
| 5. | Производная log x Доказательство с использованием производной ln x |
| 6. | Часто задаваемые вопросы о производной log x |
Что такое производная log x?
Производная от logₐ x (log x с основанием a) равна 1/(x ln a). Здесь интересно то, что у нас есть «ln» в производной от «log x». Обратите внимание, что «ln» называется натуральным логарифмом (или) это логарифм с основанием «e». т. е. ln = logₑ. Кроме того, производная от log x равна 1/(x ln 10), потому что база log по умолчанию равна 10, если база не записана.
Производная log x (по основанию 10) по x обозначается как d/dx (log x) или (log x)’. Таким образом,
- d/dx(logₐx) (или) (logₐx)’ = 1/(x ln a)
- d/dx(log x) (или) (log x)’ = 1/(x ln 10)
Поскольку производная от log x напрямую следует из производной от logₐ x, достаточно доказать последнее. Давайте докажем эту формулу, используя различные методы в следующих разделах.
Производные бревна
Мы собираемся обсудить производные журналов. т. е. производные как десятичных, так и натуральных логарифмов. Мы уже видели, что производная от logₐx равна 1/(x ln a). Здесь logₐ x называется десятичным логарифмом. Но у нас есть другой тип логарифма, называемый натуральным логарифмом. Он представлен как ln x. Это логарифм с основанием «е», поэтому его можно записать как ln x = log e x. Теперь у нас есть
d/dx (logₐ x) = 1 / (x ln a)
Подставьте a = e с обеих сторон. Тогда получаем:
Тогда получаем:
d/dx (log e x) = 1 / (x ln e)
По свойствам натуральных логарифмов, ln e = 1. Итак,
d/dx (log e x ) = 1 / (x · 1)
Таким образом, d/dx (log e x) = 1.
Заменив log e x на ln x назад, мы получим d/dx (ln x) = 1. /Икс.
Следовательно, производных от log равны:
- d/dx (logₐ x) = 1 / (x ln a) (это производная десятичного логарифма)
- d/dx (ln x) = 1/x (это производная натурального логарифма)
Производная log x Доказательство по первому принципу
Докажем, что d/dx(logₐx) = 1/(x ln a), используя первый принцип (определение производной).
Доказательство:
Предположим, что f(x) = logₐ x.
По первому принципу производная функции f(x) (обозначаемой через f'(x)) определяется пределом,
f'(x) = limₕ→₀ [f(x + h) — f(x)] / h
Так как f(x) = logₐ x, то f(x + h) = logₐ (x + час).
Подставив эти значения в уравнение первого принципа,
f'(x) = limₕ→₀ [logₐ (x + h) — logₐ x] / h logₐ (м/н). Применяя это,
f'(x) = limₕ→₀ [logₐ [(x + h) / x]] / h
= lim ₕ→₀ [logₐ (1 + (h/x))] / h
Предположим, что h/x = t. Отсюда h = xt.
Когда h→0, h/x→0 ⇒ t→0.
Тогда приведенный выше предел принимает вид
f'(x) = limₜ→₀ [logₐ (1 + t)] / (xt)
= limₜ→₀ 1/(xt) logₐ (1 + t)
By используя свойство логарифма, m logₐ a = logₐ a m . Применяя это,
f'(x) = limₜ→₀ logₐ (1 + t) 1/(xt)
Используя свойство экспонент, a mn = (a m ) n . Применяя это,
f'(x) = limₜ→₀ logₐ [(1 + t) 1/t ] 1/x
Применяя свойство logₐ a m = m logₐ a,
f'(x) = limₜ→₀ (1/x) logₐ [(1 + t) 1/t ]
Здесь переменной предела является ‘t’. Таким образом, мы можем написать (1/x) вне предела.
f'(x) = (1/x) limₜ→₀ logₐ [(1 + t) 1/t ] = (1/x) logₐ limₜ→₀ [(1 + t) 1/t ]
Используя одну из формул пределов, limₜ→₀ [(1 + t) 1/t ] = e. Следовательно,
f'(x) = (1/x) logₐ e
= (1/x) (1/logₑ a) (поскольку «a» и «e» меняются местами)
= (1/x) (1/ ln a) (поскольку logₑ = ln)
= 1 / (x ln a)
Таким образом, мы доказали, что производная от logₐ x равна 1 / (x ln a) по первому принципу.
Производная log x Доказательство неявным дифференцированием
Мы докажем, что d/dx(logₐ x) = 1 / (x ln a), используя неявное дифференцирование.
Доказательство:
Предположим, что y = logₐ x. Преобразование этого в экспоненциальную форму даст г = х. Взяв производную с обеих сторон по x, мы получим
d/dx (a y ) = d/dx (x)
. Используя цепное правило,
(a y ln a) dy/dx = 1
dy/dx = 1/(a y ln a)
Но у нас есть y = x. Следовательно,
Следовательно,
dy/dx = 1 / (x ln a)
Следовательно, мы доказали, что производная logₐ x равна 1 / (x ln a), используя неявное дифференцирование.
Производная от log x Доказательство с использованием производной от ln x
Обратите внимание, что производная от ln x равна 1/x. Мы можем преобразовать журнал в ln, используя изменение базового правила. Давайте посмотрим, как.
Доказательство:
Предположим, что f(x) = logₐ x.
Изменив базовое правило, мы можем записать это как
f(x) = (logₑ x) / (logₑ a)
Мы знаем, что logₑ = ln. Таким образом,
f(x) = (ln x) / (ln a)
Теперь найдем ее производную.
f'(x) = d/dx [(ln x) / (ln a)]
= 1/ (ln a) d/dx (ln x)
= 1 / (ln a) · (1/x)
= 1 / (x ln a)
Таким образом, мы доказали, что производная logₐ x по x равна 1/(x ln a) .
Важные примечания о производной от log x:
Вот несколько важных замечаний о производной от log x.
- Производная от logₐ x равна 1/(x ln a).
- Производная log x равна 1/(x ln 10).
- Производные от ln x и log x НЕ совпадают.
d/dx(ln x) = 1/x, тогда как d/dx (log x) = 1/(x ln 10). - Поскольку область определения logₐ x равна x > 0, d/dx (logₐ |x|) = 1/(x ln a).
Кроме того, d/dx(log |x|) = 1/(x ln 10).
☛ Связанные темы:
Вот некоторые темы, связанные с производной от logₐ x.
- Формулы журнала
- Производные формулы
- Предельные формулы
- Расчетный калькулятор
Часто задаваемые вопросы о производной log x
Какова производная log x по основанию 10 по отношению к x?
Производная от log x (основание 10) равна 1/(x ln 10). Если бревно имеет основание «а», то его производная равна 1/(x ln a). т. е. d/dx(logₐx) = 1/(x ln a).
Является ли производная log x равной 1/x?
Нет, производная log x НЕ равна 1/x. На самом деле производная от ln x равна 1/x. Но производная log x равна 1/(x ln 10).
На самом деле производная от ln x равна 1/x. Но производная log x равна 1/(x ln 10).
Что такое n
th Производная от log x?Первая производная log x равна 1/(x ln 10). Вторая производная равна -1/(x 2 п. 10). Его третья производная равна 2/(x 3 ln 10). Если мы продолжим этот процесс, n th производная от log x равна [(-1) n-1 (n-1)!]/(x n ln 10).
Что такое производная log x по основанию a?
Производная log x по основанию a равна 1/(x ln a). Доказать это можно несколькими способами. Для получения дополнительной информации щелкните следующее:
- Производная log x по первому принципу
- Производная log x с помощью неявного дифференцирования
- Производная log x Использование производной ln x
Что такое вторая производная log x?
Первая производная log x равна 1/(x ln 10). Это можно записать как x -1 /(ln 10). Таким образом, его вторая производная равна (-1x -2 )/(ln 10) (или) -1/(x 2 ln 10).
Таким образом, его вторая производная равна (-1x -2 )/(ln 10) (или) -1/(x 2 ln 10).
Какие формулы для производных журналов?
Существует два типа формул для производных журналов. Одна формула говорит о производной десятичного логарифма, тогда как другая формула говорит о производной натурального логарифма.
- Для обычного бревна: d/dx (logₐ x) = 1 / (x ln a)
- Для натурального бревна: d/dx (ln x) = 1/x
Как найти производную log(x + 1)?
Мы знаем, что производная log x равна 1/(x ln 10). Опять же, по правилу цепочки производная log(x+1) равна 1/(x+1) · d/dx(x+1) = 1/(x+1).
Какова производная от log x весь квадрат?
Производная от (log x) 2 с использованием цепного правила равна 2 log x d/dx(log x) = 2 log x [ 1/(x ln 10)] = (2 log x) / (x ln 10 ). 92?
Мы знаем, что производная log x равна 1/(x ln 10). Применяя цепное правило, производная log x 2 равна 1/(x 2 ) · (2x) = 2/x.
Исчисление I. Производные экспоненциальной и логарифмической функций
Онлайн-заметки Пола
Дом
/
Исчисление I
/
Производные
/ Производные экспоненциальной и логарифмической функций
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. h} — 1} \right)}}{h}\end{align* }\]
9Икс}\]
h} — 1} \right)}}{h}\end{align* }\]
9Икс}\]
Итак, мы застряли. Нам нужно знать производную, чтобы получить производную!
Есть одно значение \(a\), с которым мы можем работать на данный момент. Еще в разделе «Экспоненциальные функции» главы «Обзор» мы заявили, что \({\bf{e}} = \mbox{2,71828182845905} \ldots \) Однако мы на самом деле не определили, где \(\bf{e} \) происходит от. На самом деле существует множество способов определить \(\bf{e}\). Вот три из них.
Некоторые определения \(\bf{e}\) 9х}\ln \влево( а \вправо)\]
Функции логарифмирования
Давайте теперь кратко получим производные для логарифмов. В этом случае нам нужно будет начать со следующего факта о функциях, обратных друг другу.
Факт 2
Если \(f(x)\) и \(g(x)\) обратны друг другу, то
\[g’\left( x \right) = \frac{1}{{f’\left( {g\left( x \right)} \right)}}\]
Чем же нам полезен этот факт? Напомним, что натуральная экспоненциальная функция и натуральный логарифм обратны друг другу, и мы знаем, что такое производная натуральной экспоненциальной функции! 9{\ пер х}}}} = \ гидроразрыва {1} {х} \]
Последний шаг просто использует тот факт, что две функции являются обратными друг другу.
Если все это собрать вместе, получается
\[\ frac{d}{{dx}}\left( {\ln x} \right) = \frac{1}{x}\hspace{0,5in}x > 0\]
Обратите внимание, что нам нужно потребовать, чтобы \(x > 0\), так как это требуется для логарифма и, следовательно, также должно требоваться для его производной. Можно также показать, что
\[\frac{d}{{dx}}\left( {\ln \left| x \right|} \right) = \frac{1}{x}\hspace{0.5in}x \ne 0\]
Используя это, нам нужно избегать \(x = 0\).
В этом случае, в отличие от экспоненциальной функции, мы действительно можем найти производную функции общего логарифма. Все, что нам нужно, это производная от натурального логарифма, которую мы только что нашли, и замена формулы основания. Используя формулу замены основания, мы можем записать общий логарифм как
\[{\log _a}x = \frac{{\ln x}}{{\ln a}}\]
Дифференциация довольно проста.
\[\begin{align*}\frac{d}{{dx}}\left( {{{\log }_a}x} \right) & = \frac{d}{{dx}}\left({ \frac{{\ln x}}{{\ln a}}} \right)\\ & = \frac{1}{{\ln a}}\frac{d}{{dx}}\left( { \ln x} \right)\\ & = \frac{1}{{x\ln a}}\end{align*}\]
Мы воспользовались тем фактом, что \(a\) является константой, поэтому \(\ln a\) также является константой и может быть вынесено из производной. Все это вместе дает 92}}}\end{выравнивание*}\]
В действительности не так уж сложно дифференцировать натуральные логарифмы и натуральные экспоненциальные функции, если вы помните формулы. В последующих разделах по мере того, как мы будем получать больше формул, они будут усложняться.
Далее нам нужно решить нашу обязательную задачу применения/интерпретации, чтобы не забыть о них.
Пример 2. Предположим, что положение объекта задано выражением \ [s \ влево ( т \ вправо) = т {{\ bf {е}} ^ т} \] 9т} = 0\]
Теперь мы знаем, что экспоненциальные функции никогда не равны нулю, и поэтому они будут равны нулю только при \(t = — 1\). Итак, если мы собираемся допустить отрицательные значения \(t\), то объект перестанет двигаться один раз в \(t = — 1\). Если мы не собираемся допускать отрицательных значений \(t\), то объект никогда не перестанет двигаться.
Итак, если мы собираемся допустить отрицательные значения \(t\), то объект перестанет двигаться один раз в \(t = — 1\). Если мы не собираемся допускать отрицательных значений \(t\), то объект никогда не перестанет двигаться.
Прежде чем перейти к следующему разделу, нам нужно вернуться к паре производных, чтобы убедиться, что мы их не путаем. Две производные равны 9x}\ln a & \hspace{0.5in}{\mbox{Производная экспоненциальной функции}}\end{массив}\]
Важно отметить, что в правиле Степени показатель степени ДОЛЖЕН быть константой, а основание ДОЛЖНО быть переменной, в то время как для производной экспоненциальной функции требуется прямо противоположное. Для экспоненциальной функции показатель степени ДОЛЖЕН быть переменной, а основание ДОЛЖНО быть константой.
Легко зациклиться на одной из этих формул и просто использовать ее для обеих. Мы также даже не говорили о том, что делать, если и показатель степени, и основание включают переменные. Мы увидим эту ситуацию в следующем разделе.
5. Производная логарифмической функции
М. Борна
Далее На этой странице
Производная y = ln x
Производная логарифма функции
Производная логарифма с основанием, отличным от e
Сначала посмотрим на график логарифмической функции с основанием e , то есть:
f ( x ) = log e ( x ) (обычно пишется «ln х «).
Касательная при x = 2 включена в график.
1234567-1123-1-2-3-4xy12slope = 1/2Открыть изображение на новой страницеГрафик `y=ln(x)`, показывающий касательную при `x=2`
Наклон касательной y = ln x при `x = 2` составляет `1/2`. (Мы можем наблюдать это на графике, глядя на соотношение рост/рост).
Если у = ln х ,
| `х` | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| наклон графика | `1` | `1/2` | `1/3` | `1/4` | `1/5` |
| `1/х` | `1` | `1/2` | `1/3` | `1/4` | `1/5` |
Мы видим, что наклон графика для каждого значения x равно «1/x». Это работает для любого положительного значения x (конечно, у нас не может быть логарифма отрицательного числа).
Это работает для любого положительного значения x (конечно, у нас не может быть логарифма отрицательного числа).
Если бы мы сделали еще много примеров, мы могли бы заключить, что производная логарифмической функции y = ln x равна
`dy/dx = 1/x`
Примечание 1: На самом деле этот результат исходит из первых принципов.
Примечание 2: Мы используем логарифмы с основанием е . Если вам нужно напоминание о функциях журнала, ознакомьтесь с базой журнала и ранее.
Производная логарифмической функции
y = ln xПроизводная логарифмической функции y = ln x определяется как:
`d/(dx)(ln\ x)=1/x`
Вы увидите, что это написано и несколькими другими способами. Следующие эквивалентны:
`d/(dx)log_ex=1/x`
Если y = ln x , то `(dy)/(dx)=1/x`
Теперь мы покажем, откуда взялась формула для производной `log_e x`, используя первые принципы.
Доказательство формулы
Для этого доказательства нам понадобится следующая базовая математика.
Формула первых принципов для производной функции `f(x)`, то есть:
`(df)/(dx) = lim_{h->0}(f(x+h)-f(x))/h`
Законы логарифмирования 9{1″/»t}` приближается к значению `e~~2.71828`.)
Я буду писать `log(x)` так, чтобы это означало `log_e(x) = ln(x)`, чтобы его было легче читать .
У нас есть `f(x) = log(x)`, поэтому производная будет равна:
`(df)/(dx) = lim_{h->0}(log(x+h)-log(x))/h `
Теперь вершина нашей дроби равна
`log(x+h)-log(x)` `= log((x+h)/x)` `= log(1 + h/x)`.
Чтобы упростить алгебру, мы теперь заменим `t=h/x`, и это даст нам `h = xt`. Конечно 9{1″/»t})`
` = 1/x log(e)`
` = 1/x`
Совет
Для некоторых задач мы можем использовать законы логарифмирования, чтобы упростить наше логарифмическое выражение перед его дифференцированием.
Пример 1
Найдите производную числа
у = пер 2 х
Ответить
Используем логарифмический закон:
журнал аб = журнал а + журнал б
Мы можем написать наш вопрос как:
у = пер 2 х = пер 2 + пер х
Теперь производная константы равна 0, поэтому
`d/(dx)ln\ 2=0`
Итак, у нас осталось (из нашей формулы выше)
`d/(dx)(ln\ x)=1/x`
Окончательный ответ:
`(dy)/(dx)=1/x`
Из следующего графика видно, что наклон y = ln 2 x (кривая зеленого цвета, касательная пурпурного цвета) совпадает с наклоном y = ln x (кривая серого цвета, касательная серого штриха) в точке x = 2. 2=2 d/(dx)ln\ x=2/x` 92) на самом деле имеет 2 «руки», одну с отрицательной стороны и одну с положительной. На приведенном выше графике для простоты показано только положительное плечо.
2=2 d/(dx)ln\ x=2/x` 92) на самом деле имеет 2 «руки», одну с отрицательной стороны и одну с положительной. На приведенном выше графике для простоты показано только положительное плечо.
Производная от
y = ln u (где u является функцией x )К сожалению, мы можем использовать законы логарифмирования только в ограниченном числе типов вопросов на дифференциацию логарифмов.
Чаще всего нам нужно найти производную логарифма некоторой функции от х . Например, нам может понадобиться найти производную от 90 409 y 90 410 = 2 ln (3 90 409 x 90 410 90 162 2 90 163 — 1).
Для решения таких задач нам понадобится следующая формула.
Если
у = пер у
и u есть некоторая функция x , тогда:
`(dy)/(dx)=(u’)/u`
, где u’ является производным от u
Другой способ написать это
`(dy)/(dx)=1/u(du)/(dx)`
Вы также можете увидеть следующую форму. Это означает то же самое.
Это означает то же самое.
Если
y = ln f ( х ),
, то производная от y определяется как:
`(dy)/(dx)=(f'(x))/(f(x)`
Пример 3
Найдите производную из
92-1)`Пример 4
Найдите производную из
y = ln(1 − 2 x ) 3 .
Ответить
Во-первых, мы упростим наше логарифмическое выражение, используя логарифмический закон:
логарифм a n = n логарифм a
Мы можем написать
y = ln(1 − 2 x ) 3 = 3 ln(1 2+1)`
Затем мы используем следующее правило (дважды), чтобы различать два термина журнала:
`(dy)/(dx)=(u’)/u`
На первый срок
u = sin 2 x
u ‘ = 2 cos 2 x
Для второго члена ставим
u = х 2 + 1,
дача
и ‘ = 2 92+1)`
Дифференцирование логарифмических функций с основанием, отличным от
eЕсли
u = f ( x ) является функцией x ,
и
y = log b u — логарифм с основанием b ,
, то мы можем получить производную логарифмической функции с основанием b , используя:
`(dy)/(dx)=(log_be)(u’)/u`
где
`u’` является производным от u
log b e — константа.
См. изменение базового правила, чтобы узнать, как вычислить такие константы на вашем калькуляторе.)
Примечание 1: Эта формула получена из первых принципов.
Примечание 2: Если мы выберем e в качестве базы, то производная ln u , где u является функцией x , просто дает нам нашу формулу выше:
`(dy)/(dx)=(u’)/u`
[Вспомним, что журнал e e = 1. ]
[См. главу об экспоненциальных и логарифмических функциях base e , если вам нужно освежить в памяти все это.]
Пример 6
Найдите производную y = логарифм 2 6 x .
Ответ
Мы начнем с использования следующего правила журнала, чтобы упростить наш вопрос:
журнал аб = журнал а + журнал б
Мы можем написать наш вопрос как:
y = бревно 2 6 x = бревно 2 6 + бревно 2 x
Первый член, log 2 6, является константой, поэтому его производная равна 0.
Производная второго члена, используя нашу формулу, выглядит следующим образом:
`(dy)/(dx)=(log_2e) (1/x)=(log_2e)/x`
Верхний член, log 2 e , является константой. Если нам нужно десятичное значение, мы можем вычислить его, используя изменение базы следующим образом:
`log_2e=(log_10e)/(log_10 2)=1.442695041`
Пример 7
Найдите производную y = 3 log 7 ( x 2 + 1).
Ответить
Ставим
93-х``х ≠ ±sqrt(0,5)`,
`х ≠ 0`
ПРИМЕЧАНИЕ. Нам нужно быть осторожными с доменом этого решения, так как оно верно только для определенных значений. х .
График y = ln(2 x 3 − x ) 2 (который имеет степень 2 ) определен для всех x3 , кроме x3 . ` ± квадрат (0,5), 0` Его график выглядит следующим образом: График y = ln(2 x 3 − x ) 2 . (степень 2) График y = 2 ln(2 x 3 − x ), однако (у него впереди 2 × ) определен только для более ограниченного
домен (поскольку у нас не может быть логарифма отрицательного
число.) Таким образом, мы можем иметь только x в диапазоне `-sqrt 0,5 sqrt0,5.` График y = 2 ln(2 x 3 − x ). (продукт 2) Итак, когда мы находим дифференцирование логарифма, используя
указанный выше, мы должны быть осторожны, чтобы домен
заданы функция и область определения производной. 2. Найдите производную y = ln(cos x 2 ). Ответить Во-первых, График функции в упражнении 5 весьма интересен: График y = (sin x ) x . До сих пор мы научились различать различные функции, включая тригонометрические, обратные и неявные функции. В этом разделе мы исследуем производные логарифмических функций. Теперь, когда у нас есть производная натуральной экспоненциальной функции, мы можем использовать неявное дифференцирование, чтобы найти производную ее обратной, натуральной логарифмической функции. Теорема: производная функции натурального логарифма Если \(x>0\) и \(y=\ln x\), то \(\frac{dy}{dx}=\frac{1 }{Икс}\). Если \(x ≠ 0\) и \(y=\ln |x|\), то \(\frac{dy}{dx}=\frac{1}{x}\). 9{\ln x}}=\frac{1}{x}\). Использование этого результата и применение цепного правила к \(h(x)=\ln (g(x))\) дает \(h′(x)=\frac{1}{g(x)} г'(х)\). □ График \(y=lnx\) и его производной \(\frac{dy}{dx}=\frac{1}{x}\) показан на рисунке. Рисунок \(\PageIndex{3}\): Функция \(y=\ln x\) возрастает на \((0,+∞)\). Его производная \(y’=\frac{1}{x}\) больше нуля на \((0,+∞)\) Пример \(\PageIndex{1}\): взятие производной натуральный логарифм 92}\) Упростить. Пример \(\PageIndex{4}\): определение наклона касательной Найдите наклон касательной к графику \(y=log_2(3x+1)\) в точке \(x= 1\). Решение Чтобы найти наклон, мы должны оценить \(\frac{dy}{dx}\) в \(x=1\). Используя уравнение, мы видим, что \(\frac{dy}{dx}=\frac{3}{\ln 2(3x+1)}\). Вычисляя производную при \(x=1\), мы видим, что касательная имеет наклон 93x}\). Мы обрисовываем эту технику в следующей стратегии решения проблем. Стратегия решения задач: использование логарифмического дифференцирования \(\frac{d}{dx}(log_bg(x))=\frac{g′(x)}{g(x)\ln b}\) На странице Определение производной мы нашли выражение для производной функции натурального логарифма 9\prime = \frac{1}{x}. Теперь рассмотрим логарифмическую функцию с произвольным основанием и получим формулу для ее производной. Итак, возьмем логарифмическую функцию у = log а х , где основание а больше нуля и не равно 1: а > 0, а . Согласно определению производной, прибавим к независимой переменной 9 приращение Δ x > 01272 x при условии, что x + Δ x > 0. Логарифмическая функция будет увеличиваться, соответственно, на значение Δ y , где \[\Delta y = {\log _a}\left( {x + \Delta x} \right) — {\log _a}x.\] Разделить обе стороны на \(\Delta x:\) \[\frac{{\Delta y}}{{\Delta x}} = \frac{1}{{\Delta x}}\left[ {{{\log }_a}\left( {x + \ Delta x} \right) — {{\log }_a}x} \right] = \frac{1}{{\Delta x}}{\log _a}\frac{{x + \Delta x}}{x } = \frac{1}{{\Delta x}}{\log _a}\left( {1 + \frac{{\Delta x}}{x}} \right).\] 9\prime = \frac{1}{{x\ln a}}\) из первых принципов — используя предельное определение производной. Дополнительные проблемы см. на стр. 2. До сих пор мы научились различать различные функции, включая тригонометрические, обратные и неявные функции. В этом разделе мы исследуем производные экспоненциальных и логарифмических функций. Как мы обсуждали во Введении в функции и графики, экспоненциальные функции играют важную роль в моделировании роста населения и распада радиоактивных материалов. Логарифмические функции могут помочь изменить масштаб больших величин и особенно полезны для перезаписи сложных выражений. Точно так же, как когда мы находили производные других функций, мы можем найти производные экспоненциальных и логарифмических функций, используя формулы. При разработке этих формул нам необходимо сделать некоторые основные предположения. Доказательства того, что эти предположения верны, выходят за рамки этого курса. Прежде всего начнем с предположения, что функция B(x)=bx,b>0,B(x)=bx,b>0 определена для каждого действительного числа и непрерывна. В предыдущих курсах значения экспоненциальных функций для всех рациональных чисел определялись — начиная с определения bn,bn, где nn — натуральное число, — как произведение bb, умноженное само на себя nn раз. Позже мы определили b0=1,b−n=1bn,b0=1,b−n=1bn для натуральных чисел n,n и bs/t=(bt)sbs/t=(bt)s для положительных целые числа ss и t.t. Эти определения оставляют открытым вопрос о значении brbr, где rr — произвольное действительное число. Предполагая непрерывности B(x)=bx,b>0,B(x)=bx,b>0, мы можем интерпретировать brbr как limx→rbxlimx→rbx, где значения xx при переходе к пределу рациональны. 43<4π<44,43,1<4π<43,2,43,14<4π<43,15,43,141<4π<43,142,43,1415<4π<43,1416,….43<4π<44,43,1<4π<43,2,43,14<4π<43,15 ,43,141<4π<43,142,43,1415<4π<43,1416,…. Как видно из следующей таблицы, 4π≈77,88,4π≈77,88. Стол
3,6
Приближение значения 4π4π Мы также предполагаем, что для B(x)=bx,b>0,B(x)=bx,b>0 значение B′(0)B′(0) производной существует. В этом разделе мы покажем, что, сделав это одно дополнительное предположение, можно доказать, что функция B(x)B(x) дифференцируема всюду. Мы делаем последнее предположение: существует уникальное значение b>0b>0, для которого B′(0)=1.B′(0)=1. Мы определяем ee как это уникальное значение, как мы это делали в разделе «Введение в функции и графики». На рис. 3.33 представлены графики функций y=2x, y=3x, y=2,7x, y=2x, y=3x, y=2,7x и y=2,8x.y=2,8x. Визуальная оценка наклона касательных к этим функциям при 0 свидетельствует о том, что значение e лежит где-то между 2,7 и 2,8. Функция E(x)=exE(x)=ex называется естественной показательной функцией. Его обратная функция L(x)=logex=lnxL(x)=logex=lnx называется функцией натурального логарифма. Рисунок
3,33
График E(x)=exE(x)=ex находится между y=2xy=2x и y=3x.y=3x. Для лучшей оценки e,e мы можем составить таблицу оценок B′(0)B′(0) для функций вида B(x)=bx.B(x)=bx. Перед этим вспомните, что B′(0)=limx→0bx−b0x−0=limx→0bx−1x≈bx−1xB′(0)=limx→0bx−b0x−0=limx→0bx−1x≈bx−1x для значений xx, очень близких к нулю. Для наших оценок мы выбираем x=0,00001x=0,00001 и x=-0,00001x=-0,00001, чтобы получить оценку b-0,00001-1-0,00001 См. следующую таблицу. Стол
3,7
Оценка значения ee Из таблицы видно, что 2,7182 График E(x)=exE(x)=ex вместе с линией y=x+1y=x+1 показан на рисунке 3.34. Эта линия касается графика E(x)=exE(x)=ex при x=0.x=0. Рисунок
3,34
Касательная к E(x)=exE(x)=ex при x=0x=0 имеет наклон 1. Теперь, когда мы изложили наши основные предположения, мы начнем наше исследование с изучения производной от B(x)=bx,b>0.B(x)=bx,b>0. Напомним, что мы предполагали, что B′(0)B′(0) существует. Применяя предельное определение к производной, заключаем, что B′(0)=limh→0b0+h−b0h=limh→0bh−1h. (3.28) Переходя к B′(x),B′(x), получаем следующее. B′(x)=limh→0bx+h−bxhПрименить предельное определение производной.=limh→0bxbh−bxhОбратите внимание, что bx+h=bxbh.=limh→0bx(bh−1)hКоэффициент outbx.=bxlimh→0bh− 1hПрименить свойство пределов.=bxB′(0)UseB′(0)=limh→0b0+h−b0h=limh→0bh−1h.B′(x)=limh→0bx+h−bxhПрименить определение предела производная.=limh→0bxbh−bxhОбратите внимание, что bx+h=bxbh.=limh→0bx(bh−1)hКоэффициент outbx.=bxlimh→0bh−1hПрименить свойство пределов.=bxB′(0)UseB′(0)=limh →0b0+h−b0h=limh→0bh−1h. Мы видим, что на основании предположения, что B(x)=bxB(x)=bx дифференцируемо в точке 0, B(x)0,B(x) не только дифференцируемо всюду, но и его производная равна B'(x)=bxB'(0).B'(x)=bxB'(0). (3.29) Для E(x)=ex,E′(0)=1.E(x)=ex,E′(0)=1. Таким образом, мы имеем E′(x)=ex.E′(x)=ex. (Значение B′(0)B′(0) для произвольной функции вида B(x)=bx,b>0,B(x)=bx,b>0 будет получено позже. Пусть E(x)=exE(x)=ex — натуральная экспоненциальная функция. Тогда E′(x)=ex.E′(x)=ex. В общем, ddx(eg(x))=eg(x)g′(x).ddx(eg(x))=eg(x)g′(x). Найдите производную f(x)=etan(2x).f(x)=etan(2x). Используя формулу производной и цепное правило, f′(x)=etan(2x)ddx(tan(2x))=etan(2x)sec2(2x)·2.f′(x)=etan(2x )ddx(tan(2x))=etan(2x)sec2(2x)·2. Найдите производную от y=ex2x.y=ex2x. Используйте производную натуральной экспоненциальной функции, частное правило и цепное правило. y′=(ex2·2)x·x−1·ex2x2Применить частное правило. Найдите производную h(x)=xe2x.h(x)=xe2x. Начальная популяция колонии комаров составляет 1000 особей. Через tt дней популяция определяется как A(t)=1000e0,3t. A(t)=1000e0,3t. Покажите, что отношение скорости изменения популяции A'(t),A'(t) к популяции A(t)A(t) постоянно. Сначала найдите A′(t).A′(t). Используя цепное правило, мы имеем A′(t)=300e0,3t.A′(t)=300e0,3t. Таким образом, отношение скорости изменения населения к населению равно A'(t)=300e0,3t1000e0,3t=0,3.A'(t)=300e0,3t1000e0,3t=0,3. Отношение скорости изменения численности населения к численности населения является константой 0,3. Если A(t)=1000e0,3tA(t)=1000e0,3t описывает популяцию комаров через tt дней, как в предыдущем примере, какова скорость изменения A(t)A(t) через 4 дня ? Теперь, когда у нас есть производная натуральной экспоненциальной функции, мы можем использовать неявное дифференцирование, чтобы найти производную ее обратной, натуральной логарифмической функции. Если x>0x>0 и y=lnx,y=lnx, то dydx=1x.dydx=1x. (3.30) В более общем случае пусть g(x)g(x) — дифференцируемая функция. Для всех значений xx, для которых g′(x)>0,g′(x)>0, производная h(x)=ln(g(x))h(x)=ln(g(x)) определяется как h′(x)=1g(x)g′(x).h′(x)=1g(x)g′(x). (3.31) Если x>0x>0 и y=lnx,y=lnx, то ey=x.ey=x. Дифференцирование обеих частей этого уравнения приводит к уравнению eydydx=1.eydydx=1. Решение для dydxdydx дает dydx=1ey.dydx=1ey. Наконец, мы подставляем x=eyx=ey, чтобы получить dyx=1x.dydx=1x. Мы также можем получить этот результат, применяя теорему об обратной функции следующим образом. Поскольку y=g(x)=lnxy=g(x)=lnx является инверсией f(x)=ex,f(x)=ex, применяя теорему об обратной функции, мы имеем dydx=1f′(g(x))=1elnx=1x. Использование этого результата и применение цепного правила к h(x)=ln(g(x))h(x)=ln(g(x)) дает h′(x)=1g(x)g′(x).h′(x)=1g(x)g′(x). □ График зависимости y=lnxy=lnx и ее производной dydx=1xdydx=1x показан на рис. 3.35. Рисунок
3,35
Функция y=lnx Функция y=lnx возрастает на (0,+∞).(0,+∞). Его производная y′=1xy′=1x больше нуля на (0,+∞).(0,+∞). Найдите производную f(x)=ln(x3+3x−4).f(x)=ln(x3+3x−4). Используйте уравнение 3.31 напрямую. f′(x)=1×3+3x−4·(3×2+3)Useg(x)=x3+3x−4inh′(x)=1g(x)g′(x).=3×2+3×3+3x −4Rewrite.f′(x)=1×3+3x−4·(3×2+3)Useg(x)=x3+3x−4inh′(x)=1g(x)g′(x).=3×2+3×3+ 3x−4Переписать. Найдите производную f(x)=ln(x2sinx2x+1). На первый взгляд получение этой производной кажется довольно сложным. Однако, используя свойства логарифмов перед нахождением производной, мы можем значительно упростить задачу. f(x)=ln(x2sinx2x+1)=2lnx+ln(sinx)−ln(2x+1)Применить свойства логарифмов.f′(x)=2x+cotx−22x+1Применить правило сумм иh′( x)=1g(x)g′(x).f(x)=ln(x2sinx2x+1)=2lnx+ln(sinx)−ln(2x+1)Применить свойства логарифмов.f′(x)=2x +cotx−22x+1 Применить правило сумм и h′(x)=1g(x)g′(x). Дифференцировать: f(x)=ln(3x+2)5.f(x)=ln(3x+2)5. Теперь, когда мы можем дифференцировать натуральную логарифмическую функцию, мы можем использовать этот результат, чтобы найти производные от y=logbxy=logbx и y=bxy=bx для b>0,b≠1.b>0,b≠1. Пусть b>0,b≠1,b>0,b≠1, и пусть g(x)g(x) — дифференцируемая функция. dydx=1xlnb.dydx=1xlnb. (3.32) h′(x)=g′(x)g(x)lnb.h′(x)=g′(x)g(x)lnb. (3,33) dydx=bxlnb.dydx=bxlnb. (3.34) h′(x)=bg(x)g′(x)lnb .h′(x)=bg(x)g′(x)lnb. (3,35) Если y=logbx,y=logbx, то by=x.by=x. Отсюда следует, что ln(by)=lnx.ln(by)=lnx. Таким образом, ylnb=lnx.ylnb=lnx. Решая для y,y, мы имеем y=lnxlnb.y=lnxlnb. Дифференцируя и учитывая, что lnblnb — константа, мы видим, что dydx=1xlnb.dydx=1xlnb. Производная в уравнении 3. Если y=bx,y=bx, то lny=xlnb.lny=xlnb. Используя неявное дифференцирование, опять же учитывая, что lnblnb является константой, получаем, что 1ydydx=lnb.1ydydx=lnb. Решая dydxdydx и подставляя y=bx,y=bx, мы видим, что dydx=ylnb=bxlnb.dydx=ylnb=bxlnb. Более общая производная (уравнение 3.35) следует из цепного правила. □ Найдите производную h(x)=3x3x+2.h(x)=3x3x+2. Используйте правило частных и производные общих экспоненциальных и логарифмических функций. h′(x)=3xln3(3x+2)−3xln3(3x)(3x+2)2Применить правило частных.=2·3xln3(3x+2)2Упростить.h′(x)=3xln3(3x+ 2)−3xln3(3x)(3x+2)2Применить правило частных.=2·3xln3(3x+2)2Упростить. Найдите наклон линии, касательной к графику y=log2(3x+1)y=log2(3x+1) при x=1. Чтобы найти наклон, мы должны вычислить dydxdydx при x=1.x=1. Используя уравнение 3.33, мы видим, что dydx=3(3x+1)ln2.dydx=3(3x+1)ln2. Оценивая производную при x=1,x=1, мы видим, что касательная имеет наклон dydx|x=1=34ln2=3ln16.dydx|x=1=34ln2=3ln16. Найдите наклон линии, касательной к y=3xy=3x в точке x=2.x=2. Теперь мы можем брать производные функций вида y=(g(x))ny=(g(x))n для определенных значений n,n, а также функций вида y=bg( x),y=bg(x), где b>0b>0 и b≠1.b≠1. К сожалению, мы до сих пор не знаем производных таких функций, как y=xxy=xx или y=xπ.y=xπ. Эти функции требуют метода, называемого логарифмическим дифференцированием, который позволяет нам дифференцировать любую функцию вида h(x)=g(x)f(x).h(x)=g(x)f(x). Его также можно использовать для преобразования очень сложной задачи дифференцирования в более простую, например, для нахождения производной y=x2x+1exsin3x. Найдите производную y=(2×4+1)tanx.y=(2×4+1)tanx. Используйте логарифмическое дифференцирование, чтобы найти эту производную. lny=ln(2×4+1)tanxШаг 1. Возьмем натуральный логарифм обеих сторон.lny=tanxln(2×4+1)Шаг 2. Разложим, используя свойства логарифмов.1ydydx=sec2xln(2×4+1)+8x32x4+1 ·tanxШаг 3. Различайте обе стороны. Используйте правило произведения справа. +1·tanx)Шаг 5. Подставитьey=(2×4+1)tanx.lny=ln(2×4+1)tanxШаг 1. Возьмем натуральный логарифм обеих сторон.lny=tanxln(2×4+1)Шаг 2. Разложим, используя свойства логарифмов.1ydydx=sec2xln(2×4+1)+8x32x4+1·tanxШаг 3. Дифференцируем обе части. Используйте правило произведения справа. +1·tanx)Шаг 5. Замена=(2×4+1)tanx. Найдите производную y=x2x+1exsin3x.y=x2x+1exsin3x. В этой задаче действительно используются свойства логарифмов и правила дифференцирования, данные в этой главе. lny=lnx2x+1exsin3xШаг 1. Возьмем натуральный логарифм обеих частей. 3. Дифференцируем обе стороны. Найдите производную от y=xry=xr, где rr — произвольное действительное число. Процесс такой же, как в примере 3.82, но с меньшими сложностями. lny=lnxrШаг 1. Возьмем натуральный логарифм обеих сторон.lny=rlnxШаг 2. Разложим, используя свойства логарифмов.1ydydx=r1xШаг 3. Продифференцируем обе части.dydx=yrxШаг 4. Умножим на обе стороны.dydx=xrrxШаг 5. Substitutey=xr.dydx=rxr−1Simplify.lny=lnxrШаг 1. Используйте логарифмическое дифференцирование, чтобы найти производную от y=xx.y=xx. Найдите производную y=(tanx)π.y=(tanx)π. Для следующих упражнений найдите f′(x)f′(x) для каждой функции. 331. f(x)=x2exf(x)=x2ex 332. f(x)=e−xxf(x)=e−xx 333. f(x)=ex3lnxf(x)=ex3lnx 334. f(x)=e2x+2xf(x)=e2x+2x 335. f(x)=ex-e-xex+e-xf(x)=ex-e-xex+e-x 336. f(x)=10xln10f(x)=10xln10 337. f(x)=24x+4x2f(x)=24x+4×2 338. f(x)=3sin3xf(x)=3sin3x 339. f(x)=xπ·πxf(x)=xπ·πx 340. f(x)=ln(4×3+x)f(x)=ln(4×3+x) 341. f(x)=ln5x−7f(x)=ln5x−7 342. f(x)=x2ln9xf(x)=x2ln9x 343. f(x)=log(secx)f(x)=log(secx) 344. f(x)=log7(6×4+3)5f(x)=log7(6×4+3)5 345. f(x)=2x·log37x2−4f(x)=2x·log37x2−4 В следующих упражнениях используйте логарифмическое дифференцирование, чтобы найти dydx.dydx. 346. у=хху=хх 347. у=(sin2x)4xy=(sin2x)4x 348. y=(lnx)lnxy=(lnx)lnx 349. у=xlog2xy=xlog2x 350. y=(x2−1)lnxy=(x2−1)lnx 351. y=xcotxy=xcotx 352. у=х+11х2-43у=х+11х2-43 353. y=x−1/2(x2+3)2/3(3x−4)4y=x−1/2(x2+3)2/3(3x−4)4 354. [T] Найдите уравнение касательной к графику f(x)=4xe(x2−1)f(x)=4xe(x2−1) в точке, где х=-1.х=-1. Начертите график функции и касательной. 355. [T] Найдите уравнение прямой, перпендикулярной графику f(x)=x·5xf(x)=x·5x в точке, где x=1.x=1. Начертите график функции и нормальной линии. 356. [T] Найдите уравнение касательной к графику x3−xlny+y3=2x+5×3−xlny+y3=2x+5 в точке (2, 1). ( Подсказка : Используйте неявное дифференцирование, чтобы найти dydx.)dydx.) Начертите кривую и касательную. 357. Рассмотрим функцию y=x1/xy=x1/x для x>0.x>0. 358. Формула I(t)=sintetI(t)=sintet – это формула затухающего переменного тока. 359. [T] Население Толедо, штат Огайо, в 2000 году составляло примерно 500 000 человек. Предположим, что население увеличивается со скоростью 5% в год. 360. [T] Изотоп элемента эрбия имеет период полураспада примерно 12 часов. Изначально присутствует 9 граммов изотопа. 361. [T] Число случаев гриппа в Нью-Йорке с начала 1960 г. по начало 1964 г. моделируется функцией N(t)=5,3e0,093t2−0,87t,(0≤ t≤4),N(t)=5,3e0,093t2−0,87t,(0≤t≤4),
где N(t)N(t) указывает количество случаев (в тысячах), а t измеряется в годах, при этом t=0t=0 соответствует началу 1960 года. 362. [T] относительная скорость изменения дифференцируемой функции y=f(x)y=f(x) определяется выражением 100·f′(x)f(x)%.100·f′ (х)f(х)%. Одной из моделей роста населения является функция роста Гомперца, определяемая как P(x)=ae-b·e-cxP(x)=ae-b·e-cx, где a,b,a,b и cc являются константами. Для следующих упражнений используйте численность населения Нью-Йорка с 1790 по 1860 год, указанную в следующей таблице. Стол
3,8
Население Нью-Йорка с течением времени
Источник: http://en.

9x(x\ cot\ x+ln(sin x))`
3.9: Производные Ln, общие экспоненциальные и логарифмические функции; и Логарифмическое дифференцирование
 Логарифмические функции могут помочь изменить масштаб больших величин и особенно полезны для перезаписи сложных выражений.
Логарифмические функции могут помочь изменить масштаб больших величин и особенно полезны для перезаписи сложных выражений. Производная логарифмической функции

Шаг 1.  Возьмем натуральный логарифм обеих частей.
Возьмем натуральный логарифм обеих частей. \(\ln y=\ln x+\frac{1}{2}ln(2x+1)−x\ln e−3\ln \sin x\) Шаг 2. Разложить, используя свойства логарифмов. \(\ frac {1} {y} \ frac {dy} {dx} = \ frac {1} {x} + \ frac {1} {2x + 1} −1 − 3 \ frac {\ cos х}{\sin х}\) Шаг 3. Дифференцируйте обе стороны. \(\frac{dy}{dx}=y(\frac{1}{x}+\frac{1}{2x+1}−1−3\cot x)\) 9{g(x)}g′(x)\ln b\) Глоссарий
Авторы
Производные логарифмических функций
 \]
\] y }.\) Тогда 9\prime = \frac{1}{{\sin x}} \cdot \cos x = \frac{{\cos x}}{{\sin x}} = \cot x.\]
y }.\) Тогда 9\prime = \frac{1}{{\sin x}} \cdot \cos x = \frac{{\cos x}}{{\sin x}} = \cot x.\] 3.9 Производные экспоненциальных и логарифмических функций. Исчисление, том 1
Цели обучения
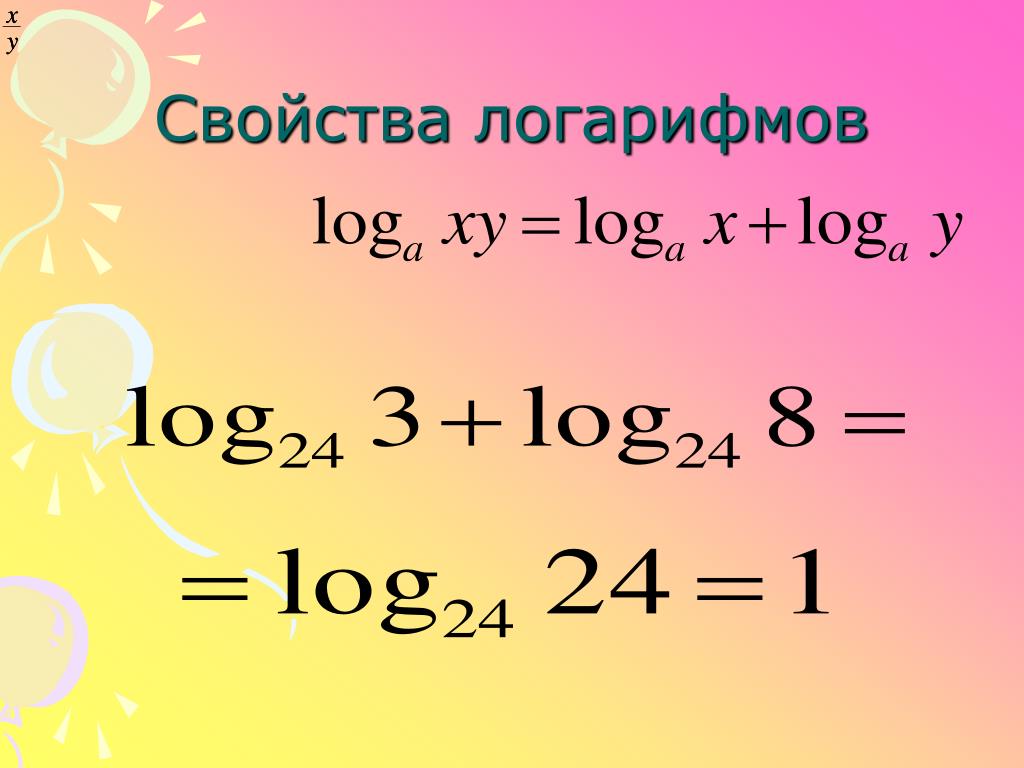
Производная показательной функции
 Например, мы можем рассматривать 4π4π как число, удовлетворяющее
Например, мы можем рассматривать 4π4π как число, удовлетворяющее хх 4x4x хх 4x4x 4343 64 43.14159343.141593 77.8802710486 43.143.1 73,5166947198 43.  141643.1416
141643.1416 77.8810268071 43.1443.14 77.7084726013 43.14243.142 77, 51944
43.14143.141 77,8162741237 43.1543.15 78.7 4541 43.141543.1415 77.8702309526 43.243.2 84.4485062895 43.1415943.14159 77.  8799471543
8799471543 4444 256 
бб b-0,00001-1-0,00001 бб b-0,00001-1-0,00001 22 0,6 2.  71832.7183
71832.7183 1,000002 2.72.7 0,9 2.7192.719 1,000259 2.712.71 0,996944 2.722.72 1,000627 2.7182.718 0,999891 2.  82.8
82.8 1,029614 2.71822.7182 0,999965 33 1,098606  B′(0)=limh→0b0+h−b0h=limh→0bh−1h.
B′(0)=limh→0b0+h−b0h=limh→0bh−1h. )
) Теорема
3.14
Производная естественной показательной функции
Пример
3,74
Производная показательной функции
Решение
Пример
3,75
Объединение правил дифференцирования
Решение
 =ex2(2×2−1)x2Упростить.y′=(ex2·2)x·x−1·ex2x2Применить частное правило.= ex2(2×2−1)x2Упростить.
=ex2(2×2−1)x2Упростить.y′=(ex2·2)x·x−1·ex2x2Применить частное правило.= ex2(2×2−1)x2Упростить. Контрольно-пропускной пункт
3,50
Пример
3,76
Применение естественной экспоненциальной функции
Решение
Контрольно-пропускной пункт
3,51
Производная логарифмической функции

Теорема
3.15
Производная натурального логарифма
Доказательство
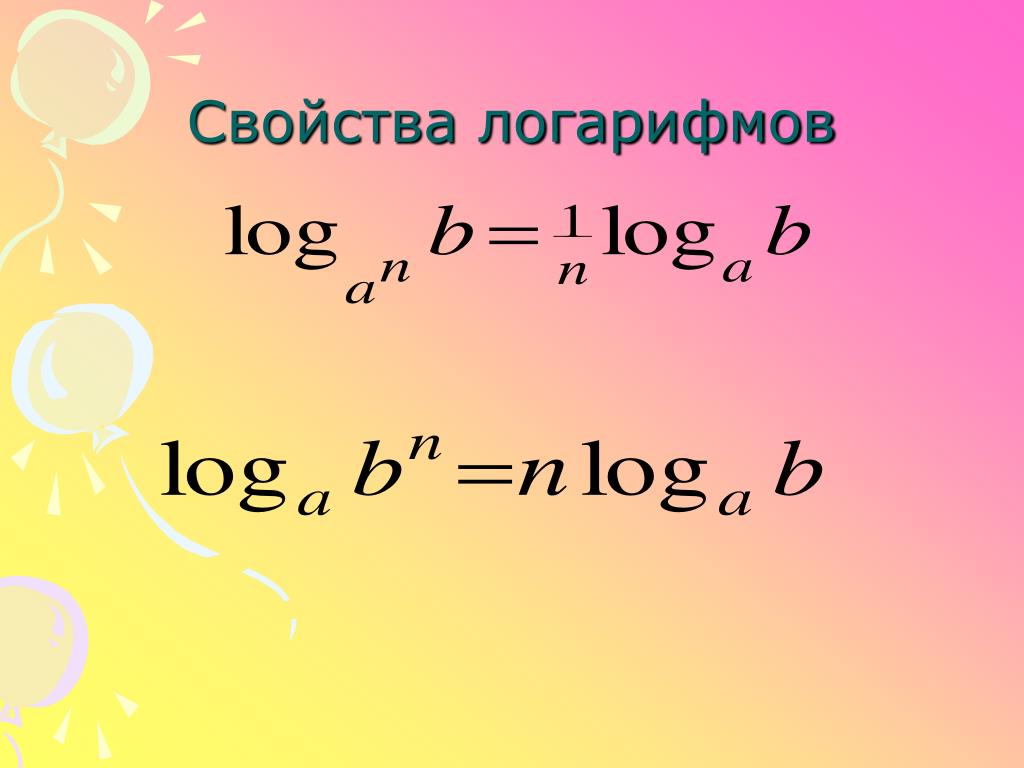 dydx=1f′(g(x))=1elnx=1x.
dydx=1f′(g(x))=1elnx=1x. Пример
3,77
Вычисление производной натурального логарифма
Решение
Пример
3,78
Использование свойств логарифмов в производной
 f(x)=ln(x2sinx2x+1).
f(x)=ln(x2sinx2x+1). Решение
Контрольно-пропускной пункт
3,52
Теорема
3.16
Производные общих экспоненциальных и логарифмических функций

В более общем случае, если h(x)=logb(g(x)),h(x)=logb(g(x)), то для всех значений x , для которых g(x )>0,g(x)>0,
В более общем случае, если h(x)=bg(x),h(x)=bg(x), то Доказательство
 33 теперь следует из цепного правила.
33 теперь следует из цепного правила.Пример
3,79
Применение формул производных
Решение
Пример
3,80
Определение наклона касательной
 x=1.
x=1. Решение
Контрольно-пропускной пункт
3,53
Логарифмическое дифференцирование
 y=x2x+1exsin3x. Мы обрисовываем эту технику в следующей стратегии решения проблем.
y=x2x+1exsin3x. Мы обрисовываем эту технику в следующей стратегии решения проблем. Стратегия решения проблем
Стратегия решения проблем: использование логарифмического дифференцирования
Пример
3,81
Использование логарифмического дифференцирования
Решение

Пример
3,82
Использование логарифмического дифференцирования
Решение
 dydx=y(1x+12x+1−1−3cotx)Шаг 4. Умножаем на обе стороны.dydx=x2x+1exsin3x(1x+12x+1−1−3cotx)Шаг 5. Подставляемy=x2x +1exsin3x.lny=lnx2x+1exsin3xШаг 1. Возьмем натуральный логарифм обеих частей.lny=lnx+12ln(2x+1)−xlne-3lnsinxШаг 2. Разложим, используя свойства логарифмов. 3cosxsinxШаг 3. Дифференцируем обе стороны.dydx=y(1x+12x+1−1−3cotx)Шаг 4. Умножаем на обе стороны.dydx=x2x+1exsin3x(1x+12x+1−1−3cotx)Шаг 5. Подставляем= x2x+1exsin3x.
dydx=y(1x+12x+1−1−3cotx)Шаг 4. Умножаем на обе стороны.dydx=x2x+1exsin3x(1x+12x+1−1−3cotx)Шаг 5. Подставляемy=x2x +1exsin3x.lny=lnx2x+1exsin3xШаг 1. Возьмем натуральный логарифм обеих частей.lny=lnx+12ln(2x+1)−xlne-3lnsinxШаг 2. Разложим, используя свойства логарифмов. 3cosxsinxШаг 3. Дифференцируем обе стороны.dydx=y(1x+12x+1−1−3cotx)Шаг 4. Умножаем на обе стороны.dydx=x2x+1exsin3x(1x+12x+1−1−3cotx)Шаг 5. Подставляем= x2x+1exsin3x. Пример
3,83
Расширение степенного правила
Решение
 Возьмем натуральный логарифм обеих частей.lny=rlnxШаг 2. Разложим, используя свойства логарифмов.1ydydx=r1xШаг 3. Продифференцируем обе части.dydx=yrxШаг 4. Умножим на yon обе стороны.dydx=xrrxШаг 5. Substitutey=xr.dydx=rxr-1Упрощение.
Возьмем натуральный логарифм обеих частей.lny=rlnxШаг 2. Разложим, используя свойства логарифмов.1ydydx=r1xШаг 3. Продифференцируем обе части.dydx=yrxШаг 4. Умножим на yon обе стороны.dydx=xrrxШаг 5. Substitutey=xr.dydx=rxr-1Упрощение. Контрольно-пропускной пункт
3,54
Контрольно-пропускной пункт
3,55
Раздел 3.9 Упражнения



тт синтетинтет 0 (и) π2π2 (ii) ππ (iii) 3π23π2 (iv) 2π2π (в) 5π25π2 (ви) 3π3π (vii) 7π27π2 (viii) 4π4π (икс) 


Годы с 1790 года Население человек 0 33 131 10 60 515 20 96 373 30 123 706 40 202 300 50 312 710 60 515 547 70 813 669 


 С.. Настоящий сборник задач призван максимально отразить существующие требования к курсам дифференциальной геометрии и топологии как со стороны новых программ, так исо стороны других курсов…
С.. Настоящий сборник задач призван максимально отразить существующие требования к курсам дифференциальной геометрии и топологии как со стороны новых программ, так исо стороны других курсов… См. изменение базового правила, чтобы узнать, как вычислить такие константы на вашем калькуляторе.)
См. изменение базового правила, чтобы узнать, как вычислить такие константы на вашем калькуляторе.)