Производная по x и y онлайн: Дифференцирование функции, заданной неявно

Найти производную методом логарифмического дифференцирования онлайн. Сложные производные

Пусть
(1)
есть дифференцируемая функция от переменной x . В начале мы рассмотрим ее на множестве значений x , для которых y принимает положительные значения: . В дальнейшем мы покажем, что все полученные результаты применимы и для отрицательных значений .

В некоторых случаях, чтобы найти производную функции (1), ее удобно предварительно прологарифмировать
,
а затем вычислить производную. Тогда по правилу дифференцирования сложной функции ,
.
Отсюда
(2) .

Производная от логарифма функции называется логарифмической производной:
.

Логарифмическая производная функции y = f(x) — это производная натурального логарифма этой функции: (ln f(x))′ .

Случай отрицательных значений y

Теперь рассмотрим случай, когда переменная может принимать как положительные, так и отрицательные значения. В этом случае возьмем логарифм от модуля и найдем его производную:
.
Отсюда
(3)

.
То есть, в общем случае, нужно найти производную от логарифма модуля функции .

Сравнивая (2) и (3) мы имеем:
.
То есть формальный результат вычисления логарифмической производной не зависит от того, взяли мы по модулю или нет. Поэтому, при вычислении логарифмической производной, мы можем не беспокоится о том, какой знак имеет функция .

Прояснить такую ситуацию можно с помощью комплексных чисел. Пусть, при некоторых значениях x , отрицательна: . Если мы рассматриваем только действительные числа, то функция не определена. Однако, если ввести в рассмотрение комплексные числа, то получим следующее:
.
То есть функции и отличаются на комплексную постоянную :
.
Поскольку производная от постоянной равна нулю, то
.

Свойство логарифмической производной

Из подобного рассмотрения следует, что логарифмическая производная не изменится, если умножить функцию на произвольную постоянную :
.
Действительно, применяя свойства логарифма , формулы производной суммы и производной постоянной , имеем:

.

Применение логарифмической производной

Применять логарифмическую производную удобно в тех случаях, когда исходная функция состоит из произведения степенных или показательных функций. В этом случае операция логарифмирования превращает произведение функций в их сумму. Это упрощает вычисление производной.

Пример 1

Найти производную функции:
.

Решение

Логарифмируем исходную функцию:
.

Дифференцируем по переменной x .
В таблице производных находим:
.
Применяем правило дифференцирования сложной функции .
;
;
;
;
(П1.1) .
Умножим на :

.

Итак, мы нашли логарифмическую производную:
.
Отсюда находим производную исходной функции:
.

Примечание

Если мы хотим использовать только действительные числа, то следует брать логарифм от модуля исходной функции:
.
Тогда
;
.
И мы получили формулу (П1.1). Поэтому результат не изменился.

Ответ

Пример 2

С помощью логарифмической производной, найдите производную функции
.

Решение

Логарифмируем:
(П2.1) .
Дифференцируем по переменной x :
;
;

;
;
;
.

Умножим на :
.
Отсюда мы получаем логарифмическую производную:
.

Производная исходной функции:
.

Примечание

Здесь исходная функция неотрицательная: . Она определена при . Если не предполагать, что логарифм может быть определен для отрицательных значений аргумента, то формулу (П2.1) следует записать так:
.
Поскольку

и
,
то это не повлияет на окончательный результат.

Ответ

Пример 3

Найдите производную
.

Решение

Дифференцирование выполняем с помощью логарифмической производной. Логарифмируем, учитывая что :
(П3.1) .

Дифференцируя, получаем логарифмическую производную.
;
;
;
(П3.2) .

Поскольку , то

.

Примечание

Проделаем вычисления без предположения, что логарифм может быть определен для отрицательных значений аргумента. Для этого возьмем логарифм от модуля исходной функции:
.
Тогда вместо (П3.1) имеем:
;

.
Сравнивая с (П3.2) мы видим, что результат не изменился.

Вам кажется, что до экзамена еще много времени? Это месяц? Два? Год? Практика показывает, что ученик лучше всего справляется с экзаменом в том случае, если начал готовиться к нему заблаговременно. В ЕГЭ немало сложных заданий, который стоят на пути школьника и будущего абитуриента к высшим баллам. Эти преграды нужно научиться преодолевать, к тому же, делать это несложно. Вам необходимо понять принцип работы с различными заданиями из билетов. Тогда и с новыми не возникнет проблем.

Логарифмы на первый взгляд кажутся невероятно сложными, но при детальном разборе ситуация значительно упрощается. Если вы хотите сдать ЕГЭ на высший балл, вам стоит разобраться в рассматриваемом понятии, что мы и предлагаем сделать в этой статье.

Для начала разделим эти определения. Что такое логарифм (log)? Это показатель степени, в которую надо возвести основание, чтобы получить указанное число. Если непонятно, разберем элементарный пример.

В этом случае основание, стоящее внизу, необходимо возвести во вторую степень, чтобы получить число 4.

Теперь разберемся со вторым понятием. Производная функции в любом виде называется понятие, характеризующее изменение функции в приведенной точке. Впрочем, это школьная программа, и если вы испытываете проблемы с данными понятиями по отдельности, стоит повторить тему.

Производная логарифма

В задания ЕГЭ по этой теме можно привести несколько задач в качестве примера. Для начала самая простая логарифмическая производная. Необходимо найти производную следующей функции.

Нам нужно найти следующую производную

Существует специальная формула.

В этом случае x=u, log3x=v. Подставляем значения из нашей функции в формулу.

Производная x будет равняться единице. С логарифмом немного труднее. Но принцип вы поймете, если просто подставите значения. Напомним, что производной lg x называется производная десятичного логарифма, а производная ln х — это производная от натурального логорифма (по основанию e).

Теперь просто подставьте полученные значения в формулу. Попробуйте сами, далее сверим ответ.

В чем здесь может быть проблема для некоторых? Мы ввели понятие натурального логарифма. Расскажем о нем, а заодно разберемся, как решать задачи с ним. Ничего сложного вы не увидите, особенно, когда поймете принцип его работы. К нему вам стоит привыкнуть, так как он нередко используется в математике (в высших учебных заведениях тем более).

Производная натурального логарифма

По своей сути, это производная логарифма по основанию e (это иррациональное число, которое равняется примерно 2,7). На деле ln очень прост, поэтому часто используется в математике в целом. Собственно, решение задачи с ним тоже не станет проблемой.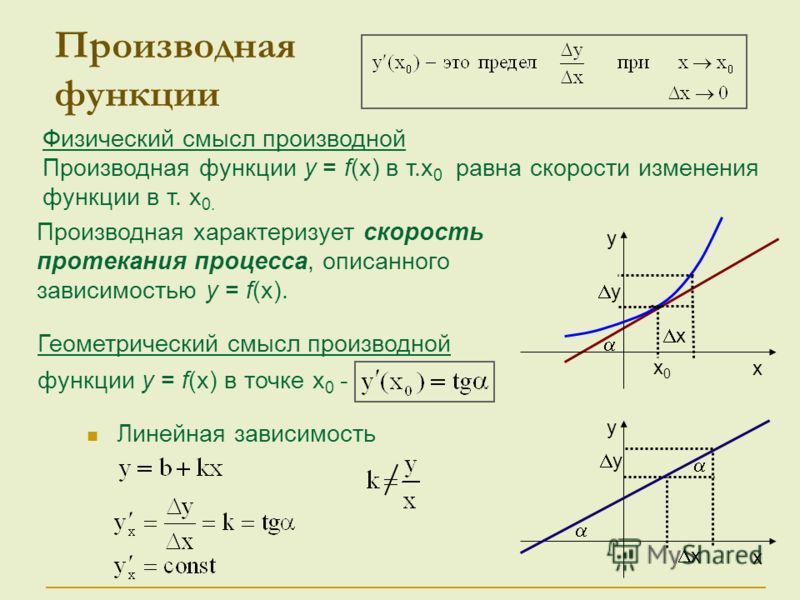 Стоит запомнить, что производная от натурального логарифма по основанию е будет равно единице поделенной на x. Самым показательным будет решение следующего примера.

Представим ее как сложную функцию, состоящую из двух простых.

Достаточно преобразовать

Ищем производную от u по x

Когда нам нужно выполнить дифференцирование показательно степенной функции вида y = (f (x)) g (x) или преобразовать громоздкое выражение с дробями, можно использовать логарифмическую производную. В рамках этого материала мы приведем несколько примеров применения этой формулы.

Чтобы понять эту тему, необходимо знать, как пользоваться таблицей производных, быть знакомым с основными правилами дифференцирования и представлять себе, что такое производная сложной функции.

Как вывести формулу логарифмической производной

Для получения этой формулы нужно сначала произвести логарифмирование по основанию e, а затем упростить получившуюся функцию, применив основные свойства логарифма. После этого надо вычислить производную неявно заданной функции:

y = f (x) ln y = ln (f (x)) (ln y) » = (ln (f (x))) » 1 y · y » = (ln (f (x))) » ⇒ y » = y · (ln (f (x))) «

Примеры использования формулы

Покажем на примере, как это делается.

Пример 1

Вычислить производную показательно степенной функции переменной x в степени x .

Решение

Проводим логарифмирование по указанному основанию и получаем ln y = ln x x . С учетом свойств логарифма это можно выразить как ln y = x · ln x . Теперь дифференцируем левую и правую части равенства и получаем результат:

ln y = x · ln x ln y » = x · ln x » 1 y · y » = x » · ln x + · ln x » ⇒ y » = y · 1 · ln x + x · 1 x = y · (ln x + 1) = x x · (ln x + 1)

Ответ: x x » = x x · (ln x + 1)

Такую задачу можно решить и другим способом, без логарифмической производной. Сначала нам надо преобразовать исходное выражение так, чтобы перейти от дифференцирования показательно степенной функции к вычислению производной сложной функции, например:

y = x x = e ln x x = e x · ln x ⇒ y » = (e x · ln x) » = e x · ln x · x · ln x » = x x · x » · ln x + x · (ln x) » = = x x · 1 · ln x + x · 1 x = x x · ln x + 1

Рассмотрим еще одну задачу.

Пример 2

Вычислите производную функции y = x 2 + 1 3 x 3 · sin x .

Решение

Исходная функция представлена в виде дроби, значит, мы можем решить задачу с помощью дифференцирования. Однако эта функция довольно сложная, значит, преобразований потребуется много. Значит, нам лучше использовать здесь логарифмическую производную y » = y · ln (f (x)) » . Поясним, почему такое вычисление удобнее.

Начнем с нахождения ln (f (x)) . Для дальнейшего преобразования нам потребуются следующие свойства логарифма:

• логарифм дроби можно представить в виде разности логарифмов;
• логарифм произведения можно представить в виде суммы;
• если у выражения под логарифмом есть степень, мы можем вынести ее в качестве коэффициента.

Преобразуем выражение:

ln (f (x)) = ln (x 2 + 1) 1 3 x 3 · sin x 1 2 = ln (x 2 + 1) 1 3 — ln (x 3 · sin x) 1 2 = = 1 3 ln (x 2 + 1) — 3 2 ln x — 1 2 ln sin x

В итоге у нас получилось достаточно простое выражение, производную которого вычислить несложно:

(ln (f (x))) » = 1 3 ln (x 2 + 1) — 3 2 ln x — 1 2 ln sin x » = = 1 3 ln (x 2 + 1) » — 3 2 ln x » — 1 2 ln sin x » = = 1 3 (ln (x 2 + 1)) » — 3 2 (ln x) » — 1 2 (ln sin x) » = = 1 3 · 1 x 2 + 1 · x 2 + 1 » — 3 2 · 1 x — 1 2 · 1 sin x · (sin x) » = = 1 3 · 2 x x 2 + 1 — 3 2 x — cos x 2 sin x

Теперь то, что у нас получилось, нужно подставить в формулу логарифмической производной.

Ответ: y » = y · ln (f (x)) » = x 2 + 1 3 x 3 · sin x · 1 3 · 2 x x 2 + 1 — 3 2 x — cos x 2 sin x

Чтобы закрепить материал, изучите еще пару следующих примеров. Здесь будут приведены только вычисления с минимумом комментариев.

Пример 3

Дана показательно степенная функция y = (x 2 + x + 1) x 3 . Вычислите ее производную.

Решение:

y » = y · (ln (f (x))) » = (x 2 + x + 1) x 3 · ln (x 2 + x + 1) x 3 » = = (x 2 + x + 1) x 3 · x 3 · (x 2 + x + 1) » = = (x 2 + x + 1) x 3 · x 3 » · ln (x 2 + x + 1) + x 3 ln (x 2 + x + 1) » = = (x 2 + x + 1) x 3 · 3 x 2 · ln (x 2 + x + 1) + x 3 · 1 x 2 + x + 1 · x 2 + x + 1 » = = (x 2 + x + 1) x 3 · 3 x 2 · ln (x 2 + x + 1) + x 3 2 x + 1 x 2 + x + 1 = = (x 2 + x + 1) x 3 · 3 x 2 · ln (x 2 + x + 1) + 2 x 4 + x 3 x 2 + x + 1

Ответ: y » = y · (ln (f (x))) » = (x 2 + x + 1) x 3 · 3 x 2 · ln (x 2 + x + 1) + 2 x 4 + x 3 x 2 + x + 1

Пример 4

Вычислите производную выражения y = x 2 + 1 3 · x + 1 · x 3 + 1 4 x 2 + 2 x + 2 .

Решение

Применяем формулу логарифмической производной.

y » = y · ln x 2 + 1 3 · x + 1 · x 3 + 1 4 x 2 + 2 x + 2 » = = y · ln x 2 + 1 3 + ln x + 1 + ln x 3 + 1 4 — ln x 2 + 2 x + 2 » = = y · 1 3 ln (x 2 + 1) + 1 2 ln x + 1 + 1 4 ln (x 3 + 1) — 1 2 ln (x 2 + 2 x + 2) » = = y · (x 2 + 1) » 3 (x 2 + 1) + x + 1 » 2 (x + 1) + (x 3 + 1) » 4 x 3 + 1 — x 2 + 2 x + 2 » 2 x 2 + 2 x + 2 = = x 2 + 1 3 · x + 1 · x 3 + 1 4 x 2 + 2 x + 2 · 2 x 3 (x 2 + 1) + 1 2 (x + 1) + 3 x 2 4 (x 3 + 1) — 2 x + 2 2 (x 2 + 2 x + 2)

Ответ:

y » = x 2 + 1 3 · x + 1 · x 3 + 1 4 x 2 + 2 x + 2 · 2 x 3 (x 2 + 1) + 1 2 (x + 1) + 3 x 2 4 (x 3 + 1) — 2 x + 2 2 (x 2 + 2 x + 2) .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Калькулятор частных производных по X и Y и решение

Введение в калькулятор частных производных

Калькулятор частных производных шаг за шагом — это онлайн-инструмент, который помогает найти частную производную функции. Калькулятор частных производных использует дифференциальное правило для нахождения частной производной заданной функции.

Поскольку частная производная является частью исчисления, она также имеет сходство с производной. Так что эта концепция как-то сбивает с толку студентов. Итак, здесь мы представляем онлайн-программное обеспечение, способное различать эти две концепции.

Что такое калькулятор частичной дифференциации?

Частичный калькулятор — это онлайн-инструмент, который дифференцирует функцию нескольких переменных для одной переменной и рассматривает другие переменные как константы. Калькулятор частных производных с шагами следует всем правилам производных, таким как цепное правило, правило произведения и правило частного, для выполнения частичного дифференцирования функции.

При вычислении частных производных вручную иногда вы можете запутаться или забыть переменную для дифференцирования. Калькулятор частных производных с несколькими переменными помогает легко и просто справиться с такими случаями.

Связанный: Найдите калькулятор второй производной и калькулятор тройной производной для расчета двойных и тройных производных бесплатно онлайн.

Как рассчитать частичную производную

Есть несколько простых шагов для использования калькулятора частных производных; это:

1. Напишите функцию в поле «Введите функцию». Или, если вы не знаете, как его использовать, вы можете попробовать вариант «Загрузить пример».
2. На втором шаге необходимо выбрать переменную из выпадающего списка поля «По отношению к».
3. Теперь выберите число в поле «Время»; это то, сколько раз вы хотите вычислить частную производную функции.
4. На последнем этапе нажмите кнопку «Рассчитать».

После нажатия кнопки «Рассчитать» калькулятор частных производных по цепному правилу начнет выполнение и выполнит вывод по заданной функции. Вы получите результат в течение нескольких секунд!!

Формула, используемая Частичным Калькулятором

Поскольку производная функции вычисляет скорость изменения переменной. Но в случае частичного дифференцирования функция может содержать более одной или двух переменных, для которых рассчитывается скорость изменения.

Калькулятор производной с несколькими переменными следует правилу производной, цепному правилу, правилу произведения и правилу степени. Он вычисляет производную функции для одной переменной, рассматривая другие переменные как константы.

Вы можете использовать калькулятор производной цепного правила, чтобы найти производную составной функции и производную векторного калькулятора, чтобы вычислить производные по направлению.

Расчет частной производной калькулятора функции многих переменных можно понять на примере ниже.

Пример:

Пусть (?, ?) = ? + ? куда ? знак равно 2 и = ? 2 . Частная производная будет вычисляться по следующей формуле:

$$ \frac{df}{dx} \;=\; \frac{df}{du} \frac{du}{dx} \;+\; \frac{df}{dv} \frac{dv}{dx} $$

И

$$ \frac{df}{dy} \;=\; \frac{df}{du} \frac{du}{dy} \;+\; \frac{df}{dv} \frac{dv}{dy} $$

Теперь продифференцируем u по x и по y.

$$ \frac{du}{dx} \;=\; 2x $$ $$ \frac{du}{dy} \;=\; 0 $$

И дифференцирование v по x и y.

$$ \frac{dv}{dx} \;=\; 0 $$

(Поскольку v содержит только переменную y, поэтому она будет рассматриваться как константа для дифференцирования по x и наоборот)

$$ \frac{dv}{dy} \;=\; 2 года $$

Дифференцировать f(x,y) по u и v.

$$ \frac{df}{du} \;=\; 1 $$ $$ \frac{df}{dv} \;=\; 1 $$

Итак,

$$ f_x \;=\; \frac{df}{dx} \;=\; 2x $$

И

$$ f_y \;=\; \frac{df}{dy} \;=\; 2 года $$

fx и fy представляют собой частную производную от f по x и y соответственно. Частные производные полезны при анализе поверхностей для точек максимума и минимума.

Зачем использовать многомерный калькулятор частных производных?

Как и производная, частная производная также является важной частью исчисления, поскольку оба являются фундаментальными решениями различных задач в исчислении. Калькулятор частных производных с шагами поможет вам найти эти полные решения шаг за шагом.

Этот калькулятор не только вычисляет частную производную заданной функции. Он также представляет функцию графически по отношению к ее изменению, чтобы пользователи могли легко понять решение.

В математике есть много понятий, по которым учащиеся всегда ищут помощь в Интернете. Частичные калькуляторы помогают им прояснить понятия. Поскольку это помогает учащимся сосредоточиться на идее, вам необходимо использовать этот калькулятор производных.

Преимущества использования калькулятора частных производных функций многих переменных

Калькулятор частных производных — эффективный инструмент со многими преимуществами. Это:

1. Это эффективный инструмент, потому что он работает быстро и показывает результаты в течение нескольких секунд.
2. Этот калькулятор прост в использовании, поскольку содержит простые шаги. Вам нужно написать функцию на своем сайте.
3. Частичный калькулятор — это бесплатный онлайн-инструмент, предназначенный только для образовательных целей.
4. Калькулятор частных производных строит трехмерный график в соответствии со скоростью изменения заданной функции.
5. Калькулятор частной производной быстро упрощает решение и предоставляет все возможные шаги.
6. Вы также можете выбрать число, до которого хотите найти частную производную.
7. Этот калькулятор не взимает никакой платы, потому что он бесплатен.
8. Этот инструмент вычисляет частные производные функции и объясняет каждый шаг, чтобы пользователь мог легко его понять.
9. Калькулятор частных производных шаг за шагом проверяет результаты, интегрируя их.
10. Этот решатель частных производных вычисляет производную заданной функции по одной переменной и рассматривает другие переменные как константы.
11. Вы можете сосредоточиться на понимании концепции вместо того, чтобы тратить время на расчеты вручную.

Другие родственные калькуляторы

1. Калькулятор неявной производной с шагами
2. Производная функция калькулятора
3. Калькулятор линеаризации
4. Калькулятор правила продукта с шагами
5. Калькулятор дифференцирования правила частного
6. Уравнение нормального линейного калькулятора
7. Калькулятор производных в точке

Часто задаваемые вопросы

Является ли калькулятор частных производных по цепному правилу точным?

Да, калькулятор частичного дифференцирования точен, и вы можете вычислять частичное дифференцирование с полной точностью.

Предоставляет ли калькулятор фундаментальных производных шаги?

Да, решатель фундаментальных производных обеспечивает пошаговые результаты. Таким образом, вы можете учиться и практиковаться, используя этот многовариантный калькулятор производных с бесплатными шагами.

Должны ли учащиеся использовать решатель частных производных?

Да, этот калькулятор цепных правил в частных производных создан специально для учащихся. Вы можете вводить свои данные несколько раз и изучать частичную дифференциацию отсюда.

Шон Мерфи

Последнее обновление 28 марта 2022 г.

Профессиональный автор контента, который любит писать о науке, технологиях и образовании.

Mathway-Find-The-Devative-Google Suce

ALLBILDERVIDEOSBüchermApsNewshopping

Sucoptionen

Деривативный калькулятор-Derivative-Calculate

WWW. в редакторе. Калькулятор производных поддерживает вычисление первой, второй…., четвертой производных, а также …

Найти производную — d/d@VAR f(x)=1/x | Матвей

www.mathway.com › Popular-Problems › Исчисление

Дифференцируйте, используя правило степени, которое утверждает, что ddx[xn] d d x [ x n ] равно nxn−1 n x n — 1 , где n=−1 n = — 1 . −x−2 — x — 2.

Ähnliche Fragen

Можете ли вы найти производные на Photomath?

Примеры вычислений | Нахождение производной с помощью цепного правила

www.mathway.com › исчисление › производные › нахождение…

Дифференцирование с использованием цепного правила, которое утверждает, что ddx[f(g(x))] d d x [ f ( g ( x ) ) ] равно f'(g(x))g'(x) f ′ ( g ( x ) ) g ′ ( x ), где f(x)=x8 f ( x ) …

Примеры вычислений | Нахождение производной с помощью правила отношения

www.mathway.com › исчисление › производные › нахождение…

Нахождение производной с помощью правила отношения — d/dx. x+3×2−1 x + 3 x 2 — 1. Шаг 1. Дифференцируйте, используя правило частных, которое утверждает, что ddx[f(x)g(x)] d d x …

Примеры исчисления | производные | Неявное дифференцирование — Mathway

www.mathway.com › примеры › неявное дифференцирование…

Производные. Найдите dx/dy. (x−y)2=x+y−1 ( x — y ) 2 = x + y — 1. Шаг 1. Дифференцируем обе части уравнения. ddy((x−y)2)=ddy(x+y−1) d d y ( ( x — y ) …

Нахождение производной с помощью фундаментальной теоремы исчисления

www.mathway.com › применения дифференцирования

Ищете английскую версию Mathway? Мэтуэй. Посетите Mathway в Интернете. Скачать бесплатно в Google Play. Скачать бесплатно в iTunes. Скачать бесплатно на Амазоне.

Примеры вычислений | Поиск производной с помощью правила произведения

www.mathway.com › исчисление › производные › поиск…

Ищете английскую версию Mathway? Мэтуэй. Посетите Mathway в Интернете. Скачать бесплатно в Google Play. Скачать бесплатно в iTunes. Скачать бесплатно на Амазоне.

Примеры вычислений | производные | Нахождение производной — Mathway

www.mathway.com › примеры › нахождение производной…

Бесплатное средство решения математических задач отвечает на ваши домашние вопросы по алгебре, геометрии, тригонометрии, исчислению и статистике с пошаговыми инструкциями объяснения, .