Производные по направлению градиент: 4.1.3. Производная по направлению. Градиент

Содержание

4.1.3. Производная по направлению. Градиент

Пусть функция U = F (X, Y, Z) непрерывна в некоторой области D и имеет в этой области непрерывные частные производные. Выберем в рассматриваемой области точку M(X,Y,Z) и проведем из нее вектор S, направляющие косинусы которого cosA, cosB, cosG. На векторе S на расстоянии DS от его начала найдем точку М1(Х+DХ, у+DУ, Z+DZ), где

Представим полное приращение функции F в виде:

После деления на ΔS получаем:

Поскольку

Предыдущее равенство можно переписать в виде:

Предел отношения

Называется Производной от функции U = F (

X, Y, Z) По направлению вектора S и обозначается

При этом

Замечание 1. Частные производные являются частным случаем производной по направлению. Например, при

Получаем:

Замечание 2. Выше определялся геометрический смысл частных производных функции двух переменных как угловых коэффициентов касательных к линиям пересечения поверхности, являющейся графиком функции, с плоскостями Х = х0 И У = у0. Аналогичным образом можно рассматривать производную этой функции по направлению L в точке М(х0 , у0) как угловой коэффициент линии пересечения данной поверхности и плоскости, проходящей через точку М параллельно оси OZ и прямой L.

Вектор, координатами которого в каждой точке некоторой области являются частные производные функции U = F (X, Y, Z) в этой точке, называется Градиентом функции U = F (X, Y, Z).

Обозначение:

Свойства градиента

1. Производная по направлению некоторого вектора S Равняется проекции вектора grad U на вектор S.

Доказательство.

Единичный вектор направления S имеет вид ES ={cosα, cosβ, cosγ}, поэтому правая часть формулы (4.7) представляет собой скалярное произведение векторов grad U и Es, то есть указанную проекцию.

2. Производная в данной точке по направлению вектора

S имеет наибольшее значение, равное |grad U |, если это направление совпадает с направлением градиента.

Доказательство.

Обозначим угол между векторами S И grad U Через J. Тогда из свойства 1 следует, что

Следовательно, ее наибольшее значение достигается при J=0 и равно |gradU|.

3. Производная по направлению вектора, перпендикулярного к вектору grad U , равна нулю.

Доказательство.

В этом случае

4. Если Z = F (X,Y) – функция двух переменных, то

Направлен перпендикулярно к линии уровня F (X,Y) = C, проходящей через данную точку.

< Предыдущая		Следующая >

Математический анализ. Начальный курс

Ильин В. А. и др. Математический анализ. Начальный курс/В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Под ред. А. Н. Тихонова,— 2-е изд., перераб., — М.: Изд-во МГУ, 1985. — 662 с.

Учебник представляет собой первую часть трехтомного курса математического анализа для высших учебных заведений СССР, Болгарии и Венгрии, написанного в соответствии с соглашением о сотрудничестве между Московским, Софийским и Будапештским университетами. Книга включает в себя теорию вещественных чисел, теорию пределов, теорию непрерывности функций, дифференциальное и интегральное исчисления функций одной переменной и их приложения, дифференциальное исчисление функций многих переменных и теорию неявных функций.

ПРЕДИСЛОВИЕ ТИТУЛЬНОГО РЕДАКТОРА
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА
Глава 2. ВЕЩЕСТВЕННЫЕ ЧИСЛА
2. Недостаточность рациональных чисел для измерения отрезков числовой оси.
3. Упорядочение множества бесконечных десятичных дробей.
§ 2. ОГРАНИЧЕННЫЕ СВЕРХУ (ИЛИ СНИЗУ) МНОЖЕСТВА ЧИСЕЛ, ПРЕДСТАВИМЫХ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ
2. Существование точных граней.
§ 3. ПРИБЛИЖЕНИЕ ЧИСЕЛ, ПРЕДСТАВИМЫХ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ, РАЦИОНАЛЬНЫМИ ЧИСЛАМИ
§ 4. ОПЕРАЦИИ СЛОЖЕНИЯ И УМНОЖЕНИЯ. ОПИСАНИЕ МНОЖЕСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ
2. Существование и единственность суммы и произведения вещественных чисел.

§ 5. СВОЙСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ
2. Некоторые часто употребляемые соотношения.
3. Некоторые конкретные множества вещественных чисел.
§ 6. ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
2. Аксиоматическое введение множества вещественных чисел.
§ 7. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
2. Операции над множествами.
3. Счетные и несчетные множества. Несчетность сегмента [0, 1]. Мощность множества.
4. Свойства операций над множествами. Отображение множеств.
Глава 3. ТЕОРИЯ ПРЕДЕЛОВ
§ 1. ПОСЛЕДОВАТЕЛЬНОСТЬ И ЕЕ ПРЕДЕЛ
2. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности.
3. Основные свойства бесконечно малых последовательностей.
4. Сходящиеся последовательности и их свойства.
§ 2. МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
2. Теорема о сходимости монотонной ограниченной последовательности.
4. Примеры сходящихся монотонных последовательностей.
§ 3. ПРОИЗВОЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ

2. Расширение понятий предельной точки и верхнего и нижнего пределов.

3. Критерий Коши сходимости последовательности.
§ 4. ПРЕДЕЛ (ИЛИ ПРЕДЕЛЬНОЕ ЗНАЧЕНИЕ) ФУНКЦИИ
2. Предел функции по Гейне и по Коши.
3. Критерий Коши существования предела функции.
4. Арифметические операции над функциями, имеющими предел.
5. Бесконечно малые и бесконечно большие функции.
§ 5. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ ПО БАЗЕ
Глава 4. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
§ 1. ПОНЯТИЕ НЕПРЕРЫВНОСТИ ФУНКЦИИ
2. Арифметические операции над непрерывными функциями.
3. Сложная функция и ее непрерывность.
§ 2. СВОЙСТВА МОНОТОННЫХ ФУНКЦИЙ
2. Понятие обратной функции.
§ 3. ПРОСТЕЙШИЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
2. Логарифмическая функция.
3. Степенная функция.
4. Тригонометрические функции.
5. Обратные тригонометрические функции.
6. Гиперболические функции.

§ 4. ДВА ЗАМЕЧАТЕЛЬНЫХ ПРЕДЕЛА
2. Второй замечательный предел.
§ 5. ТОЧКИ РАЗРЫВА ФУНКЦИИ И ИХ КЛАССИФИКАЦИЯ
2. О точках разрыва монотонной функции.
§ 6. ЛОКАЛЬНЫЕ И ГЛОБАЛЬНЫЕ СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ
2.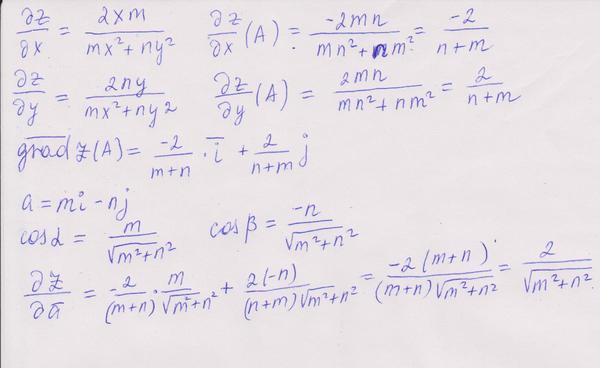

Глобальные свойства непрерывных функций.
3. Понятие равномерной непрерывности функции.
4. Понятие модуля непрерывности функции.
§ 7. ПОНЯТИЕ КОМПАКТНОСТИ МНОЖЕСТВА
2. О покрытиях множества системой открытых множеств.
3. Понятие компактности множества.
Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
§ 1. ПОНЯТИЕ ПРОИЗВОДНОЙ
2. Определение производной.
3. Геометрический смысл производной.
§ 2. ПОНЯТИЕ ДИФФЕРЕНЦИРУЕМОСТИ ФУНКЦИИ
2. Дифференцируемость и непрерывность.
3. Понятие дифференциала функции.
§ 3. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ И ОБРАТНОЙ ФУНКЦИИ
2. Дифференцирование обратной функции.
3. Инвариантность формы первого дифференциала.
4. Применение дифференциала для установления приближенных формул.
§ 4. ДИФФЕРЕНЦИРОВАНИЕ СУММЫ, РАЗНОСТИ, ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ФУНКЦИЙ
§ 5. ПРОИЗВОДНЫЕ ПРОСТЕЙШИХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
2. Производная логарифмической функции.
3. Производные показательной и обратных тригонометрических функций.

4. Производная степенной функции.
5. Таблица производных простейших элементарных функций.
6. Таблица дифференциалов простейших элементарных функций.
7. Логарифмическая производная. Производная степенно-показательной функции.
§ 6. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
2. n-ые производные некоторых функций.
3. Формула Лейбница для n-й производной произведения двух функций.
4. Дифференциалы высших порядков.
§ 7. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ
§ 8. ПРОИЗВОДНАЯ ВЕКТОРНОЙ ФУНКЦИИ

Глава 6. ОСНОВНЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
§ 1. ВОЗРАСТАНИЕ (УБЫВАНИЕ) ФУНКЦИИ В ТОЧКЕ. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ
§ 2. ТЕОРЕМА О НУЛЕ ПРОИЗВОДНОЙ
§ 3. ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ (ФОРМУЛА ЛАГРАНЖА)
§ 4. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ФОРМУЛЫ ЛАГРАНЖА
2. Условия монотонности функции на интервале.
3. Отсутствие разрывов первого рода и устранимых разрывов у производной.
4. Вывод некоторых неравенств.
§ 5. ОБОБЩЕННАЯ ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ (ФОРМУЛА КОШИ)
§ 6.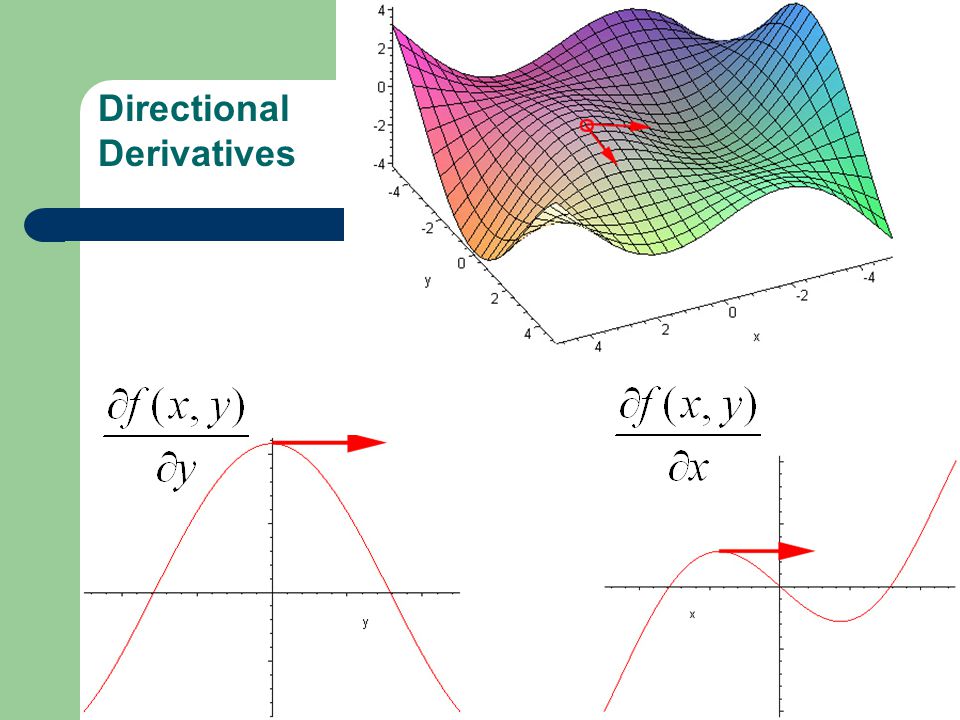

РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ (ПРАВИЛО ЛОПИТАЛЯ)
2. Раскрытие неопределенности вида oo/oo
3. Раскрытие неопределенностей других видов.
§ 7. ФОРМУЛА ТЕЙЛОРА
§ 8. РАЗЛИЧНЫЕ ФОРМЫ ОСТАТОЧНОГО ЧЛЕНА. ФОРМУЛА МАКЛОРЕНА
2. Другая запись формулы Тейлора.
3. Формула Маклорена.
§ 9. ОЦЕНКА ОСТАТОЧНОГО ЧЛЕНА. РАЗЛОЖЕНИЕ НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
2. Разложение по формуле Маклорена некоторых элементарных функций.
§ 10. ПРИМЕРЫ ПРИЛОЖЕНИЙ ФОРМУЛЫ МАКЛОРЕНА
2. Доказательство иррациональности числа е.
3. Вычисление значений тригонометрических функций.
4. Асимптотическая оценка элементарных функций и вычисление пределов.
Глава 7. ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ И ОТЫСКАНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИИ
§ 1. ОТЫСКАНИЕ СТАЦИОНАРНЫХ ТОЧЕК
2. Отыскание стационарных точек.
3. Первое достаточное условие экстремума.
4. Второе достаточное условие экстремума.
5. Третье достаточное условие, экстремума.
6. Экстремум функции, недифференцируемой в данной точке.

7. Общая схема отыскания экстремумов.
§ 2. ВЫПУКЛОСТЬ ГРАФИКА ФУНКЦИИ
§ 3. ТОЧКИ ПЕРЕГИБА
2. Первое достаточное условие перегиба.
3. Некоторые обобщения первого достаточного условия перегиба.
4. Второе достаточное условие перегиба.
5. Третье достаточное условие перегиба.
§ 4. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
§ 6. ГЛОБАЛЬНЫЕ МАКСИМУМ И МИНИМУМ ФУНКЦИИ НА СЕГМЕНТЕ. КРАЕВОЙ ЭКСТРЕМУМ
2. Краевой экстремум.
3. Теорема Дарбу.
ДОПОЛНЕНИЕ
Алгоритм отыскания экстремальных значений функции, использующий только значения этой функции
Глава 8. ПЕРВООБРАЗНАЯ ФУНКЦИЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ И НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
2. Неопределенный интеграл.
3. Основные свойства неопределенного интеграла.
4. Таблица основных неопределенных интегралов.
§ 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
2. Интегрирование по частям.
§ 3. КЛАССЫ ФУНКЦИЙ, ИНТЕГРИРУЕМЫХ в ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
2. Краткие сведения о корнях алгебраических многочленов.

3. Разложение алгебраического многочлена с вещественными коэффициентами на произведение неприводимых множителей.
4. Разложение правильной рациональной дроби на сумму простейших дробей.
5. Интегрируемость рациональной дроби в элементарных функциях.
6. Интегрируемость в элементарных функциях некоторых тригонометрических и иррациональных выражений.
§ 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ
Глава 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА
ИНТЕГРАЛ РИМАНА: § 2. ВЕРХНИЕ И НИЖНИЕ СУММЫ И ИХ СВОЙСТВА
2. Основные свойства верхних и нижних сумм.
§ 3. ТЕОРЕМЫ О НЕОБХОДИМЫХ И ДОСТАТОЧНЫХ УСЛОВИЯХ ИНТЕГРИРУЕМОСТИ ФУНКЦИЙ. КЛАССЫ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ
2. Классы интегрируемых функций.
§ 4. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. ОЦЕНКИ ИНТЕГРАЛОВ. ТЕОРЕМЫ О СРЕДНЕМ ЗНАЧЕНИИ
2. Оценки интегралов.
§ 5. ПЕРВООБРАЗНАЯ НЕПРЕРЫВНОЙ ФУНКЦИИ. ПРАВИЛА ИНТЕГРИРОВАНИЯ ФУНКЦИЙ
2. Основная формула интегрального исчисления.
3. Важные правила, позволяющие вычислять определенные интегралы.

4. Остаточный член формулы Тейлора в интегральной форме.
§ 6. НЕРАВЕНСТВА ДЛЯ СУММ И ИНТЕГРАЛОВ
2. Неравенство Гёльдера для сумм.
3. Неравенство Минковского для сумм.
4. Неравенство Гёльдера для интегралов.
5. Неравенство Минковского для интегралов.
§ 7. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ РИМАНА
2. Критерий интегрируемости Лебега.
ДОПОЛНЕНИЕ 1. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
2. Критерий Коши сходимости несобственного интеграла первого рода.
3. Абсолютная и условная сходимость несобственных интегралов.
4. Замена переменных под знаком несобственного интеграла и формула интегрирования по частям.
§ 2. Несобственные интегралы второго рода
§ 3. Главное значение несобственного интеграла
ДОПОЛНЕНИЕ 2. Интеграл Стилтьеса
2. Свойства интеграла Стилтьеса.
Глава 10. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
§ 1. ДЛИНА ДУГИ КРИВОЙ
2. Понятие параметризуемой кривой.
3. Длина дуги кривой. Понятие спрямляемой кривой.

m.
3. Предел функции m переменных.
4. Бесконечно малые функции m переменных.
5. Повторные пределы.
§ 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ m ПЕРЕМЕННЫХ
2. Непрерывность функции m переменных по одной переменной.
3. Основные свойства непрерывных функций нескольких переменных.
§ 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
2. Дифференцируемость функции нескольких переменных.
3. Геометрический смысл условия дифференцируемости функции двух переменных.
4. Достаточные условия дифференцируемости.
5. Дифференциал функции нескольких переменных.
6. Дифференцирование сложной функции.
7. Инвариантность формы первого дифференциала.
8. Производная по направлению. Градиент.
§ 5. ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
2. Дифференциалы высших порядков.
3. Формула Тейлора с остаточным членом в форме Лагранжа и в интегральной форме.
4. Формула Тейлора с остаточным членом в форме Пеано.
§ 6. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ m ПЕРЕМЕННЫХ
2.

Достаточные условия локального экстремума функции m переменных.
3. Случай функции двух переменных.
ДОПОЛНЕНИЕ 1. Градиентный метод поиска экстремума сильно выпуклой функции
1. Выпуклые множества и выпуклые функции.
2. Существование минимума у сильно выпуклой функции и единственность минимума у строго выпуклой функции.
3. Поиск минимума сильно выпуклой функции.
ДОПОЛНЕНИЕ 2. Метрические, нормированные пространства
2. Открытые и замкнутые множества.
3. Прямое произведение метрических пространств.
4. Всюду плотные и совершенные множества.
5. Сходимость. Непрерывные отображения.
6. Компактность.
7. Базис пространства.
Топологические пространства
Линейные нормированные пространства, линейные операторы
ДОПОЛНЕНИЕ 3. Дифференциальное исчисление в линейных нормированных пространствах
2. Формула Лагранжа конечных приращений.
3. Связь между слабой и сильной дифференцируемостью.
4. Дифференцируемость функционалов.
5. Интеграл от абстрактных функций.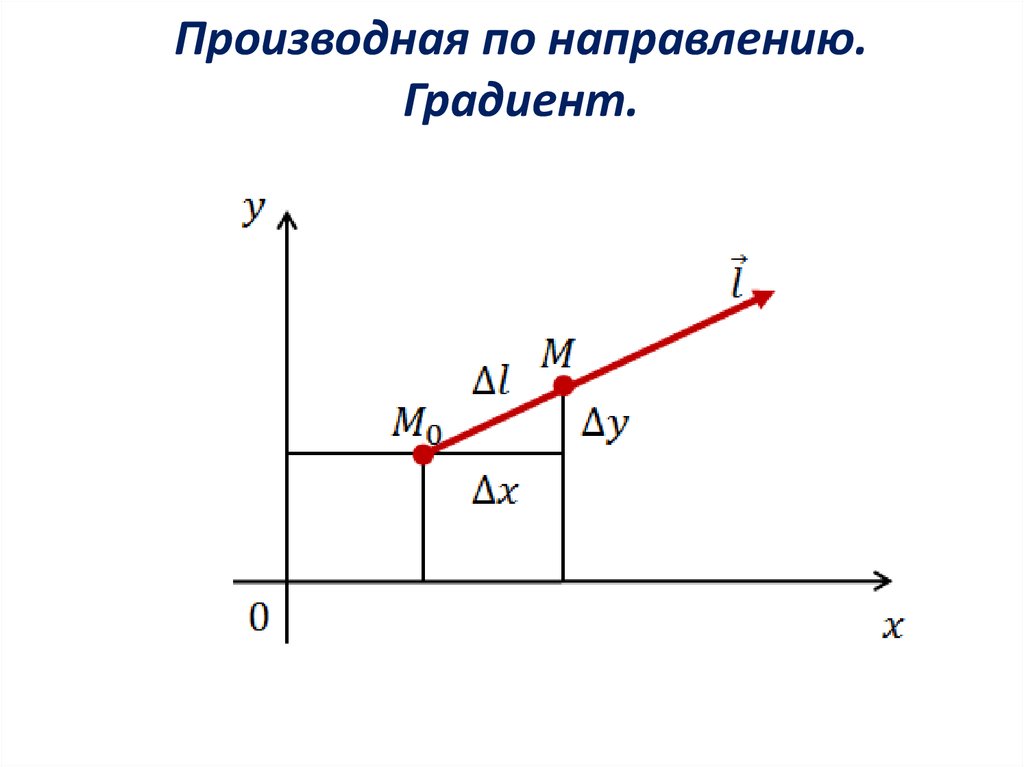

6. Формула Ньютона — Лейбница для абстрактных функций.
7. Производные второго порядка.
8. Отображение m-мерного евклидова пространства в n-мерное.
9. Производные и дифференциалы высших порядков.
10. Формула Тейлора для отображений одного нормированного пространства в другое.
Исследование на экстремум функционалов в нормированных пространствах
2. Достаточные условия экстремума.
Глава 13. НЕЯВНЫЕ ФУНКЦИИ
§ 1. СУЩЕСТВОВАНИЕ И ДИФФЕРЕНЦИРУЕМОСТЬ НЕЯВНО ЗАДАННОЙ ФУНКЦИИ
2. Вычисление частных производных неявно заданной функции.
3. Особые точки поверхности и плоской кривой.
4. Условия, обеспечивающие существование для функции y=f(x) обратной функции.
§ 2. НЕЯВНЫЕ ФУНКЦИИ, ОПРЕДЕЛЯЕМЫЕ СИСТЕМОЙ ФУНКЦИОНАЛЬНЫХ УРАВНЕНИЙ
2. Вычисление частных производных функций, неявно определяемых посредством системы функциональных уравнений.
3. Взаимно однозначное отображение двух множеств m-мерного пространства.
§ 3. ЗАВИСИМОСТЬ ФУНКЦИЙ
2. Функциональные матрицы и их приложения.

§ 4. УСЛОВНЫЙ ЭКСТРЕМУМ
2. Метод неопределенных множителей Лагранжа.
3. Достаточные условия.
4. Пример.
ДОПОЛНЕНИЕ
Отображения банаховых пространств. Аналог теоремы о неявной функции
2. Случай конечномерных пространств.
3. Особые точки поверхности в пространстве n измерений. Обратное отображение.
4. Условный экстремум в случае отображений нормированных пространств.

Производные по направлению и градиент · Исчисление

Определить производную по заданному направлению для функции двух переменных.
Определить вектор градиента заданной функции с действительным знаком.
Объясните значение вектора градиента в отношении направления изменения вдоль поверхности.
Используйте градиент, чтобы найти касательную к кривой уровня заданной функции.
Расчет производных по направлению и градиентов в трех измерениях.

В разделе «Частные производные» мы ввели частную производную. Функция z=f(x,y)

имеет две частные производные: ∂z/∂x

и ∂z/∂y.

Эти производные соответствуют каждой из независимых переменных и могут быть интерпретированы как мгновенные скорости изменения (то есть как наклоны касательной). Например, ∂z/∂x

представляет наклон касательной, проходящей через заданную точку на поверхности, определяемой z=f(x,y),

, предполагая, что касательная параллельна оси x . Точно так же ∂z/∂y

представляет собой наклон касательной, параллельной оси Y.

Теперь рассмотрим возможность касательной, параллельной ни одной из осей.

Направленные производные

Начнем с графика поверхности, определяемой уравнением z=f(x,y).

Дана точка (a,b)

в домене f,

мы выбираем направление движения из этой точки. Измеряем направление с помощью угла θ,

, который измеряется против часовой стрелки в плоскости x , y , начиная с нуля от положительной оси x ([ссылка]). Расстояние, которое мы проходим, равно h

, а направление, в котором мы движемся, задается единичным вектором u=(cosθ)i+(sinθ)j.

Следовательно, координата z второй точки на графике задается как z=f(a+hcosθ,b+hsinθ).

Мы можем рассчитать наклон секущей, разделив разницу значений z на

на длину отрезка, соединяющего две точки домена. Длина отрезка равна h.

Следовательно, наклон секущей равен

мс=f(a+hcosθ,b+hsinθ)−f(a,b)h.

Чтобы найти наклон касательной в том же направлении, мы принимаем предел как h

приближается к нулю.

Определение

Предположим, что z=f(x,y)

является функцией двух переменных с областью определения D.

Пусть (a,b)∈D

и определить u=cosθi+sinθj.

Тогда производная по направлению от f

в направлении u

определяется выражением

Duf(a,b)=limh→0f(a+hcosθ,b+hsinθ)−f(a,b) h,

при наличии ограничения.

[ссылка] дает формальное определение производной по направлению, которое во многих случаях можно использовать для расчета производной по направлению.

Нахождение производной по направлению из определения

Пусть θ=arccos(3/5).

Найдите производную по направлению Duf(x,y)

от f(x,y)=x2−xy+3y2

в направлении u=(cosθ)i+(sinθ)j.

Что такое Duf(−1,2)?

Прежде всего, поскольку cosθ=3/5

и θ

является острым, отсюда следует

sinθ=1−(35)2=1625=45.

Используя f(x,y)=x2−xy+3y2,

, мы сначала вычисляем f(x+hcosθ,y+hsinθ):

f(x+hcosθ,y+hsinθ)=(x+hcosθ) 2−(x+hcosθ)(y+hsinθ)+3(y+hsinθ)2=x2+2xhcosθ+h3cos2θ−xy−xhsinθ−yhcosθ−h3sinθcosθ+3y2+6yhsinθ+3h3sin2θ=x2+2xh(35)+9h325-xy-4xh5-3yh5-12h325+3y2+6yh(45)+3h3(1625)=x2-xy+3y2+2xh5+9h35+21yh5.

Подставляем это выражение в [ссылка]:

Duf(a,b)=limh→0f(a+hcosθ,b+hsinθ)−f(a,b)h=limh→0(x2−xy+3y2 +2xh5+9h35+21yh5)−(x2−xy+3y2)h=limh→02xh5+9h35+21yh5h=limh→02×5+9h5+21y5=2x+21y5.

Чтобы вычислить Duf(−1,2),

, подставим x=−1

и y=2

в этот ответ:

Duf(−1,2)=2(−1)+21( 2)5=-2+425=8.

(см. следующий рисунок)

Другой подход к вычислению производной по направлению включает частные производные, как указано в следующей теореме.

Производная по направлению функции двух переменных

Пусть z=f(x,y)

будет функцией двух переменных xandy,

, и предположим, что fx

и fy

существуют. Тогда производная по направлению от f

в направлении u=cosθi+sinθj

определяется как

Duf(x,y)=fx(x,y)cosθ+fy(x,y)sinθ.

Доказательство

[ссылка] утверждает, что производная по направлению от f в направлении u=cosθi+sinθj

дается

Duf(a,b)=limt→0f(a+tcosθ,b+tsinθ)−f(a,b)t.

Пусть x=a+tcosθ

и y=b+tsinθ,

и определить g(t)=f(x,y).

Начиная с FX

ф.г.

существуют, мы можем использовать цепное правило для функций двух переменных для вычисления g′(t):

g′(t)=∂f∂xdxdt+∂f∂ydydt=fx(x,y)cosθ+fy(x,y)sinθ.

Если t=0,

, тогда х=х0

и у=у0,

так

g′(0)=fx(x0,y0)cosθ+fy(x0,y0)sinθ.

По определению g′(t),

верно и то, что

g′(0)=limt→0g(t)−g(0)t=limt→0f(x0+tcosθ,y0+tsinθ)−f(x0,y0)t.

Следовательно, Duf(x0,y0)=fx(x,y)cosθ+fy(x,y)sinθ.

□

Нахождение производной по направлению: альтернативный метод

Пусть θ=arccos(3/5).

Найти производную по направлению Duf(x,y)

от f(x,y)=x2−xy+3y2

в направлении u=(cosθ)i+(sinθ)j.

Что такое Duf(−1,2)?

Сначала мы должны вычислить частные производные f:

fx=2x−yfy=−x+6y,

Затем мы используем [ссылка] с θ=arccos(3/5):

Duf(x, y)=fx(x,y)cosθ+fy(x,y)sinθ=(2x−y)35+(−x+6y)45=6×5−3y5−4×5+24y5=2x+21y5.

Для вычисления Duf(−1,2),

пусть x=−1

и y=2:

Duf(−1,2)=2(−1)+21(2)5=−2 +425=8.

Это тот же ответ, полученный в [ссылка].

Найдите производную по направлению Duf(x,y)

от f(x,y)=3x2y−4xy3+3y2−4x

в направлении u=(cosπ3)i+(sinπ3)j

, используя [ссылка] . Что такое Дуф(3,4)?

Duf(x,y)=(6xy−4y3−4)(1)2+(3×2−12xy2+6y)32Duf(3,4)=72−256−42+(27−576+24)32= −94−52532

Подсказка

Вычислите частные производные и определите значение θ.

Если вектор, заданный для направления производной, не является единичным вектором, то делить нужно только на норму вектора. Например, если мы хотим найти производную по направлению функции из [ссылка] в направлении вектора 〈−5,12〉,

мы должны сначала разделить на его величину, чтобы получить u.

Это дает нам u=〈−(5/13),12/13〉.

Затем

Duf(x,y)=∇f(x,y)·u=−513(2x−y)+1213(−x+6y)=−2213x+1713y.

Градиент

Правая часть [ссылки] равна fx(x,y)cosθ+fy(x,y)sinθ,

, которое можно записать как скалярное произведение двух векторов. Определим первый вектор как ∇f(x,y)=fx(x,y)i+fy(x,y)j

и второй вектор как u=(cosθ)i+(sinθ)j.

Тогда правая часть уравнения может быть записана как скалярное произведение этих двух векторов:

Duf(x,y)=∇f(x,y)·u.

Первый вектор в [ссылка] имеет специальное имя: градиент функции f.

Символ ∇

называется набла , а вектор ∇f

читается как «дельф».

Определение

Пусть z=f(x,y)

будет функцией xandy

такой, что fx

и fy

существуют. Вектор ∇f(x,y)

называется градиентом f

и определяется как

∇f(x,y)=fx(x,y)i+fy(x,y)j.

Вектор ∇f(x,y)

также записывается как «gradf».

Поиск градиентов

Найдите градиент ∇f(x,y)

каждой из следующих функций:

f(x,y)=x2−xy+3y2
f(x,y)=sin3xcos3y

Для обеих частей a. и б., мы сначала вычисляем частные производные fx

и fy,

, затем используем [ссылка].

fx(x,y)=2x−yandfy(x,y)=−x+6y, поэтому∇f(x,y)=fx(x,y)i+fy(x,y)j=(2x− у)i+(−x+6y)j.
fx(x,y)=3cos3xcos3yandfy(x,y)=-3sin3xsin3y, поэтому∇f(x,y)=fx(x,y)i+fy(x,y)j=(3cos3xcos3y)i-(3sin3xsin3y )ж.

Найдите градиент ∇f(x,y)

функции f(x,y)=(x2−3y2)/(2x+y).

∇f(x,y)=2×2+2xy+6y2(2x+y)2i−x2+12xy+3y2(2x+y)2j

Подсказка

Вычислите частные производные, затем используйте [ссылка].

Градиент имеет несколько важных свойств. Мы уже видели одну формулу, использующую градиент: формулу для производной по направлению. Вспомните из скалярного произведения, что если угол между двумя векторами равен

и б

это φ,

, то a·b=‖a‖‖b‖cosφ.

Следовательно, если угол между ∇f(x0,y0)

и u=(cosθ)i+(sinθ)j

это φ,

у нас есть

Duf(x0,y0)=∇f(x0,y0)·u=‖∇f(x0,y0)‖‖u‖cosφ=‖∇f(x0,y0)‖cosφ.

‖у‖

исчезает, потому что ты

— единичный вектор. Следовательно, производная по направлению равна величине градиента, оцененной в (x0,y0)

умножить на cosφ.

Напомним, что cosφ

колеблется от -1

до 1.

Если φ=0,

тогда cosφ=1

и ∇f(x0,y0)

и у

оба указывают в одном направлении. Если φ=π,

, тогда cosφ=−1

и ∇f(x0,y0)

и у

точки в противоположных направлениях. В первом случае значение Duf(x0,y0)

развернуто; во втором случае значение Duf(x0,y0)

свернуто. Если ∇f(x0,y0)=0,

, то Duf(x0,y0)=∇f(x0,y0)·u=0

для любого вектора u.

Эти три случая изложены в следующей теореме.

Свойства градиента

Предположим, что функция z=f(x,y)

дифференцируема в точке (x0,y0)

([ссылка]).

Если ∇f(x0,y0)=0,
, затем
Duf(x0,y0)=0
для любого единичного вектора
ты
Если ∇f(x0,y0)≠0,
, затем
Duf(x0,y0)
максимизируется, когда
u
указывает в том же направлении, что и
∇f(x0,y0).
Максимальное значение
Duf(x0,y0)
равно
‖∇f(x0,y0)‖.
Если ∇f(x0,y0)≠0,
, затем
Duf(x0,y0)
минимизируется, когда
u
точек в противоположном направлении от
∇f(x0,y0).
Минимальное значение
Duf(x0,y0)
равно
−‖∇f(x0,y0)‖.

Нахождение максимальной производной по направлению

Найдите направление, для которого производная по направлению от f(x,y)=3×2−4xy+2y2

при (−2,3)

является максимальной. Каково максимальное значение?

Максимальное значение производной по направлению возникает, когда ∇f

и единичный вектор указывают в одном направлении. Поэтому начнем с вычисления ∇f(x,y):

fx(x,y)=6x−4yandfy(x,y)=−4x+4y, поэтому∇f(x,y)=fx(x, y)i+fy(x,y)j=(6x−4y)i+(−4x+4y)j.

Затем мы оцениваем градиент в (−2,3):

∇f(−2,3)=(6(−2)−4(3))i+(−4(−2)+4(3))j=−24i+20j.

Нам нужно найти единичный вектор, который указывает в том же направлении, что и ∇f(−2,3),

, поэтому следующим шагом будет деление ∇f(−2,3)

на его величину, которая равна (−24)2+(20)2=976=461.

Следовательно,

∇f(−2,3)‖∇f(−2,3)‖=−24461i+20461j=−66161i+56161j.

Это единичный вектор, который указывает в том же направлении, что и ∇f(−2,3).

Чтобы найти угол, соответствующий этому единичному вектору, решим уравнения

cosθ=-66161andsinθ=56161

для θ.

Поскольку косинус отрицательный, а синус положительный, угол должен лежать во втором квадранте. Следовательно, θ=π−arcsin((561)/61)≈2,45 рад.

Максимальное значение производной по направлению в точке (−2,3)

равно ‖∇f(−2,3)‖=461

(см. следующий рисунок).

Найдите направление, для которого производная по направлению g(x,y)=4x−xy+2y2

при (−2,3)

является максимальной. Каково максимальное значение?

Градиент g

в точке (−2,3)

равен ∇g(−2,3)=i+14j.

Единичный вектор, который указывает в том же направлении, что и ∇g(−2,3)

, равен ∇g(−2,3)‖∇g(−2,3)‖=1197i+14197j=197197i+14197197j,

, что дает угол θ=arcsin((14197)/197)≈1,499 рад.

Максимальное значение производной по направлению составляет ‖∇g(−2,3)‖=197.

Подсказка

Оцените градиент g

в точке (−2,3).

[ссылка] показывает часть графика функции f(x,y)=3+sinxsiny.

Дана точка (a,b)

в домене f,

максимальное значение градиента в этой точке определяется выражением ‖∇f(a,b)‖.

Это было бы равно скорости наибольшего подъема, если бы поверхность представляла собой топографическую карту. Если бы мы пошли в противоположном направлении, это была бы скорость наибольшего спуска.

При использовании топографической карты самый крутой склон всегда находится в том направлении, где горизонтали ближе всего друг к другу (см. [ссылка]). Это аналогично контурной карте функции, если предположить, что кривые уровня получены для равноотстоящих значений во всем диапазоне этой функции.

Градиенты и кривые уровня

Напомним, что если кривая параметрически задана парой функций (x(t),y(t)),

, то вектор x′(t)i+y′(t)j

касается кривой для каждого значения t

в домене. Теперь предположим, что z=f(x,y)

— дифференцируемая функция xandy,

и (x0,y0)

находится в его домене. Предположим далее, что x0=x(t0)

и y0=y(t0)

для некоторого значения t,

и рассмотрим кривую уровня f(x,y)=k.

Определить g(t)=f(x(t),y(t))

и вычислить g′(t)

на кривой уровня. По правилу цепи,

g′(t)=fx(x(t),y(t))x′(t)+fy(x(t),y(t))y′(t).

Но g′(t)=0

, потому что g(t)=k

для всех т.

Следовательно, с одной стороны,

fx(x(t),y(t))x′(t)+fy(x(t),y(t))y′(t)=0;

с другой стороны,

fx(x(t),y(t))x′(t)+fy(x(t),y(t))y′(t)=∇f(x,y)·〈x′(t ),y′(t)〉.

Следовательно,

∇f(x,y)·〈x′(t),y′(t)〉=0.

Таким образом, скалярное произведение этих векторов равно нулю, что означает, что они ортогональны. Однако второй вектор касается кривой уровня, что означает, что градиент должен быть нормален к кривой уровня, что приводит к следующей теореме.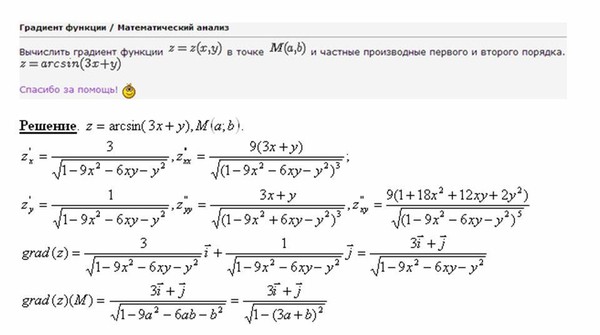

Градиент нормален к кривой уровня

Предположим, что функция z=f(x,y)

имеет непрерывные частные производные первого порядка в открытом круге с центром в точке (x0,y0).

Если ∇f(x0,y0)≠0,

, то ∇f(x0,y0)

нормальна кривой уровня f

в точке (x0,y0).

Мы можем использовать эту теорему, чтобы найти касательные и нормальные векторы к линиям уровня функции.

Нахождение касательных к кривым уровня

Для функции f(x,y)=2×2−3xy+8y2+2x−4y+4,

найти касательный вектор к кривой уровня в точке (−2,1).

Нарисуйте кривую уровня, соответствующую f(x,y)=18

, и начертите ∇f(−2,1)

и касательный вектор.

Сначала мы должны вычислить ∇f(x,y):

fx(x,y)=4x−3y+2andfy=−3x+16y−4so∇f(x,y)=(4x−3y+2 )i+(−3x+16y−4)j.

Затем мы оцениваем ∇f(x,y)

в точке (−2,1):

∇f(−2,1)=(4(−2)−3(1)+2)i+( −3(−2)+16(1)−4)j=−9i+18j.

Этот вектор ортогонален кривой в точке (−2,1).

Мы можем получить касательный вектор, поменяв местами компоненты и умножив любой из них на −1.

Так, например, −18i−9j

— касательный вектор (см. следующий график).

Для функции f(x,y)=x2−2xy+5y2+3x−2y+4,

найти касательную к кривой уровня в точке (1,1).

Нарисуйте график кривой уровня, соответствующей f(x,y)=8

, и нарисуйте ∇f(1,1)

и касательный вектор.

∇f(x,y)=(2x−2y+3)i+(−2x+10y−2)j

∇f(1,1)=3i+6j

Касательный вектор: 6i−3j

или −6i+3j

Подсказка

Рассчитать градиент в точке (1,1).

Трехмерные градиенты и производные по направлениям

Определение градиента можно распространить на функции более чем двух переменных.

Определение

Пусть w=f(x,y,z)

функция трех переменных такая, что существуют fx,fy,fz

. Вектор ∇f(x,y,z)

называется градиентом f

и определяется как

∇f(x,y,z)=fx(x,y,z)i+fy(x ,y,z)j+fz(x,y,z)k.

∇f(x,y,z)

также можно записать как gradf(x,y,z).

Вычисление градиента функции с тремя переменными очень похоже на вычисление градиента функции с двумя переменными. Сначала мы вычисляем частные производные fx,fy,

и фз,

, а затем используем [ссылка].

Поиск градиентов в трех измерениях

Найдите градиент ∇f(x,y,z)

каждой из следующих функций:

f(x,y)=5×2−2xy+y2−4yz+z2+3xz
f(x,y,z)=e−2zsin2xcos2y

Для обеих частей a. и б., мы сначала вычисляем частные производные fx,fy,

и fz,

, а затем используем [ссылка].

fz(x,y,z)=10x−2y+3z,fy(x,y,z)=−2x+2y−4zandfz(x,y,z)=3x−4y+2z, поэтому∇f(x ,y,z)=fx(x,y,z)i+fy(x,y,z)j+fz(x,y,z)k=(10x−2y+3z)i+(−2x+2y− 4z)j+(−4x+3y+2z)k.
fx(x,y,z)=−2e−2zcos2xcos2y,fy(x,y,z)=−2e−2zsin2xsin2yandfz(x,y,z)=−2e−2zsin2xcos2y, поэтому∇f(x,y,z )=fx(x,y,z)i+fy(x,y,z)j+fz(x,y,z)k=(2e−2zcos2xcos2y)i+(−2e−2z)j+(−2e−2z )=2e−2z(cos2xcos2yi−sin2xsin2yj−sin2xcos2yk).

Найдите градиент ∇f(x,y,z)

функции f(x,y,z)=x2−3y2+z22x+y−4z.

∇f(x,y,z)=2×2+2xy+6y2−8xz−2z2(2x+y−4z)2i−x2+12xy+3y2−24yz+z2(2x+y−4z)2j+4×2− 12y2−4z2+4xz+2yz(2x+y−4z)2k.

Производная по направлению также может быть обобщена на функции трех переменных. Чтобы определить направление в трех измерениях, необходим вектор с тремя компонентами. Этот вектор является единичным вектором, и компоненты единичного вектора называются направленными косинусами . Учитывая трехмерный единичный вектор u

в стандартной форме (т.е. начальная точка находится в начале координат), этот вектор образует три различных угла с положительными x−,y−,

и оси z-. Назовем эти углы α,β,

и γ.

Тогда косинусы направления задаются как cosα,cosβ,

и cosγ.

Это компоненты единичного вектора u;

— единичный вектор, верно, что cos2α+cos2β+cos2γ=1.

Определение

Предположим, что w=f(x,y,z)

является функцией трех переменных с областью определения D.

Пусть (x0,y0,z0)∈D

и пусть u=cosαi+cosβj +cosγk

— единичный вектор. Тогда производная по направлению от f

в направлении u

определяется как

Duf(x0,y0,z0)=limt→0f(x0+tcosα,y0+tcosβ,z0+tcosγ)−f(x0 ,y0,z0)t,

при условии существования предела.

Мы можем вычислить производную по направлению функции трех переменных, используя градиент, что приводит к формуле, аналогичной [ссылка].

Производная по направлению функции трех переменных

Пусть f(x,y,z)

— дифференцируемая функция трех переменных, а u=cosαi+cosβj+cosγk

— единичный вектор. Тогда производная по направлению от f

в направлении u

определяется выражением

Duf(x,y,z)=∇f(x,y,z)·u=fx(x,y,z) cosα+fy(x,y,z)cosβ+fz(x,y,z)cosγ.

Три угла α,β иγ

определяют единичный вектор u.

На практике мы можем использовать произвольный (неединичный) вектор, а затем разделить его на его величину, чтобы получить единичный вектор в нужном направлении.

Нахождение производной по направлению в трех измерениях

Вычислить Duf(1,−2,3)

в направлении v=−i+2j+2k

для функции

f(x,y,z)= 5×2−2xy+y2−4yz+z2+3xz.

Сначала находим величину v:

‖v‖=(−1)2+(2)2=3.

Следовательно, v‖v‖=−i+2j+2k3=−13i+23j+23k

является единичным вектором в направлении v,

, так что cosα=−13,cosβ=23 и cosγ=23.

Далее вычисляем частные производные от f:

fx(x,y,z)=10x−2y+3zfy(x,y,z)=−2x+2y−4zfz(x,y,z)=−4y+2z+3x,

затем замените их в [ссылка]:

Duf(x,y,z)=fx(x,y,z)cosα+fy(x,y,z)cosβ+fz(x,y,z)cosγ=(10x−2y +3z)(-13)+(-2x+2y-4z)(23)+(-4y+2z+3x)(23)=-10×3+2y3-3z3-4×3+4y3-8z3-8y3+4z3+6×3 =-8×3-2y3-7z3.

Наконец, чтобы найти Duf(1,−2,3),

подставим x=1,y=−2,andz=3:

Duf(1,−2,3)=−8(1) 3−2(−2)3−7(3)3=−83+43−213=−253.

Вычислить Duf(x,y,z)

и Duf(0,−2,5)

в направлении v=−3i+12j−4k

для функции f(x,y,z)=3×2+xy−2y2+4yz−z2+2xz.

Duf(x,y,z)=−313(6x+y+2z)+1213(x−4y+4z)−413(2x+4y−2z)Duf(0,−2,5)=38413

Подсказка

Сначала разделите v

на его величину, вычислите частные производные f,

, затем используйте [ссылка].

Ключевые понятия

Производная по направлению представляет скорость изменения функции в любом заданном направлении.
Градиент можно использовать в формуле для расчета производной по направлению.
Градиент указывает направление наибольшего изменения функции более чем одной переменной.

Ключевые уравнения

производная по направлению (два измерения)
Duf(a,b)=limh→0f(a+hcosθ,b+hsinθ)−f(a,b)h

или

Duf(x,y)=fx(x,y)cosθ+fy(x,y)sinθ

градиент (два измерения)
∇f(x,y)=fx(x,y)i+fy(x,y)j
градиент (три измерения)
∇f(x,y,z)=fx(x,y,z)i+fy(x,y,z)j+fz(x,y,z)k
производная по направлению (три измерения)
Duf(x,y,z)=∇f(x,y,z)·u=fx(x,y,z)cosα+fy(x,y,z)cosβ+fx(x,y,z) cosγ

В следующих упражнениях найдите производную по направлению, используя только определение предела.

f(x,y)=5−2×2−12y2

в точке P(3,4)

в направлении u=(cosπ4)i+(sinπ4)j

f(x,y)=y2cos(2x)

в точке P(π3,2)

в направлении u=(cosπ4)i+(sinπ4)j

−33

Найдите производную по направлению от f(x,y)=y2sin(2x)

в точке P(π4,2)

в направлении u=5i+12j.

Для следующих упражнений найдите производную функции по направлению в точке P

в направлении д.

f(x,y)=xy,P(0,−2),v=12i+32j

−1

h(x,y)=exsiny,P(1,π2),v=−i

h(x,y,z)=xyz,P(2,1,1),v=2i+j−k

f(x,y)=xy,P(1,1),u=〈22,22〉

f(x,y)=x2−y2,u=〈32,12〉,P(1,0)

f(x,y)=3x+4y+7,u=〈35,45〉,P(0,π2)

f(x,y)=excosy,u=〈0,1〉,P=(0,π2)

−1,0

f(x,y)=y10,u=〈0,−1〉,P=(1,−1)

f(x,y)=ln(x2+y2),u=〈35,45〉,P(1,2)

2225

f(x,y)=x2y,P(−5,5),v=3i−4j

f(x,y)=y2+xz,P(1,2,2),v=〈2,−1,2〉

Для следующих упражнений найдите производную функции по направлению в направлении единичного вектора u=cosθi+sinθj.

f(x,y)=x2+2y2,θ=π6

f(x,y)=yx+2y,θ=−π4

−2(x+y)2(x+2y)2

f(x,y)=cos(3x+y),θ=π4

w(x,y)=yex,θ=π3

ex(y+3)2

f(x,y)=xarctan(y),θ=π2

f(x,y)=ln(x+2y),θ=π3

1+232(x+2y)

Для следующих упражнений найдите градиент.

Найдите градиент f(x,y)=14−x2−y23.

Затем найдите градиент в точке P(1,2).

Найдите градиент f(x,y,z)=xy+yz+xz

в точке P(1,2,3).

〈5,4,3〉

Найти градиент f(x,y,z)

в точке P

и в направлении u:

f(x,y,z)=ln(x2+2y2+3z2),P(2, 1,4),u=-313i-413j-1213k.

f(x,y,z)=4x5y2z3,P(2,−1,1),u=13i+23j−23k

−320

Для следующих упражнений найдите производную функции по направлению в точке P

в направлении Q.

f(x,y)=x2+3y2,P(1,1),Q(4,5)

f(x,y,z)=yx+z,P(2,1,−1),Q(−1,2,0)

311

Для следующих упражнений найдите производную функции в P

в сторону ул.

f(x,y)=−7x+2y,P(2,−4),u=4i−3j

f(x,y)=ln(5x+4y),P(3,9),u=6i+8j

31255

[T] С помощью технологии нарисуйте кривую уровня f(x,y)=4x−2y+3

, которая проходит через P(1,2)

, и нарисуйте вектор градиента в точке P.

[T] Используйте технологию, чтобы нарисовать кривую уровня f(x,y)=x2+4y2

, который проходит через P(−2,0)

, и нарисуйте вектор градиента в точке P.

![Верх половины эллипса с центром в начале координат с горизонтальной большой осью, длиной 4 и малой осью 2. Точка (–2, 0) отмечена, и от нее влево направлена стрелка, отмеченная –4i.](/calculus-book/resources/CNX_Calc_Figure_14_06_202.jpg)

Для следующих упражнений найдите вектор градиента в указанной точке.

f(x,y)=xy2−yx2,P(−1,1)

f(x,y)=xey−ln(x),P(−3,0)

43i−3j

f(x,y,z)=xy−ln(z),P(2,−2,2)

f(x,y,z)=xy2+z2,P(−2,−1,−1)

2i+2j+2k

Для следующих упражнений найдите производную функции.