2. Равенства и неравенства (введение терминов).
В первом классе дети знакомятся с понятиями «равенство» и «неравенство» и убеждаются в том, что равенства бывают верные и неверные.
1 способ – путем показа готовых равенств и неравенств (остенсивное определение).
2 способ – можно образовать равенства и неравенства путем сравнения двух произвольных выражений (генетическое определение).
Далее вводятся понятия «верные равенства и неравенства» и «неверные равенства и неравенства».
С целью усвоения понятий проводятся различные виды упражнений.
Задание 11. По учебнику М1 подобрать различные виды упражнений с целью усвоения этих понятий.
Формирование представлений об уравнении в начальном курсе математики. Методика обучения решению простейших уравнений.
Уравнение
в начальном курсе математики трактуется
как равенство, содержащее неизвестное
число, которое надо найти. Решить
уравнение — значит найти такое значение х,
при котором равенство будет верным.
Решить
уравнение — значит найти такое значение х,
при котором равенство будет верным.
В начальных классах учащиеся решают простейшие уравнения способом подбора и на основе правила зависимости между компонентами и результатами действий.
В формировании у младших школьников представлений об уравнении можно выделить следующие этапы:
I этап Состав числа | II этап Способ подбора | III этап Связь между компонентами и результатом действий | ||||
| +
3 = 7 5 – = 2 – 3 = 5 | х + 4 = 6 3 + х = 8 х – 5 = 2 9 – х = 4 | х + 12 = 20 43 + х = 60 25 – х = 10 х – 8 = 32 | х 3 = 21 5 х = 35 40 : х = 8 x : 4 = 7 | |||
I э т а п — подготовительный (при изучении нумерации чисел в пределах
10).
1. Способом подбора дети решают примеры с «окошками» (М-1, ч. 1, с. 84). В процессе выполнения таких упражнений дети привыкают к мысли, что неизвестным может быть не только сумма или разность (с. 56), но и одно из слагаемых (уменьшаемое, вычитаемое) – с. 70. Следует иметь в виду, что упражнения с «окошками» можно использовать с различной целью (в зависимости от этого формулируется задание):
а) с целью закрепления и проверки состава чисел:
— Вставь в окошко нужное число 3 + = 7;
б) с целью подготовки к решению уравнений способом подстановки:
— Какое число нужно вставить в «окошко», чтобы получить верное равенство?
— Объясни, почему числа 1, 2, 3, 5 нельзя вставить в «окошко»?
— Какое равенство получим, если вставим в «окошко» число 6?
2. Раскрывается связь между слагаемыми и
суммой (правило нахождения неизвестного
слагаемого) — М-1, ч. 2 с. 24. Это правило
вводится либо сразу (где вводится
взаимосвязь) или на последующих уроках
(дедуктивный путь). Для этого надо
переосмыслить взаимосвязь и подвести
детей к выводу-правилу: «Чтобы найти
слагаемое …».
Раскрывается связь между слагаемыми и
суммой (правило нахождения неизвестного
слагаемого) — М-1, ч. 2 с. 24. Это правило
вводится либо сразу (где вводится
взаимосвязь) или на последующих уроках
(дедуктивный путь). Для этого надо
переосмыслить взаимосвязь и подвести
детей к выводу-правилу: «Чтобы найти
слагаемое …».
а) повторяем взаимосвязь:
5 + 3 = 8
8 – 5 = 3
8 – 3 = 5
б) учитель предлагает одно из слагаемых сделать неизвестным:
+ 3 = 8
Прочитаем: к какому числу надо прибавить 3, чтобы получить 8. Давайте найдем это число. Какое из этих равенств поможет найти первое слагаемое? (8 – 3 = 5)
в)
аналогично проводится работа со вторым
неизвестным слагаемым и делается общий
вывод: чтобы найти неизвестное
слагаемое, надо … .
3. Раскрывается связь между компонентами и результатом действий:
— вычитания, М2, ч. 1, с. 73,
умножения, М2, ч. 2, с. 62,
деления, М3, ч. 2, с. 16.
4. Выполнение упражнений в виде таблиц (М1, ч. 2, с. 89).
Индивидуальная карточка по теме «Числовые равенства и числовые неравенства».
Индивидуальная карточка по теме «Числовые равенства и числовые неравенства».| 12+ Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058 | Пользовательское соглашение Контактная и правовая информация |
Педагогическое сообщество | Бесплатные всероссийские конкурсы | Бесплатные сертификаты | Нужна помощь? Инструкции для новых участников | Бесплатная онлайн-школа для 1-4 классов |
Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости
Библиотека
▪Учебно-дидактические материалы
▪Задачи / упражнения / практикумы
Материал опубликовала
11
#2 класс #Математика #ФГОС #Учебно-дидактические материалы #Задача / упражнение / практикум #Учитель начальных классов #Педагог дополнительного образования #Студент-практикант #Школьное образование #УМК «Перспективная начальная школа» #УМК любой
Тема:
«Числовые равенства и числовые неравенства» (1 урок)
Изучение данной темы носит, прежде всего, терминологический характер. Математическая запись в виде числового равенства или числового неравенства учащимся хорошо знакома. Но до настоящего момента мы не использовали соответствующую терминологию. После изучения данной темы введенная терминология будет применяться постоянно и систематически. При этом особое внимание следует обратить на распознавание верных и неверных записей.
Математическая запись в виде числового равенства или числового неравенства учащимся хорошо знакома. Но до настоящего момента мы не использовали соответствующую терминологию. После изучения данной темы введенная терминология будет применяться постоянно и систематически. При этом особое внимание следует обратить на распознавание верных и неверных записей.
Задачи урока:
— введение терминов «числовые равенства и числовые неравенства»;
— верные и неверные числовые равенства; конструирование верных равенств;
— верные и неверные числовые неравенства; конструирование верных неравенств;
— формирование УУД: поиск рациональных способов решений без вычилений на основе применения изученныхетических положений;коммуникативные УУД.
Данная карточка разработана в качестве дидактического материала к уроку математики для обучающихся 2 класса. В ресурсе представлено 4 карточки. карточки можно использовать на этапе закрепления изученного материала, а также повторение изученного.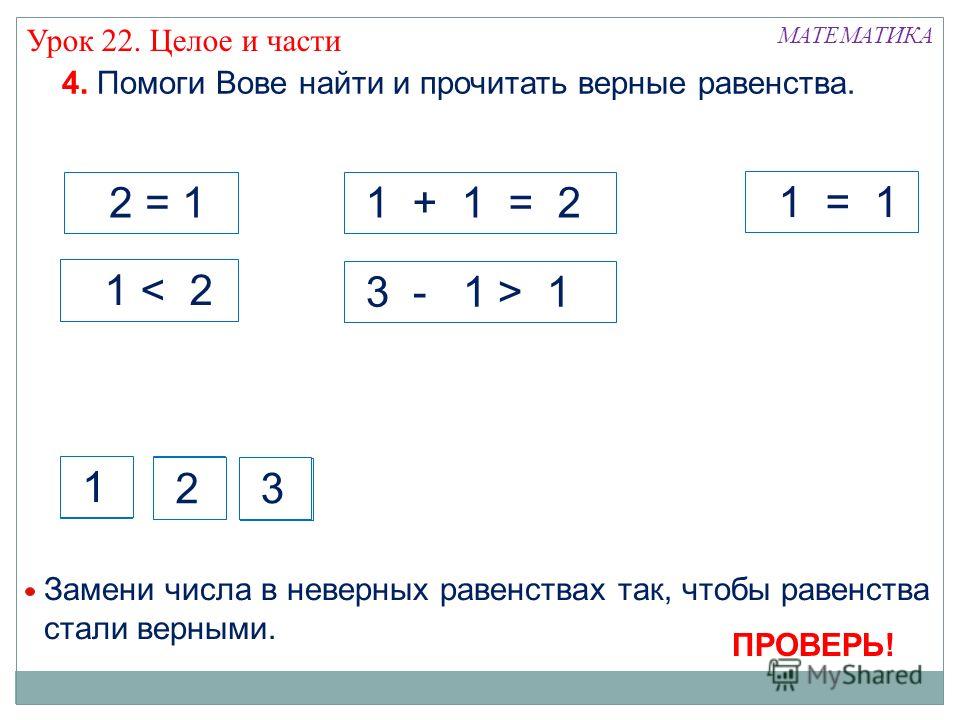
Для печати
DOCX / 14.51 Кб
Опубликовано в группе «Перспективная начальная школа»
Лилия Вильевна, спасибо за индивидуальные карточки к урокам математики. Понравились задания,где нужно соотнести неравенство и цвет, то есть для его выполнения нужно осмыслить учебную задачу.
Голдина Лилия Вильевна, 22.07.20 в 18:13 0ОтветитьПожаловаться
Ирина, благодарю за первый отзыв к моей работе. Буду рада, если карточки пригодятся в работе.
Чтобы написать комментарий необходимо авторизоваться.
Закрыть
Верные и ложные утверждения Образовательные ресурсы Обучение K12, выражения и уравнения, предварительная алгебра, планы уроков по математике, упражнения, эксперименты, помощь на дому
Аудио:
Новый аттракцион на ярмарке имеет требования к высоте.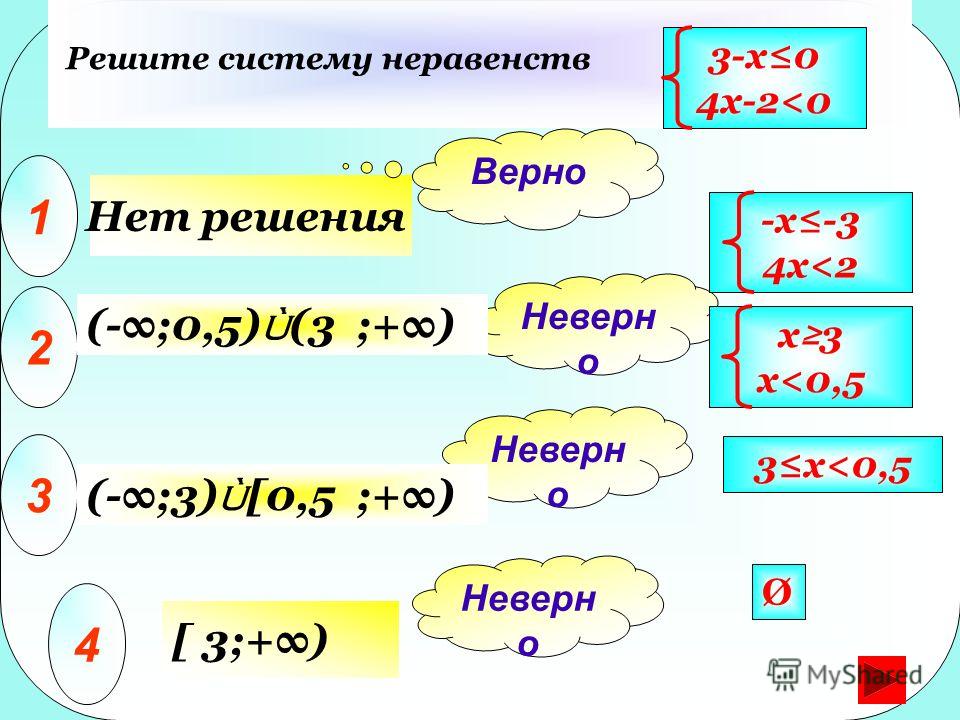
Минимальная высота — 36 дюймов, максимальная — 72 дюйма. Если ваш рост 62 дюйма, можете ли вы кататься? Какой будет высота, на которой нельзя будет кататься?
Знаете ли вы, что иногда в математике вам не нужно находить точный ответ?
Большую часть времени вы пытаетесь решить уравнение с одним ответом. Уравнение включает знак равенства (=) и представляет два выражения с одинаковыми значениями. Но иногда два выражения больше или меньше друг друга и представляются с помощью неравенства. Неравенства говорят о выражениях, которые имеют разные значения.
Посмотрите видео, чтобы узнать о неравенстве. Ответьте на следующие вопросы в своем математическом дневнике:
- Нарисуйте символ, обозначающий каждое сравнение: равно, не равно, больше, меньше, больше или равно, меньше или равно.
- Почему используются неравенства?
- Как можно использовать неравенства для представления реальных проблем?
Обсудите приведенные выше вопросы с родителями или учителем после просмотра видеоклипа «Математика — это весело» (окончание в 5:40),
Как вы видели в видео выше, с неравенствами используются специальные знаки:
| равно | = |
| не равно | ≠ |
| менее | < |
| меньше или равно | ≤ |
| больше | > |
| больше или равно | ≥ |
При использовании приведенных выше символов убедитесь, что широкая часть знака обращена к большему значению, а меньшая часть указывает на меньшее число.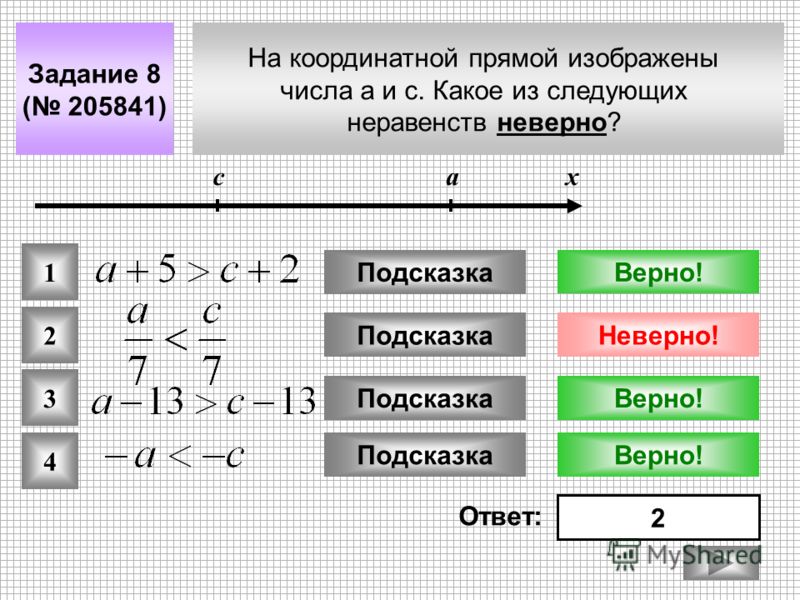 Например, чтобы показать, что 15 больше 12, вы должны написать 15 > 12.
Например, чтобы показать, что 15 больше 12, вы должны написать 15 > 12.
Один из способов запомнить это — думать о знаке как о пасти аллигатора, а аллигатор всегда хочет съесть большую часть неравенства!
Уравнение или неравенство могут быть истинными или ложными, в зависимости от используемого символа. В некоторых задачах вам нужно будет подставить значение переменной и решить ее. В других задачах вам, возможно, придется найти значение, которое приведет к истинному или ложному числовому предложению. Числовое предложение — это математическое предложение, обычно уравнение или неравенство, записанное с помощью чисел и математических символов.
Пример Подставьте 3 вместо x в каждое уравнение или неравенство и оцените. Определите, приводит ли оно к истинному числовому предложению или ложному числовому предложению:
- 6 + x = 19
- Замените x на 3, так что 6 + 3 = 9. 9 ≠ 19, так что это числовое выражение ложно.
- 4x = 12
- Замените x на 3, так что 4(3) = 12.
 Эта задача означает умножение, и 4 x 3 = 12, так что это числовое выражение верно.
Эта задача означает умножение, и 4 x 3 = 12, так что это числовое выражение верно.
- Замените x на 3, так что 4(3) = 12.
- 8 + х ≤ 12
- Замените x на 3, так что 8 + 3 = 11. 11 ≤ 12 означает, что 11 меньше или равно 12, что верно. Знак неравенства указывает, что выражение в левой части должно быть меньше или равно правому.
- Найдите значение x, чтобы это числовое предложение стало ложным: 39 — x ≥ 26.
- Сначала найдите число, при котором неравенство будет верным, если оно будет равно 26. Поскольку 39 — 13 = 26, если x = 13, левая часть выражения равна правой.
- Левая часть выражения также должна быть больше 26, чтобы быть истинной, так что оно будет включать числа меньше 13. Если вы хотите, чтобы выражение было ложным, вам нужно выбрать числа, которые сделают левую часть выражения уравнение меньше 26. В этом примере x должен быть числом, которое больше или равно 14, чтобы быть ложным.
Пример В начале урока вам была предложена такая словесная задача:
Новый аттракцион на ярмарке требует высоты. Минимальная высота составляет 36 дюймов, а максимальная — 72 дюйма. Если ваш рост 62 дюйма, можете ли вы кататься? Какой будет высота, на которой нельзя будет кататься?
Минимальная высота составляет 36 дюймов, а максимальная — 72 дюйма. Если ваш рост 62 дюйма, можете ли вы кататься? Какой будет высота, на которой нельзя будет кататься?
Минимальная высота составляет 36 дюймов, что означает, что это наименьшее значение, которое разрешено для езды. Максимальная высота составляет 72 дюйма, а это значит, что это максимальное значение, которое разрешено для езды. Если «h» означает рост, неравенства будут h ≥ 36 и h ≤ 72. Рост всадника должен быть равен или больше 36 дюймов, но меньше или равен 72 дюймам. Если у вас 62 дюйма, то это меньше 72 дюймов, так что вы сможете покататься. Если бы ваш рост был 32 дюйма или 75 дюймов, вы бы не смогли кататься, поскольку ваш рост меньше 36 дюймов или больше 72 дюймов.
В своем математическом журнале напишите ответы на следующие вопросы:
- Опишите разницу между этими символами: < и ≤.
- Как определить, является ли числовое выражение истинным или ложным?
Теперь вы перейдете к Понял? , чтобы завершить интерактивную практику, чтобы определить, верны или нет утверждения об уравнениях и неравенствах.
1. Определите, верно ли следующее утверждение или ЛОЖЬ. Заявление 66. Выберите правильный ответ ниже. A. Неверно, символ неравенства может быть обращен вправо или влево, но его отверстие должно быть обращено к меньшему числу. B.Правда, символы неравенства означают одно и то же вещь, поэтому заявления равны. C.Верно, символ неравенства может быть обращен вправо или влево, но его отверстие должно быть обращено к большему числу D. False, символ неравенства может быть обращен только вправо, и его отверстие должно быть обращено к большему числу. 2. Уравнение |x|=b, где b — a положительное число, сколько всегда будет решений? Почему? Выберите правильный ответ ниже. A. Всегда будет два решения: x=b и x=−b. С b>0, значения b и −b всегда разные числа. B. Всегда будет одно решение, x=−b, потому что абсолютное значение числа всегда отрицательно. C. Всегда будет одно решение, x=b, потому что абсолютное значение числа всегда положительно. D. Не будет решения. Поскольку b>0, значения b и −b всегда разные числа.
 2. Мария работает официанткой и зарабатывает 4,50 доллара в час плюс
средние чаевые 7 за каждый обслуживаемый стол. Сколько столов она должна
служить, чтобы заработать более 67 за 4-часовую смену? Опишите
ситуации с линейным неравенством, а затем решить
неравенство.
а. Выберите правильное неравенство ниже.
А. 18+7x>67
Б. 4,50х+67>18
В. 18+7х
2. Мария работает официанткой и зарабатывает 4,50 доллара в час плюс
средние чаевые 7 за каждый обслуживаемый стол. Сколько столов она должна
служить, чтобы заработать более 67 за 4-часовую смену? Опишите
ситуации с линейным неравенством, а затем решить
неравенство.
а. Выберите правильное неравенство ниже.
А. 18+7x>67
Б. 4,50х+67>18
В. 18+7хВопрос
Пошаговый ответ
AI Рекомендуемый ответ:
1.Начните с символа неравенства:
2. Добавьте числа слева от символа неравенства:
3. Вычтите число справа от символа неравенства:
Видеорекомендация лучшего совпадения:
Решено от проверенного эксперта
У нас нет запрошенного вами вопроса, но вот рекомендуемое видео, которое может помочь.
«Эшли решает уравнение 0,4(2,5 x — 8) — 4 и утверждает, что решение равно x — -0,8. В таблице ниже показаны шаги, которые она предприняла, и причины каждого шага. Шаг
1
2
Уравнение
0,4(2,5 х-8)=-4
Х-32=-4
х — 32+3,2 = -4 +32
х=-08
Причина
Данный
Ассоциативное свойство
Аддитивное свойство равенства
Свойство вычитания равенства
Определите, является ли каждое утверждение ниже верным или ложным относительно причин, указанных в таблице. Выберите True или False для каждого утверждения.
Верно Ложно
Причина шага 1 верна
Причиной шага 1 должно быть Распределительное свойство
Причина шага 2 верна
Причиной шага 2 должно быть свойство Additive Identity.
Причина шага 3 верна
Причина для шага 3 должна быть аддитивным обратным свойством и / или объединением подобных терминов.
Эшли решает уравнение 0,4(2,5 x _ 81 C4) и утверждает, что решение
-0,84 В приведенной ниже таблице показаны шаги, которые она предприняла, и причины
Шаг
Уравнение 4 (2,5 * — 8) =-4 X-J2=_ ‘X-32+32 74t32
Причина указана
Свойство сложения ассоциативных свойств 0f Equally Свойство Subtaction 0f Equally
С8
Определите, является ли каждое утверждение ниже истинным или ложным в отношении причин, указанных в (obble; выберите «Верно» или «Неверно» для каждого утверждения).
Шаг
1
2
Уравнение
0,4(2,5 х-8)=-4
Х-32=-4
х — 32+3,2 = -4 +32
х=-08
Причина
Данный
Ассоциативное свойство
Аддитивное свойство равенства
Свойство вычитания равенства
Определите, является ли каждое утверждение ниже верным или ложным относительно причин, указанных в таблице. Выберите True или False для каждого утверждения.
Верно Ложно
Причина шага 1 верна
Причиной шага 1 должно быть Распределительное свойство
Причина шага 2 верна
Причиной шага 2 должно быть свойство Additive Identity.
Причина шага 3 верна
Причина для шага 3 должна быть аддитивным обратным свойством и / или объединением подобных терминов.
Эшли решает уравнение 0,4(2,5 x _ 81 C4) и утверждает, что решение
-0,84 В приведенной ниже таблице показаны шаги, которые она предприняла, и причины
Шаг
Уравнение 4 (2,5 * — 8) =-4 X-J2=_ ‘X-32+32 74t32
Причина указана
Свойство сложения ассоциативных свойств 0f Equally Свойство Subtaction 0f Equally
С8
Определите, является ли каждое утверждение ниже истинным или ложным в отношении причин, указанных в (obble; выберите «Верно» или «Неверно» для каждого утверждения).

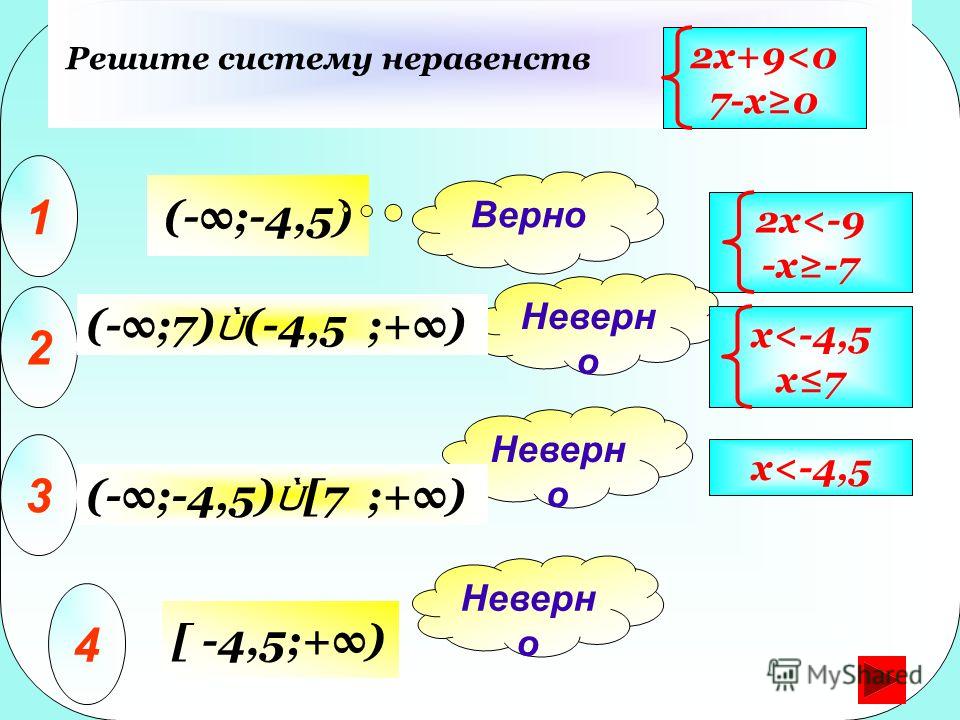 Эта задача означает умножение, и 4 x 3 = 12, так что это числовое выражение верно.
Эта задача означает умножение, и 4 x 3 = 12, так что это числовое выражение верно.