Двоичный калькулятор
+−×÷
Количество знаков после запятой в ответе
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100
Что такое двоичная система счисления
Двоичная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа. Для записи числа в двоичной системе счисления используется две цифры 0 и 1. Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием системы счисления. Например, 10012 или 10001012.
Как складывать, вычитать, делить и умножать числа в двоичной системе счисления
Для того чтобы выполнить математическую операцию с двоичными числами необходимо:
- Перевести эти числа в десятичную систему счисления.

- Выполнить математическую операцию (сложение, вычитание, умножение, деление) с десятичными числами.
- Перевести полученный результат в двоичную систему счисления.
Приведем пример на сложение, допустим необходимо сложить два числа 110 и 101.
Первым делом переведем эти числа в десятичную систему счисления:
Переведем число 1102 в десятичную систему счисления, для этого сначала запишем позицию каждой цифры в числе с права налево, начиная с нуля
| Позиция в числе | 2 | 1 | 0 |
| Число | 1 | 1 | 0 |
Каждая позиция цифры будет степенью числа 2, так как система счисления 2-ичная. Необходимо последовательно умножить каждое число 1102 на 2 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
1102 = 1 ⋅ 22 + 1 ⋅ 21 + 0 ⋅ 20 = 610
Переведем число 1012 в десятичную систему счисления, для этого сначала запишем позицию каждой цифры в числе с права налево, начиная с нуля
| Позиция в числе | 2 | 1 | 0 |
| Число | 1 | 0 | 1 |
Каждая позиция цифры будет степенью числа 2, так как система счисления 2-ичная. Необходимо последовательно умножить каждое число 1012 на 2 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
1012 = 1 ⋅ 22 + 0 ⋅ 21 + 1 ⋅ 20 = 510
Теперь сложим получившиеся десятичные числа 610 + 510 = 1110 и переведем ответ в двоичную систему счисления
Переведем число 1110 в 2-ичную систему счисления, при помощи последовательного деления на 2, до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.
В результате будет получено число из остатков деления записанное справа налево.
| 11 | : | 2 | = | 5 | остаток: 1 |
| 5 | : | 2 | = | 2 | остаток: 1 |
| 2 | : | 2 | = | 1 | остаток: 0 |
| 1 | : | 2 | = | 0 | остаток: 1 |
1110 = 10112
110 + 101 = 1011 2
Вычитание двоичных чисел выполняется аналогичным образом, если бы нам было необходимо из числа 110 вычесть число 101, то также как в примере на сложения необходимо перевести эти числа в десятичную систему счисления, получим 1102 = 610 и 1012 = 510. Затем произведем вычитание 610 – 510 = 110. И далее переведем число 1 в двоичную систему счисления
Переведем число 110 в 2-ичную систему счисления, при помощи последовательного деления на 2, до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.
В результате будет получено число из остатков деления записанное справа налево.
| 1 | : | 2 | = | 0 | остаток: 1 |
110 – 101 = 1
Умножение и деление также, как и сложение и вычитание требует сначала перевести числа из двоичной системы счисления в десятичную, а затем выполнить математические вычисления с последующим переводом результата в двоичное число.
Приведем пример, возьмём два двоичных числа 110 и 101 из предыдущего примера, (так будет удобнее, так как мы уже перевели их в десятичную систему счисления) и выполним умножение данных чисел.
Итак 1102 = 610 и 1012 = 510, тогда 610 × 510 = 3010. И далее переведем число 3010 в двоичную систему счисления
Переведем число 3010 в 2-ичную систему счисления, при помощи последовательного деления на 2, до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.
В результате будет получено число из остатков деления записанное справа налево.
| 30 | : | 2 | = | 15 | остаток: 0 |
| 15 | : | 2 | = | 7 | остаток: 1 |
| 7 | : | 2 | = | 3 | остаток: 1 |
| 3 | : | 2 | = | 1 | остаток: 1 |
| 1 | : | 2 | = | 0 | остаток: 1 |
110 × 101 = 111102
И в завершении, чтобы научиться делить двоичные числа разделим 110 на 101.
1102 = 610 и 1012 = 510, тогда 610 : 510 = 1.210.
Переведем число 1.210 в двоичную систему счисления:
Переведем целую часть 1 числа 1.210 в 2-ичную систему счисления, при помощи последовательного деления на 2, до тех пор, пока неполное частное не будет равно нулю.
| 1 | : | 2 | = | 0 | остаток: 1 |
110 = 12
Переведем дробную часть 0.2 числа 1.210 в 2-ичную систему счисления, при помощи последовательного умножения на 2, до тех пор, пока в дробной части произведения не получиться ноль или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
0. 2 2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
0.210 = 0.001100112
1.210 = 1.001100112
Нужно сразу оговориться, что, умножая дробную часть на 2 мы все равно не получим ноль, так как десятичная дробь 1.2 в двоичной системе бесконечная. Поэтому, для примера оставим 8 знаков после запятой. Получим 110 : 101 = 1.00110011.2
Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь калькулятором систем счисления с подробным решением онлайн.
Двоичная арифметика : сложение, вычитание, умножение, деление
Выполнение арифметических действий в любых позиционных системах счисления производится по тем же правилам, которые используются в десятичной системе счисления.
Так же, как и в десятичной системе счисления, для выполнения арифметических действий необходимо знать таблицы сложения (вычитания) и умножения.
Таблица сложения, вычитания и умножения для двоичной системы счисления
| Сложение | Вычитание | Умножение |
| 0 + 0 = 0 | 0 — 0 = 0 | 0 ∙ 0 = 0 |
| 0 + 1= 1 | 1 — 0 = 1 | 0 ∙ 1 = 0 |
| 1 + 0 = 1 | 1 — 1 = 0 | 1 ∙ 0 = 0 |
| 1 + 1 = 10 | 10 — 1 = 1 | 1 ∙ 1 = 1 |
Сложение двоичных чисел
Сложение в двоичной системе счисления выполняется по тем же правилам, что и в десятичной. Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями. Сложение начинается с крайнего правого разряда. Две единицы младшего разряда объединяются в единицу старшего.
Пример: 1011,12 + 1010,112
Интересна также ситуация, когда складываются больше двух чисел. В этом случае возможен перенос через несколько разрядов.
Пример: 111,12 + 1112 + 101,12
При сложении в разряде единиц (разряд 0) оказывается 4 единицы, которые, объединившись, дают 1002. Поэтому из нулевого разряда в первый разряд переносится 0, а во второй — 1.
Аналогичная ситуация возникает во втором разряде, где с учетом двух перенесенных единиц получается число 5 = 1012. 1 остается во втором разряде, 0 переносится в третий и 1 переносится в четвёртый.
Вычитание двоичных чисел
В случаях, когда занимается единица старшего разряда, она дает две единицы младшего разряда. Если занимается единица через несколько разрядов, то она дает по одной единице во всех промежуточных нулевых разрядах и две единицы в том разряде, для которого занималась.
Пример: 10110,012 — 1001,12
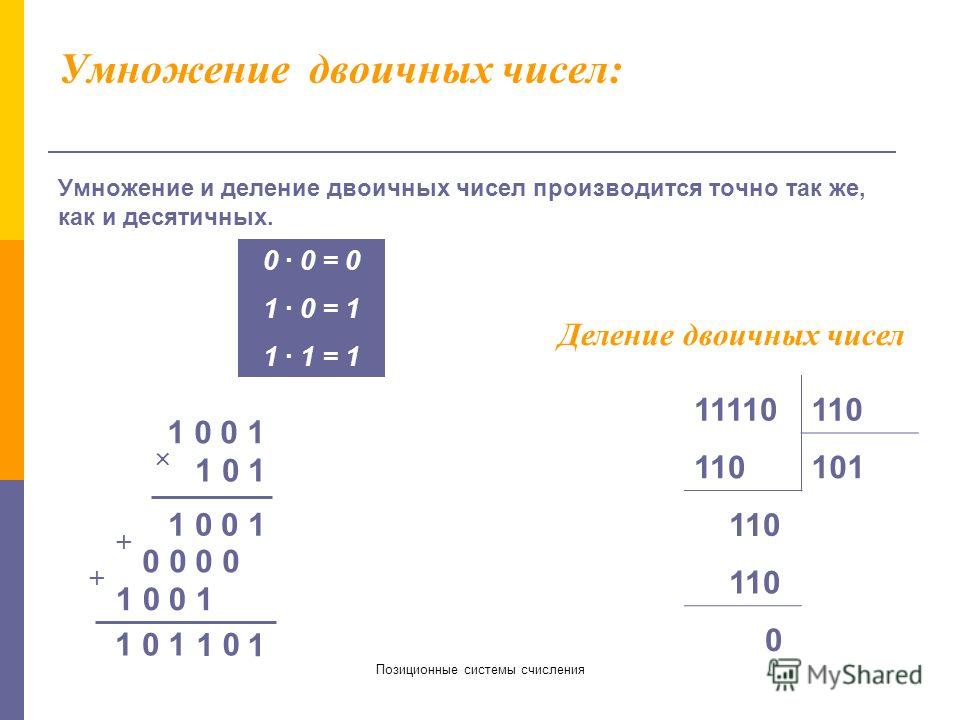
Умножение и деление двоичных чисел
Зная операции двоичной арифметики, можно переводить числа из двоичной системы счисления в любую другую.
Пример: Перевести число 1011110112 в десятичную систему счисления.
Поскольку 1010 = 10102, запишем
Полученные остатки, 10012 = 910, =1112 = 710, 112 = 310. Искомое число 1011110112 = 37910.
Назад: Представление данных и архитектура ЭВМ
Калькулятор двоичного умножения
Создано Филиппом Маусом
Отзыв Стивена Вудинга
Последнее обновление: 02 февраля 2023 г.
Содержание:- Как умножать двоичные числа?
- Каковы правила двоичного умножения?
- Как пользоваться калькулятором двоичного умножения?
- Часто задаваемые вопросы
Калькулятор двоичного умножения описывает, как умножать двоичные числа (которые можно получить с помощью двоичного преобразователя). В этой статье вы также узнаете сходства и различия между двоичной и десятичной системами счисления и см. пошаговую инструкцию по умножению двоичных чисел .
В этой статье вы также узнаете сходства и различия между двоичной и десятичной системами счисления и см. пошаговую инструкцию по умножению двоичных чисел .
🔎 Не ограничивайтесь умножением. Вы можете вычитать, умножать и делить эти типы чисел с помощью нашего двоичного калькулятора.
Как умножать двоичные числа?
В то время как десятичная система счисления, с которой мы все знакомы, основана на степенях 10, двоичная система имеет основание 2 . Это означает, что каждая цифра двоичного числа, так называемый бит, может представлять только два логических значения: 0 или 1 . Поэтому двоичные числа обычно используются в цифровой электронике и связи, представляя два состояния «включено» и «выключено». Мы можем преобразовать двоичные числа в десятичную систему. Они также позволяют применять арифметические операции, такие как сложение, вычитание, деление и, как мы увидим в этом двоичном калькуляторе, умножение. Кроме того, двоичные числа позволяют выполнять операции, уникальные для двоичной системы, такие как сдвиг битов и побитовые операции AND, OR и XOR.
Кроме того, двоичные числа позволяют выполнять операции, уникальные для двоичной системы, такие как сдвиг битов и побитовые операции AND, OR и XOR.
Эти операции также можно выполнять с отрицательными двоичными числами, как показано в нашем калькуляторе дополнения до двух , в котором первая цифра указывает на знак числа . Этот калькулятор двоичного деления использует представление со знаком, что означает, что первый бит ваших входных чисел будет считаться битом со знаком. Будьте осторожны, чтобы не получить ложные результаты из-за этого , и при необходимости увеличьте битовое представление.
Каковы правила двоичного умножения?
Двоичное умножение имеет 4 основных правила :
-
0×0=0 -
0×1=0 -
1×0=0 -
1×1=1
На основе этих правил двоичное умножение очень похоже на десятичное длинное умножение . Мы можем даже считать это немного проще, поскольку нам нужно иметь дело только с цифрами 9.0036 0 и
Мы можем даже считать это немного проще, поскольку нам нужно иметь дело только с цифрами 9.0036 0 и 1 .
Умножение является коммутативной операцией , что означает, что произведение не зависит от порядка множителей. Тем не менее, рекомендуется для длинного деления устанавливать более длинное число в качестве множителя (множитель 1), а более короткое число — в качестве множимого (множитель 2), чтобы уменьшить количество шагов.
В качестве примера рассмотрим умножение 1011 и 0101 (13 и 5 в десятичной системе):
Пошаговая процедура умножения этих двоичных чисел:
- Установите большее число в качестве множителя .

1011имеет четыре значащих бита и поэтому имеет коэффициент 1. - Умножить множитель на последнюю цифру множимого :
- Следуя основным правилам, упомянутым выше,
1011×1=1011. Это первый промежуточный продукт, начиная с позиции последней цифры множимого.
- Умножить множитель на предпоследнюю цифру множимого :
1011×0=0000. Это второй промежуточный продукт, начиная со второй до последней цифры множимого.
- Умножьте множитель на третью до последней цифры множимого :
1011×1=1011. Это третий промежуточный продукт, начиная с позиции третьей до последней цифры множимого.
- Умножьте множитель на предпоследнюю (первую) цифру множимого :
1011×0=0000.Это четвертый промежуточный продукт, начиная с позиции четвертой и заканчивая последней цифрой множимого.
- Конечный продукт представляет собой сумму промежуточных продуктов :
1011+00000+101100+0000000=0110111
Как использовать калькулятор двоичного умножения?
Теперь вы знаете, как выполнять умножение двоичных чисел, так что давайте научиться пользоваться калькулятором двоичного умножения . В качестве примера, давайте проверим правильность нашей пошаговой процедуры выше и умножим 1011 и 101 :
- . представлен в.
- Как мы уже знаем, максимальное число битов произведения равно 6, поэтому 8 битов вполне достаточно.
- Введите коэффициенты.
 Поскольку операция умножения коммутативна, порядок не имеет значения.
Поскольку операция умножения коммутативна, порядок не имеет значения.
1011и101
- Калькулятор двоичного умножения представляет произведение в двоичной и десятичной системе . Это результат вашего умножения двоичных чисел:
- Двоичный:
0011 0111- Десятичный:
13
Если ваш двоичный результат имеет значение 1 в старшем разряде и может быть понят как положительный результат в записи без знака или отрицательный результат в записи со знаком, будут отображаться оба результата .
Часто задаваемые вопросы
Как умножать двоичные числа?
Чтобы умножить двоичные числа , выполните следующие действия:
- Установите более длинное число в качестве множителя и более короткое число как множимое .

- Умножьте множитель на каждую цифру множимого , чтобы получить промежуточные произведения, последняя цифра которых находится на месте соответствующей цифры множимого.
- Суммируйте промежуточные продукты , чтобы получить конечный продукт.
Как умножать двоичные числа с помощью битового сдвига?
Двоичное умножение, особенно с коэффициентами, равными степени двойки, можно выполнить с помощью сдвига битов влево . Умножение на 2 — это сдвиг на один бит, 4 — 2 бита, 8 — 3-битный сдвиг и т. д. Благодаря своей математической эффективности этот метод обычно используется в цифровых приложениях.
Как умножить двоичные числа 101 и 11?
Чтобы умножить двоичные числа 101 и 11 , выполните следующие действия: 0019 11 как множимое .
101 на последнюю цифру 11 : 101 × 1 = 101 . Это первый промежуточный продукт .
Это первый промежуточный продукт . 101 на первую цифру 11 : 101 × 1 = 101 . Добавьте 0 в конце, чтобы представить позицию цифры множимого: 1010 . Это второй промежуточный продукт . 101 + 1010 = 1111 .Филип Маус
Двоичное представление
Вы можете записывать двоичные числа, содержащие не более 8 цифр. Вам не нужно вводить лидирующие нули.
Фактор 1
Фактор 2
Ознакомиться с 11 похожими бинарными калькуляторами 1️0️
Двоичное сложениеДвоичное делениеДвоичная дробь… 8 еще
Двоичный калькулятор — Изучение двоичного кода
Операнд 1
Введите двоичное число (например, 110.001) (без запятых, пробелов, показателей степени, дробей, операторов)Операция
Выберите +, -, * или /+-*/
Операнд 2
Введите двоичное число (например, 110. 001) (без запятых, пробелов, показателей степени, дробей, операторов)
001) (без запятых, пробелов, показателей степени, дробей, операторов)Результат
Результатом является это двоичное число: Количество цифр:Опции:
- Сократить бесконечные двоичные дроби до бит (применяется только к делению).
(Хотите выполнять вычисления с десятичными операндами? Вы должны сначала преобразовать их.)
О двоичном калькуляторе
Это двоичный калькулятор произвольной точности . Он может складывать, вычитать, умножать или делить два двоичных числа. Он может работать с очень большими целыми числами и очень маленькими дробными значениями, а также с их комбинациями.
Этот калькулятор устроен очень просто. Вы можете использовать его для изучения двоичных чисел в их самой простой форме. Он работает с «чистыми» двоичными числами, а не с компьютерными числовыми форматами, такими как дополнение до двух или двоичные числа с плавающей запятой IEEE.
Как использовать двоичный калькулятор
Ввод
- Введите по одному операнду в каждое поле.
 Каждый операнд должен быть положительным или отрицательным числом без запятых и пробелов, не выраженным в виде дроби и не в экспоненциальном представлении. Дробные значения обозначаются точкой счисления («.», , а не «,»), а перед отрицательными числами ставится знак «минус» («-»).
Каждый операнд должен быть положительным или отрицательным числом без запятых и пробелов, не выраженным в виде дроби и не в экспоненциальном представлении. Дробные значения обозначаются точкой счисления («.», , а не «,»), а перед отрицательными числами ставится знак «минус» («-»). - Выберите операцию (+, – *, /).
- Измените количество битов, которое вы хотите отобразить в двоичном результате, если оно отличается от значения по умолчанию (это относится только к делению и только тогда, когда ответ имеет бесконечную дробную часть).
- Нажмите «Рассчитать», чтобы выполнить операцию.
- Нажмите «Очистить», чтобы сбросить форму и начать с нуля.
Если вы хотите изменить операнд, просто введите исходное число и нажмите «Рассчитать» — нет необходимости сначала нажимать «Очистить». Точно так же вы можете изменить оператор и оставить операнды как есть.
Вывод
Помимо результата операции отображается количество цифр в операндах и результат.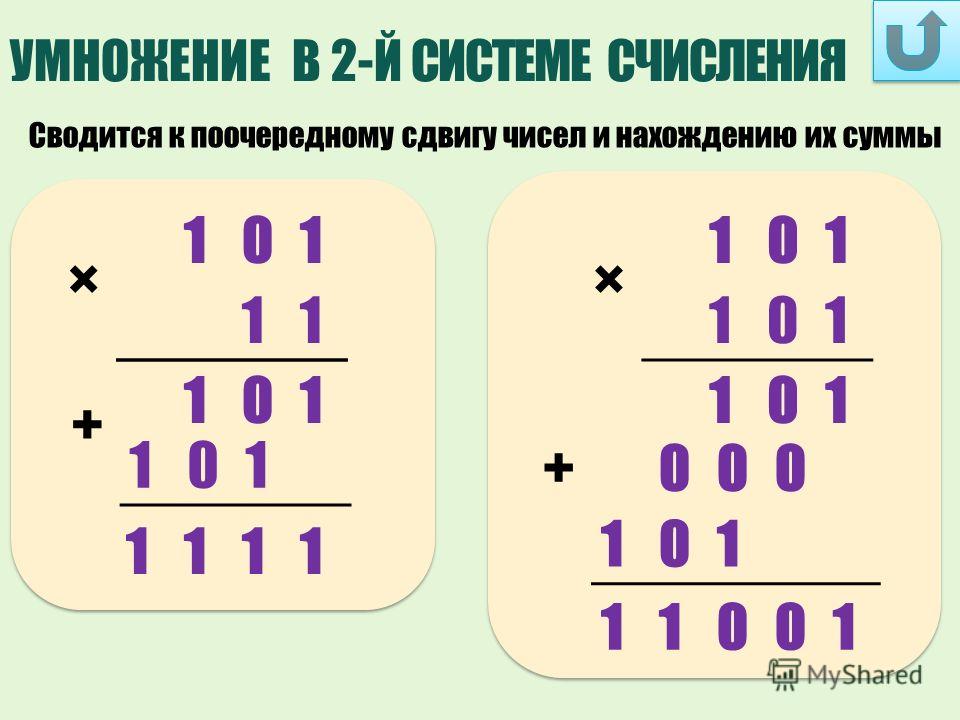 Например, при вычислении 1,1101 * 111,100011 = 1101,1010110111 в поле «Число цифр» отображается «1,4 * 3,6 = 4,10». Это означает, что операнд 1 имеет одну цифру в целой части и четыре цифры в дробной части, операнд 2 имеет три цифры в целой части и шесть цифр в дробной части, а результат состоит из четырех цифр в целой части и десяти цифр. в его дробной части.
Например, при вычислении 1,1101 * 111,100011 = 1101,1010110111 в поле «Число цифр» отображается «1,4 * 3,6 = 4,10». Это означает, что операнд 1 имеет одну цифру в целой части и четыре цифры в дробной части, операнд 2 имеет три цифры в целой части и шесть цифр в дробной части, а результат состоит из четырех цифр в целой части и десяти цифр. в его дробной части.
Сложение, вычитание и умножение всегда дают конечный результат, но деление может (на самом деле, в большинстве случаев) давать бесконечное (повторяющееся) дробное значение. Бесконечные результаты усекаются, а не округляются до указанного количества битов. Бесконечные результаты отмечены многоточием (…), добавленным к результату, и символом «∞» в качестве количества дробных цифр. Для делений, представляющих двоичные дроби, результат будет конечным и будет отображаться с полной точностью — независимо от настройки количества дробных битов.
Например, от 1/1010 до 24 дробных битов равно 0,000110011001100110011001…, где «Число цифр» = «1,0 / 4,0 = 0,∞»; 11/100 = 0,11, где «Число цифр» = «2,0 / 3,0 = 0,2».
Использование калькулятора для изучения арифметики с плавающей запятой
Хотя этот калькулятор реализует чисто двоичную арифметику, вы можете использовать его для изучения арифметики с плавающей запятой. Например, предположим, что вы хотите знать, почему, используя двоичную арифметику двойной точности IEEE с плавающей запятой, 129,95 * 10 = 1299,5, но 1290,95 * 100 = 12994,999999999998181010596454143524169921875.
В таких вычислениях есть два источника неточности: преобразование десятичных чисел в числа с плавающей запятой и двоичная арифметика с ограниченной точностью. Преобразование десятичного числа в число с плавающей запятой приводит к неточности, потому что десятичный операнд может не иметь точного эквивалента с плавающей запятой; двоичная арифметика с ограниченной точностью вносит неточность, потому что двоичное вычисление может произвести больше битов, чем может быть сохранено. В этих случаях происходит округление.
10 и 100 (оба десятичные) имеют точные эквиваленты с плавающей запятой (1010 и 1100100 соответственно), но 129,95 имеет только приблизительное представление. Мой конвертер из десятичной системы в двоичную скажет вам, что в чистом двоичном формате число 129,95 имеет бесконечную повторяющуюся дробь:
Мой конвертер из десятичной системы в двоичную скажет вам, что в чистом двоичном формате число 129,95 имеет бесконечную повторяющуюся дробь:
10000001.111100110011001100110011001100110011001100110011…
Округление до 53 бит двойной точности, это
10000001.11110011001100110011001100110011001100110011
, что равно 129,94999999999998863131622783839702606201171875 в десятичном формате.
129,95 * 10
129,95 * 10 вычисляется как
что равно 10100010011.0111111111111111111111111111111111111111111
(Попробуйте!) становится
10100010011,1 = 1299,5
129,95 * 100
129,95 * 100 вычисляется как
10000001.11110011001100110011001100110011001100110011 * 1100100
что равно 11001011000010.111111111111111111111111 1111111111111111011
Это 56 значащих битов, поэтому при округлении до 53 битов получается
11001011000010.111111111111111111111111111111111111111111
что равно 12994.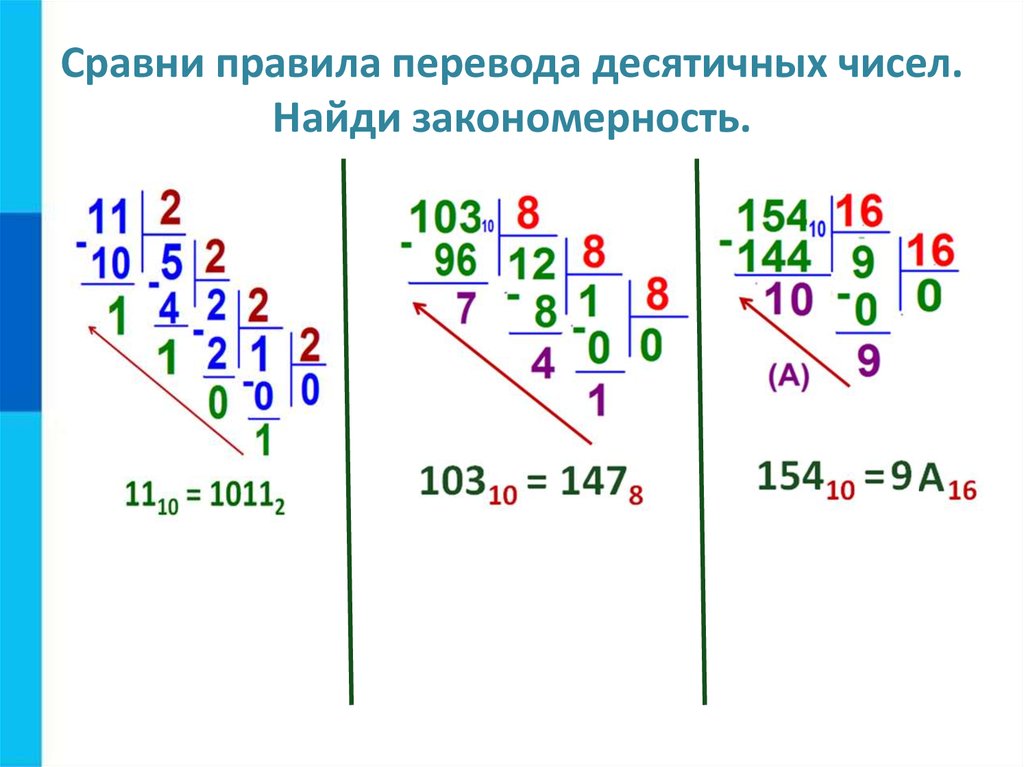



 Это четвертый промежуточный продукт, начиная с позиции четвертой и заканчивая последней цифрой множимого.
Это четвертый промежуточный продукт, начиная с позиции четвертой и заканчивая последней цифрой множимого. Поскольку операция умножения коммутативна, порядок не имеет значения.
Поскольку операция умножения коммутативна, порядок не имеет значения.
 Каждый операнд должен быть положительным или отрицательным числом без запятых и пробелов, не выраженным в виде дроби и не в экспоненциальном представлении. Дробные значения обозначаются точкой счисления («.», , а не «,»), а перед отрицательными числами ставится знак «минус» («-»).
Каждый операнд должен быть положительным или отрицательным числом без запятых и пробелов, не выраженным в виде дроби и не в экспоненциальном представлении. Дробные значения обозначаются точкой счисления («.», , а не «,»), а перед отрицательными числами ставится знак «минус» («-»).