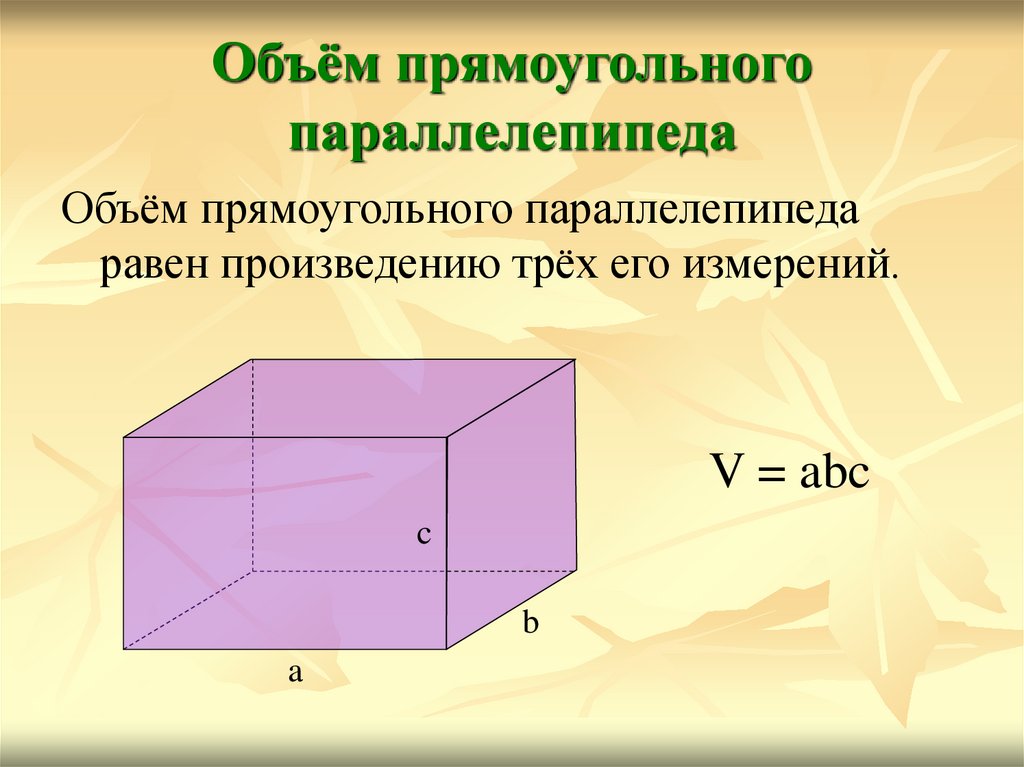
Объем прямоугольника – формула
4.6
Средняя оценка: 4.6
Всего получено оценок: 155.
4.6
Средняя оценка: 4.6
Всего получено оценок: 155.
Для учеников свойственно путать трехмерные и двумерные объекты. Это связано с тем, что на уроках математики изучаются в основном плоские фигуры, а ученик непроизвольно ищет примеры в реальной жизни, где существуют в основном 3д фигуры. Из-за этого возникает и частый вопрос: как найти объем прямоугольника?
Формула объема прямоугольника
Нужно запомнить раз и навсегда: формулы объема прямоугольника не существует.
Характеристики объема у прямоугольника нет, так же как нет ее и у любой двухмерной фигуры.
Аналогом объема служит площадь. Но словосочетание «объем прямоугольника» или объем треугольника» являются грубой ошибкой, и показывает незнание основных геометрических параметров.
Существует формула площади прямоугольника, она равна произведению длины на ширину и известна всем практически с первого класса.
Существует так же и формула объема прямоугольного параллелепипеда. Это фигура, которая состоит из шести граней, каждая из которых является прямоугольником. Очень часто именно эту фигуру по инерции называют прямоугольником, но это ошибка, от которой нужно избавляться.
Объем прямоугольного параллелепипеда равен произведению трех измерений: длины и ширины основания на высоту.
Объем и площадь
Объем и площадь – понятия во многом сходные, но есть и разница, которую стоит понимать. Площадь – это занимаемая часть плоскости. Если любую фигуру вырезать из бумаги, а затем приложить к плоскости, например к другому, более большому, листу, то фигура займет какую-то площадь.
Если фигуру обвести, а затем получившийся контур разбить на квадратики, то получится подсчитать площадь фигуры.
Объем показывает пространство, которое занимает объемная фигура.
Лучше всего объем прямоугольного параллелепипеда представляется так: если в пространстве поместить прямоугольник, провести перпендикулярно плоскости отрезок и плавно поднимать прямоугольник вверх, то результатом движения и станет объем этой фигуры.
Практически любую объемную фигуру можно представить в виде результата движения плоской фигуры. Например: конус это результат движения прямоугольного треугольника вокруг одного из катетов, а цилиндр результат вращения прямоугольника вокруг своей оси. Прямоугольный параллелепипед это результат вертикального движения прямоугольника-основания вверх
Рис. 2. Результаты вращения плоских фигур.Двух и трехмерные фигуры
Как отличить двухмерную фигуру от трехмерной? Двухмерная фигура существует исключительно на плоскости. Трехмерная фигура всегда имеет в своем составе элементы плоских фигур: окружности, линии, прямоугольники и т.д.
Рис. 3. Двухмерные и трехмерные фигуры.Если в составе фигуры можно разглядеть несколько плоских фигур, то фигура трехмерная, если же нет, и фигура состоит только из прямых, отрезков, точек и плоских углов, а саму фигуру можно изобразить на листе бумаги, то перед вами плоская фигура.
Что мы узнали?
Мы узнали, в чем разница двухмерных и трехмерных фигур.
Решили, что объема прямоугольника не существует. Существует только площадь прямоугольника или объем прямоугольного параллелепипеда.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Мадия Аманджолова
5/5
Елена Рассказова
5/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 155.
А какая ваша оценка?
Самые распространенные фигуры технического анализа
Что такое фигура в трейдинге? С виду это обычная геометрическая форма, которая очерчивает некоторую часть графика цены.
Зачем она нужна? Если трейдер выявляет фигуру технического анализа на графике, то он понимает, в каком направлении с большей вероятностью продолжится движение. Также она предоставляет возможность комфортного входа в сделку.
Сигнал на покупку или продажу возникает по окончанию формирования фигуры, когда цена выходит за ее пределы.
Как правило, именно в этот момент совершается сделка.
Важно помнить, что технические фигуры — не панацея. Есть фигуры, которые показывают отличную результативность на одних акциях, а на других просто «не работают». Для большей уверенности в прогнозе, их нередко используют в сочетании с различными техническими индикаторами.
Рассмотрим распространенные фигуры технического анализа. Они подразделяются на три группы: фигуры продолжения тренда, разворотные фигуры и двусторонние фигуры.
Фигуры продолжения тренда. Вымпел
Фигура «Вымпел» представляет собой горизонтально расположенный треугольник. Движение цены внутри вымпела — затухающее: диапазон колебаний на графике постепенно сужается. Вместе с этим снижаются и объемы торгов.
При восходящем тренде успешная реализация фигуры предполагает пробой верхней границы вымпела и продолжение up-тренда. Обратная ситуация происходит в случае «медвежьей» тенденции.
Один из основных критериев формирования вымпела — интенсивное движение по направлению тенденции перед ее остановкой.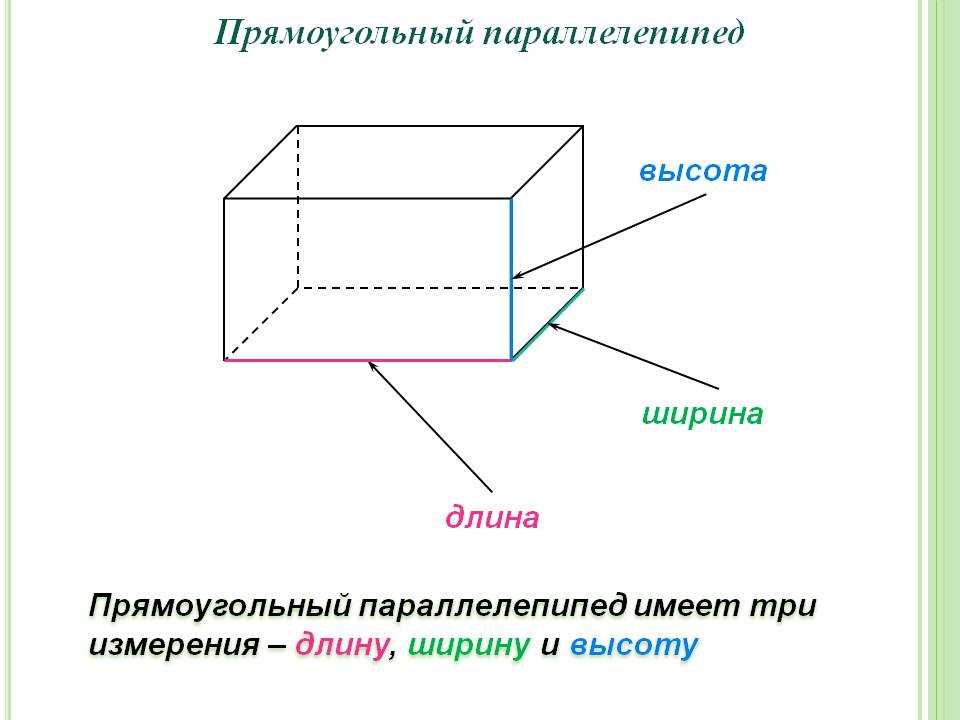
Соответствующая линия тренда на графике называется «древко» или «флагшток» (синяя линяя на графике).
Потенциал движения по тренду после выхода из вымпела равен в теории высоте «древка».
Флаг
Это еще одна фигура, возникающая перед продолжением тенденции. Линии фигуры должны быть расположены практически параллельно друг другу. Главное условие флага — направленность против тренда. При этом диапазон колебаний не должен быть слишком широким.
Как и вымпел, флаг имеет «древко» — импульсное движение на графике по тренду перед началом формирования фигуры.
Открытие сделки производится после того, как цена пробила границу флага по направлению тренда. В качестве метода входа можно использоваться стоп-заявку с ценой несколько выше (ниже) границы фигуры. Из-за постоянного сдвига канала цен стоп-ордер рекомендуется периодически редактировать.
Например, мы хотим совершить сделку на покупку в случае пробоя верхней границы нисходящего флага.
Тогда нам нужно выставить стоп-заявку по цене несколько выше актуального значения верхней границы флага. Через определенное время, в зависимости от таймфрейма, мы уменьшаем цену в заявке соразмерно падению границ флага.
Прямоугольник
Прямоугольник — это горизонтальный канал, в пределах которого колеблется цена. Фигура возникает, когда котировки не в состоянии продолжить движение по тренду.
Иногда рынку нужно «передохнуть», поскольку цена выросла (упала) больше, чем обычно. На это может указывать превышение TR* своего среднего значения ATR. Если фигура возникает на часовом графике, то TR берется с 4-часового или дневного графика, то есть со старшего таймфрейма.
* True Range — Истинный диапазон. Рассчитывается для конкретной свечи на определенном таймфрейме
Идея прямоугольника проста. Если движение по тренду останавливается на какое-то время, но при этом цена не в состоянии развернуться против тренда, то с большей вероятностью актуальная тенденция будет продолжена.
Отметим, что чем дольше котировки находятся в прямоугольнике, тем выше шансы на его скорое завершение. При этом, как правило, чем более узкий прямоугольник, тем с более сильным импульсом цена выйдет за его пределы.
Разворотные фигуры. Ромб
Графический паттерн «Ромб» предшествует в теории смене тренда.
Начало ромба возникает в конце импульсного движения по тренду. Цена затормаживается, после чего ее колебания постепенно возрастают, но происходят в пределах расходящегося треугольника (левая половина ромба). Затем происходит обратное — волатильность плавно снижается, и мы наблюдаем окончательное формирование ромба.
Сигнал на сделку против тренда возникает при пробое грани ромба вниз (вверх). Как правило, чем более узкий ромб относительно горизонтальной оси, тем импульсивней выход за его пределы. Однако при этом он не должен быть слишком вытянутым, иначе фигура превратится в боковик.
Как и в случае с другими фигурами, объемы торгов являются отличным вспомогательным инструментом при определении границ и момента завершения ромба.
Например, импульсный рост объемов возле границы ромба увеличивает вероятность завершения фигуры.
Двойная и тройная вершина (дно)
Двойное (тройное) дно формируется на падающем тренде, в то время как двойная (тройная вершина) — на растущей тенденции. В остальном эти формации схожи. Обе фигуры выступают предвестниками разворота тренда.
Рассмотрим двойную вершину и тройное дно. Двойная вершина формируется при восходящей тенденции: цена растет, потом отскакивает вниз от определенного уровня (первая вершина) и незначительно падает, формируя локальный минимум — сигнальную линию (синяя линия на графике). Затем цена поднимается и упирается в уровень первого максимума, образуя вторую вершину. Далее — разворот с успешным пробоем вниз сигнальной линии, после которого цена продолжает падать. Таким образом, происходит смена тренда на нисходящий.
Сигнал для входа в короткую позицию — пробой вниз сигнальной линии. Для большей уверенности можно дождаться тестирования снизу сигнальной линии после ее пробоя.
Риск продолжения up-тренда в таком случае снижается, однако присутствует вероятность упустить движение при импульсном падении.
Тройное дно — противоположный паттерн, суть которого заключается в том, что цена трижды касается уровня дна, дважды отскакивая сверху от сигнальной линии. В третий раз котировки пробивают наверх сигнальную линию, формируя растущий тренд.
Потенциал будущего движения в теории равен расстоянию между сигнальной линией и уровнем дна (вершины).
Голова и плечи
Эта фигура очень похожа на тройную вершину. Единственное отличие — вторая вершина находится выше первой и третьей, при этом крайние максимумы (плечи) расположены примерно на одном уровне. На практике допускается различие в высоте плеч.
Сигналом на продажу также выступает пробой линии шеи. Приведем еще один вариант входа в сделку: дождаться успешного пробоя линии шеи, а затем открыть позицию после тестирования уровня сопротивления, расположенного ниже уровня шеи.
Точка входа в таком случае надежней, но часть потенциальной прибыли упускается.
Перевернутая голова и плечи — противоположная формация, возникающая на падающем тренде и формирующая новый «бычий» тренд.
Двусторонние фигуры. Клин
Клин — это направленная вверх или вниз фигура с формой треугольника. В отличие от вымпела, линии клина имеют одну направленность — восходящую или нисходящую. От флага клин отличает разный наклон этих линий.
Как и большинство фигур, формируется после остановки тренда, когда колебания цены начинают затухать. Существует две вариации паттерна:
1) восходящий клин — с растущими минимумами и максимумами;
2) нисходящий клин — с падающими минимумами и максимумами.
Может представлять собой как фигуру продолжения тренда, так и разворотную формацию. Необходимо помнить один ключевой момент: успешная реализация клина закачивается выходом цены в сторону, противоположную направленности клина.
Сигналом для открытия короткой позиции по «бычьему» клину является пробой вниз линии поддержки.
Сделка на покупку по «медвежьему» клину совершается после пробоя наверх линии сопротивления.
Необходимые условия возникновения клина:
— линии клина сходятся, но при этом они обе направлены вверх или вниз;
— одна из линий должна быть проведена хотя бы по трем точкам, при этом вторая линия может быть построена по двум точкам.
Восходящий и нисходящий треугольник
Восходящий треугольник представляет собой затухающие колебания цены в виде треугольника с горизонтальным уровнем сопротивления. Нисходящий треугольник имеет горизонтальный уровень поддержки.
Оба паттерна не зависят от предыдущей динамики цен и тренда. «Бычий» треугольник реализуется в последующем росте, «медвежий» треугольник — предвестник падения.
Сигналы на вход в сделку:
— пробой вверх сопротивления восходящего треугольника — покупка;
— пробой вниз поддержки нисходящего треугольника — продажа.
«Бычий» и «медвежий» треугольники используются для совершения сделок на различных таймфреймах.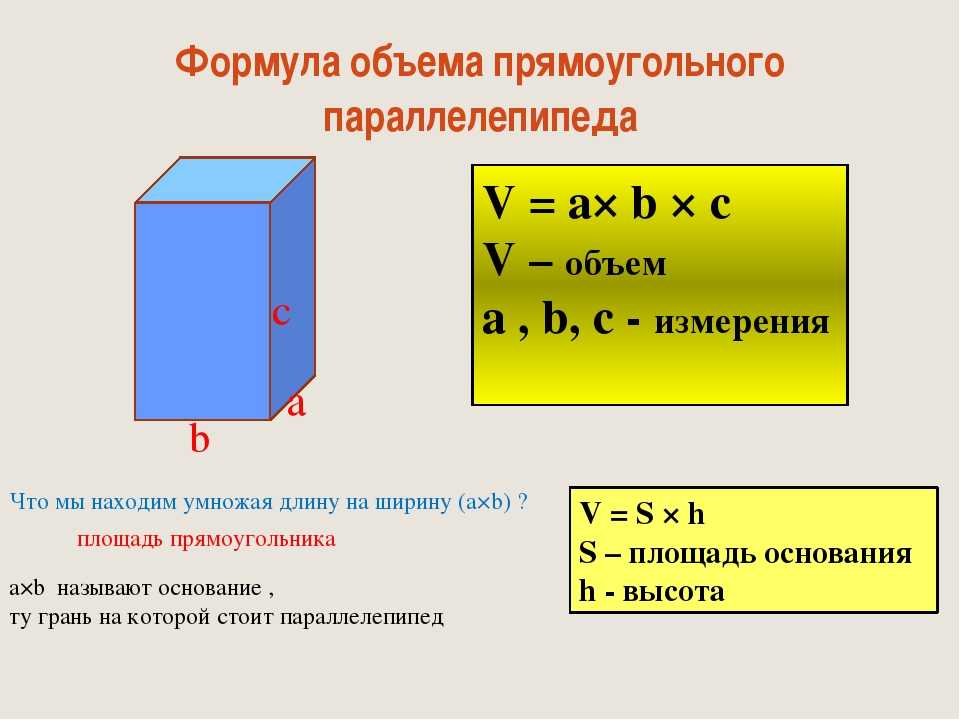
Однако любую фигуру рекомендуется использовать, начиная с часового графика и старше. В этом случае ее достоверность и надежность сигнала будут выше.
Начать торговать
БКС Брокер
Что такое объем прямоугольной призмы? Определение, формула, пример
Вы видите это в коробках, когда берете салфетку или открываете коробку с хлопьями. Вы видите это в книгах, когда удаляете закладки, чтобы начать читать. Вы видите это в ноутбуках, когда заканчиваете печатать свое последнее задание.
Да, речь идет о прямоугольной призме.
Что такое прямоугольная призма?
Прямоугольная призма представляет собой трехмерную фигуру с шестью гранями. Все грани (верхняя, нижняя и боковые грани) призмы прямоугольные, так что все пары противоположных граней конгруэнтны. Он также известен как кубоид. Короче говоря, прямоугольная призма имеет четыре прямоугольные грани и два параллельных прямоугольных основания.
Чем прямоугольная призма отличается от прямоугольника?
Начнем с того, почему важно знать разницу между разными типами форм?
Каждая фигура имеет определенные свойства, и эти свойства помогают узнать такие величины, как объем, площадь поверхности и т.
д. Помните, что вы не поймете, что нельзя класть прямоугольник поверх треугольника, если не знаете, чем они отличаются.
Разница между прямоугольником и прямоугольной призмой
| Прямоугольник | Прямоугольная призма |
| Это двумерная фигура. | Это трехмерная фигура. |
| Имеет четыре стороны. | Шесть граней, восемь вертикалей и двенадцать ребер. |
| Состоит из четырех сторон, причем противоположные стороны имеют одинаковую длину. | Он состоит из шести прямоугольников, соединенных вместе. |
| Имеет ширину и длину. | Имеет ширину, высоту и длину. |
| Состоит из двух пар лесок. | Состоит из трех пар прямоугольников. |
Теперь, когда мы знаем, что такое прямоугольные призмы, давайте посмотрим, как мы можем вычислить их объем.
Формула объема прямоугольной призмы
Умножив площадь основания призмы на ее высоту, вы получите объем призмы.
Другими словами, объем призмы = площадь основания × высота.
Поскольку основанием прямоугольной призмы является сам прямоугольник, объем прямоугольной призмы по формуле, приведенной выше, будет:
Объем прямоугольной призмы (V) = l × w × h
Где,
«l» означает длину основания,
«w» означает ширину основания,
«h» означает высоту объем прямоугольной призмы с длиной основания 9дюймов, ширина основания 6 дюймов и высота 18 дюймов соответственно.
Решение:
Здесь
Длина (l) = 9 дюймов
Ширина (b) = 6 дюймов l × w × h = 9 × 6 × 18 = 972 кубических дюйма.
Пример 2: Найдите высоту прямоугольной призмы, площадь основания которой равна 20 квадратных единиц, а объем равен 60 кубическим единицам.
Решение:
Дана площадь основания прямоугольной призмы = 20 квадратных единиц
И объем прямоугольной призмы = 60 кубических единиц
Теперь, применяя формулу объема прямоугольной призмы,
площадь основания × высота = 60 куб.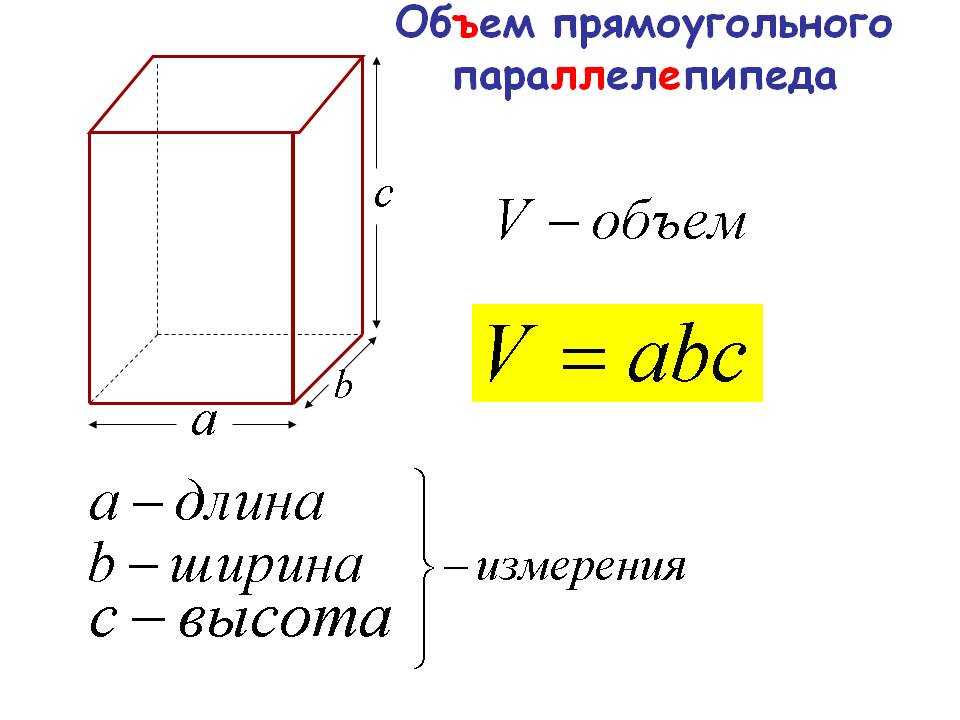
ед.
⇒ 20 × высота = 60
⇒ высота = 60 ÷ 20 ед.
⇒ высота = 3 ед. дюймов, высота = 20 дюймов, а объем = 2160 кубических дюймов.
Решение:
Здесь
Длина (l) = 12 дюймов
Высота (h) = 20 дюймов
Объем (V) = 2160 куб. ш × в
⇒ 2160 = 12 × ш × 20
⇒ 2160 ÷ (12 × 20) = ш
⇒ 9 = ш
Следовательно, ширина (ш) = 9 дюймов.
Площадь = l × w = 12 × 9 = 108 кв. дюймов.
Практические задачи
1 Выберите правильную формулу для определения объема прямоугольной призмы?V = площадь основания – высота V = площадь основания + высота V = площадь основания × высота V = площадь основания / высота Правильный ответ: V = площадь основания × высота 2 Найдите площадь основания прямоугольной призмы, высота которой 7 дюймов, а объем 343 кубических дюйма.7 кв. дюймов 2401 кв. дюймов 49 кв. дюймов 21 кв. дюймов Правильный ответ: 49 кв. дюймов 3 Найдите объем прямоугольной призмы, площадь основания которой 35 см, а высота 10 см.345 куб.см 350 куб.см 354 куб.см 360 куб.см Правильный ответ: 350 куб.см Каждая игра на SplashLearn основана на учебной программе и разработана с научной точки зрения. Чтобы расширить знания вашего ребенка по математике и позволить ему бесстрашно практиковать математику, вы можете бесплатно зарегистрироваться в SplashLearn! Часто задаваемые вопросыКак еще называется прямоугольная призма? Прямоугольная призма также известна как параллелепипед. Совпадает ли объем прямоугольной призмы с прямоугольным параллелепипедом? Да, объем прямоугольной призмы такой же, как объем прямоугольного параллелепипеда. Что такое наклонная прямоугольная призма? Наклонная прямоугольная призма представляет собой призму с шестью прямоугольными гранями, но боковые грани не перпендикулярны основаниям. Какова площадь поверхности прямоугольной призмы? Площадь поверхности прямоугольной призмы равна сумме площадей каждой из ее граней. Объем и площадь поверхности прямоугольной призмы (Видео)Стенограмма практики Здравствуйте! Сегодня мы рассмотрим самую распространенную трехмерную фигуру — прямоугольную призму, также известную как прямоугольное тело. Как и в случае с большинством трехмерных фигур, мы можем рассчитать объем и площадь поверхности, используя относительно простые формулы. Но прежде чем мы это сделаем, нам нужно определить несколько терминов. Прямоугольная призма или прямоугольное твердое тело представляет собой шестигранный объект, каждая сторона которого также называется гранью и представляет собой прямоугольник. Пример реальной проблемы объема: если нам нужно залить фундамент для прямоугольного здания — нам нужно измерить площадь каждой стороны здания, чтобы узнать, сколько бетона нам нужно подготовить. Таким образом, если нам нужно залить фундамент размером \(42,5\text{м в длину}\times{20\text{м в ширину}}\times{0,4\text{м в глубину}}\) (это высота), мы можно использовать эти размеры, чтобы найти объем нашего фундамента, подставив его в нашу формулу: \(V=lwh\) 92\). Это удачное название, потому что мы буквально находим площадь внешней поверхности объекта. Итак, все, что нам нужно сделать, это найти площадь каждой грани или стороны нашей прямоугольной призмы, а затем сложить все стороны вместе. Если мы посмотрим на призму, которую мы построили из наших маленьких сантиметровых кубиков, мы увидим квадраты на гранях. Каждый из этих квадратов равен квадратному сантиметру. С этого ракурса мы можем видеть три из шести лиц. Верхняя грань состоит из 15 квадратов. Эта задача позволяет нам увидеть квадратные сантиметры, но большинство задач на площадь поверхности не показывают нам квадраты. Мы просто узнаем размеры прямоугольной призмы, например: Здесь мы видим, что наша призма имеет длину 10 метров, ширину 5 метров и высоту 4 метра. Соответствующие ребра на противоположных сторонах будут одинаковыми, так как это прямоугольная призма. Чтобы найти площадь поверхности, я могу использовать формулу площади поверхности для прямоугольных призм: \(SA=2lw+2lh+2wh\)
Эта формула даст нам площадь поверхности, если мы подставим наши длину, ширину и высоту. Не путайте, какие стороны являются длиной, шириной и высотой. В зависимости от того, как призма ориентирована на странице, может показаться, что 10 м — это длина, но на самом деле это может быть ширина или высота. Это не имеет значения! Но для наших целей, допустим, 10 м — это длина, 5 м — ширина, 4 м — высота. Когда мы подставляем все это, это выглядит так:
Не слишком сложно, но стоит потратить время на то, чтобы посмотреть, что на самом деле делает эта формула: \(SA=2lw+2lh+2wh\)
Первый член , \(2lw\), в два раза больше длины, умноженной на ширину. |
Он определяется формулой 2(lw + wh + hl), где l — длина, w — ширина, а h — высота прямоугольной призмы.
3\)!
