Теорема Фалеса — доказательство, применение в геометрии
Краткое описание
Фалес хорошо известен в истории как талантливый геометр. Именно этому человеку многие учёные приписывают открытие и доказательство многих теорем. Фалес смог разработать весьма интересный способ определения точного расстояния от берега до видимого невооружённым взглядом водного транспорта. Некоторые историки склонны полагать, что именно для этих целей учёный использовал признак некоего сходства прямоугольных треугольников. Современные последователи великого математика высоко ценят все его достижения, что он смог вывести и доказать многочисленные теоремы, законы.
Наиболее логическое доказательство правильности предположений на основании единых положений, принятых за проверенные истины, было изобретено именно греками. Сегодня историкам трудно сказать, что именно в научном перечне принадлежит Фалесу. Конечно, благодаря этому талантливому человеку Греция обрела не только философа и математика, но и естествоиспытателя.
Перед изучением теоремы обязательно нужно понять, что параллелограмм — это самый обычный четырёхугольник, у которого все противоположные стороны попарно параллельны. А вот трапеция является специфическим четырёхугольником, у которого две стороны параллельны друг другу, а две другие стороны обладают противоположными характеристиками. Изучение этой темы состоит из нескольких частей, так как первым делом нужно ознакомиться с теорией, а только потом можно приступать к решению задач.
Основные понятия
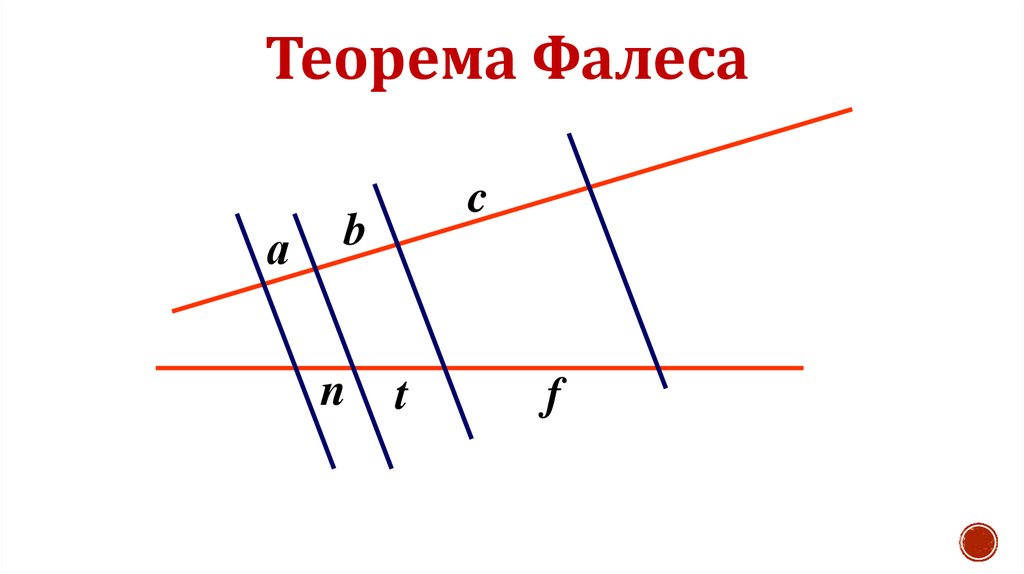
Фалесом было доказано, что две прямые линии RF и NS называются параллельными исключительно в том случае, если они проложены в одной плоскости и не пересекаются между собой вне зависимости от длины. Это правило всегда обозначают как RF || NS.
Абсолютно все существующие точки конкретной прямой располагаются на неизменном расстоянии от второй линии.
В качестве наглядного примера можно рассмотреть ситуацию, когда перпендикуляры RF, NS, EF относятся к одной и той же прямой РЕ и параллельны между собой. При этом прямая РЕ перпендикулярна ко всем остальным линиям. Итоговая длина сформированного отрезка перпендикуляра, расположенного между двумя параллельными прямыми, соответствует расстоянию средних линий. При изучении пространственной теоремы обязательно нужно понимать, что сразу восемь углов возникает при пересечении двух параллельных прямых третьей прямойю
Представленная специалистами формулировка теоремы Фалеса содержит много нюансов, в которых обязательно должен разбираться каждый человек, планирующий решать различные математические задачи.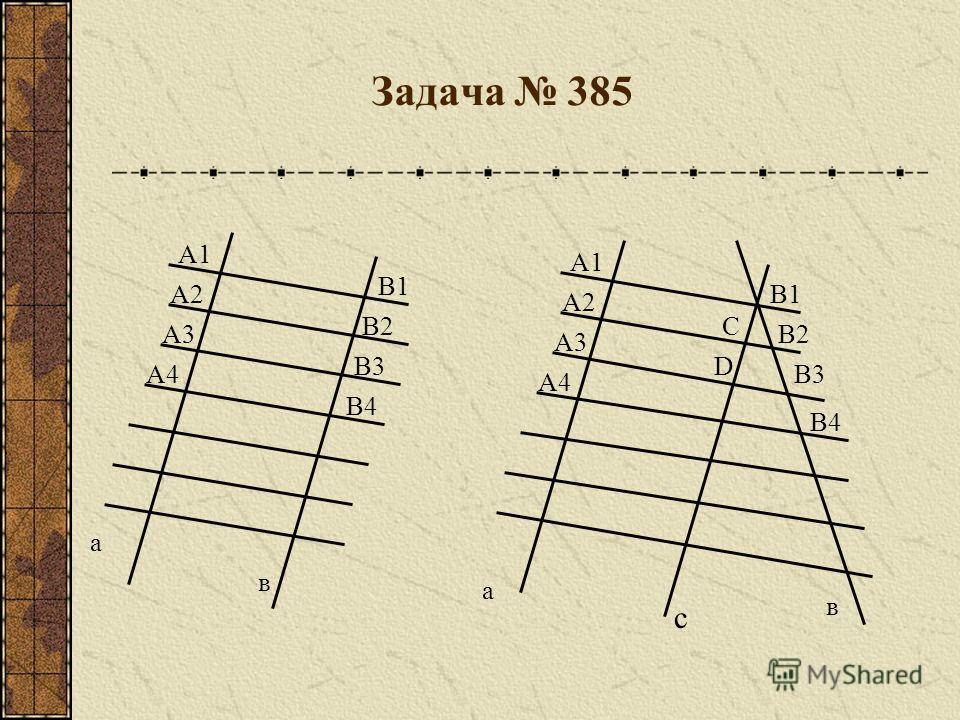 В противном случае будет сложно избежать самых распространённых ошибок. Даже кратко изложенная теория позволяет разобраться в главных математических тонкостях. Чтобы ученику стало понятно то, как именно нужно использовать теорему, можно задействовать специальные таблицы, которые помогут расширить итоговые математические возможности.
В противном случае будет сложно избежать самых распространённых ошибок. Даже кратко изложенная теория позволяет разобраться в главных математических тонкостях. Чтобы ученику стало понятно то, как именно нужно использовать теорему, можно задействовать специальные таблицы, которые помогут расширить итоговые математические возможности.
Научное пояснение значений
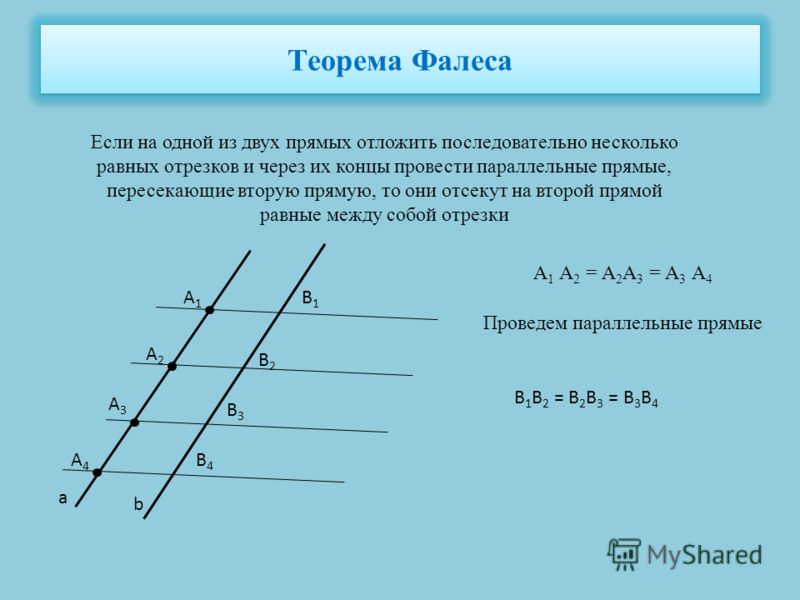
Если постараться поочерёдно отложить сразу несколько одинаковых отрезков только на одной из двух прямых линий, а потом провести прямые через конечные точки, которые смогут пересечь вторую прямую, то именно на второй прямой они смогут отсечь равные отрезки. Развёрнутая формулировка этой темы в геометрии носит название теоремы о пропорциональных геометрических отрезках. В качестве наглядного примера следует ознакомиться с этой формулой: S 1S2/N1В2 = S2S3/N2N3 = S1S3/N1N3.
Важные нюансы:
- Востребованная теорема греческого математика является частным случаем закона о пропорциональных отрезках, так как идентичные отрезки можно считать пропорциональными с элементарным коэффициентом ровности, который равняется единице.
- В изучаемой теореме нет каких-либо ограничений и требований на взаимное расположение всех секущих. Это связано с тем, что она верна как для пересекающихся прямых, так и для параллельных линий. На итоговый результат совершенно не влияет то, где находятся отрезки на секущих.
Для изучения всех нюансов этой темы необходимо рассмотреть вариант, который демонстрирует ситуацию с несвязанными парами отрезков. К примеру: существующий угол пересекает прямые LL1 || ВВ1 || СС1 || КК1 и при этом LB = СК. Через точки L и С проводят прямую линию, которая будет расположена параллельно другой стороне сформированного угла LB2В1L1 и СК2К1С1. Свойства параллелограмма тоже имеют свои особенности:
- LB2 = L1В1.

- СК2 = С1К1.
Треугольники ? JSS2 и ? СКК2 равны. Они построены на основании второго признака равенства геометрических фигур. Если целью задачи является безусловное доказательство при параллельных прямых, тогда нужно выполнить несколько несложных действий. Следует провести прямую SC. Углы SCK и JSC равны как внутренние накрест лежащие при прямых СК и JS, а также секущей SC. А вот углы JCS и CSK равны как внутренние накрест проложенные линии при параллельных прямых JC и SK, секущий SC. Тогда по второму признаку равенства треугольников геометрические фигуры JSC и KCS равны. Из этого вытекает, что JC = SK и JS = СК.
Ключевые особенности теоремы
Когда учащийся попробует на одной из двух прямых линий отложить разные отрезки, а потом через их концы провести параллельные линии, которые будут пересекать вторую прямую, то в итоге на второй прямой они обязательно отсекут идентичные между собой отрезки. Даже в школьной математике часто пользуются обобщённой теоремой Фалеса: те отрезки, которые формируются только благодаря параллельным прямым на одной линии, являются пропорциональными по отношению к другой прямой линии.
Даже в школьной математике часто пользуются обобщённой теоремой Фалеса: те отрезки, которые формируются только благодаря параллельным прямым на одной линии, являются пропорциональными по отношению к другой прямой линии.
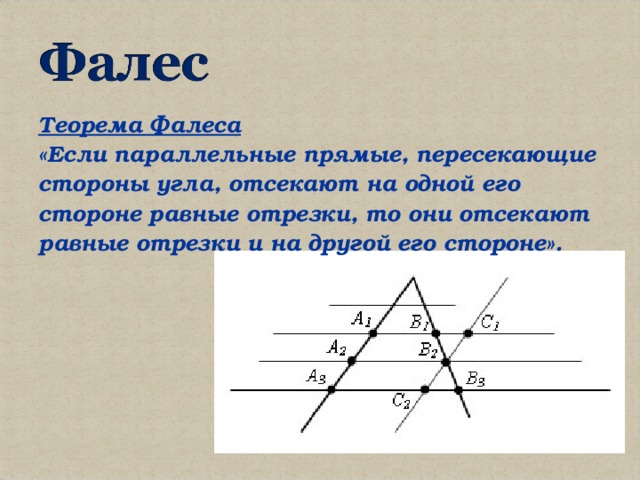
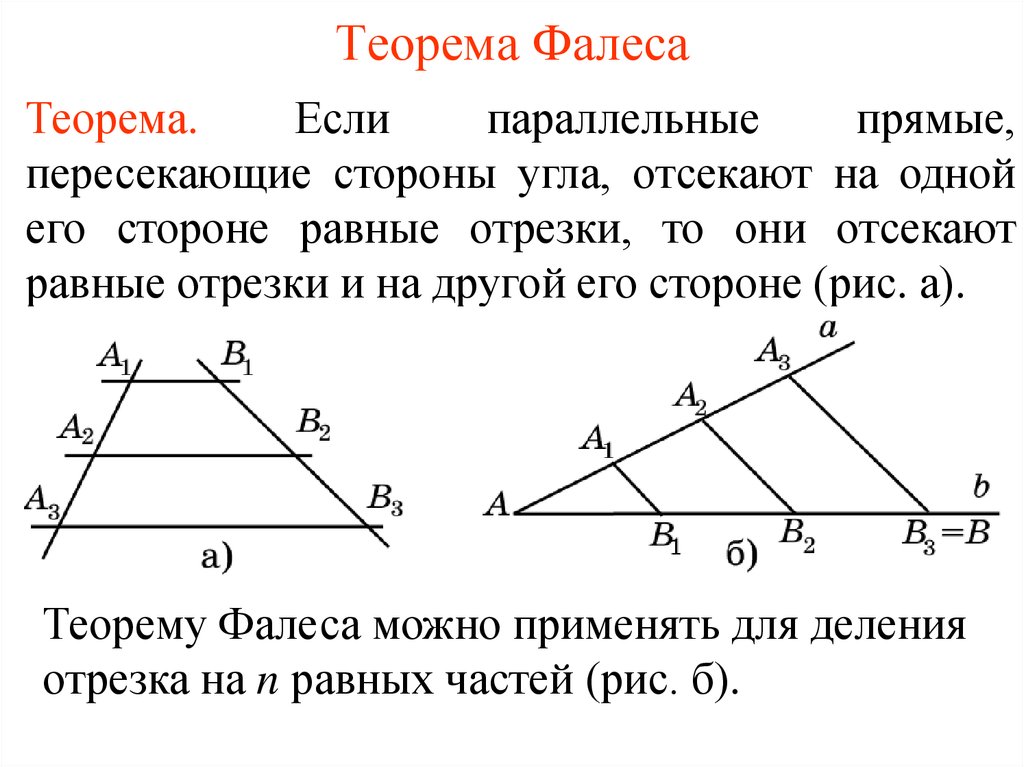
Записи с идеями Фалеса не удалось сохранить до наших дней, из-за чего историкам приходится восстанавливать информацию из разных источников. Специалистам удалось доказать, что математик из Греции вывел 7 теорем для геометрии. Основное правило гласит, что если параллельные линии, у которых пересекаются стороны угла, отсекают только на одной его стороне равные отрезки, то аналогичная ситуация происходит и на другой его стороне.
Наглядное доказательство
В качестве примера можно взять точки Н1, Н2 и Н3, которые служат для обозначения пересечения используемых параллельных отрезков только с одной стороны угла.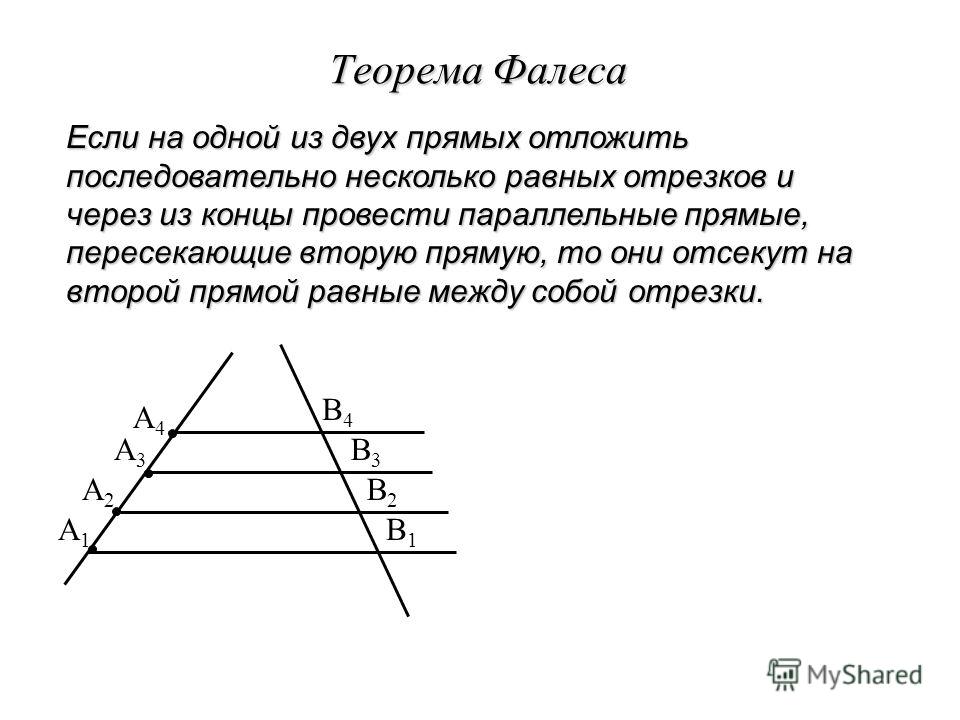 А вот для обозначения точек пересечения этих прямых с другой стороны угла используется К1, К2 и К3. Если через точку К2 провести небольшую прямую Т1 и Т2, а также параллельную Н1 и Н2, то в итоге получится обычный параллелограмм: Н1Т1КН2 и Н2К2Т2Н3. Из этого результата можно понять, что Н1Н2 = Т1К2 и Н2Н3 = К2Т2. Этот результат был достигнут благодаря тому, что Н1Н2 = Н2Н3, а Т1К1 = К2Т2.
А вот для обозначения точек пересечения этих прямых с другой стороны угла используется К1, К2 и К3. Если через точку К2 провести небольшую прямую Т1 и Т2, а также параллельную Н1 и Н2, то в итоге получится обычный параллелограмм: Н1Т1КН2 и Н2К2Т2Н3. Из этого результата можно понять, что Н1Н2 = Т1К2 и Н2Н3 = К2Т2. Этот результат был достигнут благодаря тому, что Н1Н2 = Н2Н3, а Т1К1 = К2Т2.
? Т1В2В1 = ? Т2В2В3 — это утверждение актуально только по отношению ко второму признаку равенства треугольников. Можно понять, что Т1В2 = В2Т2, < Т1В2В1 = < Т2В2В3 (как вертикальные треугольники). < В1Т1В2 = < = В3Т2В2 (как внутренние накрест лежащие треугольники при прямых линиях В1Т1 и Т2В3, а также секущем отрезке Т1Т2). Из установленного равенства треугольников получается, что В1В2 = В2В3. На этом можно считать, что теорема в геометрии полностью доказана. Если всё сделано правильно, то в итоге должна получиться следующая формула: (АВ = ВТ, АА1 || ВВ1 ||ТТ1) А1В1 = В1Т1.
Интересные нюансы из истории
Обобщение теоремы позволило современным математикам понять пропорциональность конкретного отрезка. Действующее правило гласит, что параллельные прямые, которые пересекают стороны угла, отсекают пропорциональные отрезки. Формула выглядит следующим образом: АА1 || ВВ1 || ТТ1 → АВ ВС = А1В1/В1Т1.
Применение обобщённой теоремы имеет несколько интересных исторических фактов:
- За пределами русской литературы широко распространённой теоремой известного математика Фалеса принято называть раздел евклидовой геометрии. Утверждение касается того, что сформированный угол, который базируется на определённом диаметре окружности, является прямым. Доказательство этой удивительной теоремы действительно приписывают Фалесу, так как этому есть письменное доказательство, которое удалось сберечь.
- Теоремы Менелая, Фалеса и Чевы используются в первую очередь тогда, когда в условиях задачи были даны соотношения между отрезками.
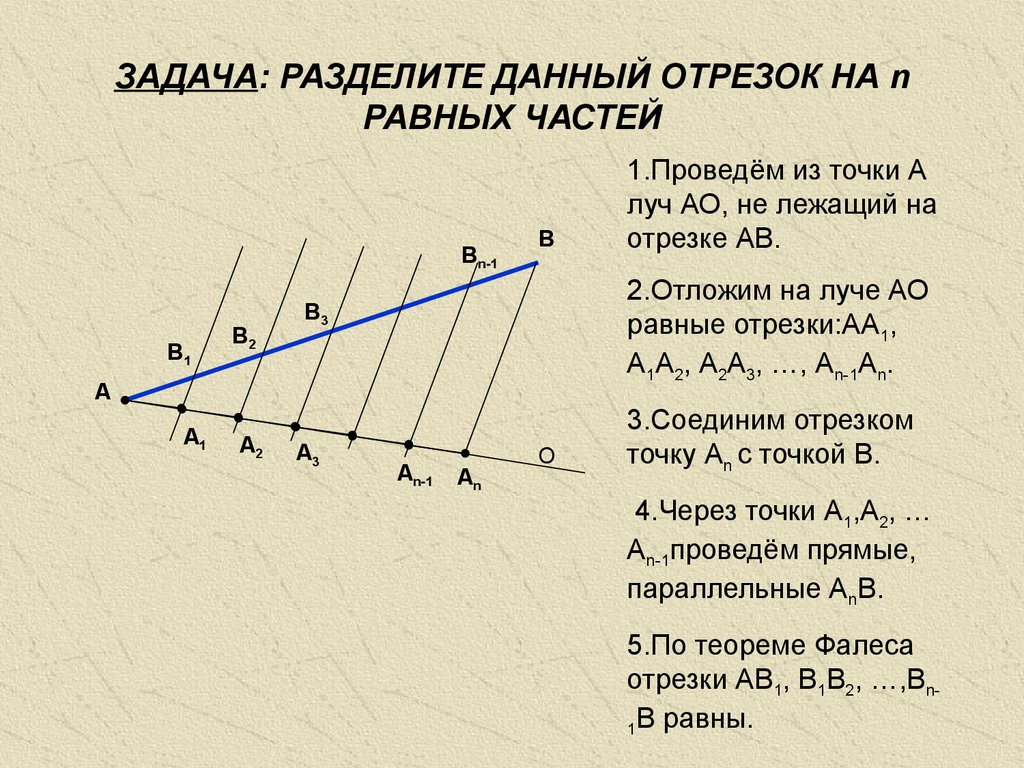
 Чаще всего для поиска правильного решения приходится проводить вспомогательный отрезок.
Чаще всего для поиска правильного решения приходится проводить вспомогательный отрезок. - В морской отрасли активно используется теорема при построении навигации. Она применяется в качества основного правила о том, что столкновение кораблей, которые движутся по волнам с одинаковой скоростью, неизбежно, если сохранится ранее заданный курс движения.
- Известная в Аргентине группа представила песню, которая посвящена теореме. В представленном клипе для этой песни было приведено доказательство для прямой теоремы используемых пропорциональных отрезков.
- Все азы геометрии Фалес постигал на территории Древнего Египта.
Теорему талантливого учёного из Греции активно изучают в 8 классе на уроках геометрии.
Вариации и обобщения
Используемая в геометрии теорема Фалеса с доказательством имеет много нюансов, которые нужно учитывать тем, кто решил изучить эту тему. Если абсолютно идентичные отрезки начинаются от вершины треугольника, то и обратная форма теоремы будет уместной. Для пересекающихся линий предназначена следующая формулировка: если 2 линии пересекают ближайшие прямые, отсекая при этом равные между собой отрезки начиная от самой верхней части, то такие прямые считаются параллельными. Эти нюансы часто не учитывают учащиеся, из-за чего допускают грубые ошибки.
Если абсолютно идентичные отрезки начинаются от вершины треугольника, то и обратная форма теоремы будет уместной. Для пересекающихся линий предназначена следующая формулировка: если 2 линии пересекают ближайшие прямые, отсекая при этом равные между собой отрезки начиная от самой верхней части, то такие прямые считаются параллельными. Эти нюансы часто не учитывают учащиеся, из-за чего допускают грубые ошибки.
Максимального сходства отрезков на обеих секущих линиях нужно требовать в том случае, если секущие являются параллельными. В противном случае утверждение становится неактуальным. Учащимся нелишним будет узнать следующий закон: L является математическим соответствием между двумя точками прямых линий w и q. Тогда элементарное множество прямых D L (D) будет множеством касательных к некоторому коническому сечению. В приведённой Фалесом теореме в роли конического сечения будет выступать удалённая точка, которая максимально соответствует направлению параллельных линий.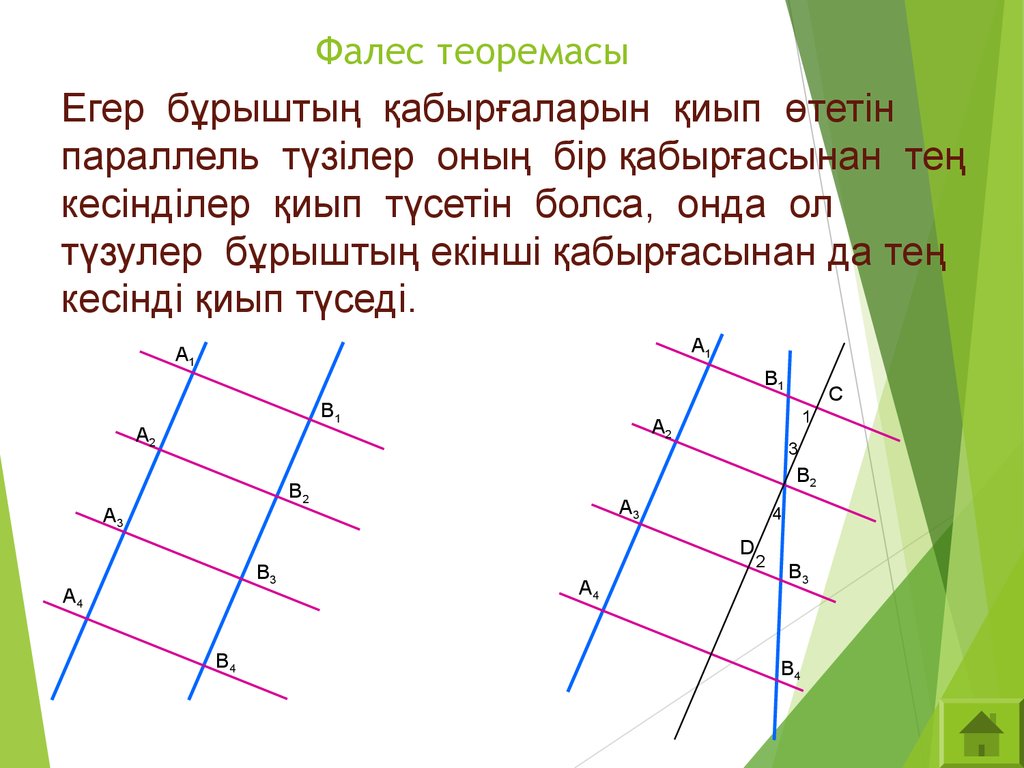
Огромные заслуги талантливого математика
В своё время Фалес Милетский был главным основателем Ионийской школы. Неоценимой заслугой этого человека было создание многофункциональной научной геометрии. Великий учёный специфического египетского искусства измерения смог самостоятельно создать полезную для человечества дедуктивную геометрию.
Благодаря целеустремлённости Фалеса все доступные в то время знания были оперативно переведены в научную категорию. Математик смог донести результаты своих наблюдений до того уровня, который подходит для учеников школ, указав при этом на определённый комплекс понятий. Доказанная талантливым и наблюдательным Фалесом теорема играет одну из самых важных ролей в геометрии. Она была хорошо известна не только в Древнем Египте, но и в других крупных странах. Актуальность и многогранность теоремы позволяет специалистам ежедневно строить новые здания, дороги и другие конструкции.
Фалес смог при помощи обычного посоха и тени установить габариты египетской пирамиды. Для этого он в обычный ясный день закрепил свой массивный посох на том участке, на котором заканчивалась тень от величественного сооружения. Он весь день прождал того момента, когда итоговая длина имеющейся тени от посоха максимально сравнялась с его высотой, после он измерил длину тени.
Благодаря этому он смог доказать всем, что длина одной тени имеет прямое отношение к другой тени, а вот сама высота посоха прямо пропорциональна высоте пирамиды. Эти соображения учёного поразили могущественного фараона по имени Амасис.
Разноцветные кусочки случайных отражений — ЖЖ
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Фалес и дедуктивный метод
Древнегреческая математика
Когда мы думаем о древней математике, на ум приходят древние греки как основоположники расчетов, которыми мы пользуемся каждый день. Работы великих древнегреческих математиков пронизывают все сферы жизни, от запуска ракет в космос до бухгалтерского учета и от архитектуры до DIY. Греческий дедуктивный подход к математике, вероятно, является величайшим наследием, которое они передали миру, и одной из основ современного общества.
Работы великих древнегреческих математиков пронизывают все сферы жизни, от запуска ракет в космос до бухгалтерского учета и от архитектуры до DIY. Греческий дедуктивный подход к математике, вероятно, является величайшим наследием, которое они передали миру, и одной из основ современного общества.
Откройте для себя еще 44 статьи по этой теме
Не пропустите эти статьи по теме:
- История научного метода
- Евклид
- Психология Аристотеля
- Кто изобрел научный метод?
- Медицина
Даже великие физики-теоретики, такие как Стивен Хокинг, опираются на работы греков как на основу своих изящных теорий о том, как устроена Вселенная. Такие математики, как Пифагор, Евклид и Архимед, все еще знакомы нам, спустя более двух тысячелетий, и их труды до сих пор преподаются в школах и колледжах по всему миру.
Истоки древнегреческой математики
| Фалес Милетский (общественное достояние) |
признать, но греки были первыми, кто переместил математику в область теории, рассуждений и дедукции, а не измерений. Египтяне стремились использовать математику в практических целях и применяли грубую силу для решения задач; например, они не беспокоились о том, чтобы найти точное число Пи, и, пока оно служило их целям, было достаточно приблизительного значения. Вавилоняне смотрели на отношения, лежащие в основе чисел, немного больше, чем египтяне, но даже их немного более абстрактная работа носила в основном эмпирический характер.
Египтяне стремились использовать математику в практических целях и применяли грубую силу для решения задач; например, они не беспокоились о том, чтобы найти точное число Пи, и, пока оно служило их целям, было достаточно приблизительного значения. Вавилоняне смотрели на отношения, лежащие в основе чисел, немного больше, чем египтяне, но даже их немного более абстрактная работа носила в основном эмпирический характер.
Греки изменили это, отыскав основополагающие правила и отношения, управляющие числами и функциями. Они полагали, что, поскольку Вселенная совершенна, они могут использовать дедуктивные рассуждения для установления математических фактов без примеси неточных эмпирических измерений. Это смещение фокуса подпитывало большие успехи, которых они достигли в геометрии, алгебре и исчислении, а математические рассуждения даже стали основой логических аргументов.
Фалес (467 г. до н.э. — 49 г.7 г. до н.э.)
Фалес Милетский заслужил свое место в истории как первый из греческих математиков, хотя его часто несправедливо упускают из виду в пользу Пифагора, Архимеда и Евклида. Поскольку у нас нет первоисточников, описывающих его вклад, нам приходится полагаться на более поздних математиков, чтобы заполнить детали. Хотя его вклад, несомненно, был огромен, отсутствие информации помешало ему стать таким же влиятельным, как Евклид или Пифагор, чьи тексты изучались великими исламскими учеными и учеными эпохи Возрождения. 9Теорема Фалеса — углы при основании равнобедренного треугольника равны (Creative Commons) и ошибочные методы решения математических задач и астрономии. Вскоре он начал превосходить своих учителей и начал задаваться вопросом, как числа сочетаются друг с другом, полагая, что этим методам проб и ошибок не хватает элегантности и проверки. Ходят слухи, хотя и не подтвержденные, что он также путешествовал в Вавилон: даже если нет, вполне вероятно, что ему были доступны работы вавилонских математиков.
Поскольку у нас нет первоисточников, описывающих его вклад, нам приходится полагаться на более поздних математиков, чтобы заполнить детали. Хотя его вклад, несомненно, был огромен, отсутствие информации помешало ему стать таким же влиятельным, как Евклид или Пифагор, чьи тексты изучались великими исламскими учеными и учеными эпохи Возрождения. 9Теорема Фалеса — углы при основании равнобедренного треугольника равны (Creative Commons) и ошибочные методы решения математических задач и астрономии. Вскоре он начал превосходить своих учителей и начал задаваться вопросом, как числа сочетаются друг с другом, полагая, что этим методам проб и ошибок не хватает элегантности и проверки. Ходят слухи, хотя и не подтвержденные, что он также путешествовал в Вавилон: даже если нет, вполне вероятно, что ему были доступны работы вавилонских математиков.
Вернувшись в Грецию, Фалес основал школу, чтобы обучать других тому, что знал сам, и пытался установить аксиомы (математические доказательства). Как только эти первые принципы были установлены, он рассудил, что можно вывести все остальные математические законы. Его четыре основных математических доказательства были следующими:
Как только эти первые принципы были установлены, он рассудил, что можно вывести все остальные математические законы. Его четыре основных математических доказательства были следующими:
- Диаметр окружности точно делит окружность пополам
- Углы при основании равнобедренного треугольника равны
- Две пары углов, образованные двумя пересекающимися прямыми, идентичны
- Если одна сторона и два смежных угла треугольника являются общими для другого треугольника, треугольники идентичны.
| Теорема Фалеса — две пары углов, образованные двумя пересекающимися прямыми, идентичны (Creative Commons) . Однако это был первый случай, когда математик попытался заложить основы дедуктивного процесса, и эти первые принципы вызвали взрыв в изучении математики. Используя эти аксиомы, он пришел к выводу, что любой треугольник можно описать окружностью, которая касается всех трех вершин. В Египте он поразил фараона, измерив высоту пирамиды по тени, отбрасываемой солнцем, используя пропорцию. Наследие Фалеса, отца греческой математикиФалес был отцом греческой математики и начал процесс вывода теорем из первых принципов, которыми мы пользуемся до сих пор. Это было лишь частью его наследия, потому что он обучал многих математиков, которые последовали за ним и основывались на его теориях. Одним из них был Пифагор, имя, известное бесчисленному количеству школьников благодаря его знаменитой теории. Круговая теорема: все, что вам нужно знатьGCSE или Общий аттестат о среднем образовании — это академическая квалификация. Этот курс включает в себя многочисленные предметы, изучаемые учащимися средних школ Англии, Уэльса и Северной Ирландии. Все ученики должны изучать английский язык, математику и естественные науки наряду с различными предметами. Теоремы о кругахявляются числом
теорем, связанных с кругом. Термины, которые необходимо знать, чтобы понять теоремы о кругахВам необходимо знать некоторые правила, термины и уравнения для кругов, чтобы решать задачи на различные теоремы о кругах:
Теперь, когда вы знаете все основные термины, давайте разберемся с теоремами о кругах. в деталях. Знакомство с типами теорем о кругахТеоремы о кругах включают несколько теорем. Некоторые фундаментальные теоремы включены в учебную программу GCSE:
Давайте подробно обсудим каждую теорему.
Это одна из важных теорем среди теорем об угле окружности . Рисунок 1: Схема вписанного угла Теорема Величина вписанного угла равна половине значения дуги, на которую он опирается. Обычно доказательство начинается со случая, когда одна сторона вписанного угла является диаметром. Тогда углы внутри окружности являются внешними углами равнобедренного треугольника. В ситуациях, когда сторона вписанного угла не является диаметром, его можно привести к первому соответствующими вспомогательными линиями.
Теорема Фалеса является частным случаем теоремы о вписанном угле. Это было доказано в пропорции 31 st третьей книги Евклида Элементы. Изображение 2: Схема теоремы Фалеса Теорема Фалеса используется для нахождения центра окружности. в
фигура, прямой угол, вершина которого лежит на окружности, всегда отсекает
диаметр окружности.
Теорема об альтернативном отрезке помогает находить углы в окружности. Изображение 3: Диаграмма теоремы об альтернативном отрезке Теорема о альтернативном отрезке утверждает, что угол между касательной и хорда, проходящая через точку касания, равна углу в перекрестном сегмент.
Теорема названа в честь греческого математика и астронома Птолемей. Птолемей использовал эту теорему для создания своей таблицы аккордов. тригонометрическая таблица, которая применялась в астрономии. Теорема Птолемея Произведение диагоналей равно сумме произведений двух пар противоположных сторон.Рисунок 4: Теорема Птолемея Теорема Птолемея утверждает, что если выпуклый четырехугольник ABCD
вписанной в окружность сумма произведений двух пар противоположных сторон равна
произведение двух диагоналей.
Теорема Милна-Томсона о круге — это утверждение, которое обеспечивает новый поток функция потока жидкости. Изображение 5: Обобщенное изображение теоремы Милна-Томсона Пусть w = f (z) будет комплексной функцией тока для течения жидкости без жестких границ и особенностей в пределах |z| = а. Если круговой цилиндр |z| = A помещается в этот поток, сложный потенциал для нового потока определяется: Изображение 6: Формула
Изображение 6: Теорема о пяти кругах, диаграмма Теорема о пяти окружностях утверждает, что если центры пяти окружностей общей шестой окружности, и они пересекаются друг с другом по цепочке на одном и том же круг, затем линии, соединяющиеся со вторыми точками пересечения, образуют пентаграмма.
I маг 7: Диаграмма теоремы о шести кругах
в треугольнике каждая окружность касается двух сторон треугольника.
Теорема касательной окружности включает две теоремы: Теорема 1:Радиус получается соединением центра и точки касания. касательная в точке окружности лежит под прямым углом к радиусу. Рисунок 8: Диаграмма теоремы 1 Теорема 2:Теорема утверждает, что если провести две касательные из внешней точки на окружность, то они имеют две равные касательные. Касательный сегмент подразумевает что линия должна соединять внешнюю точку с точкой касания. Здесь АС=ВС. Взгляните на следующую схему: Изображение 9. Теорема диаграммы 2
в программе ЕГЭ. Получение высоких оценок по теореме о круге во многом зависит от способностей
Учащийся должен распознавать и запоминать различные правила углов и формулы окружности. |

 Чаще всего для поиска правильного решения приходится проводить вспомогательный отрезок.
Чаще всего для поиска правильного решения приходится проводить вспомогательный отрезок. 19, 2008 03:44 pm Теорема
19, 2008 03:44 pm Теорема
 Врага надо знать в лицо. А остальные части тела (ну это опять о теореме) у геометрии меня мало интересовали:)))
Врага надо знать в лицо. А остальные части тела (ну это опять о теореме) у геометрии меня мало интересовали:))) вот до чего сегодняшние дети прогрессивные.
вот до чего сегодняшние дети прогрессивные.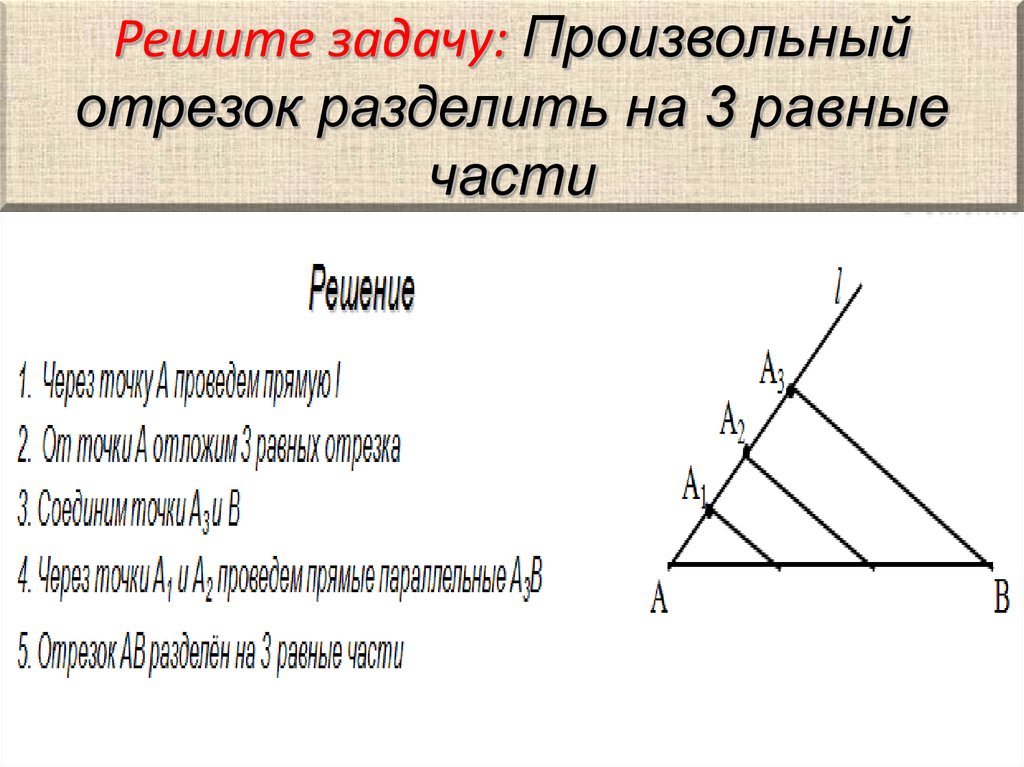 Я потом напишу. 🙂 Жду теперь следующей возможности проверить д.з. по истории с нетерпением!
Я потом напишу. 🙂 Жду теперь следующей возможности проверить д.з. по истории с нетерпением!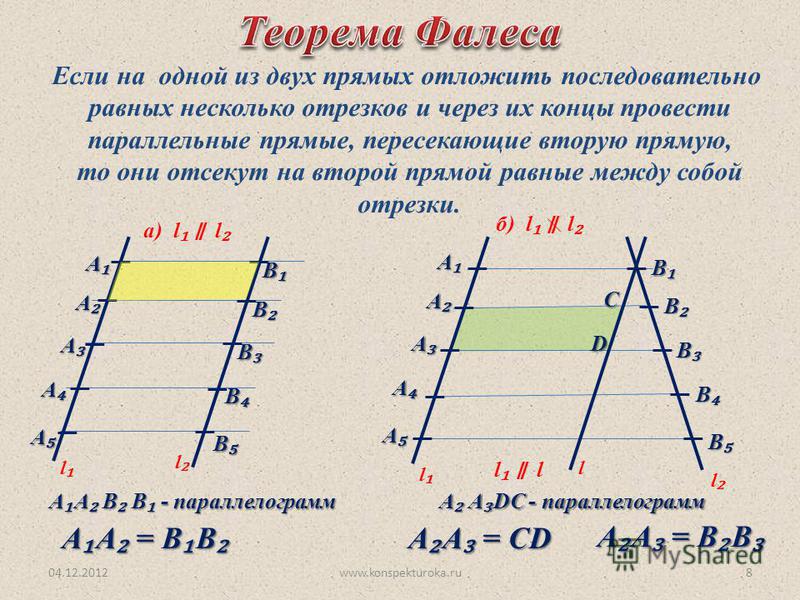 .
. Говорю, что хорошо, что папа спросил, а не учительница, на что отпрыск ответствовал, чсто никто бы не заметил, но я думаю, как минимум, учительница оценила бы. 🙂
Говорю, что хорошо, что папа спросил, а не учительница, на что отпрыск ответствовал, чсто никто бы не заметил, но я думаю, как минимум, учительница оценила бы. 🙂 . Но, думаю, что — да, потому что он только что развлекался фотошопом, а не геометрией. 🙂
. Но, думаю, что — да, потому что он только что развлекался фотошопом, а не геометрией. 🙂 мне тоже стыдно, но я не помнила точное название теоремы, пока не посмотрела в комментах. только помнила что что-то похожее на «фаллос» 🙂
мне тоже стыдно, но я не помнила точное название теоремы, пока не посмотрела в комментах. только помнила что что-то похожее на «фаллос» 🙂 з., но приходилось, потому что, эх, без контроля уроки переставали делаться. И я как-то сформулировала намерение, чтобы мне было приятно это делать. Приятно стало — не то слово — ярчайшие впечатления! :)))
з., но приходилось, потому что, эх, без контроля уроки переставали делаться. И я как-то сформулировала намерение, чтобы мне было приятно это делать. Приятно стало — не то слово — ярчайшие впечатления! :))) :)) Чтобы не повадно было.
:)) Чтобы не повадно было.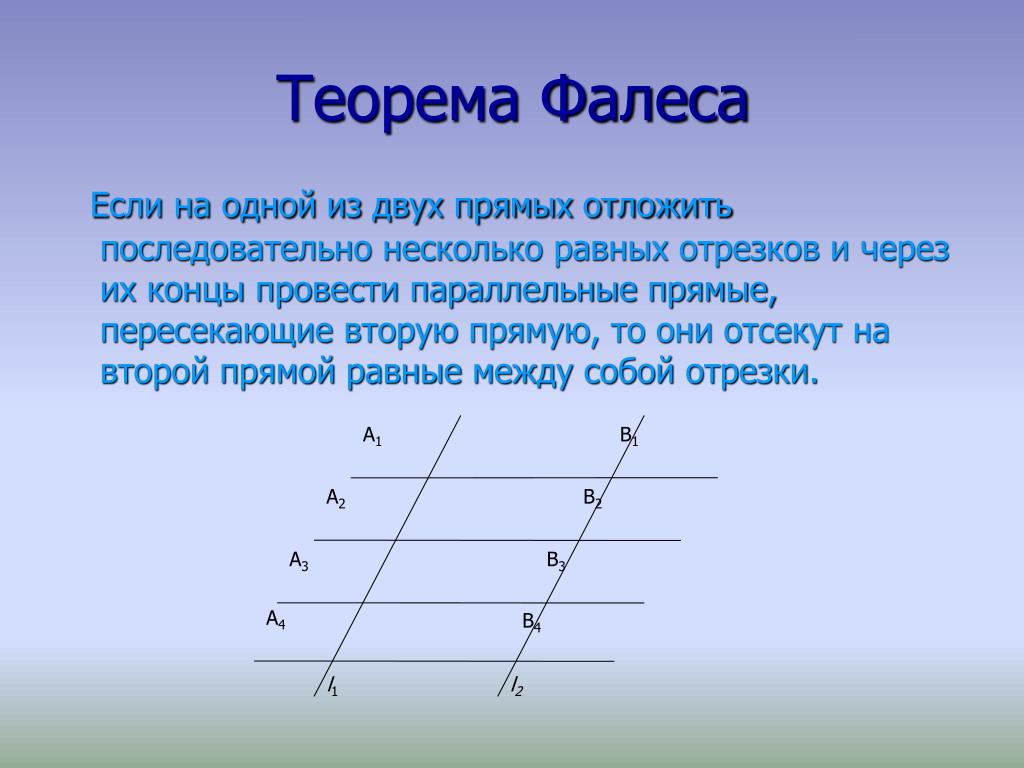 Он рассудил, что если солнце отбрасывает тень от посоха, длина которой равна длине посоха, то тень, отбрасываемая пирамидой, также будет такой же, как и ее высота.
Он рассудил, что если солнце отбрасывает тень от посоха, длина которой равна длине посоха, то тень, отбрасываемая пирамидой, также будет такой же, как и ее высота.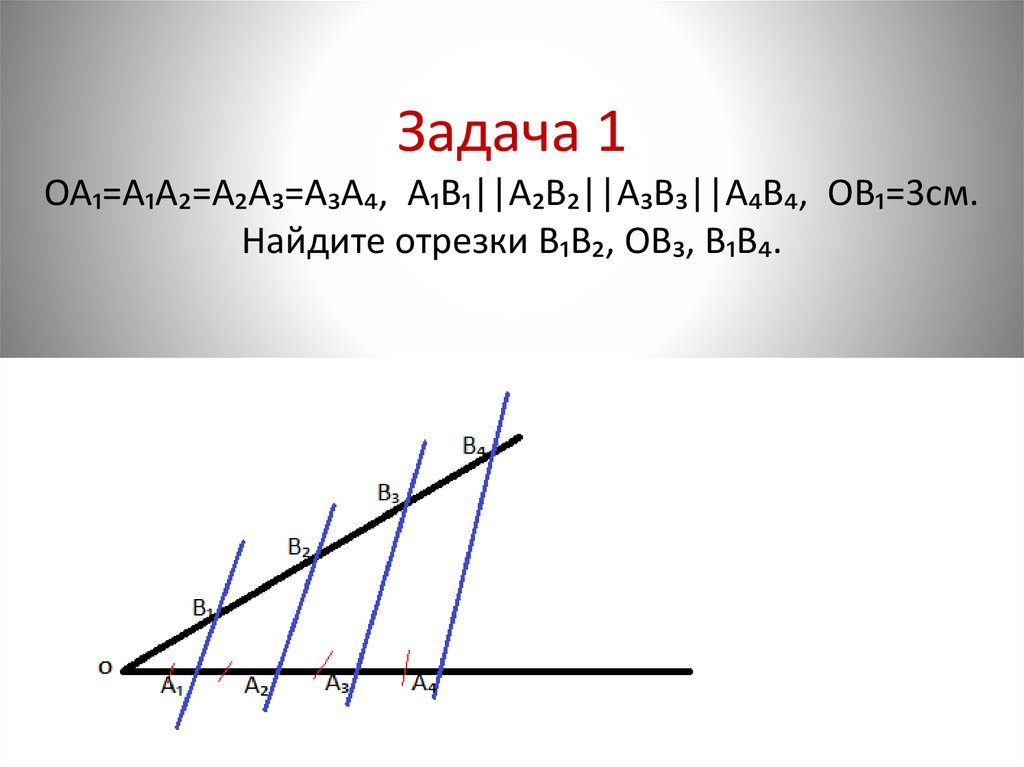 Это важный компонент GCSE
учебный план. Давайте подробно обсудим тонкости теорем круга.
Это важный компонент GCSE
учебный план. Давайте подробно обсудим тонкости теорем круга.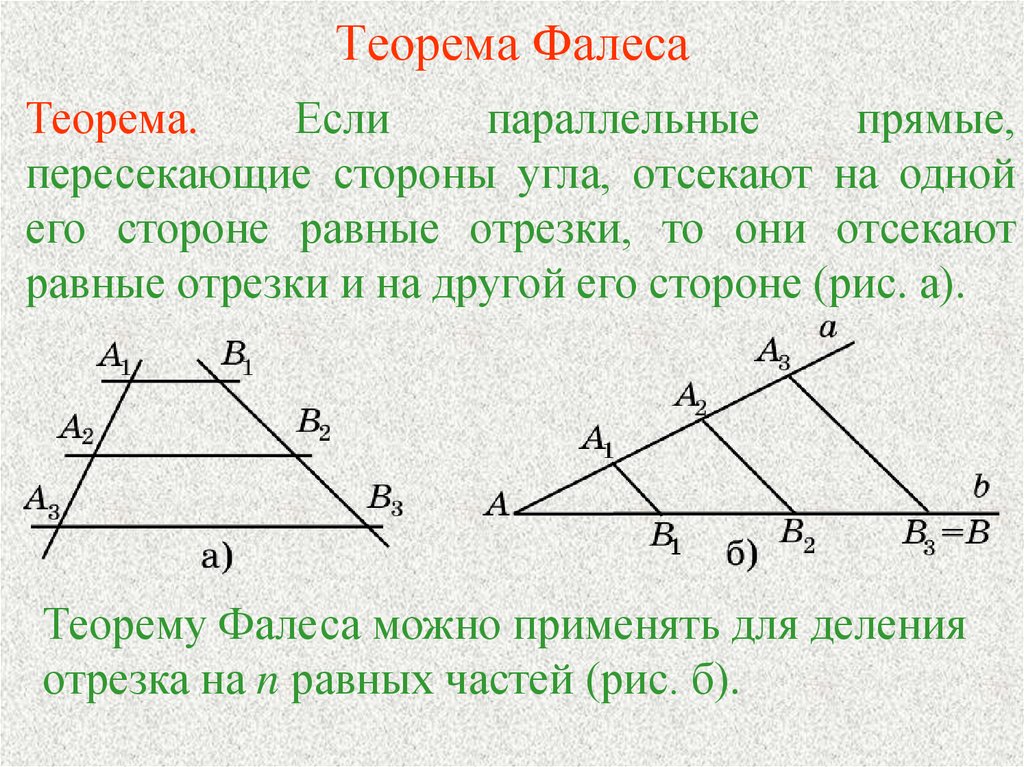
 Теорема связана с измерением
вписанный угол к центральному углу, опирающийся на ту же дугу.
Теорема связана с измерением
вписанный угол к центральному углу, опирающийся на ту же дугу.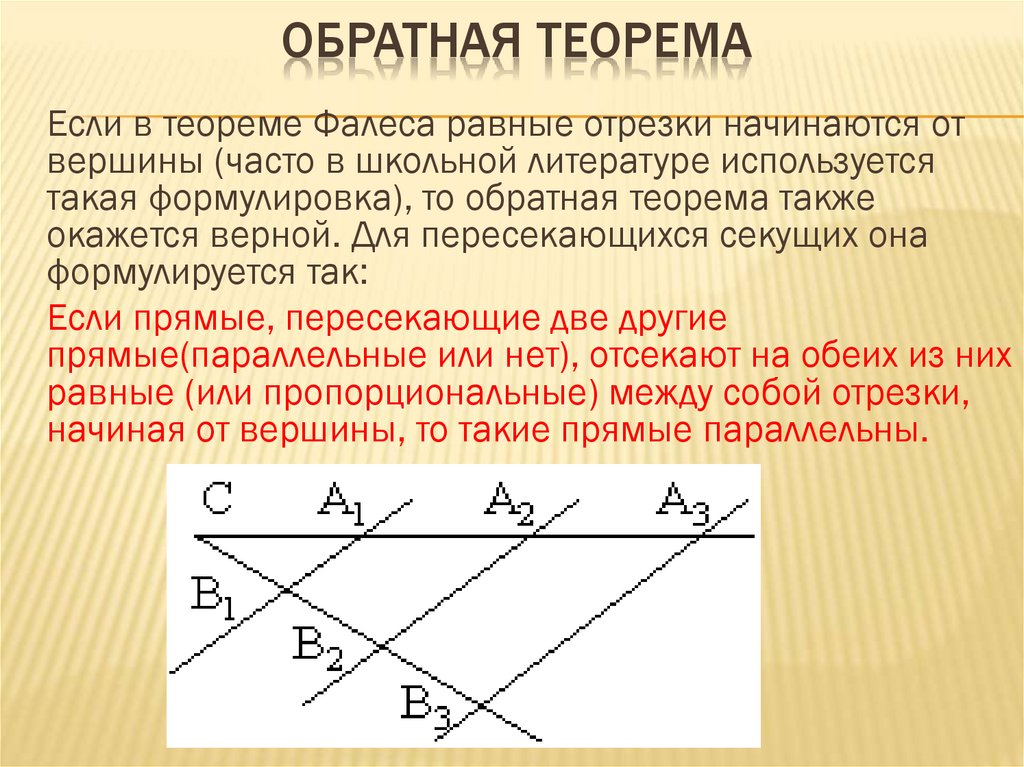 Точки P и Q всегда находятся в конце
линия диаметра. При проведении двух диаметров центр находится в точке, где
диаметры пересекаются.
Точки P и Q всегда находятся в конце
линия диаметра. При проведении двух диаметров центр находится в точке, где
диаметры пересекаются.
 Это
также должен предшествовать кругу в цепочке. Цепочка должна замкнуться в пути
что шестая окружность всегда касается первой окружности.
Это
также должен предшествовать кругу в цепочке. Цепочка должна замкнуться в пути
что шестая окружность всегда касается первой окружности.