Трапеция. Свойства и признаки равнобедренной трапеции
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Трапецией называется четырехугольник, у которого
две стороны параллельны, а две другие не
параллельны.
В
A
основание
основание
С
D
№ 387.
Найдите углы трапеции
В
основание
С
1170
360
A
основание
D
4. Трапеция
От греческогостолик
trapezion
—
Трапеция — приспособление для выполнения
перекладина, подвешенная на двух тросах
или веревках.

Трапеция, один из углов которой прямой, называется
прямоугольной.
В
A
С
D
№ 392 (а)
В
4
С
300
?6
A
М
7
600
3
D
Трапеция называется равнобедренной, если ее боковые
стороны равны.
АВ = СD
В
A
С
D
№ 388 (а) Свойства равнобедренной трапеции.
В равнобедренной трапеции углы при каждом основании
равны.
Дано:
С =1800- 1
В =1800- 3
АВСD – р/б трапеция
Доказать:
А = D
B = C
2
3
A
Е
1
D
№ 388 (б) Свойства равнобедренной трапеции.
В равнобедренной трапеции диагонали равны.
В
A
Дано:
АВСD – р/б трапеция
Доказать:
АC = BD
С
D
№ 390. Найдите все углы равнобедренной трапеции, если
известен один из её углов.
В
1120
С
680
A
D
Свойства равнобедренной трапеции.
В равнобедренной трапеции углы при каждом основании
равны.
В равнобедренной трапеции диагонали равны.

Признаки равнобедренной трапеции.
Если углы при основании трапеции равны, то она
равнобедренная.
Если диагонали трапеции равны, то она равнобедренная.
№ 389 (а) Признаки равнобедренной трапеции.
Если углы при основании трапеции равны, то она
равнобедренная.
Дано:
С
В
АВСD – р/б трапеция
Доказать:
3
2
A
1
Е
D
А = D
B = C
№ 389 (б)
Признаки равнобедренной трапеции.
Если диагонали трапеции равны, то она равнобедренная.
Дано: АВСD – р/б трапеция
В
С
Доказать:
АC = BD
2
1
A
D
К
Решение задач на готовых чертежах
АВСD – трапеция. Найти АОВ.
1800
В
С
О
A
D
Решение задач на готовых чертежах
В
х
С
2х
D
A
Из АСD: х+2х=90
Решение задач на готовых чертежах
АВСD – трапеция. ВЕ II СD
Найти углы трапеции.
В
С
0
750 65
400
A
1150
650
Е
D
Дополнительные задачи по теме «Трапеция»
Задача 1.

Найдите углы М и Р трапеции МNPQ с основаниями МQ и
0
0
NP, если угол N равен 109 , а угол Q равен 37 .
Задача 2.
0
Один из углов равнобедренной трапеции равен 115 . Найдите
остальные углы трапеции.
Задача 3.
В трапеции АВСД основание АД образует с боковыми
0
0
сторонами АВ и СД углы, равные 70 и 40 . Определите
остальные углы трапеции.
English Русский Правила
Описанная окружность и трапеция
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2015-12-05
Описанная окружность и трапеция. Здравствуйте! Для вас ещё одна публикация, в которой рассмотрим задачи с трапециями. Задания входят в состав экзамена по математике. Здесь они объединены в группу, дана не просто одна трапеция, а комбинация тел – трапеция и окружность. Большинство из таких задачек решаются устно. Но есть и такие на которые нужно обратить особое внимание, например, задача 27926.
Какую теорию необходимо помнить? Это:
1.
Свойство сторон четырёхугольника описанного около окружности.
2. Теорему Пифагора. *Куда мы без неё )
3. Понятие средней линии трапеции.
Задачи с трапециями, которые имеются на блоге можно посмотреть здесь.
27924. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Отметим, что описать окружность можно только около равнобедренной трапеции. Нам дана средняя линия, значит можем определить сумму оснований, то есть:
Значит сумма боковых сторон будет равна 22–10=12 (периметр минус основания). Так как боковые стороны равнобедренной трапеции равны, то одна сторона будет равна шести.
Ответ: 6
27925. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 600, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Если вы решали задачи с окружностью и вписанным в неё шестиугольником, то сразу озвучите ответ – радиус равен 6. Почему?
Почему?
Посмотрите: равнобедренная трапеция с углом при основании равным 600 и равными сторонами AD, DC и CB, представляет собой половину правильного шестиугольника:
В таком шестиугольнике отрезок соединяющий противоположные вершины проходит через центр окружности. *Центр шестиугольника и центр окружности совпадают, подробнее здесь п.6
То есть большее основание этой трапеции совпадает с диаметром описанной окружности. Таким образом радиус равен шести.
*Конечно, можно рассмотреть равенство треугольников ADO, DOС и OCB. Доказать что они равносторонние. Далее сделать вывод о том, что угол AOB равен 1800 и точка О равноудалена от вершин A, D, C и B, а и значит АО=ОВ=12/2=6.
Ответ: 6
27926. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.
Отметим, что центр описанной окружности лежит на оси симметрии, при чём если построить высоту трапеции проходящую через этот центр, то она при пересечении с основаниями разделит их пополам. Покажем это на эскизе, также соединим центр с вершинами:
Покажем это на эскизе, также соединим центр с вершинами:
Отрезок EF является высотой трапеции, его нам нужно найти.
В прямоугольном треугольнике OFC нам известна гипотенуза (это радиус окружности), FC=3 (так как DF=FC). По теореме Пифагора можем вычислить OF:
В прямоугольном треугольнике OEB нам известна гипотенуза (это радиус окружности), EB=4 (так как AE=EB). По теореме Пифагора можем вычислить OE:
Таким образом EF=FO+OE=4+3=7.
Ответ: 7
Теперь важный нюанс!
В этой задаче на рисунке чётко показано, что основания лежат по разные стороны от центра окружности, поэтому задача решается именно так.
А если бы в условии не было дано эскиза?
Тогда у задачи было бы два ответа. Почему? Посмотрите внимательно – в любую окружность можно вписать две трапеции с заданными основаниями:
*То есть при данных основаниях трапеции и радиусе окружности существует две трапеции.
И решение будет «второго варианта» будет следующим.
По теореме Пифагора вычисляем OF:
Также вычислим OE:
Таким образом EF=FO–OE=4–3=1.
Конечно, в задаче с кратким ответом на ЕГЭ двух ответов быть не может, и подобная задача без эскиза дана не будет. Поэтому обратите особое внимание на эскиз! А именно: как расположены основания трапеции. А вот в заданиях с развёрнутым ответом такая в прошлые годы присутствовала (немного с усложнённым условием). Тот, кто рассматривал только один вариант расположения трапеции теряли балл на этом задании.
27937. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Здесь сразу следует вспомнить свойство четырёхугольника описанного около окружности:
Суммы противоположных сторон любого четырёхугольника описанного около окружности равны.
Значит
А средняя линия равна половине суммы оснований, то есть 10.
Ответ: 10
27938. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Найдите радиус окружности.
Радиус окружности равен половине высоты. Используя свойство указанное в предыдущей задаче получим:
Большая сторона у нас это СВ, следовательно можем вычислить AD=11–CB=11–7=4. Таким образом, радиус будет равен 2.
Ответ: 2
27915. Найдите высоту трапеции, в которую вписана окружность радиуса 1.
Посмотреть решение
27936. Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
Посмотреть решение
На этом всё, успеха вам!
С уважением, Александр Крутицких.
*Расскажите о сайте в социальных сетях.
Категория: Четырёхугольники | ЕГЭ-№1Трапеция
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Trapezoid Charms — Etsy.de
Etsy больше не поддерживает старые версии вашего веб-браузера, чтобы обеспечить безопасность пользовательских данных. Пожалуйста, обновите до последней версии.
Воспользуйтесь всеми преимуществами нашего сайта, включив JavaScript.
Найдите что-нибудь памятное, присоединяйтесь к сообществу, делающему добро.
( 829 релевантных результатов, с рекламой Продавцы, желающие расширить свой бизнес и привлечь больше заинтересованных покупателей, могут использовать рекламную платформу Etsy для продвижения своих товаров. Вы увидите результаты объявлений, основанные на таких факторах, как релевантность и сумма, которую продавцы платят за клик. Узнать больше. )
Контрольная точка Shapes
Этот файл содержит двунаправленный текст Unicode, который может быть интерпретирован или скомпилирован не так, как показано ниже.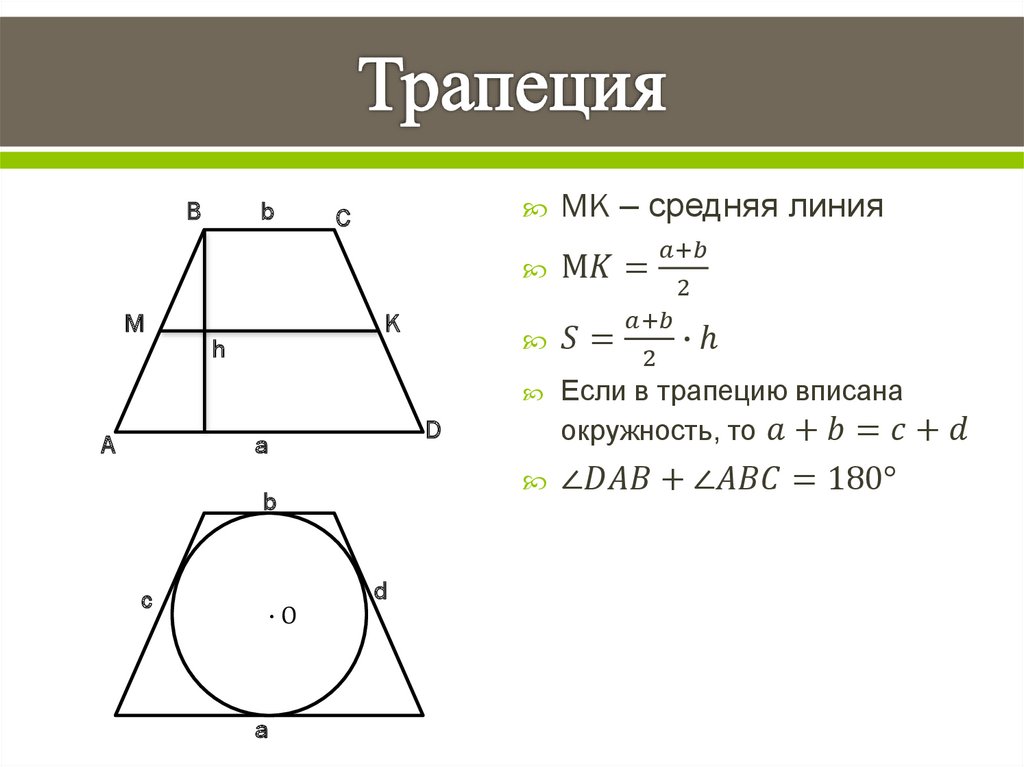 Для просмотра откройте файл в редакторе, который показывает скрытые символы Unicode.
Узнайте больше о двунаправленных символах Unicode
Для просмотра откройте файл в редакторе, который показывает скрытые символы Unicode.
Узнайте больше о двунаправленных символах Unicode
Показать скрытые символы
| класс Круг | |
| определение инициализации (радиус) | |
| @радиус = радиус | |
| конец | |
| по периметру | |
| 2 * Math::pi * г | |
| конец | |
| зона защиты | |
| Математика::пи * г * г | |
| конец | |
| конец |
Этот файл содержит двунаправленный текст Unicode, который может быть интерпретирован или скомпилирован не так, как показано ниже. Для просмотра откройте файл в редакторе, который показывает скрытые символы Unicode.
Узнайте больше о двунаправленных символах Unicode
Для просмотра откройте файл в редакторе, который показывает скрытые символы Unicode.
Узнайте больше о двунаправленных символах Unicode
Показать скрытые символы
| требуется «rspec» | |
| require_relative ‘круг’ | |
| описать Круг сделать | |
| «вычисляет периметр» do | |
| круг = Круг.новый(1.0) | |
| ожидать(окружность.периметр).to eq(6.283185307179586) | |
| конец | |
| «вычисляет площадь» do | |
Круг = Круг.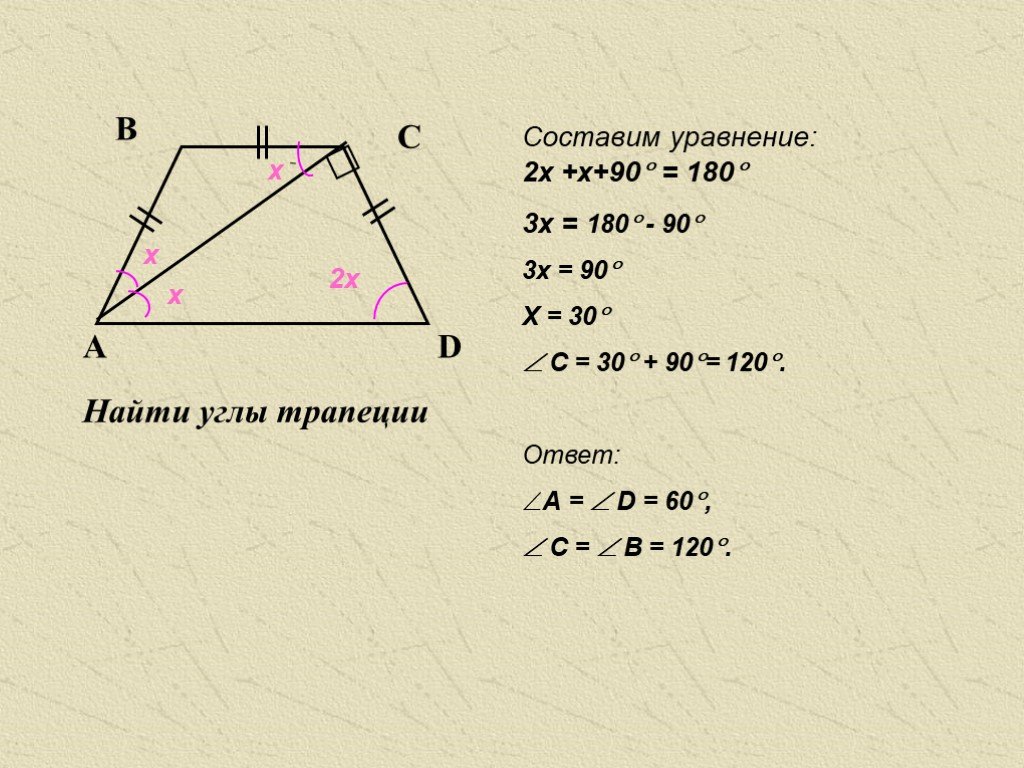 новый(1.0) новый(1.0) | |
| ожидать (квадрат.площадь).to eq(Math::Pi) | |
| конец | |
| конец |
Этот файл содержит двунаправленный текст Unicode, который может быть интерпретирован или скомпилирован не так, как показано ниже. Для просмотра откройте файл в редакторе, который показывает скрытые символы Unicode. Узнайте больше о двунаправленных символах Unicode
Показать скрытые символы
| класс Прямоугольник | |
| определение инициализации (длина, ширина) | |
| @длина = длина | |
| @ширина = ширина | |
| конец | |
| по периметру | |
| 2 * @длина + 2 * @ширина | |
| конец | |
| зона защиты | |
| @длина * @ширина | |
| конец | |
| конец |
Этот файл содержит двунаправленный текст Unicode, который может быть интерпретирован или скомпилирован не так, как показано ниже. Для просмотра откройте файл в редакторе, который показывает скрытые символы Unicode.
Узнайте больше о двунаправленных символах Unicode
Для просмотра откройте файл в редакторе, который показывает скрытые символы Unicode.
Узнайте больше о двунаправленных символах Unicode
Показать скрытые символы
| требуется «rspec» | |
| require_relative ‘прямоугольник’ | |
| описать Square do | |
| «вычисляет периметр» do | |
| прямоугольник = Rectangle.new(10.0, 5.0) | |
| ожидать(прямоугольник.периметр).to eq(30.0) | |
| конец | |
| «вычисляет площадь» do | |
прямоугольник = Rectangle. new(10.0, 5.0) new(10.0, 5.0) | |
| ожидать(прямоугольник.область).to eq(50.0) | |
| конец | |
| конец |
Этот файл содержит двунаправленный текст Unicode, который может быть интерпретирован или скомпилирован не так, как показано ниже. Для просмотра откройте файл в редакторе, который показывает скрытые символы Unicode. Узнайте больше о двунаправленных символах Unicode
Показать скрытые символы
| класс Квадрат | |
| деф инициализировать (сторона) | |
| @сторона = сторона | |
| конец | |
| по периметру | |
| сбоку * 4 | |
| конец | |
| зона защиты | |
| сторона * сторона | |
| конец | |
| конец |
Этот файл содержит двунаправленный текст Unicode, который может быть интерпретирован или скомпилирован не так, как показано ниже.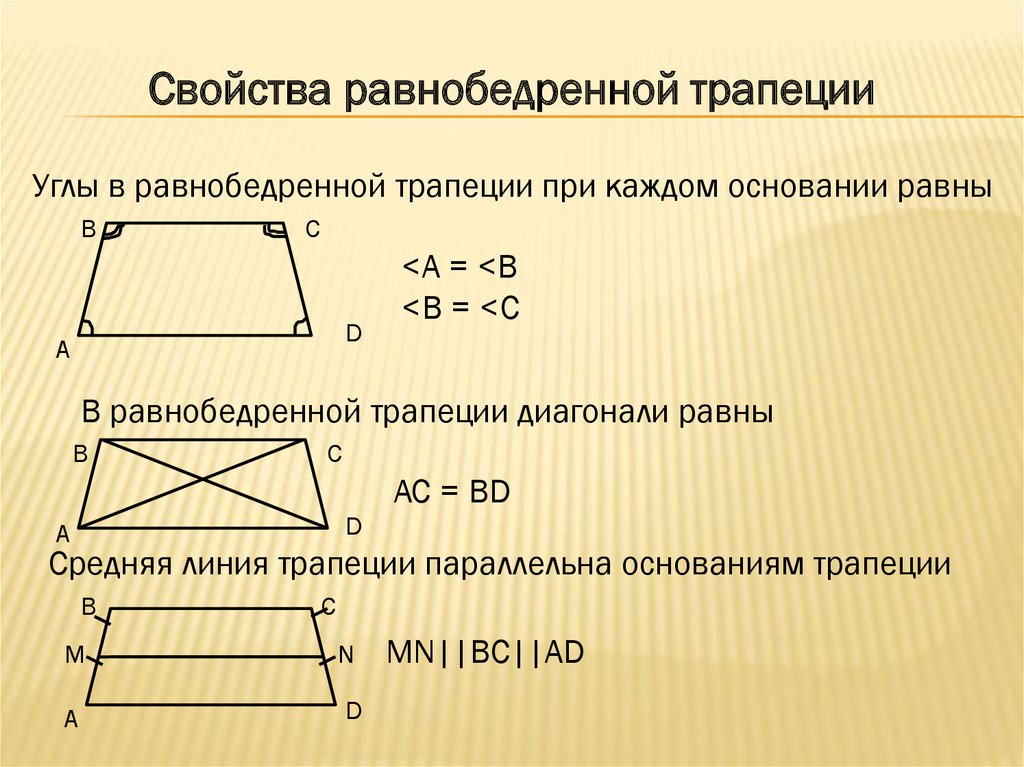 Для просмотра откройте файл в редакторе, который показывает скрытые символы Unicode.
Узнайте больше о двунаправленных символах Unicode
Для просмотра откройте файл в редакторе, который показывает скрытые символы Unicode.
Узнайте больше о двунаправленных символах Unicode
Показать скрытые символы
| требуется «rspec» | |
| require_relative ‘квадрат’ | |
| описать Square do | |
| «вычисляет периметр» do | |
| квадрат = Square.new(10.0) | |
| ожидать(квадрат.периметр).to eq(40.0) | |
| конец | |
| «вычисляет площадь» do | |
квадрат = Square. new(10.0) new(10.0) | |
| ожидать(квадрат.площадь).to eq(100.0) | |
| конец | |
| конец |
Этот файл содержит двунаправленный текст Unicode, который может быть интерпретирован или скомпилирован не так, как показано ниже. Для просмотра откройте файл в редакторе, который показывает скрытые символы Unicode. Узнайте больше о двунаправленных символах Unicode
Показать скрытые символы
| класс Трапеция | |
| определение инициализации (база1,база2,сторона1,сторона2) | |
| @base1 = base1 | |
| @base2 = base2 | |
| @сторона1 = сторона1 | |
| @сторона2 = сторона2 | |
| конец | |
| по периметру | |
| @side1 + @side2 + @base1 + @base2 | |
| конец | |
| зона защиты | |
height = Math. sqrt(((@base1 + @side1 — @base2 + @side2) * (-@base1 + @side1 + @base2 + @side2) * (@base1 — @side1 — @base2 + @side2) * (@base1 + @side1 — @base2 — @side2)) / (4 * {(@base1 — @base2)*(@base1 — @base2)))) sqrt(((@base1 + @side1 — @base2 + @side2) * (-@base1 + @side1 + @base2 + @side2) * (@base1 — @side1 — @base2 + @side2) * (@base1 + @side1 — @base2 — @side2)) / (4 * {(@base1 — @base2)*(@base1 — @base2)))) | |
| (((@base1 + @base2) / 2) * высота).round(2) | |
| конец | |
| конец |
Этот файл содержит двунаправленный текст Unicode, который может быть интерпретирован или скомпилирован не так, как показано ниже. Для просмотра откройте файл в редакторе, который показывает скрытые символы Unicode. Узнайте больше о двунаправленных символах Unicode
Показать скрытые символы
 to eq(67.05)
to eq(67.05)Этот файл содержит двунаправленный текст Unicode, который может быть интерпретирован или скомпилирован не так, как показано ниже. Для просмотра откройте файл в редакторе, который показывает скрытые символы Unicode. Узнайте больше о двунаправленных символах Unicode
Показать скрытые символы
| класс Треугольник | |
| деф инициализировать (сторона 1, сторона 2, сторона 3) | |
| @сторона1 = сторона1 | |
| @сторона2 = сторона2 | |
| @сторона3 = сторона3 | |
| конец | |
| по периметру | |
| @сторона1 + @сторона2 + @сторона3 | |
| конец | |
| зона защиты | |
| р = периметр/2 | |
sprintf(‘%. 2f’, Math.sqrt(p * (p — @side1) * (p — @side2) * (p — @side3))).to_f 2f’, Math.sqrt(p * (p — @side1) * (p — @side2) * (p — @side3))).to_f | |
| конец | |
| конец |
Этот файл содержит двунаправленный текст Unicode, который может быть интерпретирован или скомпилирован не так, как показано ниже. Для просмотра откройте файл в редакторе, который показывает скрытые символы Unicode. Узнайте больше о двунаправленных символах Unicode
Показать скрытые символы
| требуется «rspec» | |
| require_relative ‘треугольник’ | |
| описать треугольник сделать | |
| «вычисляет периметр» do | |
треугольник = Triangle. |

 Свойство сторон четырёхугольника описанного около окружности.
Свойство сторон четырёхугольника описанного около окружности.