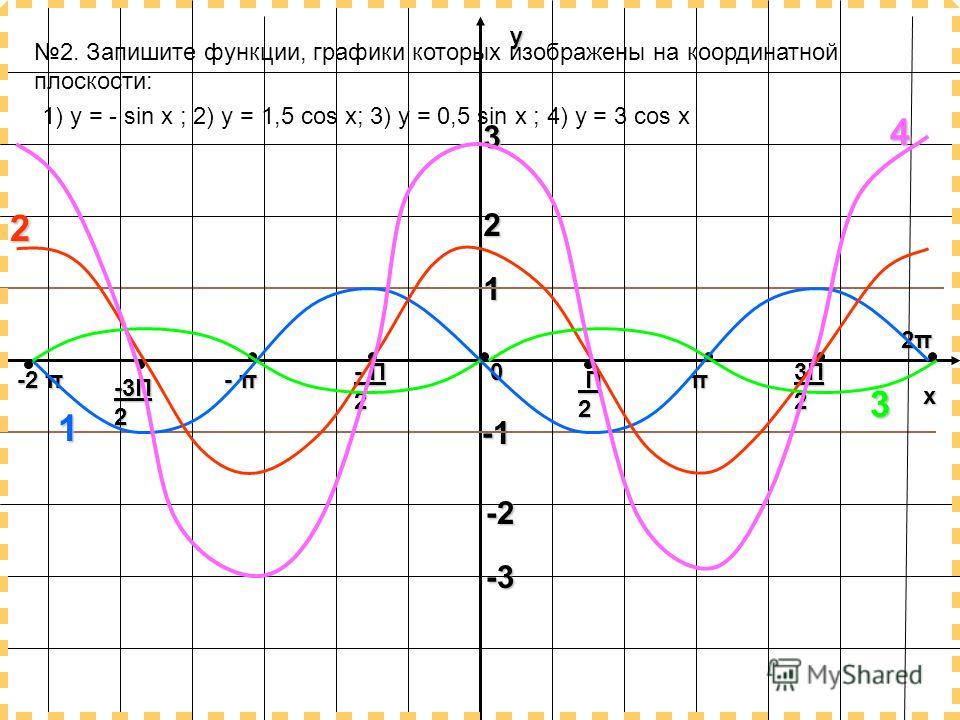
График функций синуса и косинуса
График функций синуса и косинуса Зарисовка синуса и
косинус
функции формы
Графические параметры
Амплитуда = |а|Период = 2?/|k|
Горизонтальное смещение (перевод) = d , влево, если (- d) положительное, и вправо, если (- d) отрицательное.
Вертикальный сдвиг (перевод) = c , вверх, если c положительное, и вниз, если c отрицательное.
Круг единиц
Чтобы набросать преобразованные функции синуса и косинуса, нам нужно знать, как рисовать основные функции синуса и косинуса. Единичный круг (радиус = 1) дает значения sin(x) и cos(x) в 5 ключевых точках, которые можно использовать для построения графиков более сложных функций синуса и косинуса. Координаты любой точки на единичной окружности дают косинус и синус угла в стандартном положении, соответствующем этой точке.
Примеры
вращению 0 соответствует точка (1,0) = (cos(0),sin(0))повороту на ?/2 (или 90°) соответствует точка (0,1) = (cos(?/2),sin(?/2))
для вращения? (или 180°) соответствует точка (-1,0) = (cos(?),sin(?))
повороту на 3?/2 (или 270°) соответствует точка (0,-1) = (cos(3?/2), sin(3?/2))
к вращению 2 ? (или 360°) соответствует точке (1,0) = (cos(2?),sin(2?)) как показано ниже.
Пример 1
Нарисуйте график y = 2 cos(x) + 1 за один период.Раствор
Графические параметры
Амплитуда = |2| = 2
Период = 2?
Сдвиг по вертикали (перевод) = 1 , вверх на 1 единицу.
Горизонтальный сдвиг (перевод) = 0
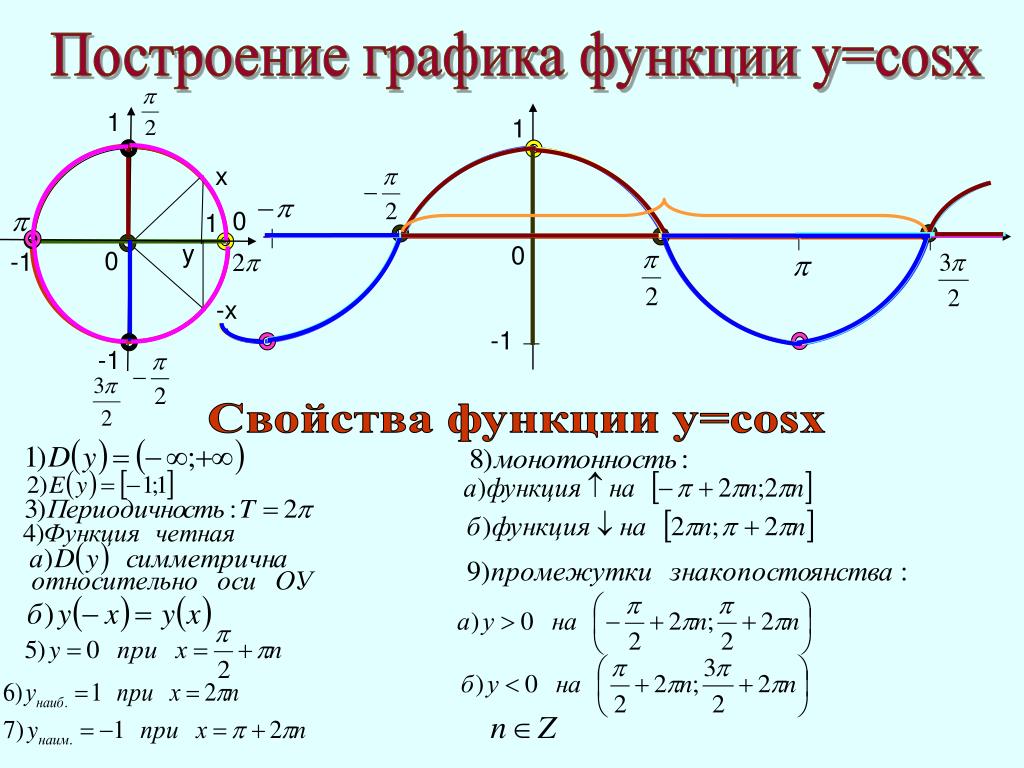
Начнем с построения эскиза y = cos(x), используя значения x и y из единичного круга (синяя диаграмма ниже).
| х = 0 | ?/2 | ? | 3?/2 | 2? |
| у = 1 | 0 | -1 | 0 | 1 |
Затем мы рисуем y = 2 cos(x), растягивая y = cos(x) на 2 (зеленый график ниже) и, наконец, y = 2 cos(x) + 1, сдвигая вверх на 1 единицу (красный график ниже).
Пример 2
Нарисуйте график зависимости y = — 2 sin(x) — 1 за один период.Раствор
Графические параметры
Амплитуда = |-2| = 2
Период = 2?
Сдвиг по вертикали (перевод) = — 1 , вниз на 1 единицу.
Горизонтальный сдвиг (перевод) = 0
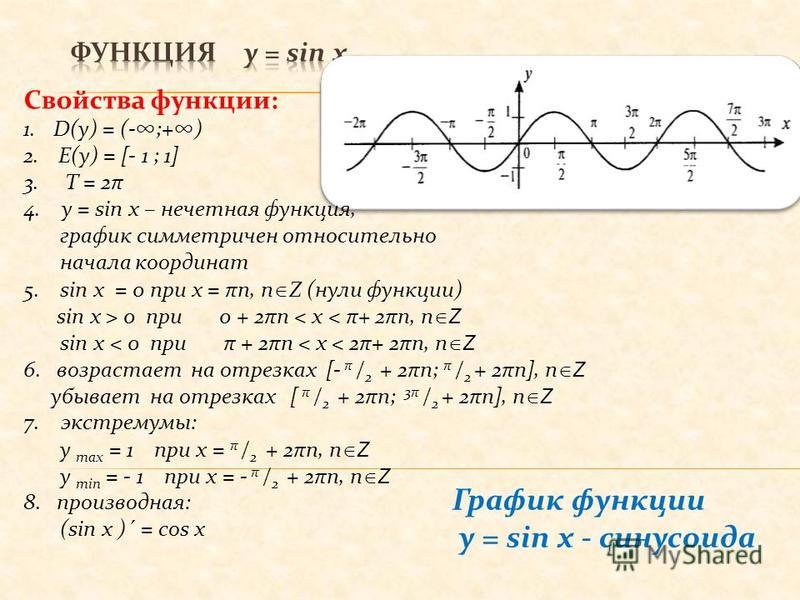
Начнем с построения эскиза y = sin(x), используя значения x и y из единичного круга (синяя диаграмма ниже).
| х = 0 | ?/2 | ? | 3?/2 | 2? |
| у = 0 | 1 | 0 | — 1 | 0 |
Затем мы рисуем y = — 2 sin(x), растягивая y = sin(x) на 2 и отражая его по оси x (зеленый график ниже) и, наконец, y = — 2 sin(x) — 1 на сдвиг вниз на 1 единицу (красный график ниже).
Пример 3
Нарисуйте график зависимости y = 3 cos(2 x + ?/3) — 1 за один период.Раствор
Графические параметры
Амплитуда = |3| = 3
Период = 2?/2 = ?
Сдвиг по вертикали (перевод) = — 1 , вниз на 1 единицу.
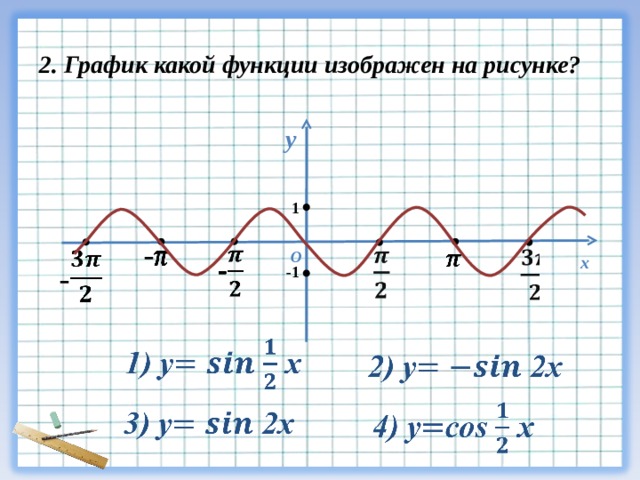
Горизонтальное смещение: из-за члена ?/3 график смещается по горизонтали. Сначала мы перепишем данную функцию как: y = 3 cos [ 2( x + ?/6)] — 1, и теперь мы можем записать сдвиг влево как равный ?/6.
Начнем с рисования 3 cos(2 x) с минимальным и максимальным значениями — 3 и + 3 за один период = ? (синий график ниже).
Затем мы рисуем y = 3 cos(2 x) — 1, переводя предыдущий график на 1 единицу вниз (зеленый график ниже). Теперь мы сдвинем предыдущий график ?/6 влево (красный график внизу) так, чтобы нарисованный период начинался с — ?/6 и заканчивался на — ?/6 + ? = 5?/6, что является одним периодом = ?.
Пример 4
Нарисуйте график зависимости y = — 0,2 sin(0,5 x — ?/6) + 0,1 за один период.Решение
Графические параметры
Амплитуда = |- 0,2| = 0,2
Период = 2?/0,5 = 4?
Вертикальный сдвиг (перевод) = 0,1 , вверх на 0,1 единицы.
Горизонтальное смещение: Из-за термина — ?/6 график сдвинут по горизонтали.
Сначала мы перепишем данную функцию как: y = — 0,2 cos [ 0,5( x — ?/3)] + 0,1, и теперь мы можем записать сдвиг вправо равным ?/3. Начнем с наброска — 0,2 sin(0,5 x) с минимальным и максимальным значениями — 0,2 и + — 0,2 за один период = 4 ? (синий график ниже).
Пример 5
Нарисуйте график зависимости y = 2 cos(2 x — 60°) — 2 за один период.Раствор
Графические параметры
Амплитуда = |2| = 2
Сдвиг по вертикали (перевод) = — 2 , вниз на 2 единицы.
Период = 360/2 = 180°
Horizontal Shift: Из-за термина -60° график смещен по горизонтали. Сначала мы перепишем данную функцию как: y = 2 cos[2( x — 30°)] — 2, и теперь мы можем записать сдвиг равным 30° вправо.
Начнем с наброска y = 2 cos(2 x) с минимальным и максимальным значениями — 2 и + 2 за один период = 180° (синий график ниже).
Затем мы рисуем y = 2 cos(2 x) — 2, переводя предыдущий график на 2 единицы вниз (зеленый график ниже). Затем мы сдвигаем предыдущий график на 30° вправо (красный график ниже), так что нарисованный период начинается с 30° и заканчивается на 30° + 180° = 210°, что составляет один период = 180°.
Пример 6
Нарисуйте график зависимости y = — 2 sin(x/3 + ?/3) — 1 за один период.Раствор
Графические параметры
Амплитуда = |- 2| = 2
Период = 2?/(1/3) = 6?
Сдвиг по вертикали (перевод) = — 1 , вниз на 1 единицу.
Горизонтальное смещение: из-за члена ?/3 график смещается по горизонтали. Сначала мы перепишем данную функцию как: y = — 2 sin[(1/3)(x + ?)] — 1, и теперь мы можем записать сдвиг как равный ? Слева.
Начнем с наброска — 2 sin(x/3) с минимальным и максимальным значениями — 2 и + 2 за один период = 6 ? (синий график ниже).
Затем мы рисуем y = — 2 sin(x/3) — 1, переводя предыдущий график на 1 единицу вниз (зеленый график ниже). Затем мы сдвигаем предыдущий график? влево (красный график внизу) так, чтобы нарисованная точка начиналась с -? и заканчивается на 5? что один период = 6?.
Дополнительные ссылки Синусоидальная функция
Функция косинуса
Используйте синусоидальные функции для моделирования проблем
Функция косинуса HTML5-апплет
Учебное пособие по синусоидальным функциям (1) — Проблемы
Математика средней школы (10, 11 и 12 классы) — Бесплатные вопросы и задачи с ответами
Математика в средней школе (6, 7, 8, 9 классы) — бесплатные вопросы и задачи с ответами
Домашняя страница
Графики тригонометрических функций ‹ OpenCurriculum
Цели статьи
Первая функция, которую мы нарисуем, это синусоидальная функция.
Мы видим на рисунке 1, что любая точка на единичной окружности имеет координаты ( x , y ) = (cos θ ,sin θ ), где θ — угол, который отрезок прямой от начала координат до ( x , y ) составляет с положительной осью x (по определению синуса и косинуса). ). Так как точка ( x , y ) движется по окружности, ее координата y равна sin θ .
Таким образом, мы получаем соответствие между y -координатами точек на единичной окружности и значениями f ( θ ) = sin θ , как показано горизонтальными линиями от единичной окружности к графику 
Мы можем расширить приведенное выше изображение, включив в него углы от 0 до 2 π радиан, как на рисунке 3. Это иллюстрирует то, что иногда называют определением единичного круга функции синуса .
Поскольку тригонометрические функции повторяются каждые 2 π радиан (360º), получим, например, следующий график функции y = sin x для x в интервале [−2 π ,2 π ]:
Чтобы построить график функции косинуса, мы могли бы снова использовать идею единичного круга (используя координату x точки, которая движется по кругу), но есть более простой способ. Напомним, что cos x = sin ( x +90º) для всех x . Таким образом, cos 0º имеет то же значение, что и sin 9.0º, cos 90º имеет то же значение, что и sin 180º, cos 180º имеет то же значение, что и sin 270º, и так далее. Другими словами, график функции косинуса — это просто график функции синуса, сдвинутый от влево от на 90º = π /2 радиан, как на рисунке 5:
Для построения графика функции тангенса используйте тангенс x = \(\frac{sin x}{cos x}\), чтобы получить следующий график:
Вспомните, что тангенс положителен для углов в QI и QIII и отрицателен в QII и QIV, и это действительно что показывает график на рисунке 6.
Мы знаем, что загар x не определено, когда cos x = 0, то есть при нечетных кратных \(\frac{π}{2}\) : x = ± \(\frac{π}{2}\) , ± \(\frac{3π}{2}\) , ± \(\frac{5}{2}\) и т. д. Мы можем понять, что происходит 90 213 вблизи 90 214 этих углов, взглянув на функции синуса и косинуса. Например, для
Аналогично, для x в QII очень близко к \(\frac{π}{2}\) , sin x очень близко к 1, а cos x отрицательно и очень близко к 0, поэтому частное загара x = \(\frac{sin x}{cos x}\) – очень большое отрицательное число, и оно тем больше в отрицательном направлении, чем ближе x приближается к \(\frac{π}{2} \) .
График показывает это. Точно так же мы получаем вертикальные асимптоты при x = −\(\frac{π}{2}\) , x = \(\frac{3π}{2}\) и x = −\( \frac{3π}{2}\) , как на рисунке 6. Обратите внимание, что график функции тангенса повторяется каждые π радиан, т.е. в два раза быстрее, чем повторяются графики синуса и косинуса.
Графики остальных тригонометрических функций можно определить, посмотрев на графики их обратных функций. Например, используя csc x = \(\frac{1}{sin x}\), мы можем просто посмотреть на график y = sin x и инвертировать значения. Вертикальные асимптоты получим при sin x = 0, а именно при кратных π : x = 0, ± π , ±2 π и т. д. На рис. 7 показан график y = csc x , с графиком y = sin x (пунктирная кривая) для справки.
Аналогичным образом, на рис. 8 показан график y = sec x с графиком y = cos x (пунктирная кривая) для справки.
Обратите внимание на вертикальные асимптоты при x = ± \(\frac{π}{2}\) , ± \(\frac{3π}{2}\). Заметьте также, что график представляет собой просто график функции косеканса, сдвинутый влево на \(\frac{π}{2}\) радиан.
График y = кроватка x также может быть определен с помощью кроватки x = \(\frac{1}{cot x}\). В качестве альтернативы мы можем использовать соотношение cot 90 213 x 90 214 = −tan ( 90 213 x 90 214 +90º), так что график функции котангенса представляет собой просто график функции тангенса, сдвинутый влево на \(\frac{π} {2}\) радиан, а затем отразить относительно оси x , как показано на рисунке 9:
Пример 1
Нарисуйте график y = −sin x для 0 ≤ x ≤ 2 π .
Решение : Умножение функции на -1 просто отражает ее график вокруг оси x . Таким образом, отображение графика y = sin x вокруг оси x дает нам график y = −sin x :
.