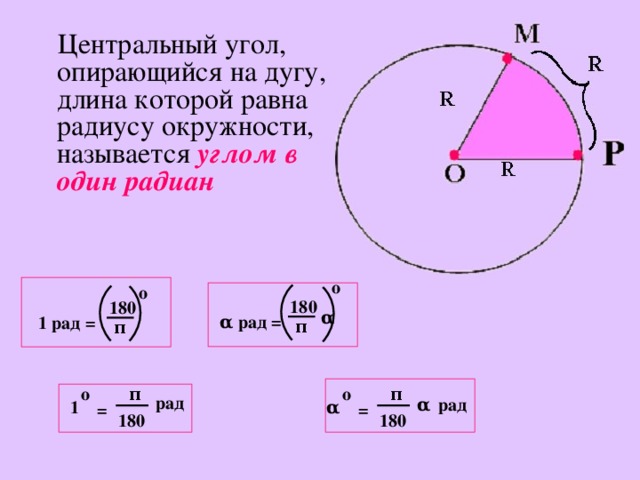
Центральный угол окружности. Центральный угол больше вписанного.
- Альфашкола
- Статьи
- Центральный угол окружности
Что такое центральный угол?
Центральный угол окружности образуется двумя радиусами. Окружность состоит из дуг и центральных углов. Центральный угол измеряется с помощью длины дуги и радиуса. Задачи центрального угла могут быть решены с помощью формулы центрального угла.
На рисунке ниже, центральный угол окружности, угол \(θ\), образованный между двумя радиусами:
Мера центрального угла равна градусной мере дуги, на которую он опирается.
\(∠ MON =MN\)
Формула для центрального угла в градусах окружности вычисляетяс следующим образом, если известна длина дуги в метрах, сантиметрах и др.
\( a=\frac{L*360}{2*π×r}\)
\(L-\)длина дуги
Пример 1. Найдите Центральный угол, если длина радиуса \(11\) см, а длина дуги около \(14\) см?
Решение:
Найдем Центральный угол окружности по формуле:
\(θ =\frac{ 14 × 360}{2 × 3.14 × 11}=\frac{5040}{69,08}=72,95\)
Центральный угол равен \(72,95\) градуса
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Зульашет Мовсуровна Гадаева
Репетитор по математике
Стаж (лет)
Образование:
Чеченский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Фёдор Владимирович Каузов
Репетитор по математике
Стаж (лет)
Образование:
Государственное образовательное учреждение высшего профессионального образования Ивановский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Райхан Талгатовна Иманбаева
Репетитор по математике
Стаж (лет)
Образование:
Санкт-Петербургский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ЕГЭ по математике (профильный уровень)
- Репетитор по химии для подготовки к ЕГЭ
- Репетитор для подготовки к ОГЭ по физике
- Подготовка к олимпиадам по физике
- Репетитор по разговорному английскому
- ВПР по физике
- Репетитор для подготовки к ЕГЭ по обществознанию
- Репетитор по информатике для подготовки к ОГЭ
- Подготовка к ОГЭ по литературе
- Программирование Pascal
Похожие статьи
- Задачи на движение
- Основные формулы: треугольник, параллелограмм и четырехугольник
- Как легко разделить на 0,25
- Признак делимости на 19
- Интегралы от тригонометрических функций
- ЕГЭ по математике, базовый уровень.
Преобразование алгебраических выражений - Готовимся к ЕГЭ по математике
- Что такое новогодний адвент-календарь, как его сделать и зачем он нужен?
Преобразование алгебраических выраженийНажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
Как найти угол сектора круга с учетом радиуса и длины дуги окружности? / Справочник :: Бингоскул
Угол сектора круга или центральный угол – это угол, образованный двумя лучами, выходящими из центра круга. Соответственно, сектор круга – это его часть, которая заключена между двумя лучами с началом в центре круга и дугой, проходящей между точками пересечения лучей с линией окружности. На приведенном ниже рисунке изображен круг, буквами R обозначены два луча, которые выходят из его центра О под углом α, участок окружности АВ – это дуга, длина которой равна L, а часть круга, ограниченная точками О, А и В – сектор.
2.
Заметим, что начиная со второго действия эту задачу можно решить другим, более простым способом. По сути дела, сектор представляет собой равнобедренный треугольник, у которого основанием является дуга окружности, а радиус – сторонами и одновременно высотой. Как известно, площадь равнобедренного треугольника равна половине произведения основания на высоту. Используя эту формулу, проверим наши вычисления:
S_α = \frac { LR } { 2 } = \frac { 9 * 10,7 } { 2 } = 48,15 см.
Как можно заметить, мы получили практически одинаковые результаты, которые отличаются лишь вторым знаком после запятой. Это вызвано тем, что мы использовали округленное значение числа π.
Угловые радиусы | Национальная ассоциация городских транспортных служащих
Ссылки
Выберите категорию или оставьте поле пустым для всех. Ресурсы для совместного использования велосипедов. Руководство по проектированию транспортных улиц. Руководство по проектированию городских велосипедных дорожек.
Руководство по проектированию городских улиц. LanesDedicated Median Bus LanesDesign ControlsDesign HourDesign SpeedDesign VehicleDesign YearDowntown 1-Way StreetDowntown 2-Way StreetDowntown StreetsDowntown ThoroughfareFixed vs. Actuated SignalizationFlow-Through PlantersFrom Pilot to PermanentFunctional ClassificationGatewayGreen AlleyInterim Design StrategiesInterim Public PlazasIntersection Design ElementsIntersection Design PrinciplesIntersectionsIntersections of Major and Minor StreetsLane WidthLeading Pedestrian IntervalMajor IntersectionsMidblock CrosswalksMini RoundaboutMinor IntersectionsMoving the CurbNeighborhood Main StreetNeighborhood StreetParkletsPedestrian Safety IslandsPerformance MeasuresPervious PavementPervious StripsPhases of TransformationPinchpointRaised IntersectionsResidential BoulevardResidential Shared StreetSidewalksSignal Cycle LengthsSignalization PrinciplesSpeed CushionSpeed HumpsSpeed Reduction MechanismsSpeed TableSplit-PhasingStormwater ManagementStreet Design ElementsStreet Design PrinciplesStreet Design in ContextStreetsTemporary Street ClosuresTraffic SignalsTransit CorridorTransit StreetsVertical Speed Control ElementsVisibility/Sight DistanceYield Street—USDG Цитата
Austin, TXBerkeley, CABoston, MABrisbane, AUCChicago, ILDenver, COFort Worth, TXHouston, TXLondon, UKLos AngelesLyon, FRMelbourne, AUMinneapolis, MNMontreal, QCNew York, NYORParis, FRPhiladelphia, PAPhoenix, AZPortoWashtoWa, DC9ron5ron, CASeattle, ON
Ссылки для угловых радиусов: найдено 4.
- Американская ассоциация государственных служащих автомобильных дорог и транспорта. «Политика геометрического проектирования автомагистралей и улиц». Американская ассоциация государственных служащих автомобильных дорог и транспорта, Американская ассоциация государственных служащих автомобильных дорог и транспорта, Вашингтон, округ Колумбия.
- Шарлотта Департамент транспорта. «Руководство по проектированию городских улиц, Приложение C: Руководство по проектированию радиусов возврата бордюров». Департамент транспорта Шарлотты, город Шарлотта, Шарлотта, Северная Каролина.
- Левин, Кендра. «Радиус бордюра и тяжесть травм на перекрестках». Библиотека Института транспортных исследований Калифорнийского университета, Беркли, Калифорния.
- Варат, Адам и Кристина Олеа. «План улучшения улиц Сан-Франциско, глава 6: элементы городского пейзажа». Департамент планирования и Агентство муниципального транспорта, город Сан-Франциско, Сан-Франциско, Калифорния.
Нет результатов. Пожалуйста, уточните параметры поиска и повторите попытку.
Как угловой радиус влияет на обработку на станках с ЧПУ
Помимо ограничений размера того, что может вместить станок с ЧПУ, еще одним важным фактором является радиус угла. При обработке радиуса угла на станке с ЧПУ, как правило, невозможно получить идеально острый угол на внутренних углах. Радиусы углов, которые вы выбираете для своей конструкции, могут существенно повлиять на эффективность ее обработки и на конечное качество обработанной детали.
В этом блоге мы углубимся в концепцию углового радиуса при обработке с ЧПУ и о том, как выбрать идеальный угловой радиус для ваших требований и бюджета.
Что такое угловой радиус?
При обработке на станках с ЧПУ под радиусом угла понимается внутренний радиус углов детали.
Все фрезерные станки с ЧПУ имеют цилиндрическую форму и создают радиус при вырезании внутреннего кармана. Радиус инструмента, используемого в процессе обработки с ЧПУ, будет определять, какие радиусы углов возможны.
Почему угловой радиус имеет значение?
Радиус угла чрезвычайно важен для обработки с ЧПУ, поскольку он будет иметь прямое влияние на качество обработки , которое может быть достигнуто, а также на количество времени, которое потребуется для обработки детали .
При обработке внутренних элементов с ЧПУ радиус угла, который вы пытаетесь получить, повлияет на отделку внутренней части вашей детали. Попытка получить узкий радиус угла относительно радиуса инструмента увеличит степень контакта инструмента с внутренними сторонами вашей детали, что приведет к снижению качества отделки.
Траектория инструмента может поворачиваться на 90 градусов, чтобы создать радиус угла, равный радиусу инструмента (минимально возможный). Однако делать это не рекомендуется, так как это вызовет большую нагрузку как на инструмент, так и на деталь. Когда инструмент достигает угла, он должен остановиться и повернуться. Это может привести к появлению следов вибрации из-за повышенной вибрации инструмента и замедлит время резания. Можно использовать инструмент меньшего размера для достижения более узких радиусов углов, но инструмент меньшего размера требует некоторых предостережений.
Инструмент большего размера обеспечивает больший радиус скругления углов, но работает быстрее, что сокращает время, необходимое для обработки детали. Следовательно, меньшие инструменты приведут к увеличению затрат. Меньшие инструменты также более ограничены по глубине элемента (глубине кармана), которую они могут достичь. Это создает обратную зависимость между радиусами углов и глубиной элемента.
Короче говоря, использование максимально возможных радиусов для вашей конструкции повысит качество обработки поверхности и снизит затраты на механическую обработку. Более крупные инструменты, создающие больший радиус, работают быстрее и снижают затраты.
Минимальные требования для угловых радиусов
Существуют минимальные требования к угловым радиусам, поскольку инструмент не может физически вписаться в угол 90°, который меньше его радиуса, как показано на рисунке ниже.
Чтобы лучше понять, почему увеличивается зацепление инструмента, полезно посмотреть на траектории, необходимые для формирования острых углов. Вот GIF-файл, который помогает проиллюстрировать зацепление инструмента на основе углового радиуса.
На рисунке показаны два разных радиуса скругления углов. Красная линия указывает траекторию инструмента, а выделенная желтым цветом область указывает на зацепление инструмента.
В первом примере траектория инструмента составляет 90 градусов, что показывает широкую желтую область для зацепления инструмента.
Вторая последовательность GIF показывает более закругленную траекторию инструмента, которая показывает меньшую желтую область, которая представляет меньшее вовлечение инструмента. Увеличенное зацепление инструмента создает большую нагрузку на материал и инструмент, что приводит к снижению качества обработки поверхности.
Эта вторая последовательность в gif иллюстрирует резкое увеличение угловых радиусов из-за гораздо большей дуги на траектории движения инструмента. Больший радиус угла значительно снижает силы резания на инструменте и улучшает качество обработки. Это также позволило бы сократить время резки и, следовательно, снизить стоимость.
Сравнение различных радиусов скругления с помощью одного и того же инструмента
Ниже приведен пример изображения четырех различных скруглений скругления, полученных с помощью одного и того же инструмента.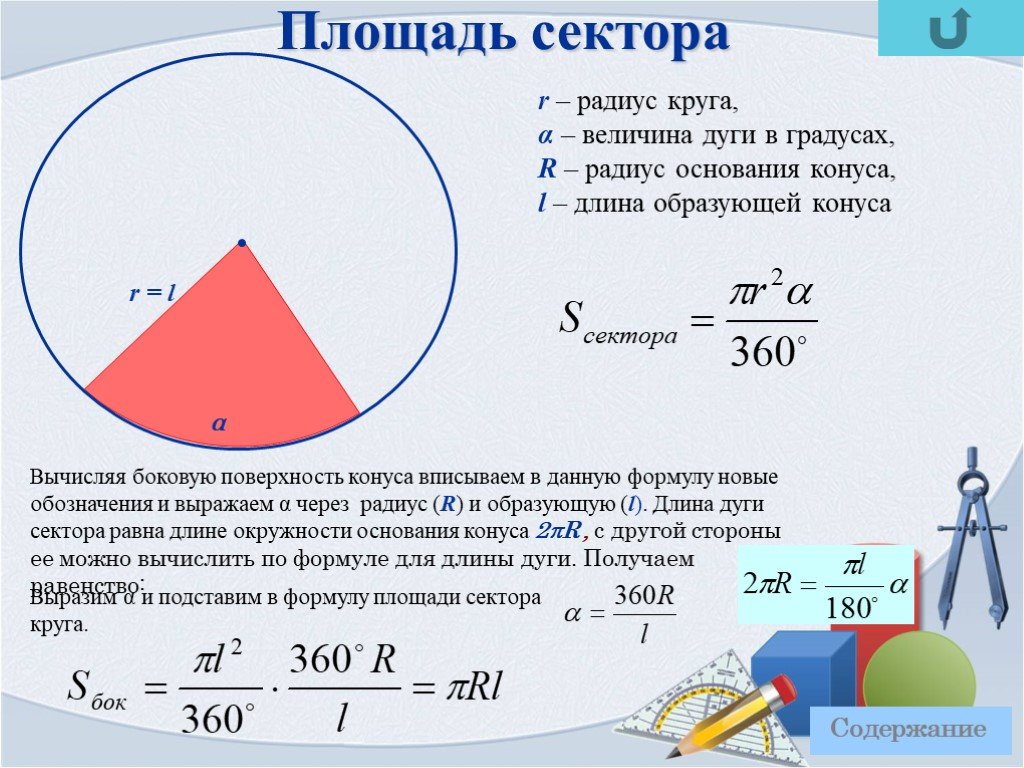
Зеленый = наибольший угол для траектории, что делает его идеальным вариантом.
Желтый = Этот угловой радиус достаточен, однако лучше всего использовать 200% радиуса инструмента.
Оранжевый = Радиус инструмента 120 % не идеален.
Красный = Этот угловой радиус не рекомендуется, так как это приведет к ухудшению качества поверхности.
Как выбрать угловой радиус?
Как описано в этом сообщении в блоге, выбранный вами радиус скругления может существенно повлиять на эффективность обработки вашей детали, а также на достигнутое качество продукции.
В приведенной ниже таблице показаны минимальные значения радиуса, которые мы рекомендуем для глубины элемента.
Дальний столбец «Рекомендуемый минимальный радиус» означает, что у нас есть процессы для этих значений, которые работают хорошо.
Минимальный радиус — это теоретический минимум, которого мы можем достичь, но этот радиус ниже рекомендованного.
При выборе минимального радиуса стоимость увеличится, а качество обработки поверхности может пострадать.
Мы всегда рекомендуем использовать как можно большие радиусы.
| Глубина элемента | Минимальный радиус | Рекомендуемый минимальный радиус |
|---|---|---|
| 0,47 дюйма (11,938 мм) | 0,016 дюйма (0,406 мм) | 0,031 дюйма (0,787 мм) |
| 0,75 дюйма (19,05 мм) | 0,032 дюйма (0,813 мм) | 0,063 дюйма (1,6 мм) |
| 2 дюйма (50,8 мм) | 0,063 дюйма (1,6 мм) | 0,094 дюйма (2,388 мм) |
| 3 дюйма (76,2 мм) | 0,125 дюйма (3,175 мм) | 0,15 дюйма (3,81 мм) |
| 3,25 дюйма (82,55 мм) | 0,25 дюйма (6,35 мм) | 0,275 дюйма (6,985 мм) |
| 4,25 дюйма (107,95 мм) | 0,3 дюйма (7,62 мм) | 0,325 дюйма (8,255 мм) |
| 5,75 дюйма (146,05 мм) | 0,75 дюйма (19,05 мм) | 0,8 дюйма (20,23 мм) |
Заключение
В конечном счете, при проектировании деталей, обработанных на станках с ЧПУ, вам необходимо сбалансировать свои требования с ограничениями, которые исходят от инструментов.