Как найти радиус сферы формула. Сфера, шар, сегмент и сектор
Если известна длина радиуса (r), то площадь поверхности сферы (S) будет составлять учетверенное произведение возведенного в квадрат радиуса на число Пи (π): S=4∗π∗r². Например, при длине радиуса сферы в три метра его площадь составит 4∗3,14∗3²=113,04 квадратных метров.
Если известен (V) пространства, ограниченного сферой, то сначала можно найти ее диаметр (d), а затем воспользоваться формулой, приведенной в первом шаге. Так как объем одной шестой части Пи на возведенную в куб длину диаметра сферы (V=π∗d³/6), то диаметр можно , как кубический корень из шести объемов, разделенных на число Пи: d=³√(6∗V/π). Подставив это значение в формулу из первого шага, получим: S=π∗(³√ (6∗V/π))². Например, при ограниченного сферой пространства равном 500 кубометров вычисление ее площади будет выглядеть так: 3,14∗(³√(6∗500/3,14))² = 3,14∗(³√955,41)² = 3,14∗9,85² = 3,14∗97,02 = 304,64 квадратных метра. (2/3)».
(2/3)».
Все планеты солнечной системы имеют форму
Инструкция
Если взять или круг и провернуть его вокруг своей оси, получится тело, называемое шаром. Иными словами, шаром называется тело, ограниченное сферой. Сфера представляет собой оболочку шара , и ее окружность. От шара она отличается тем, что является полой. Ось как у шара , так и у сферы совпадает с диаметром и проходит через центр. Радиусом шара называется отрезок, проложенный от его центра до любой внешней точки. В противоположность сфере, сечения шара представляют собой круги. Форму, близкую к шарообразной, имеет большинство и небесных тел.
Шар и сфера — взаимозаменяемые тела, в отличие от конуса, несмотря на то, что также является телом вращения. Сферические поверхности всегда в своем сечении образуют окружность, независимо от того, как именно она — по горизонтали или по вертикали. Коническая же поверхность получается лишь при вращении треугольника вдоль его оси, перпендикулярной основанию. Поэтому конус, в отличие от шара , и не считается взаимозаменяемым телом вращения.
Самый большой из возможных кругов получается при сечении шара , проходящей через центр О. Все круги, которые через центр О, пересекаются между собой в одном диаметре. Радиус всегда равен половине диаметра. Через две точки A и B, располагающиеся в любом месте поверхности
 2
2Данная может быть полезна в том случае, если известен либо диаметр, либо радиус шара или сферы. Однако, эти параметры приведены в качестве условий не во всех геометрических задачах. Существуют и такие задачи, в которых шар вписан в цилиндр. В этом случае, следует воспользоваться теоремой Архимеда, суть которой заключается в том, что площадь поверхности шара в полтора раза меньше полной поверхности цилиндра:S = 2/3 S цил., где S цил. —площадь полной поверхности цилиндра.
Видео по теме
Зная лишь длину диаметра окружности, можно вычислить не только площадь круга, но и площади некоторых других геометрических фигур. Это вытекает из того, что диаметры вписанных или описанных вокруг таких фигур окружностей совпадают с длинами их сторон либо диагоналей.
Инструкция
Если надо найти площадь (S) по известной длине его диаметра (D), умножайте число пи (π) на возведенную в длину диаметра , а результат делите на четыре: S=π ²*D²/4. Например,
Например,
Шар и сфера — это прежде всего геометрические фигуры, и если шар — это геометрическое тело, то сфера — это поверхность шара. Этими фигурами интересовались еще многие тысячи лет назад до н.э.
Впоследствии когда было открыто, что Земля — это шар, а небо — небесная сфера, получило развитие новое увлекательное направление в геометрии — геометрия на сфере или сферическая геометрия. Для того, чтобы рассуждать о размере и объеме шара, нужно сначала дать ему определение.
Шар
Шаром радиуса R с центром в точке О в геометрии называют тело, которое создано всеми точками пространство, имеющими общее свойство. Эти точки находятся на расстоянии, не превышающем радиуса шара, то есть заполняют все пространство меньше радиуса шара во все стороны от его центра. Если мы рассмотрим только те точки, которые равноудалены от центра шара — мы будем рассматривать его поверхность или оболочку шара.
Как можно получить шар? Мы можем вырезать из бумаги круг и начать его вращать вокруг его же диаметра.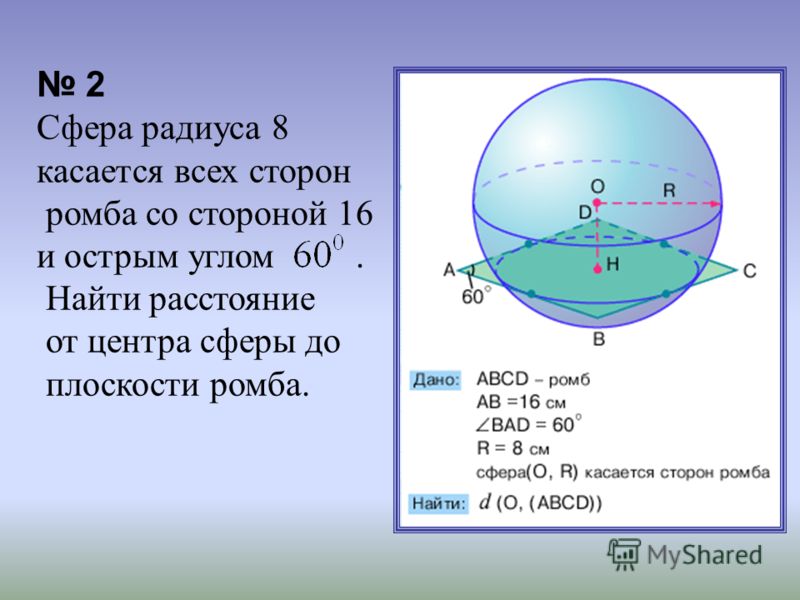 То есть диаметр круга будет осью вращения. Образованная фигура — будет шар. Поэтому шар называют также телом вращения. Потому что он может быть образован путем вращения плоской фигуры — круга.
То есть диаметр круга будет осью вращения. Образованная фигура — будет шар. Поэтому шар называют также телом вращения. Потому что он может быть образован путем вращения плоской фигуры — круга.
Возьмем какую-нибудь плоскость и разрежем ею наш шар. Подобно тому как мы режем ножом апельсин. Кусок, который мы отсечем от шара, называется шаровым сегментом.
В Древней Греции умели не только работать с шаром и сферой, как с геометрическими фигурами, например, использовать их при строительстве, а также умели расчитывать площадь поверхности шара и объем шара.
Сферой иначе называется поверхность шара. Сфера — это не тело — это поверхность тела вращения. Однако так как и Земля и многие тела имеют сферическую форму, например капля воды, то изучение геометрических соотношений внутри сферы получило большое распространение.
Например, если мы соединим две точки сферы между собой прямой линией, то эта прямая линия назовется хордой, а если эта хорда пройдет через центр сферы, который совпадает с центром шара, то хорда назовется диаметром сферы.
Если мы проведем прямую линию, которая коснется сферы всего в одной точке, то эта линия будет называться касательной. Кроме того, эта касательная к сфере в этой точке будет перпендикулярна к радиусу сферы, проведенному в точку касания.
Если мы продолжим хорду до прямой в одну и другую сторону от сферы, то эта хорда станет называться секущей. Или можно сказать иначе — секущая к сфере содержит в себе ее хорду.
Объем шара
Формула для вычисления объема шара имеет вид:
где R — радиус шара.
Если нужно найти объем шарового сегмента — воспользуйтесь формулой:
V сег =πh 2 (R-h/3), h — высота шарового сегмента.
Площадь поверхности шара или сферы
Чтобы вычислить площадь сферы или площадь поверхности шара (это одно и то же):
где R — радиус сферы.
Архимед очень любил шар и сферу, он даже попросил оставить на его гробницу рисунок, на котором в цилиндр вписан шар. Архимед считал, что объем шара и его поверхность равны двум третьим от объема и поверхности цилиндра, в который вписан шар»
Определение.
Сфера (поверхность шара ) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).
Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение.
Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).
Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).
Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.
Формула. Объём шара :
| V = | 4 | π R 3 = | 1 | π D 3 |
| 3 | 6 |
Формула. Площадь поверхности сферы через радиус или диаметр:
S = 4π R 2 = π D 2
Уравнение сферы
1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат :
x 2 + y 2 + z 2 = R 2
2. Уравнение сферы с радиусом R и центром в точке с координатами (x 0 , y 0 , z 0) в декартовой системе координат :
(x — x 0) 2 + (y — y 0) 2 + (z — z 0) 2 = R 2
Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.
Основные свойства сферы и шара
1. Все точки сферы одинаково удалены от центра.
2. Любое сечение сферы плоскостью является окружностью.
3. Любое сечение шара плоскостью есть кругом.
4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.
5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.
6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.
7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.
8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются , а в плоскости пересечения образуется круг.
Секущая, хорда, секущая плоскость сферы и их свойства
Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках.
Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).
Определение. Секущая плоскость — это плоскость, которая пересекает сферу.
Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг . Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Любая хорда, проходящая через центр сферы (шара) является диаметром.
Хорда является отрезком секущей прямой.
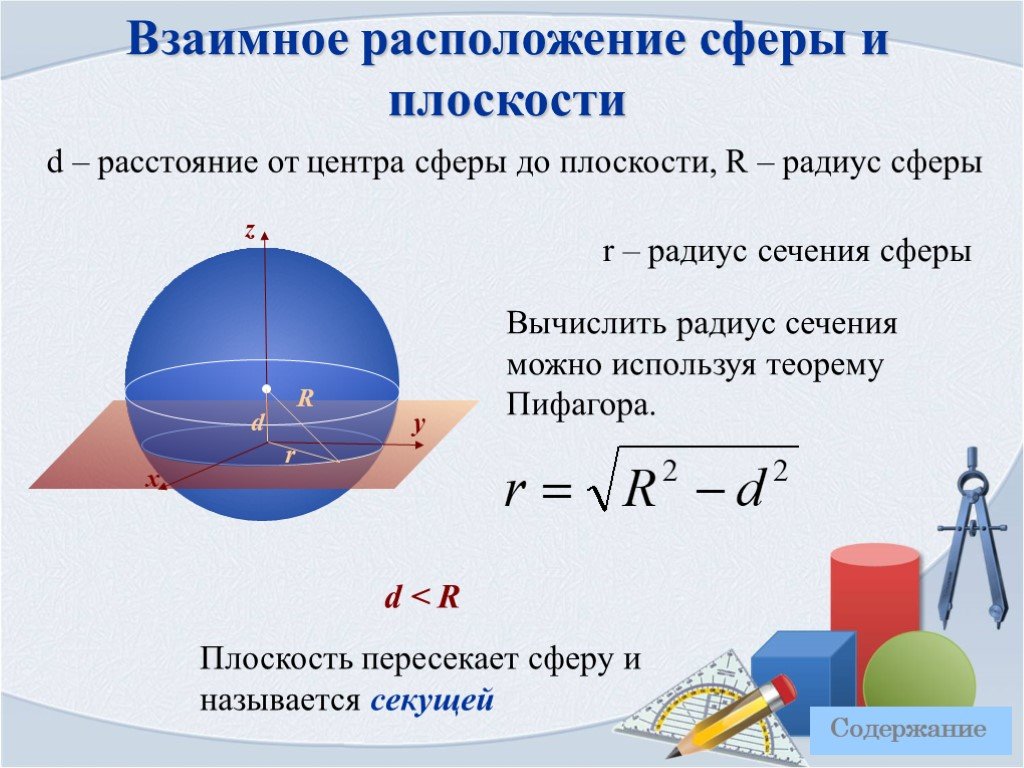
Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:
d
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m
Местом сечения секущей плоскости на сфере всегда будет малая окружность , а на шаре местом сечения будет малый круг . Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r
такого круга можно найти по формуле:
Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r
такого круга можно найти по формуле:
r = √R 2 — m 2 ,
Где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.
Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.
Касательная, касательная плоскость к сфере и их свойства
Определение. Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Определение. Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.
Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
Определение.
 Высотой сегмента h
называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Высотой сегмента h
называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:
S = 2π Rh
В сферу вписан конус, образующая которого равна l, а угол при вершине осевого сечения равен 60 градусов. Найдите площадь сферы.
Решение .
Площадь сферы найдем по формуле:
Поскольку в сферу вписан конус, проведем сечение через вершину конуса, которое будет равнобедренным треугольником. Поскольку угол при вершине осевого сечения равен 60 градусам, то треугольник — равносторонний (сумма углов треугольника — 180 градусов, значит остальные углы (180-60) / 2 = 60 , то есть все углы равны).
Поскольку угол при вершине осевого сечения равен 60 градусам, то треугольник — равносторонний (сумма углов треугольника — 180 градусов, значит остальные углы (180-60) / 2 = 60 , то есть все углы равны).
Откуда радиус сферы равен радиусу окружности, описанного вокруг равностороннего треугольника. Сторона треугольника по условию равна l . То есть
Таким образом площадь сферы
S = 4π(√3/3 l) 2
S = 4/3πl 2
Ответ : площадь сферы равна 4/3πl 2 .
Задача
Емкость имеет форму полусферы (полушара). Длина окружности основания равна 46 см. На 1 квадратный метр расходуется 300 граммов краски. Сколько необходимо краски, чтобы покрасить емкость?
Решение .
Площадь поверхности фигуры будет равна половине площади сферы и площади сечения сферы.
Поскольку нам известна длина окружности основания, найдем ее радиус:
L = 2πR
Откуда
R = L / 2π
R = 46 / 2π
R = 23 / π
Откуда площадь основания равна
S = πR
2
S = π (23/π) 2
S = 529 / π
Площадь сферы найдем по формуле:
S = 4πr 2
Соответственно площадь полусферы
S = 4πr 2 / 2
S = 2π (23/π) 2
S = 1058 / π
Общая площадь поверхности фигуры равна:
529 / π + 1058 / π = 1587 / π
Теперь вычислим расход краски (учтем, что расход дан на квадратный метр, а вычисленное значение в квадратных сантиметрах, то есть в одном метре 10 000 квадратных сантиметров)
1587 / π * 300 / 10 000 = 47,61 / π граммов ≈ 15,15 г
Задача
Решение. Рiшення .
Рiшення .
Для пояснения решения прокомментируем каждую из приведенных формул
| Для пояснення рішення прокоментуємо кожну з приведених формул
| |
| 8. Разделим объемы первого и второго шара друг на друга 9. Сократим получившуюся дробь. Заметим, что соотношение объема двух шаров равно соотношению кубов их радиусов. Учтем выражение, полученное нами ранее в формуле 4 и подставим его. Поскольку корень квадратный — это число в степени 1/2, преобразуем выражение 10. Раскроем скобки и запишем полученное соотношение в виде пропорции. Ответ получен .  | 8. Розділимо об»єми першої і другої кулі один на одного 9. Скоротимо дріб, що вийшов. Відмітимо, що співвідношення об»єму двох куль дорівнює співвідношенню кубів їх радіусів. Врахуємо вираження, отримане нами раніше у формулі 4 і підставимо його. Оскільки корінь квадратний — це число в мірі 1/2, перетворимо вираження 10. Розкриємо дужки і запишемо отримане співвідношення у вигляді пропорції. Відповідь отримана . |
| Примечание . Это часть урока с задачами по геометрии (раздел стереометрия, задачи о сфере). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом на форуме . В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√». Задача В сферу вписан конус, образующая которого равна l, а угол при вершине осевого сечения равен 60 градусов. Найдите площадь сферы. Решение . Поскольку в сферу вписан конус, проведем сечение через вершину конуса, которое будет равнобедренным треугольником. Поскольку угол при вершине осевого сечения равен 60 градусам, то треугольник — равносторонний (сумма углов треугольника — 180 градусов, значит остальные углы (180-60) / 2 = 60 , то есть все углы равны). Откуда радиус сферы равен радиусу окружности, описанного вокруг равностороннего треугольника. Сторона треугольника по условию равна l . То есть Таким образом площадь сферы S = 4π(√3/3 l) 2 Ответ : площадь сферы равна 4/3πl 2 . ЗадачаЕмкость имеет форму полусферы (полушара). Длина окружности основания равна 46 см. На 1 квадратный метр расходуется 300 граммов краски. Сколько необходимо краски, чтобы покрасить емкость? Решение . Откуда площадь основания равна Площадь сферы найдем по формуле: Соответственно площадь полусферы Общая площадь поверхности фигуры равна: Теперь вычислим расход краски (учтем, что расход дан на квадратный метр, а вычисленное значение в квадратных сантиметрах, то есть в одном метре 10 000 квадратных сантиметров) ЗадачаРешение.
|
Калькулятор радиуса сферы-Cuemath
Калькулятор радиуса сферы — это бесплатный онлайн-инструмент, который помогает найти радиус сферы.
Что такое калькулятор радиуса сферы?
«Калькулятор радиуса сферы» — это бесплатный онлайн-инструмент, который вычисляет радиус сферы, когда заданы другие измерения. Калькулятор радиуса сферы дает вам радиус сферы в течение нескольких секунд.
Калькулятор радиуса сферы
ПРИМЕЧАНИЕ. Вводите числа, состоящие только из трех цифр.
Как пользоваться калькулятором радиуса сферы?
Выполните шаги, указанные ниже, чтобы найти радиус сферы.
- Шаг 1 : Выберите вариант из раскрывающегося списка для ввода значений диаметра, площади поверхности или объема сферы.
- Шаг 2 : Введите значение параметра, выбранного вами на первом шаге, и нажмите « Вычислить », чтобы найти радиус сферы.
- Шаг 3 : Нажмите « Сбросить », чтобы очистить поля и ввести новое значение.
Как рассчитать радиус сферы?
Расстояние от центра до любой точки на окружности сферы называется радиусом. Мы знаем, что размер сферы меняется, когда изменяется длина радиуса. Теперь давайте посмотрим, как найти радиус сферы, когда известны другие измерения. Когда диаметр сферы известен, формула, используемая для радиуса сферы:
Радиус = Диаметр / 2
Когда указана площадь поверхности, для радиуса сферы используется следующая формула:
Радиус = ⎷[Площадь поверхности / (4 π)]
формула, используемая для радиуса сферы:
Радиус = ³⎷[3 * Объем / (4 π)]
Давайте рассмотрим следующий пример, чтобы лучше понять это.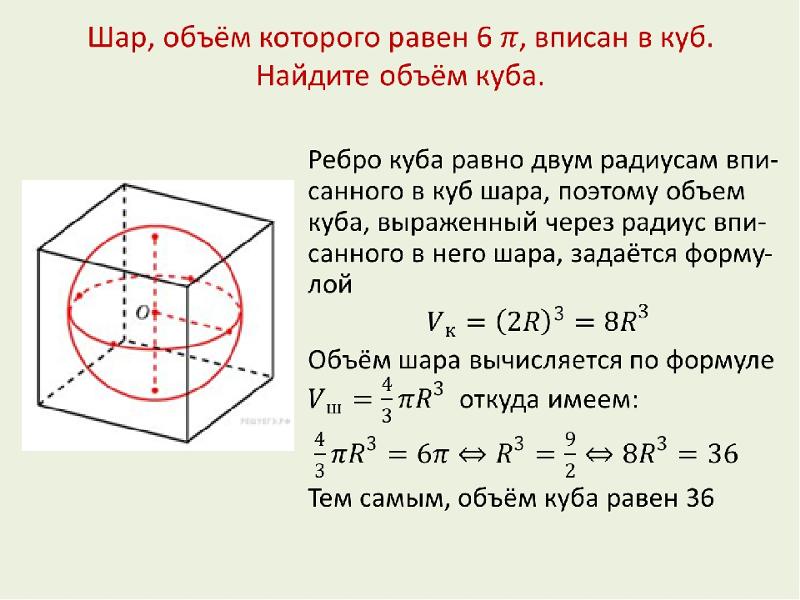
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Решенные примеры на калькуляторе радиуса сферыПример 1:
Если диаметр сферы равен 7 единицам, найдите радиус.
Решение:
Диаметр = 7 единиц
Радиус = диаметр / 2
= (7/2) Единицы
= 3,5 единицы
Пример 2:
Если диаметр сферной единиц, найдите радиус.
Решение:
Диаметр = 8 единиц
Радиус = диаметр / 2
= (8/2) единиц
= 4 единицы
Пример 3:
Если диаметр сферы равен 2 единицам .
Решение:
Диаметр = 21 единица
Радиус = Диаметр / 2
= (21/2) единицы
= 10,5 единицы
Аналогично, если найти радиус, можно использовать соответствующую формулу поверхности. дана площадь и объем сферы.
дана площадь и объем сферы.
Теперь воспользуйтесь нашим онлайн-калькулятором радиуса и найдите радиус сферы для следующих размеров:
- Диаметр = 15 единиц
- Площадь поверхности = 100 единиц
- Сфера
- Площадь поверхности сферы
- Объем сферы
Решение | Резка сфер | Окружности
Сфера на диаграмме имеет радиус \(r\) и разрезана двумя параллельными плоскостями на расстоянии \(h\) друг от друга. 92\) (вся сфера), а при \(h=0\) получаем нулевую площадь.
Итак, если нам удастся получить общую формулу, мы сможем проверить ее в этих частных случаях.
Другая возможная идея, когда \(x=0\), состоит в том, чтобы рассмотреть, что происходит, когда \(h\) очень мало. В этом случае площадь поверхности очень похожа на круг, но радиус круга не кажется особенно простым для определения, поэтому, возможно, мы оставим это на мгновение. (Есть вещи, которые мы можем сделать, чтобы приблизить радиус, используя более продвинутые методы, но в настоящее время они нам недоступны.) 92)}{\sin\theta}.\] Здесь \(R\) — радиус основания усеченного конуса, \(r\) — радиус вершины, \(h\) — высота перпендикуляра , \(s\) — длина наклона, а \(\theta\) — угол, который наклон составляет с вертикалью.
(Есть вещи, которые мы можем сделать, чтобы приблизить радиус, используя более продвинутые методы, но в настоящее время они нам недоступны.) 92)}{\sin\theta}.\] Здесь \(R\) — радиус основания усеченного конуса, \(r\) — радиус вершины, \(h\) — высота перпендикуляра , \(s\) — длина наклона, а \(\theta\) — угол, который наклон составляет с вертикалью.
Как ни странно, в этой задаче также использовалось \(r\) (для обозначения радиуса вершины пирамиды), но в нашей задаче используется \(r\) для обозначения радиуса сферы. Поэтому нам нужно быть очень осторожными при использовании формулы здесь, чтобы не запутаться.
Давайте нарисуем тонкий срез нашей сферы, чтобы увидеть, какое из этих значений легко вычислить.
Перпендикулярная высота этой усеченной части равна \(h\), толщине нашего среза.
Радиусы основания и вершины усеченного конуса примерно равны \(r\cos\varphi\), как видно из диаграммы; разница между двумя радиусами крошечная.
Длину наклона \(s\) определить немного сложнее, но угол наклона легче увидеть на диаграмме.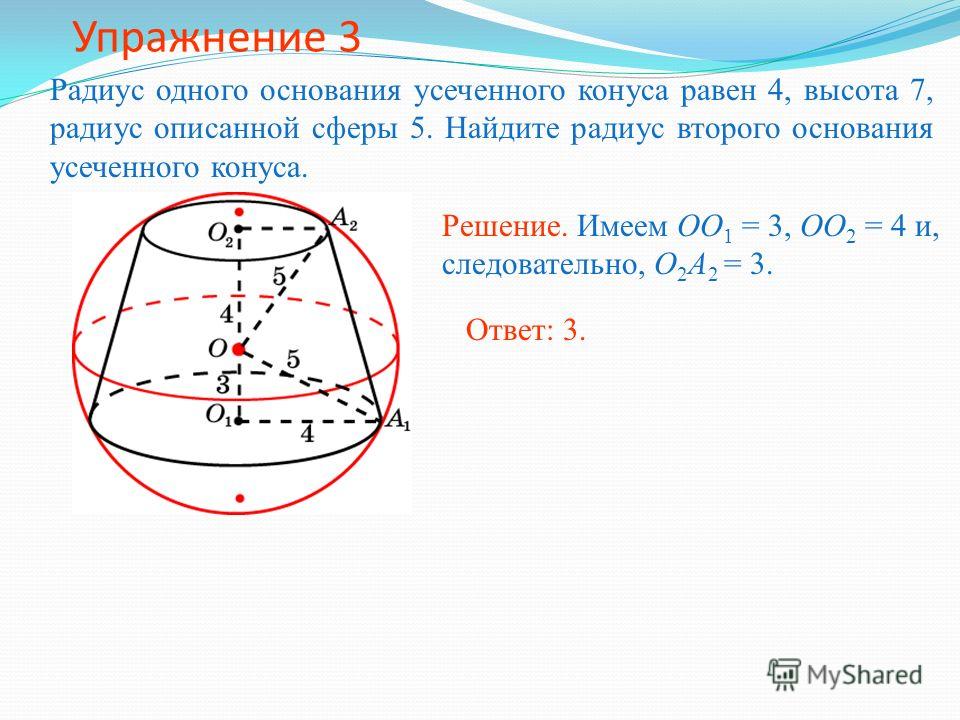 Поскольку наклон среза перпендикулярен радиусу встречающейся с ним сферы, наклон составляет угол \(\varphi\) к вертикали: 92\), поэтому мы не можем использовать третью формулу.
Поскольку наклон среза перпендикулярен радиусу встречающейся с ним сферы, наклон составляет угол \(\varphi\) к вертикали: 92\), поэтому мы не можем использовать третью формулу.
Подставляем наши значения: оба радиуса равны \(r\cos\varphi\), высота перпендикуляра равна \(h\) и угол, который образует наклон с вертикалью, равен \(\varphi\), поэтому площадь равна \[\dfrac{\pi(r\cos\varphi+r\cos\varphi)h}{\cos\varphi}=2\pi rh.\]
Это настоящий сюрприз! Ответ вообще не зависит от \(\varphi\) (или, что то же самое, \(x\))! И это то же самое, что площадь поверхности цилиндра также радиуса \(r\) и высоты \(h\).
Итак, когда \(h\) действительно мало, площадь полосы сферы составляет около \(2\pi rh\). Чем меньше мы делаем \(h\), тем точнее становится эта оценка, так как срез будет все больше и больше походить на усеченный конус.
Теперь мы можем решить основную проблему. У нас есть сечение сферы высотой \(h\). Если мы нарежем его на \(n\) кусочков, каждый высотой \(h/n\), то площадь поверхности каждого из них будет примерно \(2\pi rh/n\), поэтому в сумме площадь будет примерно \[n\times 2\pi rh/n=2\pi rh.

 Скоротимо отриманий дріб. Неважко відмітити, що співвідношення площ двох куль дорівнює співвідношенню квадратів їх радіусів. По умові завдання це співвідношення рівне m/n
Скоротимо отриманий дріб. Неважко відмітити, що співвідношення площ двох куль дорівнює співвідношенню квадратів їх радіусів. По умові завдання це співвідношення рівне m/n

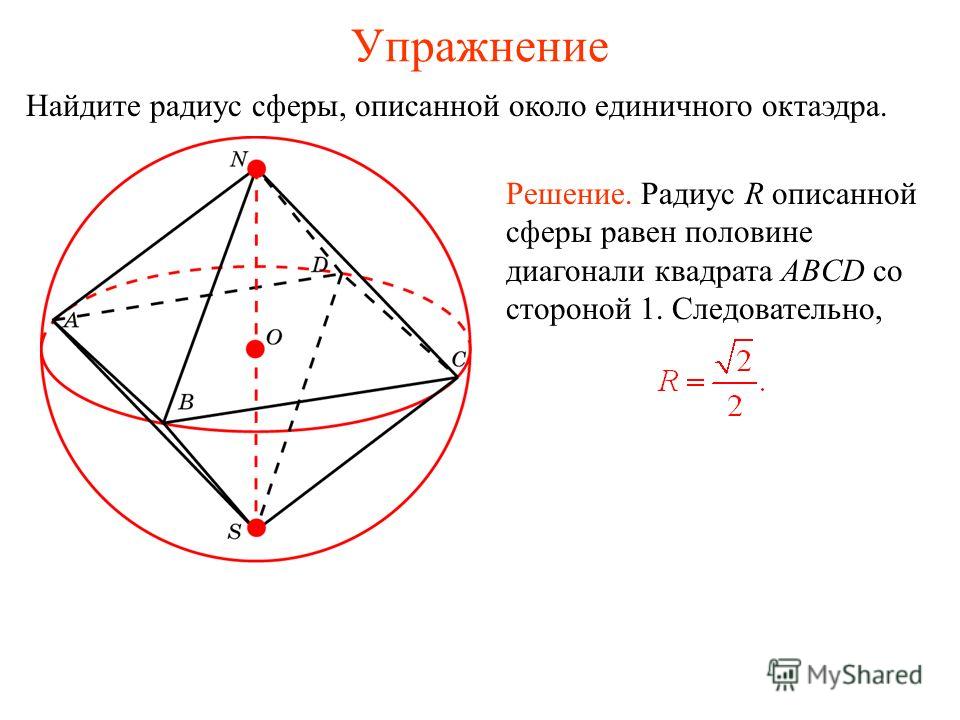 Радиус является основным параметром и очень важно уметь вычислять его значение. Для проведения этой операции существует множество способов, как практических, так и теоретических. В большинстве из них фигурирует понятие числа «Пи», в котором обязательно нужно разобраться. Число «Пи» является постоянным иррациональным трансцендентным числом. Это значит, что его десятичная запись является бесконечной. Сама константа определяется отношением длины окружности к её радиусу. С древности учёные вычисляли значение этого числа, на данный момент известно уже более миллиарда знаков после запятой. На практике и, в частности, в данной статье понадобится не слишком точное значение данной константы. И хоть первые десять знаков выглядят как 3.3, чтобы найти радиус сферы будет использоваться округлённое значение 3,4.
Радиус является основным параметром и очень важно уметь вычислять его значение. Для проведения этой операции существует множество способов, как практических, так и теоретических. В большинстве из них фигурирует понятие числа «Пи», в котором обязательно нужно разобраться. Число «Пи» является постоянным иррациональным трансцендентным числом. Это значит, что его десятичная запись является бесконечной. Сама константа определяется отношением длины окружности к её радиусу. С древности учёные вычисляли значение этого числа, на данный момент известно уже более миллиарда знаков после запятой. На практике и, в частности, в данной статье понадобится не слишком точное значение данной константы. И хоть первые десять знаков выглядят как 3.3, чтобы найти радиус сферы будет использоваться округлённое значение 3,4. 3 = (V * 3/4) / Pi. После извлечения корня кубического получится R = sqrt((V * 3/4) / Pi) . Обозначение “sqrt” означает кубический корень. Теперь стоит подставить объём в формулу и произвести вычисления: R = sqrt((48 * 3/4) / Pi) = sqrt(36 / Pi) = sqrt(1,8) = 2,4. Важное внимание следует уделить размерности в этом случае, ведь объём дан в литрах, а ответ требуется дать в величинах, измеряющих длину.
3 = (V * 3/4) / Pi. После извлечения корня кубического получится R = sqrt((V * 3/4) / Pi) . Обозначение “sqrt” означает кубический корень. Теперь стоит подставить объём в формулу и произвести вычисления: R = sqrt((48 * 3/4) / Pi) = sqrt(36 / Pi) = sqrt(1,8) = 2,4. Важное внимание следует уделить размерности в этом случае, ведь объём дан в литрах, а ответ требуется дать в величинах, измеряющих длину. Далее производить действия по аналогии с последней задачей.
Далее производить действия по аналогии с последней задачей.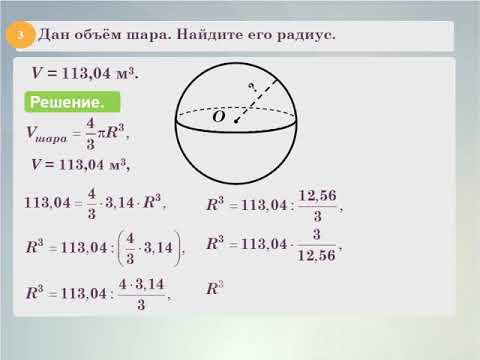
 Рiшення .
Рiшення .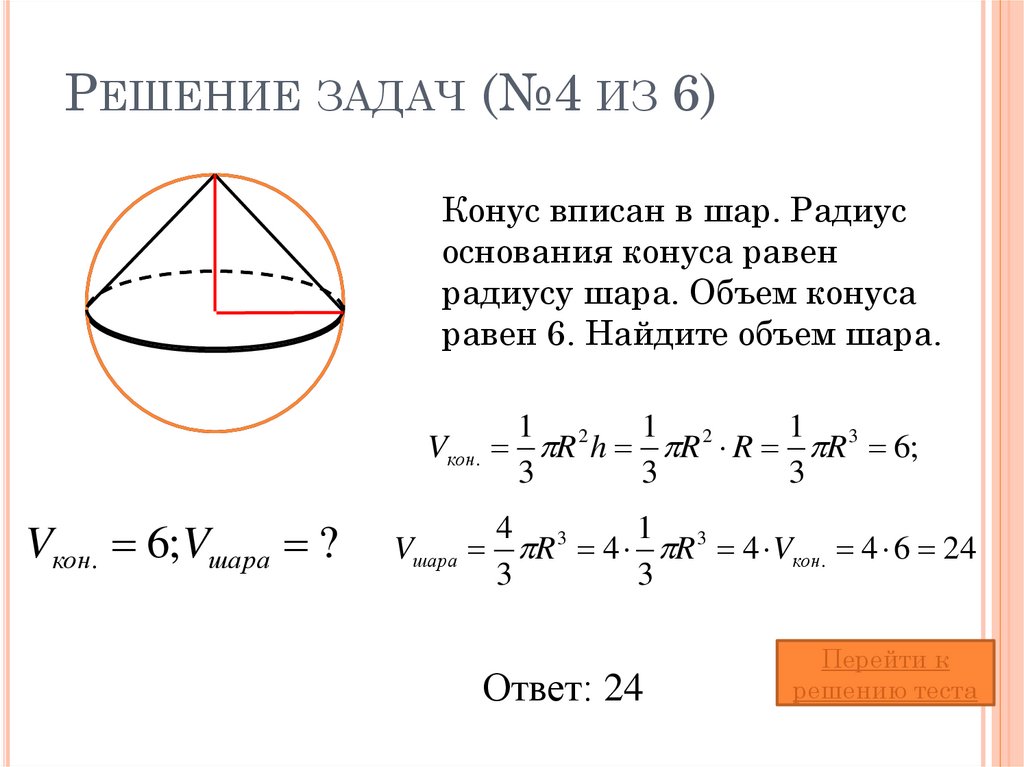 Скоротимо отриманий дріб. Неважко відмітити, що співвідношення площ двох куль дорівнює співвідношенню квадратів їх радіусів. По умові завдання це співвідношення рівне m/n
Скоротимо отриманий дріб. Неважко відмітити, що співвідношення площ двох куль дорівнює співвідношенню квадратів їх радіусів. По умові завдання це співвідношення рівне m/n
 17.5). Еще
17.5). Еще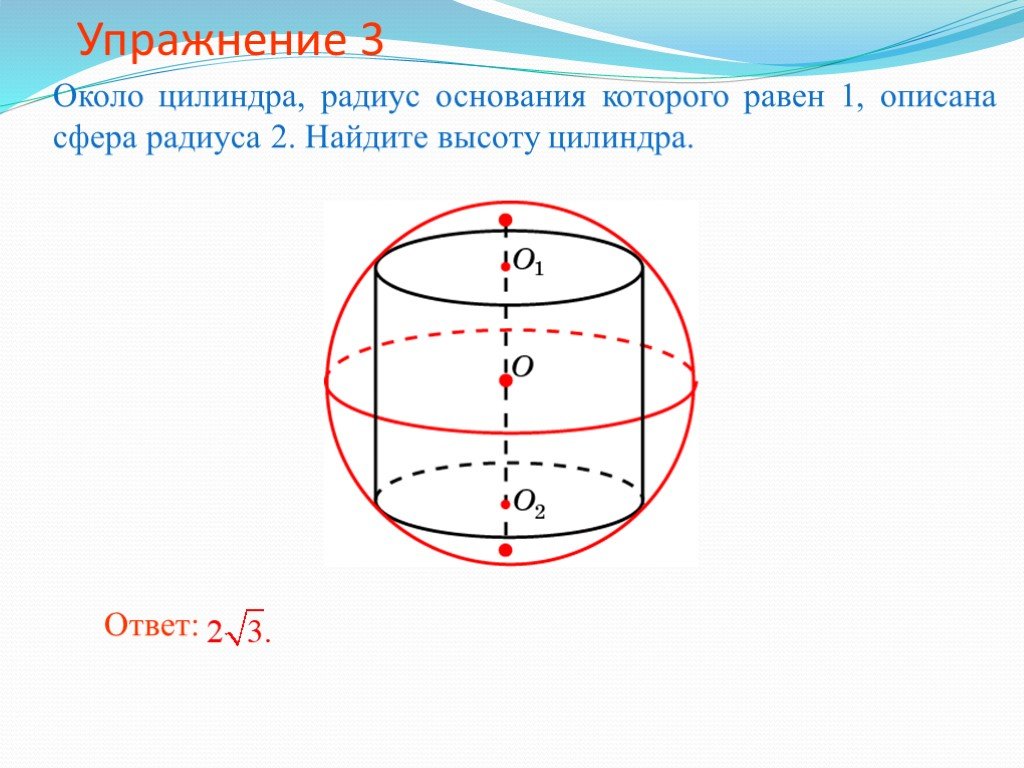 Площадь сферы радиуса R выражается формулой:
Площадь сферы радиуса R выражается формулой: