Расчет диаметра ствола | дерева
Расчет диаметра ствола | дерева
|
./img/transparent.png»/>
./img/transparent.png»/>
./img/transparent.png»/>
./img/transparent.png»/>
suКарта сайта
Наверх
Длина окружности: формулы поиска по радиусу, равному половине диаметра
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты, устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
…
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.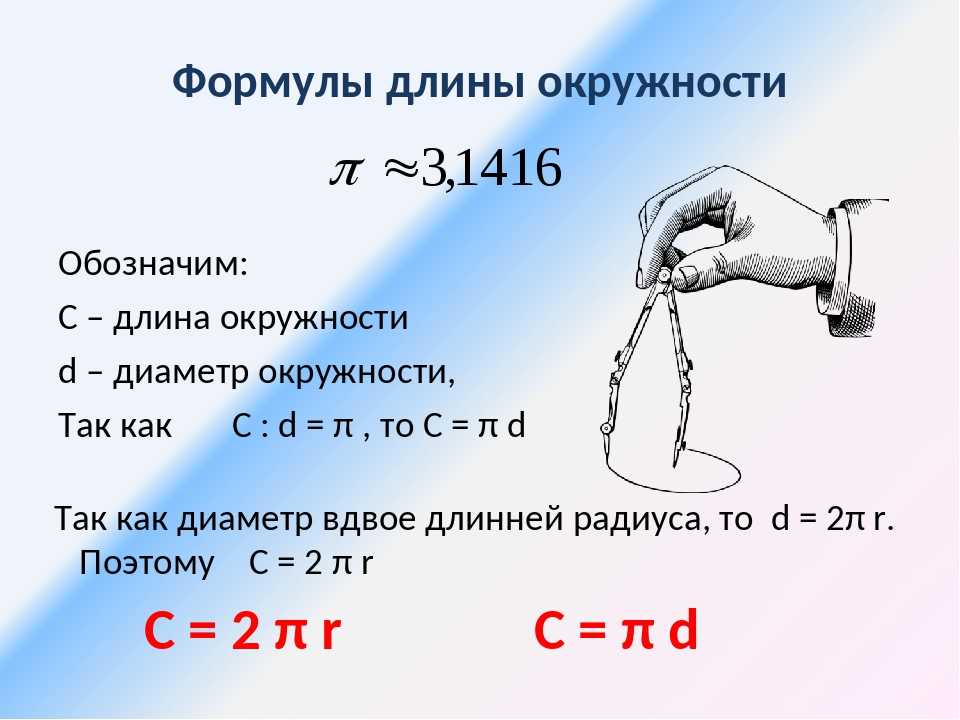
В пределах окружности имеются точки Х такие, что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда. Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками, проходящее через центр фигуры.
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
- длину фигуры вычисляют умножением диаметра на число π и записывают таким образом: C = π*D.
- Величина диаметра в два раза превышает длину радиуса. Иной способ вычисления радиуса — необходимо разделить длину круга на удвоенное π: R = C/(2* π) = D/2.
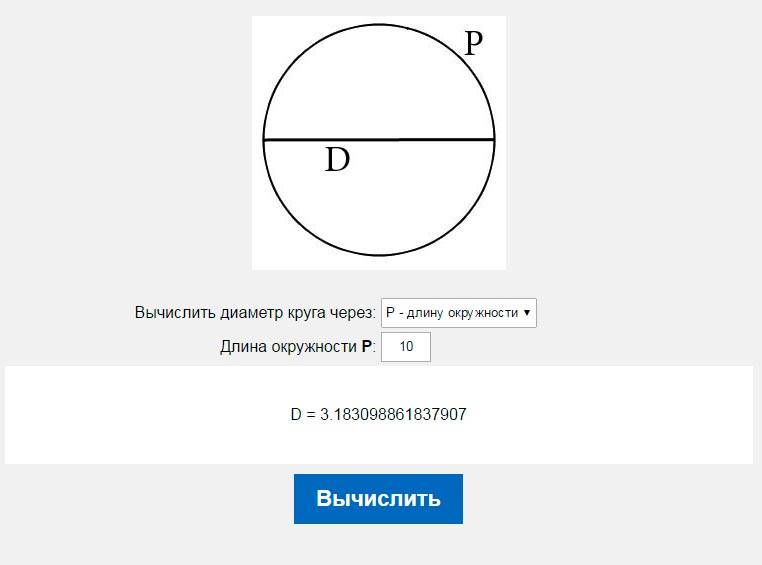
- Диаметр рассчитывается с помощью радиуса или делением длины окружности на число π. Формула нахождения диаметра: D = C/π = 2*R.
- Площадь круга, ограниченного окружностью, можно найти двумя способами: через радиус или диаметр. По формуле площадь равна четвёртой части произведения числа π и диаметра в квадрате или радиусу в квадрате, умноженному на π: S = π*R2 = π*D2/4.
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него.
В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
- При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
- Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
- Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.
Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Форму колеса имеет гончарный круг, большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
Калькулятор окружности| Математические вкусности
Форма поиска
Поиск
Используйте наш Калькулятор окружности, чтобы определить длину окружности.
При расчете длины окружности вы бегаете по кругу? Наш калькулятор окружности — это простой способ найти длину окружности любого круглого объекта. Просто введите радиус круга и нажмите «рассчитать». Вы можете нажать кнопку «сброс», если вам нужно очистить калькулятор окружности, чтобы найти ответ для другого круга.
Попробуйте наш калькулятор окружности
прямо сейчас! А если вы не знаете, что такое радиус или как его найти, ниже мы познакомим вас с некоторыми основами нахождения длины окружности.
Какова длина окружности?
Окружность круга — это измерение вокруг края круга. Это можно сравнить с нахождением периметра фигуры (хотя слово периметр зарезервировано специально для многоугольников). Если бы вы вырезали круг и разложили контур, длина созданной им линии была бы его окружностью. Окружность может быть измерена в любой единице или системе, в которой традиционно измеряется длина, — в британской (дюймы, футы и т. д.) или метрической (сантиметры, метры и т. д.). В какой бы единице измерения ни измерялся радиус, такой же единицей считается и длина окружности.
Уравнение, используемое для нахождения длины окружности, имеет вид C = 2Πr, где C обозначает длину окружности, R обозначает радиус, а Π обозначает Pi, математическую константу, эквивалентную примерно 3,14 (подробнее см. ниже).
Вы также можете рассчитать длину окружности, используя диаметр, с помощью уравнения C = Π * d. Если у вас есть только диаметр круга и вы все равно хотите использовать этот калькулятор, вы можете найти радиус, разделив диаметр пополам.
Мы предлагаем решить некоторые задачи самостоятельно и проверить свой ответ с помощью калькулятора, так как он предлагает решение для каждой задачи, но не показывает работу, которая с ней связана.
Части круга
- Окружность: Расстояние по кругу. Его также можно понимать как периметр круга.
- Радиус : Расстояние от центра круга до его края. Независимо от того, в каком направлении вы измеряете, радиус будет одинаковым из любой точки на краю круга.
- Диаметр: Прямая линия, пересекающая окружность и пересекающаяся через центральную точку. Это измерение всегда равно вдвое больше радиуса (2r).
Значение
Пи Пи ( Π) – это бесконечное число, что означает, что оно продолжается вечно и не имеет конца. Его значение составляет около 3,1415926535897… Пи также является константой, что означает, что оно всегда равно одному и тому же значению.
Греческая буква p (произносится как «пирог») используется для описания этого числа. Это отношение между длиной окружности любого круга и его диаметром, и это верно для всех кругов. Это означает, что длина окружности любого круга примерно в 3,14 раза больше его диаметра.
Пример уравнения окружности
Какова длина окружности, радиус которой равен 24 дюймам?
Длина окружности = 2×Π×r
C = 2 × 3,14 × 24
C = 150,79 дюйма более точный ответ. Это связано с тем, что для числа Пи используется более точное число, а не округление до 3,14.
Наш калькулятор длины окружности вычисляет длину окружности путем ввода ее радиуса. Наш калькулятор окружности можно использовать бесплатно в любое время, когда вы хотите определить длину окружности!
У нас также есть забавное обучающее видео о диаметре, радиусе и длине окружности прямо здесь: Видео о окружности окружности .
Прочие калькуляторы
Подпишитесь на нашу БЕСПЛАТНУЮ рассылку!
Подпишитесь на нашу БЕСПЛАТНУЮ рассылку новостей!
Адрес электронной почты *
Радиус, диаметр, длина окружности и площадь кругов
By: Mary Jane Sterling and
Updated: 07-07-2021
From The Book: Trigonometry For Dummies
Trigonometry For Dummies
Explore Book Buy On Amazon
A circle is a геометрическая фигура, для идентификации и классификации которой нужны только две части: ее центр (или середина) и ее радиус (расстояние от центра до любой точки на окружности).
После того, как вы выбрали точку в качестве центра круга и знаете, как далеко эта точка находится от всех точек, лежащих на круге, вы можете нарисовать довольно приличную картину.С помощью меры радиуса можно многое сказать о круге: его диаметр (расстояние от одной стороны до другой, проходящее через центр), его окружность (насколько далеко вокруг него) и его площадь (сколько квадратных дюймов, футов, ярдов, метров — сколько у вас — влезет в него).
Древние математики выяснили, что длина окружности всегда чуть больше, чем в три раза превышает диаметр окружности. С тех пор они сузили это «чуть более трех раз» до значения, называемого 9.0011 pi (произносится как «пирог»), обозначаемый греческой буквой π .
Десятичное значение π не является точным — оно продолжается вечно, но в большинстве случаев люди называют его приблизительно равным 3,14 или 22/7, в зависимости от того, какая форма лучше подходит для конкретных вычислений.
Формула для вычисления длины окружности связана с π и диаметром:
Длина окружности: C = πd = 2 πrd
Точно так же формула площади круга связана с π и радиусом:
Площадь круга: A = πr 2Эта формула гласит: «Площадь равна пи в квадрате».
Найдите радиус, длину окружности и площадь круга, если его диаметр равен 10 футам в длину.
Если диаметр ( d ) равен 10, вы записываете это значение как d = 10 . Радиус равен половине диаметра, поэтому радиус равен 5 футам, или r = 5 . Вы можете найти длину окружности, используя формулу
Итак, длина окружности составляет около 31,5 фута. Вы находите площадь, используя формулу
, поэтому площадь составляет около 78,5 квадратных футов.