Способ раскрытия модуля
Разделы: Математика
Одним из типов упражнений, рассматриваемых в курсе алгебры, особо выделяются упражнения, содержащие модули. Актуальность данных упражнений вызвана тем, что материалы ЕГЭ и вступительные работы в вузы содержат данный тип упражнений.
Если в задании модуль только один, то он легко раскрывается по определению. Но в решении упражнений, где количество модулей более чем один, у учащихся возникают затруднения, так как нужно определять знаки в одном и том же промежутке, но для различных подмодульных выражений и ещё учесть знаки из упражнения, стоящие перед модулем. В таких случаях мы пользуемся способом “решетки”. Название условно, так как просто сопутствующий чертеж напоминает обычную оконную решетку.
Рассмотрим алгоритм решения упражнения способом “решетки”:
Пример 1:
Решить уравнение
Ответ: -7.
Пример 2:Решить систему неравенств
Решим неравенство I , используя определение модуля.
Решение неравенства I:
Решим неравенство II используя метод “решетки”.
Общее решение системы:
Ответ:
Методика использования показала, что такие упражнения могут успешно решать как учащиеся математического профиля, так и учащиеся общеобразовательного и гуманитарного профиля, так как наглядность чертежа резко снижает количество ошибок по невнимательности.
8.02.2009
Поделиться страницей:Раскрытие модуля и комбинирование функций
Очень часто в уравнениях и неравенствах задачи 18 присутствует модуль. При этом многие ученики плохо представляют себе, что это такое.
Но ещё хуже дело обстоит в том случае, когда под модулем стоит что-то сложное — например, функция от двух переменных. Если с одной переменной мы ещё более-менее справляемся, приравнивая подмодульное выражение к нулю, то уж с двумя переменными начинается треш.:)
Сегодня мы разберёмся с этим вопросом раз и навсегда. Для этого нужно чётко усвоить две простых вещи:
- Любое выражение, стоящее под модулем, каким бы сложным оно ни казалось, можно и нужно приравнивать к нулю. И считать корни;
- Далеко не всегда корнями будут конкретные числа. Модуль может обнуляться на множестве точек, выстраивающихся в одну прямую, либо даже в параболу или окружность. Как это понять и где применять — сегодня мы об этом и поговорим.
В целом, хотел бы отметить: не бойтесь приравнивать к нулю выражения, содержащие несколько переменных. Как правило, такие уравнения очень легко решаются. В этом вы убедитесь, когда будете решать домашнюю работку в сегодняшнем уроке.:)
Хорошая новость: задачи, рассмотренные в сегодняшнем уроке, полностью соответствуют тому, что ждёт вас на настоящем экзамене. Если вы поймёте инструкции из видео и немного потренируетесь, то велика вероятность, что и настоящую задачу 18 на экзамене вы одолеете с максимальным результатом.
Кстати, о домашке. В этот раз предстоит решить три обязательных задачи, которые опять же вполне доступны любому среднестатистическому ученику. Сразу скажу: все они решаются графически, а в последних двух задачах придётся вспомнить кое-что из предыдущих уроков.
И ещё. Если вы внимательно посмотрите на задачи из домашней работы, то обнаружите, что в некоторых задания вообще отсутствует модуль. Зато присутствует уравнение с несколькими переменными. Попробуйте свои силы — и убедитесь, что все эти уравнения вам вполне по силам.:)
- Платный курс
Этот урок является частью платного курса. Пожалуйста, перейдите на страницу этого курса — там можно посмотреть его содержание и при желании купить курс.
Обратите внимание: оплатив курс всего один раз, вы получаете доступ ко всем урокам из этого курса — как уже опубликованным, так и тем, что будут опубликованы в будущем.:)
- Перейти на страницу курса
Смотрите также:
- Более сложные задачи с параметром: аналитическое решение.
- Новый урок по задачам с параметром: применение доказательств для упрощения задач
- Пробный ЕГЭ-2011 по математике, вариант №2
- Пробный ЕГЭ 2012. Вариант 2 (без логарифмов)
- Тест: простейшие показательные уравнения (2 вариант)
- Изюм и виноград (смеси и сплавы)
www.berdov.com
раскрыть модуль
По вашим просьбам!
6. Упростить тригонометрическое выражение:

17. Найти положительное число, которое в сумме с обратным ему числом, дают наименьшее значение.

18. Решите уравнение:
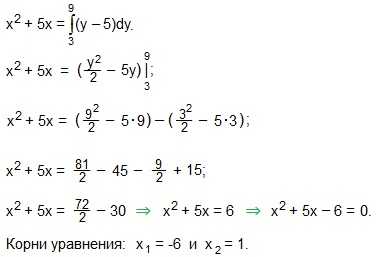
20. Раскройте модуль:

21. Упростите выражение:
Сначала выполним действия в скобках. 1) Разложим знаменатели дробей в скобках на множители по формулам сокращенного умножения: a2-b2=(a-b)(a+b) и (a+b)2=a2+2ab+b2.
22. Решить неравенство: cos(3π/2+2x)+3sin2x<2.
Применяем правило для формул приведения: 1) перед приведенной функцией ставим знак приводимой. Так как у нас угол (3π/2+2x) находится в 4 четверти, а косинус в 4 четверти положителен, то знак не поменяется. 2) если в записи аргумента π/2 взято нечетное число раз, то функцию меняем на кофункцию. У нас π/2 взято 3 раза — нечетное число, поэтому косинус поменяется на синус. Получаем равносильное данному неравенство:
sin2x+3sin2x<2. Приводим подобные слагаемые: 4sin2x<2. Разделим обе части неравенства на 4:
sin2x<½. Пусть 2х=t. Осталось решить простейшее неравенство sint<½. Изобразим в одной системе координат tOy графики функций y=sint и у=½ и определим промежуток значений аргумента, при которых синусоида лежит ниже прямой у=½.
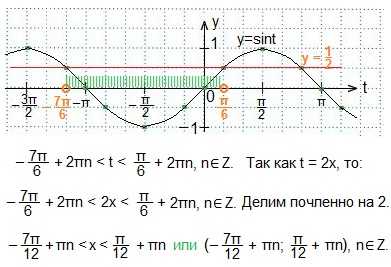
23. В наклонном параллелепипеде перпендикулярное к основанию сечение, площадь которого 340 см2, проходит через диагональ лежащего в основании прямоугольника со сторонами 8 см и 15 см. Вычислите объем параллелепипеда.

24. Найдите модуль вектора а, если модуль вектора b равен 19, модуль суммы этих векторов — 20, а модуль разности — 18.
Похожие задания были и в прошлом году. Посмотрите видео решение № 24 варианта 0009 из сборника ЕНТ-2013.
а затем краткое решение этого задания.

Всем желаю удачи и успехов!
test-training.ru
Как извлечь из модуля | Сделай все сам
Модуль – это безусловная величина числа либо выражения. Если требуется раскрыть модуль, то, согласно его свойствам, итог этой операции неизменно должен быть неотрицательным.

Инструкция
1. Если под знаком модуля находится число, значение которого вам знаменито, то раскрыть его дюже примитивно. Модуль числа a, либо |a|, будет равен самому этому числу, если a огромнее либо равно 0. Если a поменьше нуля, то есть является негативным, то его модуль будет равен противоположному ему, то есть |-a|=a. Согласно этому свойству, модули противоположных чисел равны, то есть |-a|=|a|.
2. В том случае, если подмодульное выражение возведено в квадрат либо в иную четную степень, то дозволено легко опустить скобки модуля, потому что всякое число, возведенное в четную степень, является неотрицательным. Если необходимо извлечь квадратный корень из квадрата числа, то это также будет модуль этого числа, следственно модульные скобки дозволено опустить и в этом случае.
3. Если в подмодульном выражении имеются неотрицательные числа, то их дозволено перенести за пределы модуля. |c*x|=c*|x|, где с – неотрицательное число.
4. Когда имеет место уравнение вида |x|=|c|, где x является желанной переменной, а c действительным числом, то раскрыто оно должно быть дальнейшим образом: x=+-|c|.
5. Если надобно решить уравнение, содержащее модуль выражения, итогом которого должно быть вещественное число, то знак модуля раскрывают, исходя из свойств этой неопределенности. К примеру, если имеется выражение |x-12|, то, если (x-12) – неотрицательное, оно останется постоянным, то есть модуль раскроется как (x-12). Но |x-12| превратится в (12-x), если (x-12) поменьше нуля. То есть, модуль раскрывается в зависимости от значения переменной либо выражения в скобках. Когда знак итога выражения неведом, то задача превращается в систему уравнений, первое из которых рассматривает вероятность негативного значения подмодульного выражения, а второе – правильного.
6. Изредка модуль дозволено однозначно раскрыть, даже если его значение неведомо по условиям задачи. Скажем, если под модулем находится квадрат переменной, то итог будет правильным. И напротив, если там заведомо негативное выражение, то модуль раскрывается с противоположным знаком.
jprosto.ru
Как раскрыть модуль? |3-2x|=5 помогите!
Модуль равен совокупности двух систем: 1-я система уравнений: { 3-2х=5, 3-2х >=0, 2-я система уравнений: {3-2х=-5, 3-2х<0. 1-я: х=-1, проверяем второе условие подстановкой х=-1. 5>=0 верно. 2-я: х=4, проверяем второе условие подстановкой х=4. -5<0 верно. Ответ: {-1; 4}.
два уравнения будет -3+2х=5 и 3-2х=5
3 — 2х = 5 2х = 3 — 5 2х = -2 х = -1 или 3 — 2х = -5, т. к. модуль минус пяти тоже равно 5 2х = 3 + 5 2х = 8 х = 4 Ответ: х = -1; 4
3-2x=5 или 3-2x=-5 1 случай 2x=-2 x=-1 2случай 2x=-8 x=-4
-2х=2 х=-1 модуль показывает на положительное значение разности, 3-2(-1)=3+2=5
touch.otvet.mail.ru
