Онлайн урок: Признаки делимости на 10, на 5 и на 2 по предмету Математика 6 класс
Число 10 можно разложить на пять двоек.
\(\mathbf{10=5\cdot2}\)
Это означает, что десять всегда делится нацело на 2
Если натуральное число делится нацело на 2, оно называется чётным.
Если же появляется остаток 1, тогда такое число называют нечётным.
Из однозначных чисел числа 0, 2, 4, 6 и 8 чётны, а числа 1, 3, 5, 7 и 9 нечётны.
Поэтому и цифры 0, 2, 4, 6, 8 называют чётными, а цифры 1, 3, 5, 7, 9— нечётными.
Полный десяток всегда является чётным числом, т.к. делится на 2 без остатка.
Если в разряде единиц стоит чётная цифра, значит число будет чётным.
И наоборот, если в разряде единиц стоит нечётная цифра, то и само число будет нечётным.
Довольно легко запомнить!

Когда в записи натурального числа на конце стоит чётная цифра, то такое число чётное (делится нацело на 2), а если в записи числа на конце стоит нечётная цифра, то это число нечётное.
Например, числа:
2, 88, 174, 2374 четные
3, 37, 541, 2391 нечетные
Пример 1
Можно ли, используя только цифры 2, 3, 4, 5, 7 записать число, делящееся на 2?
Решение:
Не всегда. Можно, если в разряд единиц поставить 2 или 4 например: 32574 или 73542
Можно придумать и другие числа, меняя местами предложенные цифры, но всегда в разряде единиц должны стоять четные.
Пример 2
Найдите среди чисел 154, 161, 174, 178, 191, 315, 320, 346, 425, 475
числа, кратные 2Решение:
По признаку делимости на 2, нам надо выбрать только четные числа.
Значит, выбираем 154, 174, 178, 320, 346
ladle.ru
рассуждаем логически и даем ответ!
Рассмотрим основные признаки делимости чисел на 2, 5 и 10. Начнем с десятки
Признак делимости на десять
- Если натуральное число оканчивается цифрой нуль, то это число делится без остатка на 10.
Для того чтобы в таком случае получить частное от деления, необходимо просто отбросить один нуль.
- Например, 350 делится без остатка на 10. Результатом деления будет 35.
А теперь попробуем другое число, например, 357. При делении на 10 получим неполное частное 35 и остаток 7. То есть, в качестве остатка будет цифра, записанная на последнем месте в числе.
Если же в записи натурального числа, на последнем месте стоит другая цифра, то оно не делится без остатка на 10. Остатком от деления в таком случае будет последняя цифра.
Заметим, что число 10 является произведением чисел 2 и 5. Другими словами десятка делится на 2 и на 5 без остатка. А следовательно, любое число, которое делится без остатка на 10 делится и на 2, и на 5. А учитывая предыдущий признак, получаем, что любое число, в записи котоого на последнем месте стоит нуль, делится на 2 и на 5.
- Например, 70 = 7*10 = 7*(2*5) = (7*2)*5=14*5, то есть 70:5=14
Аналогично для двойки,
- 70=7*10 = 7*(2*5)=(7*5)*2=35*2, то есть 70:2=35.
Признаки делимости на 5
Заметим так же тот факт, что любое многозначное натуральное число можно представить в виде полных десятков и единиц. Например, 23=20+3, или 1253= 1250+3.
Так как число полных десятков всегда оканчивается нулем, то эта часть числа всегда делится на 5. Следовательно, делимость числа на 5 зависит от числа, которое записано на последнем месте. Т.е. от числа единиц. Там могут быть цифры 1,2,3,4,5,6,7,8,9, из этих чисел, только 5 делится на 5 без остатка. Следовательно, можем сформулировать признак делимости числа на 5.
- Если запись натурального числа оканчивается на 5 или на 0, то это число делится на 5 без остатка. Если же запись числа оканчивается на другую цифру, то это число не делится на 5 без остатка.
Например, число 355 делится на 5 без остатка, и число 350 тоже делится на 5 без остатка, а числа 654 и 348 не делятся без остатка на 5.
Признаки делимости на 2
Аналогичными рассуждениями можно получить признак делимости числа на 2.
- Если запись натурального числа оканчивается четной цифрой, то это число делится на 2 без остатка. Если же запись числа оканчивается нечетной цифрой, то это число не делится на 2 без остатка.
Четными называются числа, не имеют остатка при делении на 2. Из однозначных, цифры 0,2,4,6,8 являются четными. Цифры 1,3,5,7,9 – являются нечетными. Нечетные числа при делении на 2, дают остаток 1.
Например, числа 4,18, 26, 4352, четные, а числа 123, 3, 987, 545 – нечетные.
Нужна помощь в учебе?
Предыдущая тема: Основное свойство дроби: если числитель и знаменатель умножить или…
Следующая тема:   Признаки делимости на 3 и на 9: рассмотрим на примере и выведем правило
Все неприличные комментарии будут удаляться.
www.nado5.ru
Сформулируйте признаки делимости на 2,5,10
На 2: делятся все четные числа На 5: делятся числа, оканчивающиеся на «5» или «0» На 10: делятся числа, оканчивающиеся на «0»Признак делимости на 2 Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2, то есть является чётной. Признак делимости на 5 Число делится на 5 тогда и только тогда, когда последняя цифра делится на 5 (то есть равна 0 или 5). Признак делимости на 10 Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль
touch.otvet.mail.ru
Признаки делимости на 10, на 5 и на 2
Признаки делимости на 10, на 5 и на 2
Вопрос: что такое признаки делимости чисел ?
Ответ: признаки делимости чисел — это
Знать эти признаки необходимо при решении многих арифметических задач.
Признак делимости на 10
Рассмотрим несколько чисел, запись которых оканчивается цифрой 0, например,
60, 130, 2340
Каждое из этих чисел делится без остатка на 10
Чтобы получить частное, достаточно отбросить цифру 0.
60 : 10 = 6
130 : 10 = 13
2340 : 10 = 234
Вывод: любое натуральное число, запись которого оканчивается цифрой 0, делится без остатка на 10
Если последняя цифра в записи натурального числа отлична от нуля,
то это число не делится без остатка на 10Проверим это утверждение, например, на числе 234
234 : 10 = 23 целых в остатке 4
(неполное частное 23 и остаток 4 — последняя цифра в записи числа 234)
Вывод: если последняя цифра в записи натурального числа отлична от нуля, то это число не делится без остатка на 10.
Определение
Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10.
Если запись натурального числа оканчивается другой цифрой, то оно не делится без остатка на 10.
Остаток в этом случае равен последней цифре в записи числа.
Обратим внимание на то, что число 10 = 2 · 5 (число 10 делится без остатка и на 2, и на 5).
Вывод: число, запись которого оканчивается цифрой 0, делится без остатка и на 5, и на 2.
Например, 70 = 7 · 10 = 7 · (2 · 5) = (7 · 2) · 5 = 14 · 5, значит, 70 : 5 = 14.
А из того что 70 = 7 · (5 · 2) = (7 · 5) · 2 = 35 · 2, получаем, что 70 : 2 = 35.
Полные десятки
Существует такое понятие, как «круглое» число — это целое число, запись которого оканчивается одним или несколькими нулями.
Такие числа принято называть «круглыми» («полными«) десятками.
Например, числа 40, 530, 3270, 3200 являются полными десятками.
40 — четыре десятка
530 — пятьдесят три десятка
3270 — триста двадцать семь десятков
3200 — триста двадцать десятков
Полные десятки делятся и на 10, и на 5, и на 2.
Признак делимости на 5
Каждое число можно представить в виде суммы полных десятков и единиц, например,
46 = 40 + 6, 539 = 530 + 9, 3278 = 3270 + 8.
Так как полные десятки делятся на 5, то и всё число делится на 5 лишь в том случае, когда на 5 делится число единиц
Это возможно только тогда, когда в разряде единиц стоит цифра 0 или 5.
Определение
Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5.
Например, числа 270 и 275 делятся без остатка на 5
Если же запись числа оканчивается другой цифрой, то число без остатка на 5 не делится.
Например, числа 272 и 273 на 5 без остатка не делятся.
Четные и нечетные числа
Определение
Числа, делящиеся без остатка на 2, называют чётными, а числа, которые при делении на 2 дают остаток 1, называют нечётными.
Из однозначных чисел числа 0, 2, 4, 6 и 8 чётные, а числа 1, 3, 5, 7 и 9 нечётные
Цифры 0, 2, 4, 6, 8 называют чётными, а цифры 1, 3, 5, 7, 9 — нечётными.
Все полные десятки делятся на 2 без остатка (т. е. они чётны).
Вывод: любое натуральное число чётно, когда в разряде единиц стоит чётная цифра, и нечётно, когда в разряде единиц стоит нечётная цифра.
Определение
Если запись натурального числа оканчивается чётной цифрой, то это число чётно (делится без остатка на 2), а если запись числа оканчивается нечётной цифрой, то это число нечётно.
Например, числа 2, 30, 74, 56, 108 чётные, а числа 3, 31, 75, 57, 109 нечётные.
Это интересно

Древнегреческий философ (профессиональный мыслитель), математик и мистик (верил в существование сверхъестественных сил) Пифагор Самосский, чётные числа считал женскими, а нечётные — мужскими
На рисунке числа от 1 до 100 (чётные и нечётные числа разного цвета)

В старину люди верили в магию чисел, где всё хорошее ассоциировалось с нечётными цифрами, а плохое – с чётными. Поэтому, например, в Рождество на стол всегда ставили нечётное количество блюд. Люди верили, что нечётные числа символизируют постоянное продолжение жизни, незавершенность. А чётные, наоборот, означают конечность всего живого, остановку движения.
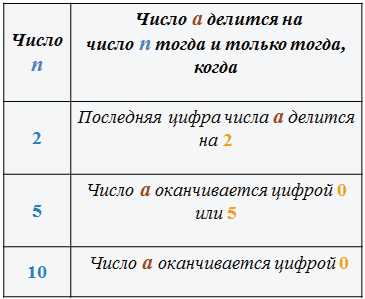
Таблица признаков делимости чисел
budu5.com
