формула и шаги • BUOM
30 августа 2021 г.
Если вы работаете в сфере финансов или экономики, расчет коэффициента корреляции может помочь вам лучше проанализировать и понять набор переменных. Если вы владелец бизнеса, определение этого значения может помочь вам определить будущие продажи вашей компании, а также общие тенденции рынка. В этой статье мы определяем, что такое коэффициент корреляции, и представляем вам шаги для его расчета.
Что такое коэффициент корреляции?
Коэффициент корреляции относится к измерению силы между двумя отдельными переменными. В то время как корреляция определяет отношение между этими двумя переменными, коэффициент корреляции связан с состоянием отношения. Коэффициент корреляции часто обозначается как r. Как только вы узнаете, какие переменные или данные вы используете, вы сможете выбрать наиболее подходящий тип коэффициента корреляции. Существует три типа коэффициентов корреляции, и они следующие:
Корреляция Пирсона: эта корреляция измеряет линейную связь между двумя переменными.
 Тем не менее, он не может определить разницу между независимыми и зависимыми переменными. Чем сильнее корреляция между этими двумя наборами данных, тем ближе она будет к +1 или -1. Это наиболее часто используемый тип коэффициента корреляции.
Тем не менее, он не может определить разницу между независимыми и зависимыми переменными. Чем сильнее корреляция между этими двумя наборами данных, тем ближе она будет к +1 или -1. Это наиболее часто используемый тип коэффициента корреляции.Корреляция Спирмена: корреляция Спирмена используется для определения монотонной связи между двумя наборами данных. Это измерение основано на ранжированных значениях для каждого набора данных и использует искаженные или порядковые переменные, а не те, которые имеют нормальное распределение.
Корреляция Кендалла: Корреляция Кендалла измеряет силу зависимости между двумя наборами данных.
Когда вы начнете понимать коэффициент корреляции, важно рассмотреть значение его значений как таковых:
Программы для Windows, мобильные приложения, игры — ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале — Подписывайтесь:)
Коэффициент корреляции представляет собой значение от -1 до 1.
Когда коэффициент корреляции близок к нулю, связь между этими переменными считается слабой.

Если значения положительные, корреляция положительная.
Аналогично, если значения отрицательные, корреляция отрицательна.
Корреляция -1 и корреляция 1 считаются идеальными корреляциями.
Как рассчитать коэффициент корреляции
Если вы хотите измерить силу связи между двумя переменными, вы можете сделать это с помощью расширенного или онлайн-калькулятора. Вы также можете использовать свои математические способности и вычислить его вручную. При расчете коэффициента корреляции вручную следует иметь в виду следующие представления:
(x(i), y(i)) = пара данных
x̅ = среднее значение x (i)
ȳ = среднее значение y (i)
s(x) = стандартное отклонение первых координат x(i)
s(y) = стандартное отклонение второй координаты y(i)
Вот шаги, которые необходимо предпринять для расчета коэффициента корреляции:
Определите свои наборы данных.
Рассчитайте стандартизированное значение для ваших переменных x.

Рассчитайте стандартизированное значение для ваших переменных y.
Умножьте и найдите сумму.
Разделите сумму и определите коэффициент корреляции.
1. Определите наборы данных.
Начните расчет с определения того, какими будут ваши переменные. Как только вы узнаете свои наборы данных, вы сможете включить эти значения в свое уравнение. Разделите эти значения переменными x и y.
2. Рассчитайте стандартизированное значение для ваших переменных x.
После того, как вы определили свои наборы данных, используйте следующее уравнение для расчета стандартизированного значения для каждой переменной x(i):
(z(x))(i) = (x(i) — x̅) / s(x)
3. Рассчитайте стандартизированное значение для ваших переменных y.
Теперь, когда вы определили стандартизированное значение для каждого x(i), сделайте то же самое для каждого y(i) со следующим уравнением:
(z(y))(i) = (y(i) — ȳ) / s(y)
4. Умножьте и найдите сумму.

Теперь, когда у вас есть стандартизированные значения, перемножьте их. Например:
(г(х))(я) * (г(у))(я)
После того, как вы умножили значения, сложите их вместе, чтобы найти сумму.
5. Разделить сумму и определить коэффициент корреляции.
На следующем шаге мы будем использовать n для представления общего количества точек в этой паре данных. Разделите сумму из четвертого шага на n — 1. Получится коэффициент корреляции.
Пример коэффициента корреляции
Чтобы лучше понять коэффициент корреляции, рассмотрим следующий пример:
Допустим, у вас есть магазин одежды, и вы пытаетесь определить, будете ли вы продавать больше купальных костюмов летом. Хотя ваш магазин открыт круглый год, вы можете предположить, что в более жаркие дни купальных костюмов будет продано больше. С другой стороны, покупатели могут быть более склонны покупать купальные костюмы зимой, когда на них, скорее всего, будет скидка. Чтобы рассчитать коэффициент корреляции, вам нужно определить набор данных о среднем количестве продаж купальных костюмов и самых высоких температурах в течение лета. Тем не менее, продажи купальных костюмов и температура будут двумя переменными, которые вы будете использовать в своих расчетах.
Тем не менее, продажи купальных костюмов и температура будут двумя переменными, которые вы будете использовать в своих расчетах.
Теперь, когда мы знаем наши переменные, рассмотрим следующие данные:
Вы совершили 5 продаж купальных костюмов при температуре 70 градусов.
Вы совершили 10 продаж купальных костюмов, когда температура достигла 80 градусов.
Вы совершили 15 продаж купальных костюмов, когда температура достигла 90 градусов.
Вы продали 20 купальных костюмов, когда температура достигла 100 градусов.
Вы продали 15 купальных костюмов при температуре 110 градусов.
Вы можете назначить x для продаж купальных костюмов и y для температурных переменных. Среднее значение ваших значений x в этом примере равно 15, а среднее значение ваших значений y равно 90. После вычисления коэффициента корреляции вы обнаружите, что r равно 1. Это означает, что если вы должны были создать точечную диаграмму , точки будут постепенно подниматься вверх по склону. Это свидетельствует о сильной положительной и «идеальной» корреляции.
Это свидетельствует о сильной положительной и «идеальной» корреляции.
Основываясь на этом расчете, вы можете определить, что по мере повышения температуры будет расти и количество продаж ваших купальных костюмов.
Коэффициент корреляции в Excel (и корреляционная матрица)
Друзья, приветствую вас на WiFiGid! Буквально на днях разрабатывал модель для одной рыночно-нейтральной торговой стратегии, где как раз и нужно было рассчитывать коэффициенты корреляции (на самом деле корреляционную матрицу). Лично я сделал это на «питоне» – все равно потом ее как-то же надо обрабатывать, ведь миллионы ячеек глазом не просмотришь. Но на этапе предварительного анализа кому-то может быть проще использовать именно Excel. Поэтому в этой статье я и покажу вам основные варианты расчета коэффициента корреляции в Excel.
А если вдруг останутся какие-то вопросы или дополнения – добро пожаловать в комментарии. По мере возможности буду отвечать.
И как дополнение, конечно, можно ввести стандартную формулу любой корреляции в Excel, и на ее основе рассчитать коэффициент.
Но в этой статье предлагаю все-таки остановиться на уже встроенных способах в Excel.
Содержание
- Коротко про коэффициент корреляции
- Способ расчета 1 – Формула
- Способ 2 (корреляционная матрица) – Пакет анализа
- Видео по теме
- Задать вопрос автору статьи
Коротко про коэффициент корреляции
Коэффициент корреляции отражает зависимость одного ряда от другого. Принимает значение от -1 до +1 (включая все промежуточные дробные значения):
- +1 – обе величины абсолютно зависимы, куда идет первая, туда идет и вторая. Например, на рынке криптовалюты все очень зависимо от биткоина. Куда он, туда и все. И коэффициент корреляции к «битку» для среднего альткоина обычно стремится к единице (но не так сильно).
- 0 – нет никакой зависимости. Каждый ходит, куда хочет.
- -1 – обратная зависимость. Т.е. если один вверх, то второй строго вниз.
Т. е. для двух рядов значений можно строго определять какое-то одно число – коэффициент корреляции. А если вдруг нам нужно проверить очень много рядов между собой, то удобнее построить таблицу, где на пересечении значений нужных строк и столбцов и будут находиться значения коэффициента корреляции для выбранной пары. Такую таблицу называют корреляционной матрицей.
е. для двух рядов значений можно строго определять какое-то одно число – коэффициент корреляции. А если вдруг нам нужно проверить очень много рядов между собой, то удобнее построить таблицу, где на пересечении значений нужных строк и столбцов и будут находиться значения коэффициента корреляции для выбранной пары. Такую таблицу называют корреляционной матрицей.
Напоследок, существует несколько математических способов расчета коэффициента корреляции. Самый популярный (и как раз он используется в Excel) – метод Пирсона. Кому нужны другие варианты (тот же Спирмен), как по мне, гораздо проще перейти на любой более-менее развитый язык программирования. Ну или уже вручную вбить формулу здесь.
Что-то я увлекся теорией, предлагаю уже переходить к практике.
Способ расчета 1 – Формула
Очень надеюсь, что вас не нужно учить писать формулы. Иначе просто закройте Excel
А теперь непосредственно попробуем посчитать коэффициент корреляции.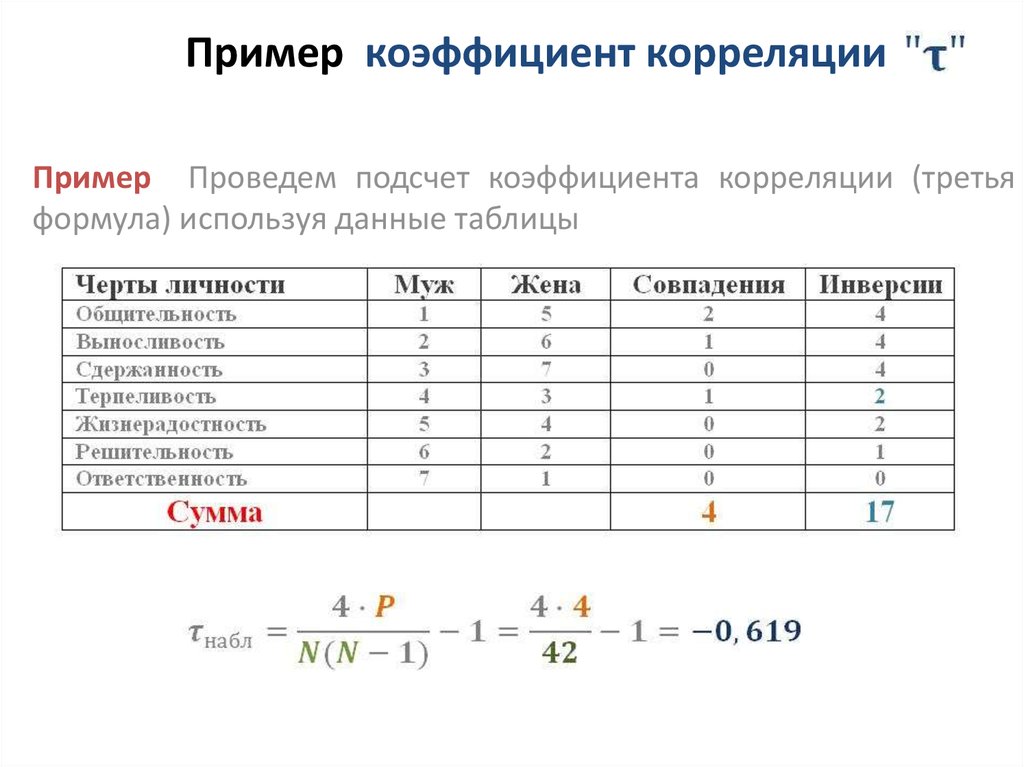 Если вы пришли сюда за формулой, то вот она (можно найти и через мастер функций, но руками быстрее):
Если вы пришли сюда за формулой, то вот она (можно найти и через мастер функций, но руками быстрее):
=КОРРЕЛ(массив1;массив2)
Под массивами подразумеваем ряды данных величин, между которыми и хотим найти корреляцию. Показываю на примере:
В данном примере у меня на очень малом промежутке времени получился коэффициент корреляции 0,29. Но главное, что способ работает. Так что если нужно получить быстро значение корреляции – круче формулы ничего и не придумаешь.
Способ 2 (корреляционная матрица) – Пакет анализа
В Excel есть еще глубоко запрятанный «Пакет анализа», который тоже содержит надстройку для расчета коэффициента корреляции. Но лично я им не пользуюсь – это очень долго. Поэтому этот раздел больше для интересующихся, чем для практикующих.
- Сначала нужно активировать этот пакет. Переходим в «Файл – Параметры – Надстройки».
- В списке находим «Пакет анализа» (обычно он в разделе неактивных надстроек), выделяем его, убеждаемся что внизу установлено «Надстройки Excel» и нажимаем по кнопке «Перейти».

- Ставим галочку напротив «Пакет анализа» и нажимаем кнопку «Ок». Это должно активировать пакет.
- Теперь переходим на вкладку «Данные». Именно тут справа должна добавить кнопка «Анализ данных». Щелкаем по ней.
- В списке выбираем «Корреляцию».
- Задаем настройки. Во входной интервал нужно передать сразу все столбцы, для которых будем рассчитывать корреляцию. Выходные данные можно переместить на новый лист или задать им место здесь же.
Если вы задали всего два столбца, то и получите то же самое число, что и через формулу. Но если передали сразу несколько столбцов, то и на выходе должна получиться целая корреляционная матрица:
Пользоваться можно, но лично мне не нравится здесь, что нельзя сразу передать названия столбцов и пустые ячейки в верхнем «треугольнике». Работать с этим можно только при небольшом количестве данных. Для остального нужно закрывать Excel.
Видео по теме
Прикладываю видео по теме, где кроме основ есть те же понятия корреляции Спирмена и поля корреляции.
11. Корреляция и регрессия
Слово корреляция используется в повседневной жизни для обозначения той или иной формы ассоциации. Можно сказать, что мы заметили корреляцию между туманными днями и приступами хрипов. Однако в статистических терминах мы используем корреляцию для обозначения связи между двумя количественными переменными. Мы также предполагаем, что связь является линейной, что одна переменная увеличивается или уменьшается на фиксированную величину при увеличении или уменьшении на единицу другой. Другой метод, который часто используется в этих обстоятельствах, — это регрессия, которая включает в себя оценку наилучшей прямой линии для обобщения ассоциации.
Коэффициент корреляции
Степень ассоциации измеряется коэффициентом корреляции, обозначаемым r. Его иногда называют коэффициентом корреляции Пирсона по имени его создателя, и он является мерой линейной связи. Если кривая линия необходима для выражения взаимосвязи, необходимо использовать другие, более сложные меры корреляции.
Коэффициент корреляции измеряется по шкале, которая варьируется от + 1 через 0 до – 1. Полная корреляция между двумя переменными выражается либо + 1, либо -1. Когда одна переменная увеличивается по мере увеличения другой, корреляция положительна; когда одно уменьшается по мере увеличения другого, оно отрицательно. Полное отсутствие корреляции представлено цифрой 0. На рис. 11.1 приведены некоторые графические представления корреляции.
Рисунок 11.1 Проиллюстрирована корреляция.
Просмотр данных: диаграммы рассеяния
Когда исследователь собрал две серии наблюдений и хочет увидеть, есть ли между ними взаимосвязь, он должен сначала построить диаграмму рассеяния. Вертикальная шкала представляет собой один набор измерений, а горизонтальная шкала — другой. Если один набор наблюдений состоит из экспериментальных результатов, а другой состоит из временной шкалы или какой-либо классификации наблюдений, обычно результаты экспериментов помещают на вертикальную ось. Они представляют собой так называемую «зависимую переменную». «Независимая переменная», такая как время, рост или какая-либо другая наблюдаемая классификация, измеряется вдоль горизонтальной оси или базовой линии.
Вертикальная шкала представляет собой один набор измерений, а горизонтальная шкала — другой. Если один набор наблюдений состоит из экспериментальных результатов, а другой состоит из временной шкалы или какой-либо классификации наблюдений, обычно результаты экспериментов помещают на вертикальную ось. Они представляют собой так называемую «зависимую переменную». «Независимая переменная», такая как время, рост или какая-либо другая наблюдаемая классификация, измеряется вдоль горизонтальной оси или базовой линии.
Слова «независимый» и «зависимый» могут озадачить новичка, потому что иногда непонятно, что от чего зависит. Эта путаница является триумфом здравого смысла над вводящей в заблуждение терминологией, потому что часто каждая переменная зависит от какой-то третьей переменной, которая может упоминаться или не упоминаться. Разумно, например, думать о росте детей как о зависимости от возраста, а не наоборот, но учитывать положительную корреляцию между средним выходом смолы и выходом никотина в некоторых марках сигарет». в смоле: оба изменяются параллельно с каким-то другим фактором или факторами в составе сигарет. Урожайность одного, по-видимому, не «зависит» от другого в том смысле, что в среднем рост ребенка зависит от его возраста. В таких случаях часто не имеет значения, какой масштаб на какой оси диаграммы рассеяния нанесен. Однако, если намерение состоит в том, чтобы сделать выводы об одной переменной из другой, наблюдения, из которых должны быть сделаны выводы, обычно помещаются в основу. В качестве еще одного примера, график ежемесячных смертей от болезней сердца и ежемесячных продаж мороженого будет показывать отрицательную связь. Однако вряд ли употребление мороженого защищает от сердечных заболеваний! Просто уровень смертности от сердечных заболеваний обратно пропорционален, а потребление мороженого положительно связано с третьим фактором, а именно с температурой окружающей среды.
в смоле: оба изменяются параллельно с каким-то другим фактором или факторами в составе сигарет. Урожайность одного, по-видимому, не «зависит» от другого в том смысле, что в среднем рост ребенка зависит от его возраста. В таких случаях часто не имеет значения, какой масштаб на какой оси диаграммы рассеяния нанесен. Однако, если намерение состоит в том, чтобы сделать выводы об одной переменной из другой, наблюдения, из которых должны быть сделаны выводы, обычно помещаются в основу. В качестве еще одного примера, график ежемесячных смертей от болезней сердца и ежемесячных продаж мороженого будет показывать отрицательную связь. Однако вряд ли употребление мороженого защищает от сердечных заболеваний! Просто уровень смертности от сердечных заболеваний обратно пропорционален, а потребление мороженого положительно связано с третьим фактором, а именно с температурой окружающей среды.
Расчет коэффициента корреляции
Детский регистратор измерил анатомическое мертвое пространство легких (в мл) и рост (в см) у 15 детей. Данные приведены в таблице 11.1, а диаграмма рассеяния показана на рисунке 11.2. Каждая точка представляет одного ребенка и находится в точке, соответствующей измерению высоты (горизонтальная ось) и мертвого пространства (вертикальная ось). Теперь регистратор проверяет шаблон, чтобы увидеть, кажется ли вероятным, что область, покрытая точками, сосредоточена на прямой линии или необходима изогнутая линия. В этом случае педиатр решает, что прямая линия может адекватно описать общий тренд точек. Поэтому его следующим шагом будет вычисление коэффициента корреляции.
Данные приведены в таблице 11.1, а диаграмма рассеяния показана на рисунке 11.2. Каждая точка представляет одного ребенка и находится в точке, соответствующей измерению высоты (горизонтальная ось) и мертвого пространства (вертикальная ось). Теперь регистратор проверяет шаблон, чтобы увидеть, кажется ли вероятным, что область, покрытая точками, сосредоточена на прямой линии или необходима изогнутая линия. В этом случае педиатр решает, что прямая линия может адекватно описать общий тренд точек. Поэтому его следующим шагом будет вычисление коэффициента корреляции.
При построении точечной диаграммы (рис. 11.2), чтобы показать высоту и анатомические мертвые зоны легких у 15 детей, педиатр разместил цифры, как в столбцах (1), (2) и (3) таблицы 11.1. Полезно располагать наблюдения в последовательном порядке независимой переменной, когда одна из двух переменных четко идентифицируется как независимая. Соответствующие цифры для зависимой переменной затем могут быть исследованы по отношению к возрастающему ряду для независимой переменной. Таким образом, мы получаем ту же картину, но в числовом виде, как показано на диаграмме рассеяния.
Таким образом, мы получаем ту же картину, но в числовом виде, как показано на диаграмме рассеяния.
Рис. 11.2. Диаграмма рассеивания соотношения роста и анатомического мертвого пространства легких у 15 детей.
Коэффициент корреляции рассчитывается следующим образом, где x представляет собой значение независимой переменной (в данном случае рост), а y представляет значение зависимой переменной (в данном случае анатомическое мертвое пространство). Используемая формула:
, которая может быть равна:
Процедура расчета
Найдите среднее значение и стандартное отклонение x, как описано в
Найдите среднее значение и стандартное отклонение y:
Вычтите 1 из n и умножьте на SD(x) и SD(y), (n – 1)SD(x)SD(y)
Это даст нам знаменатель формулы. (Не забудьте выйти из режима «Stat».)
Для числителя умножьте каждое значение x на соответствующее значение y, сложите эти значения вместе и сохраните их.
110 x 44 = Мин.
116 x 31 = M+
и т. д.
Сохраняет в памяти. Вычесть
MR – 15 x 144,6 x 66,93 (5426,6)
Наконец, разделите числитель на знаменатель.
г = 5426,6/6412,0609 = 0,846.
Коэффициент корреляции 0,846 указывает на сильную положительную корреляцию между размером легочного анатомического мертвого пространства и ростом ребенка. Но при интерпретации корреляции важно помнить, что корреляция не является причинно-следственной связью. Между двумя коррелирующими переменными может быть или не быть причинно-следственной связи. Более того, если и есть связь, то она может быть косвенной.
Часть вариации одной из переменных (измеряемая ее дисперсией) может рассматриваться как обусловленная ее взаимосвязью с другой переменной, а другая часть как вызванная неопределенными (часто «случайными») причинами. Часть, обусловленная зависимостью одной переменной от другой, измеряется Rho. Для этих данных Rho = 0,716, поэтому мы можем сказать, что 72% различий между детьми в размере анатомического мертвого пространства приходится на рост ребенка. Если мы хотим обозначить силу ассоциации, для абсолютных значений r, 0-0,19считается очень слабой, 0,2-0,39 — слабой, 0,40-0,59 — умеренной, 0,6-0,79 — сильной и 0,8-1 — очень сильной корреляцией, но это довольно условные пределы, и следует учитывать контекст результатов.
Для этих данных Rho = 0,716, поэтому мы можем сказать, что 72% различий между детьми в размере анатомического мертвого пространства приходится на рост ребенка. Если мы хотим обозначить силу ассоциации, для абсолютных значений r, 0-0,19считается очень слабой, 0,2-0,39 — слабой, 0,40-0,59 — умеренной, 0,6-0,79 — сильной и 0,8-1 — очень сильной корреляцией, но это довольно условные пределы, и следует учитывать контекст результатов.
Тест значимости
Чтобы проверить, является ли связь просто очевидной и могла ли она возникнуть случайно, используйте тест t в следующем расчете:
t Приложение Таблица B.pdf 2 степени свободы.
Например, коэффициент корреляции для этих данных составил 0,846.
Количество пар наблюдений было 15. Применяя уравнение 11.1, мы имеем:
Вводя таблицу B при 15 – 2 = 13 степенях свободы, мы находим, что при t = 5,72, P < 0,001, поэтому коэффициент корреляции можно считать как весьма значительное. Таким образом (как сразу видно из графика рассеяния) мы имеем очень сильную корреляцию между мертвым пространством и высотой, которая вряд ли возникла бы случайно.
Допущения, лежащие в основе этого теста:
- Обе переменные имеют правдоподобное нормальное распределение.
- Между ними существует линейная зависимость.
- Нулевая гипотеза состоит в том, что между ними нет связи.
Тест не следует использовать для сравнения двух методов измерения одного и того же количества, например, двух методов измерения пиковой скорости выдоха. Его использование таким образом, по-видимому, является распространенной ошибкой, когда важный результат интерпретируется как означающий, что один метод эквивалентен другому. Причины широко обсуждались(2), но стоит напомнить, что значимый результат мало что говорит нам о силе взаимосвязи. Из формулы должно быть понятно, что даже при очень слабой связи (скажем, r = 0,1) мы получили бы значимый результат при достаточно большой выборке (скажем, n более 1000).
Ранговая корреляция Спирмена
На графике данных могут быть обнаружены отдаленные точки от основной части данных, что может ненадлежащим образом повлиять на расчет коэффициента корреляции. В качестве альтернативы переменные могут быть количественными дискретными, такими как количество родинок, или упорядоченными категориальными, такими как оценка боли. Непараметрическая процедура, по Спирмену, заключается в замене наблюдений их рангами при вычислении коэффициента корреляции.
В качестве альтернативы переменные могут быть количественными дискретными, такими как количество родинок, или упорядоченными категориальными, такими как оценка боли. Непараметрическая процедура, по Спирмену, заключается в замене наблюдений их рангами при вычислении коэффициента корреляции.
Это приводит к простой формуле ранговой корреляции Спирмена, Rho.
где d — разница рангов двух переменных для данного индивидуума. Таким образом, мы можем вывести таблицу 11.2 из данных таблицы 11.1.
Отсюда получаем, что
В этом случае значение очень близко к значению коэффициента корреляции Пирсона. Для n> 10 коэффициент ранговой корреляции Спирмена может быть проверен на значимость с использованием приведенного ранее t-критерия.
Уравнение регрессии
Корреляция описывает силу связи между двумя переменными и является полностью симметричной, корреляция между A и B такая же, как корреляция между B и A. Однако, если две переменные связаны, это означает что когда одно изменяется на определенную величину, другое изменяется в среднем на определенную величину. Например, у описанных ранее детей больший рост в среднем связан с большим анатомическим мертвым пространством. Если y представляет зависимую переменную, а x независимую переменную, это отношение описывается как регрессия y на x.
Например, у описанных ранее детей больший рост в среднем связан с большим анатомическим мертвым пространством. Если y представляет зависимую переменную, а x независимую переменную, это отношение описывается как регрессия y на x.
Связь может быть представлена простым уравнением, называемым уравнением регрессии. В этом контексте «регрессия» (этот термин является исторической аномалией) просто означает, что среднее значение у является «функцией» от х, то есть изменяется вместе с х.
Уравнение регрессии, показывающее, насколько изменяется y при любом заданном изменении x, можно использовать для построения линии регрессии на диаграмме рассеяния, и в простейшем случае предполагается, что это прямая линия. Направление наклона линии зависит от того, является ли корреляция положительной или отрицательной. Когда два набора наблюдений увеличиваются или уменьшаются вместе (положительно), линия наклоняется вверх слева направо; когда один набор уменьшается, а другой увеличивается, линия наклоняется вниз слева направо. Поскольку линия должна быть прямой, она, вероятно, пройдет через несколько точек, если таковые имеются. Учитывая, что ассоциация хорошо описывается прямой линией, мы должны определить две характеристики линии, если мы хотим правильно разместить ее на диаграмме. Первый из них — это расстояние над базовой линией; второй — его наклон. Они выражаются в следующих уравнение регрессии :
Поскольку линия должна быть прямой, она, вероятно, пройдет через несколько точек, если таковые имеются. Учитывая, что ассоциация хорошо описывается прямой линией, мы должны определить две характеристики линии, если мы хотим правильно разместить ее на диаграмме. Первый из них — это расстояние над базовой линией; второй — его наклон. Они выражаются в следующих уравнение регрессии :
С помощью этого уравнения мы можем найти ряд значений переменной, которые соответствуют каждому из ряда значений x, независимой переменной. Параметры α и β должны быть оценены по данным. Параметр означает расстояние над базовой линией, на котором линия регрессии пересекает вертикальную ось (y); то есть, когда y = 0. Параметр β (коэффициент регрессии ) означает величину, на которую необходимо умножить изменение x, чтобы получить соответствующее среднее изменение y, или величину изменения y для единичного увеличения x. Таким образом, он представляет собой степень наклона линии вверх или вниз.
Уравнение регрессии часто бывает более полезным, чем коэффициент корреляции. Это позволяет нам предсказывать y по x и дает нам лучшее представление о взаимосвязи между двумя переменными. Если для конкретного значения x, x i уравнение регрессии предсказывает значение y fit , ошибка предсказания равна . Можно легко показать, что любая прямая линия, проходящая через средние значения x и y, даст общую ошибку предсказания, равную нулю, поскольку положительные и отрицательные члены точно сокращаются. Чтобы удалить отрицательные знаки, мы возводим в квадрат различия и уравнение регрессии, выбранное для минимизации суммы квадратов ошибок прогнозирования. Мы обозначаем выборочные оценки альфа и бета как a и b. Можно показать, что единственная прямая, минимизирующая оценку методом наименьших квадратов, задается как
и
можно показать, что
можно использовать, потому что мы рассчитали все компоненты уравнения (11.2) при расчете коэффициента корреляции.
Расчет коэффициента корреляции по данным таблицы 11.2 дал следующее:
Применяя эти цифры к формулам для коэффициентов регрессии, имеем:
Следовательно, в этом случае уравнение регрессии у на х становится
Это означает, что в среднем на каждое увеличение роста на 1 см увеличение анатомического мертвого пространства составляет 1,033 мл по диапазону измерений составило .
Линия, представляющая уравнение, показана наложенной на диаграмму рассеяния данных на рисунке 11.2. Чтобы нарисовать линию, нужно взять три значения x, одно в левой части диаграммы рассеяния, одно в середине и одно справа, и подставить их в уравнение следующим образом:
Если x = 110 , y = (1,033 x 110) – 82,4 = 31,2
Если x = 140, y = (1,033 x 140) – 82,4 = 62,2
Если x = 170, y = (1,033 x 170) – 82,4 = 93.2
Хотя для определения линии достаточно двух точек, для проверки лучше использовать три точки. Нанеся их на точечную диаграмму, мы просто проводим через них линию.
Рисунок 11.3 Линия регрессии, начерченная на диаграмме рассеяния относительно роста и легочного анатомического мертвого пространства у 15 детей Можно показать, что это алгебраически равно
Нам уже нужно передать все термины в этом выражении. Таким образом, квадратный корень из . Знаменатель (11.3) равен 72,4680. Таким образом, SE(b) = 13,08445/72,4680 = 0,18055.
Мы можем проверить, значительно ли наклон отличается от нуля, с помощью:
t = b/SE(b) = 1,033/0,18055 = 5,72.
Опять же, здесь n – 2 = 15 – 2 = 13 степеней свободы. Предположения, определяющие этот тест, следующие:
- Ошибки предсказания приблизительно распределены по нормальному закону. Обратите внимание, что это не означает, что переменные x или y должны иметь нормальное распределение.
- Что связь между двумя переменными является линейной.
- То, что разброс точек вокруг линии приблизительно постоянен – мы бы не хотели, чтобы изменчивость зависимой переменной росла по мере увеличения независимой переменной.
 Если это так, попробуйте логарифмировать обе переменные x и y.
Если это так, попробуйте логарифмировать обе переменные x и y.
Обратите внимание, что критерий значимости для наклона дает точно такое же значение P, что и критерий значимости для коэффициента корреляции. Хотя эти два теста выводятся по-разному, они алгебраически эквивалентны, что интуитивно понятно.
Мы можем получить 95% доверительный интервал для b из
, где tстатистика имеет 13 степеней свободы и равна 2,160.
Таким образом, 95% доверительный интервал составляет
1,033 – 2,160 х 0,18055 до 1,033 + 2,160 х 0,18055 = 0,643 до 1,422.
Линии регрессии дают нам полезную информацию о данных, из которых они получены. Они показывают, как одна переменная в среднем меняется с другой, и их можно использовать, чтобы выяснить, какой, вероятно, будет одна переменная, когда мы знаем другую — при условии, что мы задаем этот вопрос в рамках диаграммы рассеяния. Проецировать линию с любого конца — экстраполировать — всегда рискованно, потому что соотношение между x и y может измениться или может существовать какая-то точка отсечки. Например, можно провести линию регрессии, связывающую хронологический возраст некоторых детей с их костным возрастом, и это может быть прямая линия между, скажем, возрастом 5 и 10 лет, но спроецировать ее до возраста 30 лет. явно приведет к ошибке. Компьютерные пакеты часто выдают результат уравнения регрессии без предупреждения о том, что это может быть совершенно бессмысленно. Рассмотрим регресс артериального давления в зависимости от возраста у мужчин среднего возраста. Коэффициент регрессии часто бывает положительным, что указывает на повышение артериального давления с возрастом. Перехват часто близок к нулю, но было бы неправильно делать вывод, что это надежная оценка артериального давления у новорожденных младенцев мужского пола!
Например, можно провести линию регрессии, связывающую хронологический возраст некоторых детей с их костным возрастом, и это может быть прямая линия между, скажем, возрастом 5 и 10 лет, но спроецировать ее до возраста 30 лет. явно приведет к ошибке. Компьютерные пакеты часто выдают результат уравнения регрессии без предупреждения о том, что это может быть совершенно бессмысленно. Рассмотрим регресс артериального давления в зависимости от возраста у мужчин среднего возраста. Коэффициент регрессии часто бывает положительным, что указывает на повышение артериального давления с возрастом. Перехват часто близок к нулю, но было бы неправильно делать вывод, что это надежная оценка артериального давления у новорожденных младенцев мужского пола!
Более продвинутые методы
Возможно использование более одной независимой переменной – в таком случае метод известен как множественная регрессия. (3,4) Это наиболее универсальный из статистических методов, который можно использовать во многих ситуациях. Примеры включают в себя: разрешить использование более одного предиктора, возраста и роста в приведенном выше примере; чтобы учесть ковариаты — в клиническом исследовании зависимая переменная может быть исходом после лечения, первая независимая переменная может быть бинарной, 0 для плацебо и 1 для активного лечения, а вторая независимая переменная может быть исходной переменной, измеренной до лечения, но вероятно, повлияет на результат.
Примеры включают в себя: разрешить использование более одного предиктора, возраста и роста в приведенном выше примере; чтобы учесть ковариаты — в клиническом исследовании зависимая переменная может быть исходом после лечения, первая независимая переменная может быть бинарной, 0 для плацебо и 1 для активного лечения, а вторая независимая переменная может быть исходной переменной, измеренной до лечения, но вероятно, повлияет на результат.
Общие вопросы
Если две переменные коррелируют, связаны ли они причинно-следственной связью?
Путать корреляцию и причинно-следственную связь — распространенная ошибка. Все, что показывает корреляция, это то, что две переменные связаны. Может быть третья переменная, смешанная переменная, которая связана с ними обоими. Например, ежемесячная смертность от утопления и ежемесячная продажа мороженого имеют положительную корреляцию, но никто не скажет, что эта связь была причинно-следственной!
Как проверить предположения, лежащие в основе линейной регрессии?
Во-первых, всегда смотрите на точечную диаграмму и спрашивайте, является ли она линейной? Получив уравнение регрессии, вычислите остатки. Гистограмма покажет отклонения от нормальности, а график сравнения покажет, увеличиваются ли остатки в размере по мере увеличения.
Гистограмма покажет отклонения от нормальности, а график сравнения покажет, увеличиваются ли остатки в размере по мере увеличения.
Ссылки
- Russell MAH, Cole PY, Idle MS, Adams L. Содержание угарного газа в сигаретах и его связь с выходом никотина и типом фильтра. БМЖ 1975; 3:713.
- Бланд Дж. М., Альтман Д. Г. Статистические методы оценки соответствия между двумя методами клинических измерений. Ланцет 1986; я: 307-10.
- Браун Р.А., Суонсон-Бек Дж. Медицинская статистика на персональных компьютерах, 2-е изд. Лондон: BMJ Publishing Group, 1993.
- Армитаж П., Берри Г. В: Статистические методы в медицинских исследованиях, 3-е изд. Оксфорд: Научные публикации Блэквелла, 1994: 312–41.
Упражнения
11.1 Было проведено исследование посещаемости больниц людьми из 16 различных географических районов за фиксированный период времени. Расстояние центра от больницы каждого района измерялось в милях. Результаты были следующими:
(1) 21%, 6,8; (2) 12%, 10,3; (3) 30%, 1,7; (4) 8%, 14,2; (5) 10%, 8,8; (6) 26%, 5,8; (7) 42%, 2,1; (8) 31%, 3,3; (9) 21%, 4,3; (10) 15%, 9,0; (11) 19%, 3,2; (12) 6%, 12,7; (13) 18%, 8,2; (14) 12%, 7,0; (15) 23%, 5,1; (16) 34%, 4. 1.
1.
Каков коэффициент корреляции между уровнем посещаемости и средней удаленностью географического района?
11.2 Найдите ранговую корреляцию Спирмена для данных, приведенных в 11.1.
11.3 Если значения x из данных в 11.1 представляют собой среднее расстояние от района до больницы, а значения y представляют показатели посещаемости, то каким уравнением будет регрессия y на x? Что это значит?
11.4 Найдите стандартную ошибку и 95% доверительный интервал для наклона
Ответы на упражнения Ch 11.pdf
Как найти коэффициент корреляции в Excel
Карьера в области анализа данных, статистики или исследований требует овладения корреляцией формула коэффициента и расчеты. Если вы хотите попрактиковаться в своих статистических навыках и научиться использовать функции статистического расчета Excel, это руководство для вас, так как в нем объясняется, как найти коэффициент корреляции в Excel.
В этом руководстве представлены пошаговые инструкции, которые помогут вам найти сильную корреляцию и определить положительную или отрицательную связь между двумерными переменными данных. Продолжайте читать, чтобы найти коэффициент корреляции в Excel и формулу расчета его корреляции.
Продолжайте читать, чтобы найти коэффициент корреляции в Excel и формулу расчета его корреляции.
Найди свой учебный лагерь
- Career Karma подберет для тебя лучшие технологические учебные курсы
- Доступ к эксклюзивным стипендиям и подготовительным курсам
Выберите интересующий вас вопрос
Разработка программного обеспеченияДизайнОбработка и анализ данныхАналитика данныхUX-дизайнКибербезопасностьИмя
Фамилия
Электронная почта
Номер телефона
Продолжая, вы соглашаетесь с нашими Условиями обслуживания и Политикой конфиденциальности, а также соглашаетесь получать предложения и возможности от Career Karma by телефон, текстовое сообщение и электронная почта.
Что такое коэффициент корреляции в Excel?
Коэффициент корреляции в Excel — это математическая формула, используемая для измерения взаимосвязи между двумя переменными. Эта формула измеряет линейную зависимость между двумя переменными, чтобы определить отрицательную или положительную корреляцию. Положительная корреляция указывает на то, что если одна переменная повышается, другая переменная также повышается. Отрицательные корреляции, с другой стороны, указывают на то, что если одна переменная растет, переменная снижается.
Положительная корреляция указывает на то, что если одна переменная повышается, другая переменная также повышается. Отрицательные корреляции, с другой стороны, указывают на то, что если одна переменная растет, переменная снижается.
Наборы переменных, не демонстрирующие линейной корреляции, называются не имеющими корреляции. Коэффициент корреляции, равный единице, представляет собой полную положительную корреляцию. Точно так же идеальный отрицательный коэффициент корреляции представляет собой идеальный отрицательный коэффициент.
Если вы хотите стать статистиком или аналитиком данных, вам необходимо освоить коэффициент корреляции между зависимыми и независимыми переменными. Excel предлагает встроенную функцию для расчета коэффициентов корреляции двух или более случайных наборов переменных.
Почему полезно научиться находить коэффициент корреляции в Excel
- Простое прогнозирование данных. Нелинейный или линейный график коэффициента корреляции позволяет исследователям и статистикам легко находить корреляции случайных величин.
 Встроенное в Excel диалоговое окно корреляции упрощает этот процесс прогнозирования, выполняя быстрые вычисления для точечной диаграммы.
Встроенное в Excel диалоговое окно корреляции упрощает этот процесс прогнозирования, выполняя быстрые вычисления для точечной диаграммы. - Повышение производительности бизнеса. Научиться находить коэффициент корреляции в Excel полезно для повышения производительности вашего бизнеса. Есть несколько способов, которыми технологии помогают бизнес-профессионалам. Например, формула коэффициента корреляции Excel позволяет легко измерить корреляцию между производительностью труда и поведением для получения более высокой прибыли.
- Простое обновление для случайных величин. Надстройки Excel для функций коэффициента корреляции позволяют легко обновлять данные. Когда вы обновляете свои наборы данных, статистическая функция Excel автоматически изменяет расчеты коэффициента корреляции для этого диапазона значений ячеек, а также любые графики корреляции.
Как найти коэффициент корреляции в Excel: пошаговое руководство
Шаг 1.
 Введите переменные данные для таблицы корреляции
Введите переменные данные для таблицы корреляции Первым шагом к нахождению коэффициента корреляции в Excel является ввод данных в пустую ячейку. Вам нужно будет разделить наборы данных на два или более заголовков. Не забудьте добавить все соответствующие переменные, которые вы хотите учитывать при расчете коэффициента линейной корреляции. Также важно убедиться, что у вас есть правильные ссылки на ячейки.
Шаг 2. Найдите коэффициент корреляции с помощью инструмента корреляции
Следующим шагом будет использование формулы КОРРЕЛ для нахождения коэффициента корреляции. Это просто требует, чтобы вы написали формулу «=CORREL([Диапазон 1 первая ячейка], [Диапазон 1 последняя ячейка]: [Диапазон 2 первая ячейка], [Диапазон 2 последняя ячейка])». На этом шаге вам необходимо выбрать диапазон значений ячеек, для которых вы хотите получить значение корреляции.
Если обе переменные увеличиваются, у вас положительная связь, а если одна переменная увеличивается, а другая уменьшается, то у вас отрицательная связь.
Шаг 3. Использование надстройки корреляционного анализа Excel для определения коэффициента корреляции
Excel также предлагает диалоговое окно для расчета коэффициента корреляции анализа данных. Вам нужно будет получить надстройку Excel и включить пакет инструментов анализа. После того, как вы установили набор инструментов для анализа данных, следующим шагом будет переход на вкладку файла данных. Затем выберите вариант анализа данных.
Шаг 4. Выполните корреляционный анализ с помощью формулы корреляции Excel
На следующем шаге вам необходимо выбрать параметр корреляционного анализа Excel на вкладке анализа данных. Затем вы выберете таблицу коэффициентов корреляции, выбрав метки, которые вы создали, используя ваши переменные данных. Затем выберите диапазон входных ячеек и параметр вывода, выбирая метки вашего набора данных.
Шаг 5: Получите результаты для вашего коэффициента корреляции
После выбора меток ввода, вывода и данных рассчитайте коэффициент корреляции с помощью инструментария анализа данных Excel. Вам просто нужно нажать кнопку OK, чтобы создать график корреляции. В зависимости от значений вашей таблицы корреляции вы получите сильную или слабую корреляцию. Он будет подпадать под положительный, отрицательный или нулевой коэффициент корреляции.
Вам просто нужно нажать кнопку OK, чтобы создать график корреляции. В зависимости от значений вашей таблицы корреляции вы получите сильную или слабую корреляцию. Он будет подпадать под положительный, отрицательный или нулевой коэффициент корреляции.
Как сразу найти коэффициент корреляции в Excel
Excel также предлагает быстрый способ найти коэффициенты корреляции с помощью формулы КОРРЕЛ. Для этого вам просто нужно выбрать два или более набора данных и ввести формулу коэффициента корреляции. Формула имеет вид «=CORREL([Диапазон 1 первая ячейка], [Диапазон 1 последняя ячейка]: [Диапазон 2 первая ячейка], [Диапазон 2 последняя ячейка])». Вам нужно будет выбрать соответствующие ячейки, чтобы правильно рассчитать корреляцию между наборами.
Затем будет сразу рассчитан коэффициент корреляции и предложена положительная, отрицательная или диаграмма отсутствия корреляции для ваших переменных.
Преимущества поиска коэффициента корреляции в Excel
- Простые показатели для исследователей операций.
 По данным Бюро статистики труда, прогнозируется, что количество рабочих мест для аналитиков по исследованию операций вырастет на 25 процентов в период с 2020 по 2030 год. Статистический анализ и расчет коэффициента корреляции широко используются в этих профессиях. Excel предлагает простую разбивку метрик, которая предлагает логические значения для положительных, отрицательных значений и отсутствия корреляции.
По данным Бюро статистики труда, прогнозируется, что количество рабочих мест для аналитиков по исследованию операций вырастет на 25 процентов в период с 2020 по 2030 год. Статистический анализ и расчет коэффициента корреляции широко используются в этих профессиях. Excel предлагает простую разбивку метрик, которая предлагает логические значения для положительных, отрицательных значений и отсутствия корреляции. - Простой анализ данных для множества профессий. Для ответов на корреляцию, предлагаемых Excel, требуется ввести только формулу КОРРЕЛ. Вы также можете получить корреляционную матрицу через диалоговое окно надстроек анализа данных Excel. Эти быстрые расчеты позволяют специалистам в области бизнеса, маркетинга, здравоохранения и исследований выявлять основные закономерности в поведенческих и рыночных результатах.
- Отлично подходит для расчета показателей опроса. Встроенная в Excel формула корреляции обеспечивает оптимальный результат визуализации данных.
 Это позволяет исследователям получить правильную количественную шкалу метрик взаимосвязи между случайными комбинациями переменных.
Это позволяет исследователям получить правильную количественную шкалу метрик взаимосвязи между случайными комбинациями переменных.
Важность изучения того, как использовать листы Excel
Важность изучения того, как использовать листы Excel, полезно для широкого круга профессиональных профессий. Если вы хотите стать менеджером проекта, инженером-механиком или бизнес-аналитиком, работа с таблицами Excel является нормой. Таблицы Excel предлагают решения для простого анализа данных, корреляционных расчетов и сбора данных о сотрудниках. Если вы хотите изучить Excel, изучение терминологии Excel — отличное начало.
Освоение Excel также очень полезно для студентов, которым нужна эффективная рабочая тетрадь с большим объемом памяти. Согласно отчету Statista 2022, более миллиона компаний по всему миру используют Office 365. Научившись использовать листы Excel, вы удовлетворяете базовым требованиям к программному обеспечению множества компаний.
Как найти коэффициент корреляции в Excel Часто задаваемые вопросы
Что такое формула коэффициента корреляции в Excel?
Формула коэффициента корреляции в Excel: =CORREL([Диапазон 1 первая ячейка], [Диапазон 1 последняя ячейка]: [Диапазон 2 первая ячейка], [Диапазон 2 последняя ячейка]).

 Тем не менее, он не может определить разницу между независимыми и зависимыми переменными. Чем сильнее корреляция между этими двумя наборами данных, тем ближе она будет к +1 или -1. Это наиболее часто используемый тип коэффициента корреляции.
Тем не менее, он не может определить разницу между независимыми и зависимыми переменными. Чем сильнее корреляция между этими двумя наборами данных, тем ближе она будет к +1 или -1. Это наиболее часто используемый тип коэффициента корреляции.

 Но в этой статье предлагаю все-таки остановиться на уже встроенных способах в Excel.
Но в этой статье предлагаю все-таки остановиться на уже встроенных способах в Excel.
 Если это так, попробуйте логарифмировать обе переменные x и y.
Если это так, попробуйте логарифмировать обе переменные x и y. Встроенное в Excel диалоговое окно корреляции упрощает этот процесс прогнозирования, выполняя быстрые вычисления для точечной диаграммы.
Встроенное в Excel диалоговое окно корреляции упрощает этот процесс прогнозирования, выполняя быстрые вычисления для точечной диаграммы.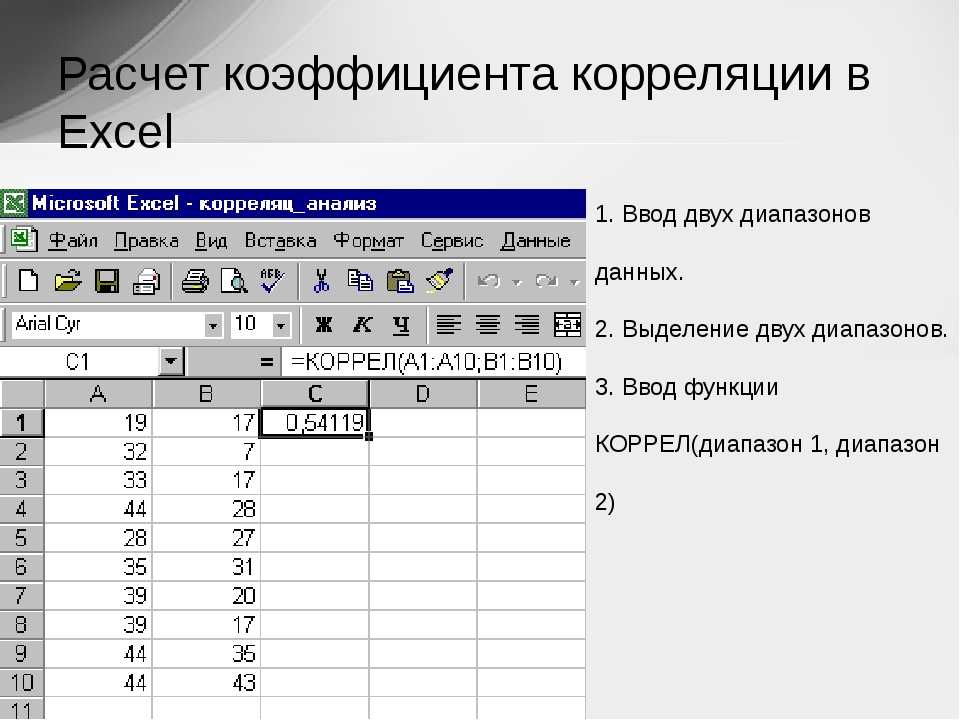 По данным Бюро статистики труда, прогнозируется, что количество рабочих мест для аналитиков по исследованию операций вырастет на 25 процентов в период с 2020 по 2030 год. Статистический анализ и расчет коэффициента корреляции широко используются в этих профессиях. Excel предлагает простую разбивку метрик, которая предлагает логические значения для положительных, отрицательных значений и отсутствия корреляции.
По данным Бюро статистики труда, прогнозируется, что количество рабочих мест для аналитиков по исследованию операций вырастет на 25 процентов в период с 2020 по 2030 год. Статистический анализ и расчет коэффициента корреляции широко используются в этих профессиях. Excel предлагает простую разбивку метрик, которая предлагает логические значения для положительных, отрицательных значений и отсутствия корреляции. Это позволяет исследователям получить правильную количественную шкалу метрик взаимосвязи между случайными комбинациями переменных.
Это позволяет исследователям получить правильную количественную шкалу метрик взаимосвязи между случайными комбинациями переменных.