Теорема о пересечении высот треугольника / Окружность / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Окружность
- Теорема о пересечении высот треугольника
Теорема
| Высоты треугольника (или их продолжения) пересекаются в одной точке. |
Доказательство
Дано: АВС, АА1, ВВ1 и СС1 — прямые, содержащие высоты треугольника.
Доказать: АА1, ВВ1 и СС1 пересекаются в одной точке.
Доказательство:
Проведём через каждую вершину АВС прямую, параллельную противоположной стороне.
Получим А2В2С2. Точки А, В и С являются серединами сторон этого треугольника. Действительно, АВ = А2С и АВ = СВ2 как противоположные стороны параллелограммов АВА2С и АВСВ2, поэтому А2С = СВ2. Аналогично С2А = АВ2 и С2В = ВА2. Кроме того, как следует из построения, СС1А2В2, АА1В2С2 и ВВ1А2С2. Таким образом, прямые АА1, ВВ1 и СС1 являются серединными перпендикулярами к сторонам треугольника А2В2С2. Следовательно, они пересекаются в одной точке. Теорема доказана.
Таким образом, прямые АА1, ВВ1 и СС1 являются серединными перпендикулярами к сторонам треугольника А2В2С2. Следовательно, они пересекаются в одной точке. Теорема доказана.
Замечательные точки треугольника: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот (или их продолжений).
Взаимное расположение прямой и окружности
Касательная к окружности
Градусная мера дуги окружности
Теорема о вписанном угле
Свойство биссектрисы угла
Свойства серединного перпендикуляра к отрезку
Вписанная окружность
Описанная окружность
Окружность
Теорема о пересечении высот треугольника
Урок 33. Геометрия 8 класс ФГОС
В этом уроке мы узнаем, что высоты треугольника (или их продолжения) пересекаются в одной точке. Эту точку называют ортоцентром и она является еще одной замечательной точкой треугольника.
Эту точку называют ортоцентром и она является еще одной замечательной точкой треугольника.
Конспект урока «Теорема о пересечении высот треугольника»
Сегодня на уроке мы продолжим изучение темы замечательные точки треугольника и познакомимся с теоремой о пересечении высот треугольника.
На прошлых уроках мы доказали, что биссектрисы треугольника пересекаются в одной точке и серединные перпендикуляры к сторонам треугольника также пересекаются в одной точке. До этого мы также доказали, что медианы треугольника пересекаются в одной точке. Оказывается, таким же свойством обладают и высоты треугольника.
Теорема. Высоты треугольника (или их продолжения) пересекаются в одной точке.
Доказательство.
Рассмотрим .
Значит, четырехугольник параллелограмм.
Значит, четырехугольник параллелограмм.
Точка является серединой отрезка серединный перпендикуляр .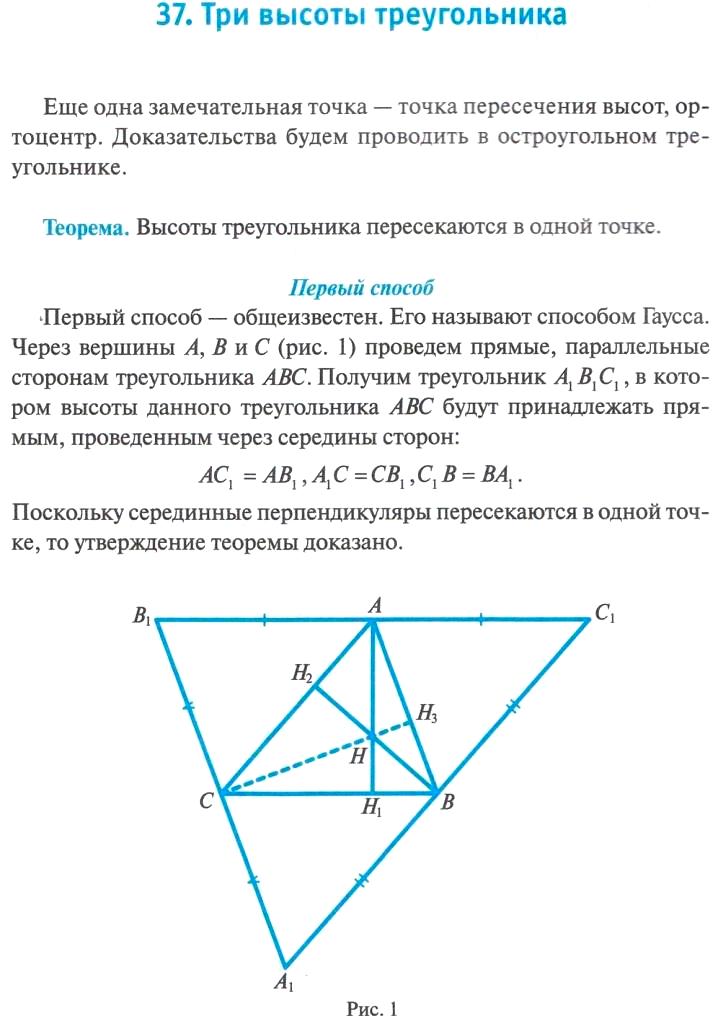
Точка является серединой отрезка серединный перпендикуляр .
Точка является серединой отрезка серединный перпендикуляр .
Значит, высоты пересекаются в одной точке, в точке .
Что и требовалось доказать.
В любом треугольнике медианы и биссектрисы принадлежат самому треугольнику. Чего нельзя сказать о высотах треугольника. Три высоты треугольника всегда пересекаются в одной точке. Точку их пересечения называют ортоцентром треугольника. В остроугольном и прямоугольном треугольниках высоты принадлежат треугольнику. Их точка пересечения – ортоцентр – в остроугольном треугольнике находится внутри треугольника, в прямоугольном треугольнике находится в прямом угле. А вот в тупоугольном треугольнике точка пересечения высот – ортоцентр – находится вне треугольника.
Рассмотрим тупоугольный .
У него –
тупой, –
высота. Докажем, что точка –
основание высоты –
не принадлежит отрезку .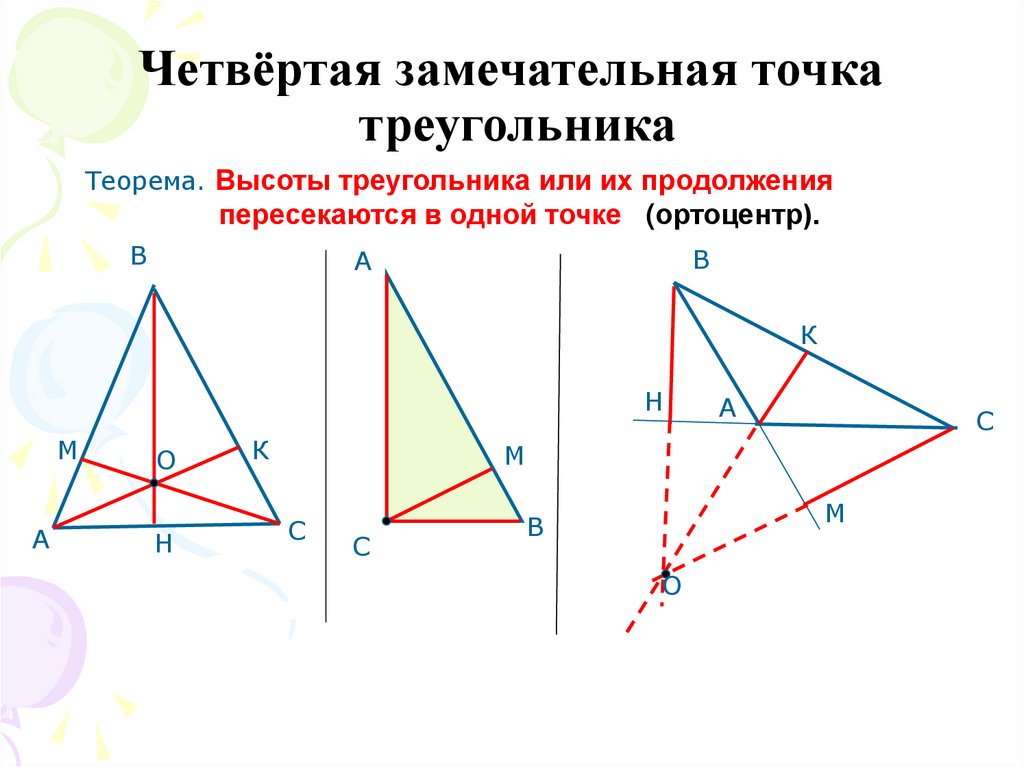
Доказательство.
Пусть точка .
.
Что не может быть.
Точка пересечения тупоугольного треугольника лежит вне треугольника.
Итак, с каждым треугольником связаны четыре точки: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам треугольника и точка пересечения высот (или их продолжений). Эти четыре точки называются замечательными точками треугольника.
Из истории замечательных точек треугольника. В четвертой книге «Начал» Евклид решает задачу: «Вписать круг в данный треугольник». Из решения вытекает, что три биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанного круга.
Из решения другой задачи
Евклида вытекает, что перпендикуляры, восстановленные к сторонам
треугольника в их серединах, тоже пересекаются в одной точке – центре
описанного круга.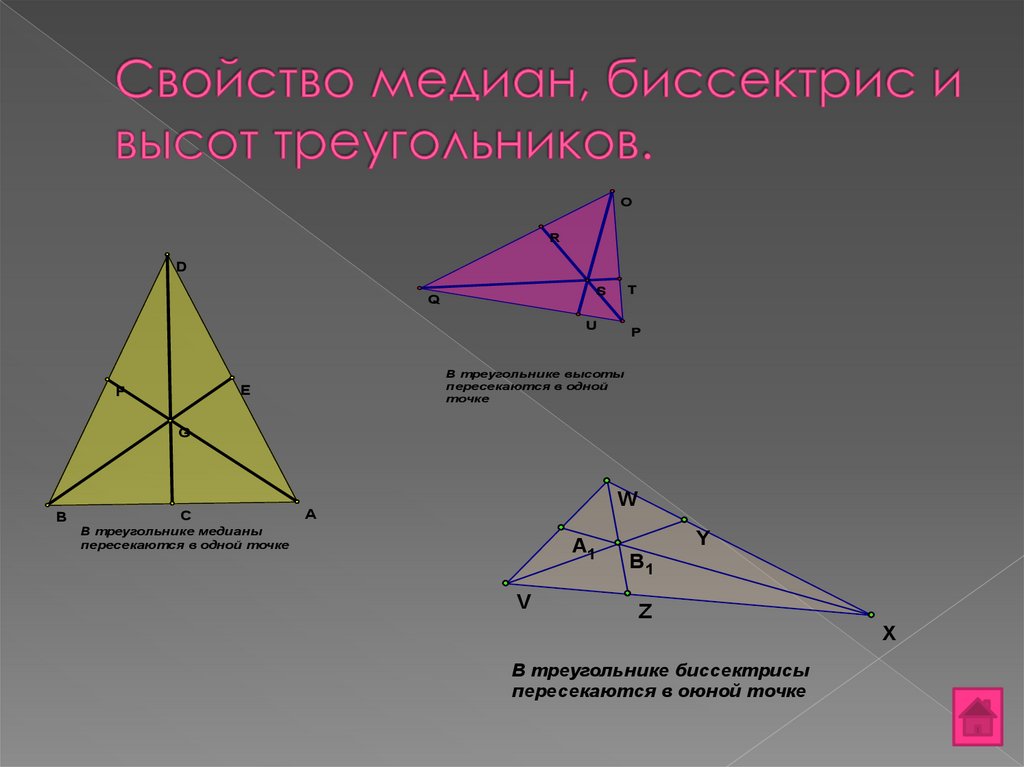
Четвертой особенной точкой треугольника является точка пересечения медиан. Архимед доказал, что она является центром тяжести (барицентром) треугольника. На вышеназванные четыре точки было обращено особое внимание, и начиная с XVIII века они были названы «замечательными» или «особенными» точками треугольника.
Исследование свойств треугольника, связанных с этими и другими точками, послужило началом для создания новой ветви элементарной математики – «геометрии треугольника» или «новой геометрии треугольника», одним из родоначальников которой стал Леонард Эйлер.
Повторим главное:
На этом уроке мы узнали, что высоты треугольника (или их продолжения) пересекаются в одной точке. Эту точку называют
Предыдущий урок 32 Свойство серединного перпендикуляра к отрезку
Следующий урок 34 Вписанная окружность
Получите полный комплект видеоуроков, тестов и презентаций Геометрия 8 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Как найти ортоцентр треугольника
Автор:
Малкольм МакКинзи
Чтобы найти наклон линии MR , вы подставляете координаты как изменение значений y по сравнению с изменением значений x :
7 MR 1 90 8 сторона нашего треугольника например:Вернитесь к уравнению и подставьте 3 вместо m :
У вас уже есть x и y значения, поэтому используйте любую заданную точку и подставьте ее числа. Используйте Point M , например:
Вы можете проверить это, используя Point R (это даст тот же ответ):
Таким образом, для отрезка линии MR уравнение линии y=3xy=3xy =3x
Повторите это для отрезка RE , и вы обнаружите, что вопрос стороны RE равен y=−1(x)+12y=-1(x)+12y=−1(x)+12 Это был всего лишь шаг один!
Второй шаг
Для второго шага найдите наклонов перпендикуляров к данным сторонам. Вам нужен наклон каждого отрезка:
Вам нужен наклон каждого отрезка:
Для стороны MR , m=3m=3m=3
Для стороны ME, m=−1m=-1m=−1
Найти наклон линии, перпендикулярной данной линии, вам нужна ее отрицательная обратная величина:
−1m\frac{-1}{m}m−1
Для бокового MR, −13\frac{- 1}{3}3−1
Для стороны RE −1−1=1\frac{-1}{-1}=1−1−1=1
Третий шаг
Для третьего шага используйте эти новые наклоны и координаты противоположных вершин, чтобы найти уравнений прямых , образующих две высоты:
Как найти ортоцентр треугольника шаг третий — добавление высотыE в (10, 2), и m=−13m=\frac{-1}{3}m=3−1:
Уравнение для высоты AE : y=−13x+163y=\frac{-1}{3}x+\frac{16}{3}y=3−1x+316.
Для стороны RE высота равна VM , с вершиной M на (1, 3) , а m=1m=1m=1:
y= 8VM высота х+2у=х+2у=х+2.
Шаг четвертый
Вы можете найти две перпендикулярные прямые, что означает, что их координаты x и y будут пересекаться:
Решить для каждой координаты; сначала для x:
Решите для y , используя любое уравнение и подставив найденное x :
уравнение: Ортоцентр треугольника находится в точке (2,5, 4,5) .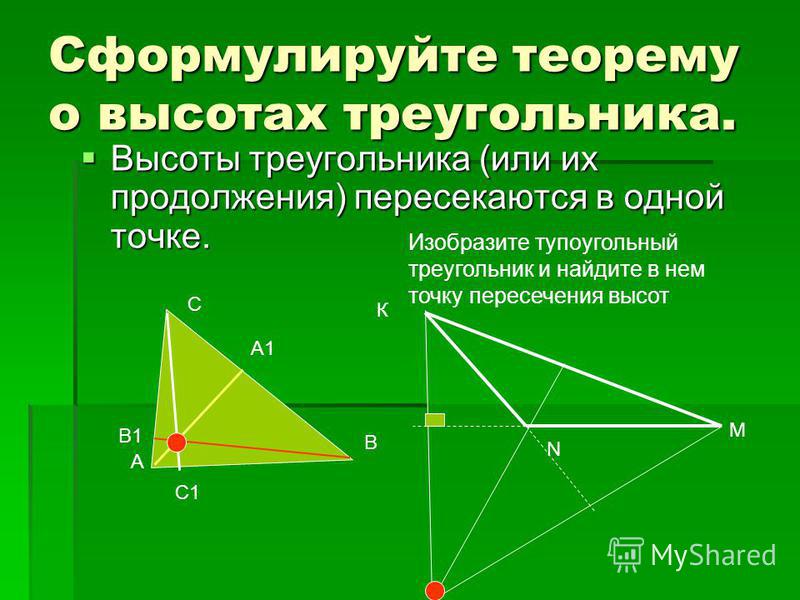 Вау! Четыре (длинных), но ценных шага.
Вау! Четыре (длинных), но ценных шага.
Орфический треугольник и описанная окружность
Работая с этими примерами, вы, возможно, заметили, что основания трех высот образуют меньший треугольник. Этот меньший треугольник называется ортотреугольником. Вы можете открыть для себя много интересных свойств ортотреугольника, например, описанную окружность ортотреугольника, также называемую девятиконечной окружностью треугольника.
геометрия — Докажите, что прямая, проходящая через пересечение прямой, проходящей через основания высот и противоположную прямую, и ортоцентр перпендикулярны медиане.
Изменено 9 лет, 11 месяцев назад
Просмотрено 2к раз
$\begingroup$
$BB’$ и $CC’$ — высоты данного $\треугольника ABC$ ($AB\ne AC$).
$M$ — середина $BC$, $H$ — ортоцентр $\треугольника ABC$, а $D$ — пересечение прямых $B’C’$ и $BC$. Докажите $DH \perp AM$.
Моя идея состоит в том, чтобы доказать, что $AC’EHB’$ (или $C’BME$, или $B’EMC$) является циклическим. Я пробовал много чего, но я думаю, что главное, чего мне не хватало во всех моих выводах, это использование $M$ в качестве средней точки.
Другая идея состоит в том, чтобы доказать, что $H$ является ортоцентром $\треугольника AMD$, так как у нас уже есть $AH\perp MD$, достаточно доказать $MH\perp AD$. Если $MH\cap AD=\{G\}$, то нужно доказать, что $G$ лежит на окружности вокруг $AC'(E)HB’$. Таким образом, другой идеей было бы доказать, что некоторые из треугольников, «составленных» из $A,C’,E,H,B’,G$, по крайней мере с одной вершиной, равной $E$ или $G$, имеют радиус описанной окружности $AH/2$. . Немного тригонометрии?
Другая идея состоит в том, чтобы пометить $E’$ как основание высоты от $D$ до $AM$, а затем с помощью теоремы Менелая доказать, что $A-H-E’$, то есть $E\equiv E’$.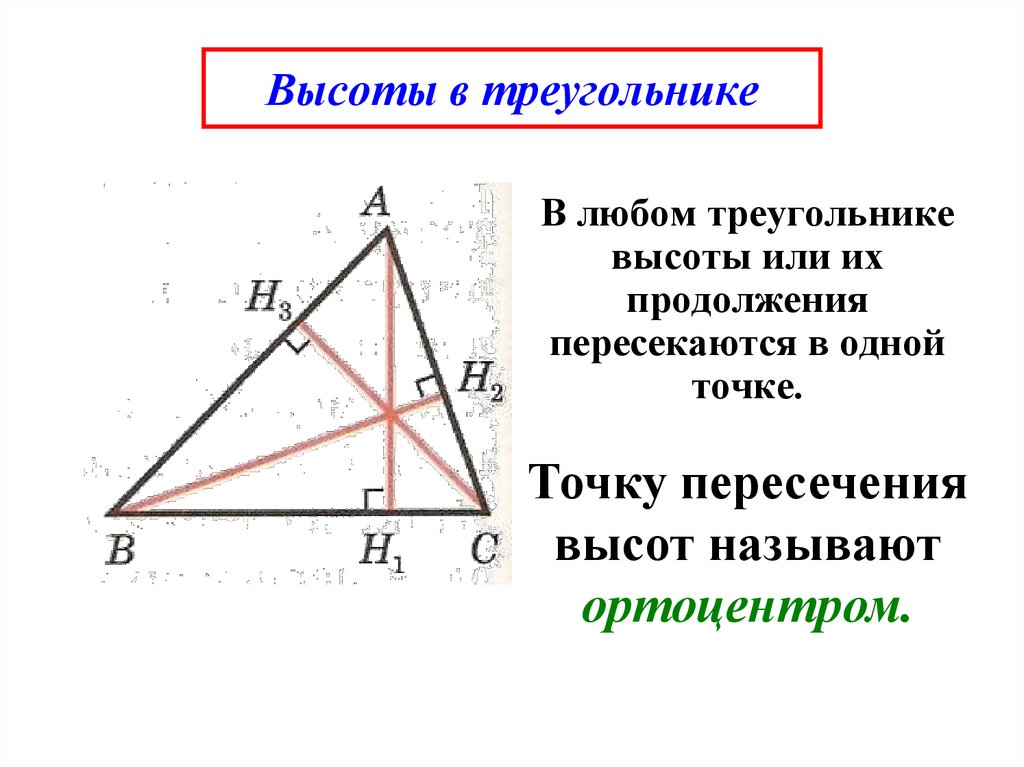
РЕД. Единственное место, где я думаю, что могу использовать тот факт, что $M$ является серединой $BC$, это то, что $BM=C’M=B’M=CM$, так что есть некоторые равные углы. Это
РЕДАКТИРОВАТЬ 2. Я также подумал об использовании того факта, что $\треугольник CMA$ и $\треугольник BMA$ имеют одинаковую площадь. Тогда у нас есть $AC\sin\alpha_1=BC\sin\alpha_2$, где $\alpha_1=\angle CAM=\angle CAE$ и $\alpha_2=\angle BAM=\angle BAE$, так что мы могли бы быть в состоянии использовать это как-то для идеи о том, что радиус описанной окружности равен $AH/2$, потому что мы можем использовать законы синусов для треугольников $\triangle AC’E$ и $AEB’$ (нам нужно доказать $\angle C’EA=\angle B=\beta$ и/или $\angle B’EA=\angle C=\gamma$), откуда мы может свести это к доказательству подобия некоторых треугольников. Кажется, хорошая идея, которая может сработать, но пока я не могу многого от нее добиться.
Кажется, хорошая идея, которая может сработать, но пока я не могу многого от нее добиться.
Еще по поводу идеи доказать, что $H$ является ортоцентром $\треугольника AMD$. Я не уверен, что лучше отметить $MH\cap AD=\{G\}$ и доказать $MH\perp AD$ или наоборот? Или, может быть, пометить пересечение $AD$ и описанной окружности $AC’HB’$ и $\треугольника ABC$ (может быть, это важно?) как $G$ и затем доказать $H\in GM$?
Просто добавляю идеи, так как мне кажется, что я ничего не могу сделать, как будто нам чего-то не хватает, и все идеи могут на самом деле работать очень похоже.
Кроме того, поскольку люди задавались вопросом, олимпиадная это задача или домашнее задание: она из сербского математического журнала для старшеклассников, она находится в разделе, где находятся одни из самых сложных задач. Но мне все равно сложнее, чем обычные из геометрии.
Пожалуйста, не используйте аналитическую геометрию или комплексные числа и старайтесь избегать векторов, если они не используются только для менее значимых лемм.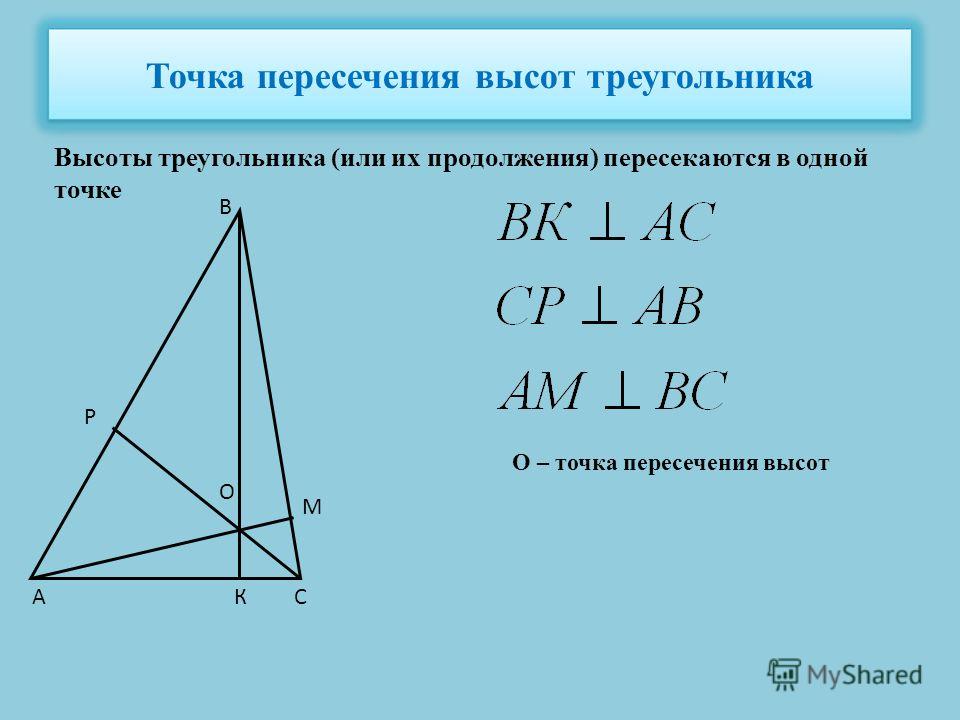
- геометрия
$\endgroup$
7
$\begingroup$
Предположим, что данный треугольник $ABC$ остроугольный. Проведите окружность с центром $M$ через $B$, $C$, $B’$, $C’$; затем проведите касательные от $A$ (лежащего снаружи) к окружности. Проведите красную линию $g$ через две точки касания; эта прямая пересекает прямую $B\vee C$ в точке $D$.
Нашу чертежную плоскость можно вложить в проективную плоскость $P$, добавив бесконечно удаленные элементы (они нам не понадобятся). Во всяком случае, существует перспективная инволюция $\iota:\P\to P$ с центром $A$, сохраняющая $g$ поточечно неподвижной и обладающая следующим дополнительным свойством: для любой прямой $\ell$, проходящей через $A$ который пересекает окружность, он меняет местами две точки пересечения. (Проективно эта $\iota$ сопряжена обычному отражению $\iota’$ на оси $x$ $g’$.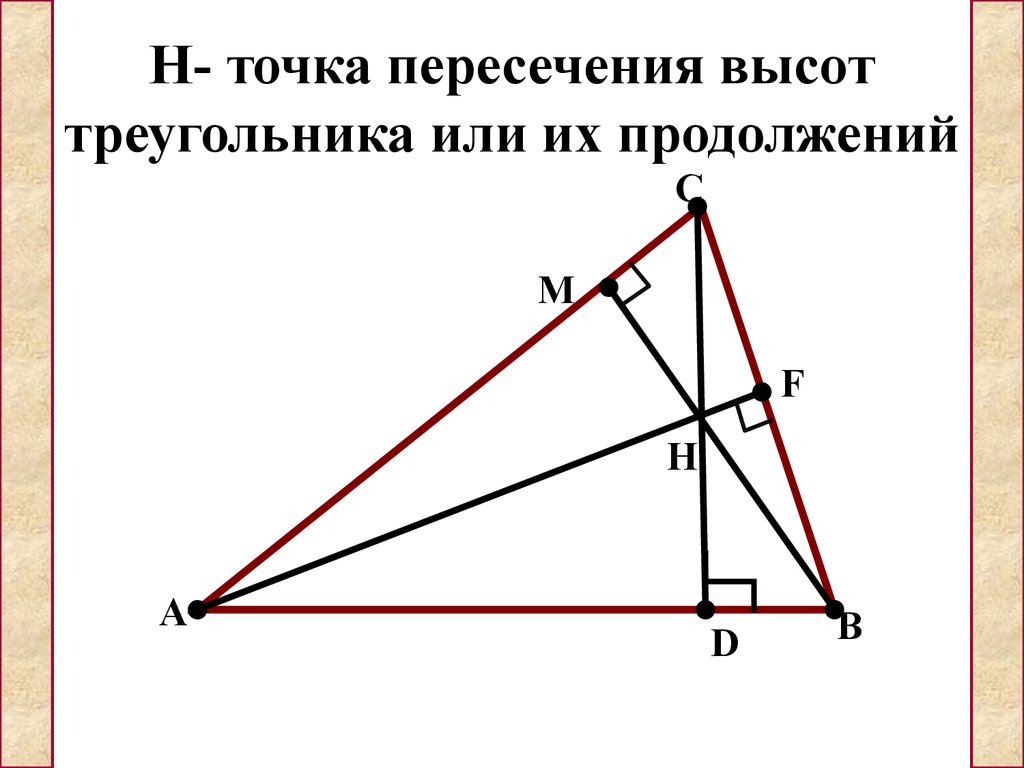 Отображение $\iota’$ имеет центр $A’$ в точке $y=\ pm\infty$, сохраняет $g’$ поточечно фиксированным и меняет местами точки на единичной окружности, лежащие на одной вертикали.)
Отображение $\iota’$ имеет центр $A’$ в точке $y=\ pm\infty$, сохраняет $g’$ поточечно фиксированным и меняет местами точки на единичной окружности, лежащие на одной вертикали.)
В частности, $\iota(B)=C’$, $\iota(C’)=B$, $\iota(C)=B’$, $\iota(B’)=C$. Следовательно, $\iota(C’\vee B’)=B\vee C$. Следовательно, $C’\vee B’$ и $B\vee C$ пересекаются на $g$, а это означает, что наша точка $D$ совпадает с точкой $D$ в вопросе. Таким же образом следует, что $B\vee B’$ и $C\vee C’$ пересекаются на $g$, откуда следует, что точка $H$ также лежит на $g$.
Поскольку прямая $A\vee M$ ортогональна $g$, она, как сказано, ортогональна $D\vee H$.
$\endgroup$ 9\prime|}$$
завершая доказательство.
$\endgroup$
3
$\begingroup$
Это частный случай следующего хорошо известного результата:
Пусть $ABCD$ — вписанный четырехугольник с центром описанной окружности $O$.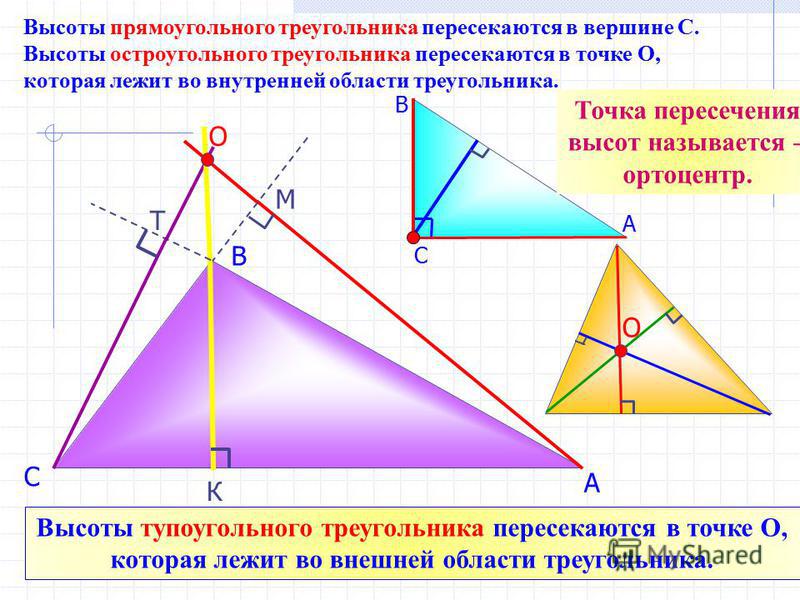 Пусть $BD$ пересекает $AC$ в точке $H$, $AB$ пересекает $CD$ в точке $E$, $BC$ пересекает $AD$ в точке $F$. Тогда $H$ является ортоцентром треугольника $EOF$.
Пусть $BD$ пересекает $AC$ в точке $H$, $AB$ пересекает $CD$ в точке $E$, $BC$ пересекает $AD$ в точке $F$. Тогда $H$ является ортоцентром треугольника $EOF$.
Доказательство: (Гармонические сопряжения и полюса и поляры): Достаточно доказать, что $OE \perp HF$, так как по симметрии мы будем иметь и $OF \perp HE$, так что $H$ действительно является ортоцентром $EOF$. Пусть $FH$ пересекает $CD$ в точке $X$, $AB$ в точке $Y$. Тогда $D, X, C, E$ гармоничны, как и $A, Y, B, E$. Отсюда следует, что $XY$ является полярой $E$ относительно описанной окружности, так что у нас действительно есть $OE \perp HF$, и мы закончили.
Редактировать: Чтобы увидеть, как это решает вашу задачу, примените его к вписанному четырехугольнику $BCB’C’$ с центром описанной окружности $M$.
В приведенном выше доказательстве я неявно использовал следующие свойства гармонических сопряжений, полюсов и поляр. Если вы не знакомы с этой темой, я также предоставил доказательства для них. Помимо приведенных выше ссылок, вы можете попробовать поискать в Google «Гармонические сопряжения» и «Полюсы и поляры», чтобы найти дополнительную информацию.
Помимо приведенных выше ссылок, вы можете попробовать поискать в Google «Гармонические сопряжения» и «Полюсы и поляры», чтобы найти дополнительную информацию.
Свойство 1: На приведенной ниже диаграмме $A, B$ и $C, D$ являются гармонически сопряженными.
Доказательство. По теореме Чевы о треугольнике $LAB$ имеем $\frac{AD}{DB}=\frac{NL}{BN}\frac{MA}{LM}$. По теореме Менелая о треугольнике $LAB$ и прямой $MNC$ имеем $\frac{AC}{CB}=\frac{NL}{BN}\frac{MA}{LM}$. Таким образом, $\frac{AD}{DB}=\frac{AC}{CB}$, поэтому $A, B$ и $C, D$ являются гармонически сопряженными. Можно также сказать, что $A, D, B, C$ образуют гармонический диапазон.
Свойство 2: Если прямая $l$ является полярой точки $P$ относительно базовой окружности с центром $O$, то $OP \perp l$.
Доказательство: Очевидно по определению полюсов и полярных.
Свойство 3: Рассмотрим точку $P$ вне базовой окружности с центром $O$, и пусть $PA, PB$ касаются этой окружности. 2$, поэтому $C$ — образ $P$ при инверсии относительно опорной окружности, поэтому $AB$ — поляра $P$ относительно опорной окружности. 92$, поэтому треугольник $XOP$ подобен треугольнику $COX$. Теперь $\frac{XP}{OX}=\frac{CX}{OC}$. Точно так же $\frac{YP}{OY}=\frac{CY}{OC}$. Деление дает $\frac{XP}{YP}=\frac{CX}{CY}$. Аналогичным образом мы можем показать, что $\frac{XZ}{YZ}=\frac{CX}{CY}$, так что действительно $P, Z$ и $X, Y$ являются гармонически сопряженными.
2$, поэтому $C$ — образ $P$ при инверсии относительно опорной окружности, поэтому $AB$ — поляра $P$ относительно опорной окружности. 92$, поэтому треугольник $XOP$ подобен треугольнику $COX$. Теперь $\frac{XP}{OX}=\frac{CX}{OC}$. Точно так же $\frac{YP}{OY}=\frac{CY}{OC}$. Деление дает $\frac{XP}{YP}=\frac{CX}{CY}$. Аналогичным образом мы можем показать, что $\frac{XZ}{YZ}=\frac{CX}{CY}$, так что действительно $P, Z$ и $X, Y$ являются гармонически сопряженными.
$\endgroup$
$\begingroup$
эта проблема действительно ортогональные круги, давайте с точки зрения чистой геометрии, чтобы решить ее.
первым нашел две ортогональные окружности треугольника ABC. см. рисунок ниже:
смотри BC’B’C: $ {CC’} \perp {AB} $,$BB’ \perp AC$, значит, BC’B’C является циклическим, а M является центром.
посмотрите на AC’HB’, они тоже циклические. центр — это N середины AH.
BTW, A’C’NBM является циклическим, который представляет собой окружность с 9 точкамиhttp://en.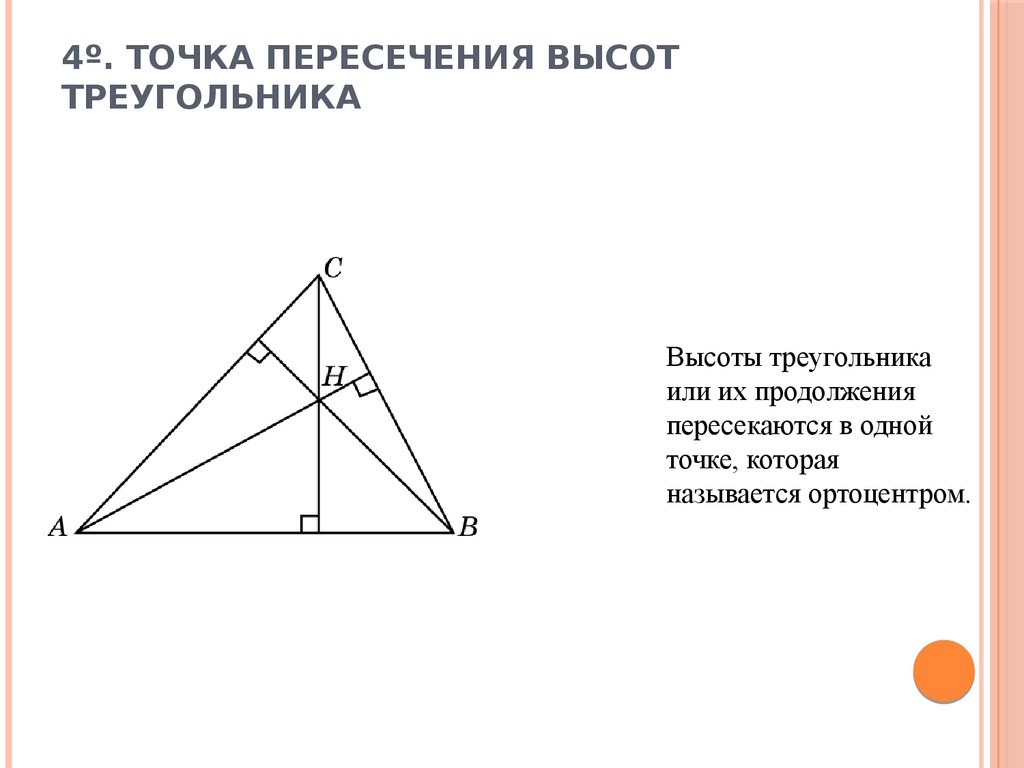 wikipedia.org/wiki/Nine_points_circle и $C’N \perp C’M $, поскольку NM — это диаметр.
wikipedia.org/wiki/Nine_points_circle и $C’N \perp C’M $, поскольку NM — это диаметр.
, поэтому окружность NA и окружность MC являются ортогональными окружностями.
2-й: мы докажем, что если DM — это диаметр окружности, то эта окружность и окружность NA также являются ортогональными окружностями. Я использую другую картинку, чтобы доказать это. 92$.
, поэтому окружность GF и окружность B являются ортогональными окружностями. посмотрите на диаметр JK круга A, обратите внимание, что A является серединой JK. Кстати, круг G (красный) должен проходить через E.
3-й: ортогональные круги имеют интересный факт, который уже доказан, см. другую картинку:
окружности P и Q ортогональны, затем возьмите A в окружности P, сделайте AB диаметром, E и F — точками пересечения окружностей P и Q, AE пересекает окружность Q в точке C, затем $ CQ \perp AB$ и CQ пересечь окружность Q в D, BC должна проходить через E, D должна быть ортоцентром ABC.
Я оставил подробное доказательство в качестве упражнения, вы можете найти подробности в статье «Заметки об ортоцентрическом тетраэдре» в Интернете, которая рекомендуется в SE.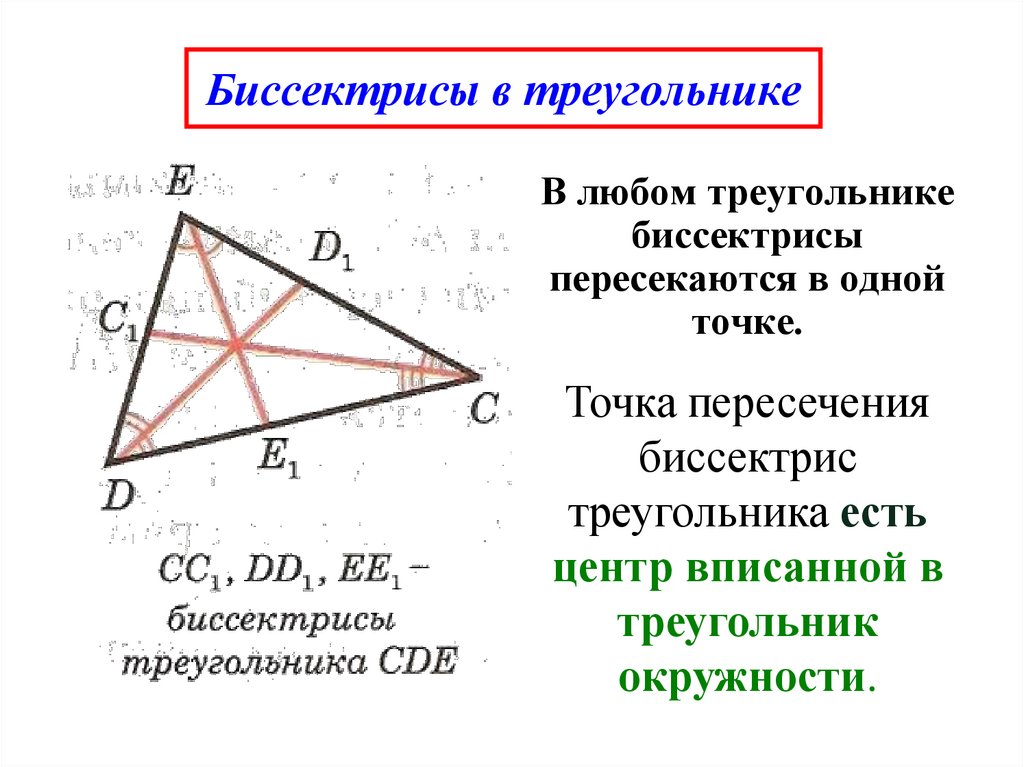
последний шаг: см. финальное изображение:
K — середина DM, сделайте круг KM, затем круг KM и круг NA — ортогональные круги. посмотрите на треугольник ADM (вам может понадобиться доказать, что A должна быть точкой, равной точке 3-го шага C, это не сложно, когда вы закончите 3-й шаг). должен быть ортоцентром АДМ. это сделано.
Я добавляю подробное доказательство для последнего шага:
окружность KD имеет общие точки E и F. прямая KE,NE, так как две окружности являются ортогональными окружностями, что ii доказывается на шаге 2, поэтому $KE \perp NE$,прямая ME , предположим, пересечение на окружности NA в A2, линия A2N, $\угол NA2E=\угол NEA2,\угол KEM=\угол KME, \угол KEM+\угол NEA2=\dfrac{\pi}{2},$ так $\угол KME+\angle NE2A=\dfrac{\pi}{2} $, то есть $A2N \perp DM$, так как AN и A2N имеют общую точку N, A2 должен быть A. По той же причине, DF расширяет окружность NA, это должны пересекаться в точке A. если мы соединяем DE,HE, так как DM диаметр, то $ DE\perp AM$, так как AH диаметр, то $HE \perp AM$, оба имеют общую точку E, значит, H должен находиться на DE . и H должен находиться в центре треугольника ADM. что закончено.
и H должен находиться в центре треугольника ADM. что закончено.
$\endgroup$
3
$\begingroup$
Обратите внимание, что приведенное здесь частичное решение на самом деле не является ответом (потому что я не дошел до него) — я оставил его здесь для пользы людей, которые хотели бы увидеть мыслительный процесс в проблеме.
Обратите внимание, что треугольник $BC’B’C$ на самом деле циклический, поскольку треугольники $BC’C$ и $BB’C$ прямоугольные. Тогда $M$ является центром окружности, описанной вокруг $BC’B’C$, поскольку она является серединой диаметра $BC$.
Игра с GeoGebra показала мне, что точки касания от $A$ к описанной окружности $BCB’C’$ (точки касания двух прямых от $A$ к окружности) лежат на $DH$. Пусть эти две точки будут $T_1$ и $T_2$. Если мы воспользуемся этим фактом, то увидим, что $AT_1 = AT_2$ и $MT_1 = MT_2$, поэтому $AT_1MT_2$ — воздушный змей, а значит, $AM$ и $T_1T_2$ перпендикулярны; поэтому $AM$ и $DH$ также перпендикулярны (потому что $DH$ и $T_1T_2$ — одна и та же прямая).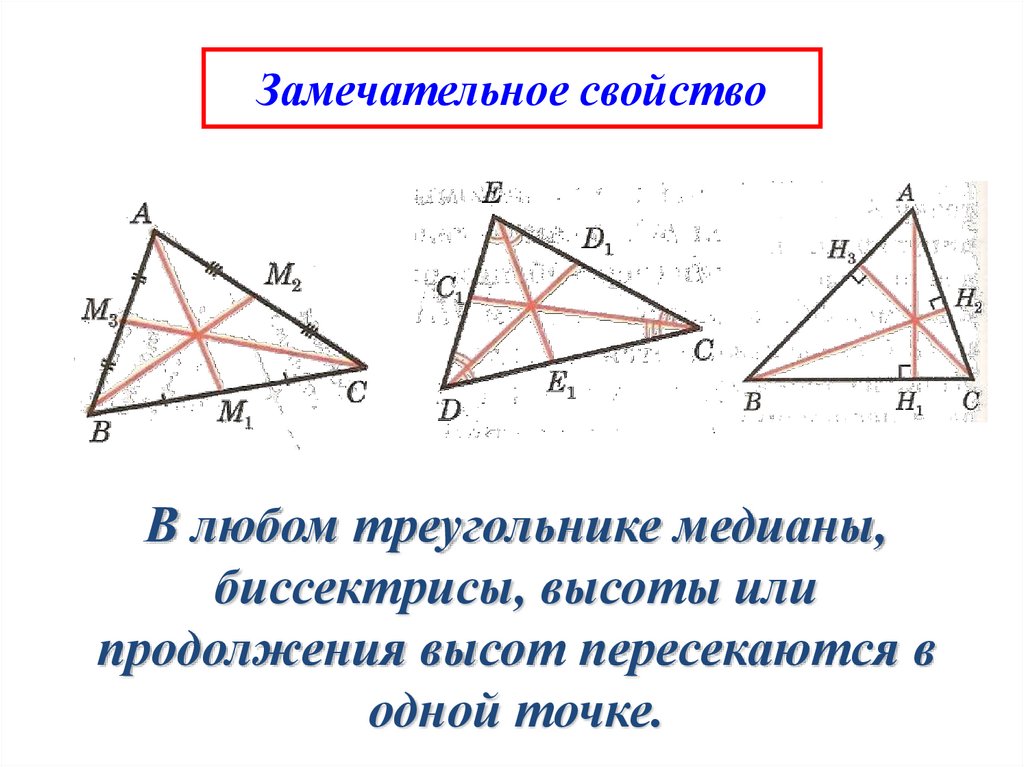

 $M$ — середина $BC$, $H$ — ортоцентр $\треугольника ABC$, а $D$ — пересечение прямых $B’C’$ и $BC$. Докажите $DH \perp AM$.
$M$ — середина $BC$, $H$ — ортоцентр $\треугольника ABC$, а $D$ — пересечение прямых $B’C’$ и $BC$. Докажите $DH \perp AM$.