заказ решений на аукционе за минимальную цену с максимальным качеством
Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:
- решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
- написание лабораторных, рефератов и курсовых
- выполнение заданий по литературе, русскому или иностранному языку.
Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Объединение сервисов в одну систему
Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:
- Форум, где посетители обмениваются идеями и помогают друг другу
- Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
- Аукцион, где цена за товар или услугу определяется в результате торгов
- Система рейтингов, где участники могут оценивать ответы друг друга.
Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Причем, чем больше рейтинг пользователя, тем более значимым становится его голосПринцип работы
Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.
Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.
Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте).
Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
За счет чего будет развиваться сервис
Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.
Второе – удобный сервис для заказчиков и для желающих заработать на решениях.
Преимущества для заказчиков
Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Преимущества для решающих задания
Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.
Преимущества для владельца сервиса
Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике.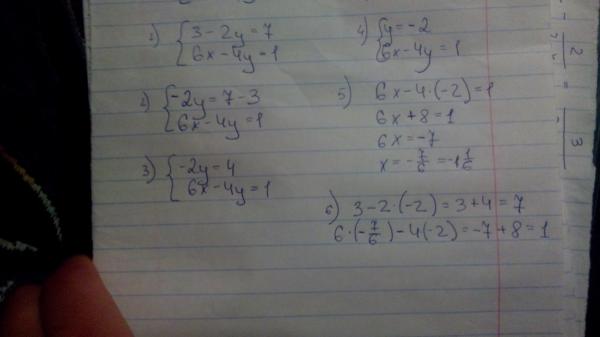
И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Что необходимо для создания сервиса
- Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.
- Выбрать платежную систему.
- Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
- Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
заказ решений на аукционе за минимальную цену с максимальным качеством
Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:
- решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
- написание лабораторных, рефератов и курсовых
- выполнение заданий по литературе, русскому или иностранному языку.
Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Объединение сервисов в одну систему
Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:
- Форум, где посетители обмениваются идеями и помогают друг другу
- Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
- Аукцион, где цена за товар или услугу определяется в результате торгов
- Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Принцип работы
Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.
Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом).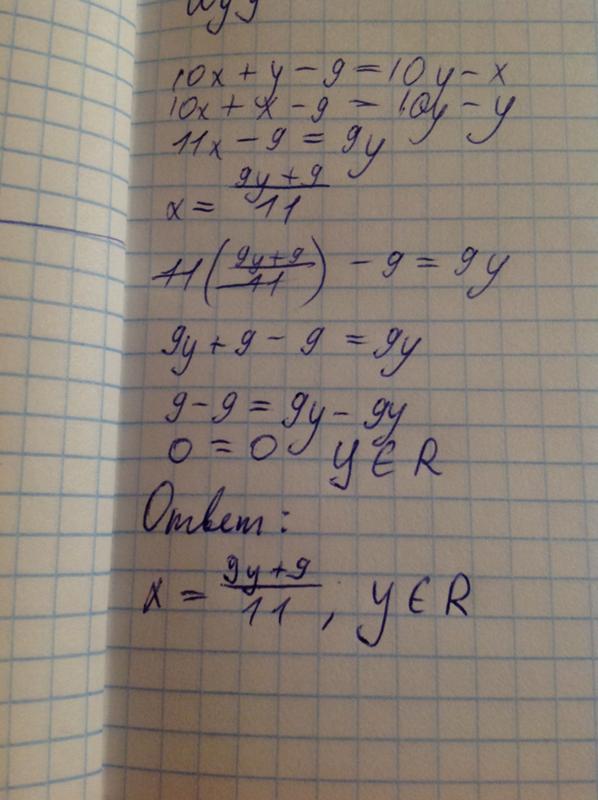
Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.
Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально.
Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
За счет чего будет развиваться сервис
Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.
Второе – удобный сервис для заказчиков и для желающих заработать на решениях.
Преимущества для заказчиков
Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег).
Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Преимущества для решающих задания
Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.
Преимущества для владельца сервиса
Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа.
Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Что необходимо для создания сервиса
- Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.
- Выбрать платежную систему.
- Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
- Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
Решение линейных уравнений с одним неизвестным 5y=4y-5.2 Решатель алгебры тигра
Переформатирование ввода:
Изменения, внесенные во ввод, не должны влиять на решение:
(1): «5.2» заменено на «(52/ 10)».
Переставить:
Переставить уравнение, вычитая то, что находится справа от знака равенства из обеих частей уравнения:
5*y-(4*y-(52/10))=0
Шаг за шагом Шаг решения:
Шаг 1 :
26
Упростить ——
5
Уравнение в конце шага 1 :
26
5у - (4у - ——) = 0
5
Шаг 2 :
Преобразование целого в виде эквивалентной дроби:
2.1 Вычитание дроби из целого
Преобразование целого в виде дроби с использованием 5 в качестве знаменателя:
4y 4y • 5
4у = —— = ——————
1 5
Эквивалентная дробь: Полученная таким образом дробь выглядит иначе, но имеет то же значение, что и целое число
Общий знаменатель: Эквивалентная дробь и другая дробь, участвующая в вычислении, имеют один и тот же знаменатель знаменатель
Соедините числители, подставьте сумму или разность к общему знаменателю, затем приведите к наименьшему числу, если возможно:
4y • 5 - (26) 20y - 26
знак равно
5 5
Уравнение в конце шага 2 :
(20 - 26)
5г - —————————— = 0
5
Шаг 3 :
Преобразование целого в виде эквивалентной дроби:
3.
1 Вычитание дроби из целого
Преобразование целого в виде дроби с использованием 5 в качестве знаменателя:
5y 5y • 5
5y = —— = ——————
1 5
Шаг 4 :
Вытягивание одинаковых членов:
4.1 Вытягивание одинаковых факторов :
20г — 26 = 2 • (10г — 13)
Сложение дробей, имеющих общий знаменатель:
4.2 Сложение двух эквивалентных дробей
(18 - 5г)) + 26
знак равно
5 5
Уравнение в конце шага 4 :
5y + 26
——————— = 0
5
Шаг 5 :
Когда дробь равна нулю:
5.1 Когда дробь равна нулю...
Если дробь равна нулю, ее числитель, часть над чертой дроби, должен быть равен нулю.
Теперь, чтобы избавиться от знаменателя, Тайгер умножает обе части уравнения на знаменатель.
Вот как:
5 лет+26
————— • 5 = 0 • 5
5
Теперь в левой части 5 уравновешивает знаменатель, а в правой части ноль, умноженный на что-либо, по-прежнему равен нулю.
Теперь уравнение принимает форму :
5y+26 = 0
Решение единого переменного уравнения:
5.2 Решение: 5y+26 = 0
Вычитание 26 с обеих сторон уравнения:
5y = -26
Разделите обе стороны уравнения на 5:
y = -26/ 5 = -5,200
Найдено одно решение:
y = -26/5 = -5,200
Дифференциальные уравнения — Решение IVP с помощью преобразований Лапласа
Онлайн-заметки Пола
Главная
/
Дифференциальные уравнения
/
Преобразования Лапласа
/ Решение IVP с помощью преобразований Лапласа
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 4.5. Решение IVP с помощью преобразований Лапласа 92}Y\left( s \right) — sy\left( 0 \right) — y’\left( 0 \right)\end{align*}\]
Обратите внимание, что две оценки функций, которые появляются в этих формулах, \(y\left( 0 \right)\) и \(y’\left( 0 \right)\), часто используются для начальное условие в наших IVP. Итак, это означает, что если мы собираемся использовать эти формулы для решения IVP, нам понадобятся начальные условия в точке \(t = 0\).
В то время как преобразования Лапласа особенно полезны для неоднородных дифференциальных уравнений, которые имеют функции Хевисайда в вынуждающей функции, мы начнем с пары довольно простых задач, чтобы проиллюстрировать, как работает этот процесс.
Пример 1. Решите следующую IVP. \[y» — 10y’ + 9y = 5t,\hspace{0.25in}y\left( 0 \right) = — 1\,\,\,\,\,\,\,y’\left( 0 \справа) = 2\]
Показать решение
Первый шаг в использовании Лапласа Преобразования для решения IVP — это преобразование каждого члена в дифференциальном уравнении.
\[\mathcal{L}\left\{ {y»} \right\} — 10\mathcal{L}\left\{ {y’} \right\} + 92}\left( {s — 9} \right)\left( {s — 1} \right)}} + \frac {{12 — s}}{{\left( {s — 9} \right)\ влево( {s — 1} \вправо)}}\]
Здесь удобно вспомнить, что мы пытаемся сделать. Мы пытаемся найти решение \(y(t)\) для IVP. То, что нам удалось найти на данный момент, — это не решение, а его Лапласовское
трансформировать. Итак, чтобы найти решение, все, что нам нужно сделать, это выполнить обратное преобразование.
Прежде чем сделать это, заметим, что в его нынешнем виде нам придется делать дроби дважды. Однако, если мы объединим два термина, мы будем делать частичные дроби только один раз. Мало того, знаменатель объединенного члена будет идентичен знаменателю первого члена. Это означает, что мы собираемся дробить термин с этим знаменателем, несмотря ни на что, поэтому мы могли бы также сделать числитель немного более беспорядочным, а затем просто разделить дробь один раз. 92}\влево( {s — 9} \вправо)\]
Выбор соответствующих значений \(s\) и решение для констант дает,
\[\begin{align*} & s = 0 & 5 & = 9B & \Rightarrow \hspace{0.25in}B & = \frac{5}{9}\\ & s = 1 & 16 & = — 8D & \Rightarrow \hspace{0.25in}D & = — 2\\ & s = 9 & 248 & = 648C & \Rightarrow \hspace{0.25in}C & = \frac{{31}}{{81}}\\ & s = 2 & 45 & = — 14A + \frac{{4345}}{{81}} & \Rightarrow \hspace{0,25in}A & = \frac{{50}}{{81}}\end{ выровнять*}\] 9т}\]
Это было довольно много работы для проблемы, которую, вероятно, можно было бы решить гораздо быстрее, используя методы из предыдущей главы.
Однако смысл этой задачи состоял в том, чтобы показать, как мы будем использовать Лапласа.
преобразуется для решения IVP.
Здесь следует отметить несколько моментов, касающихся использования преобразований Лапласа для решения IVP. Во-первых, с помощью Лапласа Преобразования сводят дифференциальное уравнение к алгебраической задаче. В случае с последним примером алгебра, вероятно, была более сложной, чем прямой подход из предыдущей главы. Однако в более поздних задачах это будет наоборот. Алгебра, хотя и очень запутанная, часто будет проще, чем прямой подход.
Во-вторых, в отличие от подхода из предыдущей главы, нам не нужно было сначала находить общее решение, дифференцировать его, подставлять начальные условия и затем искать константы, чтобы получить решение. С преобразованиями Лапласа начальные условия применяются на первом этапе, и в конце мы получаем фактическое решение вместо общего решения.
Во многих более поздних задачах Лаплас
преобразования значительно упростят решение задач, чем если бы мы использовали прямой подход, описанный в предыдущей главе.
3}}}\end{align*}\]
90}: & 8A — 4B — 2C — D & = — 15\end{выровнено}} \right\}\hspace{0.25in} \Стрелка вправо \hspace{0.25in}\begin{align}A & = — \frac {{192}}{{125}} & B & = \frac{{96}}{{125}}\\ C & = — \frac{2}{{25}} & D & = — \frac{ 1}{5}\конец{выровнено}\]
Мы получим общий знаменатель, равный 125, для всех этих коэффициентов и вычтем его, когда будем подключать их обратно к преобразованию. Выполнение этого дает,
\[Y\влево( s \вправо) = \frac{1}{{125}}\left( {\frac{{ — 190}: & 15B + 9D & = 24\end{выровнено}\right\}\hspace{0.25in} \Rightarrow \hspace{0.25in}\begin{align} A & = \frac{1}{{10} } & B & = \frac{1}{{10}}\\ C & = — \frac{{11}}{{10}} & D & = \frac{5}{2}\end{align} \]
Теперь подставьте их в разложение, возведите в квадрат знаменатель второго члена, а затем подправьте числители для процесса обратного преобразования.
\[\begin{align*}Y\left( s \right) & = \frac{1}{{10}}\left( {\frac{{s + 1}}{{{s^2} + 9{3t}}\sin\left( {\sqrt 6 t}\right)}\right)\]
До сих пор мы рассматривали только IVP, в которых начальные значения были равны \(t = 0\).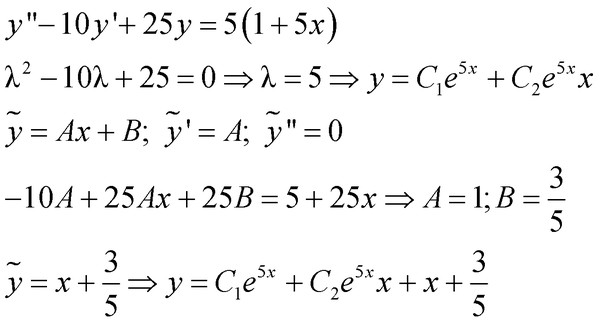
Это потому, что нам нужно, чтобы начальные значения были в этой точке, чтобы взять Лапласа
преобразование производных. Проблема со всем этим заключается в том, что в мире есть IVP, которые имеют начальные значения в местах, отличных от \(t = 0\). Лаплас
преобразования не были бы такими полезными, если бы мы не могли использовать их на этих типах IVP. Итак, нам нужно взглянуть на пример, в котором начальные условия не равны \(t = 0\), чтобы увидеть, как справляться с такими проблемами.
Пример 4. Решите следующую IVP. \[y» + 4y’ = \cos \left( {t — 3} \right) + 4t,\hspace{0.25in}y\left( 3 \right) = 0\,\,\,\,\ ,\,\,y’\влево( 3 \вправо) = 7\]
Показать решение
Первое, что нам нужно сделать здесь, это позаботиться о том, чтобы начальные условия не были равны \(t = 0\). Единственный способ, которым мы можем использовать преобразование Лапласа производных, — это иметь начальные условия в точке \(t = 0\).
Это означает, что нам нужно будет сформулировать IVP таким образом, чтобы начальные условия были при \(t = 0\). На самом деле это довольно просто сделать, однако нам нужно будет изменить переменную, чтобы это заработало. Мы собираемся определить
\[\eta = t — 3\hspace{0.25in} \Rightarrow \hspace{0.25in}\,\,\,t = \eta + 3\]
Начнем с исходного дифференциального уравнения.
\[y»\left( t \right) + 4y’\left( t \right) = \cos \left( {t — 3} \right) + 4t\]
Обратите внимание, что мы добавили часть \(\left( t \right)\) к производным, чтобы убедиться, что здесь все правильно. Далее мы заменим \(t\).
\[y»\left( {\eta + 3} \right) + 4y’\left({\eta + 3} \right) = \cos \left(\eta \right) + 4\left({\ эта + 3} \справа)\]
Теперь, чтобы немного упростить жизнь, давайте определимся,
\[и\влево(\эта\вправо) = у\влево({\эта + 3} \вправо)\]
Тогда по цепному правилу для первой производной получаем следующее.
\[u’\left( \eta \right) = \frac{{du}}{{d\eta }} = \frac{{dy}}{{dt}}\frac{{dt}}{{d \eta}} = y’\left( {\eta + 3} \right)\]
Аналогичным образом для второй производной получаем следующее.
\[u»\влево(\eta\вправо) = y»\влево({\eta + 3} \вправо)\]
Начальные условия для \(u\left( \eta \right)\):
\[\begin{align*}u\left( 0 \right) & = y\left( {0 + 3} \right) = y\left( 3 \right) = 0\\ u’\left( 0 \ справа) & = y’\left( {0 + 3} \right) = y’\left( 3 \right) = 7\end{align*}\]
Тогда IVP для этих новых переменных будет
\[u» + 4u’ = \cos \left( \eta \right) + 4\eta + 12,\hspace{0.25in}u\left(0 \right) = 0\,\,\,\, \,\,\,\,u’\влево( 0 \вправо) = 7\] 93}\left( {s + 4} \right)}}\end{align*}\]
Обратите внимание, что, в отличие от предыдущих примеров, на этот раз мы не полностью объединили все термины.
Во всех предыдущих примерах мы делали это потому, что знаменатель одного из слагаемых был общим знаменателем для всех слагаемых. Таким образом, при объединении все, что мы сделали, это сделали числитель немного более беспорядочным и уменьшили количество требуемых частичных дробей с двух до одной. Обратите внимание, что все члены в этом преобразовании, у которых в знаменателе были только степени \(s\), были объединены именно по этой причине.
Однако в этом преобразовании, если бы мы объединили оба оставшихся члена в один член, мы остались бы с довольно сложной проблемой частичной дроби. Поэтому в этом случае, вероятно, было бы проще просто сделать частичные дроби дважды. Мы решили несколько задач на неполные дроби в этом разделе и много задач на неполные дроби в предыдущих парах разделов, поэтому мы собираемся оставить детали частичного дробления на ваше усмотрение. Частичное дробление каждого из членов нашего преобразования дает нам следующее. 9{ — 4\eta }} + \frac{1}{{17}}\left( {4\sin \left( \eta \right) — \cos \left( \eta \right)} \right)\]
Конечно, это не то решение, которое нам нужно.