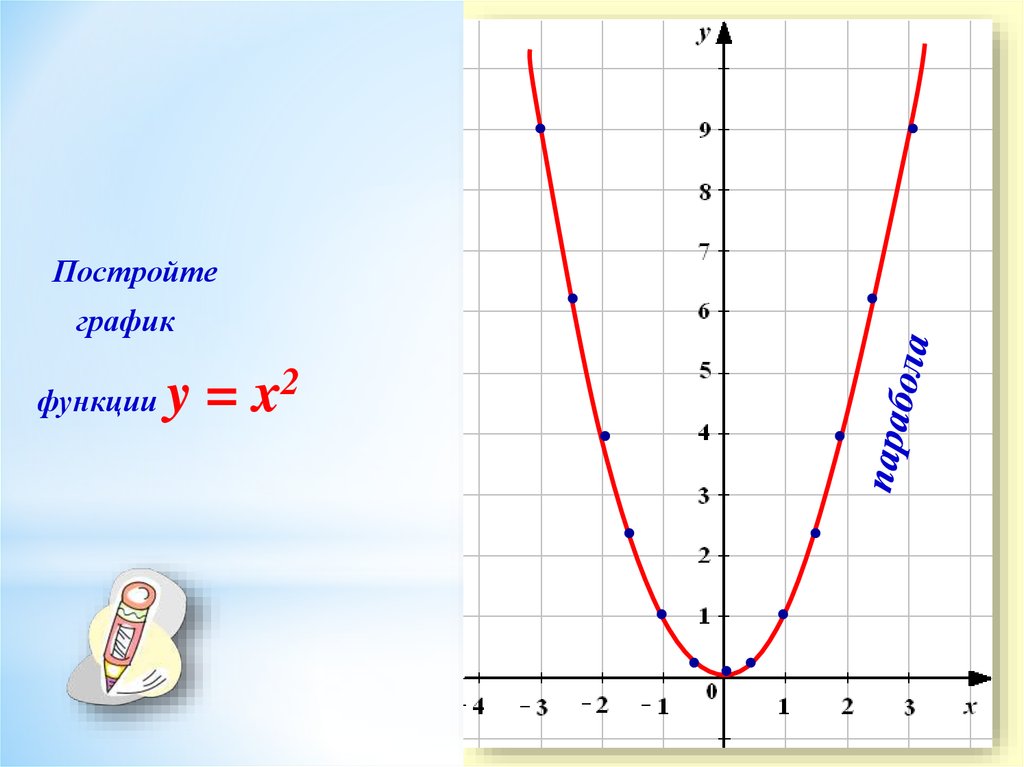
Урок по теме «Как построить графики функций y=f(x)+m, если известен график функции y=f(x)?» | План-конспект урока по алгебре (8 класс) на тему:
Слайд 1
Как построить график функции y=a + m , если известен график y=a Подготовила: Деревянкина Елена Алексеевна МБОУ СОШ № 120 г. о. Самара
Слайд 2
Как с помощью графика квадратичной функции создать подобный рисунок?
Слайд 3
Область определения функции… Область значений функции … Нули функции … Положительные и отрицательные значения функции … Монотонность функции … Наибольшее и наименьшее значение функции … Непрерывность … Ограниченность … Выпуклость … Устная работа на повторение Перечислите свойства функции, заданной графиком.
Слайд 4
Задание 1 . Постройте в одной координатной плоскости графики следующих функций и сделайте вывод о их взаимном расположении: Группа № 1. y = 2 x 2 y = 2 x 2 — 3 Группа № 3. y = — 3 x 2 y = — 3 x 2 — 1 Группа № 2. y = x 2 y = x 2 + 1 Группа № 4.
y = — х 2 y = 2 — х 2
Слайд 5
Задание 2 . Постройте в одной координатной плоскости графики следующих функций и сделайте вывод о их взаимном расположении: Группа № 1. y = ( x -3) 2 y = x 2 — 3 Группа № 3. y = -( x -1) 2 y = — x 2 — 1 Группа № 2 . y = ( x +1) 2 y = x 2 + 1 Группа № 4 . y = (2- х) 2 y = 2 — х 2
Слайд 6
Составьте алгоритм построения графика, дополнив следующие утверждения: Чтобы построить график квадратичной функции y=f (x)+m , где m -заданное положительное число, надо сдвинуть график функции y=f (x) вдоль оси … на … единиц масштаба … Чтобы построить график квадратичной функции y=f (x) ─ m , где m -заданное положительное число, надо сдвинуть график функции y=f (x) вдоль оси … на … единиц масштаба …
Слайд 7
7 m > 0 m 0, или на — m единиц вниз, если m
Слайд 8
Х У 1 1 4 9 2 3 -1 Х У 1 1 4 9 2 3 -1 2 Х 1 1 4 9 3 -1 У Установите соответствие между графиком функции формулой и координатами вершины параболы :
Слайд 9
Х У 1 1 4 9 2 3 -1 Х У 1 1 4 9 2 3 -1 2 Х 1 1 4 9 3 -1 У Установите соответствие между графиком функции формулой и координатами вершины параболы : ;
Слайд 10
Задание 3 .
Укажите координаты вершины параболы, которая получена сдвигом вдоль оси у: параболы y = 3x 2 на 2 ед. вниз параболы y = -4 x 2 на 1 ед. вверх параболы y = 0,5 x 2 на 4 ед. вверх параболы y = -0,1 x 2 на 3 ед. вниз (0; -2) (0; 1) (0; 4) (0;-3)
Слайд 11
Задание № 4 . Постройте графики функций: №1 . y = ( x +1) 2 – 0,5 №2. y = ( x -1) 2 + 4 №3 . y = ( x +2) 2 — 3 №4. y = ( x -2) 2 + 2
Слайд 12
Проверьте правильность построения графика. №1. №3. №2. №4. Х У 1 1 4 9 2 3 -1 Х У 1 1 4 9 2 3 -1 Х У 1 1 4 9 2 3 -1 Х У 1 1 4 9 2 3 -1
Слайд 13
Тест самоконтроля. Ответы. Вариант 1. Вариант 2. № задания Вариант ответа 1 б 2 г 3 в 4 б 5 а № задания Вариант ответа 1 б 2 б 3 б 4 а 5 в
Слайд 14
Учебник: п. 20 (разобрать). Задачник: № 20.7 (в , г), 20.15, 20.23 . Индивидуальное задание: проектная работа «Рисуем графиками функции».
Слайд 15
Молодцы! Спасибо за урок!
Бесплатный 3D файл Основная плитка 2×2・3D-печатная модель для загрузки・Cults
Книга
Бесплатно
Ржавый монстр
Бесплатно
Токен Грелля
Бесплатно
Руль Мегамена/Рокмена
Бесплатно
Токен Ропера
Бесплатно
Отюгский токен
Бесплатно
Beholder
Бесплатно
Имитация столба (скрыто)
Бесплатно
Лучшие файлы для 3D-принтеров в категории Архитектура
Simple Eiffel Tower — 10mins Modeling
Бесплатно
My Angkor wat(1:1000)
Бесплатно
Заколдованный сад
17 €
Cereal box, Art Nouveau house
Бесплатно
Le Moulin-Rouge
Torre del Oro — Sevilla
Бесплатно
Нью-Йорк — Манхэттен ремикс + горизонт
Бесплатно
HO tunnel entrance
0,50 €
Бестселлеры категории Архитектура
Лего — кирпичики
2,95 €
Eiffel tower
0,50 €
Ancient Raven Castle
4,98 €
The Myers House
11,38 €
СРЕДА Аддамс, Мерлина
11,07 €
1-100th scale furniture Architecture
0,76 €
Нью-Йорк — Манхэттен — модель для 3D-печати
1,30 €
НЬЮ-ЙОРК — ГОРОД МАНХЭТТЕН
3,49 €
Birdhouse -3 pieces
3,80 €
Лего — Оружие минифигурок
3,25 €
Лего — Минифигурки Волосы
3,25 €
ЭЙФЕЛЕВА БАШНЯ — ПАРИЖ
3,49 €
Ободок Asus Adapter 32» Изогнутые и плоские мониторы
5 €
Кельнский кафедральный собор
4,50 €
1:18 Coca-Cola Fridge Cans And Bottles
1 €
Lego — Ninjago Все персонажи
6,80 €
💖 Вы хотите поддержать Cults?
Вам нравятся Cults и вы хотите помочь нам продолжить наш путь самостоятельно? Обратите внимание, что мы — маленькая команда из 3 человек, поэтому поддержать нас в поддержании деятельности и создании будущих разработок очень просто.
Вот 4 решения, доступные для всех:
РЕКЛАМА:
АФФИЛИАЦИЯ: Совершайте покупки онлайн, переходя по нашим партнерским ссылкам здесь Amazon.
ДОНАТЫ: Если хотите, то можно сделать пожертвование через Ko-Fi здесь 💜.
ПРИГЛАШЕНИЕ ДРУЗЕЙ: Приглашайте своих друзей, откройте для себя платформу и великолепные 3D-файлы, которыми делится сообщество!
Обозначение | SolveTheCube
Для записи последовательности движений по кубу используем обозначение из шести основных букв:
- U для Up
- D для пуха
- L слева
- R Правый
- F для передней панели
- B для спины
Эти буквы используются в последовательностях, известных как алгоритмы , и вы просто выполняете каждую букву в алгоритме слева направо.
Вот вам пример:
F2 B2 U2 D2 L2 R2
Если вам удалось сделать это правильно, дважды повернув каждую грань куба, вы должны были получить довольно очаровательный узор в виде шахматной доски. Используйте этот простой алгоритм, чтобы произвести впечатление на своих друзей и семью!
Вы, наверное, заметили, что можете наводить курсор мыши на каждое движение в алгоритме, чтобы следить за каждым шагом. Если вы чувствуете себя немного уверенно, вы можете отключить это с помощью переключателя «Помощник по алгоритму» в нижней части меню.
Важно помнить, что каждое движение нужно делать так, как будто вы смотрите прямо на лицо, на которое влияет движение.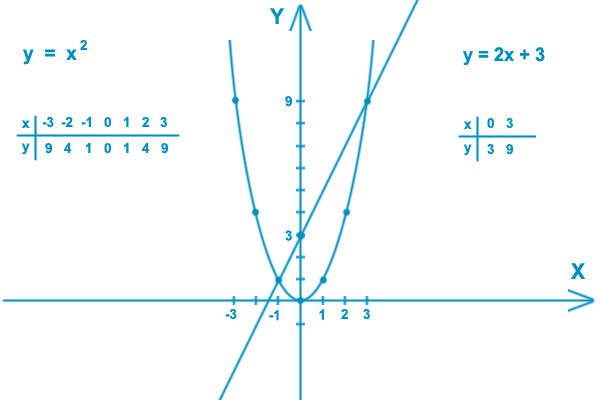
U и D — повороты по часовой стрелке для граней Up и Down, но если вы поворачиваете верхний и нижний слои одинаково, глядя на грань Up для обоих движений, вы на самом деле выполняете U и D’. Используйте этот полезный набор кнопок, чтобы увидеть, как каждое движение влияет на решенный куб, чтобы вы могли увидеть, как выполнять их правильно.
У Д л р Ф В
У’ Д’ Л’ Р’ Ф’ Б’
У2 Д2 L2 R2 F2 B2
Для промежуточного и расширенного методов будут использоваться другие буквы для обозначений. К ним относятся:
- x для вращения куба как R
- y для вращения куба как U
- z для вращения куба как F
- M для слоя между L и R
- E для слоя между U и D
- S для слоя между F и B
E и S используются очень редко, так как достаточно неудобны в исполнении и легко заменяются в алгоритмах другими поворотами.
х у г М Е S
х’ ты г’ М’ Э’ S’
x2 у2 z2 М2 Е2 S2
Существуют также строчные буквы для двухслойных поворотов, что означает одновременное поворот обычной грани и среднего слоя рядом с ним.
у д л р ф б
у’ д’ я р’ ж’ б’
у2 d2 л2 г2 f2 b2
Завершение квадратных парабол
Home > Математика > Исчисление >Заполнение квадратных парабол
Помните шаблон для парабол:
Часто параболы уже перечислены в этом формате, но иногда их нет. В этом случае вы должны перевести их в формат графика, заполнив квадрат.
Чтобы построить квадрат параболы, выполните следующие действия:
1. Определите, какая переменная возводится в квадрат. Получите оба члена с этой переменной на одной стороне уравнения и все остальное на другой стороне.
2. Вынесите на множитель константу квадрата члена.
3. Возьмите число перед членом первой степени, разделите его на два и возведите в квадрат.
4. Добавьте значение этого числа к обеим сторонам. (Будьте осторожны: вы должны добавить полное распределенное значение.)
5. Разложить полученный трехчлен на множители.
6. Переместите константу на другую сторону.
7. Упростите и измените при необходимости
Примеры: Измените эти уравнения, чтобы они соответствовали графическому образцу.
1. у =(2х) 2 -12х+23
Наш квадратный член равен х, поэтому нам нужны два члена с х на одной стороне и все остальное на другой. Это означает, что нам нужно переместить 23.
y — 23 = (2x) 2 -12x
Далее нам нужно вынести коэффициент квадрата члена: 2
y — 23 = 2(x 2 -6x)
Теперь возьмем число перед членом первой степени: -6.
Разделите его на 2 (это дает нам -3) и возведите в квадрат. Это дает нам 9.
Нам нужно добавить значение этого числа к обеим сторонам. Но это сложнее, чем кажется. Мы должны добавить 9 в скобках. Это означает, что мы на самом деле добавляем 18 к правой части (потому что 2 будет распределено на 9). Таким образом, мы должны добавить 18 к левой части.
у-23+18=2(х 2 -6х+9)
Теперь мы разложим трехчлен в скобках:
y — 5 = 2(x-3)(x-3)
И перепишем это:
y — 5 = 2(x-3) 2
Теперь мы переместим постоянный член (-5) обратно на другую сторону.
у = 2(х-3) 2 +5
Теперь это соответствует графическому шаблону и позволяет нам найти всю нашу ключевую информацию.
2.
Наш квадратный член равен y, поэтому нам нужны два члена с y на одной стороне и всем остальным на другой.
Это означает, что нам нужно переместить -x. Давайте также поменяем стороны уравнения.
Далее нам нужно вынести коэффициент квадрата члена:
Теперь возьмем число перед членом первой степени: 8. Разделим его на 2 (это дает нам 4) и возведем в квадрат. Это дает нам 16.
Нам нужно добавить значение этого числа к обеим сторонам. Но помните, мы должны быть осторожны. Мы должны добавить 16 в скобках. Это означает, что мы на самом деле добавляем только 8 к правой части (потому что 1/2 будет распределена на 16). Таким образом, мы должны добавить 8 к левой части.
Теперь мы разложим трехчлен в скобках:
И перепишите его:
Теперь мы переместим постоянный член (-3) обратно на другую сторону.
Теперь это соответствует графическому шаблону и позволяет нам найти всю нашу ключевую информацию.