Ответов пока нет | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Натуральный логарифм. Функция y=ln x, её свойства, график, дифференцирование
Вы можете ознакомиться и скачать презентацию на тему Натуральный логарифм. Функция y=ln x, её свойства, график, дифференцирование. Доклад-сообщение содержит 10 слайдов.
Презентации для любого класса можно скачать бесплатно.
Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь
им с друзьями с помощью социальных кнопок и добавьте в закладки в своем
браузере.Слайд 1
Описание слайда:
Натуральный логарифм. Функция , её свойства, график, дифференцирование
Слайд 2
Описание слайда:
Слайд 3
Описание слайда:
Слайд 4
Описание слайда:
Слайд 5
Описание слайда:
Слайд 6
Описание слайда:
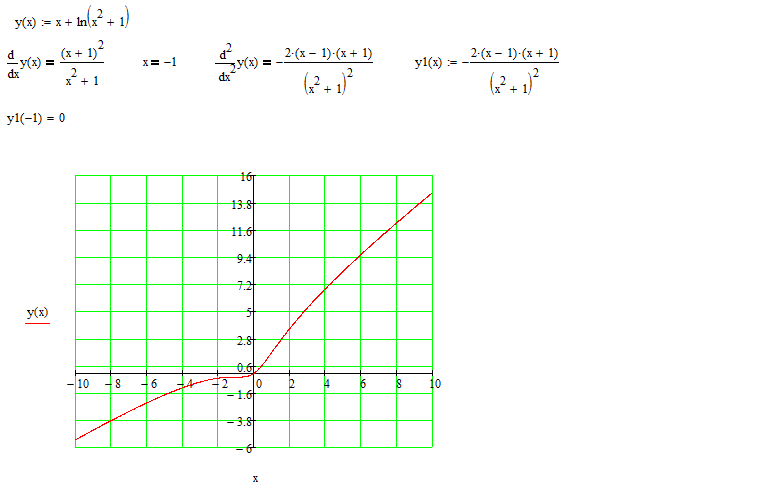
Пример:
Вычислить значение производной функции
в точке .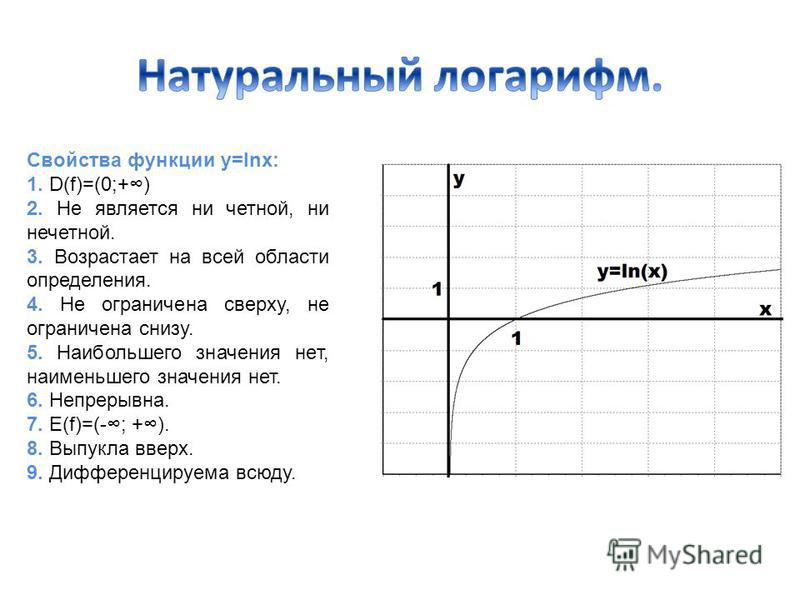
Решение:
Ответ: .
Слайд 7
Описание слайда:
Пример: Найти производную функции . Решение: Ответ: .
Слайд 8
Описание слайда:
Пример: Найти уравнение касательной к графику функции в точке . Решение: Ответ: .
Слайд 9
Описание слайда:
Пример:
Исследовать на экстремум функцию .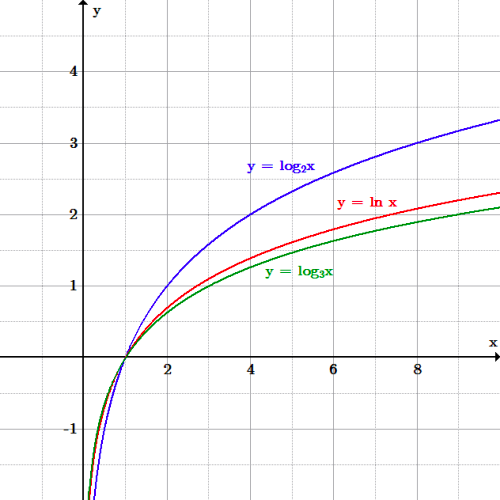
Решение:
Слайд 10
Описание слайда:
x$
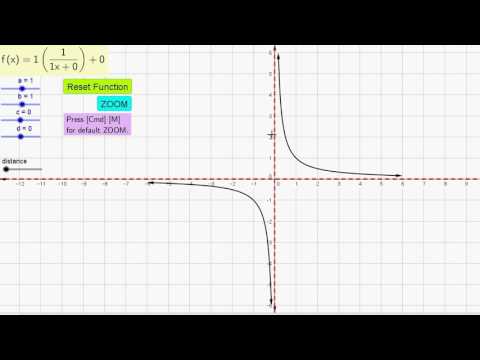
Если попытаться использовать отрицательное основание в экспоненциальной функции, точки будут разбросаны по двум кривым, и еще очень много значений функция будет неопределенной.
Логарифмическая функция является обратной показательной функции.
Вот логарифмическая функция с основанием от 0 до 1.
График функции аркгиперболического косинуса идентичен половина повернутой контактной кривой и является асимптотической логарифмической функцией.
Вот график функции аркгиперболического тангенса.
Вот график функции аркгиперболического котангенса. 9x$
Эта функция иногда используется как часть определения числа $е$. На интервале $[-1,0]$ точек разбросаны по двум кривым, со многими неопределенными значениями функции.
Эта функция часто встречается как интеграл обратной функция.
13.2: Логарифмические функции и их графики
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 49032
- Томас Тредлер и Холли Карли
- CUNY New York City College of Technology через New York City Academic College of Technology в 9CUNY City
Логарифмическая функция тесно связана с экспоненциальной функцией.
x\) с основанием \(b\). 9x) =x} \quad\quad\quad \boxed{\log_b(b)=1} \quad\quad\quad \boxed{\log_b(1)=0} \nonumber \]В общем, когда аргумент не является степенью основания, мы можем использовать калькулятор для аппроксимации значений логарифма по формулам:
\[\label{EQU:log-change-basis-calculator} \boxed{\log_b(x) = \ dfrac {\ log (x)} {\ log (b)}} \ quad \ quad \ quad \ text {или} \ quad \ quad \ quad \ boxed {\ log_b (x) = \ dfrac {\ ln ( х)}{\ln(b)}}\]
Последние две формулы будут доказаны в предложении 14.1. Сейчас мы хотим показать, как их можно использовать для вычисления любого логарифмического выражения с помощью калькулятора.
Пример \(\PageIndex{3}\)
Вычислить:
- \(\log_3(13)\)
- \(\log_{2,34}(98,765)\)
Решение
- Мы вычисляем \(\log_3(13)\), используя первую формулу в \(\ref{EQU:log-change-basis-calculator}\).
\[\log_3(13)=\dfrac{\log(13)}{\log(3)}\приблизительно 2,335 \nonumber \]
График также можно получить с помощью графического калькулятора.
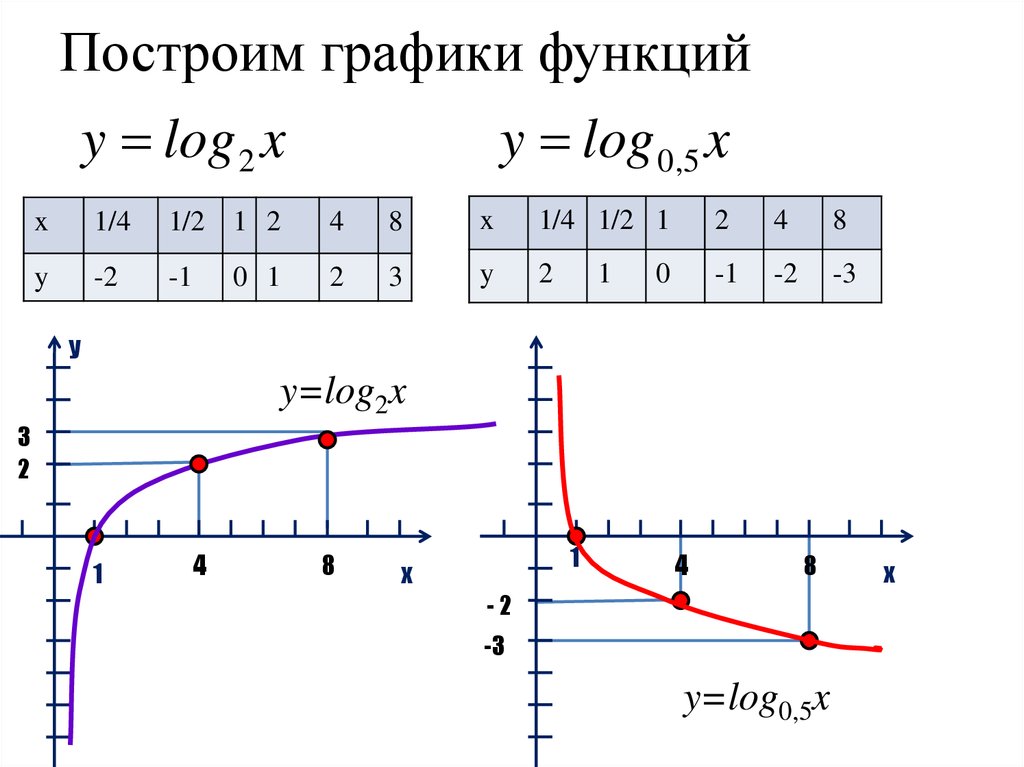
Пример \(\PageIndex{4}\)
- График функций \(f(x)=\ln(x)\), \(g(x)=\log(x)\), \(h (x)=\log_2(x)\) и \(k(x)=\log_{0,5}(x)\). Каковы домены \(f\), \(g\), \(h\) и \(k\)? Чем отличаются эти функции?
- Нарисуйте график функции \(p(x)= -3\cdot \ln(x)+4\). Какова область определения \(p\)?
- Нарисуйте график функции \(q(x)= \ln(5-x)\). Какова область определения \(q\)?
- Постройте график функции \(r(x)= \log_7(2x+8)\). Какова область определения \(r\)?
Решение
- Из определения мы знаем, что областью определения \(f\), \(g\) и \(h\) являются все действительные положительные числа, \(D_f=D_g=D_h=D_k =\{х|х>0\}\). Функции \(f\) и \(g\) можно сразу ввести в калькулятор. {-1})}=-\dfrac{1}{\ln(2)}\), так что график \(k\) является графиком \(h\), отраженным относительно \(x \)-ось.
Обратите внимание, что все эти графы имеют общий \(x\)-перехват в точке \(x=1\):
\[f(1)=g(1)=h(1)=k(1 )=0 \nonumber \]
Чтобы визуализировать различия между графиками, мы изобразим их вместе в одной системе координат.
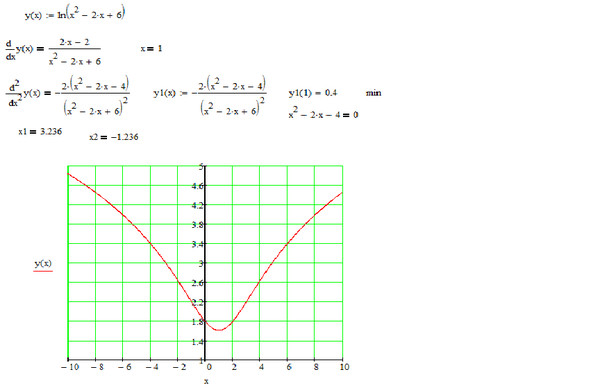
- Используя наши знания о преобразованиях графов, мы ожидаем, что \(p(x)=-3\cdot \ln(x)+4\) равно \(y=\ln(x)\) отражается и растягивается от оси \(x\) (в \(3\) раз), а затем смещается вверх в \(4\). Растянутый и отраженный график находится внизу посередине, а график сдвинутой функции \(p\) справа внизу.
Домен состоит из чисел \(x\), для которых определено \(\ln(x)\), то есть \(D_p=\{x|x>0\}\).
- Чтобы определить область определения \(q(x)=\ln(5-x)\), мы должны увидеть, для каких \(x\) логарифм имеет положительный аргумент. Точнее, нам нужно \(5-x>0\), то есть \(5>x\), чтобы домен был \(D_q=\{x|x<5\}\). Калькулятор отображает следующий график.
Обратите внимание, что график, отображаемый калькулятором, заканчивается в точке, которая находится приблизительно в точке \((5,-2,5)\). Однако реальный график логарифма не останавливается ни в какой точке , поскольку имеет вертикальную асимптоту в \(x=5\), то есть график приближается к \(-\infty\), когда \(x\) приближается к \(5\). Калькулятор отображает только приблизительное значение, которое может вводить в заблуждение, поскольку оно определяется размером окна и размером каждого пикселя. Таким образом, график будет выглядеть следующим образом.
- Область определения \(r(x)= \log_7(2x+8)\) состоит из тех чисел \(x\), для которых аргумент логарифма положителен.
\[2x+8>0 \stackrel{\text{(вычесть $8$)}}\подразумевается \quad 2x>-8 \stackrel{\text{(разделить на $2$)}}\подразумевается \quad x> -4 \nonumber \]
Следовательно, домен равен \(D_r=\{x|x>-4\}\).
Чтобы построить график функции \(r(x)= \log_7(2x+8)\), мы можем ввести \(r(x)=\dfrac{\ln(2x+8)}{\ln(7)}\ ) в калькулятор. График выглядит следующим образом.В предыдущем примере анализируется график логарифмической функции. Вот резюме.
Наблюдение: график логарифмической функции
График логарифмической функции \(y=\log_b(x)\) с основанием \(b\) представляет собой график натурального логарифма \(y=\ln(x)\), оттянутый от \(x \)-оси или сжаты к оси \(x\) при \(b>1\). Когда \(0
График \(y=\log_b(x)\) имеет область определения \(D=\{x|x>0\}\) и вертикальную асимптоту в точке \(x=0\). Горизонтальной асимптоты нет , поскольку \(f(x)\) приближается к \(+\infty\), когда \(x\) приближается к \(+\infty\) для \(b>1\), и \ (f(x)\) приближается к \(-\infty\), когда \(x\) приближается к \(+\infty\) для \(0
Эта страница под заголовком 13.
x\) с основанием \(b\). 9x) =x} \quad\quad\quad \boxed{\log_b(b)=1} \quad\quad\quad \boxed{\log_b(1)=0} \nonumber \]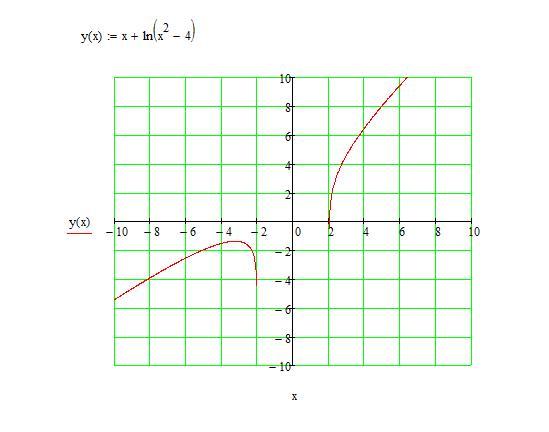
9х\) из предыдущего раздела. Напомним, что график обратной функции есть отражение графика функции относительно диагональной линии \(y=x\). Итак, в этом случае мы имеем:
{-1})}=-\dfrac{1}{\ln(2)}\), так что график \(k\) является графиком \(h\), отраженным относительно \(x \)-ось.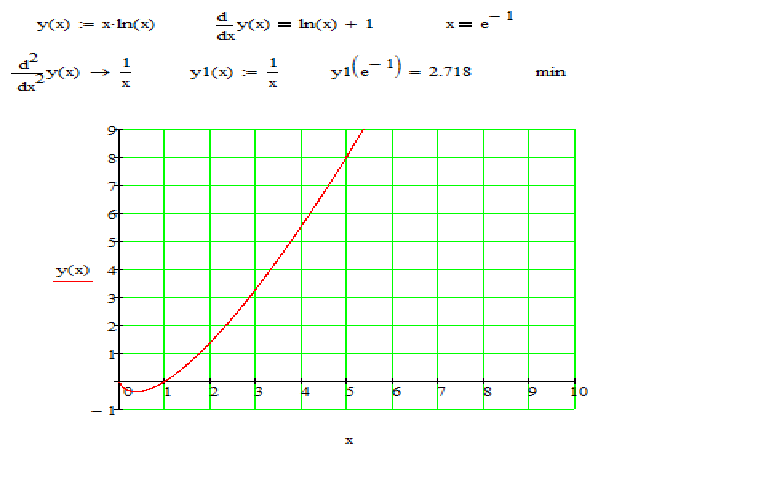
Калькулятор отображает следующий график.
Чтобы построить график функции \(r(x)= \log_7(2x+8)\), мы можем ввести \(r(x)=\dfrac{\ln(2x+8)}{\ln(7)}\ ) в калькулятор. График выглядит следующим образом.