Равнобедренная трапеция площадь: Все формулы площади трапеции и калькулятор онлайн

формулы через стороны, основания и тд

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение высоты равнобедренной (равнобокой) трапеции

В данной публикации мы рассмотрим различные формулы, с помощью которых можно вычислить высоту равнобедренной (равнобокой) трапеции.

Напомним, высотой трапеции называется перпендикуляр, соединяющий оба ее основания. Также, в равнобедренной трапеции боковые стороны равны.

• Нахождение высоты равнобедренной трапеции
  • Через длины сторон
  • Через боковую сторону и прилежащий угол
  • Через основания и прилежащий угол
  • Через площадь и основания
  • Через диагонали и угол между ними

Через длины сторон

Зная длины всех сторон равнобедренной трапеции, вычислить ее высоту можно, используя формулу ниже:

Через боковую сторону и прилежащий угол

Если известна длина боковой стороны равнобедренной трапеции и угол между ней и основанием фигуры, найти высоту можно следующим образом:

Через основания и прилежащий угол

Вычислить высоту трапеции можно, если известны длины ее оснований и угол при любом из оснований (например, при большем).

Через площадь и основания

Также высоту равнобедренной трапеции удастся найти через ее площадь и длины оснований:

Данная формула может быть представлена в другом виде, если вместо оснований дана средняя линия (m).

m – средняя линия, равняется полусумме оснований, т.е. m = ^(a+b)/₂.

Через диагонали и угол между ними

И еще один способ вычислить высоту равнобедренной трапеции, если известны ее диагонали (которые имеют одинаковую длину), угол между ними и основания.

Та же самая формула, но со средней линией (m) вместо суммы оснований:

Примечание: если диагонали равнобедренной трапеции взаимно перпендикулярны, то ее высота равняется половине суммы оснований или, другими словами, средней линии.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

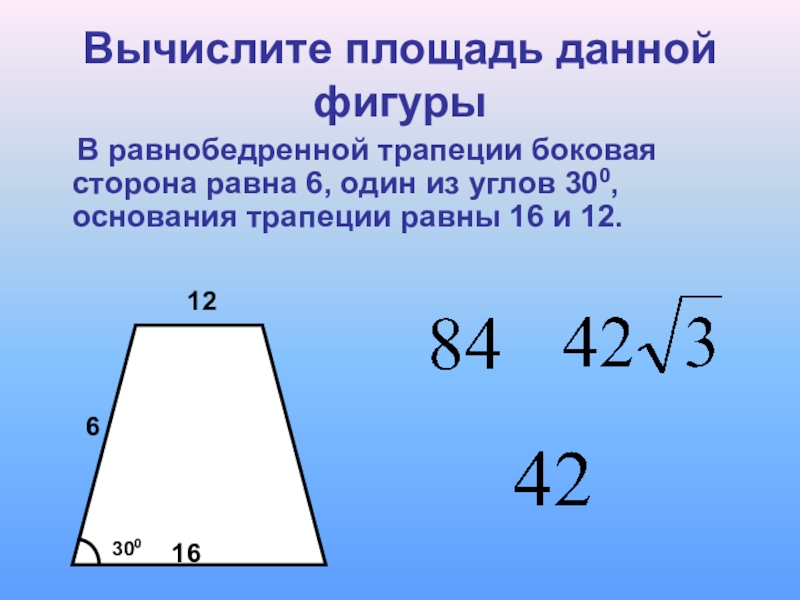
Задание 2.

Площадь равнобедренной трапеции

Задание 2. Площадь равнобедренной трапеции

Прежде чем приступить к решению примеров и задач, обязательно ознакомьтесь с теоретической частью урока 

или 

посмотрите

ВИДЕОУРОК

 1. Основания равнобедренной трапеции равны  5 см  и  13 см, а диагональ делит её острый угол пополам. Найдите площадь трапеции.

  а)   24 см²;      
 б)   27 см²;    

  в)   29 см²;      
 г)   23 см².

 2. В равнобедренной трапеции основания равны 

10 см  и  24 см, а боковая сторона – 25 см. Найдите площадь трапеции.

 а)  408 см²;      
 б)  398 см²;     

 в)  388 см²;      
 г)  416 см².

 3. В равнобедренную трапецию вписана окружность радиусом  3 см. Большое основание трапеции равно  8 см. Найдите площадь трапеции.

 а)  40,2 см²;      
 б)  39,8 см²;     

 в)  38,6 см²;      
 г)  37,5 см².

 4. Площадь трапеции равна  36 см

2, высота – 4 см, а боковые стороны равны по  5 см. Найдите периметр трапеции.

 а)  28 см;      
 б)  19 см;     

 в)  23 см;      
 г)  40 см.

 5. Периметр равнобокой трапеции равен  124 см. Меньшее основание равно боковой стороне и меньше другого основания на  20см. Найдите площадь трапеции.

 а)  880 см²;       
 б)  806 см²;

 в)  864 см²;       
 г)  872 см².

 6. Площадь равнобедренной трапеции, описанной вокруг окружности, равна  162. Найти длину боковой стороны трапеции, если острый угол при основании равен  30°.

 а)  9;         
 б)  18;     

 в)  4,5;      
 г)  15.

 7. Равнобедренная трапеция описана вокруг окружности. Боковая сторона трапеции делится точкой касания на отрезки длиной  12 см  и  48 см. Найдите площадь трапеции.

 а)  2880 см²;     

 б)  3280 см²;

 в)  1880 см²;       

 г)  1440

см².

 8. Вычислите площадь равнобедренной трапеции, если её меньшее основание равно  10 см, боковая сторона равна  8 см  и угол между ними равен  135°.

 а)  (10√͞͞͞͞͞2 + 36) см²;     

 б)  (40√͞͞͞͞͞2 + 16) см²;

 в)  (20√͞͞͞͞͞2 + 32) см²;        

 г)  (40√͞͞͞͞͞2 + 32) см².

 9. Около окружности, радиус которой  12 см, описана равнобедренная трапеция. Боковая сторона делится точкой касания в отношении  4 : 9. Найдите площадь трапеции.

 а)  628 см²;      
 б)  624

см²;     

 в)  668 см²;      
 г)  616 см².

10. Диагональ равнобедренной трапеции, равная  16 см, образует с основанием угол  45°. Вычислите площадь трапеции.

 а)  128 см²;      
 б)  118 см²;     

 в)  168 см²;      
 г)  116 см².

11. Основания равнобедренной трапеции  50 см  и  14 см, диагональ перпендикулярна к боковой стороне. Найдите площадь трапеции.

 а)  785 см²;      
 б)  698 см²;     

 в)  768 см²;      
 г)  776

см².

12. Боковая сторона равнобедренной трапеции  а, угол при большем основании  60°. Диагональ делит его пополам. Найдите площадь трапеции.

 а)  ³/₄√͞͞͞͞͞3 а²;      
 б)  ³/₂√͞͞͞͞͞5 а²;     

 в)  ⁵/₂√͞͞͞͞͞2 а²;      
 г)  ¹/₂√͞͞͞͞͞5 а².

Задания к уроку 10

• Задание 1
• Задание 3

Следующее Предыдущее Главная страница

Подписаться на: Комментарии к сообщению (Atom)

Математическая задача: Равнобедренная трапеция — вопрос № 960, планиметрия

Равнобедренная трапеция ABCD, AB||CD задается |CD| = c = 12 см, высота v = 16 см и |CAB| = 20°. Вычислите площадь трапеции.

Правильный ответ:

S = 703,3542 см ²

Пошаговое объяснение:

​−c=31,96 a=c+2x=2a1​−c=75,92 см S=2a+c​v=tan20∘v2​=703,3542 см2

Вы нашли ошибку или неточность? Не стесняйтесь

напишите нам

. Спасибо!

Советы по родственным онлайн-калькуляторам

Расчет равнобедренного треугольника.
См. также наш калькулятор тригонометрического треугольника.

You need to know the following knowledge to solve this word math problem:

• planimetrics
• area of ​​a shape
• triangle
• trapezoid
• goniometry and trigonometry
• tangent

Оценка слов Проблема:

• Практика для 14 -летнего возраста
• Средняя школа

Мы призываем вас посмотреть это учебное видео по этой математической задаче: видео1

• Isosceles 37621
  in the isosdes in the isosdes in the isosdes in in the isodesdesdesdesdesdesdeodes 37621914 , даны основания AB = 20 см, CD = 12 см и длины плеч AD = BC = 8 см. Укажите ее высоту и альфа-угол при вершине A
• Окружность 7052
  Дана трапеция ABCD (AB || CD, AB перпендикулярна AD). Вычислите его окружность, если | АБ | = 20см, | компакт-диск | = 15см, | ОБЪЯВЛЕНИЕ | = 12см. Теорема Пифагора
• Трапеция 70454
  Построить трапецию ABCD (AB // CD): | АБ | = 7 см | Британская Колумбия | = 3,5 см | компакт-диск | = 4см Величина угла ABC = 60°
• Трапеция 20873
  В трапеции ABCD (AB II CD) α = 57°, γ = 4β. Вычислите величину всех внутренних углов.
• Равнобедренная 2588
  Дана равнобедренная трапеция ABCD, в которой | АБ | = 2 | Британская Колумбия | = 2 | компакт-диск | = 2 | ДА | держит. На стороне BC точка K такова, что | БК | = 2 | KC |, на стороне CD точка L такова, что | КЛ | = 2 | LD |, а со стороны DA точка M такова, что
• Диагонали под прямым углом
  В трапеции ABCD дано: AB=12см CD=4см Диагонали пересекаются под прямым углом. Чему равна площадь этой трапеции ABCD?
• Прямоугольник 49153
  Прямоугольник ABCD, у которого | АБ | = 5см, | переменный ток | = 8 см, ∢ | КАБИНА | = 30°. Какова длина другой стороны и какова ее площадь?
• Пересечение диагонали
  Равнобедренная трапеция ABCD с длинными основаниями | АБ | = 6 см, CD | = 4 см делится на четыре треугольника диагоналями, пересекающимися в точке S. Какую часть площади трапеции составляют треугольники ABS и CDS?
• Вычислить 48073
  Вычислить площадь равнобедренной трапеции ABCD, если a = 14 см, c = 8 см, а величина угла DAB равна 52°.
• Трапеции
  В равнобедренной трапеции ABCD мы знаем: AB||CD, |CD| = c = 8 см, высота h = 7 см, |∠CAB| = 35°. Найдите площадь трапеции.
• Бассейн
  Бассейн длиной 30 м наполнен водой на глубину 1 м в мелкой части и 5 м в глубокой части, а по вертикали бассейн имеет форму трапеции с площадь определяется как S (abcd) = 1/2 (ab + cd) x ad. Что такое
• трапеция 3428
  Дана трапеция ABCD с основаниями AB, CD. Пусть K — середина стороны AB, а точка L — середина стороны CD. Площадь треугольника ALB равна 15 см ² , а площадь треугольника DKC равна 10 см². Вычислите площадь трапеции ABCD.
• Равнобедренная
  Равнобедренная трапеция ABCD ABC = 12 угол ABC = 40° b=6. Вычислите окружность и площадь.
• Равнобедренная 7929
  ABCD Равнобедренная трапеция. A = 6см, e = 7см и угол дельты = 105°. Подсчитайте оставшиеся страницы.
• Трапеция 4908
  Трапеция ABCD с основаниями AB = a, CD = c имеет высоту v. Точка S является центром плеча BC. Докажите, что площадь треугольника ASD равна половине площади трапеции ABCD.
• Прямоугольная трапеция
  Прямоугольная трапеция ABCD с основаниями AB и CD разделена диагональю AC на два равносторонних прямоугольных треугольника. Длина диагонали АС равна 62 см. Вычислите площадь трапеции в квадратных см и посчитайте, сколько различных периметров
• Диагональ
  Прямоугольная трапеция ABCD, плечо AD которой перпендикулярно основаниям AB и CD, имеет площадь 15 кв.см. Основания имеют длину AB = 6 см, CD = 4 см. Вычислите длину диагонали АС.

Площадь трапеции: формула и 5 примеров

10 января 2023 г.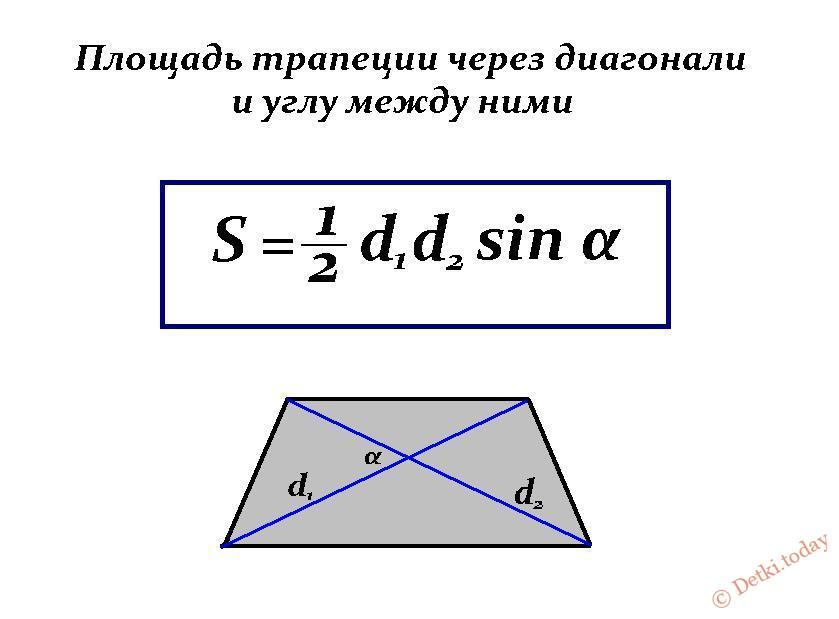

Большинство учащихся хорошо знакомы с основными формами и формулами, которые преподаются на уроках математики в средних и старших классах. Обычный человек, идущий по улице, может найти площадь квадрата или треугольника, но некоторые фигуры сложнее, чем основные. Одной из самых запутанных задач в геометрии является решение задач по формуле площади трапеции.

Площадь — это термин, используемый для описания объема пространства, занимаемого плоскостью или двумерной фигурой. Вычисление площади чего-либо часто используется для измерения того, насколько большой или маленькой может быть форма. Типичным примером из повседневной жизни является желание узнать, сколько краски нужно купить, чтобы покрыть стену или покрыть ковром спальню. Существует много формул для расчета площади, но они различаются в зависимости от формы.

Трапеция представляет собой четырехугольник с двумя параллельными сторонами. Параллельные стороны называются основаниями, непараллельные стороны называются катетами, а расстояние между двумя основаниями называется высотой.

Высоту иногда также называют высотой. Различают три типа трапеций: правильная трапеция, равнобедренная трапеция и разносторонняя трапеция. Все типы трапеций имеют одну и ту же формулу площади.

Площадь трапеции Формулы:

A предназначена для области

A для базы One

B для основания два

H предназначена для высоты или высоты

. b для трапециевидных оснований взаимозаменяемы. Основания будут сложены, разделены на 2 и умножены на высоту. Окончательный ответ для площади фигуры всегда выражается в квадратных единицах.

 

 

Пример 1:

Найдите площадь правой трапеции ниже.

Сначала определите и подставьте числа для ваших переменных.

Упрощение.

A = 15 дюймов * 20 дюймов

A = 300 дюймов ²

Площадь правой трапеции 300 дюймов 2 ^{0 9.}

 

Пример 2:

Найдите площадь равнобедренной трапеции.

Упрощение.

A = 18,5 дюймов * 7 дюймов

A = 129,5 дюймов ²

Площадь равнобедренной трапеции 9000,5 900,5 дюймов.

 

 

Пример 3:

Найдите площадь разносторонней трапеции.

Упрощение.

А = 14,5 дюйма * 4 дюйма

А = 58 в ²

Площадь разносторонней трапеции равна 58 в ² .

 

Пример 4:

Найдите площадь трапеции с основанием 4 см, основанием 6 см и высотой 3 см. Примечание: единицы измерения указаны в сантиметрах.

Сначала пометьте свои переменные соответствующими номерами. a равно равно 4, b равно 6, а h равно 3. Подставьте свои числа в площадь формулы трапеции.

 

 

Следуйте вашему порядку операций, найдите A или площадь в дюймах ² .